深圳大学大一期末高数线代复习资料

大一高等代数期末考知识点高等代数作为大一学生必修的一门数学课程，是代数学的重要分支，是培养学生抽象思维和逻辑思维的基础。

本文将系统地总结大一高等代数知识点，以帮助同学们复习期末考试。

一、集合与二元关系1. 集合及其运算：包括集合的定义、集合之间的相等关系、子集与真子集、交集、并集、补集和差集等。

2. 二元关系：掌握关系的定义、域、逆关系、复合关系、等价关系和序关系的概念。

二、数系与复数1. 自然数、整数、有理数、实数和复数的定义及其性质。

2. 复数的运算：复数的加减乘除、乘方和开方。

三、代数式与多项式1. 代数式的概念：包括代数式、项、系数和次数等。

2. 多项式的运算：多项式的加减乘除以及整式化简。

3. 多项式的因式分解：二次、三次多项式的因式分解方法。

四、方程与不等式1. 一元一次方程和不等式：一元一次方程和不等式的解集、方程组与不等式组的解集。

2. 一元二次方程与不等式：二次方程和不等式的解集、因式分解法和配方法解方程和不等式。

3. 绝对值方程与不等式：绝对值方程和不等式的解集。

五、函数与图像1. 函数的概念：函数的定义、定义域、值域、图像和性质。

2. 基本初等函数：包括幂函数、指数函数、对数函数、三角函数和反三角函数等。

3. 函数的运算：函数的加减乘除、复合函数以及函数的逆。

六、行列式与矩阵1. 行列式的概念与性质：行列式的定义、性质、性质的运算规律。

2. 矩阵的概念与性质：矩阵的定义、矩阵的加法和数乘、矩阵的乘法、矩阵的转置和矩阵的逆运算。

3. 线性方程组：线性方程组的定义、增广矩阵、齐次方程组与非齐次方程组。

七、向量与线性空间1. 向量的概念与运算：向量的定义、向量的加法、数乘和数量积。

2. 线性空间的概念与性质：线性空间的定义、线性空间的性质、线性相关与线性无关、线性空间的基与维数。

3. 子空间与线性变换：子空间的定义、子空间的性质、线性变换的定义、线性变换的性质。

八、特征值与特征向量1. 特征值与特征向量的概念：矩阵的特征值与特征向量的定义。

【整理】高数、线代大一上期末复习...高数（上册）期末复习要点第一章：1、极限（夹逼准则）2、连续（学会用定义证明一个函数连续，判断间断点类型）第二章：1、导数（学会用定义证明一个函数是否可导）注：连续不一定可导，可导一定连续2、求导法则（背）3、求导公式也可以是微分公式第三章：1、微分中值定理（一定要熟悉并灵活运用--第一节）2、洛必达法则3、泰勒公式拉格朗日中值定理4、曲线凹凸性、极值（高中学过，不需要过多复习）5、曲率公式曲率半径第四章、第五章：积分不定积分：1、两类换元法（变dx/变前面）2、分部积分法（注意加C）（最好都自己推导一遍，好记）定积分： 1、定义 2、反常积分第六章：定积分的应用主要有几类：极坐标、求做功、求面积、求体积、求弧长第七章：向量问题不会有很难1、方向余弦2、向量积3、空间直线（两直线的夹角、线面夹角、求直线方程） 3、空间平面4、空间旋转面（柱面）高数解题技巧。

（高等数学、考研数学通用）高数解题的四种思维定势●第一句话：在题设条件中给出一个函数f(x)二阶和二阶以上可导，“不管三七二十一”，把f(x)在指定点展成泰勒公式再说。

●第二句话：在题设条件或欲证结论中有定积分表达式时，则“不管三七二十一”先用积分中值定理对该积分式处理一下再说。

●第三句话：在题设条件中函数f(x)在[a,b]上连续，在(a,b)内可导，且f(a)=0或f(b)=0或f(a)＝f(b)=0，则“不管三七二十一”先用拉格朗日中值定理处理一下再说。

●第四句话：对定限或变限积分，若被积函数或其主要部分为复合函数，则“不管三七二十一”先做变量替换使之成为简单形式f(u)再说。

线性代数解题的八种思维定势●第一句话：题设条件与代数余子式Aij或A*有关，则立即联想到用行列式按行(列)展开定理以及AA*=A*A=|A|E。

●第二句话：若涉及到A、B是否可交换，即AB＝BA，则立即联想到用逆矩阵的定义去分析。

大一下高数期末知识点总结高等数学是大学理工科专业中的一门重要基础课程，对于理解和掌握其他专业课程具有至关重要的作用。

下面将对大一下学期高等数学的主要知识点进行总结。

一、极限与连续1. 极限的定义及基本性质- 数列极限的定义- 函数极限的定义- 极限的四则运算法则2. 确定极限的方法- 代入法- 夹逼准则- 单调有界准则- 极限的唯一性3. 连续函数- 连续函数的定义- 连续函数的基本性质- 连续函数的四则运算法则二、导数与微分1. 导数的概念- 导数的定义- 右导数与左导数- 导数与函数图像的关系2. 基本求导公式- 幂函数求导法则- 反函数求导法则- 乘积法则与商法则- 复合函数求导法则3. 高阶导数与高阶导数的求法 - 高阶导数的概念- 高阶导数的求法- Leibniz公式4. 函数的微分与线性化- 微分的定义- 微分的应用- 线性化的概念及应用三、不定积分1. 不定积分的概念与性质- 不定积分的定义- 不定积分的线性性质- 不定积分的换元法则2. 基本初等函数的不定积分- 幂函数的不定积分- 三角函数的不定积分- 指数函数与对数函数的不定积分3. 特殊函数的不定积分- 有理函数的不定积分- 特殊三角函数的不定积分- 分部积分法四、定积分与其应用1. 定积分的概念与性质- 定积分的定义- 定积分的性质- 定积分的换元法则2. 定积分的计算方法- 几何意义与微元法- 换元法- 分部积分法3. 积分学基本定理- 积分的存在性定理- 牛顿-莱布尼茨公式- 反常积分的收敛性五、微分方程1. 一阶常微分方程- 可分离变量的一阶方程 - 齐次方程与非齐次方程 - 线性方程与伯努利方程2. 二阶线性常微分方程- 齐次线性方程的解- 常系数非齐次线性方程的特解- 高阶线性常微分方程总结：高等数学是一门抽象而严谨的学科，其中的知识点需要通过理论学习和大量的练习才能掌握。

以上只是大一下学期高等数学的主要知识点总结，希望能为同学们的学习提供一定的参考。

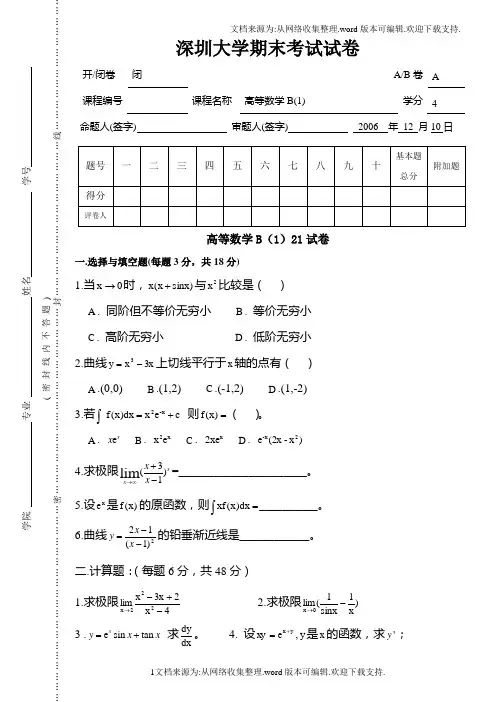
文档来源为:从网络收集整理.word 版本可编辑.欢迎下载支持.深圳大学期末考试试卷开/闭卷 闭A/B 卷 A课程编号课程名称高等数学B(1)学分 4命题人(签字) 审题人(签字) 2006 年 12 月10日高等数学B （1）21试卷一.选择与填空题(每题3分，共18分)1.当0x →时，)sinx x (x +与2x 比较是（ ） A . 同阶但不等价无穷小 B . 等价无穷小 C . 高阶无穷小 D . 低阶无穷小2.曲线3x x y 3-=上切线平行于x 轴的点有（ ） A .(0,0) B .(1,2) C .(-1,2) D .(1,-2)3.若c e x dx )x (f -x 2+=⎰ 则=)x (f （ ）。

A . e x x B . x 2e x C . x 2xe D . )x -2x (e 2-x4.求极限3()1lim xx x x →∞+-=______________________。

5.设x e 是)x (f 的原函数，则⎰=dx )x (xf __________。

6.曲线2)1(12--=x x y 的铅垂渐近线是____________。

二.计算题：（每题6分，共48分）1.求极限4x 23x x lim 222x -+-→2.求极限)x1sinx 1(lim 0x -→ 3 .e sin tan x y x x =+ 求dxdy。

4. 设y x e x y +=,y 是x 的函数，求'y ；5.设()e f x y = 求y '' ；6. 322sin , x y x y =设　求d ；7. 求2ln(1)x dx +⎰； 8. 求⎰-dx e x 3x 2；三.设f (x )=⎪⎪⎩⎪⎪⎨⎧>=<01sin 0 (0sin 1x x x x k x x x 常数） 问当k 为何值时，函数在x =0处连续？为什么？（7分）四、ln(1) 01xx x x x<+<>+ 利用拉格朗日中值定理证明不等式对一切成立．（7分） 五. 判定曲线x x e y -=的单调性、极值、凹向及拐点 （10分） 六. 某厂每批生产某种商品x 单位的费用为 2005x )x (C += （元） 得到的收益是201x .010x )x (R -= （元）求:1.生产10个单位时的边际成本和边际收益.2.每批应生产多少单位时才能使利润最大。

大一下期末高数知识点归纳大一下学期的高等数学是大学数学的重要基础课程之一，内容涵盖了微积分和线性代数等方面的知识。

这门课程通常会以考试形式来评测学生的掌握情况，因此对于期末考试来说，掌握重点知识点是非常关键的。

本文将对大一下学期高等数学的重点知识点进行归纳总结，帮助同学们更好地复习备考。

微积分部分：1. 导数与求导法则：导数是微积分的基本概念，重点掌握求导法则，包括常数和幂函数的导数、指数函数和对数函数的导数、三角函数的导数以及复合函数和反函数的求导法则。

2. 高阶导数和隐函数微分：了解高阶导数的概念和计算方法，并能够应用隐函数微分法求解问题。

3. 函数的极限与连续性：掌握函数极限的定义和性质，熟练运用夹逼准则和无穷小的性质求解极限问题；理解函数的连续性概念，掌握连续函数的性质以及间断点的分类。

4. 函数的导数与微分中值定理：熟悉导数的几何和物理意义，掌握导数的计算方法；了解罗尔定理、拉格朗日中值定理和柯西中值定理等微分中值定理，并能够灵活运用解题。

5. 不定积分和定积分：了解不定积分和定积分的概念，熟练掌握基本积分法和换元积分法，并能够应用定积分求解面积、弧长和体积等问题。

线性代数部分：1. 线性方程组与矩阵：熟悉线性方程组和矩阵的概念，了解增广矩阵和矩阵的初等变换，熟练运用高斯消元法和矩阵求逆方法解决线性方程组的问题。

2. 行列式与矩阵的运算：理解行列式的定义和性质，熟练掌握行列式的展开法则和行列式的特殊性质；了解矩阵的运算法则，并能够进行矩阵的加减、乘法运算。

3. 向量与线性相关性：了解向量的线性运算和线性相关性的概念，能够判断向量组的线性相关性，并进行线性相关性的运算。

4. 线性变换和特征值特征向量：了解线性变换的概念和性质，掌握线性变换的矩阵表示和线性变换的求解方法；熟悉特征值和特征向量的定义和求解过程。

5. 正交与正交矩阵：理解正交性的概念和性质，了解正交基和正交矩阵的定义，熟练应用正交性来解决相关问题。

大一高等数学复习资料（二）引言概述：大一高等数学是大学数学课程中的基础课程，为了帮助大家更好地复习该门课程，本文提供了一份大一高等数学复习资料（二）。

通过该资料的学习，可以帮助大家复习和巩固高等数学的重要概念和知识点，为接下来的学习打下坚实的基础。

正文：1. 微分学复习：a. 重要概念回顾：导数和微分的定义、基本导数公式；b. 导数的应用：求函数的极值与最值、函数图像的描绘；c. 高阶导数与泰勒展开式：求函数的高阶导数、利用泰勒公式研究函数的性质。

2. 积分学复习：a. 定积分与不定积分：定义及性质、基本积分公式；b. 积分方法与技巧：换元法、分部积分法、三类换元法；c. 积分应用：求函数的面积、曲线长度、曲线包围的面积。

3. 微分方程复习：a. 常微分方程与解法：一阶线性微分方程、可分离变量的微分方程；b. 高阶线性微分方程：二阶齐次线性微分方程、二阶非齐次线性微分方程；c. 变量分离和常系数齐次线性微分方程。

4. 空间解析几何复习：a. 点、线、面的方程与性质；b. 点到直线和点到平面的距离计算；c. 平面与直线的位置关系、两平面的位置关系。

5. 矩阵与行列式复习：a. 矩阵的基本概念：矩阵的定义、矩阵的运算；b. 行列式的定义与性质：二阶、三阶行列式的计算；c. 逆矩阵与矩阵的秩：逆矩阵的判定、矩阵秩的计算。

总结：通过学习本文提供的大一高等数学复习资料（二），我们可以更好地复习和巩固高等数学的重要概念和知识点，为接下来的学习打下坚实的基础。

希望这份资料对于大家的学习有所帮助，祝愿大家在学习中取得优异的成绩！。

大一高数期末考试复习知识点近年来，大学生的课程负担越来越重，而高等数学作为大学本科阶段的一门重要课程，对于理工科学生来说，尤为重要。

大一高数期末考试作为对学生掌握程度的一次大考，需要学生全面复习相关知识点，以确保自己的考试成绩。

一、极限极限是大一高数课程的核心概念之一。

在复习期间，需要重新温习极限的定义、计算方法和性质。

学生应该熟练掌握常见函数的极限计算方法，如幂函数、指数函数、对数函数等。

此外，对于无穷小量和无穷大量的概念以及他们之间的关系也需要重点掌握。

二、导数和微分导数是大一高数课程的另一个重要概念。

在复习期间，学生需要回顾导数的定义和几何意义，并通过练习来熟悉各种函数的导数计算方法。

此外，微分的概念和性质也是复习的重点之一。

学生需要了解微分的定义、微分法则以及微分的物理意义。

三、积分积分是大一高数课程的又一重要概念。

在复习期间，学生需要重新温习积分的定义和计算方法。

掌握不同类型函数的积分计算方法，如基本初等函数的积分、分部积分法、换元积分法等。

此外，对于定积分和不定积分的区别和联系也需要进行复习。

四、微分方程微分方程是大一高数课程中的一大难点。

在复习期间，学生需要重点掌握一阶线性微分方程和二阶线性齐次微分方程的解法，理解解的存在唯一性定理，并通过练习来提高解微分方程的能力。

此外，对于常微分方程和偏微分方程的区别和联系也需要进行复习。

五、级数级数是大一高数课程中的一大难点，也是复习中的一项重点内容。

学生需要回顾级数的概念、收敛性判别法以及级数求和的方法。

对于常见的数列，如等比数列、等差数列、调和数列等，学生需要熟悉它们的性质和求和公式。

六、空间解析几何空间解析几何是大一高数课程中的一项重要内容。

在复习期间，学生需要回顾空间直线和平面的方程及其性质，理解直线与平面的位置关系和相交情况。

此外，学生还需要掌握空间几何体的体积和表面积计算方法，如球体、圆柱体、圆锥体等。

七、数列和数列的极限数列和数列的极限是大一高数课程中的一项基础内容。

大一期末线代知识点线性代数是数学中的一门基础学科，对于大一学生来说，线性代数是一个重要的课程。

在期末考试中，了解和掌握各个知识点是取得好成绩的关键。

下面是大一期末线代知识点的详细介绍。

1. 向量和向量空间向量是线性代数中最基本的概念之一。

向量具有大小和方向，可以进行加法和数乘运算。

向量空间是由一组向量构成的集合，满足一定的运算规则。

2. 线性方程组线性方程组是线性代数中的核心内容之一。

线性方程组可以写成矩阵乘以向量的形式，其中矩阵是由方程组的系数构成的。

解线性方程组的方法有高斯消元法、矩阵的逆等。

3. 矩阵和矩阵运算矩阵是线性代数中的另一个重要概念。

矩阵是由数按矩形排列而成的矩形阵列。

矩阵之间可以进行加法、减法和乘法等运算。

4. 行列式行列式是一个与矩阵相对应的数。

它是一个用于描述矩阵性质的重要工具。

行列式的计算方法有代数余子式展开法、三角形法等。

5. 特征值与特征向量特征值和特征向量是描述矩阵特性的重要概念。

通过特征值和特征向量可以判断矩阵的相似性、对角化等性质。

6. 矩阵的秩矩阵的秩是描述矩阵中线性无关的向量个数。

矩阵的秩可以判断矩阵是否可逆、解线性方程组的情况等。

7. 线性变换线性变换是线性代数中的另一个重要概念。

线性变换是指将一个向量空间映射到另一个向量空间的变换。

线性变换可以用矩阵来表示。

8. 内积空间和正交内积空间是线性代数中的一个重要概念。

内积空间中定义了一个内积运算，内积满足一定的运算规则。

正交是内积空间中的一个概念，指的是两个向量的内积为零。

9. 特征分解和奇异值分解特征分解和奇异值分解是对于矩阵的一种分解方法。

特征分解可以将一个矩阵分解成特征值和特征向量的乘积形式，奇异值分解可以将一个矩阵分解成奇异值矩阵的乘积形式。

10. 线性代数的应用线性代数在很多领域都有广泛的应用，如计算机图形学、密码学、信号处理等。

了解线性代数的知识点可以为以后的学习和应用打下坚实的基础。

以上是大一期末线代的主要知识点的简要介绍。

高数大一期末复习知识点大学的第一个学期即将进入尾声，而大一阶段的数学课程也即将迎来期末考试。

高等数学作为复杂的学科，对于大多数学生来说可能会感到有些困难。

为了帮助同学们更好地复习和掌握高数知识点，本文将围绕重点内容展开讨论。

一、极限与连续在高等数学中，极限与连续是基础而重要的概念。

极限是数列或函数在某一点趋于无穷大或无穷小的过程。

通过对极限的理解和熟练应用，能够掌握数列的收敛性和函数的连续性。

在复习过程中，我们可以重点关注常见函数的极限计算方法，并应用到例题中去理解其运用。

二、微分学微分学是高等数学中的重要部分，它研究了函数的变化率及其相关性质。

微分的概念与应用都在高数课程中占据很大比重。

对于微分公式的掌握和运用往往是解题的关键。

在复习过程中，我们可以着重复习基本函数的导数计算和常见求导法则，并结合例题进行训练。

三、积分学积分学是微分学的重要补充，它研究了函数的面积、曲线长度以及其相关性质。

积分的计算方法和应用都是复习的重点。

我们需要重点复习不定积分和定积分的计算方法，例如换元法、分部积分法、曲线下面积计算等。

掌握这些方法对于解决积分题目将大有帮助。

四、级数级数是由无穷个数相加（或相减）而成的一种数列。

级数在高等数学中有广泛的应用，如级数的条件收敛性判别法、函数展开为级数等。

复习时，我们需要熟悉并巩固级数求和常用方法，以及研究级数的收敛性质和敛散判别法。

五、多元函数微分学多元函数微分学是高等数学中的拓展内容，它主要研究多元函数的导数和极值问题。

在复习中，我们需要熟悉多元函数的偏导数的计算方法和极值判定法则。

此外，掌握多元函数微分学的基本概念和性质，对于理解三维几何图形和解决相关问题有非常大的帮助。

六、方程与不等式方程与不等式既是高等数学的基础又是复习和考试重点。

回顾前面学过的内容，我们需要熟练掌握常用的一元方程和一元二次方程的解法，以及一元不等式的解法。

同时，我们还需了解二元方程、二元一次方程组和二元一次不等式组的解法，以及线性规划问题的求解思路。

大一下期末高数知识点一、导数与微分在微积分中，导数是用来描述曲线斜率变化的概念。

它的求解可以通过求导函数得到，表示函数在某一点上的瞬时变化率。

导数的数学表示为f'(x)，也可以表示为dy/dx。

微分是导数的重要应用，它描述了函数在某一点上的局部线性近似。

二、极限与连续极限是微积分中的基本概念，它用来描述函数在某一点附近的趋势。

极限的计算需要应用一系列的极限运算法则，如极限的四则运算、夹逼定理等。

连续是极限的重要应用，当函数在某一点处的左极限、右极限和函数值相等时，该函数称为在该点连续。

三、微分中值定理微分中值定理是微积分中的重要定理，它描述了函数在某一区间内的平均变化率与瞬时变化率之间的关系。

常见的微分中值定理包括拉格朗日中值定理、柯西中值定理和罗尔中值定理等。

四、反函数与隐函数在微积分中，反函数与隐函数是两种常见的函数关系。

反函数是指函数f(x)与其反函数f^(-1)(x)之间的关系，可以通过互换自变量和因变量得到。

隐函数则是指函数关系不容易直接用显式函数表示出来，但可以通过偏导数计算出函数的性质。

五、定积分与不定积分定积分是微积分中的重要概念，用来描述曲线下方的面积或者曲线长度。

它的计算需要应用积分的性质和一些常见的积分法则，如换元法、分部积分法等。

不定积分是定积分的反向操作，表示求解函数的原函数。

六、级数与收敛性级数是微积分中的一种数学运算，是对无穷多个数相加或相乘得到的一种结果。

级数的收敛性是判断级数是否有有限的和，常用的收敛判别法有比较判别法、积分判别法和绝对收敛判别法等。

七、微分方程微分方程是描述函数和其导数之间的关系的方程。

它在物理、工程、生物等领域中有广泛的应用。

常见的微分方程包括一阶微分方程、二阶微分方程和常微分方程等，可以通过解方程得到函数的解析表达式。

八、空间解析几何空间解析几何是微积分的重要应用，通过坐标系和方程式来描述三维空间中的几何问题。

常见的空间解析几何问题包括平面与直线的位置关系、平面曲线与曲面的切线与法线等。

大一高等数学期末考试试卷及复习资料详解大一高等数学期末考试试卷（一）一、选择题（共12分）1.（3分）若/3= 2XXV0,为连续函数,则d的值为（）.a+ x,x>0（A）I （B） 2 （C）3 （D）-I2.（3分）已知厂⑶=2,则Ii y "7⑶的值为（）.λ→0 2hOOl （B） 3 （C）-I （D）I23.（3分）定积分∫>Λ∕1-COS23Xdx的值为（）•■⑷ 0 （B）-2 （C）I （D） 24.（3分）若/⑴在“勺处不连续,则/3在该点处（）・（A）必不可导（B）—定可导（C）可能可导（D）必无极限二、填空题（共12分）1.（3分）平面上过点（0,1）,且在任意一点（Λ∙,y）处的切线斜率为3疋的曲线方程为_________________________ .2.（ 3 分）∫ ι（x2+x4 Sin XyIX = _______ 1-3.（3 分）IilnX2 Sin丄= ・.r→υX4.（3分）y = 2√ -3√的极大值为________________ —2 （6分）设尸冕,求*JT + 1三、计算题（共42分）1.（6 分）求Iim史S.∙*→υ Sin 3x^3.（6分）求不定积分JXIn（I+十）厶.x .v<ι4.（6 分）求J /（X-1）JΛ∖其中/（x）= < l + cosχ,e' +l,x> 1.5.（6分）设函数y = f（x）由方程JO e,M + ［cos∕d∕ = 0所确定,求dy.6.（ 6 分）设 f f{x）dx = Sin + C,求j + 3）dx.7.（6 分）求极限IinJI÷-Γn→30k 2/7 7四、解答题（共28分）1.（7 分）设,Γ（lnx） = l+x,且/（0） = 1,求32.（7分）求由曲线y = cosx［-^-<x<^及X轴所围成图形绕着X轴旋I 2 2）转一周所得旋转体的体积.3.（7分）求曲线y = x3-3√÷24x-19在拐点处的切线方程•4.（7分）求函数y = x + √∏7在［-5,1］上的最小值和最大值.五、证明题（6分）设厂（X）在区间［“］上连续,证明i a f^dx = ¥ ［/（“） + f（b）］+1 ［（X - a）（x - b）fj）dx.（二）一、填空题（每小题3分，共18分）1.设函数/（χ）= 2χ2~1 ,则"1是心）的第_________ 类间断点.X -3x + 23.=∙v→∞V X)4・ 曲线 V 在点(扣)处的切线方程 为 ・5 .函数J = 2X 3-3X 2在［-1,4］上的最大值 _________________ ,最小值 __________ .二、 单项选择题(每小题4分，共20分)1.数列&”｝有界是它收敛的( )•(A)必要但非充分条件； (C)充分必要条件； 2.下列各式正确的是((B)充分但非必要条件; (D)无关条件.)・(A) je-χdx=e"x+C i(B) J In X(IX = _ + C ; (C)JI 2∕x=2hl (l 2x)+C ；(D) f —5—JX = Inlllx+ C ・' ,J XInX3-设/(x)在RM 上，广(x)>O 且厂(x)>0,则曲线y = f(x)在［“问上•6.∣∙arctanx J l +x 2(IX(小沿X轴正向上升且为凹(B)沿兀轴正向下降且为凹的；的；(D)沿X轴正向下降且为凸(C)沿兀轴正向上升且为凸的；的.则/(x)在兀=0处的导? :( )•4. 设/(*)=XInX ’⑷等于1;（C）等于O ；（D）不存在•5.已知Ihn/（x）= 2,以下结论正确的是（）•G）函数在工=1处有定义且/（1）=2 ; （B）函数在；V = I处的某去心邻域内有定义；（C）函数在2 1处的左侧某邻域内有定义；（D）函数在21处的右侧某邻域内有定义.三、计算（每小题6分，共36分）1.求极限:HlnX2 sinx→0X2.已知y = ln（l + χ2）,求几3.求函数J = >0）的导数.5.J X COS XdX ・丄 16.方程y x =X y确定函数y = f（x）f求八四、（H）分）已知/为/（X）的一个原函数，求∫x2∕（x}∕x.五、（6分）求曲线,=壮7的拐点及凹凸区间.六、（10 分）设J广（√∑）/X = X（e、' +1）+C ,求/（X）・（三）填空题（本题共5小题，每小题4分，共20分）・±J_(1)⅛(COSX)r = ________ 石________ .(2)曲线A = Xlnx上及直线X-y + l= °平行的切线方程为y =x-∖(3 )已知f f(e x) = xe~x,且/(D = O ,则大一高等数学期末考试试卷及复习资料详解/(X)= _________ /Cv)= 2(In X)________ .X 211(4)曲线V =3777的斜渐近线方程为 _______ V= 3Λ^9,二、选择题(本题共5小题，每小题4分，共20分)・(1)下列积分结果正确的是(D )(2)函数/W 在［恥］内有定义，其导数广⑴的图形如图1-1所示, 则(D ) •(A)刁宀都是极值点.⑻ g ，/3))，(£，/(£))都是拐点.(C) F 是极值点.，U 是拐点. (D) WJy))是拐点，勺是极值点.(3) 函数y = qe v ÷C 2e-÷A -e'满足的一个微分方程是(D ).(A) /-y-2>∙ = 3xe t . (B) /-y-2y = 3e v . (C) / + y-2y = 3Λ∙e c .(D) / + y~2y = 3e r .lim∕(⅞)-∕(⅞~z0 (4) 设/W 在％处可导，则I h 为(A ) •⑷ 广仇). (B) -f ,M.(C) O. (D)不存在.(5)下列等式中正确的结果是((A) (J* /(x)"∙χ)'Z=/W-(C) 町 /(χ)"χ]=/W -) 微分方程= (V+1)-的通解为三、计算J (本 共4小题，每小题6分，共24分).y =3 _5 "3 O(或令 √Γ+χ = r)四、解答题（本题共4小题，共29分）•1. （本题6分）解微分方程r-5∕÷6j = xe -.解：特征方程r 2-5r + 6 = 0 ------------- 1分 特征解斤=2,r 2 =3. ------------ 1分 3x大一高等数学期末考试试卷及复习资料详解 恤（丄—丄）1∙求极限j X-I In —X 11. xlnx-x+1Iim (—— _ ——)IIm ---------In XIUn I XTl x-1 I---- + In xh ∖x Iim x →,X -1 + xln1.1 + In X 1 IUn -------- =— j 1 + In X +1 2Λ = In Sin t2.方程尸COSWSinf 确定V 为X 的函数,dy y ,(f)-=-一 =∕sm∕, 解 JX 十⑴求dx 及Jx 2 .（3分） (6分)arctan JX3. 4.计算不定积分J石(1+『. arctanA∕√7—— (i + χ)=21 arctan √7t∕ arctan y ∕x ——解 Hatan 仇=2 J √x(l + x)=(arctan2+C ——「一 dx4.计算定积分如+曲.'3χ(l -VTTX) 0解 分）oT7⅛7_ V dx = 一J(：(I-、/i+x)〃X（6分）LL i∖l4/1 «\ ? r V 八2.(本题7分)一个横放着的圆柱形水桶(如图4-1),桶内盛有半桶水，设桶的底半径为R ,水的比重为乙计算桶的一端面上所受的压力.解：建立坐标系如图3.(本题8分)设/B在S】上有连续的导数，f(u) = f(b) = θ9且∫O∕2(X)JΛ =1^试求∫>∕ω∕解:J：Xf(X)f∖x)dx = £ Xf(X)df(x) 2 分= -∫n^^W ------------ 2 分=IV 2(Λ-)⅛-|£72(X)厶一一2 分4.(本题8分)过坐标原点作曲线＞, = h^的切线，该切线及曲线y =lnx及X轴围成平面图形D.⑴(3) 求D的面积A;⑵(4) 求D绕直线X = e旋转一周所得旋转体的体积V.解:(1)设切点的横坐标为"，则曲线y = In Λ在点(⅞Jn ⅞)处的切线方程y = Inx0 + —(X-X0).氐__I分由该切线过原点知山心-1 = 0,从而心=匕所以该切线的方程为1y = -X.平面图形D的面积1V = -X(2)切线"及X轴及直线Xe所围成的三角形绕直线Xe旋转V I = -7te1所得的圆锥体积为,3 2分曲线尸IZ及X轴及直线所围成的图形绕直线Xe旋转所得的旋转体体积为V2=(oπ(e-e>)2dy9】分因此所求旋转体的体积为V=V l-V2=-^2-e y)2dy = -(5e2-∖2e + 3).五、证明题(本题共1小题，共7分)•1.证明对于任意的实数Y , eJl + x.e x = l + x + —Λ2≥l + x2解法二设fM = e x-x~^则/(0) = 0.因为f f M = e x-∖. 1 分当Xno时，f,M≥o.f(χ)单调增加，/(χ)≥∕(θ)=o.当x≤0时，∕,ω≤0.∕(Λ∙)单调增加，/(X)≥/(0) =0. 所以对于任意的实数X, ∕3≥°∙即e'≥l + I 解法三：由微分中值定理得，R -1 = “ -60 =^(X-O) = ^Xt 其中§位于0 到X 之一1分2分A = V -ey)dy = ~e~^∙解法一:2分2分1分2分间。

大一高数期末冲刺知识点高等数学是大一学生的必修课程之一，也是大多数理工科专业的基础课程。

期末考试是对学生在这门课上所学知识的全面检验，因此，为了取得好成绩，有必要进行冲刺复习。

下面将总结大一高数期末考试的核心知识点，以便帮助同学们有针对性地复习。

一、导数与微分1. 导数的定义与求法a. 导数的定义：导数表示函数在某一点上的变化率，可以通过导数来研究函数的增减性、极值和曲线的形状等。

b. 导数的求法：常用求导法则包括函数的基本求导法则、乘积、商的求导法则以及复合函数求导法则等。

2. 高阶导数a. 高阶导数的定义：高阶导数表示导数的导数，即导函数的导函数。

b. 高阶导数的求法：通过多次应用求导法则，可以求得高阶导数。

3. 隐函数求导a. 隐函数的定义：若函数y=f(x)在某一区间内满足方程F(x,y)=0，则方程F(x,y)=0所确定的函数y=f(x)称为隐函数。

b. 隐函数求导的方法：利用隐函数的导数公式，可以求得隐函数的导数。

4. 微分a. 微分的定义：函数y=f(x)在点x处的微分表示函数在该点附近的变化量，可以近似地描述函数在该点上的变化情况。

b. 微分的求法：使用微分公式，可以求得函数在某一点处的微分。

二、积分1. 不定积分a. 不定积分的定义：不定积分是反导数的概念，与导数相互逆运算，表示函数的原函数。

b. 不定积分的法则：常用的不定积分法则包括基本积分法、分部积分法、换元积分法等。

2. 定积分a. 定积分的定义：定积分是将函数在某一区间上的各点微小部分的变化量相加而得到一个区间上的整体变化量。

b. 定积分的计算方法：可以利用定积分的性质、基本积分法则以及数值积分法等来计算定积分。

3. 曲线与定积分a. 曲线下面积的计算：可利用定积分的概念计算曲线下的面积。

b. 与坐标轴围成的面积：通过分割区间，以及利用定积分的性质，可以计算曲线与坐标轴所围成的面积。

三、常微分方程1. 一阶线性常微分方程a. 一阶线性常微分方程的定义：一阶线性常微分方程是指形如dy/dx+p(x)y=q(x)的微分方程。

高等代数大一下期末知识点高等代数是大一下学期的一门重要课程，它是线性代数的延伸与拓展，主要涉及到矩阵、向量、行列式、特征值与特征向量等内容。

下面，我将针对高等代数大一下期末的知识点进行全面的总结和归纳。

一、矩阵与行列式1. 矩阵的定义和性质：矩阵是由一些数按一定规律排列成的矩形数组。

矩阵的加法、数乘和乘法满足一定的运算规律，具有结合律、分配律等性质。

2. 矩阵的转置：矩阵的转置是将矩阵的行和列互换得到的新矩阵。

3. 矩阵的逆：对于可逆矩阵，存在一个逆矩阵，使得矩阵与其逆矩阵相乘得到单位矩阵。

逆矩阵的求解可以利用伴随矩阵和行列式的性质。

4. 行列式的定义和性质：行列式是一个标量，它根据矩阵的排列规律计算而得。

行列式的计算可以使用代数余子式和代数余子式的行列式展开式。

二、向量空间1. 向量与线性相关性：向量的线性组合、线性相关与线性无关的概念是研究向量空间的基础。

线性相关性可以通过求解线性方程组或利用行列式判断。

2. 向量空间的定义和性质：向量空间是由一组向量和定义在其上的加法和数乘运算构成的。

3. 向量空间的子空间：子空间是向量空间的一个更小的子集，它同样满足向量空间的定义和性质。

判断一个子空间是否成立可以利用子空间的闭包性和线性组合的定义。

三、特征值与特征向量1. 特征值与特征向量的定义：对于矩阵A，如果存在一个非零向量X，使得AX=kX，其中k为一个常数，则称k为矩阵A的特征值，X为对应的特征向量。

2. 特征多项式和特征方程：特征多项式是由特征值和对应特征向量所构成的多项式。

特征方程是特征多项式为零的解方程。

3. 对角化和相似矩阵：对于可对角化矩阵，存在一个可逆矩阵P，使得PAP^{-1}为对角矩阵。

相似矩阵具有相同的特征值，但特征向量可能不同。

四、正交性与正交矩阵1. 内积空间与正交性：内积空间是带有内积运算的向量空间。

向量的内积可以用来衡量向量之间的夹角和长度。

2. 正交向量与正交集：两个向量的内积为零时，称这两个向量正交。

大一期末必备知识点1.数学-高等数学核心内容：函数与极限、导数与微分、积分与定积分、微分方程-线性代数：矩阵的基本运算、行列式与矩阵的逆、线性方程组、向量空间和线性映射-概率与统计：基本概念与性质、随机变量与概率分布、常见离散型分布、连续型分布、统计推断等2.物理学-力学：牛顿运动定律、运动学、动量与动量守恒、功与能量、万有引力等-电磁学：电场与电荷、电势与电势差、电场与电势的关系、电容与电容器、电流与电阻、电路基本定律等-热学：温度与热量、热传导、热容与比热容、热力学第一定律与第二定律等3.化学-基础概念：原子结构、分子结构、化学键、离子式、化学方程式、氧化还原反应等-物质的性质：酸碱性、pH值、溶解度、氧化性与还原性、化学反应速率等-物质的组成：元素周期表、主要元素的性质、常见化合物等4.生物学-细胞结构与功能：细胞膜结构、细胞器功能、细胞分裂、细胞信号传导等-遗传与进化：基因的结构与功能、DNA复制、基因突变、遗传变异、自然选择等-生态与环境：生态系统的结构与功能、生物的适应性与生存策略、环境保护与可持续发展等5.社会科学-政治学：国家与政府、政治体制与制度、选举制度与民主、国际关系等-经济学：市场经济与计划经济、供需关系与价格、货币与通货膨胀、经济增长与发展等-社会学：社会结构与社会组织、社会化与社会心理、社会问题与社会变迁等6.英语-词汇与语法：常用单词与短语、时态与语态、句子结构与用法、语法规则与语法错误等-阅读与理解：文章主旨与段落结构、关键信息与推理、语义推断与词汇理解等-写作与口语：表达能力与写作技巧、常见写作形式与内容、口语交际能力与场景应对等7.计算机科学-编程基础：编程语言、变量与常量、数据类型、流程控制、函数与模块、数据结构与算法等-网络基础：网络协议、IP地址与子网掩码、网络拓扑与设备、网络安全与防火墙等-数据库基础：数据库类型与表结构、SQL语言、数据库管理与备份、数据查询与报表等这些知识点是大一期末考试的基本内容，建议同学们在备考阶段逐一复习，并通过做相关的习题和模拟试题来提高自己的理解和应用能力。

大一高数复习资料大一高数复习资料大一高数是大部分理工科学生都要修习的一门基础课程，它是数学的一大分支，对于理解和掌握高等数学的基本概念和方法具有重要意义。

然而，由于大一学生的学习压力较大，时间有限，很多人在高数学习中遇到了困难。

为了帮助大家更好地复习高数，本文将介绍一些高效的复习资料和方法。

一、教材与课件大一高数的教材通常是由教授编写的教材，这些教材系统地介绍了高数的各个知识点和解题方法。

复习时，可以将教材作为主要参考资料，着重阅读和理解教材中的例题和习题解析。

此外，许多学校会提供高数的课件，这些课件通常包含了教材中的重点内容和难点解析，可以帮助学生更好地理解和掌握知识点。

二、习题集习题集是复习高数的重要资料，它包含了大量的习题和答案，可以帮助学生巩固知识和提高解题能力。

在选择习题集时，建议选择与教材相对应的习题集，这样可以更好地对照教材进行复习。

在做习题时，可以按照章节顺序，先做一些基础题，逐渐过渡到难度较大的题目。

同时，要注意查看习题的解析，理解解题思路和方法。

三、辅导书籍除了教材和习题集，还有一些辅导书籍也可以作为复习资料。

这些书籍通常以更简洁明了的方式介绍高数的知识点和解题方法，适合用来查漏补缺和快速复习。

在选择辅导书籍时，可以根据自己的学习风格和需求进行选择。

有的人喜欢图文并茂的书籍，有的人喜欢重点突出的书籍，可以根据自己的喜好选择适合自己的辅导书籍。

四、网络资源互联网是一个宝藏般的资源库，里面有大量的高数学习资料和解题技巧。

在复习高数时，可以利用搜索引擎搜索相关的学习资料和视频教程。

有一些知名的教育网站和学习平台也提供了大量的高数学习资源，可以免费或付费使用。

在使用网络资源时，要注意选择正规和可信的网站，避免受到错误或误导性的信息。

五、刷题APP随着智能手机的普及，刷题APP成为了许多学生复习高数的选择。

这些APP通常提供了大量的高数习题和解题思路，可以随时随地进行刷题练习。

在选择刷题APP时，可以参考其他用户的评价和推荐，选择功能齐全、题目质量较高的APP。

大一高等数学复习资料大一高等数学复习资料大一高等数学是大学数学的一门重要课程，对于理工科学生来说尤为重要。

它是数学的基础，也是后续学习更高级数学课程的基石。

因此，对于大一学生来说，复习高等数学是至关重要的。

一、复习方法1. 制定复习计划复习高等数学需要有一个明确的计划。

可以根据教材的章节和重点，制定每天的复习内容和时间安排。

合理的计划可以帮助你合理分配时间，有针对性地复习重点知识点。

2. 多做习题高等数学是一门需要多做题来巩固理论知识的学科。

可以通过做教材后面的习题，或者找一些习题集进行练习。

重点是要理解每道题目的解题思路和方法，而不是死记硬背答案。

3. 结合实际应用高等数学中的很多概念和方法都是为了解决实际问题而提出的。

在复习的过程中，可以将数学知识与实际问题相结合，通过解决实际问题来理解和巩固相关的数学知识。

二、复习重点1. 极限与连续极限与连续是高等数学的重要概念。

在复习时，要掌握极限的定义和性质，理解极限的概念在数学和物理等领域中的应用。

同时，要熟练掌握连续函数的定义和性质，理解连续函数的图像和性质。

2. 导数与微分导数与微分是高等数学中的重要内容。

在复习时，要掌握导数的定义和性质，理解导数在函数图像上的几何意义。

同时，要掌握常见函数的导数公式和求导法则。

微分是导数的应用，要理解微分的定义和性质，并能够应用微分解决实际问题。

3. 积分与定积分积分与定积分是高等数学中的重要内容。

在复习时，要掌握积分的定义和性质，理解积分的几何意义和物理意义。

同时，要熟练掌握常见函数的积分公式和求积法则。

定积分是积分的应用，要理解定积分的定义和性质，并能够应用定积分解决实际问题。

4. 一元函数的级数级数是高等数学中的重要内容。

在复习时，要掌握级数的定义和性质，理解级数的收敛和发散的概念和判别法则。

同时，要熟练掌握常见级数的求和公式和级数的收敛性质。

三、常见问题解答1. 为什么要复习高等数学？复习高等数学可以巩固和加深对数学知识的理解和掌握，为后续学习更高级数学课程打下坚实的基础。

一、定积分及其应用1、计算定积分（1）10xxe dx -⎰ （2）x x x x d )(tan 114⎰-+（3）⎰++70311x dx . （4）⎰+41)1(x x dx .（5）⎰51ln xdx2. 判断广义积分1ln edxx x ⎰的敛散性3、求曲线1y x=与,2y x x ==所围成图形的面积。

4、求曲线2y x=与直线3,0x y ==围成的图形绕x轴旋转所得的旋转体体积。

二、无穷级数1.填空 （1）若=xe∑∞=0!n nn x , 那么2x xe =（2）级数∑∞=031n n 的和________________（3）幂级数11(1)n nn x n -∞=-∑的收敛半径________________2.判断级数敛散性1）1+322121+++323131+++324141++ +2）12(1)nn n n ∞=+∑3）132()41nn n n ∞=-+∑ 4）∑∞=+-122)1(n n an5）∑∞=+121sin n n na3、求级数下列级数的收敛半径和收敛域 1）∑∞=1n nnx 2）1123111(1)1(1)n n n n n x x x x x ∞----=-=-+-++-+∑4、将函数ln x 展开成(x -1)的幂级数,并求展开式成立的区间.5.将函数341)(2++=x x x f 展开成x - 1的幂级数. 6.将函数341)(2+-=x x x f 展开成x + 1的幂级数.三、多元函数1． 填空（1）设22),(y x y x y x f -=-+, 则f (x , y ) = .（2）若y x z 2e =, 那么=∂∂)1,1(xz.（3）若xy z =, 那么=∂∂)2,1(xz.2.求下列函数的全微分d z . (1)22y x z +=（2）xy z =(3) xy z = (4) x y z arctan =3．求下列偏导数 （1）22yxz +=,求yx z ∂∂∂2 （2）)ln(y x z +=，求yx z∂∂∂2 （3）已知arctan yz x =，求22x z ∂∂,22yz ∂∂和yx z∂∂∂2 （4）设3323sin z x y xy x y =+-+，求2zx y∂∂∂4. 设),2(22y x xy f z +=, 其中f 具有一阶连续的偏导数, 求xz ∂∂,yz ∂∂.5. 设),(xy y x f z +=, 其中f 具有一阶连续的偏导数, 求xz ∂∂,yz ∂∂.6. 设生产某种产品的数量与所用两种原料A 、B 的数量x 、y间有关系式y x y x f 25.0),(=. 现在用300元购买原料, 已知A 、B 两种原料的单价分别为2元、5元, 问A 、B 两种原料各购进多少时, 可使产品的数量最多?7.工厂生产两种产品Ⅰ、Ⅱ, 总成本为52222121+++=Q Q Q Q C , Q 1及Q 2分别为Ⅰ、Ⅱ两种产品的产量, 两种产品的需求函数为1126P Q -=, 224110P Q -=, P 1、P 2分别是两种产品的出售单价. 若生产的产品都能卖出, 问两种产品的产量Q 1、Q 2各为多少时, 工厂取得的利润最大?四、二重积分1. 设D 为正方形区域: ∣x ∣≤ 1, ∣y ∣≤ 1, 则⎰⎰Ddxdy2. 设D 为圆域: 222a y x ≤+,求⎰⎰Dy x d d 23. 计算⎰⎰Dydxdy x 2, 其中D 由2x y =与y = x 所围成的平面区域.4. 设区域D 为01x ≤≤，01y ≤≤，求⎰⎰Dxydxdy5. 计算⎰⎰Dy x xy d d , 其中D 是由xy 1=, y = x , x = 2所围成的平面区域.。