自动控制原理及其应用(第2版)黄坚第三章习题课

自动控制原理黄坚课后习题答案解析GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-4s(s+5)G(s)=1s(s+1)G(s)=1.3tc(t)10.1解:t p ==0.121-ζπωn =0.3e -ζζπ1-2e ζζπ1-2=3.3ωn 2 ζ1- 3.140.1==31.4ζ21-ζπ/=ln3.3=1.19)21-ζπ2/ζ(=1.42=1.42-1.429.862ζ2ζζ=0.35=33.4ωn s(s+2 ωn ωn ζ)G(s)=21115.6s(s+22.7)=G(s)=s(s+1)(0.5s 2+s+1)K(0.5s+1)3-1 设温度计需要在一分钟内指示出响应值的98%，并且假设温度计为一阶R =20 k Ω R =200 k Ω(2) 求系统的单位脉冲响应，单位斜坡响应,及单位抛物响应在t 时刻的3-3 已知单位负反馈系统的开环传递函数，3-4 已知单位负反馈系统的开环传递函数，求系3-7 设二阶系统的单位阶跃响应曲线如图，系统的为单3-11 已知闭环系统的特征方程式，试用劳斯判据判断系统的稳定性。

3-12 已知单位负反馈系统的开环传3-13 已知系统结构如图，试确r(t)=I(t)+2t+t 2s 2R(s)=1s2+s 32+K r(s+1)G(s)=3-14 已知系统结构如图，试确3-16 已知单位反馈系统的开环传递函3-18 已知系统结构如图。

为使ζ=0.7时,单位斜坡输入的稳态误差e ss =0.25确定K 和τ值 。

4-1 已知系统的零、极点分布如图，大致绘制出系统的根轨迹。

4-2 已知开环传递函数，试用解析法绘制出系统4-5 已知系统的开环传递函数。

(1)试绘制出根轨迹图。

(2)增益K r 为何值时，复数特征根的实部为-2。

5-1 已知单位负反馈系统开环传递函数，当输入信号r(t)=sin(t+30o )，试求系统的稳态输出。

3-1 设系统特征方程式：试按稳定要求确定T 的取值范围。

解：利用劳斯稳定判据来判断系统的稳定性，列出劳斯列表如下：欲使系统稳定，须有故当T>25时,系统是稳定的。

3-2 已知单位负反馈控制系统的开环传递函数如下，试分别求出当输入信号为,21(),t t t 和 时，系统的稳态误差(),()().ssp ssv ssa e e e ∞∞∞和解：（1）根据系统的开环传递函数可知系统的特征方程为：由赫尔维茨判据可知，n=2且各项系数为正，因此系统是稳定的。

由G(s)可知，系统是0型系统，且K=10，故系统在21(),t t t 和输入信号作用下的稳态误差分别为：(2)根据系统的开环传递函数可知系统的特征方程为：由赫尔维茨判据可知，n=2且各项系数为正，且2212032143450,/16.8a a a a a a a ∆=-=>∆>=以及，因此系统是稳定的。

由G(s)可知，系统式I 型系统，且K=7/8,故系统在21(),t t t 和 信号作用下的稳态误差分别为：(3)根据系统的开环传递函数可知系统的特征方程为：由赫尔维茨判据可知，n=2且各项系数为正，且21203 3.20a a a a ∆=-=>因此系统是稳定的。

由G(s)可知，系统是Ⅱ型系统，且K=8,故系统在21(),t t t 和 信号作用下的稳态误差分别为：3-3 设单位反馈系统的开环传递函数为试求当输入信号2()12r t t t =++时，系统的稳态误差.解：由于系统为单位负反馈系统，根据开环传递函数可以求得闭环系统的特征方程为：由赫尔维茨判据可知，n=2且各项系数为正，因此系统是稳定的。

由G(s)可知，系统是Ⅱ型系统，且K=8,故系统在21(),t t t 和 信号作用下的稳态误差分别为10,,K∞，故根据线性叠加原理有：系统的稳态误差为： 3-4 设舰船消摆系统如图3-1所示，其中n(t)为海涛力矩产生，且所有参数中除1K 外均为已知正值。

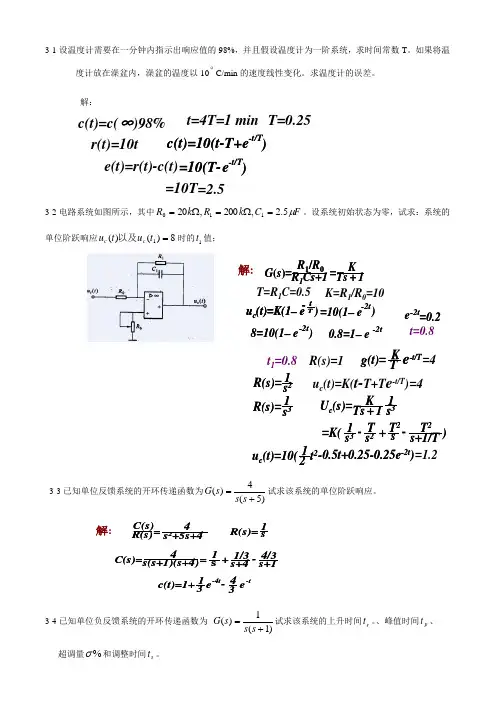
3-1设温度计需要在一分钟内指示出响应值的98%，并且假设温度计为一阶系统，求时间常数T 。

如果将温度计放在澡盆内，澡盆的温度以10C/min 的速度线性变化。

求温度计的误差。

解：c(t)=c(∞)98%t=4T=1 min r(t)=10te(t)=r(t)-c(t)c(t)=10(t-T+e )-t/T =10(T-e )-t/T =10T =2.5T=0.253-2电路系统如图所示，其中F C k R k R μ5.2,200,20110=Ω=Ω=。

设系统初始状态为零，试求：系统的单位阶跃响应8)()(1=t u t u c c 以及时的1t 值；解:R 1Cs+1R 1/R 0G (s )= u c (t)=K(1–e t T -)KTs +1=T=R 1C=0.5 K=R 1/R 0=10=10(1–e -2t )8=10(1–e -2t)0.8=1–e-2te -2t =0.2 t=0.8g(t)=e -t/T T Kt 1=0.8=4u c (t)=K(t-T+T e -t/T )=4R(s)=1s 2R(s)=1R(s)=1s 3T 2=K(s s+1/T +T s 2-1s 3-T 2)=1.2Ts 1s 3K +1U c (s)= -0.5t+0.25-0.25e -2t )12t 2u c (t)=10(3-3已知单位反馈系统的开环传递函数为)5(4)(+=s s s G 试求该系统的单位阶跃响应。

解:C(s)=s 2+5s+4R(s)4s(s+1)(s+4)C(s)=4R(s)=s1s+41+1/3s =4/3s +1-c(t)=1+ 4e 13-4t -t 3-e3-4已知单位负反馈系统的开环传递函数为 )1(1)(+=s s s G 试求该系统的上升时间r t 。

、峰值时间p t 、超调量%σ和调整时间s t 。

1s(s+1)G(s)=t p =d ωπ 3.140.866= =3.63t s = ζ3ωn=6t s = ζ4ωn =8解:C(s)=s 2+s+1R(s)12= 1ωn 2ωn ζ=1ζ=0.5=1ωn =0.866d ω= ωn 2 ζ1-=60o -1ζ=tg β21-ζt r =d ωπβ-= 3.14-3.14/30.866=2.42σ%=100%e -ζζπ1-2=16%-1.8e3-6已知系统的单位阶跃响应为t te et c 10602.12.01)(---+= ，试求：（1）系统的闭环传递函数；（2）系统的阻尼比ζ和无阻尼自然震荡频率n ω；解:s+601+0.2s C(s)= 1.2s +10-s(s+60)(s+10)=600=s 2+70s+600C(s)R(s)600R(s)=s 12=600ωn2ωn ζ=70ζ=1.43=24.5ωn3-7设二阶控制系统的单位阶跃响应曲线如图所示，如果该系统为单位负反馈系统，试确定其开环传递函数。

《⾃动控制原理》黄坚课后习题答案解析word版本2-1试建⽴图所⽰电路的动态微分⽅程-u o+u o解：u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解：)-R 2(u i -u o )=R 1u 0-CR 1R 2(dui dt dt duo CR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉⽒变换。

(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解：(2) f(t)=t 3+e 4t解：L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解：(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解：2-3求下列函数的拉⽒反变换。

A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解：A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解：= A 2s+1s+2+ A 3+A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds s s+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解：= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++(4) F(s)=s+2s(s+1)2(s+3)解：=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分⽅程。

自动控制原理黄坚课后习题答案第一题题目：请简要说明自动控制系统的基本组成部分。

答案：自动控制系统的基本组成部分包括：1.被控对象（Plant）：被控对象是指系统中需要被控制的实际物理过程或设备，可以是机械、电气、化工或其他领域的设备。

被控对象接收输入信号并产生相应的输出响应。

2.传感器（Sensor）：传感器用于测量被控对象的某些状态或物理量，并将这些信息转换成适合控制器处理的电信号。

传感器的信号反映了被控对象的实际状态，如温度、压力、速度等。

3.控制器（Controller）：控制器接收传感器提供的信息，并通过执行算法来生成适当的控制策略。

控制器的输出作为被控对象的输入信号，用于调节被控对象的状态或物理量。

4.执行器（Actuator）：执行器接收来自控制器的控制信号，并将其转换为适合被控对象的输入形式。

执行器能够执行动作，例如打开或关闭阀门，调节电机速度等。

5.参考信号（Reference Signal）：参考信号是用于指导控制系统工作的期望值或目标值。

控制系统通过与参考信号进行比较，并调节控制策略以使输出达到期望值。

6.反馈信号（Feedback Signal）：反馈信号是被控对象产生的响应信号，可用于评估控制系统的性能。

控制系统可以根据反馈信号进行修正和调整，以实现更精确的控制。

第二题题目：请简要说明比例控制器、积分控制器和微分控制器的工作原理及特点。

答案：•比例控制器：比例控制器是通过比较被控对象的实际值与期望值之间的差异，并将该差异乘以比例增益系数来生成控制信号的。

比例控制器的输出正比于误差信号，可以快速响应系统的变化，但可能会导致稳定性问题。

•积分控制器：积分控制器是对误差信号进行积分，并将积分结果乘以积分增益系数后生成控制信号的。

积分控制器的作用是消除稳态误差，提高系统的稳定性和精度，但可能会引入超调和振荡问题。

•微分控制器：微分控制器是对误差信号进行微分，并将微分结果乘以微分增益系数后生成控制信号的。

3-1（1） )(2)(2.0t r t c= （2） )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。

已知全部初始条件为零。

解：（1） 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应：s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c（2）)()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s φ 单位脉冲响应：124.004.01)(2++=s s s C t e t g t 4sin 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s Ct e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ，用其测量容器内的水温，1min 才能显示出该温度的98%的数值。

若加热容器使水温按10ºC/min 的速度匀速上升，问温度计的稳态指示误差有多大？解法一 依题意，温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知：o o T c 98)4(=，因此有 min 14=T ，得出 min 25.0=T 。

视温度计为单位反馈系统，则开环传递函数为Ts s s s G 1)(1)()(=Φ-Φ= ⎩⎨⎧==11v T K用静态误差系数法，当t t r ⋅=10)( 时，C T Ke ss ︒===5.21010。

解法二 依题意，系统误差定义为 )()()(t c t r t e -=，应有 1111)()(1)()()(+=+-=-==ΦTs TsTs s R s C s R s E s e C T s Ts Ts ss R s s e s e s ss ︒==⋅+=Φ=→→5.210101lim )()(lim 23-3 已知二阶系统的单位阶跃响应为)1.536.1sin(5.1210)(2.1o tt et c +-=-试求系统的超调量σ％、峰值时间ｔp 和调节时间ｔs 。