实际流体恒定总流的伯努利方程讲解

浅析气体动力学原理——伯努利方程例解气体动力学作为一门研究物体运动的科学，是研究物理学的重要组成部分。

在气体动力学中有许多定律，伯努利方程是其中最基础也最重要的定律之一。

本文将对伯努利方程的原理及其在例题中的解法进行浅析。

一、伯努利方程原理伯努利方程（Bernoulli equation），又称为贝纳方程，是气体动力学的基本方程，由拉丁物理学家Daniel Bernoulli于1738年发现，他发现在一个恒定的系统中，当沿着系统上流动的流体（一般情况下是气体）改变速度和高度，其内能总量是不变的，这一定律叫做伯努利定律。

伯努利方程可以概括为：P +γV +gh = k（γ是气体的比容系数，V是气体流速，h是气体高度，P是气体压强，g是重力加速度，k是常数）式中，其中P +γV体现了气体的动能，gh表示气体的位能，两者之和即为气体的总能量，而k则表示该总能量在系统中是恒定的。

二、伯努利方程在例题中的解法1.设有一个气体在一定的容器中，容器的高度是 h1，而此时气体的压强为P1，流速为V1，则由伯努利方程可知：P1 +γV1 +gh1 = k2.气体流出容器时，留下来的气体高度为h2，压强为P2，流速为V2，由伯努利方程可知：P2 +γV2 +gh2 = k3.上面两公式代入可得：P1 +γV1 +gh1 = P2 +γV2 +gh24.两边中的P1,V1,h1分别消去可得：P2 =γ(V2 - V1) +(h2 - h1)5.此可以看出，当流体从一个容器流出到另一容器时，流体的压强受其高度的变化以及流体的流速变化的影响。

三、结论伯努利方程是气体动力学中重要的基础定律，它描述了在一定系统中流体运动时总能量保持不变的定律。

本文通过一个具体的例子，讲解了伯努利方程的原理及其在例题中的解法，从而使我们对伯努利方程有了更深的理解。

第四章 伯努利方程4.1 伯努利方程4.1.1 理想流体沿流线的伯努利方程1. 伯努利方程的推导将欧拉运动微分方程式积分可以得到流体的压力分布规律，但只能在特殊的条件下，不可能在任何的情况下都可求得其解，故我们需对流场作出如下假设：（1）理想流体（2）定常流动（3）质量力有势（4）不可压缩流体（5）沿流线积分在定常流动的条件下，理想流体的运动微分方程（欧拉运动微分方程）可以写成 ⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂=∂∂-z v v y v v x v v z p f z v v y v v x v v y p f z v v y v v x v v x p f z z z y z x z y z y y y x y x z x y x x x ρρρ111 (4.1) 将这个方程沿流线积分，如图4.1所示，可得到伯努利方程。

为此，将式(4.1)的第一式乘以x d 得x zv v x y v v x x v v x x p x f x z x y x x x d d d d 1d ∂∂+∂∂+∂∂=∂∂-ρ （1） 按照流线方程 zy x v z v y v x d d d == 将有，y v x v x y d d =，z v x v x z d d =故式（1）可写成x x x x x x x x x v v z zv v y y v v x x v v x x p x f d d d d d 1d =∂∂+∂∂+∂∂=∂∂-ρ （2） 式(4.1)的另外两式分别乘y d 、z d 后，作类似的代换，可得y y y v v y yp y f d d 1d =∂∂-ρ （3）z z z v v z zp z f d d 1d =∂∂-ρ （4） 将式（2）、（3）和式（4）相加，得 z z y y x x z y x v v v v v v z zp y y p x x p z f y f x f d d d )d d d (1d d d ++=∂∂+∂∂+∂∂-++ρ （5） p 的全微分可以表示为 dz zp dy y p dx x p dp ∂∂+∂∂+∂∂= 质量力有势，则必存在势函数U ，满足y f y f x f z zU y y U x x U U y y x d d d d d d d ++=∂∂+∂∂+∂∂=而 2/d d d d 2v v v v v v v z z y y x x =++式中等号右端的v 为平均速度。

工程流体力学综合报告学院：机械工程学院专业：机械工程班级：学号：学生姓名：任课老师：提交日期：2017年12月27 日关于伯努利方程的应用摘要“伯努利原理“是著名的瑞士科学家丹尼尔·伯努利在1726年提出的。

这是在流体力学的连续介质理论方程建立之前，水力学所采用的基本原理，其实质是流体的机械能守恒。

理想正压流体在有势彻体力作用下作定常运动时，运动方程（即欧拉方程）沿流线积分而得到的表达运动流体机械能守恒的方程。

即：动能+重力势能+压力势能=常数。

其最为著名的推论为：等高流动时，流速大，压力就小。

伯努利方程对于确定流体内部各处的压力和流速有很大意义，在水利、造船、航空等部门有着广泛的应用。

关键词：伯努利方程 公式及原理 应用 流体力学1 伯努利方程伯努利原理往往被表述为p+1/2ρv2+ρgh=C ，这个式子被称为伯努利方程。

式中p 为流体中某点的压强，v 为流体该点的流速，ρ为流体密度，g 为重力加速度，h 为该点所在高度，C 是一个常量。

它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。

需要注意的是，由于伯努利方程是由机械能守恒推导出的，所以它仅适用于粘度可以忽略、不可被压缩的理想流体1.1 流线上的伯努利方程流线上的伯努利方程：g V g p z g V g p z C gv g p z 222222221112++=++=++ρρρ适于理想流体（不存在摩擦阻力）。

式中各项分别表示单位流体的动能、位能、静压能之差。

如果流动速度为0，则由伯努利方程可得平衡流体的流体静力学基本公式（C g p z =+ρ）。

1.2 总流的伯努利方程总流是无数元流的总和，将元流伯努利方程沿总流过流断面积分，即可推导出总流的伯努利方程，也即总流能量方程。

动能修正系数α为实际动能与按平均速度计算的动能的比值，α值反映了断面速度分布的不均匀程度。

由于气体的动力黏度值较小，过流断面速度梯度小，g V g p z g V g p z 222222221111αραρ++=++实际的气流运动的速度分布比较均匀，接近于断面平均流速。

伯努利流体动力学-概述说明以及解释1.引言1.1 概述引言是一篇文章的开头部分，旨在为读者提供一个概述，引起读者的兴趣并引导他们进入后续内容的阅读。

本文将介绍伯努利流体动力学的相关概念和原理。

伯努利流体动力学是流体力学研究的重要领域之一。

流体动力学是研究流体运动规律和性质的学科，而伯努利原理是其中一个基本概念。

伯努利原理指出，在理想流体中，当流体在沿流线流动过程中速度增加时，压力会降低，而速度减小时，则压力增加。

这一原理可以通过数学公式来描述，即伯努利方程。

伯努利方程是伯努利原理的数学表达方式，它将流体动能、压力能和势能联系起来。

通过应用伯努利方程，可以分析流体在不同位置的速度、压力和高度等参数的关系，从而帮助解释和预测流体运动中的现象和现象背后的物理本质。

本文将探讨伯努利原理的基本概念、流体动力学的基本概念，以及阐述伯努利方程的应用。

通过深入了解伯努利流体动力学，可以对流体运动的原理和性质有更清晰的认识，并且可以为未来的研究提出新的方向和可能性。

在结论部分，我们将总结伯努利流体动力学的重要性，并展望未来的研究方向。

通过本文的研究，我们能够更好地理解和应用伯努利流体动力学的原理，为工程和科学领域的相关研究提供重要的理论基础。

总而言之，本文将以伯努利流体动力学为主题，介绍伯努利原理和伯努利方程的基本概念以及应用。

通过深入研究这一领域，我们可以更好地理解流体运动的本质和特性，为相关领域的研究和应用提供有益的借鉴和启示。

1.2文章结构1.2 文章结构本篇文章将围绕伯努利流体动力学展开讨论。

文章分为引言、正文和结论三个部分。

在引言部分，将首先对伯努利流体动力学进行概述，介绍其基本概念和重要性。

然后，阐述文章的结构和目的，以及对伯努利流体动力学的总结。

正文部分将详细介绍伯努利原理及其基本概念，以及流体动力学基本概念和伯努利方程。

通过对这些理论的深入讨论和分析，读者将能够全面了解伯努利流体动力学的原理和应用。

化工原理伯努利方程
伯努利方程是描述流体在运动过程中能量守恒的基本原理之一。

根据伯努利方程，流体在稳态条件下沿着流线的总能量保持不变，即由速度势、静压力和流动压力组成的总能量在流体运动过程中保持恒定。

具体而言，伯努利方程可以写作：
P + 0.5ρv^2 + ρgh = 常数
其中，P是流体的静压力，ρ是流体的密度，v是流体的速度，g是重力加速度，h是流体的高度。

伯努利方程的原理可以通过下面的推导来理解。

考虑一个流经管道的流体元素，在单位时间内，流体元素穿过任意两个横截面之间的流体量是相等的。

由于质量守恒，流体密度是恒定的，所以这一流体元素在不同横截面位置上的体积速度亦是相等的。

根据动量定理，单位时间内流体元素受到的外力和单位时间内动量的改变量之间存在关系。

在伯努利方程中，流体受到的外力可以分为静压力和流动压力两部分。

静压力即为流体在静止不动时的压力，而流动压力则是流体在运动过程中产生的额外压力。

由于单位时间内流体元素的动量改变量为0，所以伯努
利方程成立。

根据伯努利方程，我们可以得到一些重要的结论。

首先，当流体的速度增加时，流体的静压力会下降，即压力和速度之间存在负相关关系。

其次，当流体的速度增加时，流体的动能也会
增加，即速度和动能之间存在正相关关系。

最后，当流体高度增加时，流体的静压力也会增加。

总之，伯努利方程是描述流体运动过程中能量守恒的重要原理，对于分析和理解流体力学问题具有重要意义。

恒定总流能量方程（伯努利方程）
恒定总流能量方程式也称作恒定总流伯努利方程式，是流体力学领域极其适用的一个公式，其表达式以下：
式中， h1、 h2——流体截面被研究点相关于选定基准面的高度；
p 1、p2——流体截面被研究点的压强；
v 1、v2——流体截面被研究点的均匀流速；
h l1-2——流体在两截面被研究点之间的水头损失。

注意：截面上的被研究点能够为截面上的随意点。

伯努利方程的合用性剖析：
（1）方程是在恒定流速前提下推导获得。

从理论大将讲，没有绝对的恒定流；可是，关于多半流动，流速随时间变化迟缓，由此所致使的惯性力较小，方程仍旧合用。

（2）方程的推导以不行压缩流体为基础。

当在工程应用中，它仍旧合用于压缩性极小的液体流动，也合用于惯例的大部分气体流动。

只有当气体压强变化较大、流速很高时，才需要考虑气体的可压缩性。

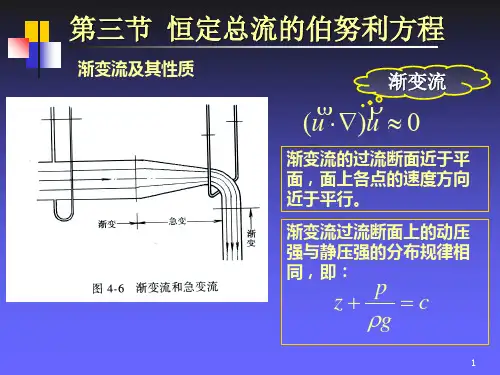
（3）方程推导所选流体截面处于渐变流段。

渐变流是指各流线靠近于平行直线的流动。

这在一般条件下是要恪守的，特别是断面流速特别大时，更应当严格恪守。

伯努利方程的扩展应用：
（1）关于两截面之间有能量输出（水轮机或汽轮机）或输入（水泵或风机）的场合。

（2）关于两截面之间有分流或合流的场合。

方程的推导是依据两截面间没有分流或合流的状况下推获得的。

可是，关于两截面间存在两分流或合流的状况，方程仍旧合用。

热工流体综合实验－气动基础部分不可压粘性流体定常总流伯努利方程实验一、实验目的和要求1．在流体在管内作定常稳定流动过程中，观察和记录垂直测压管测压管水头（z +p/γ）、速度水头（v2/(2g)）沿流程的变化情况, 验证流体恒定总流的伯努利方程关系式(机械能形式的沿总流束的能量方程)，以加深对实际运动流体伯努利方程关系式的认知和理解。

2．通过对有关现象的实验分析和讨论，进一步掌握有压管流中三种机械能分量之间的能量转换特性，对比实际水流总水头线与理想流体总水头线，深化因粘性而引起流动沿程水头损失和局部水头损失的工程实际概念。

3．掌握流体过水断面流量、平均流速、静压和总压的实验测量的基本技能。

4. 要求原始记录数据及处理数据手填，曲线手绘，回答问题手写。

二、实验装置与测量仪器图1 所示为航空工程实验中心自循环水流伯努利方程验证实验装置。

图1 自循环水流伯努利方程实验装置示意l 自循环供水器（下水箱） 2. 实验台桌 3 可控硅无级调速器 4 溢流板 5 多孔稳水板6 恒压水箱（上水箱） 7液柱式测压仪 8 可滑动测量尺 9竖直测压管 10 实验管道11各个测压点（从左往右按小字编号） 12 总压毕托管测点示意 13手轮式流量调节阀本实验装置中，测压管测到的压强有两种类型：1．表1.1中上标标有*号的测点所连接的测压管为毕托管，用以测读毕托管所正对水流点处的总水头值H ’（= Z+gu p22+γ）。

H ’值与当地过流断面上的总水头值H （=Z＋g v p 22+γ）是不同的，因为u ≠ v ，所以毕托管测得的水头线只能定性表示总水头的变化趋势。

2．表1.1中未标*号的测点所连接的测压管为壁面点测压管，用以定量测定当地过流断面上对应的测压管静水头值（z + p/γ）。

3．实验管道水流流量用阀门13来控制调节，体积流量值采用体积（量筒）－时间（秒表）方法进行测定（Q=体积/时间）, 有的也可采用重量-时间法等来测定。

伯努利方程的原理及其应用摘要：伯努利方程是瑞士物理学家伯努利提出来的，是理想流体做稳定流动时的基本方程，是流体定常流动的动力学方程，意为流体在忽略粘性损失的流动中，流线上任意两点的压力势能、动能与位势能之和保持不变。

伯努利方程对于确定流体内部各处的压力和流速有很大意义，在水利、造船、航空等部门有着广泛的应用。

关键词：伯努利方程 发展和原理 应用1.伯努利方程的发展及其原理：伯努利方程是瑞士物理学家伯努利提出来的，是理想流体做稳定流动时的基本方程，流体定常流动的动力学方程，意为流体在忽略粘性损失的流动中，流线上任意两点的压力势能、动能与位势能之和保持不变。

对于确定流体内部各处的压力和流速有很大意义，在水利、造船、航空等部门有着广泛的应用。

伯努利方程的原理，要用到无黏性流体的运动微分方程。

无黏性流体的运动微分方程：无黏性元流的伯努利方程：实际恒定总流的伯努利方程：z 1+g p ρ1+g v 2121α=z 2+gp ρ2+g v 2222α+h w总流伯努利方程的物理意义和几何意义：Z ----总流过流断面上某点（所取计算点）单位重量流体的位能，位置高度或高度水头；gpρ----总流过流断面上某点（所取计算点）单位重量流体的压能，测压管高度或压强水头；g2v 2α----总流过流断面上单位重量流体的平均动能，平均流速高度或速度水头； hw ----总流两端面间单位重量流体平均的机械能损失。

总流伯努利方程的应用条件：（1）恒定流；（2）不可压缩流体；（3）质量力只有重力；（4）所选取的两过水断面必须是渐变流断面，但两过水断面间可以是急变流。

（5）总流的流量沿程不变。

（6）两过水断面间除了水头损失以外，总流没有能量的输入或输出。

（7）式中各项均为单位重流体的平均能（比能），对流体总重的能量方程应各项乘以ρgQ。

2.伯努利方程的应用:伯努利方程在工程中的应用极其广泛，下面介绍几个典型的例子：※文丘里管：文丘里管一般用来测量流体通过管道时的流量。

液压传动实验报告姓名：陈国庆学号：0806110902班级：机械1107班0 / 6实验一伯努利方程实验一、实验目的要求1．验证流体恒定流动时的总流伯努利方程；2．进一步掌握有压管流中，流动液体能量转换特性；3．掌握流速、流量、压强等动水力学水流要素的实际量测技能。

二、实验原理实际流体在做稳定管流时的总流伯努利方程为：22p??p??211212z???z???h21?2f1?g2g?g2g选测压点⑴～⒁，从相应各测压管的水面读数测得z+p/r值，并分别计算各测点速度水头，并将各过流断面处速度水头与z+p/r相加，据此，可在管流轴线图上方绘制出测压管水头线P-P和总水头线E-E (见图2-1)。

液体流动时的机械能，以位能、压力能和动能三种形式出现，这三种形式的能量可以互相转换，在无流动能量损失的理想情况下，它们三者总和是一定的。

伯努利方程表明了流动液体的能量守恒定律。

对不可压缩流体恒定流动的理想情况，总流伯努利方程可表示为：22p??P??211212z???z???C (C为常数)21?g2g?g2g对实际液体要考虑流动时水头损失，此时方程变为：22p??p??212211z???z???h212?f1?g2g?g2gh为1、2两个过流断面间单位重量流体的水头损失。

2?f1三、实验方法和步骤：1．选择实验管B上的⑴～⒁十四个过流断面，每个过流断面对应有一根测压管。

2．开启水泵。

使恒压水箱溢流杯溢流，关闭节流阀31后，检查所有测压管水面是否平齐(以工作台面为基准)。

如不平，则应仔细检查，找出故障原因(连通管受阻、漏气、有气泡) ，并加以排除，直至所有测压管水面平齐。

1 / 6○○14的水位变化趋势，观察流量增大或减小时测压管水位如何变化。

1～3．打开节流阀31，观察测压管p?z的值)，同时测量出实验管B31的开度固定后，记测各测压管液位高度(即中的流量。

4．当节流阀?g? )。

5．测记恒压水箱实验水温(以备计算用6．改变流量再做一次。

理想流体和实际流体的伯努利方程
伯努利方程是描述流体力学中流动的基本定律之一，但在现实应用中，理想流体和实际流体的伯努利方程有所不同。

理想流体是指在流动中不存在黏性、摩擦、热传导等现象，而实际流体则存在这些现象。

在理想流体中，伯努利方程可以简化为P1+ρv12/2= P2+ρv22/2，其中P1和P2分别是两点处的压力，ρ是流体的密度，v1和v2分别是两点处的流速。

这个方程描述了流体在不同位置处的压力和流速之间的关系。

在实际流体中，伯努利方程的形式略有变化，需要考虑黏性和摩擦对流体的影响。

这些现象会导致流体在流动中损失能量，所以在实际流体中，伯努利方程需要添加一项损失项，即P1+ρv12/2+ρgh1= P2+ρv22/2+ρgh2-K，其中h1和h2分别是两点处的高度，g是重力加速度，K是损失项，描述了流体在流动中损失的能量。

因此，在实际应用中，我们需要根据具体的情况选择合适的伯努利方程，考虑到流体的黏性、摩擦等因素，来准确描述流体的流动。

- 1 -。

总流伯努利方程各项的物理意义和几何意义总流伯努利方程是流体力学中的基本方程之一，描述了沿着流体流动方向的能量守恒。

它可以用于研究流体在不同位置和状态下的压力、速度和高度之间的关系。

总流伯努利方程包含压力项、速度项和高度项，每一项都有其物理意义和几何意义。

首先，我们来详细介绍总流伯努利方程的各个项及其物理意义和几何意义：1.压力项（P/ρ）：这一项表示单位体积流体所具有的压力能。

物理上，这一项描述了由于压力差造成的流体运动，即流体沿着压力梯度从高压区向低压区运动。

几何上，这一项表示为等压线，即流体在等压面上的运动。

2.速度项（v^2/2）：这一项表示单位质量流体所具有的动能。

物理上，这一项描述了流体由于速度差而具有的能量。

它表示为流体的动能，即流体的速度越大，动能越大。

几何上，这一项表示为等速度线，即流体沿着速度矢量方向运动。

3. 高度项（gz）：这一项表示流体所具有的势能，即流体的重力势能。

物理上，这一项描述了由于流体被提升或下降而产生的能量。

几何上，这一项表示为等高线，即流体在不同位置的高度。

综上所述，总流伯努利方程的各项分别表示了流体在不同形式的能量下的运动情况。

通过这些项，我们可以了解到流体的运动方式、速度分布以及压力分布等信息。

总流伯努利方程在流体力学中具有重要的应用，可以用于研究流体的各种运动现象，如管道流动、风洞实验、飞行器气动力学等。

总流伯努利方程的几何意义在于描述了流体在不同位置的动力学变化，即流体在不同速度、压力、高度条件下的运动情况。

通过总流伯努利方程，我们可以了解到流体在不同位置的压力和速度的变化规律，从而推断出流体的流动情况。

同时，总流伯努利方程还可以用于分析流体流动中的能量损失、能量转化等问题，是流体力学中不可或缺的基本方程。

总流伯努利方程的物理意义在于描述了流体在不同状态下的能量变化情况。

通过总流伯努利方程，我们可以了解到流体所具有的压力能、动能和势能之间的关系，从而了解流体的能量转化和守恒的规律。