平行线中的拐点问题 ppt课件

格式：ppt
大小：759.00 KB
文档页数：11

下载文档原格式

平行线中的几何探究--'拐点'问题(优秀课件)

再见！
华东师大版七年级上册第五章《相交线与平行线》
知识奠基
对顶角、邻补角
相
交
线
垂线及直角
平
判定
行
线
性质
找找感觉
1．如图，AB∥EF，CD⊥EF于点D.若 ∠ABC＝40°，则∠BCD的度数为(130°)
引入探究
如图，AB∥CD，探讨下面四个图形中∠APC与 ∠PAB，∠PCD的数量关系．
探究1：自主探究
探究2：深入探究
如图，AB∥CD，在下面图形中，选择一个探讨∠APC与∠PAB，∠PCD的数量关系.
小组汇报
如图，AB∥CD，你选择哪一个图形探讨∠APC与∠PAB， ∠PCD的数量关系.
方法小结
图形中探讨角的数量关系，方法或思想上有什么共同点？
寻找（构造）角所在的基本图形，通过基本图形中的数量关系，实现角的等量转化。
【升华感觉】
1、如图1，已知a∥b，∠1=130°，∠2=90°，则 ∠3=_______.
（图1）
（图2）
2、如图2，将两张长方形纸片如图摆放，使其中一张纸片的一个顶点恰好落在另一张纸片的一条边上，则 ∠1＋∠2＝________.
【升华感觉】
3、如图3，已知AB∥ED，∠B=58°，∠C=35°，则∠D 的度数为．
(2)如图②，AB∥CD，试问∠2＋∠4＋∠6与∠1＋∠3＋∠5＋ ∠7还有类似的数量关系吗？若有，请直接写出，并将它们推广到一般情况，用一句话写出你的结论．
【课后延伸】
2.如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，P为直线l3上一点，A、B分别是直线l1、l2上的不动点．其中PA与l1相交为∠1，PA、 PB相交为∠2，PB与l2相交为∠3．（1）若P点在线段CD（C、D两点除外）上运动，问∠1、∠2、∠3之间的关系是什么？这种关系是否变化？（2）若P点在线段CD之外时，∠1、∠2、∠3之间的关系有怎样？说明理由．

七年级数学下册第五章方法专题1两平行线间的拐点问题ppt课件新版新人教版

七年级数学下册人教版
第五章相交线与平行线
方法专题1 两平行线间的“拐点”问题
类型一含一个“拐点”的平行线问题 1.(2019·鄂州)如图，一块直角三角尺的一个顶点落在直尺的一边上，若∠2
＝35°，则∠1的度数为( B ) A.45° B.55° C.65° D.75°
2.如图，直线AB∥EF，C是直线AB上一点，D是直线AB外一点.若∠BCD＝ 95°，∠CDE＝25°，则∠DEF的度数是( C ) A.110° B.115° C.120° D.125°
3.如图，直线m∥n，∠1＝70°，∠2＝30°，则∠A等于___4_0_°___.
4.如图，AB∥EF，CD⊥EF于点D，若∠ABC＝40°，则∠BCD＝__1_3_0_°___.

5.如图，正方形ABCD的顶点A，C分别在直线a，b上，且a∥b，∠1＝60°，则∠2＝___6_0_°___.
6.如图，AB∥CD，E为AB，CD之间的一点.
(1)若∠B＝130°，∠C＝30°，则∠BEC的度数为__8_0_°____；
(2)探究∠B，∠C，∠BEC三者之间有怎样的数量关系，试说明理由. 解：(2)∠B＋∠BEC－∠C＝180°.理由如下：过点E向左侧作EF∥AB，又∵AB∥CD，∴EF∥CD，∴∠FEC＝∠C. ∵∠BEF＝∠BEC－∠FEC，∴∠BEF＝∠BEC－∠C. ∵AB∥EF，∴∠B＋∠BEF＝180°， ∴∠B＋∠BEC－∠C＝180°.
(2)如图2，当点P在直线AB的上面、直线AC的右边时，试确定α，β，γ之间的数量关系；
(2)过点P向左侧作PE∥AB. ∵AB∥CD，∴PE∥AB∥CD， ∴∠PAB＝∠APE，∠PCD＝∠CPE， ∴∠APC＝∠CPE－∠APE＝∠PCD－∠PAB，∴γ＝β－α.

初中数学_平行线中的“拐点”问题教学课件设计

A
B
A
A ④ E B E③
B
E
E
②E
E①
C 图1 D
C 图2
D
C
⑥
E
D
E⑤
E
A
BE
A
B
A
B
A
B
C 图3 D
C 图4 D
C 图5 D E
C
D
图6 E
变式探究—多拐点
变式1：如图AB∥EF，你知道∠B、∠C 、∠D、 ∠E 之间的数量关系吗？
A
B
C
∠B+∠C +∠D+∠E=540°
D
F
E
变式探究—多拐点
A
B
A
B
C
D
E F
C
DALeabharlann BFEC
D
变式探究
若AB∥CD，则∠B，∠BED，∠D之间有何数量关系？并说明理由
A E
C ∠B+ ∠D= ∠E
B
F
E D
思考：显然，根据图1和图2的结论，点E的位置不同，
∠BED 、∠B与∠D 之间的关系也不同。改变点E的
位置，你还能得到∠BED 、∠B与∠D 的哪些关系？E
变式2：如图，AB∥GF，试判断∠B、∠C 、∠D、 ∠E 、∠F之间的数量关系。
A
B
C
D
E
G
F
∠B+∠C +∠D+∠E +∠F=720°
归纳1. A E
B
A
C1
DF
BA
C1 C2
E
G
B C1 C2 C3 F
两条平行线之间的拐点个数n=1时，形成的三个

初中数学课件平行线间的拐点问题

度，并说明理由．
-21如图，已知//，若按图中规律继续下去，则∠1 + ∠2 + ⋯ + ∠ =
(
)
A.n⋅180 °
B.2n⋅180 °
C.(n−1)⋅180 °
D.(n−1)2⋅180 °
应用练习
如图，直线//，则∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 =______.
√
平行线间的拐点问题
—子弹图
如图，已知//，∠1 = 120 ° ，∠2 = 90 ° ，则∠3的度数是（）
确认预判Ⅱ
如图所示，//、是、之间的一条折线，则∠1 +
∠2 + ∠3 + ∠4 = ________．
思维导图
课程目标
1、根据关键特征识别子弹图模型，能独立推导并掌握模型结论；
2、掌握作辅助线方法及规范的几何语言；
3、能灵活运用子弹图模型解决延伸问题。
课程导入
A
B
E
E
C
1、子弹图（铅笔型）
D
2、猪手图（燕尾型）
E
A
B
A
B
C
C
D
D
E
3、靴子图（燕尾型）
课程导入
A
F
E
B
E
F
C
D
E
A
B
A
B
C
C
D
D
E
核心方法：过拐点作已知直线的平行线
简单说成：逢拐点作平行线，一般而言，有几个拐点，就做几条平行线
出∠ + ∠ + ∠的大小吗？
解：过点画//
∵//(________)

平行线与拐点问题公开课获奖课件百校联赛一等奖课件

变式训练：1.如下图所示，直线AB∥CD， ∠B=23°，∠D=42°，则∠E= 65°。
教材母题（教材P23第7(2)题）
假如AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF=( )
(A)180°(B)270°(C)360°(D)540°
A
B
C
D
E
F
措施指导
（1）铅笔型
如图1，已知：AB∥CD，点E是平面内一点，那么∠BED与∠B、∠D之间旳数量关系是什么呢？
B
G
F
E
H
C
D
解：过点E作EG∥AB，过点F作FH∥AB， ∵AB∥CD ∴AB||CD||EG||FH ∴∠A=∠1，∠2=∠3，∠4=∠D ∴∠A+∠3+∠4=∠1+∠2+∠D ∴∠A+∠EFD=∠AEF+∠D
若左边有n个角，右边有m个角；你能找到规律吗？
A
F1 F2 Fn
B E1
E2
Em
C
D
①点在两平行线之间
A
B
E
C
D
图1
②点在两平行线之外
E
A
B
A
B
C 图3
D
C
D
图4 E
A
C
图2
B E
D
E
A
A
B
B
C
D
图5
C
D
图6
E
措施指导
（2）燕尾型（或M型）如图2，已知：AB∥CD，点E是平面内
一点，那么∠BED与∠B、∠D之间旳数量关系是什么呢？
A
B
E
C
图1

小专题12巧解平行线中的拐点问题ppt课件

1．(随州中考)如图，在平行线 l1，l2 之间放置一块直角三角板，三角板的锐角顶点 A，B 分别在直线 l1，l2 上，若 ∠1＝65°，则∠2 的度数是( A )
A．25° B．35° C．45° D．65°
采用PP管及配件：根据给水设计图配置好PP 管及配件，用管件在管材垂直角切断管材，边剪边旋转，以保证切口面的圆度，保持熔接部位干净无污物
变式 2 当点 C 运动到平行线的外边已知 AB∥ED，点 C 为 AB，ED 之外任意一点． (1)如图 1，∠B，∠BCD，∠D 之间的关系是∠B＝
∠BCD＋∠D ； (2)如图 2，∠B，∠EDC，∠C 之间的关系是∠EDC
＝∠B＋∠C ；
采用PP管及配件：根据给水设计图配置好PP 管及配件，用管件在管材垂直角切断管材，边剪边旋转，以保证切口面的圆度，保持熔接部位干净无污物
解：(2)∠EFD＝∠BEF＋30°. 理由：分别过点 E，F 作 EM∥AB，FN∥AB. ∴EM∥AB∥FN. ∴∠B＝∠BEM＝30°，∠MEF＝∠EFN.
采用PP管及配件：根据给水设计图配置好PP 管及配件，用管件在管材垂直角切断管材，边剪边旋转，以保证切口面的圆度，保持熔接部位干净无污物
3．(莱芜中考)如图，AB∥CD，∠BED＝61°，∠ABE 的平分线与∠CDE 的平分线交于点 F，则∠DFB＝( B )
A．149° C．150°
பைடு நூலகம்
B．149.5° D．150.5°
采用PP管及配件：根据给水设计图配置好PP 管及配件，用管件在管材垂直角切断管材，边剪边旋转，以保证切口面的圆度，保持熔接部位干净无污物

平行线拐点问题PPT课件

精选ppt
3
学习验收
.如图，CD∥AB，∠DCB=70°，
∠CBF=20°，∠EFB=130°，问直线EF 与AB有怎样的位置关系，为什么？
精选ppt
4
感谢亲观看此幻灯片，此课件部分内容来源于网络，如有侵权请及时联系我们删除，谢谢配合！
平行线
—拐点问题
精选ppt
1
学习目标
1、正确解决常见的拐点问题。 2、灵活运用平行线的性质与判定解决相关问题。 3、培养自己一题多解，拓展提升的思维能力。
精选ppt
2
如图（1）所示，AB∥CD，根据平行线的性质可知内错角∠B与∠C相等，观察图（2），（3）与（4），回答下列问题．
①如图（2）所示，AB∥CD，试问∠E+∠C与∠B+∠F哪个大？请说明理由； ②如图（3）所示，AB∥CD，试问∠E+∠∠C与∠B+∠H+∠F哪个大？（直接写出答案，不必说明理由） ③根据第①，②小题的结论，在图（4）中，若AB∥CD，你又能得到什么结论？

平行线与拐点问题(经典)

A
B
C
图6
D
E
∠BED=∠D－∠B
C
D
图7
E
∠BED=∠B－∠D
4.已知：如图，AB//CD，试解决下列问题：（1）∠1＋∠2＝___ _1_8_0；° （2）∠1＋∠2＋∠3＝___ __；360° （3）∠1＋∠2＋∠3＋∠4＝_ __ __；540° （4）试探究∠1＋∠2＋∠3＋∠4＋…＋∠n
A
B
G
F
E
H
C
D
解：过点E作EG∥AB，过点F作FH∥AB， ∵AB∥CD ∴AB||CD||EG||FH ∴∠A=∠1，∠2=∠3，∠4=∠D ∴∠A+∠3+∠4=∠1+∠2+∠D ∴∠A+∠EFD=∠AEF+∠D
若左边有n个角，右边有m个角；你能找到规律吗？
A
F1 F2 Fn
B E1
E2
Em
∴ BE∥CF
（内错角相等，两直线平行）
平行线与“拐点”问题
〖情景导入〗
已知如图，AB∥CD，若线段AC是拉直的橡皮筋，上任取一点E，向不同的方向拉动点E，那么
∠A、∠C、∠AEC之间有何关系呢？
A
B
在AC
E
C
D
右上
左上
一个动点与两条平行线的位置关系
①点在两平行线之间
②点在两平行线之外
一个动点与两条平行线的位置关系
A
B
D
E
C
5.如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，P为直线l3上一点，A、B分别是直线l1、 l2上的不动点．其中PA与l1相交为∠1，PA、PB相交为∠2，PB与l2相交为∠3．

初中数学人教七年级下册第五章相交线与平行线平行线中的拐点问题PPT

问题导入
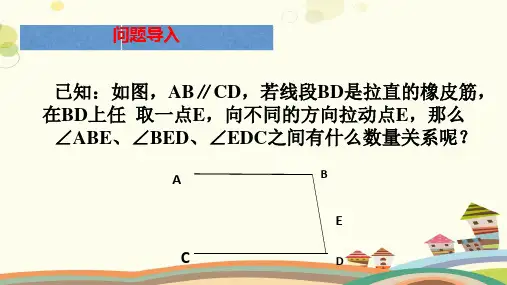
已知：如图，AB∥CD，若线段BD是拉直的橡皮筋，在BD上任取一点E，向不同的方向拉动点E，那么
∠ABE、∠BED、∠EDC之间有什么数量关系呢？
A
B
E
C
D
一个动点与两条平行线的位置关系
①点在两平行线之间
A
B
A
B
E
C
图2
D
②点在两平行线之外
E
A
B
A
B
C 图3
D
C
D
图4 E
E
C
D
图1
E
A
B
C
D
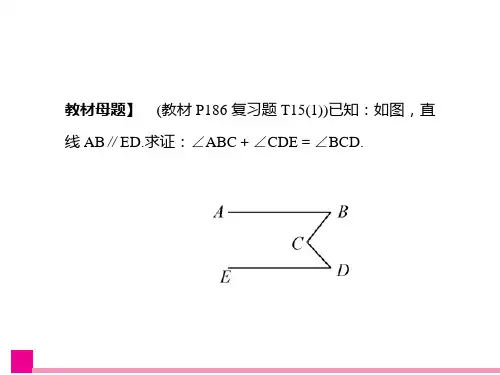
解：过点E 作EF∥AB
∵AB∥CD（已知）
∴AB∥CD∥EF
∴∠B=∠BEF, ∠D=∠DEF
∴∠B=∠BEF =∠BED+∠DEF
∴∠B= ∠BED +∠D
F
∠B=∠BED+∠D
新知探究三：‘靴子’型
F
A
E
B
∠B=∠BED+∠D
C
D
解：过点E 作EF∥AB
∵AB∥CD（已知）
∴AB∥CD∥EF
放置(∠ABC＝30°)，其中A，B两点分别落在直线m，n上。若∠1
＝20°，则∠2的度数为( )
D
A．20° B．30° C．45° D．50°
新知探究三“靴子“型
若将点E向线段AB的左上方拉动（如图）. 已知AB∥CD，问∠B、∠D、∠BED的关系.
E
A
B
C
D
图5
新知探究三：‘靴子’型
E
A
∴∠ABE+∠BEF=180°∴∠D+∠FED=180°

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A 1
BA 1
BA 1
B
A 1
B
E2
E2
E2
2 C
3
D
C
F 34
D
C
Nn
D
C
D
平行线中的拐点问题
13
拓展提升 “牙齿”模型
（1）如图1，已知AB∥CD，求证：∠BED＝ ∠1+∠2．（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、 ∠BEG之间数量关系，并加以证明．（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．
即∠B＋∠E＝∠BCE．
D
B
1
F
2
E
平行线中的拐点问题
5
知识点二：‘凹’进去的模型
学以致用
1、如图，AB∥CD，∠A=65°－ α ，∠P=80°+α，
∠C=60°－α，则α= 15°。
A
B
P
C
D
平行线中的拐点问题
6
知识点二：‘凹’进去的模型
学以致用
2、如图，有一块含有45°角的三角尺放在直尺上，如果
∠2=20°，那么∠1= 25°。
1
0 1 2 3 4 5 6 7 8 9 1 0 1 1
孝感市文昌中学学生专用尺 2
C m
平行线中的拐点问题
7
知识点三：“猪手图”模型
新知究
P1 A
C
F
B D
A
C
1
P
解：过点P作PF∥AB，则PF∥CD（
）
∴∠CPF＋∠C=180°∠1＋∠A=180°（
新知究
A
B
P
例2、已知AB∥DE，试问∠B、∠E、
C
∠BCE有什么关系。
A
解：过点C作CF∥AB，
C
则_∠_B_=_∠__1_ （两直线平行，内错角相等）
又∵AB∥DE，AB∥CF，
D
∴_C_F_∥__D_E____（平行于同一直线的两条直线互相平行）
∴∠E＝∠__2__（两直线平行，内错角相等） ∴∠B＋∠E＝∠1＋∠2
∠1+∠3 与∠ABE+∠CDE的关系吗？
平行线中的拐点问题
11
知识点三：“猪手图”模型
学以致用
变式：将上题中的∠ABE的平分线改为它
140º
的补∠ABG的角平分线，其它条件不变，
则∠F= 20°。
平行线中的拐点问题
12
知识点三：“猪手图”模型
拓展提升
已知：如图，AB//CD，试解决下列问题：（1）∠1＋∠2＝_1_8_0°；（2）∠1＋∠2＋∠3＝_36_0_° ；（3）∠1＋∠2＋∠3＋∠4＝_ 54_0°_ ；（4）试探究∠1＋∠2＋∠3＋∠4＋…＋∠n= 180°（n-1) ；
5.3 平行线的性质
5.3.1：平行线的性质 ----“拐点”问题
a 1 3
b2
平行线中的拐点问题
1
知识点一：‘凸’出来的模型
A
B
P
例1 已知：如图，AB//CD，∠A=100°
C
D
∠C=110°求∠AEC的度数
A
B
解：过点E作EF//AB
1
∵AB//CD，EF//AB（已知）
E2
F
∴ CD // EF 。(平行于同一直线的两直线平行）
）
∴∠CPF=180°－∠C ,∠1=180°－∠A
∴∠APC＝∠CPF－∠1
=(180°－∠C)－(180°－∠A)=∠A－∠C
平行线中的拐点问题
B D
F
8
知识点三：“猪手图”模型
新知究
A
B
C
D
Hale Waihona Puke P∠APC＝∠A－∠C
P
A
B
C
D
∠APC＝∠C－∠A
平行线中的拐点问题
9
知识点三：“猪手图”模型
归纳总结
M
1
a
P
2 3
b
N
平行线中的拐点问题
3
知识点一：‘凸’出来的模型
学以致用
2、如图，AB//CD,FG⊥CD于N，若∠EMB=α,则
∠EFG=( B )。 A
A.180°－α B.90°＋α
C.180°＋α D.270°－α C
∟
E Mα F
N
G
平行线中的拐点问题
B D
4
知识点二：‘凹’进去的模型
C
D
∴∠A+∠1 =180o，∠C+∠ 2=180o(两直线平行，同旁内角互补）
又∵∠A=100°，∠C=110°（已知）
∴ ∠ 1 = 80 °, ∠2 = 70 ° （等量代换）
∴∠AEC=∠1+∠2= 80 ° + 70 °=150 °
平行线中的拐点问题
2
知识点一：‘凸’出来的模型
学以致用
1、如图，a//b,M、N分别在a、b上，P为两平行线间一点，如果∠3= 135° ，∠2=60°那么∠1= 165º。
某学习小组发现一个结论：已知直线a∥b，若直线c∥a，则c∥b．他们发现这个结论运用很广，请你利用这个结论解决以下问题：已知直线AB∥CD，点E在AB、CD之间，点P、Q分别在直线AB、CD上，连接PE、EQ．（1）如图1，运用上述结论，探究∠PEQ与∠APE+∠CQE之间的数量关系，并说明理由；（2）如图2，PF平分∠BPE，QF平分∠EQD，当∠PEQ＝140°时，求出∠PFQ的度数；
当“拐点”在平行线的外部时，“拐角” 等于两个边角之差.
(即：折角=大边角-小边角)
平行线中的拐点问题
10
知识点三：“猪手图”模型
学以致用
例3：已知AB∥CD，∠ABE和∠CDE的平分线相交于F，∠E = 140º，则∠F= 11。0°
（1）由基本图形二，你能得到∠F与∠1+∠3的关系吗？（2）由基本图形一，你能得到∠ABE+∠CDE的值吗？（3）由BF和DF分别平分∠ABE和∠CDE，你能得到
平行线中的拐点问题
14
思维导图
平行线性质与判定
“拐点” 问题
‘凸’出来的模型 ‘凹’进去的模型 “猪手图”模型
平行线中的拐点问题
15
综合应用
如图所示，已知CD∥EF，∠C+∠F＝∠ABC，求证：AB∥GF．
平行线中的拐点问题
16
综合应用
（3）如图3，若点E在CD的下方，PF平分∠BPE，QH平分∠EQD，QH的反向延长线交PF于点F．当∠PEQ＝70°时，请求出∠PFQ的度数．
3）如图3，若点E在CD的下方，PF平分∠BPE，QH平分∠EQD，QH的反向延长线交PF于点F．当∠PEQ＝70°时，请求出∠PFQ的度数．
平行线中的拐点问题