平行线中的拐点(拐角)问题专题

平行线拐点问题
一、平行线拐点基本模型
模型一“铅笔”模型
点P在EF右侧，在AB、CD内部“铅笔”模型
模型二“猪蹄”模型（M模型）
点P在EF左侧，在AB、CD内部“猪蹄”模型
模型三“臭脚”模型
点P在EF右侧，在AB、CD外部“臭脚”模型
模型四“骨折”模型
点P在EF左侧，在AB、CD外部“骨折”模型
二、平行线拐点模型的证明
三、平行线拐点模型的进阶
1、处理方法
⎩⎨⎧拐点作平行
构造三角形关键作有效截线“铅笔”模型“铅笔”模型
3、模型二“猪蹄”模型（M 模型）
“猪蹄”模型
注意：铅笔模型与M 模型在一定程度可以相互转换。

4、核心
平行线拐点模型的核心在于平行线间的点，这些点有一个，两个和多个，这些点决定模型的类型和处理手段。

例1、平行线拐点模型的简单应用
例2、平行线拐点模型的探究问题
∠，F A平分HAD ECD
∠，若
例3、平行线拐点模型的具体应用
的度数为.
课后作业。

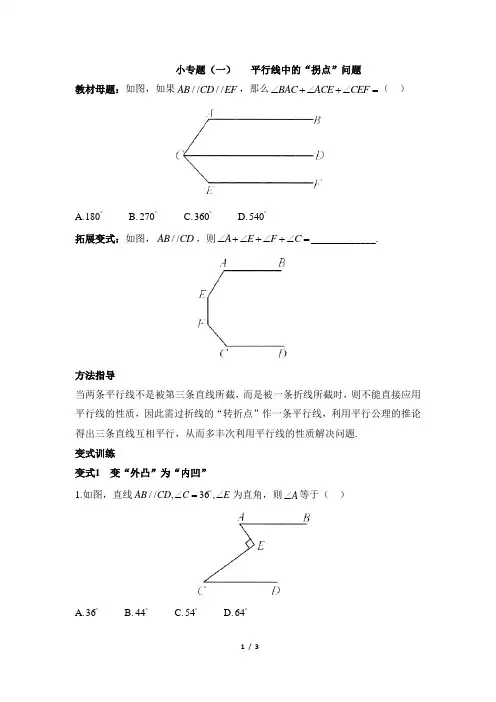
小专题（一） 平行线中的“拐点”问题教材母题：如图，如果////AB CD EF ，那么BAC ACE CEF ∠+∠+∠=（ ）A.180︒B.270︒C.360︒D.540︒拓展变式：如图，//AB CD ，则A E F C ∠+∠+∠+∠=_____________.方法指导当两条平行线不是被第三条直线所截，而是被一条折线所截时，则不能直接应用平行线的性质，因此需过折线的“转折点”作一条平行线，利用平行公理的推论得出三条直线互相平行，从而多丰次利用平行线的性质解决问题.变式训练变式1 变“外凸”为“内凹”1.如图，直线//,36,AB CD C E ︒∠=∠为直角，则A ∠等于（ ）A.36︒B.44︒C.54︒D.64︒2.如图，已知//AB CD ，试判断,B BED ∠∠和D ∠之间的关系，并说明理由.变式2 变“平行线间”为“平行线的外部”3.已知//AB CD ，点E 为,AB CD 之外任意一点.（1）如图1，探究BED ∠与,B D ∠∠的数量关系，并说明理由（2）如图2，探究CDE ∠与,B BED ∠∠的数量关系，并说明理由.变式3 变“一次”为“多次” 4.（1）如图1，//AB CD ，则E G ∠+∠与B F D ∠+∠+∠有何关系？（2）如图2，若//AB CD ，又能得到什么结论？请直接写出结论.参考答案教材母题 C拓展变式 540变式训练1.C2.解：BED B D ∠=∠+∠.理由如下：过点E 作//EF AB ，则.//B BEF AB CD ∠=∠，//..EF CD DEF D BED ∴∴∠=∠∠=BEF DEF ∠+∠，BED B D ∴∠=∠+∠.3.解：（1）B BED D ∠=∠+∠.理由如下：过点E 作//EF AB .又//AB CD ， ////.,.EF AB CD BEF B D DEF BEF ∴∴∠=∠∠=∠∠BED DEF =∠+∠， B BED D ∴∠=∠+∠.（2）CDE B ∠=∠+BED ∠.理由如下：过点E 作//EF AB .又//AB CD ，////.180,180EF AB CD B BEF CDE DEF ︒︒∴∴∠+∠=∠+∠=. 又,DEF BEF BED CDE BEF BED B BEF ∠=∠-∠∴∠+∠-∠=∠+∠， 即CDE B BED ∠=∠+∠.4.解：（1）过点E 作//EM AB ，过点F 作//FN AB ，过点G 作//GH CD .//,////////.1,2AB CD AB EM FN GH CD B ∴∴∠=∠∠=3,45,6D ∠∠=∠∠=∠.125634B D ∴∠+∠+∠+∠=∠+∠+∠+∠，即BEF FGD B EFG D ∠+∠=∠+∠+∠.（2）12112n n B F F F D E E E -∠+∠+∠++∠+∠=∠+∠++∠.。

第思维导图核心考点聚焦与生活有关的平行线拐点问题【变式训练】2．如图，AB∥EF，则3．【变式】已知：AB EF∥、、满足的数量关系．∠∠∠B F C6．（1）如图①，如果AB ∥（2）如图②，AB CD ∥，根据上面的推理方法，直接写出___________．考点三、平行线中含多个拐点问题例题：7．如图，直线AB CD ∥，则23415∠+∠+∠-∠-∠的度数为(1)如图1， 1l ∥2l ， 若65P ∠= ， 计算并直接写出A B ∠∠+的大小．A．28︒B．54︒【变式训练】11．“绿水青山，就是金山银山”在两个景区之间建立上的一段观光索道如图所示，索道A ．110︒B ．11512．七年级四班在项目学习中研究生活中的平行关系，小明发现家中的护眼灯，如图是一款长臂折叠LED 护眼灯示意图，MN 平行时，120,DEF ∠=︒∠过关检测一、选择题13．如图，AB DE ∥，BC CD ⊥，系正确的是（ ）A ．90αβ-=C ．180αβ+= 14．如图，平行于主光轴MN 的光线的反向延长线交于主光轴MN16．如图，AB CD ∥，B ∠为 ．三、解答题17．已知一个角的两边与另一个角的两边分别平行，请结合图形回答下列问题：(1)如图①，AB CD ，BE DF ∥，直接写出1∠与2∠的关系__________________(2)如图②，AB CD ，BE DF ∥，猜想1∠与2∠的关系，并说明理由；(3)由（1）（2），我们可以得出结论：一个角的两边与另一个角的分别平行，那么这两个角__________________；(4)应用：两个角的两边分别平行，且一个角比另一个角的3倍少60︒，求出这两个角的度数分别是多少度？①当点P在A，B两点之间运动时，②当点P在A，B两点外侧运动时(点α∠，∠β之间的数量关系，并说明理由．．19．已知AB CD(1)如图1，AB CD ∥，点E 为AB 、CD 之间的一点．求证：12360MEN ∠+∠+∠=︒．(2)如图2，AB CD ∥，点E 、F 、G 、H 为AB 、CD 之间的四点．则123456∠+∠+∠+∠+∠+∠=______．(3)如图3，AB CD ∥，则123n ∠+∠+∠++∠= ______．1．66︒##66度【分析】如图所示，过点E 作EF AB ∥，则AB CD EF ∥∥，根据两直线平行内错角相等分别求出4026AEF CEF =︒=︒∠，∠，则66AEC AEF CEF =+=︒∠∠∠．【详解】解：如图所示，过点E 作EF AB ∥，∵EF AB AB CD ∥，∥，∴AB CD EF ∥∥，∴4026AEF A CEF C ==︒==︒∠∠，∠∠，∴66AEC AEF CEF =+=︒∠∠∠，故答案为：66︒．【点睛】本题主要考查了平行线的性质，正确作出辅助线求出4026AEF CEF =︒=︒∠，∠是解题的关键．2．360A C E ∠+∠+∠=︒【分析】根据两直线平行，同旁内角互补可直接得到答案．【详解】如下图所示，过点C 作//CD AB ，∵//CD AB ，∴180A ACD ∠+∠=︒（两直线平行，同旁内角互补），∵//AB EF ，//CD AB ，∴//CD EF ，∴180E DCE ∠+∠=︒（两直线平行，同旁内角互补），∴360A ACD E DCE ∠+∠+∠+∠=︒，∴360A ACE E ∠+∠+∠=︒，∴在原图中360A C E ∠+∠+∠=︒，故答案为：360A C E ∠+∠+∠=︒．【点睛】本题考查平行直线的性质，解题的关键是熟练掌握两直线平行，同旁内角互补．3．(1)见解析(2)见解析【分析】（1）利用平行线的性质即可求解．（2）过点C 作CG AB ∥，即可得出BCG B ∠=∠，由平行线公理的推论可得出∥CG EF ，故GCF F ∠=∠，即可得出BCG GCF B F ∠+∠=∠+∠，即可得出C ∠与B F ∠∠、之间的数量关系是：B F BCF ∠+∠=∠．【详解】（1）解：图（1）C ∠与B F ∠∠、之间的数量关系是：B F C ∠+∠=∠．理由：过点C 作CG AB ∥，∴BCG B ∠=∠，∵AB EF ∥，∴∥CG EF ，∴GCF F ∠=∠，∴BCG GCF B F ∠+∠=∠+∠，∴B F BCF ∠+∠=∠；图（2）C ∠与B F ∠∠、之间的数量关系是：F B C ∠-∠=∠．理由：过点C 作CG AB ∥，∴BCG B ∠=∠，∵AB EF ∥，∴∥CG EF ，∴GCF F ∠=∠，∴GCF BCG F B ∠-∠=∠-∠，∴F B BCF ∠-∠=∠；图（3）C ∠与B F ∠∠、之间的数量关系是：B F C ∠-∠=∠．理由：过点C 作CG AB ∥，∴BCG B ∠=∠，∵AB EF ∥，∴∥CG EF ，∴GCF F ∠=∠，∴BCG GCF B F ∠-∠=∠-∠，∴B F BCF ∠-∠=∠；图(4)C ∠与B F ∠∠、之间的数量关系是：360B F C ∠+∠+∠=︒．理由：过点C 作CG AB ∥，∴180BCG B ∠+∠=︒，∵AB EF ∥，∴∥CG EF ，∴180GCF F ∠+∠=︒，∴180180BCG B GCF F ∠+∠+∠+∠=︒+︒，∴360B F BCF ∠+∠+∠=︒；图（5）C ∠与B F ∠∠、之间的数量关系是：B F C ∠-∠=∠．理由：过点C 作CG AB ∥，∴BCG B ∠=∠，∵AB EF ∥，∴∥CG EF ，∴GCF F ∠=∠，∴BCG GCF B F ∠-∠=∠-∠，∴B F BCF ∠-∠=∠；图（6）C ∠与B F ∠∠、之间的数量关系是：F B C ∠-∠=∠．理由：过点C 作CG AB ∥，∴BCG B ∠=∠，∵AB EF ∥，∴∥CG EF ，∴GCF F ∠=∠，∴GCF BCG F B ∠-∠=∠-∠，∴F B BCF ∠-∠=∠；故B C F ∠∠∠、、之间的数量关系如下表：∠=∠，∴BCG B∵AB EF∥，CG EF，∴∥∠=∠，∴GCF F【详解】解：连接BD，如图，∵AB∥CD，∴∠ABD+∠CDB=180°，∵∠2+∠3+∠EBD+∠FBD=360°，∴∠2+∠3+∠EBD+∠FDB+∠ABD+∠CDB=540°，即∠1+∠2+∠3+∠4=540°．故答案为：540°．【点睛】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．5．30°##30度【分析】过A点作AB∥直线l1，过C点作CD∥直线l2，由平行线的性质可得∠5=∠1=40°，∠4=∠8，∠6=∠7，结合∠2比∠3大10°可得∠5+∠6-∠7-∠8=10°，进而可求解．【详解】解：过A点作AB∥直线l1，过C点作CD∥直线l2，∴∠5=∠1=40°，∠4=∠8，∵直线l1∥l2，∴AB∥CD，∴∠6=∠7，∵∠2比∠3大10°，∴∠2-∠3=10°，∵∠5+∠6=∠2，∠7+∠8=∠3，∴∠5+∠6-∠7-∠8=10°，∴40°-∠4=10°，解得∠4=30°．故答案为：30°．【点睛】本题主要考查平行线的性质，角的计算，作适当的辅助线是解题的关键．6．（1）见解析；（2）540︒；（3）x z y+-【分析】（1）过P 作PM AB ∥，利用平行线的判定与性质证明即可；（2）过点P 作PE AB ∥，过点Q 作QF AB ∥，根据平行线的性质即可求解；（3）过点P 作PN AB ∥，过点Q 作QM AB ∥，根据平行线的性质求解即可．【详解】（1）证明：过P 作PM AB ∥，如图，∴A APM ∠=∠，∵PM AB AB CD ∥，∥（已知），∴PM CD ∥，∴C CPM ∠=∠，∵APC APM CPM ∠=∠+∠，∴APC A C ∠=∠+∠；（2）如图，过点P 作PE AB ∥，过点Q 作QF AB ∥，∵AB DC ∥，PE AB ∥，QF AB ∥，∴AB PE QF CD ∥∥∥，∴180A APE ∠+∠=︒，180EPQ PQF ∠+∠=︒，=180FQC QCD ∠+∠︒，∴=540A APQ PQC C ∠+∠+∠+∠︒，故答案为：540︒；（3）过点P 作PE AB ∥，过点Q 作QF AB ∥，∵AB DC ∥，PE AB ∥，QF AB ∥，∴AB PE QF CD ∥∥∥，∴B BPE ∠=∠，QPE PQF ∠=∠，=FQC C ∠∠，∴=B PQC C BPQ ∠+∠∠+∠，即=x z m y ++，∴=m x z y +-，故答案为：x z y +-．【点睛】本题考查平行线的判定与性质，灵活运用平行线的性质和判定是解题的关键．7．360【分析】过E 作EF ∥CD ，过G 作GH ∥CD ，过M 作MN ∥CD ，根据平行线的判定得出EF ∥GH ∥MN ∥AB ∥CD ，根据平行线的性质得出即可．【详解】过E 作EF ∥CD ，过G 作GH ∥CD ，过M 作MN ∥CD ，如图所示：∵CD ∥AB ，∴EF ∥GH ∥MN ∥AB ∥CD ，∴∠1=∠BEF ，∠GEF +∠EGH =180°，∠HGM +∠GMN =180°，∠NMC =∠5，∵∠2=∠BEF +∠GEF ，∠3=∠EGH +∠HGM ，∠4=∠GMN +∠NMC ，∴23415∠+∠+∠-∠-∠BEF GEF EGH HGM GMN NMC BEF NMC=∠+∠+∠+∠+∠+∠-∠-∠360GEF EGH HGM GMN =∠+∠+∠+∠=︒．故答案为：360．【点睛】本题考查了平行线的性质，能灵活运用平行线的性质进行推理是解此题的关键．8．(1)65°(2)见解析(3)∠1+∠3+∠5=∠2+∠4【分析】（l）过P作PE∥l1，根据平行线的性质和角的和差即可得到结论；（2）过点P、Q分别作l1和l2的平行线分别记为l3和l4，根据平行线的性质和等量代换即可得到结论；（3）分别过P，Q，M作PC∥l1，QD∥l1，ME∥l1，根据平行线的性质和角的和差即可得到结论．【详解】（1）解：过P作PE∥l1∵l1∥l2∴PE∥l2∥l1∴∠A=∠1，∠B=∠2∴∠APB=∠1+∠2=∠A+∠B=65°即∠A+∠B=65°；（2）证明：过点P、Q分别作l1和l2的平行线分别记为l3和l4∵l1∥l2∴l1∥l2∥l3∥l4∵l1∥l3（已知）∴∠A=∠1（两直线平行，内错角相等）∵l3∥l4（已知）∴∠2＝∠3（两直线平行，内错角相等）∵l2∥l4（已知）∴∠4+∠B=180°（两直线平行，同旁内角互补）∴∠A+∠3+∠4+∠B=∠1+∠2+180°又∵∠1+∠2=∠P ，∠3+∠4=∠Q ∴∠A +∠B +∠Q =∠P +180°．（3）解：如图，分别过P ，Q ，M 作PC ∥l 1，QD ∥l 1，ME ∥l 1，∵12l l ∥，∴12////////PC QD ME l l ∴∠1=∠APC ，∠QPC =∠PQD ，∠DQM =∠EMQ ，∠EMB =∠5，∴∠2=∠1+∠PQD ，∠4=∠5+∠DQM ，∴∠2+∠4=∠1+∠PQD +∠5+∠DQM =∠1+∠3+∠5，∴∠1+∠3+∠5=∠2+∠4．【点睛】本题考查了平行线的性质及平行公理的推论，熟练掌握平行线的性质是解题的关键．9．（1）A C AFC ∠∠∠＋＝；A C AFC ∠-∠∠＝；C A AFC∠-∠∠＝（2）360（3）-1180n ⨯︒（）【分析】（1）根据平行线的性质可直接得到结论；（2）过点F 作AB 的平行线，利用平行线的性质，计算出A C AFC ∠∠∠＋＋的度数；（3）过点E 作AB 的平行线，过点F 作AB 的平行线，利用平行线的性质，计算出A AEF EFC C ∠∠∠∠＋＋＋度数；通过前面的计算，找出规律．利用规律得到有n 个折点的结论；【详解】解：（1）如图1：A C AFC ∠∠∠＋＝，如图2：A C AFC ∠-∠∠＝，如图3：C A AFC ∠-∠∠＝，如图1说明理由如下：∵AB CD EF ∥∥，∴A AFE C EFC ∠∠∠∠＝，＝，∴A C AFE EFC ∠∠∠∠＋＝＋，即A C AFC ∠∠∠＋＝；（2）如下图：过F 作FH AB ∥，∴180A AFH ∠∠︒＋＝，又∵AB CD ∥，∴CD FH ∥，∴180C CFH ∠∠︒＋＝，∴360A AFH C CFH ∠∠∠∠︒＋＋＋＝，即360A C AFC ∠∠∠︒＋＋＝；故答案为：360；（3）如下图：AB CD ∥，过E 作EG AB ∥，过F 作FH AB ∥，∵AB CD ∥，∴AB EG FH CD ∥∥∥，∴180A AEG ∠∠︒＋＝，180GEF EFH ∠∠︒＋＝，180HFC C ∠∠︒＋＝，∴1803A AEG GEF EFH HFC C ∠∠∠∠∠∠︒⨯＋＋＋＋＋＝，即540A AEF EFC C ∠∠∠∠︒＋＋＋＝；综上所述：由当平行线AB 与CD 间没有点的时候，180A C ∠∠︒＋＝，当A 、C 之间加一个折点F 时，2180A AFC C ∠∠∠⨯︒＋＋＝；当A 、C 之间加二个折点E 、F 时，则3180A AEF EFC C ∠∠∠∠⨯︒＋＋＋＝；以此类推，如图5，1n A B A D ∥，当1A 、5A 之间加三个折点234A A A 、、时，则123454180A A A A A ∠+∠∠∠∠⨯︒＋＋＋＝；…当1A 、n A 之间加n 个折点231n A A A -⋯、、时，则123-1180n A A A A n ∠∠∠⋯∠⨯︒＋＋＋＝（），即1234n ∠∠∠∠∠＋＋＋＋＋ 的度数是-1180n ⨯︒（）．【点睛】本题是探索型试题，主要考查了平行线的性质，根据题意作出辅助线，利用平行线的性质及三角形外角的性质等知识求解是解答此题的关键．10．B【分析】延长DC 交AE 于F ，依据AB CD ∥，77BAE ∠=︒，可得77CFE ∠=︒，再根据三角形外角性质，即可得到E DCE CFE ∠=∠-∠．【详解】解：如图，延长DC 交AE 于F ，∵AB CD ∥，77BAE ∠=︒，77CFE BAE ∴∠=∠=︒，又131DCE ∠=︒ ，E CFE DCE ∠+∠=∠，1317754E DCE CFE ∴∠=∠-∠=︒-︒=︒．故选：B ．【点睛】本题主要考查了平行线的性质，解决问题的关键是掌握：两直线平行，同位角相等．11．C 【分析】过点B 作∥BD AM ，则BD AM CN ∥∥，由平行线的性质可得65ABD MAB ∠=∠=︒，55CBD NCB ∠=∠=︒，由此进行计算即可得到答案．【详解】解：如图，过点B 作∥BD AM ，，AM CN ∥，A BD M CN ∴∥∥，65MAB ∠=︒，55NCB ∠=︒，65ABD MAB ∴∠=∠=︒，55CBD NCB ∠=∠=︒，6555120ABC ABD CBD ∴∠=∠+∠=︒+︒=︒，故选：C ．【点睛】本题考查了平行线的性质，熟练掌握两直线平行，内错角相等是解此题的关键．12．100︒##100度【分析】过点D 作DG AB ∥，过点E 作EH AB ∥，根据平行线的性质和垂直的定义，进行求解即可．【详解】解：过点D 作DG AB ∥，过点E 作EH AB ∥，∵EF MN ⊥，∴90MFE ∠=︒，∵AB MN ∥，∴AB DG EH MN ∥∥∥，∴180ACD CDG ∠+∠=︒，DEH GDE ∠=∠，90HEF MFE ∠=∠=︒∵120,110DEF BCD ∠=︒∠=︒，∴30GDE DEH ︒∠=∠=，18011070CDG ∠︒=︒-︒=，∴100CDE CDG GDE =∠+∠=︒∠．故答案为：100︒【点睛】本题考查了平行线的判定和性质，解题的关键是过拐点构造平行线．13．A【分析】过C 作CM ∥AB ，得到CM ∥DE ，因此ABC BCM ∠=∠，MCD EDC β∠=∠=，由垂直的定义得到90ABC β∠=︒-，由邻补角的性质即可得到答案．【详解】解：过C 作CM ∥AB ，AB ∥DE ，CM DE ∴∥，ABC BCM ∴∠=∠，MCD EDC β∠=∠=，BC CD ⊥ ，9090BCM MCD β∴∠=︒-∠=︒-，90ABC β∴∠=︒-，180ABC ABF ∠+∠=︒ ，90180βα∴︒-+=︒，∴90αβ-= ．故选：A ．【点睛】本题考查平行线的性质，关键是过C 作//CM AB ，得到//CM DE ，由平行线的性质来解决问题．14．C【分析】首先求出ABP ∠和CDP ∠，再根据平行线的性质求出BPN ∠和DPN ∠即可．【详解】解：∵150160ABE CDF ∠=︒∠=︒，∴18030ABP ABE ∠=︒-∠=︒，18020CDP CDF ∠=︒-∠=︒，∵AB CD MN ∥∥，∴30BPN ABP ∠=∠=︒20DPN CDP ∠=∠=︒，∴50BPN D EPF PN ∠+∠=︒∠=，故选：C ．【点睛】本题考查了平行线的性质，熟知两直线平行，内错角相等是解题的关键．15．65︒##65度【分析】过点P 作PE AB ，得到PE AB CD ∥∥，进而得到1,2180A CDP ∠=∠∠=︒-∠，再利用12∠+∠计算即可．本题考查平行线的判定和性质，解题的关键是过拐点作平行线．【详解】解：过点P 作PE AB ，∵AB CD ∥，∴PE AB CD ∥∥，∴125,218040A CDP ∠=∠=︒∠=︒-∠=︒，∴1265APD ∠=∠+∠=︒；故答案为：65︒．16．120EFG BEF DGF ∠=∠+∠-︒【分析】如图，过E 作EQ AB ∥，过F 作FN AB ∥，过G 作GK AB ∥，再证明AB EQ FN GK CD ∥∥∥∥，再结合平行线的性质可得结论．【详解】解：如图，过E 作EQ AB ∥，过F 作FN AB ∥，过G 作GK AB ∥，∵AB CD ∥，∴AB EQ FN GK CD ∥∥∥∥，∵120B D ∠=∠=︒，∴18060QEB B ∠=︒-∠=︒，18060DGK D ∠=︒-∠=︒，∵QE FN GK ∥∥，∴QEF EFN ∠=∠，KFG GFN ∠=∠，∴EFG EFN GFN QEF KGF ∠=∠+∠=∠+∠，∵6060120QEF KGF BEF DGF BEF DGF ∠+∠=∠-︒+∠-︒=∠+∠-︒，∴120EFG BEF DGF ∠=∠+∠-︒；故答案为：120EFG BEF DGF ∠=∠+∠-︒【点睛】本题考查的是平行公理的应用，平行线的性质，作出合适的辅助线是解本题的关键．17．(1)12∠=∠(2)12180∠+∠=︒，理由见解析(3)相等或互补(4)这两个角的度数分别为30︒，30︒，或60︒，120︒【分析】（1）根据两直线平行，内错角相等，即可作答；（2）根据两直线平行，内错角相，同旁内角互补，即可作答；（3）根据（1）、（2）结论直接归纳即可；（4）①当两角相等时，设一个角为x ，另一个角为()360x -︒，可得方程360x x =-︒，解方程即可求解；②当两角互补时，设一个角为x ，另一个角为()360x -︒，可得方程()360180x x ︒+-=︒，解方程即可求解．【详解】（1）∵AB CD ，BE DF ∥，∴13∠=∠，32∠=∠，∴12∠=∠，故答案为：12∠=∠；（2）12180∠+∠=︒，证明：∥ AB CD ，13∠∠∴=，BE DF ，23180∴∠+∠=︒，12180∴∠+∠=︒；（3）根据（1）、（2）的结果可知：一个角的两边与另一个角的分别平行，那么这两个角相等或互补，故答案为：相等或互补；（4）①当两角相等时，设一个角为x ，另一个角为()360x -︒，360x x ∴=-︒，30x ∴=︒，36030x ∴-︒=︒②当两角互补时，设一个角为x ，另一个角为()360x -︒，()360180x x ︒∴+-=︒，60x ∴=︒，360120x ︒∴-=︒．综上所述：这两个角的度数分别为30︒，30︒，或60︒，120︒．【点睛】本题主要考查了平行线的性质，掌握两直线平行，内错角相，同旁内角互补，是解答本题的关键．18．(1)110APC ∠=︒；(2)①CPD αβ∠=∠+∠；②CPD βα∠=∠-∠或CPD αβ∠=∠-∠．【分析】本题考查了平行线的性质和判定的应用，解决问题的关键是作辅助线构造内错角以及同旁内角．（1）过P 作PE AB ∥，构造同旁内角，利用平行线性质，可得110APC ∠=︒；（2）①过P 作PE AD ∥交CD 于E ，推出AD PE BC ∥∥，根据平行线的性质得出DPE α∠=∠，CPE β∠=∠，即可得出答案；②画出图形（分两种情况：点P 在BA 的延长线上，点P 在AB 的延长线上），根据平行线的性质得出DPE α∠=∠，CPE β∠=∠，即可得出答案．【详解】（1）解：过P 作PE AB ∥，∵AB CD ∥，∴PE AB CD ∥∥，∵130PAB ∠=︒，120PCD ∠=︒．∴18050APE PAB ∠=︒-∠=︒，18060CPE PCD ∠=︒-∠=︒，∴5060110APC ∠=︒+︒=︒；（2）解：①CPD αβ∠=∠+∠：如图3，过P 作PE AD ∥交CD 于E ，∵AD BC ∥，∴AD PE BC ∥∥，∴DPE α∠=∠，CPE β∠=∠，∴CPD DPE CPE αβ∠=∠+∠=∠+∠；故答案为：CPD αβ∠=∠+∠；②当P 在AB 延长线时，CPD βα∠=∠-∠；理由：如图4，过P 作PE AD ∥交CD 于E ，∵AD BC ∥，∴AD PE BC ∥∥，∴DPE α∠=∠，CPE β∠=∠，∴CPD CPE DPE βα∠=∠-∠=∠-∠；当P 在BO 之间时，CPD ∠理由：如图5，过P 作PE ∥∵AD BC ∥，∴AD PE BC ∥∥，∴DPE α∠=∠，CPE β∠=∠CPD αβ∴∠=∠-∠综上所述，CPD ∠，α∠，∠βCPD αβ∠=∠-∠．19．（1）见解析；（2）见解析；【分析】()1过点E 作EM AB ∥∴∠=∠，ABE BEMAB CD，∥∴ ，CD EM∴∠=∠，CDE DEM∥AB CD，∴ ，AB EM FN CD∥，EM FN∴∠+∠=︒，MEF NFE180∥AB CD，∴ AB EM FN GH∥EM FN∥，FN GH ∴∠+∠=180 MEF NFE20．(1)证明见详解；(2)900︒；(3)()1801︒-n ；【分析】（1）过点E 作OE ∥A B ，可得OE AB CD ∥∥，根据平行线的性质可得1180MEO ∠+∠=︒，2180OEN ∠+∠=︒，再计算角度和即可证明；（2）分别过点E 、F 、G 、H 作AB 的平行线，在两相邻平行线间利用两直线平行同旁内角互补求得两角度和后，再将所有角度相加即可解答；（3）由（2）解答可知在AB 、CD 之间每有一条线段便可求得一个180°角度和，结合图3找出n 和线段条数的关系便可解答；【详解】（1）证明：如下图，过点E 作OE ∥A B ，∵AB CD ∥，OE ∥A B ，∴ OE CD ，根据两直线平行同旁内角互补可得：1180MEO ∠+∠=︒，2180OEN ∠+∠=︒，∴12360MEO OEN ∠+∠+∠+∠=︒，∴12360MEN ∠+∠+∠=︒；（2）解：如下图，分别过点E 、F 、G 、H 作1O E AB ∥，2O F AB ∥，3O G AB ∥，4O H AB ∥，结合（1）解答在两相邻平行线间可得：1180AME MEO ∠+∠=︒，12180O EF EFO ∠+∠=︒，23180O FG FGO ∠+∠=︒，34180O GH GHO ∠+∠=︒，4180O HN HNC ∠+∠=︒，将所有角度相加可得：1234561805900∠+∠+∠+∠+∠+∠=︒⨯=︒；（3）解：由（2）解答可知在AB 、CD 之间每有一条线段便可求得一个180°角度和，由图3可知：当AB 、CD 之间有2条线段时，3n =，当AB 、CD 之间有3条线段时，4n =，当AB 、CD 之间有4条线段时，5n =，当AB 、CD 之间有5条线段时，6n =，…，当AB 、CD 之间有()1n -条线段时，n n =，∴()1231801n n ∠+∠+∠++∠=︒- ；【点睛】本题考查了平行线公理的推论，平行线的性质，归纳总结的解题思路，通过作辅助线将角度按组计算是解题关键．。

专题一平行线中的拐点问题【学习目标】1.复习巩固平行线的性质和判定，找到解决平行线间拐点问题的基本方法，学会运用平行线转移角，建立分散的角之间的练习，提高几何推理能力。

2.在探究的过程中，体会观察-猜想-实验-证明的探究过程，初步体会添加辅助线的目的。

【学习过程】一、复习填空.平行线的判定：①_____________________________________________.②_____________________________________________.③_____________________________________________.④_____________________________________________.平行线的定理：①_____________________________________________.②_____________________________________________.③_____________________________________________.二、探究新知假设，两根木杆AB与CD平行放置，木杆的两端B、D用一根橡皮筋连接，现在在橡皮筋BD上任取一点P，将点P向里压：例1.如图，在平行线AB，CD内任取一点P，连接DP，BP.（1）若∠ABP=45°，∠CDP=15°则∠BPD=__________.（2）若∠BPD=50°，∠CDP=10°则∠ABP=__________.（3）试猜想∠BPD与∠ABP、∠CDP之间的数量关系，并说明理由.变式练习：1.如图，直线AB∥CD，∠A=40°，∠D=45°，则∠1的度数是__________. 2.如图，直线AB∥CD，∠C=44°，∠E为直角，则∠1的度数是_____________.（1）（2）拓展提升：如图1，AB∥CD，EOF是直线AB、CD间的一条折线．（1）如果将折一次改为折二次，如图2，则∠BEO、∠O、∠P、∠PFC之间会满足怎样的数量关系，证明你的结论．（2）如果将折一次改为折三次，如图3，则∠BEO、∠O、∠P、∠Q、∠QFD之间会满足怎样的数量关系（直接写出结果不需证明）假设，现在在橡皮筋BD上任取一点P，将点P水平向外拉：例2.如图，在平行线段AB、CD外取一点P，连接BP，DP，刚才的结论还成立吗？若不成立，你又有新的发现吗？变式练习：1.某小区地下停车场入口门栏杆的平面示意图如图所示，BA垂直地面AE于点A，CD平行于地面AE，若∠BCD=110°，则∠ABC=__________.2.如图，如果a∥b，∠1=55°，∠2=130°，则∠3=___________.（1）（2）拓展提升：已知：如图，AB∥CD，试解决下列问题：（1）∠1+∠2＝；（2）∠1+∠2+∠3＝；（3）∠1+∠2+∠3+∠4＝_；（4）试探究∠1+∠2+∠3+∠4+…+∠n＝．假设，现在在橡皮筋BD上任取一点P，将点P斜上右上方拉或者斜上左上方拉：例3.如图①②，在平行线AB、CD外取一点P，连接BP，DP，这时∠ABP，∠CDP，∠BPC之间又有怎样的数量关系呢？变式训练：1.如图，BD∥EF，AE与BD交于点C，∠B＝30°，∠A＝75°，则∠E的度数为__________.2.如图，直线AB∥EF，点C是直线AB上一点，点D是直线AB外一点，若∠BCD＝100°，∠CDE＝15°，则∠DEF的度数是___________.3.如图，已知直线a∥b，则∠1、∠2、∠3的关系是______________.（1）（2）（3）三、课后练习1.如图，直线l2∥12，∠A＝125°，∠B＝85°，则∠1+∠2＝．2.如图，如果AB∥CD，则角α、β、γ之间的关系为．3.如图，已知AB∥CD，∠ABE和∠CDE的平分线相交于F，∠E＝140°．则∠BFD的度数为____________．（1）（2）（3）4.如图，直线m∥n，AB⊥BC，∠1＝35°，∠2＝62°，则∠BCD的度数为．5.直线l1∥l2，∠A＝125°，∠B＝105°，则∠1+∠2=____________.（4）（5）6.如图，已知AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED＝75°．求∠BFD的度数．7.如图，一条公路修到湖边时需绕道，第一次拐角∠B＝110°，第二次拐角∠C＝150°，为了保持公路AB与DE平行，则第三次拐角∠D的度数为__________.8．如图，AB∥EF，BC⊥CD于C，∠ABC＝30°，∠DEF＝45°，则∠CDE等于（）A．105°B．75°C．135°D．115°9．如图所示，两平面镜α、β的夹角为60°，入射光线AO平行于β入射到α上，经两次反射后的反射光线O′B平行于α，则∠1的度数为（）A．60°B．45°C．30°D．75°10．如图，直线a∥b，直角三角形如图放置，∠DCB＝90°．若∠1+∠B＝70°，则∠2的度数为（）A．20°B．40°C．30°D．25°（8）（9）（10）11．阅读第（1）题解题过程，解答第（2）题．（1）如图1，AB∥CD，E为AB、CD之间的一点，已知∠B＝40°，∠C＝30°，求∠BEC的度数．解：过点E作EM∥AB，∴∠B＝（）．∵AB∥CD，AB∥EM，∴EM∥（）．∴∠2＝（）．∴∠BEC＝∠1+∠2＝∠B+∠C＝40°+30°＝70°．（2）如图2，AB∥ED，试探究∠B、∠BCD、∠D之间的数量关系．。

第二讲平行线的拐点问题（一）情景引入1、设计情景：如图.一条公路修到湖边时.需拐弯绕湖而过.如果第一次拐的角ZA是12L,第二次拐的角ZR是15『・第三次拐的角是,C・这时的道路恰好和第一次拐弯之前的道路平行.则z（-（）.2、知识点归纳：我们把实际问题图形抽象成几何图形，来看看ZA、ZB、ZC之间有什么数量关系？下而我们就来研究下。

（二）新课教学：Q讲点1巧作一条平行线,木杆与FC平行，（1>图（肿中■之间冇何关系？（2>图（C中.ZA・ZB・ZC之间冇何关系？（3）图W）中.ZA<ZB<ZCX间有何关系？⑷图⑺中,ZA，ZB，ZC之间有何关系？师：观察以上几个图形，由题目所给的平行线我们能否利用所学的平行线的性质得角度的关系？师：如果不行，是什么原因？师：有两直线却没有截线，下而教师来给大家演示增添一条辅助线，使得平行线都有截线。

师：通过过拐点A作平行线，我们可以把原本的两直线平行转化为多组两直线平行，从而运用平行线的性质来找ZA> ZB、ZC之间的数呈关系。

板书：解析：以（1〕为例：过A点做AD〃EB ・•・ZB=ZBAD・・・EB〃FC , AD/7EB ・・.AD〃FC ・・・ZC=ZCAD:.Z BAC= ZBAD+ ZCAD= ZB+ZC(2) ZA+ZB+ZC=180°⑶ ZA+ZB=ZC(4) ZA+ZC=ZB归纳总结：上述是常见的平行线拐点问题的根本模型，证明方法都是过拐点作平行线。

稳固练习：练1・3如图AB//CD.交宜答案:155°或如图所示.AE//BD ・Zl=a ・= 求ZC.（用含a 代数式表示〉 师：图中有没有我们如图.一条公路修到湖边时.需拐弯绕湖而过.如 果第一次拐的角ZA 是1206,第二次拐的角是 150',第三次拐的练1.1 一大门的栏杆（如图所示九BA 垂直地面AE 于凡丿 ________ D *快七'CD 平行地面AE.则ZHBC 十ZbC ：D=（）.占厂" A. 180c B. 27俨C. 280?D. 2 9贷 -- ------------- E A答案：B 解析：过B 点作BF 〃CD,那么可以得岀两组同位角，其中ZABC 的一局部等于90° ,另外一局部和Z BCD 互补。

七年级数学下册平行线中的“拐点”问题专题练习模型1M型【例1】如图，已知AB∥CD，则∠B，∠BED，∠D之间有何数量关系？请说明理由．【思路点拨】由已知条件知，AB∥CD，但图形中没有截这两条平行线的第三条直线，因而不能直接用平行线的性质解决．为此可构造第三条直线，即过点E 作EF∥AB，于是BE，DE就可以作为第三条直线了．变式当点E运动到平行线的外侧1．已知AB∥CD，点E为AB，CD之外任意一点．(1)如图1，探究∠BED与∠B，∠D的数量关系，并说明理由；(2)如图2，探究∠CDE与∠B，∠BED的数量关系，并说明理由．拓展平行线间有多个拐点2．(1)如图1中，AB∥CD，则∠E＋∠G与∠B＋∠F＋∠D有何关系？(2)在图2中，若AB∥CD，又能得到什么结论？如果出现多个拐点时，可以作多条平行线，从而将多拐点问题转化为一个拐点问题来处理．M型最终的结论为：朝左的角之和等于朝右的角之和．模型2铅笔型【例2】如图，直线AB∥CD，∠B，∠BED，∠D之间有什么关系呢？为什么？拓展平行线间有多个拐点3．(1)①如图1，MA1∥NA2，则∠A1＋∠A2＝度；②如图2，MA1∥NA3，则∠A1＋∠A2＋∠A3＝度；③如图3，MA1∥NA4，则∠A1＋∠A2＋∠A3＋∠A4＝度；④图4，MA1∥NA5，则∠A1＋∠A2＋∠A3＋∠A4＋∠A5＝度；从上述结论中你发现了什么规律？(2)如图5，MA1∥NA n，则∠A1＋∠A2＋∠A3＋…＋∠A n＝度．小专题(二)利用平行线的性质求角的度数类型1直接利用平行线的性质与判定求角度1．如图，OC是∠AOB的平分线，l∥OB.若∠1＝52°，则∠2的度数为( ) A．52°B．54°C．64°D．69°2．如图，CD∥AB，点O在AB上，OE平分∠BOD，OF⊥OE，∠D＝110°，则∠AOF的度数是( )A．20°B．25°C．30°D．35°3．如图，AB∥CD，CB∥DE，∠B＝50°，则∠D＝．4．如图，已知EF∥AD，∠1＝∠2，∠BAC＝80°，求∠AGD的度数．类型2借助学具的特征求角度5．如图，将直尺与30°角的三角尺叠放在一起．若∠1＝40°，则∠2的大小是( ) A．40° B．60° C．70° D．80°6．如图，一块直角三角板的两锐角的顶点刚好落在平行线l1，l2上，已知∠C是直角，则∠1＋∠2的度数等于( )A．75° B．90° C．105° D．120°类型3折叠问题中求角度7．将一个长方形纸片折叠成如图所示的图形．若∠ABC＝26°，则∠ACD＝．8．如图，一个四边形纸片ABCD，∠B＝∠D＝90°，∠C＝130°.把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕，则∠AEB的度数是．类型4抽象出平行线模型求角度(建模思想)9．如图，∠AOB的一边OA为平面镜，∠AOB＝38°，一束光线(与水平线OB 平行)从点C射入经平面镜反射后，反射光线落在OB上的点E处，已知∠ADC ＝∠ODE.则∠DEB的度数是度．10．如图1是我们常用的折叠式小刀，图2中刀柄外形是一个梯形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是．小专题(三)平行线的性质与判定的综合运用——教材P37T13的变式与应用教材母题(教材P37T13)：完成下面的证明．(1)如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA.求证：∠FDE＝∠A.证明：∵DE∥BA，∴∠FDE＝．∵DF∥CA，∴∠A＝．∴∠FDE＝∠A.(2)如图2，AB和CD相交于点O，∠C＝∠COA，∠D＝∠BOD.求证AC∥BD.证明：∵∠C＝∠COA，∠D＝∠BOD，又∠COA＝∠BOD( )，∴∠C＝．∴AC∥BD(内错角相等，两直线平行)．(1)判定两直线平行的方法有五种：①平行线的定义；②平行公理的推论；③同位角相等，两直线平行；④内错角相等，两直线平行；⑤同旁内角互补，两直线平行．(2)判定两直线平行时，定义一般不常用，其他四种方法要灵活运用，推理时要注意书写格式．(3)由两条直线平行得到同位角相等、内错角相等或同旁内角互补，解题时应结合图形先确认所成的角是不是两平行线被第三条直线所截得的同位角或内错角或同旁内角，同时要学会简单的几何说理，做到每一步有理有据．1．如图，已知AD⊥BC，EF⊥BC，垂足分别为D，F，∠2＋∠3＝180°.试说明：∠GDC＝∠B.下面是不完整的说理过程，请你将横线上的过程和括号里的理由补充完整．解：因为AD⊥BC，EF⊥BC(已知)，①所以∠ADB＝∠EFB＝(垂直的定义)．②所以(同位角相等，两直线平行)．③所以∠1＋∠2＝(两直线平行，同旁内角互补)．④又因为∠2＋∠3＝180°( )，⑤所以∠1＝∠3( )．⑥所以AB∥DG( )．⑦所以∠GDC＝∠B( )．2．如图，点G在射线BC上，射线DE与AB，AG分别交于点H，M.若DF∥AB，∠B＝75°，∠D＝105°，求证：∠AME＝∠AGC.3．如图，AB∥CD，AE平分∠BAD，CD与AE相交于点F，∠CFE＝∠E.求证：AD∥BC.4．如图，∠E＝∠1，∠3＋∠ABC＝180°，BE是∠ABC的平分线．你能判断DF与AB的位置关系吗？请说明理由．5．如图，AB⊥BD于点B，点E是BD上的点，AE平分∠BAC，CE平分∠ACD，且∠1＋∠2＝90°.求证：CD⊥BD.6．如图，把一张长方形ABCD的纸片沿EF折叠后，ED与BC的交点为G，点D，C分别落在D′，C′的位置上．若∠EFG＝55°，求∠1，∠2的度数．7．如图，已知BC∥GE，∠AFG＝∠1＝50°.(1)求证：AF∥DE；(2)若AQ平分∠FAC，交BC于点Q，且∠Q＝15°，求∠ACQ的度数．参考答案：小专题（一）平行线中的“拐点”问题模型1M型【例1】如图，已知AB∥CD，则∠B，∠BED，∠D之间有何数量关系？请说明理由．【思路点拨】由已知条件知，AB∥CD，但图形中没有截这两条平行线的第三条直线，因而不能直接用平行线的性质解决．为此可构造第三条直线，即过点E 作EF∥AB，于是BE，DE就可以作为第三条直线了．【解答】∠BED＝∠B＋∠D.理由：过点E作EF∥AB，则EF∥CD.∴∠B＝∠BEF，∠D＝∠DEF.∴∠BED＝∠BEF＋∠DEF＝∠B＋∠D.变式当点E运动到平行线的外侧1．已知AB∥CD，点E为AB，CD之外任意一点．(1)如图1，探究∠BED与∠B，∠D的数量关系，并说明理由；(2)如图2，探究∠CDE与∠B，∠BED的数量关系，并说明理由．解：(1)∠B＝∠BED＋∠D.理由如下：过点E作EF∥AB，则AB∥CD∥EF.∴∠BEF＝∠B，∠D＝∠DEF.∵∠BEF＝∠BED＋∠DEF，∴∠B＝∠BED＋∠D.(2)∠CDE＝∠B＋∠BED.理由如下：过点E作EF∥AB，则AB∥CD∥EF.∴∠B＋∠BEF＝180°，∠CDE＋∠DEF＝180°.又∵∠DEF＝∠BEF－∠BED，∴∠CDE＋∠BEF－∠BED＝∠B＋∠BEF，即∠CDE＝∠B＋∠BED.拓展平行线间有多个拐点2．(1)如图1中，AB∥CD，则∠E＋∠G与∠B＋∠F＋∠D有何关系？(2)在图2中，若AB∥CD，又能得到什么结论？解：(1)∠BEF＋∠FGD＝∠B＋∠EFG＋∠D.理由：过点E，F，G分别作EM∥AB，FN∥AB，GH∥AB，由AB∥CD，得AB∥EM∥FN∥GH∥CD.∴∠BEM＝∠B，∠MEF＝∠EFN，∠NFG＝∠FGH，∠HGD＝∠D.∴∠BEF＋∠FGD＝∠BEM＋∠MEF＋∠FGH＋∠HGD＝∠B＋∠EFN＋∠NFG＋∠D＝∠B＋∠EFG＋∠D.(2)在图2中，有∠E1＋∠E2＋∠E3＋…＋∠E n＝∠B＋∠F1＋∠F2＋…＋∠F n－1＋∠D.如果出现多个拐点时，可以作多条平行线，从而将多拐点问题转化为一个拐点问题来处理．M型最终的结论为：朝左的角之和等于朝右的角之和．模型2铅笔型【例2】如图，直线AB∥CD，∠B，∠BED，∠D之间有什么关系呢？为什么？【解答】∠B＋∠BED＋∠D＝360°.理由：过点E作EF∥AB.∵AB∥CD，∴AB∥CD∥EF.∴∠B＋∠BEF＝180°，∠D＋∠DEF＝180°.∴∠B＋∠BEF＋∠D＋∠DEF＝360°，即∠B＋∠BED＋∠D＝360°.拓展平行线间有多个拐点3．(1)①如图1，MA1∥NA2，则∠A1＋∠A2＝180度；②如图2，MA1∥NA3，则∠A1＋∠A2＋∠A3＝360度；③如图3，MA1∥NA4，则∠A1＋∠A2＋∠A3＋∠A4＝540度；④图4，MA1∥NA5，则∠A1＋∠A2＋∠A3＋∠A4＋∠A5＝720度；从上述结论中你发现了什么规律？(2)如图5，MA1∥NA n，则∠A1＋∠A2＋∠A3＋…＋∠A n＝180(n－1)度．解：每增加一个角，度数增加180°.小专题(二)利用平行线的性质求角的度数类型1直接利用平行线的性质与判定求角度1．如图，OC是∠AOB的平分线，l∥OB.若∠1＝52°，则∠2的度数为( C ) A．52°B．54°C．64°D．69°2．如图，CD∥AB，点O在AB上，OE平分∠BOD，OF⊥OE，∠D＝110°，则∠AOF的度数是( D )A．20°B．25°C．30°D．35°3．如图，AB∥CD，CB∥DE，∠B＝50°，则∠D＝130°．4．如图，已知EF∥AD，∠1＝∠2，∠BAC＝80°，求∠AGD的度数．解：∵EF∥AD，∴∠2＝∠3(两直线平行，同位角相等)．∵∠1＝∠2，∴∠1＝∠3(等量代换)．∴AB∥DG(内错角相等，两直线平行)．∴∠BAC＋∠AGD＝180°(两直线平行，同旁内角互补)．∵∠BAC＝80°，∴∠AGD＝100°.类型2借助学具的特征求角度5．如图，将直尺与30°角的三角尺叠放在一起．若∠1＝40°，则∠2的大小是( D ) A．40° B．60° C．70° D．80°6．如图，一块直角三角板的两锐角的顶点刚好落在平行线l1，l2上，已知∠C是直角，则∠1＋∠2的度数等于( B )A．75° B．90° C．105° D．120°类型3折叠问题中求角度7．将一个长方形纸片折叠成如图所示的图形．若∠ABC＝26°，则∠ACD＝128°．8．如图，一个四边形纸片ABCD，∠B＝∠D＝90°，∠C＝130°.把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕，则∠AEB的度数是65°．类型4抽象出平行线模型求角度(建模思想)9．如图，∠AOB的一边OA为平面镜，∠AOB＝38°，一束光线(与水平线OB 平行)从点C射入经平面镜反射后，反射光线落在OB上的点E处，已知∠ADC ＝∠ODE.则∠DEB的度数是76度．10．如图1是我们常用的折叠式小刀，图2中刀柄外形是一个梯形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是90°．小专题(三)平行线的性质与判定的综合运用——教材P37T13的变式与应用教材母题(教材P37T13)：完成下面的证明．(1)如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA.求证：∠FDE＝∠A.证明：∵DE∥BA，∴∠FDE＝∠BFD(两直线平行，内错角相等)．∵DF∥CA，∴∠A＝∠BFD(两直线平行，同位角相等)．∴∠FDE＝∠A.(2)如图2，AB和CD相交于点O，∠C＝∠COA，∠D＝∠BOD.求证AC∥BD.证明：∵∠C＝∠COA，∠D＝∠BOD，又∠COA＝∠BOD(对顶角相等)，∴∠C＝∠D．∴AC∥BD(内错角相等，两直线平行)．(1)判定两直线平行的方法有五种：①平行线的定义；②平行公理的推论；③同位角相等，两直线平行；④内错角相等，两直线平行；⑤同旁内角互补，两直线平行．(2)判定两直线平行时，定义一般不常用，其他四种方法要灵活运用，推理时要注意书写格式．(3)由两条直线平行得到同位角相等、内错角相等或同旁内角互补，解题时应结合图形先确认所成的角是不是两平行线被第三条直线所截得的同位角或内错角或同旁内角，同时要学会简单的几何说理，做到每一步有理有据．1．如图，已知AD⊥BC，EF⊥BC，垂足分别为D，F，∠2＋∠3＝180°.试说明：∠GDC＝∠B.下面是不完整的说理过程，请你将横线上的过程和括号里的理由补充完整．解：因为AD⊥BC，EF⊥BC(已知)，①所以∠ADB＝∠EFB＝90°(垂直的定义)．②所以AD∥EF(同位角相等，两直线平行)．③所以∠1＋∠2＝180°(两直线平行，同旁内角互补)．④又因为∠2＋∠3＝180°(已知)，⑤所以∠1＝∠3(同角的补角相等)．⑥所以AB∥DG(内错角相等，两直线平行)．⑦所以∠GDC＝∠B(两直线平行，同位角相等)．2．如图，点G在射线BC上，射线DE与AB，AG分别交于点H，M.若DF∥AB，∠B＝75°，∠D＝105°，求证：∠AME＝∠AGC.证明：∵DF∥AB(已知)，∴∠D＝∠BHM(两直线平行，同位角相等)．又∵∠B＝75°，∠D＝105°(已知)，∴∠B＋∠BHM＝75°＋105°＝180°.∴DE∥BC(同旁内角互补，两直线平行)．∴∠AME＝∠AGC(两直线平行，同位角相等)．3．如图，AB∥CD，AE平分∠BAD，CD与AE相交于点F，∠CFE＝∠E.求证：AD∥BC.证明：∵AE平分∠BAD(已知)，∴∠1＝∠2(角平分线的定义)．∵AB∥CD(已知)，∴∠1＝∠CFE(两直线平行，同位角相等)．又∵∠1＝∠2(已证)，∠CFE＝∠E(已知)，∴∠2＝∠E(等量代换)．∴AD∥BC(内错角相等，两直线平行)．4．如图，∠E＝∠1，∠3＋∠ABC＝180°，BE是∠ABC的平分线．你能判断DF与AB的位置关系吗？请说明理由．解：DF∥AB.理由：∵BE是∠ABC的平分线，∴∠1＝∠2(角平分线的定义)．∵∠E＝∠1(已知)，∴∠E＝∠2(等量代换)．∴AE∥BC(内错角相等，两直线平行)．∴∠A＋∠ABC＝180°(两直线平行，同旁内角互补)．∵∠3＋∠ABC＝180°(已知)，∴∠A＝∠3(等量代换)．∴DF∥AB(同位角相等，两直线平行)．5．如图，AB⊥BD于点B，点E是BD上的点，AE平分∠BAC，CE平分∠ACD，且∠1＋∠2＝90°.求证：CD⊥BD.证明：∵AE平分∠BAC，CE平分∠ACD(已知)，∴∠BAC＝2∠1，∠ACD＝2∠2(角平分线的性质)．∴∠BAC＋∠ACD＝2∠1＋2∠2＝2(∠1＋∠2)．∵∠1＋∠2＝90°(已知)，∴∠BAC＋∠ACD＝180°.∴AB∥CD(同旁内角互补，两直线平行)．∴∠B＋∠D＝180°(两直线平行，同旁内角互补)．∴∠D＝180°－∠B(等式的性质)．∵AB⊥BD(已知)，∴∠B＝90°(垂直的定义)．∴∠D＝90°，即CD⊥BD.6．如图，把一张长方形ABCD的纸片沿EF折叠后，ED与BC的交点为G，点D，C分别落在D′，C′的位置上．若∠EFG＝55°，求∠1，∠2的度数．解：∵AD∥BC，∠EFG＝55°，∴∠2＝∠GED，∠DEF＝∠EFG＝55°(两直线平行，内错角相等)．由折叠，知∠GEF＝∠DEF＝55°.∴∠GED＝110°.∴∠2＝110°.∴∠1＝180°－∠2＝70°(两直线平行，同旁内角互补)．7．如图，已知BC∥GE，∠AFG＝∠1＝50°.(1)求证：AF∥DE；(2)若AQ平分∠FAC，交BC于点Q，且∠Q＝15°，求∠ACQ的度数．解：(1)证明：∵BC∥GE，∴∠E＝∠1＝50°.∵∠AFG＝∠1＝50°，∴∠E＝∠AFG＝50°.∴AF∥DE.(2)过点A作AP∥GE，∵BC∥GE，∴AP∥GE∥BC.∴∠FAP＝∠AFG＝50°，∠PAQ＝∠Q＝15°.∴∠FAQ＝∠FAP＋∠PAQ＝65°.∵AQ平分∠FAC，∴∠CAQ＝∠FAQ＝65°.∴∠CAP＝80°.∴∠ACQ＝180°－∠CAP＝100°.。

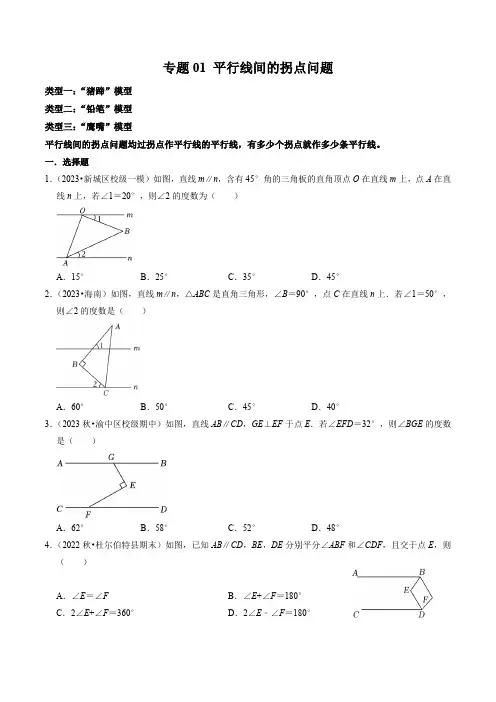
专题01 平行线间的拐点问题类型一：“猪蹄”模型类型二：“铅笔”模型类型三：“鹰嘴”模型平行线间的拐点问题均过拐点作平行线的平行线，有多少个拐点就作多少条平行线。

一．选择题1．（2023•新城区校级一模）如图，直线m∥n，含有45°角的三角板的直角顶点O在直线m上，点A在直线n上，若∠1＝20°，则∠2的度数为（）A．15°B．25°C．35°D．45°2．（2023•海南）如图，直线m∥n，△ABC是直角三角形，∠B＝90°，点C在直线n上．若∠1＝50°，则∠2的度数是（）A．60°B．50°C．45°D．40°3．（2023秋•渝中区校级期中）如图，直线AB∥CD，GE⊥EF于点E．若∠EFD＝32°，则∠BGE的度数是（）A．62°B．58°C．52°D．48°4．（2022秋•杜尔伯特县期末）如图，已知AB∥CD，BE，DE分别平分∠ABF和∠CDF，且交于点E，则（）A．∠E＝∠F B．∠E+∠F＝180°C．2∠E+∠F＝360°D．2∠E﹣∠F＝180°5．（2022秋•榆树市期末）如图，AB∥CD，则图中∠1、∠2、∠3关系一定成立的是（）A．∠1+∠2+∠3＝180°B．∠1+∠2+∠3＝360°C．∠1+∠3＝2∠2D．∠1+∠3＝∠26．（2023秋•湖北月考）将含有30°角的直角三角板在两条平行线中按如图所示摆放．若∠1＝120°，则∠2为（）A．120°B．130°C．140°D．150°二．填空题7．（2023•江油市开学）如图，AB∥CD，P为AB，CD之间的一点，已知∠2＝28°，∠BPC＝58°，则∠1＝．8．（2023秋•南岗区校级期中）如图，已知DE∥BC，∠ABC＝105°，点F在射线BA上，且∠EDF＝125°，则∠DFB的度数为．9．（2023秋•道里区校级期中）为增强学生体质，望一观音湖学校将“跳绳”引入阳光体育一小时活动．图1是一位同学跳绳时的一个瞬间．数学老师把它抽象成图2的数学问题：已知AB∥CD，∠EAB＝70°，∠ECD＝105°，则∠AEC＝．10．（2022秋•雅安期末）如图，AB∥CD，∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∠E﹣∠F＝60°，则∠E＝．11．（2023秋•南岗区校级期中）已知：如图，AB∥CD，∠ABG的平分线与∠CDE的平分线交于点M，∠M＝45°，∠F＝64°，∠E＝66°，则∠G＝°．三．解答题12．（2022秋•宝丰县期末）已知直线MN、PQ，点A、B为分别在直线MN、PQ上，点C为平面内一点，连接AC、BC，且∠C＝∠NAC+∠CBQ．（1）求证：MN∥PQ；（2）如图2，射线AE、BD分别平分∠MAC和∠CBQ，AE交直线PQ于点E，BD与∠NAC内部的一条射线AD交于点D，若∠C＝2∠D，求∠EAD的度数．13．（2022秋•莘县期末）综合与实践如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD 于点F．（1）当所放位置如图①所示时，∠PFD与∠AEM的数量关系是∠PFD+∠AEM＝90°；（2）当所放位置如图②所示时，求证：∠PFD﹣∠AEM＝90°；（3）在（2）的条件下，若MN与CD交于点O，且∠DON＝15°，∠PEB＝30°，求∠N的度数．14．（2022秋•洛宁县期末）问题情境：如图1，AB∥CD，∠P AB＝130°，∠PCD＝120°．求∠APC度数．小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC＝50°+60°＝110°．问题迁移：（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP ＝∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．15．（2023春•鼎城区期末）已知直线AB∥CD，点P为直线AB，CD所确定的平面内的一点．问题提出：（1）如图1，∠A＝120°，∠C＝130°，求∠APC的度数；问题迁移：（2）如图2，写出∠APC，∠A，∠C之间的数量关系，并说明理由；问题应用：（3）如图3，点E在射线BA上，过点E作EF∥PC，作∠PEG＝∠PEF，点G在直线CD上，作∠BEG的平分线EH交PC于点H，若∠APC＝20°，∠P AB＝150°，求∠PEH的度数．16．（2023秋•南岗区校级期中）已知：如图，AB∥CD，直线EF分别交AB，CD于点G，H，点P为直线EF上的点，连接AP，CP．（1）如图1，点P在线段GH上时，请你直接写出∠BAP，∠DCP，∠APC的数量关系；（2）如图2，点P在HG的延长线上时，连接CP交AB于点Q，连接HQ，AC，若∠ACP+∠PHQ＝∠CQH，求证：AC∥EF；（3）在（2）的条件下，如图3，CK平分∠ACP，GK平分∠AGP，GK与CK交点K，连接AK，若∠PQH＝4∠PCK+2∠PHQ，∠CKG＝∠CHQ，∠AKC+∠KAC＝159°，求∠BAC的大小．17．（2023秋•道里区校级期中）已知：直线AB与直线CD内部有一个点P，连接BP．（1）如图1，当点E在直线CD上，连接PE，若∠B+∠PEC＝∠P，求证：AB∥CD；（2）如图2，当点E在直线AB与直线CD的内部，点H在直线CD上，连接EH，若∠ABP+∠PEH＝∠P+∠EHD，求证：AB∥CD；（3）如图3，在（2）的条件下，BG、EF分别是∠ABP、∠PEH的角平分线，BG和EF相交于点G，EF和直线AB相交于点F，当BP⊥PE时，若∠BFG＝∠EHD+10°，∠BGE＝36°，求∠EHD的度数．18．（2023秋•南岗区校级期中）已知，过∠ECF内一点A作AD∥/EC交CF于点D，作AB∥/CF交CE于点B．（1）如图1，求证：∠ABE＝∠ADF；（2）如图2，射线BM，射线DN分别平分∠ABE和∠ADF，求证：BM∥DN；（3）如图3，在（2）的条件下，点G，Q在线段DF上，连接AG，AQ，AC，AQ与DN交于点H，反向延长AQ交BM于点P，如果∠GAC＝∠GCA，AQ平分∠GAD，∠QAC＝50°，求∠MP A+∠PQF的度数．19．（2023秋•南岗区校级期中）已知，射线FG分别交射线AB、DC于点F、G，点E为射线FG上一点．（1）如图1，若∠A+∠D＝∠AED，求证：AB∥CD．（2）如图2，若AB∥CD，求证：∠A﹣∠D＝∠AED．（3）如图3，在（2）的条件下，DI交AI于点Ⅰ，交AE于点K，∠EDI＝∠CDE，∠BAI＝∠EAI，∠I＝∠AED＝25°，求∠EKD的度数．20．（2023春•栾城区校级期中）【问题解决】：如图①，AB∥CD，点E是AB，CD内部一点，连接BE，DE．若∠ABE＝40°，∠CDE＝60°，求∠BED的度数；嘉琪想到了如图②所示的方法，请你帮她将完整的求解过程补充完整；解：过点E作EF∥AB∴∠ABE＝∠BEF（）；∵EF∥AB，AB∥CD（已知）；∴EF∥CD（）；∴∠CDE＝（）（）；又∵∠BED＝∠BEF+∠DEF（）；∴∠BED＝∠ABE+∠CDE（）；∵∠ABE＝40°，∠CDE＝60°（已知）；∴∠BED＝∠ABE+∠CDE＝100°（等量代换）；【问题迁移】：请参考嘉琪的解题思路，解答下面的问题：如图③，AB∥CD，射线OM与直线AB，CD分别交于点A，C，射线ON与直线AB，CD分别交于点B，D，点P在射线ON上运动，连接AP，CP，设∠BAP＝α，∠DCP＝β．（1）如图③，当点P在B，D两点之间运动时（点P不与点B，D重合），写出α，和∠APC之间满足的数量关系，并说明理由；（2）当点P在B，D两点外侧运动时（点P不与点B，D重合），请画出图形，并直接写出α，β和∠APC之间满足的数量关系．。

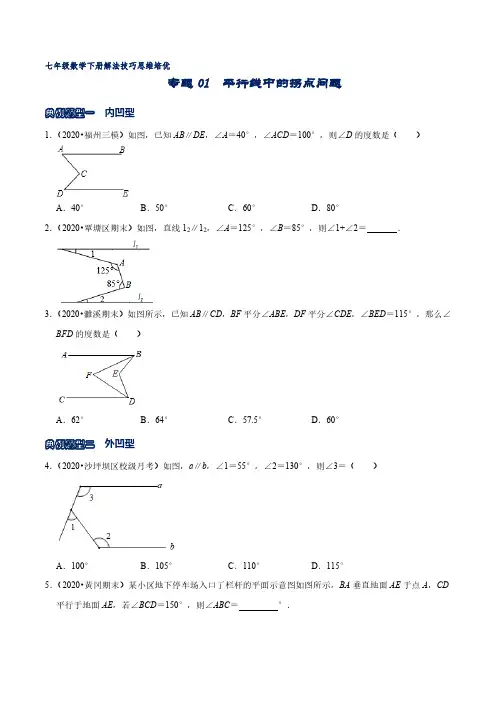
七年级数学下册解法技巧思维培优专题01 平行线中的拐点问题典例题型一内凹型1．（2020•福州三模）如图，已知AB∥DE，∠A＝40°，∠ACD＝100°，则∠D的度数是（ ）A．40°B．50°C．60°D．80°2．（2020•覃塘区期末）如图，直线12∥12，∠A＝125°，∠B＝85°，则∠1+∠2＝ ．3．（2020•濉溪期末）如图所示，已知AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED＝115°，那么∠BFD的度数是（ ）A．62°B．64°C．57.5°D．60°典例题型二外凹型4．（2020•沙坪坝区校级月考）如图，a∥b，∠1＝55°，∠2＝130°，则∠3＝（ ）A．100°B．105°C．110°D．115°5．（2020•黄冈期末）某小区地下停车场入口了栏杆的平面示意图如图所示，BA垂直地面AE于点A，CD 平行于地面AE，若∠BCD＝150°，则∠ABC＝ °．6．（2020•梁子湖区期末）如图，如果AB∥CD，那么角α，β，γ之间的关系式为（ ）A．α+β+γ＝360°B．α﹣β+γ＝180°C．α+β+γ＝180°D．α+β﹣γ＝180°典例题型三外错型7．（2020•凉山州）如图，BD∥EF，AE与BD交于点C，∠B＝30°，∠A＝75°，则∠E的度数为（ ）A．135°B．125°C．115°D．105°8．（2020•襄汾期末）如图，直线AB∥EF，点C是直线AB上一点，点D是直线AB外一点，若∠BCD＝100°，∠CDE＝15°，则∠DEF的度数是（ ）A．110°B．115°C．120°D．125°9．（2020•鸡东期末）如图，已知直线a∥b，则∠1、∠2、∠3的关系是（ ）A．∠1+∠2+∠3＝360°B．∠1+∠2﹣∠3＝180°C．∠1﹣∠2+∠3＝180°D．∠1+∠2+∠3＝180°典例题型四综合型10．（2020•文登区期末）如图，直线m∥n，AB⊥BC，∠1＝35°，∠2＝62°，则∠BCD的度数为（ ）A．97°B．117°C．125°D．152°11．（2020•北碚区期末）如图，一条公路修到湖边时需绕道，第一次拐角∠B＝120°，第二次拐角∠C＝140°，为了保持公路AB与DE平行，则第三次拐角∠D的度数应为（ ）A．130°B．140°C．150°D．160°12．（2020•潜江期末）如图，AB∥CD，∠BED＝60°，∠ABE的平分线与∠CDE的平分线交于点F，则∠DFB的度数是 ．巩固练习1．（2020•新乡二模）如图是婴儿车的平面示意图，其中AB∥CD，∠1＝120°，∠3＝40°，那么∠2的度数为（ ）A．80°B．90°C．100°D．102°2．（2020•高明区期末）如图，已知AB∥CD，直线AB，CD被BC所截，E点在BC上，若∠1＝45°，∠2＝35°，则∠3＝（ ）A．65°B．70°C．75°D．80°3．（2020•宿豫区期中）如图，把一个长方形纸片沿EF折叠后，点C、D分别落在M、N的位置．若∠EFB ＝65°，则∠AEN等于（ ）A．25°B．50°C．65°D．70°4．（2020•稷山校级一模）如图，直线a∥b，∠1＝32°，∠2＝45°，则∠3的度数是（ ）A．77°B．97°C．103°D．113°5．（2020•温岭市一模）如图，将直尺与含30°角的三角尺摆放在一起，若∠1＝20°，则∠2的度数是（ ）A．30°B．40°C．50°D．60°6．（2020•遂宁期末）如图，∠BCD＝95°，AB∥DE，则∠α与∠β满足（ ）A．∠α+∠β＝95°B．∠β﹣∠α＝95°C．∠α+∠β＝85°D．∠β﹣∠α＝85°7．（2020•河南模拟）如图，将矩形ABCD沿GH折叠，点C路在点Q处，点D落在AB边上的点E处，若∠AGE＝34°．则∠BHQ等于（ ）A．73°B．34°C．45°D．30°8．（2020•孟津期末）如图，AB∥EF，设∠C＝90°，那么x、y和z的关系是（ ）A．y＝x+z B．x+y﹣z＝90°C．x+y+z＝180°D．y+z﹣x＝90°9．（2020•福州期末）如图，BC⊥AE，垂足为C，过C作CD∥AB，若∠ECD＝43°，则∠B＝（ ）A．43°B．57°C．47°D．45°10．（2020•沙坪坝区校级期末）将一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G、D、C分别在M、N的位置上，若∠EFG＝52°，则∠2﹣∠1＝ °．11．（2020•泉州期末）如图，将一张长方形纸条沿某条直线折叠，若∠1＝116°，则∠2等于 ．。

第03讲解题技巧专题：平行线中有关拐点的模型专题问题(4类热点题型讲练)目录【考点一平行线中含一个拐点问题】 (1)【考点二平行线中含两个拐点问题】 (11)【考点三平行线中含多个拐点问题】 (21)【考点四平行线中在生活上含拐点问题】 (27)【考点一平行线中含一个拐点问题】例题：（2023上·广东揭阳·八年级统考期末）如图，直线【答案】134︒/134度【分析】本题主要考查利用平行线的性质求解相关角度，两直线平行内错角相等，直接过点∠进行分割转移，最后利用邻补角的概念，直接求出线把E【详解】见试题解答内容∴C FEC ∠=∠，BAE FEA ∠=∠，∵44C ∠=︒，90AEC ∠=︒；∴44FEC ∠=︒，904446BAE AEF ∠=∠=︒-︒=︒，∴118018046134BAE ∠=︒-∠=︒-︒=︒；故答案为：134︒．【变式训练】【答案】180APD A ∠=︒+∠-【分析】过点P 作PM AB ∥，从而可得PM CD ∥，然后利用平行线的性质可得A APM ∴∠=∠，AB CD ∥ ，PM CD ∴∥，【答案】25︒/25度【分析】本题主要考查等边三角形的性质，平行线的判定与性质，过点平行线的性质可得结论．【详解】解：过点B 作BF ∴35,ABF α∠=∠=︒∵ABC 是等边三角形，∴60,ABC ∠=︒∴FBC ABC ABF ∠=∠-∠∵12l l ∥，【答案】（1）见解析；（2）F BMF DNF ∠=∠-∠；（3）20【分析】本题主要考查平行线的判定和性质，作辅助线是解题的关键．（1）过点E作EF AB∥，根据平行线的性质可求解；∥，根据平行线的性质即可得到结论；（2）如图②，过F作FH AB∥，根据平行线的性质即可得到结论．（3）如图③，过C作CG AB【详解】（1）证明：如图①，过点E作EF AB∥，则MEF BME∠=∠，∥，又∵AB CD∥，∴EF CD∴∠=∠，NEF DNE∴∠=∠+∠，MEN MEF NEF∠=∠+∠；即MEN BME DNE（2）解：BMF MFN FND∠=∠+∠．，证明：如图②，过F作FK AB∴∠=∠，BMF MFK∥，∵AB CD，∴FK CD∴∠=∠，FND KFN∴∠=∠-∠=∠-∠，MFN MFK KFN BMF FND即：BMF MFN FND∠=∠+∠．故答案为：BMF MFN FND∠=∠+∠；∥，（3）如图③，过C作CG AB18060∴∠=︒-∠=︒，GCA BAC∥，∵AB DE∥，∴CG DEGCD CDE∴∠=∠=︒，80∴∠=︒，20ACD故答案为：20．4．（2023上·七年级课时练习）已知AB CD ，点E 为,AB CD 之外任意一点．（1）如图1，探究BED ∠与,B D ∠∠之间的数量关系，并说明理由；（2）如图2，探究CDE ∠与,B BED ∠∠之间的数量关系，并说明理由．【拓展变式】如图，“抖空竹”是国家级非物质文化遗产．在“抖空竹”的一个瞬间如图1所示，将图1抽象成一个数学问题：如图2，若,70,110AB CD EAB ECD ︒∠=∠=︒∥，则E ∠=_______________．【答案】（1）B BED D ∠=∠+∠，理由见解析；（2）CDE B BED ∠=∠+∠，理由见解析；[拓展变式]40︒．【分析】（1）过点E 作EF AB ∥，则AB CD EF ∥∥，根据平行线的性质可得,BEF B D DEF ∠=∠∠=∠，进而得出结论；（2）理由如下：过点E 作EF AB ∥，则AB CD EF ∥∥，根据平行线的性质可得B BEF ∠=∠，CDE DEF ∠=∠，进而得出结论；（3）过点E 作EF AB ∥，则AB CD EF ∥∥，根据平行线的性质得出180110AEF EAB ∠=︒-∠=︒，18070CEF ECD ∠=︒-∠=︒，进而即可求解．【详解】解：（1）B BED D ∠=∠+∠．理由如下：过点E 作EF AB ∥，则AB CD EF ∥∥．,BEF B D DEF ∴∠=∠∠=∠．BEF BED DEF ∠=∠+∠ ，B BED D ∴∠=∠+∠．（2）CDE B BED ∠=∠+∠．理由如下：过点E 作EF AB ∥，则AB CD EF ∥∥．B BEF ∴∠=∠，CDE DEF ∠=∠．DEF BEF BED ∠=∠+∠ ，CDE B BED ∴∠=∠+∠．【拓展变式】过点E 作EF AB ∥，则AB CD EF ∥∥．70,110EAB ECD ︒︒∠=∠= 180110AEF EAB ∠=︒-∠=︒，18070CEF ECD ∠=︒-∠=︒11070AEC AEF CEF ∴∠=∠-∠=︒-︒=40︒，故答案为：40︒．【点睛】本题考查了平行线的性质与判定，熟练掌握平行线的性质与判定是解题的关键．5．（2023上·吉林长春·七年级统考期末）如图，AB CD ∥，点E 、F 分别在直线AB 、CD 上，点P 是AB 、CD 之间的一个动点．【感知】如图①，当点P 在线段EF 左侧时，若50AEP ∠=︒，70PFC ∠=︒，求EPF ∠的度数．分析：从图形上看，由于没有一条直线截AB 与CD ，所以无法直接运用平行线的性质，这时需要构造出“两条直线被第三条直线所截”的基本图形，过点P 作PG AB ∥，根据两条直线都和第三条直线平行，那么这两条直线也互相平行，可知PG CD ∥，进而求出EPF ∠的度数．【探究】如图②，当点P 在线段EF 右侧时，AEP ∠、EPF ∠、PFC ∠之间的数量关系为______．【答案】感知：120︒探究：360AEP EPF PFC ∠+∠+∠=︒【分析】本题考查了平行线的判定与性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．感知：过点P 作PG AB ∥，根据猪脚模型，即可解答；探究：过点P 作PG AB ∥，根据铅笔模型，即可解答．【详解】感知：解：过点P 作PG AB ∥，50EPG AEP ∴∠=∠=︒，AB CD ∥ ，PG CD ∴∥，70GPF PFC ∴∠=∠=︒，5070120EPF EPG GPF ∴∠=∠+∠=︒+︒=︒，EPF ∠∴的度数为120︒；探究：解：过点P 作PG AB ∥，180EPG AEP ∴∠+∠=︒，AB CD ∥ ，PG CD ∴∥，180GPF PFC ∴∠+∠=︒，360AEP EPG FPG PFC ∴∠+∠+∠+∠=︒，360AEP EPF PFC ∴∠+∠+∠=︒，【答案】（1）90；（2）①56︒②见解析；（3）12290∠+∠=︒，理由见解析．【分析】（1）利用角平分线的定义可得，112PAC BAC ∠=∠=∠，122PCA ∠=∠=性质，求解即可；（2）①根据垂直可得90ACP ∠=︒，从而得到ACD ∠的度数，利用平行线的性质得到求解；②利用角平分线的定义和平行线的性质，求解即可；（3）根据角平分线的定义可得22ACD ∠=∠，再根据平行线的性质可得ACD ∠+∠∠=∠+∠．（完成下面的填空部分）(1)【基础问题】如图1，试说明：AGD A D证明：过点G作直线MN AB∥，∵72∠=︒AFC ，∴18072108GAB ∠=︒-︒=∵AH 平分GAB ∠，∴1122HAB GAB ∠=∠=【考点二平行线中含两个拐点问题】例题：如图所示，AB CD ∥、BEFD 是AB 、CD 之间的一条折线，则∠1+∠2+∠3+∠4=_____．【答案】540︒【分析】连接BD ，根据平行线的性质由AB ∥CD 得到∠ABD +∠CDB =180°，根据四边形的内角和得到∠2+∠3+∠EBD +∠FBD =360°，于是得到结论．【详解】解：连接BD ，如图，∵AB ∥CD ，∴∠ABD +∠CDB =180°，∵∠2+∠3+∠EBD +∠FBD =360°，∴∠2+∠3+∠EBD +∠FDB +∠ABD +∠CDB =540°，即∠1+∠2+∠3+∠4=540°．故答案为：540°．【点睛】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．【变式训练】【答案】34︒/34度【分析】过E 作EG AB ∥BED BEG DEG ∠=∠+∠AB CD ∥ ，AB EG FH CD ∴∥∥∥ABE BEG ∴∠=∠，DEG ∠DFH CDF ∠=∠，BFH ∠【答案】②③④【分析】①过点E作EF∥AB，由平行线的性质即可得出结论；②过点点E作EF∥AB，由平行线的性质即可得出结论；③如图3，过点C作CD∥AB，延长AB到G，由平行线的性质可得出180④过点P作PF∥AB，由平行线的性质可得出∠A=∠CPF+∠APC=∠C+②如图2，过点E 作EF ∥AB ，∵AB ∥CD ，∴AB ∥EF ∥CD ，∴∠A =∠AEF ，∠C =∠CEF ，∴∠A +∠C =∠CEF +∠AEF =∠AEC ，则②正确；③如图3，过点C 作CD ∥AB ，延长AB 到G ，∵AB ∥EF ，∴AB ∥EF ∥CD ，∴∠DCF =∠EFC ，由②的结论可知∠GBH +∠HCD =∠BHC ，又∵180GBH ABH =︒-∠∠，∠HCD =∠HCF -∠DCF∴180°-∠ABH +∠HCF -∠DCF =∠BHC ，∴180°-∠ABH +∠HCF -∠EFC =∠BHC ，∴180x αβγ︒-+-=∠∠∠∠，故③正确；④如图4，过点P 作PF ∥AB ，∵AB ∥CD ，∴AB ∥PF ∥CD ，∴∠A =∠APF ，∠C =∠CPF ，∴∠A =∠CPF +∠APC =∠C +∠APC ，则④正确；故答案为：②③④．【点睛】本题考查的是平行线的性质，根据题意作出辅助线是解答此题的关键．3．（23·24八年级上·广东江门·阶段练习）（1）如图①，如果AB CD ∥，求证：APC A C ∠=∠+∠．（2）如图②，AB CD ∥，根据上面的推理方法，直接写出A P Q C ∠+∠+∠+∠=___________．（3）如图③，AB CD ∥，若ABP x BPQ y PQC z QCD m ∠=∠=∠=∠=，，，，则m =___________（用x 、y 、z 表示）．【答案】（1）见解析；（2）540︒；（3）x z y+-【分析】（1）过P 作PM AB ∥，利用平行线的判定与性质证明即可；（2）过点P 作PE AB ∥，过点Q 作QF AB ∥，根据平行线的性质即可求解；（3）过点P 作PN AB ∥，过点Q 作QM AB ∥，根据平行线的性质求解即可．【详解】（1）证明：过P 作PM AB ∥，如图，∴A APM ∠=∠，∵PM AB AB CD ∥，∥（已知），∴PM CD ∥，∴C CPM ∠=∠，∵APC APM CPM ∠=∠+∠，∴APC A C ∠=∠+∠；（2）如图，过点P 作PE AB ∥，过点Q 作QF AB ∥，∵AB DC ∥，PE AB ∥，QF AB ∥，∴AB PE QF CD ∥∥∥，∴180A APE ∠+∠=︒，180EPQ PQF ∠+∠=︒，=180FQC QCD ∠+∠︒，∴=540A APQ PQC C ∠+∠+∠+∠︒，故答案为：540︒；（3）过点P 作PE AB ∥，过点Q 作QF AB ∥，∵AB DC ∥，PE AB ∥，QF AB ∥，∴AB PE QF CD ∥∥∥，∴B BPE ∠=∠，QPE PQF ∠=∠，=FQC C ∠∠，∴=B PQC C BPQ ∠+∠∠+∠，即=x z m y ++，∴=m x z y +-，故答案为：x z y +-．【点睛】本题考查平行线的判定与性质，灵活运用平行线的性质和判定是解题的关键．4．（2023下·海南省直辖县级单位·七年级统考期末）如图1，AB CD ∥，点P 为直线AB CD ，间一点，点E ，F 分别是直线AB CD ，上的点，连接EP FP ，.(1)【证明推断】求证：EPF AEP CFP ∠=∠+∠，请完善下面的证明过程，并在（）内填写依据.证明：过点P 作直线MN AB ∥，MN AB ∥ （已作），AEP EPN ∴∠=∠（______），又MN AB ∥ ，AB CD ∥（已知）∴______，（______）CFP FPN ∴∠=∠，AEP CFP EPN FPN ∴∠+∠=∠+∠=______.(2)如图2，若AEP ∠的平分线与PFC ∠的平分线交于点Q .①【类比探究】试猜想EPF ∠与EQF ∠之间的关系，并说明理由；②【结论运用】若240BEP DFP ∠+∠=︒，求EQF ∠的度数.(3)【拓展认知】如图3，直线AB CD ∥，点P ，H 为直线AB CD 、间的点，请直接写出AEP ∠，PHF ∠，EPH ∠，HFD ∠的数量关系：______.【答案】(1)两直线平行，内错角相等；MN CD ∥；平行于同一直线的两直线平行；EPF∠（3）过点P、H作m∥【点睛】本题考查平行的性质，角平分线的定义，添加合适的辅助线是解题关键．5．（2023上·重庆九龙坡·八年级重庆市育才中学校考开学考试）如图CD 上，点O 在直线AB 、CD 之间，且(1)求BEO OFD ∠+∠的值；(2)如图2，直线MN 分别交BEO ∠、OFC ∠的角平分线于点M 、N ，直接写出EMN ∠-(3)如图3，EG 在AEO ∠内，AEG m OEG ∠=∠；FH 在DFO ∠内，DFH m OFH ∠=∠，直线FH 分别于点M 、N ，且80FMN ENM ∠-∠=︒，直接写出m 的值．【答案】(1)280︒(2)50︒（2）解：如图2，过点M ，AB CD∥∴∥∥∥，AB MK NI CD∠∴∠=∠，KMN BEM EMK∴∠-∠=∠EMN FNM EMK（3）解：如图3，设直线FH∥，AB CD∴∠=∠，AHF DFHAHF EPH PEH∠=∠+∠=∴∠=∠+∠，DFH EPH AEG【点睛】本题考查了平行线的性质，角平分线的性质及三角形的外角性质，熟练掌握平行线的性质、角平分线的性质及三角形的外角性质并正确作出辅助线是解题关键．【考点三平行线中含多个拐点问题】例题：如图，直线AB CD ∥，则23415∠+∠+∠-∠-∠的度数为___________°．【答案】360【分析】过E 作EF ∥CD ，过G 作GH ∥CD ，过M 作MN ∥CD ，根据平行线的判定得出EF ∥GH ∥MN ∥AB ∥CD ，根据平行线的性质得出即可．【详解】过E 作EF ∥CD ，过G 作GH ∥CD ，过M 作MN ∥CD ，如图所示：∵CD ∥AB ，∴EF ∥GH ∥MN ∥AB ∥CD ，∴∠1=∠BEF ，∠GEF +∠EGH =180°，∠HGM +∠GMN =180°，∠NMC =∠5，∵∠2=∠BEF +∠GEF ，∠3=∠EGH +∠HGM ，∠4=∠GMN +∠NMC ，∴23415∠+∠+∠-∠-∠BEF GEF EGH HGM GMN NMC BEF NMC=∠+∠+∠+∠+∠+∠-∠-∠360GEF EGH HGM GMN =∠+∠+∠+∠=︒．故答案为：360．【点睛】本题考查了平行线的性质，能灵活运用平行线的性质进行推理是解此题的关键．【变式训练】【答案】88︒/88度【分析】本题考查平行线的性质、角平分线的定义等，解题的关键是会添加常用辅助线（即过2．（2023上·七年级课时练习）观察图形：已知a b ，在图1中，可得12∠+∠=_______________度，在图度……按照以上规律，则112n P P ∠+∠+∠++∠= _______________【答案】180，360，()1801n +．【详解】解：如图1，∵a b ，∴12180∠+∠= ；如图2，过1P 作11PQ a ，∵a b ，∴11PQ a b ，∴111180APQ ∠+∠=︒，112180BPQ ∠+∠=︒，∴112360APB ∠+∠+∠=；同理可得：112180(1)n P P n ∠+∠+∠++∠=+ ；故答案为：180，360，()1801n +．【点睛】本题考查平行线的性质，掌握两直线平行，同旁内角互补是解题的关键．3.如图：(1)如图1，1l ∥2l ，若65P ∠= ，计算并直接写出A B ∠∠+的大小．(2)如图2，在图1的基础上，将直线PB 变成折线PQB ，证明：180A B Q P ∠∠∠∠++=+(3)如图3，在图2的基础上，继续将且线BQ 变成折现BMQ ．请你写出一条关于1∠、2345∠∠∠∠，，，的数量关系（无需证明直接写出）【答案】(1)65°(2)见解析(3)∠1+∠3+∠5=∠2+∠4【分析】（l ）过P 作PE ∥l 1，根据平行线的性质和角的和差即可得到结论；（2）过点P 、Q 分别作l 1和l 2的平行线分别记为l 3和l 4，根据平行线的性质和等量代换即可得到结论；（3）分别过P ，Q ，M 作PC ∥l 1，QD ∥l 1，ME ∥l 1，根据平行线的性质和角的和差即可得到结论．（1）解：过P作PE∥l1∵l1∥l2∴PE∥l2∥l1∴∠A=∠1，∠B=∠2∴∠APB=∠1+∠2=∠A+∠B=65°即∠A+∠B=65°；（2）证明：过点P、Q分别作l1和l2的平行线分别记为l3和l4∵l1∥l2∴l1∥l2∥l3∥l4∵l1∥l3（已知）∴∠A=∠1（两直线平行，内错角相等）∵l3∥l4（已知）∴∠2＝∠3（两直线平行，内错角相等）∵l2∥l4（已知）∴∠4+∠B=180°（两直线平行，同旁内角互补）∴∠A+∠3+∠4+∠B=∠1+∠2+180°又∵∠1+∠2=∠P，∠3+∠4=∠Q∴∠A+∠B+∠Q=∠P+180°．（3）解：如图，分别过P，Q，M作PC∥l1，QD∥l1，ME∥l1，∵12l l ∥，∴12////////PC QD ME l l ∴∠1=∠APC ，∠QPC =∠PQD ∴∠2=∠1+∠PQD ，∠4=∠∴∠2+∠4=∠1+∠PQD +∠5∴∠1+∠3+∠5=∠2+∠4．【点睛】本题考查了平行线的性质及平行公理的推论，熟练掌握平行线的性质是解题的关键．4．猜想说理：（1）如图，AB CD EF ∥∥形说明理由：拓展应用：（2）如图4，若AB CD ，则A C AFC ∠+∠+∠=（3）在图5中，若1n A B A D ∥，请你用含n 的代数式表示【答案】（1）A C AFC ∠∠∠＋＝；A C AFC ∠-∠∠＝；∠（2）360（3）-1180n ⨯︒（）【分析】（1）根据平行线的性质可直接得到结论；度数；通过前面的计算，找出规律．利用规律得到有n 个折点的结论；【详解】解：（1）如图1：A C AFC ∠∠∠＋＝，如图2：A C AFC ∠-∠∠＝，如图3：C A AFC ∠-∠∠＝，如图1说明理由如下：∵AB CD EF ∥∥，∴A AFE C EFC ∠∠∠∠＝，＝，∴A C AFE EFC ∠∠∠∠＋＝＋，即A C AFC ∠∠∠＋＝；（2）如下图：过F 作FH AB ∥，∴180A AFH ∠∠︒＋＝，又∵AB CD ∥，∴CD FH ∥，∴180C CFH ∠∠︒＋＝，∴360A AFH C CFH ∠∠∠∠︒＋＋＋＝，即360A C AFC ∠∠∠︒＋＋＝；故答案为：360；（3）如下图：AB CD ∥，过E 作EG AB ∥，过F 作FH AB ∥，∵AB CD ∥，∴AB EG FH CD ∥∥∥，∴180A AEG ∠∠︒＋＝，180GEF EFH ∠∠︒＋＝，180HFC C ∠∠︒＋＝，∴1803A AEG GEF EFH HFC C ∠∠∠∠∠∠︒⨯＋＋＋＋＋＝，即540A AEF EFC C ∠∠∠∠︒＋＋＋＝；综上所述：由当平行线AB 与CD 间没有点的时候，180A C ∠∠︒＋＝，当A 、C 之间加一个折点F 时，2180A AFC C ∠∠∠⨯︒＋＋＝；当A 、C 之间加二个折点E 、F 时，则3180A AEF EFC C ∠∠∠∠⨯︒＋＋＋＝；以此类推，如图5，1n A B A D ∥，当1A 、5A 之间加三个折点234A A A 、、时，则123454180A A A A A ∠+∠∠∠∠⨯︒＋＋＋＝；…当1A 、n A 之间加n 个折点231n A A A -⋯、、时，则123-1180n A A A A n ∠∠∠⋯∠⨯︒＋＋＋＝（），即1234n ∠∠∠∠∠＋＋＋＋＋L 的度数是-1180n ⨯︒（）．【点睛】本题是探索型试题，主要考查了平行线的性质，根据题意作出辅助线，利用平行线的性质及三角形外角的性质等知识求解是解答此题的关键．【考点四平行线中在生活上含拐点问题】例题：（2023·广东深圳·校考模拟预测）“绿水青山，就是金山银山”在两个景区之间建立上的一段观光索道如图所示，索道支撑架均为互相平行（AM CN ∥），且每两个支撑架之间的索道均是直的，若65MAB ∠=︒，55NCB ∠=︒，则ABC ∠=（）A ．110︒B ．115︒C ．120︒D ．125︒【答案】C 【分析】过点B 作∥BD AM ，则BD AM CN ∥∥，由平行线的性质可得65ABD MAB ∠=∠=︒，55CBD NCB ∠=∠=︒，由此进行计算即可得到答案．【详解】解：如图，过点B 作∥BD AM ，，AM CN ∥，A BD M CN ∴∥∥，65MAB ∠=︒，55NCB ∠=︒，65ABD MAB ∴∠=∠=︒，55CBD NCB ∠=∠=︒，6555120ABC ABD CBD ∴∠=∠+∠=︒+︒=︒，故选：C ．【点睛】本题考查了平行线的性质，熟练掌握两直线平行，内错角相等是解此题的关键．【变式训练】1．（2023下·山西临汾·七年级统考期中）图①是某种青花瓷花瓶，图②是其抽象出来的简易轮廓图，已知AG EF ，AB DE ∥，若120DEF ∠=︒，则A ∠的度数为（）A ．60°B ．65°C ．70°D ．75°【答案】A 【分析】连接CF ，根据AB CF ，AG EF 可得出CFE BAG ∠=∠，再由平行线的性质即可得出结论．【详解】解：连接CF ，延长AG 交CF 于点H ，作MN AG ，如图AB CF DE ∥∥，120DEF ∠=︒18012060CEF ∴∠=︒-︒=︒，AHF BAG∠=∠∵AG EF ，AG MN∥∴AHF MNF ∴∠=∠，EF MN∥60CFE FNM BAG ∴∠=∠=∠=︒．故选：A ．【点睛】本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解题的关键．2．（2023下·浙江台州·七年级统考期末）如图是路政工程车的工作示意图，工作篮底部AB 与支撑平台CD 平行．若130∠=︒，3150∠=︒，则2∠=（）A ．60︒B ．50︒【答案】C 【分析】过2∠顶点作直线l 【详解】解：如图所示，过∠∵工作篮底部与支撑平台平行、直线∴直线l 支撑平台 工作篮底部，∴1430∠=∠=︒，53180∠+∠=︒∴230∠=︒，∴24560∠=∠+∠=︒，故选：C ．【答案】100︒/100度【分析】过点D 作DG AB ∥，过点【详解】解：过点D 作DG ∥∵EF MN ⊥，∴90MFE ∠=︒，∵AB MN ∥，∴AB DG EH MN ∥∥∥，∴180ACD CDG ∠+∠=︒，DEH GDE ∠=∠，90HEF MFE ∠=∠=︒∵120,110DEF BCD ∠=︒∠=︒，∴30GDE DEH ︒∠=∠=，18011070CDG ∠︒=︒-︒=，∴100CDE CDG GDE =∠+∠=︒∠．故答案为：100︒【点睛】本题考查了平行线的判定和性质，解题的关键是过拐点构造平行线．。

专题02 平行线中的拐点模型之铅笔头模型平行线中的拐点模型在初中数学几何模块中属于基础工具类问题，也是学生必须掌握的一块内容，熟悉这些模型可以快速得到角的关系，求出所需的角。

本专题就平行线中的拐点模型（铅笔头模型）进行梳理及对应试题分析，方便掌握。

拐点（平行线）模型的核心是一组平行线与一个点，然后把点与两条线分别连起来，就构成了拐点模型，这个点叫做拐点，两条线的夹角叫做拐角。

通用解法：见拐点作平行线；基本思路：和差拆分与等角转化。

模型2：铅笔头模型图1 图2 图3如图1，①已知：AM∥BN，结论：∠1+∠2+∠3=360°；②已知：∠1+∠2+∠3=360°，结论：AM∥BN.如图2，已知：AM∥BN，结论：∠1+∠2+∠3+∠4=540°如图3，已知：AM∥BN，结论：∠1+∠2+…+∠n=（n－1）180°.【模型证明】在图1中，过P作AM的平行线PQ，∵AM∥BN，∴PQ∥BN，∴∠1+∠APQ＝180°，∠3+∠BPQ＝180°，∴∠1+∠2+∠3＝360°；在图2中，过P1作AM的平行线P1C，过点P2作AM的平行线P2D，∵AM∥BN，∴AM∥P1C∥P2D∥BN，∴∠1+∠AP1C＝180°，∠P2P1C+∠P1P2D＝180°，∠BP2D+∠4＝180°，∴∠1+∠2+∠3+∠4＝540°；在图3中，过各角的顶点依次作AB的平行线，根据两直线平行，同旁内角互补以及上述规律可得：∠1+∠2+∠3+…+∠n＝（n﹣1）180°．例1．（2023·江苏南通·校考二模）如图，已知//AB CD ，140A Ð=°，120E Ð=°，则C Ð的度数是（ ）A ．80°B ．120°C ．100°D ．140°【答案】C 【分析】过E 作直线MN //AB ，根据两直线平行，同旁内角互补即可求出∠1，进而可求出∠2，然后根据平行于同一条直线的两直线平行可得MN //CD ，根据平行线性质从而求出∠C ．【详解】解：过E 作直线MN //AB ，如下图所示，∵MN //AB ，∴∠A +∠1＝180°（两直线平行，同旁内角互补），∴∠1＝180°﹣∠A ＝180°﹣140°＝40°，∵12120AEC Ð=Ð+Ð=°，∴211204080AEC Ð=Ð-Ð=°-°=°∵MN //AB ，AB //CD ，∴MN //CD ，∴∠C +∠2＝180°（两直线平行，同旁内角互补），∴∠C ＝180°﹣∠2＝180°﹣80°＝100°，故选：C ．【点睛】此题考查的是平行线的判定及性质，掌握构造平行线的方法是解决此题的关键．例 2．（2023·山西吕梁·校联考模拟预测）如图，这是路政工程车的工作示意图，工作篮底部与支撑平台平行.若132Ð=°，262Ð=°，则3Ð的度数为（ ）A ．118°B ．148°C ．150°D ．162°【答案】C 【分析】过点B 作BA ∥工作篮底部，根据平行线的性质及角的和差求解即可．【详解】解：如图，过点B 作BA ∥工作篮底部，3180MBA \Ð+Ð=°，Q 工作篮底部与支撑平台平行，BA ∥工作篮底部BA \∥支撑平台，132ABN \Ð=Ð=°，2ABN MBA Ð=Ð+ÐQ ，262Ð=°，30MBA \Ð=°，3150\Ð=°，故选：C ．【点睛】此题考查了平行线的性质，熟记“两直线平行，内错角相等”、“两直线平行，同旁内角互补”是解题的关键．例3．（2023下·江苏·七年级专题练习）如图，AB //ED ，α＝∠A +∠E ， β＝∠B +∠C +∠D ，则β与α的数量关系是（ ）A ．2β＝3αB ．β＝2αC ．2β＝5αD ．β＝3α【答案】B 【分析】作CF //ED ，利用平行线的性质求得β与α，再判断β与α的数量关系即可．【详解】解：如图，作CF //ED ， ∵AB //ED ，∴∠A +∠E =180°= α ，∵ED //CF ， ∴∠D +∠DCF =180°，∵AB //ED ，ED //CF ，∴AB //CF ，∴∠B +∠BCF =180°，∴∠D +∠DCF +∠B +∠BCF =180°+180° 即 ∠B +∠C +∠D =360°= β ， ∴ β＝2α ． 故选B ．【点睛】本题考查了平行线的性质，熟悉运用平行线的性质是解题的关键．例4．（2023下·广西南宁·七年级校考期末）如图，如果AB EF ∥，那么ABC BCD CDE DEF Ð+Ð+Ð+Ð=A ．270°B ．360°【答案】C 【分析】利用平行线的性质，结合所作的辅助线，可以得出答案．【详解】解：过点C 作CM AB ∥∵AB EF ∥，∴AB CM DN EF ∥∥∥，∴1180ABC Ð+Ð=°，23180Ð+Ð=°，Ð∴540ABC BCD CDE DEF Ð+Ð+Ð+Ð=【点睛】本题考查了平行线的性质及判定的相关知识点，掌握知识点是解答此题的关键．例5．（2023下·湖北武汉·七年级期末）如图，【答案】60°/60度【分析】根据平角定义可求出，∴180ABC BCM Ð+Ð=°，180MCF EFC +Ð=°，BCM Ð∴360ABC FCB EFC Ð+Ð+а，∵120FCB Ð=°，∴360360ABC EFC FCB Ð=-Ð=°-∵14ABP ABC Ð=Ð， 14EFP EFC Ð=Ð，A ．2360P Q Ð+Ð=°B ．2【答案】A 【分析】过点P 作PM AB ∥,EPM AEP FPM CFP Ð=ÐÐ=Ð进而得到12EQF Ð=Ð+Ð，再由角平分线的定义可得()2122PEB PFD EQF Ð+Ð=Ð+Ð=Ð，即可求解．【详解】解：如图，过点P 作PM AB ∥，过点Q 作QN AB ∥，∵AB CD P ，∴PM AB CD QN ∥∥∥，∴,EPM AEP FPM CFP Ð=ÐÐ=Ð，1,2EQN FQN Ð=ÐÐ=Ð，180,180PEB EPM PFD FPM Ð+Ð=°Ð+Ð=°，∴12EQF Ð=Ð+Ð，∵PEB Ð和PFD Ð的平分线交于点Q ，∴21,22PEB PFD Ð=ÐÐ=Ð，∴()()21222PEB PFD EQN FQN EQF Ð+Ð=Ð+Ð=Ð+Ð=Ð，∵180,180PEB EPM PFD FPM Ð+Ð=°Ð+Ð=°，∴2360EPF EQF AEP CFP PEB PFD Ð+Ð=Ð+Ð+Ð+Ð=°．故选：A ．【点睛】本题考查了平行线的性质，平行公理的推论，角平分线的定义，熟练掌握平行线的性质是解题的关键．例7．（2023下·江苏南京·七年级统考期中）从特殊到一般是数学研究的常用方法，有助于我们发现规律，探索问题的解．(1)如图1，AB CD ∥，点E 为AB 、CD 之间的一点．求证：12360MEN Ð+Ð+Ð=°．(2)如图2，AB CD ∥，点E 、F 、G 、H 为AB 、CD 之间的四点．则123456Ð+Ð+Ð+Ð+Ð+Ð=______．(3)如图3，AB CD ∥，则123n Ð+Ð+Ð++Ð=L ______．【答案】(1)证明见详解；(2)900°；(3)()1801°-n ；【分析】（1）过点E 作OE ∥A B ，可得OE AB CD ∥∥，根据平行线的性质可得1180MEO Ð+Ð=°，2180OEN Ð+Ð=°，再计算角度和即可证明；（2）分别过点E 、F 、G 、H 作AB 的平行线，在两相邻平行线间利用两直线平行同旁内角互补求得两角度和后，再将所有角度相加即可解答；（3）由（2）解答可知在AB 、CD 之间每有一条线段便可求得一个180°角度和，结合图3找出n 和线段条数的关系便可解答；【详解】（1）证明：如下图，过点E 作OE ∥A B ，∵AB CD ∥，OE ∥A B ，∴P OE CD ，根据两直线平行同旁内角互补可得：1180MEO Ð+Ð=°，2180OEN Ð+Ð=°，∴12360MEO OEN Ð+Ð+Ð+Ð=°，∴12360MEN Ð+Ð+Ð=°；（2）解：如下图，分别过点E 、F 、G 、H 作1O E AB ∥，2O F AB ∥，3O G AB ∥，4O H AB ∥，结合（1）解答在两相邻平行线间可得：1180AME MEO Ð+Ð=°，12180O EF EFO Ð+Ð=°，23180O FG FGO Ð+Ð=°，34180O GH GHO Ð+Ð=°，4180O HN HNC Ð+Ð=°，将所有角度相加可得：1234561805900Ð+Ð+Ð+Ð+Ð+Ð=°´=°；（3）解：由（2）解答可知在AB 、CD 之间每有一条线段便可求得一个180°角度和，由图3可知：当AB 、CD 之间有2条线段时，3n =，当AB 、CD 之间有3条线段时，4n =，当AB 、CD 之间有4条线段时，5n =，当AB 、CD 之间有5条线段时，6n =，…，当AB 、CD 之间有()1n -条线段时，n n =，∴()1231801n n Ð+Ð+Ð++Ð=°-L ；【点睛】本题考查了平行线公理的推论，平行线的性质，归纳总结的解题思路，通过作辅助线将角度按组计算是解题关键．例8．（2023下·江苏苏州·七年级校考期中）当光线经过镜面反射时，入射光线、反射光线与镜面所夹的角对应相等例如：在图①、图中②，都有12Ð=Ð，3=4ÐÐ，设镜子AB 与BC 的夹角αABC Ð=．(1)如图①，若α90=°，判断入射光线EF 与反射光线GH 的位置关系，并说明理由．(2)如图②，若90α180°<<°，入射光线EF 与反射光线GH 的夹角βFMH Ð=，探索α与β的数量关系，并说明理由．(3)如图③，若α120=°，设镜子CD 与BC 的夹角γ(90γ180)BCD Ð=°<<°，入射光线EF 与镜面AB 的夹角1(090)m m Ð=°<<°，已知入射光线EF 从镜面AB 开始反射，经过(n n 为正整数，且3)n £次反射，当第n 次反射光线与入射光线EF 平行时，请直接写出γ的度数(可用含有m 的代数式表示)．【答案】(1)EF GH ∥，见解析(2)2180b a =-°，见解析(3)90m °+或150°【分析】（1）在BEG V 中，23α180ÐÐ++=°，α90=°，可得2390Ð+Ð=°，根据入射光线、反射光线与镜面所夹的角对应相等可得，180FEG EGH Ð+Ð=°，进而可得//EF GH ；（2）在BEG V 中，23α180ÐÐ++=°，可得23180αÐÐ+=°-，根据入射光线、反射光线与镜面所夹的角对应相等可得，22MEG ÐÐ=，23MGE ÐÐ=，在MEG V 中，β180MEG MGE ÐÐ++=°，可得α与β的数量关系；（3）分两种情况画图讨论：①当3n =时，根据入射光线、反射光线与镜面所夹的角对应相等，及GCH △内角和，可得γ90.m =°+②当2n =时，如果在BC 边反射后与EF 平行，则α90=°，与题意不符；则只能在CD 边反射后与EF 平行，根据三角形内角和定理推出，可得γ60G Ð=-°，由EF HK ∥，且由（1）的结论可得，γ150=°．【详解】（1）EF GH ∥，理由如下：在BEG V 中，23α180ÐÐ++=°，α90=°，2390\Ð+Ð=°，12Ð=ÐQ ，3=4ÐÐ，1234180Ð+Ð+Ð+Ð=\°，12180FEG ÐÐÐ++=°Q ，34180EGH ÐÐÐ++=°，180FEG EGH \Ð+Ð=°，EF GH \∥；（2）β2α180=-°，理由如下：在BEG V 中，23α180ÐÐ++=°，23180αÐÐ\+=°-，12Ð=ÐQ ，1MEB Ð=Ð，2\Ð=ÐMEB ，22\Ð=ÐMEG ，同理可得，23MGE ÐÐ=，在MEG V 中，β180MEG MGE ÐÐ++=°，()β180MEG MGE ÐÐ\=°-+()1802223ÐÐ=°-+()180223ÐÐ=°-+()1802180α=°-°-2α180=-°；1BEG m ÐÐ==Q ，18012060BGE CGH m m ÐÐ\==°-°-=°-，180211802FEG m ÐÐ\=°-=°-(1802180260EGH BGE Ð=°-=°-°EF HK Q ∥，360FEG EGH GHK \Ð+Ð+=°，则120GHK Ð=°，则30GHC Ð=，由GCH △内角和得γ90m =°+．②当2n =时，如果在BC 边反射后与EF 平行，由（1）可知α90=°，与题意不符；则只能在CD 边反射后与EF 平行，如下图所示，设AB 与DC 的延长线交于点【答案】(1)110°(2)3603APC AQC Ð=°-Ð；(3)11n n -+【分析】（1）过点P 作PQ AB ∥，则PQ AB CD ∥∥，根据平行线的性质即可求解；（2）过点P 作PM AB ∥，过点Q 作QN AB ∥，则PM AB CD ∥∥，QN C AB D ∥∥，结合22QAP QAB QCP QCD Ð=ÐÐ=Ð，，即可得到结论；（3）过点P 作PE AB ∥，则PE ∥∵130PAB Ð=°，∴13050APQ Ð=-°=°，∵120APC Ð=°，∴5070CPQ Ð=°-°=°，∴18070110PCD Ð=°-°=°；（2）解：过点P 作PM ∥，过点Q 作QN AB ∥，则PM AB CD ∥，QN C AB D ∥∥∴180180PAB APM PCD CPM Ð+Ð=°Ð+Ð=°，，，即()360APC PAB PCD Ð=°-Ð+Ð，同理：AQC BAQ Ð=Ð课后专项训练1．（2023下·江苏苏州·七年级校考期中）如图，在五边形ABCDE 中，AE BC ∥，则C D E Ð+Ð+Ð=（ ）A ．540°B ．360°C ．270°D ．180°【答案】B 【分析】首先过点D 作DF AE ∥，交AB 于点F ，由AE BC ∥，可证得AE DF BC ∥∥，然后由两直线平行，同旁内角互补可知180E EDF Ð+Ð=°，180CDF C Ð+Ð=°，继而证得结论．【详解】解：过点D 作DF AE ∥，交AB 于点F ，AE BC Q ∥，AE DF BC \∥∥，180E EDF \Ð+Ð=°，180CDF C Ð+Ð=°，360C CDE E \Ð+Ð+Ð=°．故选：B ．【点睛】此题考查了平行线的性质，注意掌握辅助线的作法，注意数形结合思想的应用．2．（2023上·四川绵阳·八年级统考开学考试）如图，一束光线AB 先后经平面镜OM ，ON 反射后，当35ABM Ð=°时，DCN Ð的度数为（ ）A ．55°B ．70°C ．60°D ．35°【答案】A 【分析】根据入射角等于反射角以及“两直线平行，同旁内角互补”解答即可．【详解】解：∵35ABM Ð=°，ABM OBC Ð=Ð，∴35OBC Ð=°，∴1801803535110ABC ABM OBC Ð=°-Ð-Ð=°-°-°=°，∵CD AB ∥，∴180ABC BCD Ð+Ð=°，∴18070BCD ABC Ð=°-Ð=°，A．115°B．120°【答案】A【分析】直接利用平移的性质结合平行线的性质得出答案．【详解】解：过B 作h m ∥，由题意可得：m n ∥,∴h n ∥，∴1180ABD Ð+Ð=°，∴3DBC Ð=Ð，180118065115ABD Ð=°-Ð=°-°=°，∴232115DBC ABD Ð-Ð=Ð-Ð=Ð=°．故选：A ．【点睛】此题主要考查了平移的性质以及平行线的性质，正确转化角的关系是解题关键．5．（2023·安徽安庆·八年级统考期中）一把直尺与一块直角三角板按如图方式摆放，若146Ð=°，则2Ð=（ ）A ．46°B ．44°C ．42°D ．40°【答案】B 【分析】本题考查平行线的性质，掌握两直线平行，同位角相等是解题的关键，过三角板的直角顶点作直尺两边的平行线，根据平行线的性质可得1346Ð=Ð=°，24ÐÐ=，再结合角的和差关系可得答案.【详解】解：过三角板的直角顶点作直尺两边的平行线，∵直尺两边互相平行，∴1346Ð=Ð=°，24ÐÐ=，∵490344Ð=°-Ð=°，∴2444Ð=Ð=°，故选：B ．6．（2023下·山东烟台·七年级统考期末）如图，按虚线剪去长方形纸片的相邻两个角，并使1160Ð=°，AB BC ^，则2Ð的度数为（ ）A ．100°B ．110°C ．120°D ．130°【答案】B 【分析】过点B 作BE AD ∥，然后根据两直线平行，同旁内角互补得出12360ABE CBE Ð+Ð+Ð+Ð=°，再解答即可．【详解】解：过点B 作BE AD ∥，∴1360ABE Ð+Ð=°∵CF AD ∥，∴CF BE AD ∥∥，∴2360CBE Ð+Ð=°∴12360ABE CBE Ð+Ð+Ð+Ð=°，∴12360ABC Ð+Ð+Ð=°，∵AB BC ^∴90ABC Ð=°∵1160Ð=°，∴2Ð的度数为110°．故选：B ．【点睛】本题主要考查了平行线的性质，加辅助线，然后利用平行线的性质求解是解此题的关键．7．（2023下·广东中山·七年级校联考期中）如图，已知：,115,135AB CD B D Ð=°Ð=°∥，则E Ð= （ ）A ．105°B ．110°C ．115°D ．120°【答案】B 【分析】过点E 作ME AB ∥，根据平行线的性质得出180B BEM Ð+Ð=°，180D DEM Ð+Ð=°，再根据角的和差求解即可．AB CD ∥Q ，ME AB CD \∥∥115B Ð=°Q ，135D Ð=°，\Ð110BED BEM DEM \Ð=Ð+Ð=A ．40°B ．50°【答案】C 【分析】利用多边形的内角和公式求得五边形的内角和，再由平行线性质求得BAE ABC BCD Ð+Ð+Ð，最后利用角的和差即可求得答案．【详解】解：∵四边形ABCDE 为五边形，【答案】540°/540度【分析】可过点B ，【详解】解：如图，过点AE DF ∥Q ，AE BM CN \∥∥则180A ABM Ð+Ð=°，MBC ÐA ABM MBC BCN =Ð+Ð+Ð+Ð【点睛】本题主要考查平行线的判定与性质，平行公理的推论，掌握两直线平行，同旁内角互补是解决此【答案】1402n °+°【分析】首先过点E 作EF AB ∥，由平行线的传递性得得出B C D A B C n Ð=Ð=°，BAD Ð=由两直线平行，内错角相等得出BEF Ð∥Q AB CD ，∴B C D A B C n Ð=Ð=°，Ð又∵BE 平分ABC Ð，DE 平分ADC Ð，∵AB EF CD ∥∥，∴12BEF ABE n Ð=Ð=° ∴1402BED FED BEF n Ð=Ð+Ð=°+°，故答案为：【答案】50【分析】先根据平行公理判定【详解】解:如图，过点∵CM EF ∥,AB EF ∥，∵155A Ð=°，105E Ð=°∵CD 平分ACE Ð，ACD \Ð【答案】150【分析】过点B 作BF AE P ，根据平行线的性质可得90BAE Ð=°，则90ABF Ð=°，可求出CBF Ð=【详解】解：过点B 作BF AE P ，∵CD AE ∥，∴BF AE CD ∥∥∵BA AE ^，∴90BAE Ð=°，∵120ABC Ð=°，∴30CBF Ð=【点睛】本题主要考查了平行线的性质和判定，解题的关键是掌握：平行于同一直线的两直线互相平行；【答案】3b a =/13a =【点睛】本题考查平行线的性质，关键是过点平行线的性质即可解决问题．14．（2023下·贵州安顺=540°，根据以上的规律求【答案】140【分析】过点E作EM Q AB CD∥，EM AB∥Q的平分线与ABFÐ1\Ð=ÐÐ,ABE ABF【答案】①②③④【分析】根据平行公理判断到212180Ð+Ð=°，2+4=90ÐÐ得到2123360Ð+Ð=°，根据【点睛】本题考查了平行线的判定和性质，熟练应用判定定理和性质定理是解题的关键，平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．【答案】（1）55°；（2）140°【点睛】本题考查平行线的性质和三角形外角的性质，掌握两直线平行，同旁内角互补，是解题的关键．18．（2023下·江苏南京·七年级校联考期末）珠江某河段两岸安置了两座可旋转探照灯示，假如河道两岸是平行的，PQ MN ∥，且(1)填空：BAN Ð= °；(2)若灯B 射线先转动30秒，灯A 射线才开始转动，在灯A 灯转动几秒，两灯的光束互相平行？(3)如图3，若两灯同时转动，在灯A 射线到达的射线AC 与BC 交于点C ，过C 作ACD Ð交PQ 于点D ，且120ACD Ð=°，则在转动过程中，与BCD Ð的数量关系，并说明理由．①当090t <<时，如图1，PQ MN Q ∥，PBD BDA \Ð=ÐAC BD Q P ，CAM BDA \Ð=Ð，CAM PBD \Ð=Ð2t \=②当90150t <<时，如图2，PQ MN Q ∥，PBD BDA \Ð+ÐAC BD Q P ，CAN BDA \Ð=Ð180PBD CAN \Ð+Ð=°1802CAN t Ð=°-Q ，\Ð又120ABC t Ð=°-Q ，(1)如图①，点C 是夹在AB 和DE 之间的一点，当AC CD ^时，垂足为C ，你知道(2)如图②，点1C ，2C 是夹在AB 和DE 之间的两点，请想一想：12A C C Ð+Ð+Ð(3)如图③，随着AB 与DE 之间点的增加，那么121n A C C C D -Ð+Ð+Ð++Ð+ÐL 的度数为必说明理由）【答案】(1)270°(2)540°(3)()180n °【分析】（1）如图所示，过点C 作AB 的平行线CF ，则CF DE AB ∥∥，由平行线的性质得到180A ACF Ð+Ð=°，180DCF D Ð+Ð=°，进而得到360A ACD D Ð+Ð+Ð=°，再由AC CD ^，即可得到270A D Ð+Ð=°．（2）如图所示，过点2C 作2C F AB ∥，则2C AB DE ∥∥，由平行线的性质得到2180D FC D +=°∠∠，同（1）可得112360A C C C F ++=°∠∠∠，112540A C C C D D +++=°∠∠∠∠；（3）由（1）（2）可知，AD DE、之间每多增加一个点，那么所得角度之和就会增加180°，据此规律求解即可．【详解】（1）解：如图所示，过点C 作AB 的平行线CF ．∵AB DE ∥，∴CF DE ∥，∴180A ACF Ð+Ð=°，180DCF D Ð+Ð=°，∴1802360A ACD D Ð+Ð+Ð=°´=°．又∵AC CD ^，∴36090270A D Ð+Ð=°-°=°．（2）解：如图所示，过点2C 作2C F AB ∥，∵AB DE ∥，∴2C F AB DE ∥∥，∴2180D FC D +=°∠∠，同（1）可得112360A C C C F ++=°∠∠∠，∴1122540A C C C F D FC D ++++=°∠∠∠∠∠，∴112540A C C C D D +++=°∠∠∠∠，故答案为：540°；（3）解：由（1）（2）可知，AD DE 、之间每多增加一个点，那么所得角度之和就会增加180°，∴()121180n A C C C D n -Ð+Ð+Ð++Ð+Ð=°L ，故答案为：()180n °．【点睛】本题主要考查了平行线的性质，图形类的规律探索，熟知平行线的性质是解题的关键．20．（2023下·江苏·七年级专题练习）已知AB CD ∥，连接A ，C 两点．(1)如图1，CAB Ð与ACD Ð的平分线交于点E ，则AEC Ð等于(2)如图2，点M 在射线AB 反向延长线上，点N 在射线CD 4570AMN ACN Ð=°Ð=°，，求MEC Ð的度数；(3)如图3，图4，M ，N 分别为射线AB ，射线CD 上的点，()AMN ACN a b a b Ð=Ð=¹，，请直接写出图中MEC Ð的度数（用含【答案】(1)90(2)57.5°(3)1118022a b °-+或1118022b a °-+【分析】（1）根据平行线的性质得到180BAC ACD Ð+Ð=°90CAE ACE Ð+Ð=°，即可求出答案；（2）过点E 作EF ∥∵,ME CE 分别平分BMN ACD Ð，，∴122.52BME BMN Ð=Ð=°，∴3557.5MEC MEF CEF Ð=Ð+Ð=+°=°；（3）①如图3，过点E 作AB ，∵AB CD ∥，∴EF CD ∥，∵11AME AMN a Ð=Ð=，11802MEF a =°-，∵AB CD ∥，∴EF CD ∥，∴Ð∵1122ECD ACD b Ð=Ð=，∴Ð【点睛】此题考查了平行线的性质及角平分线的定义，解题的关键是正确掌握平行线的性质：两直线平行同旁内角互补，两直线平行内错角相等．【答案】(1)80°(2)36012P Ð=°-Ð-Ð；证明见详解(3)140°【分析】（1）过点P 作MN AB ∥，利用平行的性质就可以求角度，解决此问；（2）利用平行线的性质求位置角的数量关系，就可以解决此问；（3）分别过点P 、点G 作MN AB ∥、KR AB ∥，然后利用平行线的性质求位置角的数量关系即可．【详解】（1）解：如图过点P 作MN AB ∥，∵AB CD ∥，∴AB MN CD ∥∥．∴1180EPN Ð+Ð=°，2180FPN Ð+Ð=°．∵1130Ð=°，2150Ð=°，∴12360EPN FPN Ð+Ð+Ð+Ð=° ∴36013015080EPN FPN Ð+=°-°-°=°．∵P EPN FPN Ð=Ð+Ð，∴∠P =80°．故答案为：80°；（2）解：36012P Ð=°-Ð-Ð，理由如下：如图过点P 作MN AB ∥，∵AB CD ∥，∴AB MN CD ∥∥．∴1180EPN Ð+Ð=°，2180FPN Ð+Ð=°．∴12360EPN FPN Ð+Ð+Ð+Ð=°∵EPN FPN P Ð+Ð=Ð，36012P Ð=°-Ð-Ð．（3）如图分别过点P 、点G 作MN AB ∥、KR AB∥（1）如图2，AB CD P ，点M 是AEF Ð和FGC Ð平分线的交点，EFG Ð（2）如图3，AB CD P ，GM 平分CGF Ð，EM GM ^，EF 平分BEM ÐCGF Ð的度数是________．【答案】EFG BEF DGF Ð=Ð+Ð，360；（1）117°；（2）124°【答案】(1)60OFD Ð=°(2)见解析(3)2760n <<【分析】（1）过点O 作AB OH ∥，易得AB CD OH ∥P ,利用平行线的性质可求解；（2）延长EG 交CD 于Z ,由于EG 平分AEO Ð，所以AEG OEG Ð=Ð，根据此条件表示可求出两角的关系；（3）过点O 作AB OK MP NQ P P P ，设2AEG x Ð=，MNF MNG FNG Ð=Ð+Ð，求出n ，m 之间的关系，利用已知条件n m ＞，求出【详解】（1）解：证明：过点O 作AB OH ∥，∵AB CD ∥，∴AB CD OH ∥P ,∴AEO Ð又∵150AEO а＝，90EOF а＝,∴EOH Ð（2）解：GFO Ð与CFG Ð相等，理由如下：延长∵AB CD ∥，∴180AEG CZG Ð+аÐ＝，∵135EGF а＝，且CZG ZGF ZFG Ð=Ð+Ð又∵90EOF а＝，∴在四边形EOFG 中，∵EG 平分AEO Ð，∴AEG OEG Ð=Ð,∴∵AB CD ∥，∴AB CD OK MP NQ ∥P P P ∴90EOF BEO OFD Ð=Ð+Ð=°，即180又∵3EMN n а＝，5MNH m а＝，∴MNF Ð∴322MNF MNQ FNQ n x Ð=Ð+Ð=°-+(1)【特例探究】如图1，90C Ð=°．①CED CGF Ð+Ð=______度；②若CED Ð与CGF Ð的角平分线相交于点P ，则EPG Ð=______度；(2)【一般探索】如图2，C a Ð=，EPG b Ð=．①若13DEP CED Ð=Ð，13FGP CGF Ð=Ð，求a 与b 的关系；②若1DEP CED nÐ=Ð，1FGP CGF n Ð=Ð（2n ³且n 为整数），直接写出a 与b 的关系；∴180DEC ECM Ð+Ð=°，∴DEC ECM MCG Ð+Ð+Ð∵ECM MCG ECG Ð+ÐÐ=∴DEC ECG FGC Ð+Ð+Ð=②∵CED Ð与CGF Ð的角平分线相交于点∴1DEP CED Ð=Ð，FGP Ð∵12l l ∥， ∴2CM l P ，PN ∥∴180DEC ECM Ð+Ð=°，Ð∴DEC ECM MCG Ð+Ð+Ð+即DEC ECG FGC Ð+Ð+Ð=∵13DEP CED Ð=Ð，FGP Ð。

七年级下数学重难点专题训练：平行线拐点问题模型汇总模型一：“Ｍ”型（猪蹄模型）例：1．（1）如图1，已知AB∥CD，求证：∠BED＝∠1+∠2．（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、∠BEG之间数量关系，并加以证明．（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．【分析】（1）过点E作EF∥AB，依据平行线的性质，即可得到∠3+∠4＝∠1+∠2，进而得出∠BED＝∠1+∠2；（2）分别过点E、G作EF∥AB，GH∥AB，依据平行线的性质，即可得到∠1+∠5+∠6＝∠3+∠4+∠2，进而得到∠1+∠EGH＝∠2+∠BEG；（3）分别过平行线间的折点作AB的平行线，依据平行线的性质，即可得到∠1、∠3、∠5与∠2、∠4、∠6之间的关系．【解答】解：（1）证明：如图，过点E作EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠3＝∠1，∠4＝∠2，∴∠3+∠4＝∠1+∠2，即∠BED＝∠1+∠2；（2）∠1+∠EGH＝∠2+∠BEG，理由如下：如图，分别过点E、G作EF∥AB，GH∥AB，∵AB∥CD，∴AB∥EF∥GH∥CD，∴∠1＝∠3，∠4＝∠5，∠6＝∠2，∴∠1+∠5+∠6＝∠3+∠4+∠2，即∠1+∠EGH＝∠2+∠BEG；（3）由题可得，向左的角度数之和与向右的角度数之和相等，∴∠1、∠3、∠5与∠2、∠4、∠6之间的关系为：∠1+∠3+∠5＝∠2+∠4+∠6．通关训练：2．如图，已知AB∥CD，∠B＝30°，∠D＝120°．（1）若∠E＝60°，则∠F＝．（2）请探索∠E与∠F之间满足何数量关系？并说明理由；（3）如图2，已知EP平分∠BEF，FG平分∠EFD，反向延长FG交EP于点P，求∠P 的度数．3．如图，AB∥CD，点A，E，B，C不在同一条直线上．（1）如图1，求证：∠E+∠C﹣∠A＝180°（2）如图2．直线F A，CP交于点P，且∠BAF＝∠BAE，∠DCP＝∠DCE．①试探究∠E与∠P的数量关系：②如图3，延长CE交P A于点Q，若AE∥PC，∠BAQ＝α（0°＜α＜22.5°），则∠PQC的度数为（用含α的式子表示）4．如图，已知AB∥CD，现将直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F．（1）当直角三角形PMN所放位置如图①所示时，∠PFD与∠AEM存在怎样的数量关系？请说明理由．（2）当直角三角形PMN所放位置如图②所示时，请直接写出∠PFD与∠AEM之间存在的数量关系．（3）在（2）的条件下，若MN与CD交于点O，且∠AEM＝40°，∠DON＝20°，则∠N的度数为．5．已知，AB∥CD．点M在AB上，点N在CD上．（1）如图1中，∠BME、∠E、∠END的数量关系为：；（不需要证明）如图2中，∠BMF、∠F、∠FND的数量关系为：；（不需要证明）（2）如图3中，NE平分∠FND，MB平分∠FME，且2∠E+∠F＝180°，求∠FME的度数；（3）如图4中，∠BME＝60°，EF平分∠MEN，NP平分∠END，且EQ∥NP，则∠FEQ 的大小是否发生变化，若变化，请说明理由，若不变化，求出∠FEQ的度数．6．请阅读小明同学在学习平行线这章知识点时的一段笔记，然后解决问题．小明：老师说在解决有关平行线的问题时，如果无法直接得到角的关系，就需要借助辅助线来帮助解答，今天老师介绍了一个“美味”的模型﹣﹣﹣“猪蹄模型”．即已知：如图1，AB∥CD，E为AB、CD之间一点，连接AE，CE得到∠AEC．求证：∠AEC＝∠A+∠C．小明笔记上写出的证明过程如下：证明：过点E作EF∥AB，∴∠1＝∠A．∵AB∥CD，EF∥AB，∴EF∥CD．∴∠2＝∠C．∵∠AEC＝∠1+∠2，∴∠AEC＝∠A+∠C．请你利用“猪蹄模型”得到的结论或解题方法，完成下面的两个问题．（1）如图2，若AB∥CD，∠E＝60°，则∠B+∠C+∠F＝．（2）如图3，AB∥CD，BE平分∠ABG，CF平分∠DCG，∠G＝∠H+27°，E、B、H 共线，F、C、H共线，则∠H＝．7．如图1，已知AB∥CD，BP、DP分别平分∠ABD、∠BDC．（1）∠BPD＝°；（2）如图2，将BD改为折线BED，BP、DP分别平分∠ABE、∠EDC，其余条件不变，若∠BED＝140°，求∠BPD的度数；（3）如图3，若∠BEF＝152°，∠EFD＝136°，BP、DP分别平分∠ABE、∠CDF，其余条件不变，那么∠BPD＝°．8．已知AB∥CD，点E在AB与CD之间．（1）图1中，试说明：∠BED＝∠ABE+∠CDE；（2）图2中，∠ABE的平分线与∠CDE的平分线相交于点F，请利用（1）的结论说明：∠BED＝2∠BFD．（3）图3中，∠ABE的平分线与∠CDE的平分线相交于点F，请直接写出∠BED与∠BFD之间的数量关系．9．已知：点E、点G分别在直线AB、直线CD上，点F在两直线外，连接EF、FG （1）如图1，AB∥CD，求证：∠AEF+∠FGC＝∠EFG；（2）若直线AB与直线CD不平行，连接EG，且EG同时平分∠BEF和∠FGD如图2，请探索∠AEF、∠FGC、∠EFG之间的数量关系？并说明理由．10．如图，已知AB∥CD．（1）发现问题：若∠ABF＝∠ABE，∠CDF＝∠CDE，则∠F与∠E的等量关系为．（2）探究问题：若∠ABF＝∠ABE，∠CDF＝∠CDE．猜想：∠F与∠E的等量关系，并证明你的结论．（3）归纳问题：若∠ABF＝∠ABE，∠CDF＝∠CDE．直接写出∠F与∠E的等量关系．11．【引入】如图1，已知∠ABC+∠ECB＝180°，∠P＝∠Q，求证：∠1＝∠2．【变式】如图2，AB∥CD，∠1＝∠2，求证：∠F＝∠Ｍ模型二：铅笔模型例：12．模型与应用．【模型】（1）如图①，已知AB∥CD，求证∠1+∠MEN+∠2＝360°．【应用】（2）如图②，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6的度数为．如图③，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为．（3）如图④，已知AB∥CD，∠AM1M2的角平分线M1O与∠CM n M n﹣1的角平分线M n O 交于点O，若∠M1OM n＝m°．在（2）的基础上，求∠2+∠3+∠4+∠5+∠6+……+∠n ﹣1的度数．（用含m、n的代数式表示）【分析】（1）过点E作EF∥CD，根据平行线的判定得出EF∥AB，根据平行线的性质得出即可；（2）过E作EQ∥CD，过F作FW∥CD，过G作GR∥CD，过H作HY∥CD，根据平行线的判定得出EQ∥FW∥GR∥HY∥AB∥CD，根据平行线的性质得出即可；（3）过点O作SR∥AB，根据平行线的性质得出即可；【解答】（1）证明：过点E作EF∥CD，∵AB∥CD，∴EF∥AB，∴∠1+∠MEF＝180°，同理∠2+∠NEF＝180°，∴∠1+∠2+∠MEN＝360°；【应用】（2）过E作EQ∥CD，过F作FW∥CD，过G作GR∥CD，过H作HY∥CD，∵CD∥AB，∴EQ∥FW∥GR∥HY∥AB∥CD，∴∠1+∠MEQ＝180°，∠QEF+∠EFW＝180°，∠WFG+∠FGR＝180°，∠RGH+∠GHY＝180°，∠YHN+∠6＝180°，∴∠1+∠2+∠3+∠4+∠5+∠6＝5×180°＝900°，同理∠1+∠2+∠3+∠4+∠5+∠6+…+∠n＝180°（n﹣1），故答案为：900°，180°（n﹣1）；（3）解：过点O作SR∥AB，∵AB∥CD，∴SR∥CD，∴∠AM1O＝∠M1OR同理∠C M n O＝∠M n OR∴∠A M1O+∠CM n O＝∠M1OR+∠M n OR，∴∠A M1O+∠CM n O＝∠M1OM n＝m°，∵M1O平分∠AM1M2，∴∠AM1M2＝2∠A M1O，同理∠CM n M n﹣1＝2∠CM n O，∴∠AM1M2+∠CM n M n﹣1＝2∠AM1O+2∠CM n O＝2∠M1OM n＝2m°，又∵∠A M1M2+∠2+∠3+∠4+∠5+∠6+……+∠n﹣1+∠CM n M n﹣1＝180°（n﹣1），∠2+∠3+∠4+∠5+∠6+…+∠n﹣1＝（180n﹣180﹣2m）°．通关训练：13．如图1，MA1∥NA2，则∠A1+∠A2＝度．如图2，MA1∥NA3，则∠A1+∠A2+∠A3＝度．如图3，MA1∥NA4，则∠A1+∠A2+∠A3+∠A4＝度．如图4，MA1∥NA5，则∠A1+∠A2+∠A3+∠A4+∠A5＝度．从上述结论中你发现了什么规律？如图5，MA1∥NA n，则∠A1+∠A2+∠A3+…+∠A n＝度．14．如图，AB∥CD，点F在CE上，∠EAF＝∠BAF，若∠AEC＝105°，∠DCE＝115°，求∠AFC的度数．15．直线AB∥CD，E为直线AB、CD之间的一点，完成以下问题：（1）如图1，若∠B＝15°，∠BED＝90°，则∠D＝；（2）如图2，若∠B＝α，∠D＝β，求出∠BED的度数（用a、β表示）；（3）如图3，若∠B＝α，∠C＝β，则a、β与∠BEC之间有什么等量关系？请猜想证明．16．问题情境：如图1，AB∥CD，∠P AB＝135°，∠PCD＝125°．求∠APC度数．小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可求得∠APC的度数．请写出具体求解过程．问题迁移：（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．17．如图，BN∥CD，点A是直线BN上一点，P是直线AB与直线CD之间一点，连接AP，PC．（1）求证：∠BAP+∠C＝∠P；（2）过点C作CM平分∠PCD，过点C作CE⊥CM交∠NAP的角平分线于点E，过点P作PF∥AE交CM于点F，探索∠CFP和∠APC的数量关系，并说明理由；（3）在（2）的条件下，若2∠AEC﹣∠CPF＝240°，Q是直线CD上一点，请直接写出∠PFQ和∠FQD的数量关系．模型三：钩型（臭脚模型和骨折模型）例：18．（1）如图1，AB∥CD，CF平分∠DCE，若∠DCF＝30°，∠E＝20°，求∠ABE 的度数；（2）如图2，已知AB∥CD，∠EBF＝2∠ABF，CF平分∠DCE，若∠F的2倍与∠E的补角的和为190°，求∠ABE的度数；（3）如图3，若P是（2）中的射线BE上一点，G是CD上任一点，PQ平分∠BPG，PQ∥GN，GM平分∠DGP，若∠B＝30°，求∠MGN的度数．【分析】根据平行线的判定与性质，三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义解答即可．【解答】解：（1）过E作EM∥AB∵AB∥CD∴CD∥EM∥AB∴∠ABE＝∠BEM∠DCE＝∠CEM∵CF平分∠DCE∴∠DCE＝2∠DCF∵∠DCF＝30°∴∠DCE＝60°∴∠CEM＝60°又∵∠CEB＝20°∴∠BEM＝∠CEM﹣∠CEB＝40°∴∠ABE＝40°，（2）过E作EM∥AB，过F作FN∥AB∵∠EBF＝2∠ABF∴设∠ABF＝x，∠EBF＝2x，则∠ABE＝3x ∵CF平分∠DCE∴设∠DCF＝∠ECF＝y，则∠DCE＝2y∵AB∥CD∴EM∥AB∥CD∴∠DCE＝∠CEM＝2y∠BEM＝∠ABE＝3x∴∠CEB＝∠CEM﹣∠BEM＝2y﹣3x同理∠CFB＝y﹣x∵2∠CFB+（180°﹣∠CEB）＝190°∴2（y﹣x）+180°﹣（2y﹣3x）＝190°∴x＝10°∴∠ABE＝3x＝30°，（3）过P作PL∥AB∵GM平分∠DGP∴设∠DGM＝∠PGM＝y，则∠DGP＝2y ∵PQ平分∠BPG∴设∠BPQ＝∠GPQ＝x，则∠BPG＝2x∵PQ∥QN∴∠PGN＝∠GPQ＝x∵AB∥CD∴PL∥AB∥CD∴∠GPL＝∠DGP＝2y∠BPL＝∠ABP＝30°∵∠BPL＝∠GPL﹣∠BPG∴30°＝2y﹣2x∴y﹣x＝15°∵∠MGN＝∠PGM﹣∠PGN＝y﹣x∴∠MGN＝15°．通关训练：19．已知AM∥CN，点B为平面内一点，AB⊥BC于B．（1）如图1，直接写出∠A和∠C之间的数量关系；（2）如图2，过点B作BD⊥AM于点D，求证：∠ABD＝∠C；（3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF＝180°，∠BFC＝3∠DBE，求∠EBC的度数．20．为增强学生体质，感受中国的传统文化，学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间．如图是某同学“抖空竹”时的一个瞬间，王聪把它抽象成如图的数学问题：已知AB∥CD，∠EAB＝80°，∠ECD＝110°，求∠E的度数．21．如图，BE∥CF，∠A＝30°，∠C＝80°，求∠B的度数．22．（1）（问题）如图1，若AB∥CD，∠AEP＝40°，∠PFD＝130°．求∠EPF的度数；（2）（问题迁移）如图2，AB∥CD，点P在AB的上方，问∠PEA，∠PFC，∠EPF之间有何数量关系？请说明理由；（3）（联想拓展）如图3所示，在（2）的条件下，已知∠EPF＝α，∠PEA的平分线和∠PFC的平分线交于点G，用含有α的式子表示∠G的度数．23．已知AB∥CD，点E在AB上，点G在CD上，点F在直线AB、CD之间，分别连接EF、FG，∠BEF+∠DGF＝2∠EFG．（1）如图1，求∠EFG的度数；（2）如图2，若∠BEF的角平分线与FG的延长线交于点M，求证：∠AEF﹣2∠FME ＝60°；（3）如图3，已知点P在FG的延长线上，点K在CD上，点N在∠PGC内，分别连接NG，NK．若NK∥EF，∠PGN＝2∠NGC，请直接写出∠AEF﹣∠GNK的值．24．同一平面内的两条直线有相交和平行两种位置关系．（1）如图1，若AB∥CD，点P在AB、CD内部，请写出∠BPD、∠B、∠D之间的数量关系（不必说明理由）；（2）如图2，将直线AB绕点B逆时针方向转一定角度交直线CD于点Q，利用（1）中的结论求∠BPD、∠B、∠D、∠BQD之间有何数量关系？并证明你的结论；（3）如图3，设BF交AC于点M，AE交DF于点N．已知∠AMB＝140°，∠ANF＝105°，利用（2）中的结论直接写出∠B+∠E+∠F的度数和∠A比∠F大多少度．25．综合探究：已知，AB∥CD，点M、N分别是AB、CD上两点，点G在AB、CD之间，连接MG、NG．（1）如图1，若GM⊥GN，求∠AMG+∠CNG的度数；（2）如图2，若点P是CD下方一点，MG平分∠BMP，ND平分∠GNP，已知∠BMG ＝40°，求∠MGN+∠MPN的度数．26．已知直线AB∥CD．（1）如图1，请直接写出∠BME、∠E、∠END的数量关系为；（2）如图2，∠ABM＝∠MBE，∠CDN＝∠NDE，直线MB、ND交于点F，若∠F ＝10°，求∠E的度数；（3）如图3，∠BME的角平分线所在的直线与∠CNE的角平分线相交于点P，试探究∠P与∠E之间的数量关系，并证明你的结论．27．如图，已知直线AB∥CD．（1）在图1中，点M在直线AB上，点N在直线CD上，∠BME、∠E、∠END的数量关系是；（不需证明）（2）如图2，若GN平分∠CNE，FE平分∠AMG，且∠G+∠E＝60°，求∠AMG的度数；（3）如图3，直线BM平分∠ABE，直线DN平分∠CDE相交于点F，求∠F：∠E的值；（4）若∠ABM＝∠MBE，∠CDN＝∠NDE，则＝．（用含有n的代数式表示）28．如图1所示，AB∥CD，E为直线CD下方一点，BF平分∠ABE．（1）求证：∠ABE+∠C﹣∠E＝180°．（2）如图2，EG平分∠BEC，过点B作BH∥GE，求∠FBH与∠C之间的数量关系．（3）如图3，CN平分∠ECD，若BF的反向延长线和CN的反向延长线交于点M，且∠E+∠M＝130°，请直接写出∠E的度数．29．如图，平面内的直线有相交和平行两种位置关系（1）如图①，已知AB∥CD，求证：∠BPD＝∠B+∠D；（提示；可过点P作PO∥AB）（2）如图②，已知AB∥CD，求证：∠B＝∠P+∠D．30．如图，AB∥CD，分别探讨下面四个图形中∠APC与∠A，∠C的关系，请你从所得的关系中任意选取一个加以说明．图（1）结论：；图（2）结论：；图（3）结论：；图（4）结论：．你准备证明的是图，请在下面写出证明过程．31．如图1，将两根笔直的细木条MN，EF用图钉固定并平行摆放，将一根橡皮筋拉直后用图钉分别周定在MN，EF上，橡皮筋的两端点分别记为点A，点B．（1）图1中，点P在AB上，若∠1＝110°，则∠2＝°；（2）P为橡皮筋上一点，用皮筋的弹性拉动橡皮筋，使A，B，P三点不在同一直线，后用图固定点P．①如图2，若点P在两根细木条所在直线之间，且∠1+∠2＝90°，试判断线段AP与BP所在直线的位置关系，并说明理由；②如图3，若点P在两根细木条所在直线的同侧，且∠1+∠2＝90°，∠1＝31°，试求∠APB的度数；（3）如图4，P1，P2两点在两根细木条所在直线之间，拉动橡皮筋并固定，若∠1+∠2＝90°，则∠AP1P2+∠BP1P2＝°．32．阅读下面材料：小明遇到这样一个问题：如图1，AC∥BD，点E为直线AC上方一点，连接CE、DE，猜想∠C、∠D、∠E的数量关系，并证明．小明发现，可以过点E作MN∥AC来解决问题，如图2，请你完成解答；用学过的知识或参考小明的方法，解决下面的问题：如图3，AB∥CD，P是平面内一点，连接AP、CP，使AP∥BD，∠APC＝100°，BM、CM分别平分∠ABD、∠DCP交于点M，求∠M的度数．33．如图，已知直线MB∥ND，A、C分别为MB、ND上的点，E为直线MB、ND外的一点，连接AE、EC．（1）E在直线MB的上方（如图1），求证：∠AEC+∠ECD＝∠EAB；（2）若∠MAE与∠NCE两角的角平分线交于F点，请在图2中将图形补充完整，并直接写出∠AEC与∠AFC之间的数量关系；（3）若∠EAB的角平分线的反向延长线与∠NCE的角平分线交于G点（如图3），且∠AGC比∠AEC的倍多50°，求∠AEC的度数．34．已知直线AB∥CD，E为直线AB、CD外的一点，连接AE、EC．（1）E在直线AB的上方（如图1），求证：∠AEC+∠EAB＝∠ECD；（2）∠BAF＝2∠EAF，∠DCF＝2∠ECF（如图2），求证：∠AEC＝∠AFC；（3）若E在直线AB、CD之间，在（2）条件下（如图3），且∠AFC比∠AEC的倍少40°，则∠AEC的度数为（不用写出解答过程）．35．如图：已知AB∥DE，若∠ABC＝60°，∠CDE＝140°，求∠BCD的度数．36．如图，已知AB∥CD，点E在直线AB，CD之间．（1）求证：∠AEC＝∠BAE+∠ECD；（2）若AH平分∠BAE，将线段CE沿CD平移至FG．①如图2，若∠AEC＝90°，HF平分∠DFG，求∠AHF的度数；②如图3，若HF平分∠CFG，试判断∠AHF与∠AEC的数量关系并说明理由．37．如图，平面内有两条直线同AB、CD，且AB∥CD，P为一动点．（1）当点P移动到如图（1）的位置时，这时∠APC与∠A，∠C有怎样的关系？并说明理由；（2）当点P移动到如图（2）的位置时，这时∠APC与∠A，∠C又有怎样的关系？说明你的理由；（3）当点P移动到如图（3）的位置时，直接写出∠APC与∠A，∠C的关系式；（4）当点P移动到如图（4）的位置时，直接写出∠APC与∠A，∠C的关系式．38．如图所示，已知AB∥CD，分别探讨下面四个图形中，∠APC，∠P AB与∠PCD的关系．39．已知AB∥CD，点P为平面内一点，连接AP、CP．（1）探究：如图（1）∠P AB＝145°，∠PCD＝135°，则∠APC的度数是；如图（2）∠P AB＝45°，∠PCD＝60°，则∠APC的度数是．（2）在图2中试探究∠APC，∠P AB，∠PCD之间的数量关系，并说明理由．（3）拓展探究：当点P在直线AB，CD外，如图（3）、（4）所示的位置时，请分别直接写出∠APC，∠P AB，∠PCD之间的数量关系．40．探究：（1）如图a，若AB∥CD，则∠B+∠D＝∠E，你能说明为什么吗？（2）反之，若∠B+∠D＝∠E，直线AB与CD有什么位置关系？请证明；（3）若将点E移至图b所示位置，此时∠B、∠D、∠E之间有什么关系？请证明；（4）若将E点移至图c所示位置，情况又如何？（5）在图d中，AB∥CD，∠E+∠G与∠B+∠F+∠D又有何关系？（6）在图e中，若AB∥CD，又得到什么结论？七年级下数学重难点专题训练：平行线拐点问题模型汇总1．（1）如图1，已知AB∥CD，求证：∠BED＝∠1+∠2．（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、∠BEG之间数量关系，并加以证明．（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．【分析】（1）过点E作EF∥AB，依据平行线的性质，即可得到∠3+∠4＝∠1+∠2，进而得出∠BED＝∠1+∠2；（2）分别过点E、G作EF∥AB，GH∥AB，依据平行线的性质，即可得到∠1+∠5+∠6＝∠3+∠4+∠2，进而得到∠1+∠EGH＝∠2+∠BEG；（3）分别过平行线间的折点作AB的平行线，依据平行线的性质，即可得到∠1、∠3、∠5与∠2、∠4、∠6之间的关系．【解答】解：（1）证明：如图，过点E作EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠3＝∠1，∠4＝∠2，∴∠3+∠4＝∠1+∠2，即∠BED＝∠1+∠2；（2）∠1+∠EGH＝∠2+∠BEG，理由如下：如图，分别过点E、G作EF∥AB，GH∥AB，∵AB∥CD，∴AB∥EF∥GH∥CD，∴∠1＝∠3，∠4＝∠5，∠6＝∠2，∴∠1+∠5+∠6＝∠3+∠4+∠2，即∠1+∠EGH＝∠2+∠BEG；（3）由题可得，向左的角度数之和与向右的角度数之和相等，∴∠1、∠3、∠5与∠2、∠4、∠6之间的关系为：∠1+∠3+∠5＝∠2+∠4+∠6．2．如图，已知AB∥CD，∠B＝30°，∠D＝120°．（1）若∠E＝60°，则∠F＝90°．（2）请探索∠E与∠F之间满足何数量关系？并说明理由；（3）如图2，已知EP平分∠BEF，FG平分∠EFD，反向延长FG交EP于点P，求∠P 的度数．【分析】（1）分别过点E，F作EM∥AB，FN∥AB，根据平行线的性质得到∠B＝∠BEM ＝30°，∠MEF＝∠EFN，∠D+∠DFN＝180°，代入数据即可得到结论；（2）根据平行线的性质得到∠B＝∠BEM＝30°，∠MEF＝∠EFN，由AB∥CD，AB∥FN，得到CD∥FN，根据平行线的性质得到∠D+∠DFN＝180°，于是得到结论；（3）过点F作FH∥EP，设∠BEF＝2x°，则∠EFD＝（2x+30）°，根据角平分线的定义得到∠PEF＝∠BEF＝x°，∠EFG＝∠EFD＝（x+15）°，根据平行线的性质得到∠PEF＝∠EFH＝x°，∠P＝∠HFG，于是得到结论．【解答】解：（1）如图1，分别过点E，F作EM∥AB，FN∥AB，∴EM∥AB∥FN，∴∠B＝∠BEM＝30°，∠MEF＝∠EFN，又∵AB∥CD，AB∥FN，∴CD∥FN，∴∠D+∠DFN＝180°，又∵∠D＝120°，∴∠DFN＝60°，∴∠BEF＝∠MEF+30°，∠EFD＝∠EFN+60°，∴∠EFD＝∠MEF+60°∴∠EFD＝∠BEF+30°＝90°；故答案为：90°；（2）如图1，分别过点E，F作EM∥AB，FN∥AB，∴EM∥AB∥FN，∴∠B＝∠BEM＝30°，∠MEF＝∠EFN，又∵AB∥CD，AB∥FN，∴CD∥FN，∴∠D+∠DFN＝180°，又∵∠D＝120°，∴∠DFN＝60°，∴∠BEF＝∠MEF+30°，∠EFD＝∠EFN+60°，∴∠EFD＝∠MEF+60°，∴∠EFD＝∠BEF+30°；（3）如图2，过点F作FH∥EP，由（2）知，∠EFD＝∠BEF+30°，设∠BEF＝2x°，则∠EFD＝（2x+30）°，∵EP平分∠BEF，GF平分∠EFD，∴∠PEF＝∠BEF＝x°，∠EFG＝∠EFD＝（x+15）°，∵FH∥EP，∴∠PEF＝∠EFH＝x°，∠P＝∠HFG，∵∠HFG＝∠EFG﹣∠EFH＝15°，∴∠P＝15°．3．如图，AB∥CD，点A，E，B，C不在同一条直线上．（1）如图1，求证：∠E+∠C﹣∠A＝180°（2）如图2．直线F A，CP交于点P，且∠BAF＝∠BAE，∠DCP＝∠DCE．①试探究∠E与∠P的数量关系：②如图3，延长CE交P A于点Q，若AE∥PC，∠BAQ＝α（0°＜α＜22.5°），则∠PQC的度数为180°﹣8α（用含α的式子表示）【分析】（1）如图1，过E作EF∥AB，根据平行线的性质即可得到结论；（2）①设∠BAF＝x，∠BAE＝3x，∠DCP＝y，∠DCE＝3y，由（1）知，∠E＝180°﹣∠C+∠A＝180°﹣3（y﹣x），如图2，过P作PG∥CD，根据平行线的性质即可得到结论；②如图3，过P作PG∥CD，根据平行线的性质即可得到结论．【解答】解：（1）如图1，过E作EF∥AB，∵AB∥CD，∴AB∥EF∥CD，∴∠AEF＝∠A，∠C+∠FEC＝180°，∴∠E＝∠AEF+∠FEC＝∠A+180°﹣∠C，即∠E+∠C﹣∠A＝180°；（2）①∵∠BAF＝∠BAE，∠DCP＝∠DCE，∴设∠BAF＝x，∠BAE＝3x，∠DCP＝y，∠DCE＝3y，由（1）知，∠E＝180°﹣∠C+∠A＝180°﹣3（y﹣x），如图2，过P作PG∥CD，∵AB∥CD，∴AB∥PG，∴∠GP A＝∠BAF＝x，∠GPC＝∠PCD＝y，∴∠APC＝y﹣x，即∠E＝180°﹣3∠P；②如图3，过P作PG∥CD，∵∠BAQ＝α，∴∠QAE＝2α，∵AE∥PC，∴∠QAE＝∠APC＝2α，由①知，∠AEC＝180°﹣3∠APC＝180°﹣6α，∴∠PQC＝∠AEC﹣∠QAE＝180°﹣6α﹣2α＝180°﹣8α，故答案为：180°﹣8α．4．如图，已知AB∥CD，现将直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F．（1）当直角三角形PMN所放位置如图①所示时，∠PFD与∠AEM存在怎样的数量关系？请说明理由．（2）当直角三角形PMN所放位置如图②所示时，请直接写出∠PFD与∠AEM之间存在的数量关系．（3）在（2）的条件下，若MN与CD交于点O，且∠AEM＝40°，∠DON＝20°，则∠N的度数为30°．【分析】（1）作PH∥AB，根据平行线的性质得到∠AEM＝∠HPM，∠PFD＝∠HPN，根据∠MPN＝90°解答；（2）根据平行线的性质得到∠PFD+∠BHN＝180°，根据∠P＝90°解答；（3）根据对顶角相等，直角三角形的性质，平行线的性质以及三角形外角的性质计算即可求解．【解答】解：（1）如图①，作PH∥AB，则∠AEM＝∠HPM，∵AB∥CD，PH∥AB，∴PH∥CD，∴∠PFD＝∠HPN，∵∠MPN＝90°，∴∠PFD+∠AEM＝90°，故答案为：∠PFD+∠AEM＝90°；（2）猜想：∠PFD﹣∠AEM＝90°；理由如下：∵AB∥CD，∴∠PFD+∠BHN＝180°，∵∠BHN＝∠PHE，∴∠PFD+∠PHE＝180°，∵∠P＝90°，∴∠PHE+∠PEB＝90°，∵∠PEB＝∠AEM，∴∠PHE+∠AEM＝90°，∴∠PFD﹣∠AEM＝90°；（3）∵∠P＝90°，∠PEB＝∠AEM＝40°，∴∠PHE＝90°﹣∠PEB＝90°﹣40°＝50°，∵AB∥CD，∴∠HFO＝∠PHE＝50°，∵∠DON＝20°，∴∠N＝∠HFO﹣∠DON＝30°．故答案为：30°．5．已知，AB∥CD．点M在AB上，点N在CD上．（1）如图1中，∠BME、∠E、∠END的数量关系为：∠BME＝∠MEN﹣∠END；（不需要证明）如图2中，∠BMF、∠F、∠FND的数量关系为：∠BMF＝∠MFN+∠FND；（不需要证明）（2）如图3中，NE平分∠FND，MB平分∠FME，且2∠E+∠F＝180°，求∠FME的度数；（3）如图4中，∠BME＝60°，EF平分∠MEN，NP平分∠END，且EQ∥NP，则∠FEQ 的大小是否发生变化，若变化，请说明理由，若不变化，求出∠FEQ的度数．【分析】（1）过E作EH∥AB，易得EH∥AB∥CD，根据平行线的性质可求解；过F作FH∥AB，易得FH∥AB∥CD，根据平行线的性质可求解；（2）根据（1）的结论及角平分线的定义可得2（∠BME+∠END）+∠BMF﹣∠FND＝180°，可求解∠BMF＝60°，进而可求解；（3）根据培训心得性质及角平分线的定义可推知∠FEQ＝∠BME，进而可求解．【解答】解：（1）过E作EH∥AB，如图1，∴∠BME＝∠MEH，∵AB∥CD，∴HE∥CD，∴∠END＝∠HEN，∴∠MEN＝∠MEH+∠HEN＝∠BME+∠END，即∠BME＝∠MEN﹣∠END．如图2，过F作FH∥AB，∴∠BMF＝∠MFK，∵AB∥CD，∴FH∥CD，∴∠FND＝∠KFN，∴∠MFN＝∠MFK﹣∠KFN＝∠BMF﹣∠FND，即：∠BMF＝∠MFN+∠FND．故答案为∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN+∠FND．（2）由（1）得∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN+∠FND．∵NE平分∠FND，MB平分∠FME，∴∠FME＝∠BME+∠BMF，∠FND＝∠FNE+∠END，∵2∠MEN+∠MFN＝180°，∴2（∠BME+∠END）+∠BMF﹣∠FND＝180°，∴2∠BME+2∠END+∠BMF﹣∠FND＝180°，即2∠BMF+∠FND+∠BMF﹣∠FND＝180°，解得∠BMF＝60°，∴∠FME＝2∠BMF＝120°；（3）∠FEQ的大小没发生变化，∠FEQ＝30°．由（1）知：∠MEN＝∠BME+∠END，∵EF平分∠MEN，NP平分∠END，∴∠FEN＝∠MEN＝（∠BME+∠END），∠ENP＝∠END，∵EQ∥NP，∴∠NEQ＝∠ENP，∴∠FEQ＝∠FEN﹣∠NEQ＝（∠BME+∠END）﹣∠END＝∠BME，∵∠BME＝60°，∴∠FEQ＝×60°＝30°．6．请阅读小明同学在学习平行线这章知识点时的一段笔记，然后解决问题．小明：老师说在解决有关平行线的问题时，如果无法直接得到角的关系，就需要借助辅助线来帮助解答，今天老师介绍了一个“美味”的模型﹣﹣﹣“猪蹄模型”．即已知：如图1，AB∥CD，E为AB、CD之间一点，连接AE，CE得到∠AEC．求证：∠AEC＝∠A+∠C．小明笔记上写出的证明过程如下：证明：过点E作EF∥AB，∴∠1＝∠A．∵AB∥CD，EF∥AB，∴EF∥CD．∴∠2＝∠C．∵∠AEC＝∠1+∠2，∴∠AEC＝∠A+∠C．请你利用“猪蹄模型”得到的结论或解题方法，完成下面的两个问题．（1）如图2，若AB∥CD，∠E＝60°，则∠B+∠C+∠F＝240°．（2）如图3，AB∥CD，BE平分∠ABG，CF平分∠DCG，∠G＝∠H+27°，E、B、H 共线，F、C、H共线，则∠H＝51°．【分析】（1）由EM∥AB，FN∥EM，FN∥CD分别得∠1＝∠B，∠2＝∠3，∠4+∠C＝180°，由角的和差计算∠B+∠C+∠F的度数为240°；（2）由角平分线得∴∠ABG＝2∠1，∠DCG＝2∠4，根据直线EF∥AB，EF∥CD得2∠1+∠7＝180°，2∠4+∠8＝180°，等式的性质得2（∠1+∠4）＝∠BGC+180°；直线MN∥AB，MN∥CD得∠1＝∠5，∠4＝∠6，等量代换2（∠5+∠6）＝∠BGC+180°，又因∠BGC＝∠BHC+27°求得∠BHC的度数为51°．【解答】解：（1）过点E、F分别作EM∥AB，FN∥AB，如图2所示：∵EM∥AB，∴∠1＝∠B，又∵FN∥AB，∴FN∥EM，∴∠2＝∠3，又∵AB∥CD，∴FN∥CD，∴∠4+∠C＝180°，又∵∠BEF＝∠1+∠2，∠EFC＝∠3+∠4，∠BEF＝60°∴∠B+∠EFC+∠C＝∠1+∠3+∠4+∠C＝（∠1+∠2）+（∠4+∠C）＝60°+180°＝240°；（2）过点G、H作EF∥AB，MN∥AB，如图3所示：∵BE平分∠ABG，CF平分∠DCG，∴∠ABG＝2∠1，∠DCG＝2∠4，又∵EF∥AB，∴2∠1+∠7＝180°，又∵AB∥CD，∴EF∥CD，∴2∠4+∠8＝180°，∴∠7+∠8＝360°﹣2（∠1+∠4），又∵∠7+∠8+∠BGC＝180°，∴2（∠1+∠4）＝∠BGC+180°，又∵MN∥AB，∴∠1＝∠5，又∵AB∥CD，∴MN∥CD，∴∠4＝∠6，∴2（∠5+∠6）＝∠BGC+180°，又∵∠5+∠6+∠BHC＝180°，∴∠BGC+2∠BHC＝180°，又∠BGC＝∠BHC+27°，∴3∠BHC+27°＝180°，∴∠BHC＝51°；故答案为：240°，51°．7．如图1，已知AB∥CD，BP、DP分别平分∠ABD、∠BDC．（1）∠BPD＝90°°；（2）如图2，将BD改为折线BED，BP、DP分别平分∠ABE、∠EDC，其余条件不变，若∠BED＝140°，求∠BPD的度数；（3）如图3，若∠BEF＝152°，∠EFD＝136°，BP、DP分别平分∠ABE、∠CDF，其余条件不变，那么∠BPD＝54°．【分析】（1）先根据平行线的性质得出∠ABD+∠BDC＝∠180°，再根据角平分线的定义得出∠PBD+∠PDB的度数，由三角形内角和定理即可得出结论；（2）连接BD，先求出∠EBD+∠EDB的度数，再由平行线的性质得出∠ABD+∠CDB的度数，由角平分线的性质得出∠PBE+∠PDE的度数，根据∠BPD＝180°﹣∠PBE﹣PDE﹣∠EBD﹣∠EDB即可得出结论．（3）连接BD，先求出∠EBD+∠FDB的度数，再求出∠PBE+∠PDF的度数，再利用三角形内角和定理即可解决．【解答】解：（1）∵AB∥CD，∴∠ABD+∠BDC＝∠180°，∵BP、DP分别平分∠ABD、∠BDC，∴∠PBD+∠PDB＝90°，∴∠BPD＝180°﹣90°＝90°．（2）连接BD，∵∠BED＝140°，∴∠EBD+∠EDB＝40°，∵AB∥CD，∴∠ABD+∠CDB＝180°，∵BP、DP分别平分∠ABE、∠EDC，∴∠PBE＝∠ABE，∠PDE＝∠CDE，∴∠PBE+∠PDE＝×（180°﹣40°）＝70°，∴∠BPD＝180°﹣∠PBE﹣PDE﹣∠EBD﹣∠EDB＝70°．（3）连接BD，∵∠BEF＝152°，∠EFD＝136°，∴∠EBD+∠FDB＝360°﹣（152°+136°）＝72°，∵BP、DP分别平分∠ABE、∠FDC，∴∠PBE＝∠ABE，∠PDF＝∠CDF，∴∠PBE+∠PDF＝×（180°﹣72°）＝54°，∴∠BPD＝180°﹣（∠EBD+∠FDB）﹣（∠PBE+∠PDF）＝54°．故答案为：90；54°．8．已知AB∥CD，点E在AB与CD之间．（1）图1中，试说明：∠BED＝∠ABE+∠CDE；（2）图2中，∠ABE的平分线与∠CDE的平分线相交于点F，请利用（1）的结论说明：∠BED＝2∠BFD．（3）图3中，∠ABE的平分线与∠CDE的平分线相交于点F，请直接写出∠BED与∠BFD之间的数量关系．【分析】（1）图1中，过点E作EG∥AB，则∠BEG＝∠ABE，根据AB∥CD，EG∥AB，所以CD∥EG，所以∠DEG＝∠CDE，进而可得∠BED＝∠ABE+∠CDE；（2）图2中，根据∠ABE的平分线与∠CDE的平分线相交于点F，结合（1）的结论即可说明：∠BED＝2∠BFD；（3）图3中，根据∠ABE的平分线与∠CDE的平分线相交于点F，过点E作EG∥AB，则∠BEG+∠ABE＝180°，因为AB∥CD，EG∥AB，所以CD∥EG，所以∠DEG+∠CDE ＝180°，再结合（1）的结论即可说明∠BED与∠BFD之间的数量关系．【解答】解：（1）如图1中，过点E作EG∥AB，则∠BEG＝∠ABE，因为AB∥CD，EG∥AB，所以CD∥EG，所以∠DEG＝∠CDE，所以∠BEG+∠DEG＝∠ABE+∠CDE，即∠BED＝∠ABE+∠CDE；（2）图2中，因为BF平分∠ABE，所以∠ABE＝2∠ABF，因为DF平分∠CDE，所以∠CDE＝2∠CDF，所以∠ABE+∠CDE＝2∠ABF+2∠CDF＝2（∠ABF+∠CDF），由（1）得：因为AB∥CD，所以∠BED＝∠ABE+∠CDE，∠BFD＝∠ABF+∠CDF，所以∠BED＝2∠BFD．（3）∠BED＝360°﹣2∠BFD．图3中，过点E作EG∥AB，则∠BEG+∠ABE＝180°，因为AB∥CD，EG∥AB，所以CD∥EG，所以∠DEG+∠CDE＝180°，所以∠BEG+∠DEG＝360°﹣（∠ABE+∠CDE），即∠BED＝360°﹣（∠ABE+∠CDE），因为BF平分∠ABE，所以∠ABE＝2∠ABF，因为DF平分∠CDE，所以∠CDE＝2∠CDF，∠BED＝360°﹣2（∠ABF+∠CDF），由（1）得：因为AB∥CD，所以∠BFD＝∠ABF+∠CDF，所以∠BED＝360°﹣2∠BFD．9．已知：点E、点G分别在直线AB、直线CD上，点F在两直线外，连接EF、FG （1）如图1，AB∥CD，求证：∠AEF+∠FGC＝∠EFG；（2）若直线AB与直线CD不平行，连接EG，且EG同时平分∠BEF和∠FGD如图2，请探索∠AEF、∠FGC、∠EFG之间的数量关系？并说明理由．【分析】（1）过F作FQ∥AB，利用平行线的性质，即可得到∠AEF+∠FGC＝∠EFQ+∠GFQ＝∠EFG；（2）延长AB，CD，交于点P，依据∠FEP＝180°﹣∠AEF，∠FGP＝180°﹣∠FGC，即可得到∠FEP+∠FGP＝360°﹣（∠AEF+∠FGC），再根据四边形内角和，即可得到四边形EFGP中，∠F+∠P＝360°﹣（∠FEP+∠FGP）＝∠AEF+∠FGC，进而得出结论．【解答】解：（1）如图1，过F作FQ∥AB，∵AB∥CD，∴FQ∥CD，∴∠AEF＝∠QFE，∠FGC＝∠GFQ，∴∠AEF+∠FGC＝∠EFQ+∠GFQ＝∠EFG；（2）如图2，延长AB，CD，交于点P，∵EG同时平分∠BEF和∠FGD，∴∠FEG＝∠PEG，∠FGE＝∠PGE，∴∠F＝∠P，∵∠FEP＝180°﹣∠AEF，∠FGP＝180°﹣∠FGC，∴∠FEP+∠FGP＝360°﹣（∠AEF+∠FGC），∵四边形EFGP中，∠F+∠P＝360°﹣（∠FEP+∠FGP）＝360°﹣[360°﹣（∠AEF+∠FGC）]＝∠AEF+∠FGC，即2∠EFG＝∠AEF+∠FGC．10．如图，已知AB∥CD．（1）发现问题：若∠ABF＝∠ABE，∠CDF＝∠CDE，则∠F与∠E的等量关系为∠BED＝2∠BFD．（2）探究问题：若∠ABF＝∠ABE，∠CDF＝∠CDE．猜想：∠F与∠E的等量关系，并证明你的结论．（3）归纳问题：若∠ABF＝∠ABE，∠CDF＝∠CDE．直接写出∠F与∠E的等量关系．【分析】（1）首先连接FE并延长，易得∠BED＝∠BFD+∠EBF+∠EDF，又由BF、DF 分别平分∠ABE、∠CDE，以及（1）的结论，易证得∠BED＝2∠BFD；（2）过点E、F分别作AB的平行线EG、FH，由平行线的传递性可得AB∥EG∥FH∥CD，根据平行线的性质得到∠ABF＝∠BFH，∠CDF＝∠DFH，根据已知条件即可得到结论．（3）由（1）（2）即可得出∠F与∠E的等量关系．【解答】解：（1）∠BED＝2∠BFD．证明：连接FE并延长，∵∠BEG＝∠BFE+∠EBF，∠DEG＝∠DFE+∠EDF，∴∠BED＝∠BFD+∠EBF+∠EDF，∵BF、DF分别平分∠ABE、∠CDE，∴∠ABE+∠CDE＝2（∠EBF+∠EDF），∵∠BED＝∠ABE+∠CDE，∴∠EBF+∠EDF＝∠BED，∴∠BED＝∠BFD+∠BED，∴∠BED＝2∠BFD；（2）过点E、F分别作AB的平行线EG、FH，由平行线的传递性可得AB∥EG∥FH∥CD，∵AB∥FH，∴∠ABF＝∠BFH，∵FH∥CD，∴∠CDF＝∠DFH，∴∠BFD＝∠DFH+∠BFH＝∠CDF+∠ABF；同理可得∠BED＝∠DEG+∠BEG＝∠ABE+∠CDE；∵∠BFD＝∠DFH+∠BFH＝∠CDF+∠ABF＝（∠ABE+∠CDE）＝∠BED，∴∠BED＝3∠BFD．（3）由（1）（2）可得∠BED＝n∠BFD．11．【引入】如图1，已知∠ABC+∠ECB＝180°，∠P＝∠Q，求证：∠1＝∠2．【变式】如图2，AB∥CD，∠1＝∠2，求证：∠F＝∠Ｍ【分析】【引入】先判定AB∥DE，则∠ABC＝∠BCD，再由∠P＝∠Q，则∠PBC＝∠QCB，从而得出∠1＝∠2．【变式】延长EF交CD于G，利用平行线的性质得出∠1＝∠EGD，进而得出∠EGD＝∠2，再利用平行线的判定方法得出答案．【解答】【引入】证明：∵∠ABC+∠ECB＝180°，∴AB∥DE，∴∠ABC＝∠BCD，∵∠P＝∠Q，∴PB∥CQ，∴∠PBC＝∠BCQ，∵∠1＝∠ABC﹣∠PBC，∠2＝∠BCD﹣∠BCQ，∴∠1＝∠2．【变式】证明：延长EF交CD于G，如图：∵AB∥CD，∴∠1＝∠EGD∵∠1＝∠2，∴∠EGD＝∠2∴EF∥MN，∴∠EFM＝∠M．12．模型与应用．【模型】（1）如图①，已知AB∥CD，求证∠1+∠MEN+∠2＝360°．【应用】（2）如图②，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6的度数为900°．如图③，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为180°（n﹣1）．（3）如图④，已知AB∥CD，∠AM1M2的角平分线M1O与∠CM n M n﹣1的角平分线M n O 交于点O，若∠M1OM n＝m°．在（2）的基础上，求∠2+∠3+∠4+∠5+∠6+……+∠n ﹣1的度数．（用含m、n的代数式表示）【分析】（1）过点E作EF∥CD，根据平行线的判定得出EF∥AB，根据平行线的性质得出即可；（2）过E作EQ∥CD，过F作FW∥CD，过G作GR∥CD，过H作HY∥CD，根据平行线的判定得出EQ∥FW∥GR∥HY∥AB∥CD，根据平行线的性质得出即可；（3）过点O作SR∥AB，根据平行线的性质得出即可；【解答】（1）证明：过点E作EF∥CD，∵AB∥CD，∴EF∥AB，∴∠1+∠MEF＝180°，同理∠2+∠NEF＝180°，∴∠1+∠2+∠MEN＝360°；【应用】（2）过E作EQ∥CD，过F作FW∥CD，过G作GR∥CD，过H作HY∥CD，∵CD∥AB，∴EQ∥FW∥GR∥HY∥AB∥CD，∴∠1+∠MEQ＝180°，∠QEF+∠EFW＝180°，∠WFG+∠FGR＝180°，∠RGH+∠GHY＝180°，∠YHN+∠6＝180°，∴∠1+∠2+∠3+∠4+∠5+∠6＝5×180°＝900°，同理∠1+∠2+∠3+∠4+∠5+∠6+…+∠n＝180°（n﹣1），故答案为：900°，180°（n﹣1）；（3）解：过点O作SR∥AB，∵AB∥CD，∴SR∥CD，∴∠AM1O＝∠M1OR同理∠C M n O＝∠M n OR∴∠A M1O+∠CM n O＝∠M1OR+∠M n OR，∴∠A M1O+∠CM n O＝∠M1OM n＝m°，∵M1O平分∠AM1M2，∴∠AM1M2＝2∠A M1O，同理∠CM n M n﹣1＝2∠CM n O，∴∠AM1M2+∠CM n M n﹣1＝2∠AM1O+2∠CM n O＝2∠M1OM n＝2m°，又∵∠A M1M2+∠2+∠3+∠4+∠5+∠6+……+∠n﹣1+∠CM n M n﹣1＝180°（n﹣1），∠2+∠3+∠4+∠5+∠6+…+∠n﹣1＝（180n﹣180﹣2m）°．13．如图1，MA1∥NA2，则∠A1+∠A2＝180度．如图2，MA1∥NA3，则∠A1+∠A2+∠A3＝360度．如图3，MA1∥NA4，则∠A1+∠A2+∠A3+∠A4＝540度．如图4，MA1∥NA5，则∠A1+∠A2+∠A3+∠A4+∠A5＝720度．从上述结论中你发现了什么规律？如图5，MA1∥NA n，则∠A1+∠A2+∠A3+…+∠A n＝180（n﹣1）度．【分析】首先过各点作MA1的平行线，由MA1∥NA2，可得各线平行，根据两直线平行，同旁内角互补，即可求得答案，注意找到规律：MA1∥NA n，则∠A1+∠A2+∠A3+…+∠A n＝180（n﹣1）度是关键．【解答】解：如图1，∵MA1∥NA2，∴∠A1+∠A2＝180°．如图2，过点A2作A2C1∥A1M，∵MA1∥NA3，∴A2C1∥A1M∥NA3，∴∠A1+∠A1A2C1＝180°，∠C1A2A3+∠A3＝180°，∴∠A1+∠A2+∠A3＝360°．如图3，过点A2作A2C1∥A1M，过点A3作A3C2∥A1M，∵MA1∥NA3，∴A2C1∥A3C2∥A1M∥NA3，∴∠A1+∠A1A2C1＝180°，∠C1A2A3+∠A2A3C2＝180°，∠C2A3A4+∠A4＝180°，∴∠A1+∠A2+∠A3+∠A4＝540°．如图4，过点A2作A2C1∥A1M，过点A3作A3C2∥A1M，过点A4作A4C3∥A1M，∵MA1∥NA5，∴A2C1∥A3C2∥A4C3∥NA5，∴∠A1+∠A1A2C1＝180°，∠C1A2A3+∠A2A3C2＝180°，∠C2A3A4+∠A3A4C3＝180°∠C3A4A5+∠A5＝180°，∴∠A1+∠A2+∠A3+∠A4+∠A5＝720°．从上述结论中你发现了规律：如图5，MA1∥NA n，则∠A1+∠A2+∠A3+…+∠A n＝180（n ﹣1）度．故答案为：180，360，540，720，180（n﹣1）．14．如图，AB∥CD，点F在CE上，∠EAF＝∠BAF，若∠AEC＝105°，∠DCE＝115°，求∠AFC的度数．【分析】过点E作EM∥AB，由平行线的性质得到∠MEC＝65°，从而得到∠AEM＝40°，再根据平行线的性质得到∠EAB＝180°﹣∠AEM＝140°，进而得到∠EAF＝35°，最后根据三角形的外角定理即可求解．【解答】解：如图，过点E作EM∥AB，∵AB∥CD，∴EM∥CD，∴∠MEC+∠DCE＝180°，∵∠DCE＝115°，∴∠MEC＝180°﹣115°＝65°，∵∠AEC＝∠MEC+∠AEM，∠AEC＝105°，∴∠AEM＝40°，∵EM∥AB，∴∠AEM+∠EAB＝180°，∴∠EAB＝180°﹣∠AEM＝140°，∵∠EAB＝∠EAF+∠BAF，∠EAF＝∠BAF，∴∠EAF+3∠EAF＝140°，∴∠EAF＝35°，∴∠AFC＝∠EAF+∠AEC＝35°+105°＝140°．15．直线AB∥CD，E为直线AB、CD之间的一点，完成以下问题：（1）如图1，若∠B＝15°，∠BED＝90°，则∠D＝75°；（2）如图2，若∠B＝α，∠D＝β，求出∠BED的度数（用a、β表示）；（3）如图3，若∠B＝α，∠C＝β，则a、β与∠BEC之间有什么等量关系？请猜想证明．【分析】（1）过E作EF∥AB，根据两直线平行，内错角相等进行计算；（2）过E作EF∥AB，根据两直线平行，同旁内角互补进行计算；（3）过点E作EF∥AB，根据两直线平行，内错角相等，以及两直线平行，同旁内角互补进行计算．【解答】解：（1）过E作EF∥AB，∵AB∥CD，∴EF∥CD，∵∠B＝15°，∴∠BEF＝15°，又∵∠BED＝90°，∴∠DEF＝75°，∵EF∥CD，∴∠D＝75°，故答案为：75°；（2）过E作EF∥AB，∵AB∥CD，∴EF∥CD，∴∠B+∠BEF+∠DEF+∠D＝360°，又∵∠B＝α，∠D＝β，∴∠BED＝∠BEF+∠DEF＝360°﹣α﹣β，故答案为：∠BED＝360°﹣α﹣β；（3）猜想：∠BEC＝180°﹣α+β．证明：过点E作EF∥AB，则∠BEF＝180°﹣∠B＝180°﹣α，∵AB∥EF，AB∥CD，∴EF∥CD，∴∠CEF＝∠C＝β，∴∠BEC＝∠BEF+∠CEF＝180°﹣α+β．16．问题情境：如图1，AB∥CD，∠P AB＝135°，∠PCD＝125°．求∠APC度数．小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可求得∠APC的度数．请写出具体求解过程．问题迁移：（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．【分析】过P作PE∥AB，构造同旁内角，通过平行线性质，可得∠APC＝45°+55°＝100°．（1）过P作PE∥AD交CD于E，推出AD∥PE∥BC，根据平行线的性质得出∠α＝∠DPE，∠β＝∠CPE，即可得出答案；（2）分两种情况：①点P在A、M两点之间，②点P在B、O两点之间，分别画出图形，根据平行线的性质得出∠α＝∠DPE，∠β＝∠CPE，即可得出结论．【解答】解：过P作PE∥AB，∵AB∥CD，∴PE∥AB∥CD，∴∠APE＝180°﹣∠A＝45°，∠CPE＝180°﹣∠C＝55°，∴∠APC＝45°+55°＝100°；（1）∠CPD＝∠α+∠β，理由如下：。

平行线拐点问题专题作平行线的技巧当两条平行线间遇到拐点时，常过拐点作平行线构造出同位角、内错角和同旁内角．通过平行线的性质，得到题目中所求角与已知角之间的关系，从而解决问题．一般而言，有几个“拐点”就需要作几条平行线．类型1形图(燕尾型)1．如图，AB ∥CD ，P 为AB ，CD 之间的一点，已知∠1＝32°，∠2＝25°，则∠BPC＝ .2．如图，已知AB ∥CD ，∠1与∠D ，∠B 之间存在怎样的数量关系？解： 类型2形图(铅笔型)3．(1)如图1所示，若AB ∥DE ，∠B ＝135°，∠D ＝145°，求∠C 的度数；(2)如图1所示，在AB ∥DE 的条件下，你能得出∠B ，∠C ，∠D 之间的数量关系吗？请说明理由；(3)如图2所示，AB ∥EF ，根据(2)中的结果，直接写出∠B ＋∠C ＋∠D ＋∠E 的度数．解：类型3形图4．(2019·河南鹤壁一模)如图，已知AB ∥CD ，若∠A ＝25°，∠E ＝50°，则∠C ＝ .5．(2019·安徽淮北五校联考)小华在学习“平行线的性质”后，对图中∠B ，∠D 和∠BOD的关系进行了探究：(1)如图1，若点O 在CD 的上侧，试探究∠B ，∠D 和∠BOD 之间有什么关系，并说明理由；(2)如图2，若点O在AB的下侧，试探究∠B，∠D和∠BOD之间有什么关系，请直接写出它们的关系式．解：类型4形图(靴子型)6．如图，直线AB∥CD，若∠A＝100°，∠E＝15°，则∠ECD＝.7．如图，已知AB∥CD，点E为AB，CD之外任意一点，探究∠CDE与∠B，∠E之间的数量关系，并说明理由．解：类型5形图8．(2019·江苏南京二十九中模拟)如图，已知AB∥DE，∠ABC＝80°，∠CDE＝140°，求∠BCD的度数．解：方法1：如图1，过点C作FG∥AB.方法2：如图2，反向延长DE交BC于点M.类型6形图9．(2019·湖北武汉蔡甸区期末)如图，已知AB∥CD，∠ABE＝110°，∠DCE＝36°，求∠BEC的度数．解：如图，过点E作直线EF∥AB.类型7多拐点型10.如图所示，AB∥EF，∠B＝45°，∠E＝35°，则∠C＋∠D的值为.11．如图，m∥n，试说明：∠1＋∠3＝∠2＋∠4.解：如图，分别过点P1，P2作P1C∥m，P2D∥m.类型8复合“拐点”型12．已知直线AB∥CD.(1)如图1，BF，DF分别平分∠ABE，∠CDE，那么∠BFD和∠BED有怎样的数量关系？请说明理由；(3)如图2，若点E在直线BD的右侧，BF，DF仍分别平分∠ABE，∠CDE，求∠BFD 和∠BED的数量关系．解：(1)∠BFD＝12∠BED.理由：因为BF，DF分别平分∠ABE，∠CDE，所以∠ABF＝12∠ABE，∠CDF＝12∠CDE，所以∠ABF＋∠CDF＝12∠ABE＋12∠CDE＝12(∠ABE＋∠CDE)．因为∠ABE＋∠CDE＝∠BED，∠BFD＝∠ABF＋∠CDF，所以∠BFD＝1 2∠BED.(2)过点E作EG∥CD，如图所示．因为AB∥CD，EG∥CD，所以AB∥CD∥EG，所以∠ABE＋∠BEG ＝180°，∠CDE＋∠DEG＝180°，所以∠ABE＋∠CDE＋∠BED＝360°.因为∠BFD＝∠ABF＋∠CDF，BF，DF分别平分∠ABE，∠CDE，所以∠ABF＝12∠ABE，∠CDF＝12∠CDE.所以∠BFD＝12(∠ABE＋∠CDE)，所以2∠BFD＋∠BED＝360°.。

七年级下册数学《第五章 相交线与平行线》专题 巧解平行线中的拐点问题【例题1】（2022春•内乡县期末）如图，AB ∥CD ，∠1＝45°，∠2＝30°，则∠3的度数为（ ）A ．55°B ．75°C ．80°D ．105°【变式1-1】（2022春•香洲区校级期中）如图，已知AB∥DE，∠B＝150°，∠D＝145°，则∠C＝ 度．【变式1-2】（2022•博山区一模）如图，直线a∥b，点M、N分别在直线a、b上，P为两平行线间一点，那么∠1+∠2+∠3等于（ ）A．360°B．300°C．270°D．180°【变式1-3】（2022春•信都区期末）为增强学生体质，某学校将“抖空竹”引入阳光体育一小时活动．图1是一位同学抖空竹时的一个瞬间，数学老师把它抽象成图2的数学问题：已知AB∥CD，∠EAB＝80°，∠ECD＝110°．求∠AEC的度数．小明在解决过程中，过E点作EF∥CD，则可以得到EF∥AB，其理由是 ，根据这个思路可得∠AEC＝ ．【变式1-4】如图，已知AB∥DE，∠1＝120°，∠2＝110°，求∠3的度数．【变式1-5】如图，AB∥DE，∠1＝25°，∠2＝110°，求∠BCD的度数．【变式1-6】（2021秋•南召县期末）课堂上老师呈现一个问题：下面提供三种思路：思路一：过点F作MN∥CD（如图（1））；思路二：过点P作PN∥EF，交AB于点N；思路三：过点O作ON∥FG，交CD于点N．解答下列问题：（1）根据思路一（图（1）），可求得∠EFG的度数为 ；（2）根据思路二、思路三分别在图（2）和图（3）中作出符合要求的辅助线；（3）请你从思路二、思路三中任选其中一种，试写出求∠EFG的度数的解答过程．【例题2】如图，直线l 1∥l 2，∠A ＝125°，∠B ＝85°，则∠1+∠2等于（ ）A ．40°B ．35°C ．36°D ．30°【变式2-1】（2022春•新洲区期末）如图，AB ∥EF ，则∠A ，∠C ，∠D ，∠E 满足的数量关系是（ ）A ．∠A +∠C +∠D +∠E ＝360°B ．∠A +∠D ＝∠C +∠E C ．∠A ﹣∠C +∠D +∠E ＝180°D ．∠E ﹣∠C +∠D ﹣∠A ＝90°【变式2-2】如图所示，若AB ∥CD ，则∠1+∠2+∠3+∠4+∠5+∠6的度数是　　．【变式2-3】（2022春•金湖县期末）如图，AB∥CD，E、F分别是AB、CD上的点，EH、FH分别是∠AEG 和∠CFG的角平分线．若∠G＝110°，则∠H＝ °．【变式2-4】（2022春•潜山市月考）如图，AB∥CD，点E，F分别是AB，CD上的点，点M位于AB与CD之间且在EF的右侧．（1）若∠M＝90°，则∠AEM+∠CFM＝ ；（2）若∠M＝n°，∠BEM与∠DFM的角平分线交于点N，则∠N的度数为 ．（用含n的式子表示）【变式2-5】（1）填空：如图1，MA1∥NA2，则∠A1+∠A2＝ °．如图2，MA1∥NA3，则∠A1+∠A2+∠A3＝ °．如图3，MA1∥NA4，则∠A1+∠A2+∠A3+∠A4＝ °．如图4，MA1∥NA5，则∠A1+∠A2+∠A3+∠A4+∠A5＝ °．（2）归纳：如图5，MA1∥NA n，则∠A1+∠A2+∠A3+…+∠A n＝ °．（3）应用：如图6，已知AB∥CD，∠ABE和∠CDE的平分线相交于F，∠E＝80°，求∠BFD的度数．【例题3】小华在学习“平行线的性质”后，对图中∠B ，∠D 和∠BOD 的关系进行了探究：（1）如图1，AB ∥CD ，点O 在AB ，CD 之间，试探究∠B ，∠D 和∠BOD 之间有什么关系？并说明理由；小华添加了过点O 的辅助线OM ，并且OM ∥CD 请帮助他写出解答过程；（2）如图2，若点O 在CD 的上侧，试探究∠B ，∠D 和∠BOD 之间有什么关系？并说明理由；（3）如图3，若点O 在AB 的下侧，试探究∠B ，∠D 和∠BOD 之间有什么关系？请直接写出它们的关系式．【变式3-1】如图,已知∠1=70°，∠2=30°, EF平分∠BEC,∠BEF=50°，求证：AB∥CD.【变式3-2】如图，点E在线段AC上，AB∥CD，∠1=∠B，∠2=∠D．求证：BE⊥DE.【变式3-3】（2022春•阳江期末）如图1，AB∥CD，EOF是直线AB、CD间的一条折线．（1）试证明：∠O＝∠BEO+∠DFO．（2）如果将折一次改为折二次，如图2，则∠BEO、∠O、∠P、∠PFC之间会满足怎样的数量关系，证明你的结论．【变式3-4】（2022秋•驿城区校级期末）问题情境：如图1，AB∥CD，∠PAB＝135°，∠PCD＝125°．求∠APC 度数．小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可求得∠APC的度数．请写出具体求解过程．问题迁移：（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．【变式3-5】阅读下面内容，并解答问题在学习了平行线的性质后，老师请同学们证明命题：两条平行线被第三条直线所截，一组同旁内角的平分线互相垂直．小颖根据命题画出图形并写出如下的已知条件．已知：如图1，AB∥CD，直线EF分别交AB，C于点E，F．∠BEF的平分线与∠DFE的平分线交于点G．（1）直线EG，FG有何关系？请补充结论：求证：“ ”，并写出证明过程；（2）请从下列A、B两题中任选一题作答，我选择 题，并写出解答过程．A．在图1的基础上，分别作∠BEG的平分线与∠DFG的平分线交于点M，得到图2，求∠EMF的度数．B．如图3，AB∥CD，直线EF分别交AB，CD于点E，F．点O在直线AB，CD之间，且在直线EF右侧，∠BEO的平分线与∠DFO的平分线交于点P，请猜想∠EOF与∠EPF满足的数量关系，并证明它．【例题4】（2022秋•小店区校级期末）（1）问题背景：如图1，已知AB∥CD，点P的位置如图所示，连结PA，PC，试探究∠APC与∠A、∠C之间的数量关系，以下是小明同学的探索过程，请你结合图形仔细阅读，并完成填空（理由或数学式）：解：过点P作PE∥AB∵AB∥CD（已知），∴PE∥CD（ ），∴∠A＝∠APE，∠C＝∠CPE（ ），∴∠A+∠C＝ +　（等式的性质）．即∠APC，∠A，∠C之间的数量关系是 ．（2）类比探究：如图2，已知AB∥CD，线段AD与BC相交于点E，点B在点A右侧．若∠ABC＝41°，∠ADC ＝78°，则∠AEC＝ ．（3）拓展延伸：如图3，若∠ABC与∠ADC的角平分线相交于点F，请直接写出∠BFD与∠AEC之间的数量关系　．【变式4-1】（2021秋•长春期末）小明同学遇到这样一个问题：如图①，已知：AB∥CD，E为AB、CD之间一点，连接BE，ED，得到∠BED．求证：∠BED＝∠B+∠D．小亮帮助小明给出了该问的证明．证明：过点E作EF∥AB，则有∠BEF＝∠B．∵AB∥CD，∴EF∥CD，∴∠FED＝∠D，∴∠BED＝∠BEF+∠FED＝∠B+∠D．请你参考小亮的思考问题的方法，解决问题：直线l1∥l2，直线EF和直线l1、l2分别交于C、D两点，点A、B分别在直线l1、l2上，猜想：如图②，若点P在线段CD上，∠PAC＝15°，∠PBD＝40°，求∠APB的度数．拓展：如图③，若点P在直线EF上，连接PA、PB（BD＜AC），直接写出∠PAC、∠APB、∠PBD之间的数量关系．【变式4-2】（2022春•龙亭区校级期末）如图，已知AB∥CD，E、F分别在AB、CD上，点G在AB、CD之间，连接GE、GF．（1）当∠BEG＝40°，EP平分∠BEG，FP平分∠DFG时：①如图1，若EG⊥FG，则∠P的度数为 ；②如图2，在CD的下方有一点Q，EG平分∠BEQ，FD平分∠GFQ，求∠Q+2∠P的度数；（2）如图3，在AB的上方有一点O，若FO平分∠GFC．线段GE的延长线平分∠OEA，则当∠EOF+∠EGF ＝100°时，请直接写出∠OEA与∠OFC的数量关系．【变式4-3】（2021春•安徽月考）（1）如图1，直线AB∥CD．点P在直线AB，CD之间，试说明：∠BAP+∠APC+∠PCD＝360°．小明说明的过程是这样的：“过点P作PE∥AB，…”请按照小明的思路写出完整的解答说明过程．（2）①直线AB∥CD，点P，Q在直线AB，CD之间，且点P，Q在直线AC的同侧，如图2，试探究∠BAP，∠APQ，∠PQC，∠QCD之间的数量关系，并说明理由；②直线AB∥CD，点P，Q在直线AB，CD之间，且点P，Q在直线AC的两侧．如图3，试探究∠BAP，∠APQ，∠PQC，∠QCD之间的数量关系，并说明理由．请在①②任选一个问题进行解答．（3）如图4，若a∥b，直接写出图中x的度数（不用说理）．【变式4-4】（2022春•兴国县期末）【感知】（1）如图①，AB∥CD，∠AEP＝40°，∠PFD＝130°，求∠EPF 的度数．小乐想到了以下方法，请帮忙完成推理过程．解：如图①，过点P作PM∥AB，【探究】（2）如图②，AB∥CD，∠AEP＝50°，∠PFC＝120°，求∠EPF的度数；【应用】（3）如图③，在以上【探究】条件下，∠PEA的平分线和∠PFC的平分线交于点G，求∠G的度数．（4）已知直线a∥b，点A，B在直线a上，点C，D在直线b上（点C在点D的左侧），连接AD，BC，∠ABC的平分线与∠ADC的平分线所在的直线交于点E，设∠ABC＝α，∠ADC＝β（α≠β），请画出图形并求出∠BED的度数（用含α，β的式子表示）．。