概率论常用统计分布共62页
- 格式:ppt
- 大小:4.80 MB
- 文档页数:62

第四章常用概率分布为了便于读者理解统计分析的基本原理,正确掌握和应用以后各章所介绍的统计分析方法,本章在介绍概率论中最基本的两个概念——事件、概率的基础上,重点介绍生物科学研究中常用的几种随机变量的概率分布——正态分布、二项分布、波松分布以及样本平均数的抽样分布和t分布。
第一节事件与概率一、事件(一)必然现象与随机现象在自然界与生产实践和科学试验中,人们会观察到各种各样的现象,把它们归纳起来,大体上分为两大类:一类是可预言其结果的,即在保持条件不变的情况下,重复进行试验,其结果总是确定的,必然发生(或必然不发生)。
例如,在标准大气压下,水加热到100℃必然沸腾;步行条件下必然不可能到达月球等。
这类现象称为必然现象(inevitable phenomena)或确定性现象(definite phenomena)。
另一类是事前不可预言其结果的,即在保持条件不变的情况下,重复进行试验,其结果未必相同。
例如,掷一枚质地均匀对称的硬币,其结果可能是出现正面,也可能出现反面;孵化6枚种蛋,可能“孵化出0只雏”,也可能“孵化出1只雏”,…,也可能“孵化出6 只雏”,事前不可能断言其孵化结果。
这类在个别试验中其结果呈现偶然性、不确定性现象,称为随机现象(random phenomena)或不确定性现象(indefinite phenomena)。
人们通过长期的观察和实践并深入研究之后,发现随机现象或不确定性现象,有如下特点:在一定的条件实现时,有多种可能的结果发生,事前人们不能预言将出现哪种结果;对一次或少数几次观察或试验而言,其结果呈现偶然性、不确定性;但在相同条件下进行大量重复试验时,其试验结果却呈现出某种固有的特定的规律性——频率的稳定性,通常称之为随机现象的统计规律性。
例如,对于一头临产的妊娠母牛产公犊还是产母犊是事前不能确定的,但随着妊娠母牛头数的增加,其产公犊、母犊的比例逐渐接近1:1的性别比例规律。






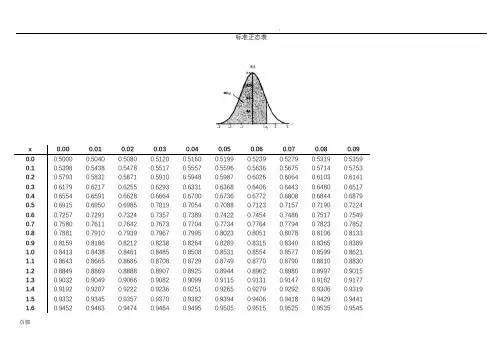
页脚标准正态表x 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359 0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753 0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141 0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517 0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879 0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224 0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549 0.7 0.7580 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852 0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.81330.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8315 0.8340 0.8365 0.83891.0 0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.8599 0.8621 1.1 0.8643 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830 1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015 1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177 1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319 1.5 0.9332 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 0.9418 0.9429 0.9441 1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545页脚n\p 0.005 0. 0.025 0.050 0.100 0.250 0.750 0.900 0.950 0.975 0.990 0.9951 0.0000 0.0002 0.0010 0.0039 0.0158 0.1015 1.3233 2.7055 3.8415 5.0239 6.6349 7.87942 0.0100 0.0201 0.0506 0.1026 0.2107 0.5754 2.7726 4.6052 5.9915 7.3778 9.2103 10.59663 0.0717 0.1148 0.2158 0.3518 0.5844 1.2125 4.1083 6.2514 7.8147 9.3484 11.3449 12.83824 0.2070 0.2971 0.4844 0.7107 1.0636 1.9226 5.3853 7.7794 9.4877 11.1433 13.2767 14.86035 0.4117 0.5543 0.8312 1.1455 1.6103 2.6746 6.6257 9.2364 11.0705 12.8325 15.0863 16.74966 0.6757 0.8721 1.2373 1.6354 2.2041 3.4546 7.8408 10.6446 12.5916 14.4494 16.8119 18.54767 0.9893 1.2390 1.6899 2.1673 2.8331 4.2549 9.0371 12.0170 14.0671 16.0128 18.4753 20.27778 1.3444 1.6465 2.1797 2.7326 3.4895 5.0706 10.2189 13.3616 15.5073 17.5345 20.0902 21.95509 1.7349 2.0879 2.7004 3.3251 4.1682 5.8988 11.3888 14.6837 16.9190 19.0228 21.6660 23.589410 2.1559 2.5582 3.2470 3.9403 4.8652 6.7372 12.5489 15.9872 18.3070 20.4832 23.2093 25.188211 2.6032 3.0535 3.8157 4.5748 5.5778 7.5841 13.7007 17.2750 19.6751 21.9200 24.7250 26.756812 3.0738 3.5706 4.4038 5.2260 6.3038 8.4384 14.8454 18.5493 21.0261 23.3367 26.2170 28.299513 3.5650 4.1069 5.0088 5.8919 7.0415 9.2991 15.9839 19.8119 22.3620 24.7356 27.6882 29.819514 4.0747 4.6604 5.6287 6.5706 7.7895 10.1653 17.1169 21.0641 23.6848 26.1189 29.1412 31.319315 4.6009 5.2293 6.2621 7.2609 8.5468 11.0365 18.2451 22.3071 24.9958 27.4884 30.5779 32.801316 5.1422 5.8122 6.9077 7.9616 9.3122 11.9122 19.3689 23.5418 26.2962 28.8454 31.9999 34.267217 5.6972 6.4078 7.5642 8.6718 10.0852 12.7919 20.4887 24.7690 27.5871 30.1910 33.4087 35.718518 6.2648 7.0149 8.2307 9.3905 10.8649 13.6753 21.6049 25.9894 28.8693 31.5264 34.8053 37.1565 页脚页脚页脚T分布n\p 0.750 0.800 0.850 0.900 0.950 0.975 0.990 0.995 0.9975 0.9990 0.99951 1.0000 1.3764 1.9626 3.0777 6.3138 12.7062 31.8205 63.6567 127.3213 318.3088 636.61922 0.8165 1.0607 1.3862 1.8856 2.9200 4.3027 6.9646 9.9248 14.0890 22.3271 31.59913 0.7649 0.9785 1.2498 1.6377 2.3534 3.1824 4.5407 5.8409 7.4533 10.2145 12.92404 0.7407 0.9410 1.1896 1.5332 2.1318 2.7764 3.7469 4.6041 5.5976 7.1732 8.61035 0.7267 0.9195 1.1558 1.4759 2.0150 2.5706 3.3649 4.0321 4.7733 5.8934 6.86886 0.7176 0.9057 1.1342 1.4398 1.9432 2.4469 3.1427 3.7074 4.3168 5.2076 5.95887 0.7111 0.8960 1.1192 1.4149 1.8946 2.3646 2.9980 3.4995 4.0293 4.7853 5.40798 0.7064 0.8889 1.1081 1.3968 1.8595 2.3060 2.8965 3.3554 3.8325 4.5008 5.04139 0.7027 0.8834 1.0997 1.3830 1.8331 2.2622 2.8214 3.2498 3.6897 4.2968 4.780910 0.6998 0.8791 1.0931 1.3722 1.8125 2.2281 2.7638 3.1693 3.5814 4.1437 4.586911 0.6974 0.8755 1.0877 1.3634 1.7959 2.2010 2.7181 3.1058 3.4966 4.0247 4.437012 0.6955 0.8726 1.0832 1.3562 1.7823 2.1788 2.6810 3.0545 3.4284 3.9296 4.317813 0.6938 0.8702 1.0795 1.3502 1.7709 2.1604 2.6503 3.0123 3.3725 3.8520 4.220814 0.6924 0.8681 1.0763 1.3450 1.7613 2.1448 2.6245 2.9768 3.3257 3.7874 4.140515 0.6912 0.8662 1.0735 1.3406 1.7531 2.1314 2.6025 2.9467 3.2860 3.7328 4.0728页脚页脚76 0.6777 0.8464 1.0436 1.2928 1.6652 1.9917 2.3764 2.6421 2.8913 3.2010 3.423277 0.6777 0.8463 1.0435 1.2926 1.6649 1.9913 2.3758 2.6412 2.8902 3.1995 3.421478 0.6776 0.8463 1.0434 1.2925 1.6646 1.9908 2.3751 2.6403 2.8891 3.1980 3.419779 0.6776 0.8462 1.0433 1.2924 1.6644 1.9905 2.3745 2.6395 2.8880 3.1966 3.418080 0.6776 0.8461 1.0432 1.2922 1.6641 1.9901 2.3739 2.6387 2.8870 3.1953 3.416381 0.6775 0.8461 1.0431 1.2921 1.6639 1.9897 2.3733 2.6379 2.8860 3.1939 3.414782 0.6775 0.8460 1.0430 1.2920 1.6636 1.9893 2.3727 2.6371 2.8850 3.1926 3.413283 0.6775 0.8460 1.0429 1.2918 1.6634 1.9890 2.3721 2.6364 2.8840 3.1913 3.411684 0.6774 0.8459 1.0429 1.2917 1.6632 1.9886 2.3716 2.6356 2.8831 3.1901 3.410285 0.6774 0.8459 1.0428 1.2916 1.6630 1.9883 2.3710 2.6349 2.8822 3.1889 3.408786 0.6774 0.8458 1.0427 1.2915 1.6628 1.9879 2.3705 2.6342 2.8813 3.1877 3.407387 0.6773 0.8458 1.0426 1.2914 1.6626 1.9876 2.3700 2.6335 2.8804 3.1866 3.405988 0.6773 0.8457 1.0426 1.2912 1.6624 1.9873 2.3695 2.6329 2.8795 3.1854 3.404589 0.6773 0.8457 1.0425 1.2911 1.6622 1.9870 2.3690 2.6322 2.8787 3.1843 3.403290 0.6772 0.8456 1.0424 1.2910 1.6620 1.9867 2.3685 2.6316 2.8779 3.1833 3.4019 100 0.6770 0.8452 1.0418 1.2901 1.6602 1.9840 2.3642 2.6259 2.8707 3.1737 3.3905 120 0.6765 0.8446 1.0409 1.2886 1.6577 1.9799 2.3578 2.6174 2.8599 3.1595 3.3735F分布n\m 1 2 3 5 6 7 8 10 15 20 301 39.86 49.50 53.59 55.83 57.24 58.91 59.44 59.86 61.22 61.74 62.262 8.53 9.00 9.16 9.24 9.29 9.35 9.37 9.38 9.42 9.44 9.46 页脚P= 0.99页脚页脚页脚页脚页脚页脚页脚页脚页脚Excel公式1.正态分布函数Excel计算正态分布时,使用NORMDIST函数,其格式如下:NORMDIST(a,μ,σ,累积)其中,“累积”:若为TRUE,则输出分布函数值,即P{X≤a};若为FALSE,则为概率密度函数值.示例:已知X服从正态分布,μ=600,σ=100,求P{X≤500}.输入公式NORMDIST(500, 600, 100, TRUE)得到的结果为0.158655,即P{X≤500}=0.158655.2、正态分布函数的反函数Excel计算正态分布函数的反函数使用NORMINV函数,格式如下:NORMINV(p,μ,σ),此公式计算a,使P{X ≤a}=p3标准正态分布反函数=NORMSINV(0.975)3、t分布Excel计算t分布的值,采用TDIST函数,格式如下:TDIST(a,自由度,侧数)其中,“侧数”:指明分布为单侧或双侧:若为1,为单侧;此命令输出P{ T >a }页脚若为2,为双侧.此命令输出P{ |T| >a}示例:设T服从自由度为24的t分布,求P(T>1.711).已知t=1.711,df=24,采用单侧,则T分布的值:TDIST(1.711,24,1)得到0.05,即P(T > 1.711)=0.05.4. t分布的反函数Excel使用TINV函数得到t分布的反函数,格式如下:TINV(α,自由度)输出T 分布的α / 2 分位点:t_α/2_(n)若求临界值tα(n),则使用公式=TINV(2*α, n)5.返回F分布的函数是FDISTFDIST(x,degrees_freedom1,degrees_freedom2)函数FDIST 的计算公式为FDIST=P( F>x ),5.F分布的反函数FINV(probability,deg_freedom1,deg_freedom2)已知probability=P( F>x ),求x页脚。