当前位置：文档之家 › 概率统计分布表(常用)

概率统计分布表(常用)

  • 格式：docx
  • 大小：310.00 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

6.2数理统计中几种常用的分布.

6.2数理统计中几种常用的分布.

性质3. 设T～t(n),则:T ～F(1,n) .
2
证明:
由t分布定义 T
2
X Y /n
其中X∼N(0,1),Y～χ (n),且X与Y相互独立. 2 2 (1) / 1 X /1 2 F T 2 Y /n ( n) / n
且 2 (1)与 2 ( n)相互独立.
由F分布定义, ∴ F = T2～F(1,n) .
2
条件: 的点χ

P ( n)
2 2



2
( n )
f ( x)dx
2
(n)为χ 2(n)分布的上分位点.
χ (n)分布 的上分位点 图形如右图.
χ2(n)分布的上分位点可以查 附表5.
2Hale Waihona Puke 13例1:求2 2 0 ( 10 ) ， )。 .05 0.1 (20
1.) 因为
P X z0.05 1 P X z0.05 1 0.05 0.95.
P X 1.64 0.9495.
P X 1.65 0.9505.
z0.05 1.64 1.65 1.645. 2
4
2.)
P X z0.005 1 PX z0.005 1 0.005 0.995.

i 1 n i 1
n
EX i2 n.
2 DX i
D D(



2n.
10
4.应用中心极限定理可得，若 若 X ~ 2 (n) ，则当n充分大时， X n 2n 的分布近似正态分布N(0,1).
11
2 (n)
分布的密度函 数的图形如右 图.

数的概率分布

数的概率分布

数的概率分布概率分布是概率论中重要的概念之一，用于描述一个随机变量取值的可能性。

在数学和统计学领域里，数的概率分布研究了在特定情况下数值出现的概率。

本文将介绍数的概率分布的基本含义、常见的概率分布类型以及其在实际应用中的重要性。

一、概率分布的基本定义概率分布是随机变量的可能取值及其对应概率的描述。

随机变量可以是离散型变量或连续型变量。

离散型变量的取值有限且可数，如掷骰子的点数；连续型变量的取值为无限个且不可数，如人的身高。

概率分布描述了随机变量每个取值的概率。

二、常见的概率分布类型1. 离散型概率分布离散型概率分布用于描述随机变量为离散型的情况。

以下是几种常见的离散型概率分布：（1）伯努利分布伯努利分布是一种简单的离散型分布，常用于描述试验只有两个可能结果的情况，如硬币的正反面。

（2）二项分布二项分布是描述n次成功失败试验的离散型分布，例如n次掷硬币中正面朝上的次数。

（3）泊松分布泊松分布用于描述单位时间内随机事件发生的次数，如单位时间内电话呼叫次数、交通事故发生次数等。

2. 连续型概率分布连续型概率分布用于描述随机变量为连续型的情况。

以下是几种常见的连续型概率分布：（1）均匀分布均匀分布描述了在一个区间内随机取值时，每个取值的概率相等，如抛硬币的落点在一个平面上的坐标。

（2）正态分布正态分布是最常见的连续型概率分布之一，也称为高斯分布。

它以钟形曲线为特征，广泛应用于自然和社会科学领域，如身高、体重等。

（3）指数分布指数分布用于描述事件发生的时间间隔或等待时间，如设备故障发生的时间间隔、用户等待的响应时间等。

三、概率分布在实际应用中的重要性概率分布在实际应用中具有重要的作用，主要体现在以下几个方面：1. 预测和决策通过分析和建模某个事件或现象的概率分布，可以对未来可能的结果进行预测。

例如，在金融领域中，通过对股票收益率的概率分析，可以帮助投资者做出决策。

2. 风险评估概率分布可以用于评估风险。

在保险行业中，通过对保险索赔次数或大小的概率分析，可以估算保险公司的风险，并确定合理的保费。

概率统计6-2 统计推断中常用的三个分布

概率统计6-2 统计推断中常用的三个分布

1 n k 其观察值 α k = ∑ x i , k = 1, 2, L . n i =1
(5)样本 k 阶中心矩 样本 1 n Bk = ∑ ( X i − X )k , k = 2, 3, L ; n i =1
1 n 其观察值 bk = ∑ ( x i − x ) k , k = 2, 3, L . n i =1
再根据第五章辛钦定理知 再根据第五章辛钦定理知 辛钦定理
11
1 n k P ∑ X i → µk , n i =1
k = 1, 2, L ;
由第五章关于依概率收敛的序列的性质知
g ( A1 , A2 ,L, Ak ) → g ( µ1 , µ 2 ,L, µ k ),
P
其中 g 是连续函数 .
n
证 X 1 , X 2 ,L, X n 相互独立 , 且与总体 X 同分布,故有 相互独立, 同分布,
E( X i ) = E( X ) = µ , D( X i ) = D( X ) = σ 2 , i = 1,2, L , n
1 n 1 n 所以 E( X ) = E( ∑ X i ) = ∑ E( X i ) = µ , n i =1 n i =1 1 n 1 n σ2 D( X ) = D( ∑ X i ) = 2 ∑ D( X i ) = . n i =1 n i =1 n
7
样本均值
1 X = ∑Xi n i=1
n
它反映了总体 均值的信息 它反映了总体 方差的信息
1 n 1 n 2 2 2 2 样本方差 S = ∑( Xi − X) = n −1 ∑Xi − nX n −1 i=1 i =1
推导： 推导：
( Xi − X)2 = ∑( Xi2 − 2Xi X + X 2 ) ∑

概率分布与统计图表

概率分布与统计图表
1. 关于
心，左右对称。 2. 在 在 处取得概率密度函数的最大值， 处有拐点，表现为 钟形曲线。即正
对称。即态分布以均数为中
态曲线在横轴上方均数处最高。
2018/10/26
6
3. 正态分布有两个参数，即均数µ 和标准差σ。
µ 是位置参数，σ是变异度参数(形状参数)。常用
N(µ ,σ2)表示均数为μ ，标准差为σ的正态分布；用
（ 2）
2018/10/26
16
（ 3）
查附表1，标准正态分布曲线下左侧面积为0.10所对应
的Z值为-1.28，所以80%的8岁男孩身高值集中在
X 1.28S 区间内，即116.9cm~129.2cm
2018/10/26
17
练习：
查附表，求标准正态分布曲线下的面积。 （-∞，-1.96），（ -∞ ，-2.58）， （-1.96，1.96），（-1，1），（ -∞ ，0.00）。
，
S=4.79 cm ，估计(1)该地8岁男孩身高在130 cm以上者占该地8岁 男孩总数的百分比；(2)身高界于120cm~128cm者占该地8岁男孩
总数的比例；(3)该地80%男孩身高集中在哪个范围？
先做标准化变化:
理论上该地8岁男孩身高在130 cm以上者占该地8岁男孩 总数的7.21%。
2018/10/26 15
分析：正常人的血红蛋白过高过低均为异常，要制
定双侧正常值范围。
该指标的95%医学参考值范围为
2018/10/26 21
例4 某地调查110名正常成年男子的第一秒肺通 气量，得均数为4.2 L，标准差为0.7 L ，试估计该地 正常成年男子第一秒肺通气量的95%参考值范围。
分析：正常人的第一秒肺通气量近似正态分布，且只

(卫生统计学)第四章 常用概率分布

(卫生统计学)第四章 常用概率分布

第二节 Poisson分布的概念与特征
一、Poisson分布概念与特征
若某一随机变量X的取值为0，1，2，…，且X=k 的概率为：
P(X k) k e
k!
记作 X~P（ λ ）
其中 自然数e≈2.7182; λ 是大于0的常数，称X服从以λ 为参数的Poisson分布。
Poisson分布主要用于描述在单位时间（空间）内稀有事件的发生数。例如：放 射性物质在单位时间内的放射次数、单位容积内充分摇匀的水中的细菌数、染色 体异变数等。
350 300 250 200
人数
150 100
50 0
109 111 113 115 117 119 121 123 125 127 129 131 133 135 137 139 141 143
不同参数µ和σ下的正态分布曲线
正态分布函数
1.Gauss函数 （Gauss, 1777~1855 德国人）
某地正常成人心率（次/分）的频率分布
频数 1 5 12 13 26 31
组段 75~ 80~ 85~ 90~ 95~ 100~105
频数 24 15 9 7 5 2
心率频数分布
35
30
25
20
人数
15
10
5
0
45
50
55
60
65
70
75
80
85
90
95 100~105
正态曲线
例4-10 某地1986年120名8岁男孩身高频数图
百分位数法
例4-13
282名正常人尿汞值（g/L）测量结果
尿汞值 0~ 8.0~
16.0~ 24.0~ 32.0~ 40~ 48.0~ 56.0~ 64.0~72.0

常用概率分布间简介

常用概率分布间简介

其中 c 为常数，解方程（1）得
f ( ) c f ( )
f
(
)
k
e
1 2
c
2
，
k
为常数.
为使 f ( ) 为概率密度函数，
f
( )d
1，
即
k
e
1 2
c
2
dy
1
故必须 c 0 ，不妨令 c 1 （ 0 ），代入（2）解得 2
k 1 ， 2 Biblioteka 于是f ( ) 1
2
e2 2 ， R ，
2
这是均值为 0，方差为 2 的正态分布的概率密度函数.
.
X
~
N(0, 2)
,
则Y
X2
~
Ga(
1 2
,
1 2
2
)
.
（1） （2）
Ga( n , 1) 2(n) . 22
m
Xi ~ N(0,1) , i 1,2,,n 且相互独立 , 则 X
X
2 i
~
2(n) .
i 1
⒊ 相当误差（比率）的概率分布
m
设
Xi
~
N(0, 2 ) ，i
1,2,, m,m 1,,m n且相互独立，则
i 1
二、随机误差的概率分布
⒈ 高斯随机误差模型 随机变量的高斯分解
可观测的指标
X
不可观测的随机干扰
指标的标准值(生产控制参数,理论均值)
原始测量误差的概率分布
由棣莫弗提出，高斯推证，拉普拉斯再证，原始测量误差的概率分布为：
~ N (0 , 2 )
高斯的推证要点如下：
设测量误差 X 的密度函数为 f ( ) ，由“最大后验概率”的原则得

第3节 常用统计分布(三个常用分布)


例2
设X
~
N
(
,
2
),
Y
2
~
2 (n),且X ,Y相互独立,
试求 T X 的概率分布.
Yn
解 因为X ~ N(, 2),所以 X ~ N(0,1)
又Y
2
~
2 (n),且X ,Y独立,则
X
与Y
2
独立,
由定理得
T (X ) / X ~ t(n) (Y / 2) / n Y n
n
事实上，它们受到一个条件的约束：
Xi nX
i 1
n
i 1
Xi
X
1
n
(
i 1
Xi
nX )
1
0
0.
例1
设X1 ,
X 2 ,
,
X
为
6
来
自
正
态
总
体N
(0,1)的
一
组
样
本,
求C1
,
C
使
2
得
Y C1( X1 X 2 )2 C2( X 3 X4 X5 X6 )2
服 从 2分 布.
解
X1
2
4
则C1 1 2 ,C2 1 4 .
3. t 分布 定义 设 X ~ N (0, 1), Y ~ 2 (n), 且 X , Y
独立,则称随机变量 T X 服从自由度为 n Y /n
的 t 分布, 记为T ~ t(n).
t 分布又称学生氏(Student)分布. t(n) 分布的概率密度函数为
2. 2分布（卡方分布）
定义、设 X1, X 2 ,L , X n 相互独立，同服从 N (0, 1)

标准正态分布表025

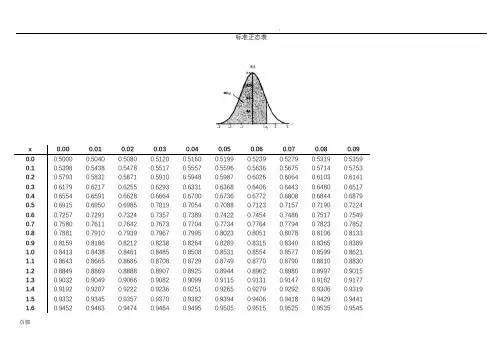
标准正态分布表025标准正态分布表025是统计学中常用的一种表格，用于计算正态分布的概率。

正态分布是一种连续概率分布，其概率密度函数呈钟形曲线，均值为0，标准差为1。

标准正态分布表025可以帮助我们在进行正态分布概率计算时节省时间，提高计算的准确性。

在标准正态分布表025中，横坐标为Z值，纵坐标为Z值对应的累积概率。

通过查表可以得到给定Z值下的累积概率，也可以通过给定累积概率来反查对应的Z 值。

这对于统计学中的假设检验、置信区间估计等问题非常有用。

使用标准正态分布表025时，首先需要计算出所关注的变量的Z值，即将原始数据转化为标准正态分布的变量。

然后根据Z值在表格中查找对应的累积概率。

例如，如果我们要计算Z值为1.96时的累积概率，可以在表格中找到Z值为1.9和0.06的交叉点，对应的累积概率为0.9750。

这意味着在标准正态分布下，Z值小于1.96的概率为0.9750。

另外，标准正态分布表025也可以用于反查。

例如，如果我们希望找到累积概率为0.95对应的Z值，可以在表格中找到累积概率为0.9500的数值，对应的Z值为1.64。

这意味着在标准正态分布下，Z值小于1.64的概率为0.95。

在实际应用中，标准正态分布表025可以帮助我们进行各种与正态分布相关的统计推断。

例如，在制造业中，我们可以利用标准正态分布表025来进行质量控制，判断产品的合格率；在医学研究中，我们可以利用标准正态分布表025来进行药效学研究，评估药物的疗效；在金融领域，我们可以利用标准正态分布表025来进行风险评估，制定投资策略。

总之，标准正态分布表025是统计学中一项非常有用的工具，它可以帮助我们快速准确地计算正态分布的概率，为决策提供科学依据。

通过熟练掌握标准正态分布表025的使用方法，我们可以更好地应用统计学原理解决实际问题，提高工作效率，取得更好的成果。

第4章 几种常见的概率分布


6. 正态分布的单双侧临界值
面积为，已知 上侧临界值 P(U> u )= α ，下侧临界值 P (U <- u )= α (附表 3 上侧临界值)
若将一定曲线下面积α，平分到两侧尾区，则每侧曲线下面积为α/2,
即 P(
U U 2
)=
α,
U 这时的
U
2
称为α的双侧临界值。
面积为，已知
u 称为的上侧临界值。 附表3 （256页）给出了u的值。
N(0，1)
x=0 时，φ(x) 达到最大值
(1) 关于点（0，0.5）对称，该点也
是它的拐点
(2)x 取值离原点越远，φ (x) 值越小 (2) 曲线以 y = 0 和 y = 1 为渐近线；
(3)关于 y 轴对称，即φ(x)= φ (- x)
(3) Ф(1.960)－Ф(－1.960) = 0.95
种变量有它各自的概率而组成一个分布。这个分布就叫做二项概率分布，或简称二项分布
（binomial distribution) 由此得到计算二项分布任何一项概率的通式为：p(x) =Cnx φ
x(1- φ)n-x
二项分布是一种离散型随机变量的概率分布
性质
n
Cnx x (1 )nx 1
x0
m
一指定时间范围内或在指定的面积或体积内某一事件出现的个体数的分布 泊松分布是一种离散型随机变量的概率分布
实例 调查某种猪场闭锁育种群仔猪畸形数，共记录 200 窝， 畸形仔猪数的分布情况如下表所
示。试判断畸形仔猪数是否服从泊松分布。 畸形仔猪数统计分布
解：根据泊松分布的平均数与方差相等这一特征，若畸形仔猪数服从泊松分布，则由观察数 据计算的平均数和方差就近于相等。样本均数和方差 S2 计算结果如下：

第5章 常用概率分布2


正态分布的参数
1
2
3
图9 标准差相同、均数不同的正态分布曲线
正态分布的参数
σ1 σ2 σ3 σ1<σ2<σ3
图10 均数相同、标准差不同的正态分布曲线
正态分布
二、正态概率密度曲线下的面积规律

正态曲线下面积总和为1；
正态曲线关于均数对称；对称的区域内面积相等； 对任意正态曲线，按标准差为单位，对应的面积相 等；

计算z值：
z1 x1


( 1.96 )

1.96
z2


x2


( 1.96 )

1.96
0.025 1.96
查附表1：确定概率 结论：95％
0.025 -1.96
正态分布
例 已知X服从均数为 、标准差 为的正态分布， 1 .96 试估计：(1)X取值在区间 上的概率； (2)X 取值在区间 上的概率。 2.58
记为N(0,1)。 标准正态分布是一条曲线。

标准正态分布曲线下的面积
μ±1范围内的面积为68.27% μ±1.96范围内的面积为95%
μ±2.58范围内的面积占99%
图12 正态曲线下的面积分布示意
标准正态分布曲线下的面积的计算
求z值，用z值查表，得到所求区间面积占总面
积的比例。 曲线下对称于0的区间，面积相等。 曲线下总面积为100％或1。

计算z值：
Z 130 123 .02 1.46 4.79

查附表1：确定概率
0.0721 0.0721 1.46

结论：7.21％
-1.46
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

标准正态表2.1 0.9821 0.9826 0.9830 0.9834 0.9838 0.9842 0.9846 0.9850 0.9854 0.9857 2.2 0.9861 0.9864 0.9868 0.9871 0.9875 0.9878 0.9881 0.9884 0.9887 0.9890 2.3 0.9893 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911 0.9913 0.9916 2.4 0.9918 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.9932 0.9934 0.9936 2.5 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952 2.6 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 0.9964 2.7 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972 0.9973 0.9974 2.8 0.9974 0.9975 0.9976 0.9977 0.9977 0.9978 0.9979 0.9979 0.9980 0.99812.9 0.9981 0.9982 0.9982 0.9983 0.9984 0.9984 0.9985 0.9985 0.9986 0.99863.0 0.9987 0.9987 0.9987 0.9988 0.9988 0.9989 0.9989 0.9989 0.9990 0.9990 3.1 0.9990 0.9991 0.9991 0.9991 0.9992 0.9992 0.9992 0.9992 0.9993 0.9993 3.2 0.9993 0.9993 0.9994 0.9994 0.9994 0.9994 0.9994 0.9995 0.9995 0.9995 3.3 0.9995 0.9995 0.9995 0.9996 0.9996 0.9996 0.9996 0.9996 0.9996 0.9997 3.4 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9998 3.5 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 3.6 0.9998 0.9998 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 3.7 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 3.8 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 3.9 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.000024 9.8862 10.8564 12.4012 13.8484 15.6587 19.0373 28.2412 33.1962 36.4150 39.3641 42.9798 45.558525 10.5197 11.5240 13.1197 14.6114 16.4734 19.9393 29.3389 34.3816 37.6525 40.6465 44.3141 46.927926 11.1602 12.1981 13.8439 15.3792 17.2919 20.8434 30.4346 35.5632 38.8851 41.9232 45.6417 48.289927 11.8076 12.8785 14.5734 16.1514 18.1139 21.7494 31.5284 36.7412 40.1133 43.1945 46.9629 49.644928 12.4613 13.5647 15.3079 16.9279 18.9392 22.6572 32.6205 37.9159 41.3371 44.4608 48.2782 50.993429 13.1211 14.2565 16.0471 17.7084 19.7677 23.5666 33.7109 39.0875 42.5570 45.7223 49.5879 52.335630 13.7867 14.9535 16.7908 18.4927 20.5992 24.4776 34.7997 40.2560 43.7730 46.9792 50.8922 53.672031 14.4578 15.6555 17.5387 19.2806 21.4336 25.3901 35.8871 41.4217 44.9853 48.2319 52.1914 55.002732 15.1340 16.3622 18.2908 20.0719 22.2706 26.3041 36.9730 42.5847 46.1943 49.4804 53.4858 56.328133 15.8153 17.0735 19.0467 20.8665 23.1102 27.2194 38.0575 43.7452 47.3999 50.7251 54.7755 57.648434 16.5013 17.7891 19.8063 21.6643 23.9523 28.1361 39.1408 44.9032 48.6024 51.9660 56.0609 58.963935 17.1918 18.5089 20.5694 22.4650 24.7967 29.0540 40.2228 46.0588 49.8018 53.2033 57.3421 60.274836 17.8867 19.2327 21.3359 23.2686 25.6433 29.9730 41.3036 47.2122 50.9985 54.4373 58.6192 61.581237 18.5858 19.9602 22.1056 24.0749 26.4921 30.8933 42.3833 48.3634 52.1923 55.6680 59.8925 62.883338 19.2889 20.6914 22.8785 24.8839 27.3430 31.8146 43.4619 49.5126 53.3835 56.8955 61.1621 64.181439 19.9959 21.4262 23.6543 25.6954 28.1958 32.7369 44.5395 50.6598 54.5722 58.1201 62.4281 65.475640 20.7065 22.1643 24.4330 26.5093 29.0505 33.6603 45.6160 51.8051 55.7585 59.3417 63.6907 66.766041 21.4208 22.9056 25.2145 27.3256 29.9071 34.5846 46.6916 52.9485 56.9424 60.5606 64.9501 68.052742 22.1385 23.6501 25.9987 28.1440 30.7654 35.5099 47.7663 54.0902 58.1240 61.7768 66.2062 69.336043 22.8595 24.3976 26.7854 28.9647 31.6255 36.4361 48.8400 55.2302 59.3035 62.9904 67.4593 70.615944 23.5837 25.1480 27.5746 29.7875 32.4871 37.3631 49.9129 56.3685 60.4809 64.2015 68.7095 71.892645 24.3110 25.9013 28.3662 30.6123 33.3504 38.2910 50.9849 57.5053 61.6562 65.4102 69.9568 73.1661T分布n\p 0.750 0.800 0.850 0.900 0.950 0.975 0.990 0.995 0.9975 0.9990 0.999519 0.6876 0.8610 1.0655 1.3277 1.7291 2.0930 2.5395 2.8609 3.1737 3.5794 3.883420 0.6870 0.8600 1.0640 1.3253 1.7247 2.0860 2.5280 2.8453 3.1534 3.5518 3.849521 0.6864 0.8591 1.0627 1.3232 1.7207 2.0796 2.5176 2.8314 3.1352 3.5272 3.819322 0.6858 0.8583 1.0614 1.3212 1.7171 2.0739 2.5083 2.8188 3.1188 3.5050 3.792123 0.6853 0.8575 1.0603 1.3195 1.7139 2.0687 2.4999 2.8073 3.1040 3.4850 3.767624 0.6848 0.8569 1.0593 1.3178 1.7109 2.0639 2.4922 2.7969 3.0905 3.4668 3.745425 0.6844 0.8562 1.0584 1.3163 1.7081 2.0595 2.4851 2.7874 3.0782 3.4502 3.725126 0.6840 0.8557 1.0575 1.3150 1.7056 2.0555 2.4786 2.7787 3.0669 3.4350 3.706627 0.6837 0.8551 1.0567 1.3137 1.7033 2.0518 2.4727 2.7707 3.0565 3.4210 3.689628 0.6834 0.8546 1.0560 1.3125 1.7011 2.0484 2.4671 2.7633 3.0469 3.4082 3.673929 0.6830 0.8542 1.0553 1.3114 1.6991 2.0452 2.4620 2.7564 3.0380 3.3962 3.659430 0.6828 0.8538 1.0547 1.3104 1.6973 2.0423 2.4573 2.7500 3.0298 3.3852 3.646031 0.6825 0.8534 1.0541 1.3095 1.6955 2.0395 2.4528 2.7440 3.0221 3.3749 3.633532 0.6822 0.8530 1.0535 1.3086 1.6939 2.0369 2.4487 2.7385 3.0149 3.3653 3.621833 0.6820 0.8526 1.0530 1.3077 1.6924 2.0345 2.4448 2.7333 3.0082 3.3563 3.610934 0.6818 0.8523 1.0525 1.3070 1.6909 2.0322 2.4411 2.7284 3.0020 3.3479 3.600735 0.6816 0.8520 1.0520 1.3062 1.6896 2.0301 2.4377 2.7238 2.9960 3.3400 3.591136 0.6814 0.8517 1.0516 1.3055 1.6883 2.0281 2.4345 2.7195 2.9905 3.3326 3.582137 0.6812 0.8514 1.0512 1.3049 1.6871 2.0262 2.4314 2.7154 2.9852 3.3256 3.573738 0.6810 0.8512 1.0508 1.3042 1.6860 2.0244 2.4286 2.7116 2.9803 3.3190 3.565739 0.6808 0.8509 1.0504 1.3036 1.6849 2.0227 2.4258 2.7079 2.9756 3.3128 3.558140 0.6807 0.8507 1.0500 1.3031 1.6839 2.0211 2.4233 2.7045 2.9712 3.3069 3.551041 0.6805 0.8505 1.0497 1.3025 1.6829 2.0195 2.4208 2.7012 2.9670 3.3013 3.544242 0.6804 0.8503 1.0494 1.3020 1.6820 2.0181 2.4185 2.6981 2.9630 3.2960 3.537743 0.6802 0.8501 1.0491 1.3016 1.6811 2.0167 2.4163 2.6951 2.9592 3.2909 3.531644 0.6801 0.8499 1.0488 1.3011 1.6802 2.0154 2.4141 2.6923 2.9555 3.2861 3.525845 0.6800 0.8497 1.0485 1.3006 1.6794 2.0141 2.4121 2.6896 2.9521 3.2815 3.520346 0.6799 0.8495 1.0483 1.3002 1.6787 2.0129 2.4102 2.6870 2.9488 3.2771 3.515047 0.6797 0.8493 1.0480 1.2998 1.6779 2.0117 2.4083 2.6846 2.9456 3.2729 3.509948 0.6796 0.8492 1.0478 1.2994 1.6772 2.0106 2.4066 2.6822 2.9426 3.2689 3.505149 0.6795 0.8490 1.0475 1.2991 1.6766 2.0096 2.4049 2.6800 2.9397 3.2651 3.500450 0.6794 0.8489 1.0473 1.2987 1.6759 2.0086 2.4033 2.6778 2.9370 3.2614 3.496051 0.6793 0.8487 1.0471 1.2984 1.6753 2.0076 2.4017 2.6757 2.9343 3.2579 3.491853 0.6791 0.8485 1.0467 1.2977 1.6741 2.0057 2.3988 2.6718 2.9293 3.2513 3.483854 0.6791 0.8483 1.0465 1.2974 1.6736 2.0049 2.3974 2.6700 2.9270 3.2481 3.480055 0.6790 0.8482 1.0463 1.2971 1.6730 2.0040 2.3961 2.6682 2.9247 3.2451 3.476456 0.6789 0.8481 1.0461 1.2969 1.6725 2.0032 2.3948 2.6665 2.9225 3.2423 3.472957 0.6788 0.8480 1.0459 1.2966 1.6720 2.0025 2.3936 2.6649 2.9204 3.2395 3.469658 0.6787 0.8479 1.0458 1.2963 1.6716 2.0017 2.3924 2.6633 2.9184 3.2368 3.466359 0.6787 0.8478 1.0456 1.2961 1.6711 2.0010 2.3912 2.6618 2.9164 3.2342 3.463260 0.6786 0.8477 1.0455 1.2958 1.6706 2.0003 2.3901 2.6603 2.9146 3.2317 3.460261 0.6785 0.8476 1.0453 1.2956 1.6702 1.9996 2.3890 2.6589 2.9127 3.2293 3.457362 0.6785 0.8475 1.0452 1.2954 1.6698 1.9990 2.3880 2.6575 2.9110 3.2270 3.454563 0.6784 0.8474 1.0450 1.2951 1.6694 1.9983 2.3870 2.6561 2.9093 3.2247 3.451864 0.6783 0.8473 1.0449 1.2949 1.6690 1.9977 2.3860 2.6549 2.9076 3.2225 3.449165 0.6783 0.8472 1.0448 1.2947 1.6686 1.9971 2.3851 2.6536 2.9060 3.2204 3.446666 0.6782 0.8471 1.0446 1.2945 1.6683 1.9966 2.3842 2.6524 2.9045 3.2184 3.444167 0.6782 0.8470 1.0445 1.2943 1.6679 1.9960 2.3833 2.6512 2.9030 3.2164 3.441768 0.6781 0.8469 1.0444 1.2941 1.6676 1.9955 2.3824 2.6501 2.9015 3.2145 3.439469 0.6781 0.8469 1.0443 1.2939 1.6672 1.9949 2.3816 2.6490 2.9001 3.2126 3.437270 0.6780 0.8468 1.0442 1.2938 1.6669 1.9944 2.3808 2.6479 2.8987 3.2108 3.435071 0.6780 0.8467 1.0441 1.2936 1.6666 1.9939 2.3800 2.6469 2.8974 3.2090 3.432972 0.6779 0.8466 1.0440 1.2934 1.6663 1.9935 2.3793 2.6459 2.8961 3.2073 3.430873 0.6779 0.8466 1.0438 1.2933 1.6660 1.9930 2.3785 2.6449 2.8949 3.2057 3.428974 0.6778 0.8465 1.0437 1.2931 1.6657 1.9925 2.3778 2.6439 2.8936 3.2041 3.426975 0.6778 0.8464 1.0436 1.2929 1.6654 1.9921 2.3771 2.6430 2.8924 3.2025 3.425076 0.6777 0.8464 1.0436 1.2928 1.6652 1.9917 2.3764 2.6421 2.8913 3.2010 3.423277 0.6777 0.8463 1.0435 1.2926 1.6649 1.9913 2.3758 2.6412 2.8902 3.1995 3.421478 0.6776 0.8463 1.0434 1.2925 1.6646 1.9908 2.3751 2.6403 2.8891 3.1980 3.419779 0.6776 0.8462 1.0433 1.2924 1.6644 1.9905 2.3745 2.6395 2.8880 3.1966 3.418080 0.6776 0.8461 1.0432 1.2922 1.6641 1.9901 2.3739 2.6387 2.8870 3.1953 3.416381 0.6775 0.8461 1.0431 1.2921 1.6639 1.9897 2.3733 2.6379 2.8860 3.1939 3.414782 0.6775 0.8460 1.0430 1.2920 1.6636 1.9893 2.3727 2.6371 2.8850 3.1926 3.413283 0.6775 0.8460 1.0429 1.2918 1.6634 1.9890 2.3721 2.6364 2.8840 3.1913 3.411684 0.6774 0.8459 1.0429 1.2917 1.6632 1.9886 2.3716 2.6356 2.8831 3.1901 3.410285 0.6774 0.8459 1.0428 1.2916 1.6630 1.9883 2.3710 2.6349 2.8822 3.1889 3.408787 0.6773 0.8458 1.0426 1.2914 1.6626 1.9876 2.3700 2.6335 2.8804 3.1866 3.405988 0.6773 0.8457 1.0426 1.2912 1.6624 1.9873 2.3695 2.6329 2.8795 3.1854 3.404589 0.6773 0.8457 1.0425 1.2911 1.6622 1.9870 2.3690 2.6322 2.8787 3.1843 3.403290 0.6772 0.8456 1.0424 1.2910 1.6620 1.9867 2.3685 2.6316 2.8779 3.1833 3.4019 100 0.6770 0.8452 1.0418 1.2901 1.6602 1.9840 2.3642 2.6259 2.8707 3.1737 3.3905 120 0.6765 0.8446 1.0409 1.2886 1.6577 1.9799 2.3578 2.6174 2.8599 3.1595 3.3735F分布19 2.99 2.61 2.40 2.27 2.18 2.06 2.02 1.98 1.86 1.81 1.7620 2.97 2.59 2.38 2.25 2.16 2.04 2.00 1.96 1.84 1.79 1.7421 2.96 2.57 2.36 2.23 2.14 2.02 1.98 1.95 1.83 1.78 1.7222 2.95 2.56 2.35 2.22 2.13 2.01 1.97 1.93 1.81 1.76 1.70 24 2.93 2.54 2.33 2.19 2.10 1.98 1.94 1.91 1.78 1.73 1.67 26 2.91 2.52 2.31 2.17 2.08 1.96 1.92 1.88 1.76 1.71 1.65 28 2.89 2.50 2.29 2.16 2.06 1.94 1.90 1.87 1.74 1.69 1.63 30 2.88 2.49 2.28 2.14 2.05 1.93 1.88 1.85 1.72 1.67 1.61P= 0.9911 9.65 7.21 6.22 5.67 5.32 4.89 4.74 4.63 4.40 4.29 4.21 4.15 4.1012 9.33 6.93 5.95 5.41 5.06 4.64 4.50 4.39 4.16 4.05 3.97 3.91 3.8613 9.07 6.70 5.74 5.21 4.86 4.44 4.30 4.19 3.96 3.86 3.78 3.72 3.6614 8.86 6.51 5.56 5.04 4.69 4.28 4.14 4.03 3.80 3.70 3.62 3.56 3.5115 8.68 6.36 5.42 4.89 4.56 4.14 4.00 3.89 3.67 3.56 3.49 3.42 3.3716 8.53 6.23 5.29 4.77 4.44 4.03 3.89 3.78 3.55 3.45 3.37 3.31 3.2617 8.40 6.11 5.18 4.67 4.34 3.93 3.79 3.68 3.46 3.35 3.27 3.21 3.1618 8.29 6.01 5.09 4.58 4.25 3.84 3.71 3.60 3.37 3.27 3.19 3.13 3.0819 8.18 5.93 5.01 4.50 4.17 3.77 3.63 3.52 3.30 3.19 3.12 3.05 3.0020 8.10 5.85 4.94 4.43 4.10 3.70 3.56 3.46 3.23 3.13 3.05 2.99 2.9421 8.02 5.78 4.87 4.37 4.04 3.64 3.51 3.40 3.17 3.07 2.99 2.93 2.8822 7.95 5.72 4.82 4.31 3.99 3.59 3.45 3.35 3.12 3.02 2.94 2.88 2.8323 7.88 5.66 4.76 4.26 3.94 3.54 3.41 3.30 3.07 2.97 2.89 2.83 2.7824 7.82 5.61 4.72 4.22 3.90 3.50 3.36 3.26 3.03 2.93 2.85 2.79 2.7425 7.77 5.57 4.68 4.18 3.85 3.46 3.32 3.22 2.99 2.89 2.81 2.75 2.7026 7.72 5.53 4.64 4.14 3.82 3.42 3.29 3.18 2.96 2.86 2.78 2.72 2.6628 7.64 5.45 4.57 4.07 3.75 3.36 3.23 3.12 2.90 2.79 2.72 2.65 2.6029 7.60 5.42 4.54 4.04 3.73 3.33 3.20 3.09 2.87 2.77 2.69 2.63 2.5730 7.56 5.39 4.51 4.02 3.70 3.30 3.17 3.07 2.84 2.74 2.66 2.60 2.55Excel公式1.正态分布函数Excel计算正态分布时，使用NORMDIST函数，其格式如下：NORMDIST（a，μ，σ，累积）其中，“累积”：若为TRUE，则输出分布函数值，即P{X≤a}；若为FALSE，则为概率密度函数值．示例：已知X服从正态分布，μ＝600，σ＝100，求P{X≤500}．输入公式NORMDIST(500, 600, 100, TRUE)得到的结果为0.158655，即P{X≤500}=0.158655．2、正态分布函数的反函数Excel计算正态分布函数的反函数使用NORMINV函数，格式如下：NORMINV（p，μ ，σ ），此公式计算a，使P{X ≤a}=p3标准正态分布反函数=NORMSINV(0.975)3、t分布Excel计算t分布的值,采用TDIST函数，格式如下：TDIST（a，自由度，侧数）其中，“侧数”：指明分布为单侧或双侧：若为1，为单侧；此命令输出P{ T >a }若为2，为双侧．此命令输出P{ |T| >a}示例：设T服从自由度为24的t分布，求P(T>1.711)．已知t＝1.711，df=24，采用单侧，则T分布的值：TDIST(1.711,24,1)得到0.05，即P(T > 1.711)=0.05．4. t分布的反函数Excel使用TINV函数得到t分布的反函数，格式如下：TINV（α，自由度）输出T 分布的α / 2 分位点：t_α/2_(n)若求临界值tα(n)，则使用公式＝TINV(2*α, n)5.返回F分布的函数是FDISTFDIST(x,degrees_freedom1,degrees_freedom2) 函数FDIST 的计算公式为FDIST=P( F>x )，5.F分布的反函数FINV(probability,deg_freedom1,deg_freedom2)已知probability=P( F>x )，求x。