(2)驻波中各点的相位
- 格式:ppt
- 大小:335.00 KB
- 文档页数:15
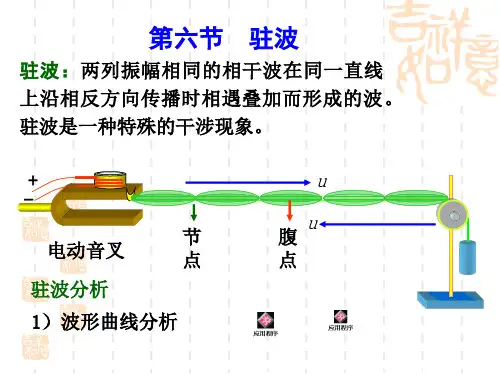



波的基本概念1.波:振动在媒质(介质)中的传播就是波,分为横波和纵波。
2.横波:媒质中各体元振动的方向与波传播的方向垂直。
例如:一根均匀柔软的细绳的振动,形成的波就是横波。
3.纵波:媒质中各体元振动的方向与波传播的方向平行。
例如:空气中的声波,空气中体元时而靠近,时而疏远。
4.表面波:在两中媒质的界面上传播的波。
例如:水面波。
5.波面:波传播时,同相位各点所组成的面。
6.波前:离波源最远,即“最前方”的波面。
7.波射线:与波面垂直且表明波的传播方向的线叫波射线。
8.平面波:波前为平面的波。
波线是互相平行的。
9.球面波:波前为球面。
点波源在均匀的和各向同性媒质中发生的波是球面波。
波线是相交于波源的直线。
平面简谐波方程一. 平面简谐波:平面波传播时,媒质中体元均按正弦(或余弦)规律运动。
二. 平面简谐波方程(从运动学角度考虑):描述不同时刻不同体元的运动状态。
设:一列平面简谐波沿'轴正向传播,选择原点-|处体元相位为0的时刻为计时起点,即该体元的相位为零,则:|处体元的运动学方程:y = Acos魏其中:「为体元距平衡位置的位移,A、「为波源的振幅和圆频率。
Ai ——经:的时间,- |处体元的振动状态传到位于二处的体元,即:t时刻,位于厂处(巧t ——的体元的振动状态应与I甘丿时刻处体元的振动状态一样,则乔处体元的运动学方程为:其中:V 为振动状态传播的速度,叫波速,也叫相速。
⑴式就是平面简谐波方程。
从⑴式时刻的波形。
T=—r由⑴可知:二处体元振动的周期、频率和圆频率:注意:•不一定是振动系统的固有频率而取决于波源频率,所以⑴中的形式不意味 着各体元作简谐振动。
由⑵知:t 一定时,y 是二的周期函数,也存在空间位置上的周期,波长即:波长是波在一个周期内传播的距离,或:沿波传播方向相邻同相位两点间的距离。
另外,由空间位置的周期性可知:A — vT =—定义: ',称为波数:看出:二处质元的振动比原点处的质元落后 X耳£誌X —F 丿。
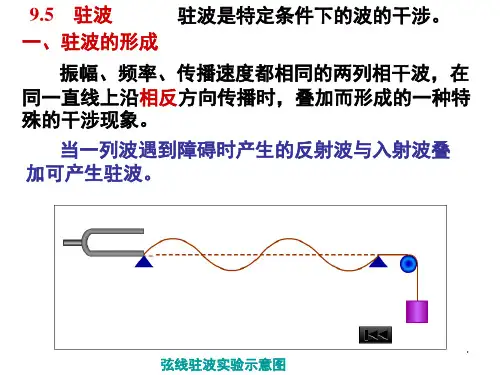

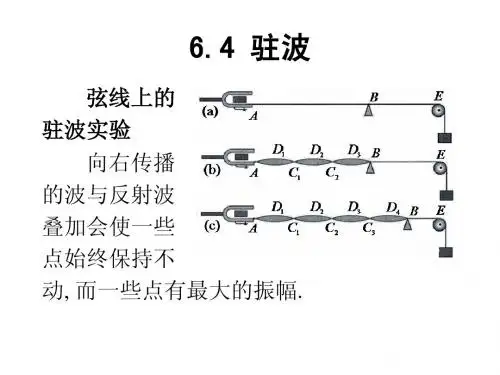
10.7 驻波教学目的1.知道驻波现象及什么是波节、波腹,驻波是一种特殊的干涉现象.2.理解驻波的形成过程,理解驻波与行波的区别,理解空气柱共鸣的条件.引入新课一列波在向前传播的途中遇到障碍物或者两种介质的分界面时,会发生反射,如果反射波和原来向前传播的波相互叠加,会发生什么现象呢?一、驻波1、驻波的演示:如课本图10-31所示,把弦线的一端A固定在电磁打点计时器的振针上,另一端跨过定滑轮拴一个砝码盘,盘上放砝码,将弦线拉平.在靠近定滑轮的B处,用一个尖劈把弦线支起来.接通电磁打点计时器的电源,振针振动时,有一列波向定滑轮的一侧传播,并在B处发生反射.改变尖劈的位置,来调节AB的长度,当尖劈调到某适当位置时,可以看到,弦线会分段振动起来.2、几个概念:①波节——弦线上有些点始终是静止不动的,这些点叫做波节.波腹——在波节和波节之间的那段弦线上,各质点以相同的频率、相同的步调振动,但振幅不同,振幅最大的那些点叫做波腹.在相邻的两段弦线上,质点的振动方向是相反的.相邻的两个波节(或波腹)之间的距离等于半个波长,即等于λ/2.②驻波——波形虽然随时间而改变,但是不向任何方向移动,这种现象叫做驻波.波形不传播,是媒质质元的一种集体振动形态。
"驻"字的第一层含义。
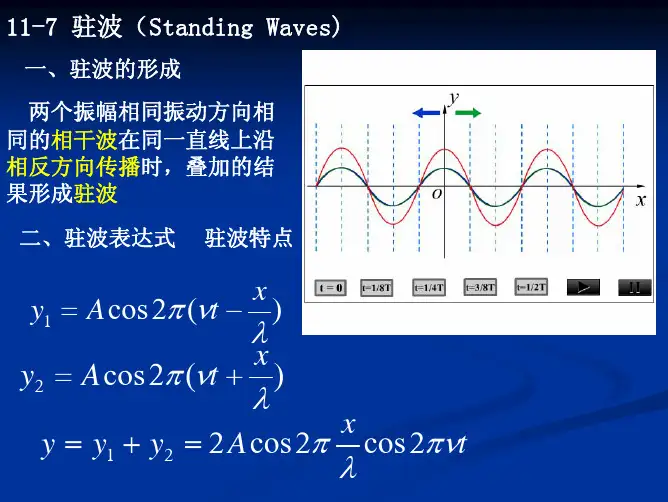
行波——驻波跟前面讲过的波形向前传播的那种波显然是不同的,相对于驻波来说波形向前传播的那种波叫行波.③驻波与行波的区别A物理意义不同:驻波是两列波的特殊干涉现象,行波是一列波在介质中的传播.B质点振动不同:相邻波节间质点运动方向一致.波节两侧质点振动方向总相反.C波形不同:波形向前传播的是行波,波形不向任何方向传播的是驻波.3、驻波的形成两列振幅相同的相干波在同一直线上沿相反方向传播时形成的叠加波。
①两列沿相反方向传播的振幅相同、频率相同的波叠加,形成驻波.②振幅相同、频率相同波的叠加.三、驻波的特点课本10-33中用虚线表示两列沿相反方向传播的振幅相同、频率相同波的叠加,用实线表示这两列波叠加后形成的合成波.图中画出了每隔T/8周期波形的变化情况.由图可以看出,合成波在波节的位置(图中的“·”表示),位移始终为零.在两波节之间,各质点以相同的步调在振动,两波节之间的中点振幅最大,就是波腹(图中用“+”表示).驻波不是振动状态的传播,也没有能量的传播。


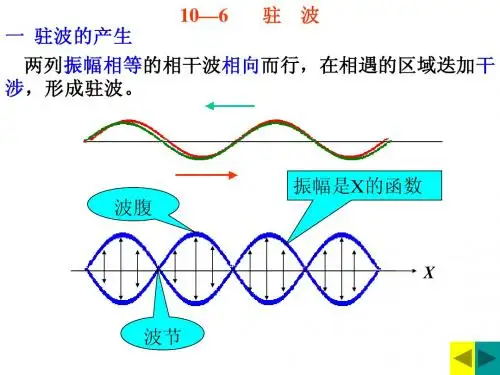
波的基本概念1.波:振动在媒质(介质)中的传播就是波,分为横波和纵波。
2.横波:媒质中各体元振动的方向与波传播的方向垂直。
例如:一根均匀柔软的细绳的振动,形成的波就是横波。
3.纵波:媒质中各体元振动的方向与波传播的方向平行。
例如:空气中的声波,空气中体元时而靠近,时而疏远。
4.表面波:在两中媒质的界面上传播的波。
例如:水面波。
5.波面:波传播时,同相位各点所组成的面。
6.波前:离波源最远,即“最前方”的波面。
7.波射线:与波面垂直且表明波的传播方向的线叫波射线。
8.平面波:波前为平面的波。
波线是互相平行的。
9.球面波:波前为球面。
点波源在均匀的和各向同性媒质中发生的波是球面波。
波线是相交于波源的直线。
平面简谐波方程一. 平面简谐波:平面波传播时,媒质中体元均按正弦(或余弦)规律运动。
二. 平面简谐波方程(从运动学角度考虑):描述不同时刻不同体元的运动状态。
设:一列平面简谐波沿轴正向传播,选择原点处体元相位为0的时刻为计时起点,即该体元的相位为零,则处体元的运动学方程:其中:为体元距平衡位置的位移,A、为波源的振幅和圆频率。
经的时间,处体元的振动状态传到位于处的体元,即:t时刻,位于处的体元的振动状态应与时刻处体元的振动状态一样,则处体元的运动学方程为:⑴其中:v为振动状态传播的速度,叫波速,也叫相速。
⑴式就是平面简谐波方程。
从⑴式看出:处质元的振动比原点处的质元落后。
若:波动沿轴负方向传播,则波动方程为:⑵⑵式可以看出:处质元的振动超前于原点处的质元。
三. 平面简谐波方程的物理意义1.当一定时,表示x处质元的振动方程,初位相是2.当t一定时,表示t时刻各个质元偏离平衡位置的位移,即t 时刻的波形。
由⑴可知:处体元振动的周期、频率和圆频率:注意:不一定是振动系统的固有频率而取决于波源频率,所以⑴中的形式不意味着各体元作简谐振动。
由⑵知:t一定时,y是的周期函数,也存在空间位置上的周期,波长:⑶即:波长是波在一个周期内传播的距离,或:沿波传播方向相邻同相位两点间的距离。