由二维视图复原三-侯洪生

考点08 由三视图还原实物图1．由空间几何体的三视图还原直观图时,遵循的原则:长对正 高平齐,宽相等的基本原则,特别注意几何体中与投影面垂直或平行的线及面的关系． 2．根据三视图还原成实物图应注意:（1）由三视图还原成实物图是由实物图画三视图的逆过程,在该过程中注意理解实物图画三视图的原理,并联想柱、锥、台、球体的三视图．（2）由三视图还原成实物图时,一般以俯视图为基础再结合正(主)视图和侧(左)视图．（3）根据三视图还原实物图:需要综合正(主)视图、侧(左)视图、俯视图的特征,确定分界线,找出组成几何体的简单几何体,再将组合还原,其中确定分界线是正确还原的关键．【例】如图是正四棱锥PABCD 的三视图，其中主视图和左视图都是边长为1的正三角形，求这个四棱锥的侧棱长．【解析】由条件知，正四棱锥底面边长AB ＝1，高PO ＝23(O 是底面中心)， OB ＝22AB ＝22，故侧棱长：PB ＝＝42＝25．1．若一个几何体的三视图都是等腰三角形，则这个几何体可能是( ) A ．正方体 B ．长方体 C ．三棱锥 D ．圆 【答案】C【解析】由三视图的知识，可知答案为C ．2．如图所示，甲、乙、丙是三个几何体的三视图，则甲、乙、丙对应的几何体分别为( )①长方体；②圆锥；③三棱锥；④圆柱． A ．④③② B ．①③② C ．①②③ D ．④②③ 【答案】A3．某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是( )图1A BC D【答案】D4．在一个几何体的三视图中，正视图和俯视图如下图所示，则相应的侧视图可以为( )A BC D【答案】D【解析】本题考查三视图，可用排除法或特例求答．由正视图知A、B不正确，又由俯视图知C不正确，选D．本题的几何体也可看成是一个圆锥的一半与一个三棱锥的组合体．5．如图是一个物体的三视图，则该物体对应的直观图为( )【答案】C【解析】从俯视图看，A，C，D均符合，再结合主视图看，只有C符合．故选C．6．给出下列命题：①如果一个几何体的三个视图是完全相同的，则这个几何体是正方体；②如果一个几何体的主视图和俯视图都是矩形，则这个几何体是长方体；③如果一个几何体的三个视图都是矩形，则这个几何体是长方体：④如果一个几何体的主视图和左视图都是等腰梯形，则这个几何体是圆台．其中正确的是______．(将正确的全都写在横线上)【答案】③1．右图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正(主)视图、俯视图如右图②存在四棱柱，其正(主)视图、俯视图如右图③存在圆柱，其正(主)视图、俯视图如右图．其中真命题的个数是( )A．3 B．2C．1 D．0【答案】A【解析】主要考查三视图知识．这一知识点近几年都有考查．①正确，比如一个平放的两底面是等腰直角三角形的直三棱柱．②显然正确，③中可以是一个平放的圆柱．2．正视图为一个三角形的几何体可以是________(写出三种)．【答案】三棱锥、三棱柱、圆锥3．如图所示为一个简单组合体的主视图和左视图，则该几何体可能是________(填序号)．【答案】①【解析】由主视图中左下角至右上角有一实对角线，可知所给的几何体中只有①符合，又根据左视图知①符合，所以选①．4．根据图中的三视图想象物体原形，并画出物体的实物草图．如何画人物素描中的轮廓画人物素描的基础就是画人物的轮廓．画轮廓要抓住头部基本形状、五官位置、明暗交界线的位置、头与肩的关系．要画准轮廓，就必须整体观察，整体比较，多运用辅助线帮助确定位置．在抓外形时要狠抓特征，要画得像．外形初见端倪，形象呼之欲出．就如公园门口的艺人用剪子剪影，轻而易举地将人物形象显现出来，尽管看不清过细的内部结构，我们照样能够认出他来．有些人不注意这一步，形还非常含糊，便匆匆忙忙去画五官了．这样画出来的画怎么能逼近形象呢！画人物素描就是要先画出人体的直观图．。

第15章由三维实体生成二维视图◆15.1 概述◆15.2 由三维实体生成三视图◆15.3 由三维实体创建剖视图15.1 概述基本视图：实体模型在投影面投影所得到的图形称为基本视图，通常可分为主视图、俯视图、左视图、右视图、仰视图、后视图。

图15-1所示的是三维零件图在各个方向的投影视图所得的效果。

(a) 三维视图(b) 主视图(c) 后视图(d) 俯视图(e) 仰视图(f) 左视图(g) 右视图图15-1 各个视图剖视图：假想用一个剖切平面将三维实体剖开，移去观察者和剖面之间的部分，而将留下的部分向投影面投影，所得视图称为剖视图。

剖面图：也叫断面图，假想用剖切面将零件的某处切断，紧画出其断面的图形，称为剖切图。

分为移出断面图和重合断面图。

图15-2是剖视图和剖面图的比较。

(a) 阶梯轴(b) 剖面图(c) 剖视图图15-2 剖面图和剖视图模型空间是为创建三维模型提供一个广阔的绘图区域，用户可以通过建立UCS，创建各种样式的模型并设置观察视点和消隐、渲染等操作。

而布局空间是用于创建最终的打印布局，是图形输出效果的布置，用户不能通过改变视点的方式来从其他角度观看图形。

它们的主要区别标志是坐标系图标。

模型空间中，坐标系图标是一个反映坐标方向的坐标架，而布局空间中，坐标系图标则是三角板形状。

利用布局空间可以把在模型空间中绘制的三维模型在同一张图纸上以多个视图的形式排列并打印出来，而在模型空间中则无法实现这一点。

15.2 由三维实体生成三视图AutoCAD将三维实体模型生成三视图的方法大致有两种：第一种方法是先使用VPORTS或MVIEW命令，在布局空间中创建多个二维视图视口，然后使用SOLPROF命令在每个视口中分别生成实体模型的轮廓线，以创建二维视图的三视图。

第二种方法是使用SOLVIEW命令后，在布局空间中生成实体模型的各个二维视图视口，然后使用SOLDRAW命令在每个视口中分别生成实体模型的轮廓线，以创建二维视图的三视图。

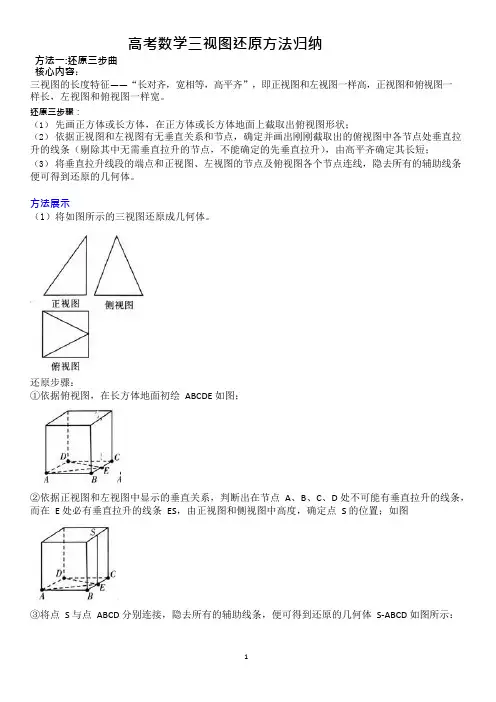
高考数学三视图还原方法归纳方法一:还原三步曲核心内容：三视图的长度特征——“长对齐，宽相等，高平齐”，即正视图和左视图一样高，正视图和俯视图一样长，左视图和俯视图一样宽。

还原三步骤：（1）先画正方体或长方体，在正方体或长方体地面上截取出俯视图形状；（2）依据正视图和左视图有无垂直关系和节点，确定并画出刚刚截取出的俯视图中各节点处垂直拉升的线条（剔除其中无需垂直拉升的节点，不能确定的先垂直拉升），由高平齐确定其长短；（3）将垂直拉升线段的端点和正视图、左视图的节点及俯视图各个节点连线，隐去所有的辅助线条便可得到还原的几何体。

方法展示（1）将如图所示的三视图还原成几何体。

还原步骤：①依据俯视图，在长方体地面初绘ABCDE 如图；②依据正视图和左视图中显示的垂直关系，判断出在节点A、B、C、D 处不可能有垂直拉升的线条，而在 E 处必有垂直拉升的线条ES，由正视图和侧视图中高度，确定点S 的位置；如图③将点S 与点ABCD 分别连接，隐去所有的辅助线条，便可得到还原的几何体S-ABCD 如图所示：3经典题型：例题 1：若某几何体的三视图，如图所示，则此几何体的体积等于（ ）cm ³。

解答：（24）例题 2：一个多面体的三视图如图所示，则该多面体的表面积为（ ）答案：21+ 计算过程：步骤如下：第一步：在正方体底面初绘制ABCDEFMN 如图；第二步：依据正视图和左视图中显示的垂直关系，判断出节点E、F、M、N 处不可能有垂直拉升的线条，而在点A、B、C、D 处皆有垂直拉升的线条，由正视图和左视图中高度及节点确定点G, G', B', D', E ', F ' 地位置如图；第三步：由三视图中线条的虚实，将点G 与点E、F 分别连接，将G'与点E ' 、F '分别连接，隐去所有的辅助线便可得到还原的几何体，如图所示。

例题3：如图所示，网格纸上小正方形的边长为4，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度是（）答案：（6）还原图形方法一：若由主视图引发，具体步骤如下： （1） 依据主视图，在长方体后侧面初绘 ABCM 如图：（2） 依据俯视图和左视图中显示的垂直关系，判断出在节点 A 、B 、C 出不可能有垂直向前拉升的线条，而在 M 出必有垂直向前拉升的线条 MD ，由俯视图和侧视图中长度，确定点 D 的位置如图：（3） 将点 D 与 A 、B 、C 分别连接，隐去所有的辅助线条便可得到还原的几何体 D —ABC 如图所示：解：置于棱长为 4 个单位的正方体中研究，该几何体为四面体 D —ABC ，且 AB=BC=4，AC=4 方法 2,DB=DC= 2 ,可得 DA=6.故最长的棱长为 6. 若由左视图引发，具体步骤如下： （1） 依据左视图，在长方体右侧面初绘 BCD 如图：（2） 依据正视图和俯视图中显示的垂直关系，判断出在节点 C 、D 处不可能有垂直向前拉升的线条，而在 B 处，必有垂直向左拉升的线条 BA ，由俯视图和左视图的长度，确定点 A 的位置，如图：5 2（3）将点A 与点B、C、D 分别连接，隐去所有的辅助线条便可得到还原的几何体D—ABC 如图：方法3：由三视图可知，原几何体的长、宽、高均为4，所以我们可以用一个正方体做载体还原：（1）根据正视图，在正方体中画出正视图上的四个顶点的原象所在的线段，用红线表示。

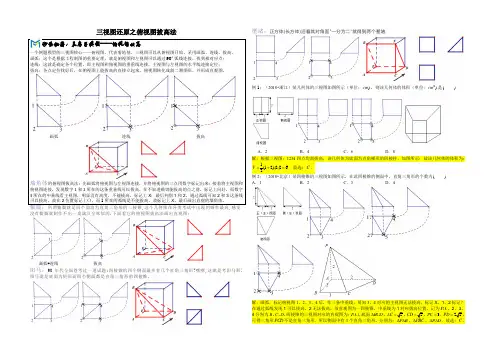
三视图还原之俯视图拔高法鳖臑：没有鳖臑就制作不出一桌满汉全席似的.下面看它的俯视图拔高法画出直观图；画弧+连线 拔高阳马：90年代全国卷考过一道试题:四棱锥的四个侧面最多有几个直角三角形?嘿嘿,这就是考阳马那!阳马就是底面为矩形而四个侧面都是直角三角形的四棱锥。

壍堵：正方体(长方体)沿着其对角面"一分为二"就得到两个壍堵.例1：（2018•浙江）某几何体的三视图如图所示（单位：)cm ，则该几何体的体积（单位：3)cm 是( )A ．2B ．4C ．6D ．8A ．1B ．2C ．3D ．4秒杀秘籍：盖房子模型——俯视图拔高一个例题模型的三视图核心——俯视图，代表着地基，三视图可以从俯视图开始，采用画弧、连线、拔高。

画弧：这个是根据工程制图的重要定理，就是俯视图和左视图可以通过90°弧线连接，找到相对应点； 连线：这就是确定各个位置，即主视图和俯视图的重垂线连接，主视图与左视图的水平线连接定位； 拔高：各点定位找好后，在俯视图上能拔高的直接立起来，俯视图转化成斜二测图形，并形成直观图。

画弧 连线 拔高墙角体的俯视图拔高法：先画弧将俯视图与左视图连接，并将俯视图的三点用数字标记出来；接着将主视图和俯视图连接，发现数字1和2所在的这条重垂线可以拔高，在不知道确切能拔高的点之前，标记上问好，而数字3所在的中垂线看主视图，明显没有高度，不能拔高，标记上Χ；最后判别1和2，通过弧线可知2和3这条线可以拔高，故在2位置标记上〇，而1所在的弧线是不能拔高，故标记上Χ。

最后画出直观的墙角体。

例3：（2015•安徽）一个四面体的三视图如图所示，则该四面体的表面积是()去底座拔高法：主视图和左视图都有的矩形部分叫做底座，故可以在三视图还原时不予考虑，最后加上去这个底座，也就是一个长方体部分，需要注意的是矩形必须为实线。

例5：（2017•新课标Ⅰ）某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为( )A．1B．1C．1D．1正四面体：最"正"的四面体,就是6条棱长都相等的三棱锥,我们有个习惯,绝大多数看到正四面体的时候,都是要把它放进正方体中去思考,三视图也不例外。

三视图还原之俯视图拔高法鳖臑：没有鳖臑就制作不出一桌满汉全席似的.下面看它的俯视图拔高法画出直观图；画弧+连线 拔高阳马：90年代全国卷考过一道试题:四棱锥的四个侧面最多有几个直角三角形?嘿嘿,这就是考阳马那!阳马就是底面为矩形而四个侧面都是直角三角形的四棱锥。

壍堵：正方体(长方体)沿着其对角面"一分为二"就得到两个壍堵.例1：（2018•浙江）某几何体的三视图如图所示（单位：)cm ，则该几何体的体积（单位：3)cm 是( )A ．2B ．4C ．6D ．8A ．1B ．2C ．3D ．4秒杀秘籍：盖房子模型——俯视图拔高一个例题模型的三视图核心——俯视图，代表着地基，三视图可以从俯视图开始，采用画弧、连线、拔高。

画弧：这个是根据工程制图的重要定理，就是俯视图和左视图可以通过90°弧线连接，找到相对应点； 连线：这就是确定各个位置，即主视图和俯视图的重垂线连接，主视图与左视图的水平线连接定位； 拔高：各点定位找好后，在俯视图上能拔高的直接立起来，俯视图转化成斜二测图形，并形成直观图。

画弧 连线 拔高墙角体的俯视图拔高法：先画弧将俯视图与左视图连接，并将俯视图的三点用数字标记出来；接着将主视图和俯视图连接，发现数字1和2所在的这条重垂线可以拔高，在不知道确切能拔高的点之前，标记上问好，而数字3所在的中垂线看主视图，明显没有高度，不能拔高，标记上Χ；最后判别1和2，通过弧线可知2和3这条线可以拔高，故在2位置标记上〇，而1所在的弧线是不能拔高，故标记上Χ。

最后画出直观的墙角体。

例3：（2015•安徽）一个四面体的三视图如图所示，则该四面体的表面积是()去底座拔高法：主视图和左视图都有的矩形部分叫做底座，故可以在三视图还原时不予考虑，最后加上去这个底座，也就是一个长方体部分，需要注意的是矩形必须为实线。

例5：（2017•新课标Ⅰ）某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为( )A．1B．1C．1D．1正四面体：最"正"的四面体,就是6条棱长都相等的三棱锥,我们有个习惯,绝大多数看到正四面体的时候,都是要把它放进正方体中去思考,三视图也不例外。

(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号 (43)申请公布日 (21)申请号 201711304096.0(22)申请日 2017.12.11(71)申请人 福州国化智能技术有限公司地址 350000 福建省福州市仓山区建新镇金山大道618号桔园洲工业园鼓楼园17号楼第三层(72)发明人 黄雄　李俊　刘李　潘小冰　吴上海　(74)专利代理机构 福州市鼓楼区京华专利事务所(普通合伙) 35212代理人 王美花(51)Int.Cl.G06T 17/00(2006.01)(54)发明名称一种利用二维三视图自动重建三维模型的方法(57)摘要本发明提供一种利用二维三视图自动重建三维模型的方法，包括导入二维三视图，获取各视图的二维坐标；根据各视图的二维坐标寻找三维坐标原点；根据创建的三维坐标寻找各视图的二维坐标所对应的三维点；构建三维边形成线框图；根据线框图上三维点的度来删除假元；从任一三维点出发，任意选取连接该三维点的两条三维边得到一个三维面，获取该三维面上的所有三维边，根据左邻边序列算法获取最小面环，且合并内环，同时继续执行完所有的三维点；使用耳切法将各面环均切割成复数个三角形，并通过unity绘制出三角面形成三维模型。

本发明优点：可实现对自动化生产所需的工件、设备等进行三维模型自动重构，可极大的提升建模效率。

权利要求书1页 说明书4页 附图3页CN 107918950 A 2018.04.17C N 107918950A1.一种利用二维三视图自动重建三维模型的方法，其特征在于：所述方法包括如下步骤：步骤1、从制图软件中导入工程图的二维三视图，并分别获取导入的各个视图的二维坐标；步骤2、根据各个视图的二维坐标寻找三维坐标原点，进行坐标规格化；步骤3、根据创建的三维坐标寻找各个视图的二维坐标所对应的三维点，构建三维点云；步骤4、连接任意两个三维点构建三维边，对构建的三维边进行三视图投影，并根据投影结果删除存在的假元；同理，继续构建完所有的三维边形成一线框图；步骤5、获取得到的线框图，并根据线框图上三维点的度来继续删除假元；步骤6、从删除完假元的线框图的任意一个三维点出发，任意选取连接该三维点的两条三维边得到一个三维面，获取该三维面上的所有三维边，并根据左邻边序列算法获取最小面环，且合并内环；同理，继续执行完所有的三维点，且每个三维面都仅执行一次；步骤7、使用耳切法将各个面环均切割成复数个三角形，并通过unity绘制出三角面形成三维模型。

机械类学生三维设计能力培养方法研究作者：刘永霞，彭如恕来源：《教育教学论坛》2013年第42期摘要：机械类学生在校期间熟练掌握三维软件，已成学生就业的基本要求。

可以从以下三个方面培养学生的三维设计能力：在《机械工程制图》课堂教学中引入三维软件的学习，尽早开展三维软件课程，多创造机会让学生参加设计大赛。

关键词：三维软件；机械工程制图；机械类学生中图分类号：G642.3？摇文献标志码：A 文章编号：1674-9324（2013）42-0073-02目前，三维设计已成为普遍应用的CAD技术[1]。

这也要求机械类学生在校期间必须熟练掌握三维软件，但目前有很多机械专业毕业生没有达到这一要求，这就给现代大学教育带来了一定的压力。

如何让学生在校期间更好地掌握现代工程设计技术，已成为机械类专业教学改革的热点问题，但到目前为止还没有形成完善的解决方案[2-4]。

本文从以下3个方面论述机械类学生三维设计能力的培养方法。

一、在《机械工程制图》课堂教学中引入三维软件的学习机械专业学生在大一第一学期就开展了《画法几何》课程，若将三维软件引入该课程的教学中，不仅有利于该课程的学习，还有利于培养学生的三维设计能力。

大一学生学习的积极性和主动性都比较高，此时接触三维软件，更能够激起他们浓厚的学习兴趣。

学生由于初学制图，缺乏感性认识，空间思维能力有限，在学习过程中出现的问题得不到及时的指导和纠正，将丧失学习兴趣。

三维软件创建的三维模型质感好、形象逼真、色彩丰富，在课堂上，教师可以利用三维软件将复杂形体的外型与内腔、相贯体中相贯线的变化趋势、装配体中零件之间的连接关系等向学生演示，使教学中的知识难点讲解得更加清晰、生动、形象。

例如讲解组合体时，已知两个视图求作第三个视图是教学中的重点和难点。

如图1所示就是已知组合体的主视图和左视图，画出俯视图，教学中应用Pro/E进行三维造型，使学生看到组合体的形成过程，分析清楚组合体各个组成部分的相对位置，明白了相交、相切、平齐的含义，再通过输出视图得到组合体的三视图。

《工程图学C》教学大纲课程编码：08297007课程名称：工程图学(C)英文名称：Engineering Graphics C开课学期：1学时/学分：40/ 2.5课程类型：学科基础课开课专业：测控技术与仪器、自动化、通信工程、信息工程、光信息科学与技术等专业选用教材：《工程图学与CAD基础》任长春李苏红主编吉林大学出版社2001。

主要参考书：1、高俊亭主编：《工程制图》，高等教育出版社2004。

2、何铭新, 钱可强主编：《机械制图》，高等教育出版社2004。

3、王秀英主编：《工程制图》，科学出版社2002。

4、侯洪生主编：《计算机绘图实用教程》，科学出版社2005。

执笔人：孟祥宝一、课程性质、目的与任务工程图学是研究绘制和阅读工程图样的一门既有系统投影理论又有较强实践环节的技术基础课。

设计制造机器和工程项目施工都离不开工程图样，使用维修设备也要通过阅读图样了解其结构性能。

因此，工程图样作为一项重要的技术文件是用来表达和交流设计思想的重要信息工具，是工程界的一门通用图形语言。

本课程培养学生的绘图、读图和空间想象能力，为后续相关课程和从事工程技术工作储备必要的工程背景和基础知识。

二、教学基本要求1．学习正投影基本理论；2．学习制图国家标准基本规定，培养查阅设计资料和相关标准的能力；3．培养绘制和阅读简单工程图样（徒手草图、尺规绘图和计算机绘图）的技能；4．培养初步的零部件表达能力和空间构思能力；5．培养认真负责的工作态度和严谨细致的工作作风，塑造动手能力、工程意识。

三、各章节内容及学时分配绪论（0. 5学时）教学目的与要求了解工程图样在生产实践中的作用。

教学内容一、本课程的主要任务二、本课程的学习方法考核要求本部分不考核。

第一章制图的基本知识（3.5学时）教学目的与要求理解、掌握并遵守国家标准基本规定（图幅、比例、字体、图线、尺寸标注等）。

正确使用绘图工具，掌握基本几何作图方法，做到作图正确、图线分明、字迹工整。

组合体教学中的形体分析法作者：韩丽艳，张孟玫，丁乔来源：《科技创新与生产力》 2014年第7期韩丽艳，张孟玫，丁乔（北京石油化工学院机械工程学院，北京 102617）摘要：针对工程制图教学中组合体教学常用的形体分析法，提出从立体的形成及工作性能角度对组合体进行分析，以提高图形分析和二维、三维图形间的转换能力。

通过读组合体、尺寸标注、画组合体3个方面对学生困惑的问题采用简单易懂的方法解决，不仅可以辅助思维，还能提高教学质量。

关键词：组合体；工程图学；形体分析；读图中图分类号：G642 文献标志码：A DOI：10.3969/j.issn.1674-9146.2014.07.0501 传统的形体分析形体分析是在反映特征比较明显的视图上将组合体划分为几个部分，通过投影关系找到各线框所表示的部分在其他投影图中的投影，进而分析各部分的形状以及它们之间的相对位置，最后综合想象组合体的整体形状[1]。

视图中表示的是构成组合体的各个表面，一个封闭线框一般情况下表示一个面的投影，线框套线框，通常是两个面凹凸不平或者是具有打通的孔，若是两个线框相邻，表示两个面高低不平或相交。

若想读懂视图，还应利用虚、实线区分各部分的相对位置关系，必要时找视图对照来看。

可以这样说，形体分析是从面的角度出发来进行组合体的分析，既然是形体，不妨从体的角度分析组合体。

图1-a是简单的立体两面视图，它的形成既可以看成是由一个小长方体和一半圆柱体组合而成（见图1-b），也可以看成是由一个大长方体挖去一部分而成（见图1-c）。

实际生活中，这个立体一定是由图1-c的方式形成的。

因此，在组合体的教学中，不仅是通过形体分析读懂视图，还能使学生的空间思维由体向零件转变，它不仅具有几何形状特征，还应符合实际设计加工要求。

2 改进后的形体分析原则上讲，形体分析适合于解决组合体的所有问题。

实际上，任何组合体都可以由长方体经过切割、挖槽、叠加等操作形成。

因此，在进行组合体读图、画图、尺寸标注时，完全从体的形成过程来分析更易于接受和理解[2-3]。

CATIA V5中三维实体模型的二维工程图表达
李苏红;侯洪生;林玉祥;庞云阶
【期刊名称】《图学学报》
【年(卷),期】2008(029)005
【摘要】介绍了在CATIA V5软件中创建二维工程图的两种方法.详细阐述了在Drafting(工程图)模块下由三维实体模型直接创建各种视图、剖视图及断面图的方法.分析所得二维工程图在图样表达上与现行国家标准图样画法不一致的地方,并提出相应的解决办法.本文内容对在三维模式下创建符合国家标准规范的工程图具有一定参考价值.
【总页数】5页(P136-140)
【作者】李苏红;侯洪生;林玉祥;庞云阶
【作者单位】吉林大学机械科学与工程学院,吉林,长春,130022;吉林大学计算机科学与技术学院,吉林,长春,130012;吉林大学机械科学与工程学院,吉林,长春,130022;吉林大学机械科学与工程学院,吉林,长春,130022;吉林大学计算机科学与技术学院,吉林,长春,130012
【正文语种】中文
【中图分类】TB23
【相关文献】
1.CATIA V5工程图模板的创建与使用 [J], 王岩
2.CATIA V5下制定工程图标准 [J], 丁仁亮
3.通过数据交换在CATIA V5中创建工程图 [J], 李苏红;孟祥宝;李军;庞云阶
4.通过数据交换在CATIA V5中创建工程图 [J], 李苏红;孟祥宝;李军;庞云阶
5.基于CATIA V5工程图的二次开发在水电工程图中的应用 [J], 皮漫;张权
因版权原因，仅展示原文概要，查看原文内容请购买。