2018届九年级数学下册3.3三视图第2课时由三视图还原几何体教案(新版)湘教版
- 格式:pdf
- 大小:69.67 KB
- 文档页数:2



29.2 三视图(第3课时)一、内容和内容解析1.内容根据三视图说出立体图形的名称,描述物体的形状,感受“综合”思考的过程。
2.内容解析学生在七年级已经接触过“从不同的方向看物体”的内容,但当时没有明确给出“视图”这个概念;本章是从投影的角度解释三视图的概念,这与从不同的方向看物体所得到的平面图形是一致的。
前一节课学生已经能够画出基本几何体的三视图,体会了从立体图形到平面图形的转化。
本节课是在上一节“由物画图”的基础上“由图想物”,让学生体会从平面图形到立体图形的转化过程,这种从“二维”到“三维”的转化,不仅使学生对投影和视图的认识水平再次提升,更能对培养学生的空间观念起到很好的促进作用。
画三视图是将一个物体从三个方向观察,分别表现这三个方面的分解过程;由三视图想出物体的立体形状,则是把物体的三个方面形状“综合”起来的过程,这两个过程是相反的,也是相互联系的。
基于以上分析,确定本节课的教学重点为:根据三视图描述基本几何体和实物原型。
二、目标和目标解析1.目标(1)能根据三视图描述基本几何体形状和实物原型。
(2)通过观察和动手实践,理解三视图中相关各线条之间的对应关系,通过它们能形成一个整体性认识,并根据这些关系由平面图形得出对应的立体图形。
2.目标解析达成目标(1)的标志是:能通过给出的三视图用语言来描述出立体图形的形状。
达成目标(2)的标志是:通过三视图描述立体图形,体会三视图在转化为立体图形的过程中所起的作用。
三、教学问题诊断分析本节课是在学习了“从不同方向看物体”的内容后,又进一步引入“三视图”的概念,并通过观察能够画出立体图形的三视图,这要准确把握三视图中的相对位置关系和大小关系,并要求学生有较强的空间想象能力,而本节课要求学生能够通过三视图想象并描述出立体图形,这对学生的空间想象能力有了较高的要求,是教学中的一个难点。
基于以上分析,确定本节课的教学难点为:根据三视图观察想象,描述出基本几何体和实物原型。


《三视图》教案设计九江科技中专桂芳一、地位和作用本课选自语文出版社《数学》第三册,依据中职学校的课程设置要求,体现文化课为专业课服务原则,数学课除了具备普通教育要求的“来源生活、构建模型、运用实际”的特性外,中职学校的数学还要根据不同专业的特点,突现通过数学教学架起与专业理论的立交桥,提高学生的实操能力。
二、教学目标1.知识目标:理解空间几何体三视图的形成原理和投影规律;掌握简单组合体的三视图;使学生了解三视图在数控专业中的应用。
2. 能力目标:在工程设计过程中,常常需要把三维形体用二维平面图形表达在纸面,要达到这个目的,我们可以靠投影法来实现。
投影法就是投射线经过三维形体,在选定的平面上得到二维图形的方法,本节课突显了职业学校数学课为专业课服务的目标。
3. 情感目标理解三视图的作用,感受数学的实用价值,激发学生学习专业的兴趣;提高学生学习专业的能力;培养学生勇于探索、合作的精神。
三、教学重难点教学重点:空间几何体三视图的画法教学难点:理解三视图的投影规律,能根据工程设计图纸绘制工件简图。
四、教学策略三视图的形成是个动态过程,用语言文字是不易描述的。
立体图形的主要特点是他们处于三维空间中。
因此本节课的特点是难说,难画,难想。
针对本节课的特点,采用的是直观教学法,任务驱动法,利用多媒体创设问题情境,使学生对本节课内容产生强烈的求知欲望;利用多媒体演示投影,正投影下物体形状,大小变化以及正投影的基本特性。
使学生直观感知三视图的形成,建构三视图的概念。
用直观的方法深入浅出地增强学生的兴趣,提高学生的动手能力。
五、学法分析根据职业学校的学生文化基础参差不齐,数学基础差,学习兴趣低,但对专业课重视程度高的特点,采用观察法、小组讨论法、讲练结合法,“学中做、做中学”,注意实效,让学生学会学习,找回自信。
六、教学用具实物(乒乓球、魔方)、多媒体课件。
七、教学过程(一)、创设情境,引入新课(用多媒体课件展示)引例1. 欣赏一幅“6”与“9”的漫画。
第2课时由三视图复原几何体1.进一步明确三视图的意义,由三视图想象出原型;(重点)2.由三视图得出实物原型并进行简单计算.(重点)一、情境导入同学们独立完成以下几个问题:1.画三视图的三条规律,即______视图、______视图长对正;______视图、______视图高平齐;______视图、______视图宽相等.2.如下列图,分别是由假设干个完全相同的小正方形组成的一个几何体的主视图和俯视图,那么组成这个几何体的小正方体的个数是多少?二、合作探究探究点一:由三视图描述几何体【类型一】由三视图确定几何体根据图①②的三视图,说出相应的几何体.解析:根据三视图想象几何体的形状,关键要熟练掌握直棱柱、圆锥、球等几何体的根本三视图.解:图①是直三棱柱,图②是圆锥和圆柱的组合体.方法总结:先根据各个视图想象从各个方向看到的几何体形状,再来确定几何体的形状.变式训练:见《》本课时练习“课堂达标训练〞第1题【类型二】由三视图确定正方体的个数一个几何体,是由许多规格相同的小正方体堆积而成的,其主视图、左视图如下列图,要摆成这样的图形,最少需用________个小正方体.解析:根据主视图、左视图是分别从物体正面、左面看,所得到的图形,结合此题进行分析即可.根据三视图可得第二层有2个小正方体,根据主视图和左视图可得第一层最少有4个小正方体,故最少需用7个小正方体.故答案为7.方法总结:由三视图判断几何体由多少个立方体组成时,先由俯视图判断底面的行列组成;再从主视图判断每列的高度(有几个立方体),并在俯视图中按照左、中、右的顺序用数字标出来;然后由左视图判断行的高度,在俯视图中按照上、中、下的顺序用数字标出来;最后把俯视图中的数字加起来.变式训练:见《 》本课时练习“课堂达标训练〞 第5题 探究点二:三视图的相关计算如图是某工件的三视图,其中圆的半径是10cm ,等腰三角形的高是30cm ,那么此工件的体积是( )A .1500πcm 3B .500πcm 3C .1000πcm 3D .2000πcm 3解析:由三视图可知该几何体是圆锥,底面半径和高.解:∵底面半径为10cm ,高为30cm.∴体积V =13π×102×30=1000π(cm 3).应选C.方法总结:依据三视图“长对正,高平齐,宽相等〞的原那么,正确识别几何体,再进行有关计算.变式训练:见《 》本课时练习“课堂达标训练〞第8题 三、板书设计本节课是在学习了简单几何体的三视图的根底上,反过来几何体的三视图想象出几何体,既是对三视图知识的完善,又是三视图知识的简单应用,培养了学生的空间想象能力,使学生初步体会到由平面图形到立体图形的转化也是一种数学方法.1.4 二次函数与一元二次方程的联系1.通过探索,理解二次函数与一元二次方程之间的联系,会用二次函数图象求一元二次方程的近似解;(重点)2.通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.(难点)一、情境导入小唐画y =x 2-6x +c 的图象时,发现其顶点在x 轴上,请你帮小唐确定字母c 的值是多少?二、合作探究探究点一:二次函数与一元二次方程的联系【类型一】 二次函数图象与x 轴交点情况的判断以下函数的图象与x 轴只有一个交点的是( ) A .y =x 2+2x -3 B .y =x 2+2x +3 C .y =x 2-2x +3 D .y =x 2-2x +1解析:选项A 中b 2-4ac =22-4×1×(-3)=16>0,选项B 中b 2-4ac =22-4×1×3=-8<0,选项C 中b 2-4ac =(-2)2-4×1×3=-8<0,选项D 中b 2-4ac =(-2)2-4×1×1=0,所以选项D 的函数图象与x 轴只有一个交点.应选D.变式训练:见《 》本课时练习“课后稳固提升〞第1题【类型二】 利用函数图象与x 轴交点情况确定字母的取值范围(2021·武汉模拟)二次函数y =kx 2-6x +3的图象与x 轴有交点,那么k 的取值范围是( )A .k <3B .k <3且k ≠0C .k ≤3D .k ≤3且k ≠0解析:∵二次函数y =kx 2-6x +3的图象与x 轴有交点,∴方程kx 2-6x +3=0(k ≠0)有实数根,即Δ=36-12k ≥0,k ≤3.由于是二次函数,故k ≠0,那么k 的取值范围是k ≤3且k ≠0.应选D.方法总结:二次函数y =ax 2+bx +c ,当b 2-4ac >0时,图象与x 轴有两个交点;当b 2-4ac =0时,图象与x 轴有一个交点;当b 2-4ac <0时,图象与x 轴没有交点.变式训练:见《 》本课时练习“课堂达标训练〞第4题【类型三】利用抛物线与x 轴交点坐标确定一元二次方程的解(2021·苏州中考)假设二次函数y =x 2+bx 的图象的对称轴是经过点(2,0)且平行于y 轴的直线,那么关于x 的方程x 2+bx =5的解为( )A.⎩⎪⎨⎪⎧x 1=0,x 2=4B.⎩⎪⎨⎪⎧x 1=1,x 2=5C.⎩⎪⎨⎪⎧x 1=1,x 2=-5D.⎩⎪⎨⎪⎧x 1=-1,x 2=5解析:∵对称轴是经过点(2,0)且平行于y 轴的直线,∴-b2=2,解得b =-4.解方程x 2-4x =5,解得x 1=-1,x 2=5.应选D.方法总结:此题容易出错的地方是不知道二次函数的图象与一元二次方程的解的关系导致无法求解.变式训练:见《 》本课时练习“课堂达标训练〞第1题 探究点二:用二次函数的图象求一元二次方程的近似解利用二次函数的图象求一元二次方程-x 2+2x -3=-8的实数根(精确到0.1). 解析:对于y =-x 2+2x -3,当函数值为-8时,对应点的横坐标即为一元二次方程-x 2+2x -3=-8的实数根,故可通过作出函数图象来求方程的实数根.解:在平面直角坐标系内作出函数y =-x 2+2x -3的图象,如图.由图象可知方程-x 2+2x -3=-8的根是抛物线y =-x 2+2x -3与直线y =-8的交点的横坐标,左边的交点横坐标在-1与-2之间,另一个交点的横坐标在3与4之间.(1)先求在-2和-1之间的根,利用计算器进行探索:x - - - - - y-----因此x ≈-是方程的一个实数根. (2)另一个根可以类似地求出:x y-----x ≈是方程的另一个实数根.方法总结:用二次函数的图象求一元二次方程满足精确度的实数根的方法:(1)作出函数的图象,并由图象确定方程解的个数;(2)由图象与y =h 的交点的位置确定交点横坐标的取值范围;(3)利用计算器求方程的实数根.变式训练:见《 》本课时练习“课堂达标训练〞第8题 探究点三:二次函数与一元二次方程在运动轨迹中的应用某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,球出手时距地面209米,与篮框中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行轨迹为抛物线,篮框距地面3米.(1)建立如下列图的平面直角坐标系,问此球能否准确投中?(2)此时,假设对方队员乙在甲面前1米处跳起盖帽拦截,乙的最大摸高为米,那么他能否获得成功?解析:这是一个有趣的、贴近学生日常生活的应用题,由条件可得到出手点、最高点(顶点)和篮框的坐标,再由出手点、顶点的坐标可求出函数表达式;判断此球能否准确投中的关键就是判断代表篮框的点是否在抛物线上;判断盖帽拦截能否获得成功,就是比较当x =1时函数y 的值与最大摸高米的大小.解:(1)由条件可得到出手点、最高点和篮框的坐标分别为A (0,209),B (4,4),C (7,3),其中B 是抛物线的顶点.设二次函数关系式为y =a (x -h )2+k ,将点A 、B 的坐标代入,可得y =-19(x -4)2+4.将点C 的坐标代入上式,得左边=3,右边=-19(7-4)2+4=3,左边=右边,即点C在抛物线上.所以此球一定能投中;(2)将x =1代入函数关系式,得y =3.因为>3,所以盖帽能获得成功. 变式训练:见《 》本课时练习“课后稳固提升〞第7题 三、板书设计教学过程中,强调学生自主探索和合作交流,通过观察二次函数与x 轴的交点个数,讨论一元二次方程的根的情况,体会知识间的相互转化和相互联系.。



九年级数学《三视图》教案课时:1课时课型:新授课教具:板书、投影仪、多媒体计算机、几何体实物模型教学目标:1.知识与技能:通过探究与学习, 理解视图、三视图的概念, 掌握三视图画法, 能够进行三视图与几何图之间的转化。
感受从不同方向观察同一物体可能看到不一样的结果, 培养学生全面观察的能力。
2.过程与方法:通过对三视图的分析, (采用实物模型)以小组探究的方法掌握三视图的基本画法, 促使学生的思维活动外显, 提高学生的合作探究能力。
3.情感态度与价值观:通过三种视图才能确定一物体, 启发学生认识问题要从多个角度进行分析。
教学重点:理解三视图, 并掌握三视图的画法教学难点:几何体与其三视图之间的相互转化教学方法:讲授法、讨论法、体验学习教学法、演示法教学内容及过程:(一)导入《题西林壁》横看成岭侧成峰, 远近高低各不同。
不识庐山真面目, 只缘身在此山中。
【设计意图】切入主题, 激发学习兴趣, 另外也能展现学科间并不是孤立的, 有其互益性, 数学也可以充满文学是色彩。
(二)授新课1、联系上节课所学的“正投影”, 讲解“视图”的概念视图:用正投影的方法, 把物体轮廓形状向投影面投影所得的图形称为视图。
2、三视图及其关系在PPT中展示几张“三视图”在生活中和工程设计中的应用的图片提问:确定一物体需要几个方向的视图?讲解:(PPT动画展示)主视图:从物体的前面向后面投射所得的视图称主视图, 反映物体的长和高俯视图:从物体的上面向下面投射所得的视图称俯视图, 反映物体的长和宽左视图:从物体的左面向右面投射所得的视图称左视图, 反映物体的宽和高关系:长对正, 高平齐, 宽相等3、小组合作探究, 学会画几何体:“四棱柱”“三棱柱”“圆柱”“圆锥”、“球体”。
(1)将学生分为十组, 每组4-5人。
将“四棱柱”“三棱柱”“圆柱”“圆锥”、“球体”的实物模型分发给各组, 其中每两个组所发模型相同。
说明活动任务:小组合作, 画出几何体的三视图。


29.2三视图(第2课时)1.理解三视图中各视图之间的位置关系和大小关系.2.会画基本几何体、组合体的三视图.画基本几何体、组合体的三视图.画基本几何体、组合体的三视图.知识回顾对一个物体(例如一个长方体)在三个投影面内进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.【设计意图】复习已经学过的三视图知识,为引出新课作铺垫.新知探究一、探究学习【探究】正对着物体看,物体左右之间的水平距离、前后之间的水平距离,上下之间的竖直距离,分别对应物体的长、宽、高.如图,将长方体三个投影面展开在一个平面内,得到这一物体的一张三视图(由主视图、教学目标教学重点教学难点教学过程俯视图和左视图组成),展开的这三个视图的位置有什么关系?【师生活动】教师提出问题,学生分小组交流并派代表回答,教师总结.【答案】主视图在左上边,它的正下方是俯视图,左视图在主视图的右边.【追问】展开的这三个视图的大小有什么关系?【师生活动】教师分析:三视图中,主视图与俯视图可以表示同一个物体的长,主视图与左视图可以表示同一个物体的高,左视图与俯视图可以表示同一个物体的宽,因此三个视图的大小是互相联系的.学生根据教师分析,思考并回答:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.教师展示动图,学生观看并体会三视图中的位置关系和大小关系.【探究】结合三视图中的位置关系和大小关系,画三视图时主视图与俯视图之间、主视图与左视图之间、左视图与俯视图之间应分别注意什么?【师生活动】学生讨论并回答问题,教师总结.【答案】画三视图时,三个视图都要放在正确的位置,并且注意主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.【设计意图】通过观察讨论三视图中的三个视图的位置关系和大小关系,体会“长对正,高平齐,宽相等”的具体含义.二、典例精讲【例1】画出图中基本几何体的三视图.【师生活动】教师分析:画这些基本几何体的三视图时,要注意从三个方面观察它们,具体方法为:(1)确定主视图的位置,画出主视图;(2)在主视图正下方画出俯视图,注意与主视图“长对正”;(3)在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;(4)为表示圆柱、圆锥等的对称轴,规定在视图中加画点划线()表示对称轴.学生根据教师分析,分小组交流讨论,教师提示:(1)正三棱柱的上、下底面均为正三角形,其余各面都是矩形;(2)从某一角度看物体时,有些部分因被遮挡而看不见.为全面反映立体图形的形状,画图时规定:看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.学生作图,教师巡查纠错并讲解.【答案】解:如图所示.【归纳】画一个几何体的三视图的几点注意:(1)在观察几何体时,要注意视线与观察面垂直,即观察到的平面图形是几何体在该观察面上的正投影;(2)要注意正确用虚线表示看不见部分的轮廓线,不要漏画.当看不见的轮廓线(虚线)和看得见的轮廓线(实线)重叠时,不用画出虚线;(3)按三视图的位置和大小要求从整体上画出几何体的三视图;(4)画出三视图后,可以擦去图中的辅助线.【例2】画出如图所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.【师生活动】教师分析:支架的形状是由两个大小不等的长方体构成的组合体.画三视图时要注意这两个长方体的上下、前后位置关系.学生根据教师分析,独立思考并尝试画图,教师巡查纠错并讲解.【答案】解:下图是支架的三视图.【提醒】画组合体的三视图时,构成组合体的各部分的视图也要遵守“长对正,高平齐,宽相等”的规律.【设计意图】通过例1、例2的练习与讲解,让学生学会画基本几何体、组合体的三视图,巩固学生对所学知识的理解及应用.课堂小结板书设计一、三视图中各视图之间的位置关系、大小关系二、三视图的画法课后任务完成教材第97页练习.。
《三视图》教学设计一、教学内容分析通用技术必修模块“技术与设计1”第六章第二节《常见的技术图样》之“正投影与三视图”(苏教版)主要描述了正投影形成三视图的方法、原理,三视图的绘制(识读)方法和规律等。
三视图作为一种技术图样是设计交流与表达的一种常用的技术语言形式。
学生通过本节的学习,掌握绘制简单三视图的基础知识和技能,本节内容也是后续知识“形体的尺寸标注”和“机械加工图”的基础。
在这里起到一个呈上启下的作用。
二、学情分析通过前面章节的学习,高中学生能够较熟练地绘制(识读)平面图和正等轴测图,也有光线投射成影的感知和体验。
教学可以从学生的现有知识和经验出发,按照直观感知、操作确认、思辩求证的认识过程展开,建构正投影与三视图的知识体系。
但学生的空间思维还受到定向模式的限制,很难发散思考一些个别现象,处理个特殊案例的能力有待提高,如不可见部分和重叠等。
三、教学目标1.知识目标:(1)理解投影法的基本概念和方法;(2)掌握正投影法方法、特性及三视图成图原理和规律;(3)掌握三视图一般绘图规则。
2.能力目标:(1)掌握简单的三视图的绘制(识读);(2)学会规范作图的方法和技能。
3.情感态度价值观:(1)经历三视图的作图过程,体验技术图样的魅力(2)形成科学的空间三围思维方式,培养学生严谨的思维与态度。
4、教学重点:(1)掌握三视图成图原理和规律;(2)掌握简单的三视图的绘制(识读)。
5、教学难点:(1)能规范绘制和识读简单的三视图。
四、教学准备准备积木,利用塑料胶纸和泡沫制作多个的模型。
五、教学策略及媒体运用在本节的教学中,将采用“主导—主体(分享—互助提升)”的设计模式,引导学生进行自主探究、知识建构和能力拓展。
总体教学流程为:“情境导入,知识建构,合作探究,总结提升,能力拓展”。
1、通过生活小故事的情景导学,激发学生对“技术语言的种类”进行回顾和复习以及注意在技术活动中选用恰当的技术语言进行交流的重要性,对本节课内容产生强烈的求知欲望。
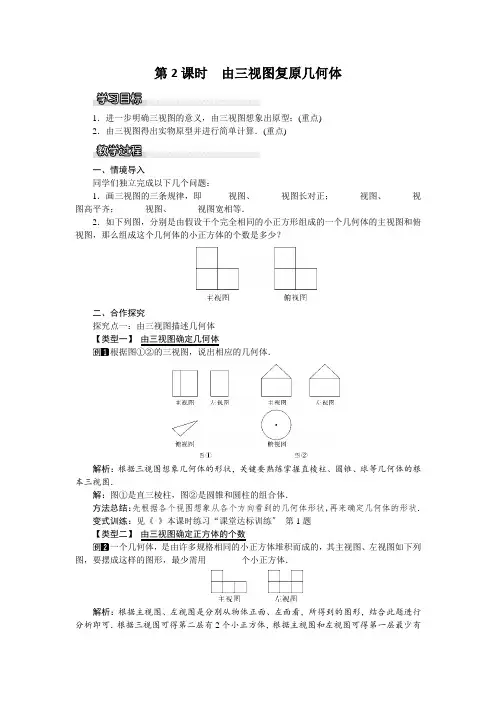
第2课时由三视图还原几何体
1.进一步明确三视图的意义,由三视
图想象出原型;(重点)
2.由三视图得出实物原型并进行简单
计算.(重点)
一、情境导入
同学们独立完成以下几个问题:
1.画三视图的三条规律,即______视图、______视图长对正;______视图、______视图高平齐;______视图、______视图宽相等.
2.如图所示,分别是由若干个完全相
同的小正方形组成的一个几何体的主视图
和俯视图,则组成这个几何体的小正方体的
个数是多少?
二、合作探究
探究点一:由三视图描述几何体
【类型一】由三视图确定几何体
根据图①②的三视图,说出相应
的几何体.
解析:根据三视图想象几何体的形状,
关键要熟练掌握直棱柱、圆锥、球等几何体的基本三视图.
解:图①是直三棱柱,图②是圆锥和圆
柱的组合体.
方法总结:先根据各个视图想象从各个方向看到的几何体形状,再来确定几何体的形状.
变式训练:见《学练优》本课时练习“课堂达标训练”第1题
【类型二】由三视图确定正方体的个
数
一个几何体,是由许多规格相同
的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的图形,最少需用
________个小正方体.
解析:根据主视图、左视图是分别从物体正面、左面看,所得到的图形,结合本题
进行分析即可.根据三视图可得第二层有2个小正方体,根据主视图和左视图可得第一
层最少有4个小正方体,故最少需用7个小正方体.故答案为7.
方法总结:由三视图判断几何体由多少
个立方体组成时,先由俯视图判断底面的行
列组成;再从主视图判断每列的高度(有几个立方体),并在俯视图中按照左、中、右
的顺序用数字标出来;然后由左视图判断行的高度,在俯视图中按照上、中、下的顺序
用数字标出来;最后把俯视图中的数字加起来.
变式训练:见《学练优》本课时练习“课堂达标训练”第5题
探究点二:三视图的相关计算
如图是某工件的三视图,其中圆
的半径是10cm,等腰三角形的高是30cm,则此工件的体积是( )
A.1500πcm3 B.500πcm3
C.1000πcm3 D.2000πcm3
解析:由三视图可知该几何体是圆锥,
底面半径和高已知.
解:∵底面半径为10cm,高为30cm.∴
体积V=1
3
π×102×30=1000π(cm3).故选
C.
方法总结:依据三视图“长对正,高平齐,宽相等”的原则,正确识别几何体,再
进行有关计算.
变式训练:见《学练优》本课时练习“课堂达标训练”第8题
三、板书设计
本节课是在学习了简单几何体的三视图的
基础上,反过来已知几何体的三视图想象出
几何体,既是对三视图知识的完善,又是三视图知识的简单应用,培养了学生的空间想象能力,使学生初步体会到由平面图形到立
体图形的转化也是一种数学方法.。