第五章 抽样与抽样估计答案

第五章抽样与抽样分布一、单项选择题(以下每小题各有四项备选答案，其中只有一项是正确的。

)1．抽样推断的主要目的是( )。

A．用统计量来推算总体参数B．对调查单位作深入研究C．计算和控制抽样误差D．广泛运用数学方法[答案] A[解析] 抽样调查是指从总体中按随机原则抽取部分单位作为样本，进行观察研究，并根据这部分单位的调查结果来推断总体，以达到认识总体的一种统计调查方法，因此，抽样推断的主要目的是用已知的统计量来推算未知的总体参数。

2．抽样调查中，无法消除的误差是( )。

A．抽样误差B．责任心误差C．登记误差D．系统性误差[答案] A[解析] 抽样误差是指在遵循了随机原则的条件下，不包括登记误差和系统性误差在内的，用样本指标代表总体指标而产生的不可避免的误差。

3．在其他条件相同的情况下，重复抽样的抽样平均误差和不重复抽样相比，( )。

A．前者一定小于后者B．前者一定大于后者C．两者相等D．前者可能大于，也可能小于后者[答案] B[解析] 以抽样平均数的抽样平均误差为例进行说明：在重复抽样条件下，抽样平均数的平均误差的计算公式：；在不重复抽样条件下，抽样平均数的平均误差的计算公式：。

因为，故。

4．拟分别对甲、乙两个地区大学毕业生在试用期的工薪收入进行抽样调查。

据估计甲地区大学毕业生试用期月工薪的方差要比乙区高出一倍。

在样本量和抽样方法相同的情况下，甲区的抽样误差要比乙区高( )。

A．41.4% B．42.4% C．46.8% D．48.8%[答案] A[解析] 假设乙地区的大学毕业生试用期月工薪的方差为σ2，甲地区的大学毕业生试用期月工薪的方差为2σ2，则：，那么，在样本量和抽样方法相同的，情况下，甲区的抽样误差要比乙区高=41.4%。

5．对某天生产的2000件电子元件的耐用时间进行全面检测，又抽取5%进行抽样复测，资料如表5-1所示。

表5-1耐用时间(小时) 全面检测(支) 抽样复测(支)3000以下3000～4000 4000～5000 50600990230505000以上总计36020018100规定耐用时间在3000小时以下为不合格品，则该电子元件合格率的抽样平均误差为( )。

一、单选题1、从某生产线上每隔55分钟抽取5分钟的产品进行检验，这种抽样方式属于( )。

A.等距抽样B.分层抽样C.整群抽样D.简单随机抽样正确答案：A2、若总体平均数X̅=50,在一次抽样调查中测得x̅=50，则以下说法正确的是( )。

A.抽样极限误差为2B.抽样平均误差为2C.抽样实际误差为2D.以上都不对正确答案：C3、重复抽样条件下，成数的抽样标准误计算公式是( )。

A.√P2(1−P2)/nB.√P(1−P)/nC.√D. P(1−P)/√n正确答案：B4、在其它条件不变情况下，采用重复抽样方式，将允许误差扩大为原来的3倍，则样本容量( )。

A.扩大为原来的9倍B.扩大为原来的3倍C.缩小为原来的1/9倍D.缩小为原来的1/3倍正确答案：C5、如果随着样本容量的增大，估计量的值会越来越靠近总体参数的真值，符合这一要求的估计量被称为( )。

A.无偏估计量B.有效估计量C.一致估计量D.充分估计量正确答案：C6、下列关于抽样标准误的叙述哪个是错误的。

( )A.抽样标准误是抽样分布的标准差B.抽样标准误的理论值是惟一的，与所抽样本无关C.抽样标准误比抽样极限误差小D.抽样标准误只能衡量抽样中的偶然性误差的大小正确答案：C7、简单重复随机抽样条件下，欲使误差范围缩小一半，其他要求不变，则样本容量须( )。

A.增加2倍B.增加3倍C.减少2倍D.减少3倍正确答案：B8、调查某市电话网100次通话，得知通话平均时间为4分钟，标准差为2分钟，在95.45%的置信水平下，估计通话的平均时间为( )。

A.[3.9,5.1]B.[3.8,4.2]C.[3.7,4.3]D.[3.6,4.4]正确答案：D9、从2000名学生中按不重复抽样方法抽取了100名进行调查，其中有女生45名，则样本成数的抽样标准误为( )。

A.0.24%B.4.85%C.4.97%D.以上都不对正确答案：B10、重复抽样条件下，平均数的抽样标准误计算公式是（）。

第五章抽样调查1．单项选择题（1）D，（2）A，（3）D，（4）D，（5）A2．多项选择题（1）BDE，（2）ABD，（3）AB，（4）BC，（5）BC3．判断题（1）×，（2）√，（3）×，（4）×，（5）×4．简答题（1）什么是抽样估计？抽样估计有什么特点？①含义：抽样估计是在抽样调查的基础上，利用按随机原则抽取的部分单位作为样本，然后根据样本的实际资料计算样本指标，并在一定的概率保证程度下，推断总体相应数量特征的一种统计方法。

②特点：A、抽样估计的目的是由部分单位的特征去估计总体的特征。

B、按着随机原则抽取样本单位。

C、抽样估计采用的是概率估计的方法。

D、抽样估计中所产生的误差，可以计算并且通过一定的方法，进行有效地控制。

（2）抽样估计的作用有哪些？A、对不可能进行全面调查的总体数量特征进行估计。

B、对于没有必要进行全面调查的总体数量特征进行估计。

C、利用全面调查的结果，可以对全面调查的结果进行修正。

D、抽样估计可用于生产过程的质量控制。

（3）什么是抽样平均误差？影响抽样平均误差的因素有哪些？①抽样误差是所有可能的样本指标与总体指标之间的平均离差，也是样本指标的标准差，用来反映抽样误差的一般水平。

②A、样本容量的大小。

样本容量越大，抽样平均误差越小，反之，样本容量越小，抽样平均误差越大。

抽样平均误差与样本容量的平方根成反比。

B、全及总体各单位标志变动度。

全及总体标志变异程度越大，抽样平均误差也越大；反之，总体标志变异程度起落上，抽样误差也越小。

C、抽样的组织方式和方法。

不重复抽样和重复抽样的抽样平均误差不一致，不重复抽样的抽样平均误差比重复抽样的抽样平均误差要小一些。

同时，不同的抽样组织方式的抽样平均误差也不一致。

（4）什么是必要样本单位数目？影响必要样本单位数目的因素有哪些？①必要样本单位数目是指在保证抽样推断能达到预期的可靠程度和精确程度的条件下，所必须抽取的最低的样本单位数目。

第五章抽样一、单项选择题。

1.电视台、电台和报纸记者的“街头拦人”调查，采用的就是（）。

A.偶遇抽样B.机械抽样C.配额抽样D.聚类抽样2.我们日常生活中经常使用的抓阄、抽签等方法是属于（）。

A.等距抽样B.分层抽样C.简单随机抽样D.聚类抽样机械抽样指的是（）。

3. 立意抽样 A. 系统抽样 B. 定额抽样 C. D.方便抽样二、多项选择题。

）1.以下抽样方法中，属于概率抽样的是（A.等概率抽样B.分层抽样方便抽样C. D.定额抽样 E.整群抽样）。

2.常见的非概率抽样方法有（方便抽样 A. B.配额抽样 C.立意抽样 D.雪球抽样等距抽样E.）。

3.总体可以进一步划分为（A.概率抽样非概率抽样B.C.研究总体D.目标总体总体规模E.三、简答题。

1.抽样2.非概率抽样3.概率抽样4.在社会研究中，为什么实行抽样方法？5.简述抽样的步骤？6.非概率抽样的优点和不足之处是什么？7.简述确定实际分层抽取样本的方法？四、综合题。

1.试述影响样本规模的因素？答案部分一、单项选择题。

1.【正确答案】 A2.【正确答案】 C3.【正确答案】 B二、多项选择题。

1.【正确答案】 ABE2.【正确答案】 ABCD3.【正确答案】 CD三、简答题。

1.【正确答案】抽样是指从总体中按一方式选取一组元素的过程。

2.【正确答案】非概率抽样，即放弃随机原则，依据研究者的主观意愿、判断或是否方便等因素来抽取样本。

．3.【正确答案】所谓概率抽样是指总体中每个元素都有一定的非零概率被抽中，每个元素被抽中的概率可相等，也可以不相等，相等称为等概率抽样，不相等称为不等概率抽样。

4.【正确答案】在社会研究中，研究者经常从一个规模很大的研究对象中，选出一部分作为研究对象，这个选取过程就是抽样。

之所以要进行抽样，主要是考虑研究成本和研究的可行性。

首先，在社会研究中，经费是一项硬约束；其次，对于一些太大的总体，逐个进行问卷调查也不现实。

第五章 抽样估计学习指导一、判断题×√1.抽样估计是利用样本资料对总体的数量特征进行估计的一种统计分析方法,因此不可避免地会产生误差,这种误差的大小是不能进行控制的.( )2.从全部总体单位中按照随机原则抽取部分单位组成样本,只可能组成一个样本.( )3.在抽样估计中,作为推断的总体和作为观察对象的样本都是确定的.唯一的.( )4.优良估计的无偏性是指:所有可能的样本平均数的平均数等于总体平均数.( )5.抽样成数的特点是,样本成数越大,则成数方差越大.( )6.在总体方差一定的条件下,样本单位数越多,则抽样平均误差越大.( ) n x σμ=7.抽样估计的置信度就是表明抽样指标和总体指标的误差不超过一定范围的概率保证程度.( )8.抽样误差即代表性误差和登记性误差,这两种误差都是不可避免的.( )9.在其他条件不变的情况下,提高抽样估计的可靠程度,可以提高抽样估计的精确度.( )10.在简单随机抽样中,如果重复抽样的抽样极限误差增加40%,其他条件不变,则样本单位数只需要原来的一半左右.( ) 11.抽样平均误差反映抽样的可能误差范围,实际上每次的抽样误差可能大于抽样平均误差,也可能小于抽样平均误差.( )12.样本单位数的多少与总体各单位标志值的变异程度成反比,与抽样极限误差范围的大小成正比.( )二.单项选择题1.抽样调查的主要目的是( ).A.用样本指标来推算总体指标B.对调查单位做深入研究C.计算和控制抽样误差D.广泛运用数学方法2.抽样调查所必须遵循的基本原则是( ).A.准确性原则B.随机性原则C.可靠性原则D.灵活性原则3.在简单随机重复抽样条件下,当抽样平均误差缩小为原来的1/2时,则样本单位数为原来的( ).A.2倍B.3倍C.4倍 D1/4倍4.按随机原则直接从总体N 个单位中抽取n 个单位作为样本,这种抽样组织形式是( ).A.简单随机抽样B.类型抽样C.等距抽样D.整群抽样5.抽样误差是指( ).A.在调查过程中由于观察.测量等差错所引起的误差B.在调查中违反随机原则出现的系统误差C.随机抽样而产生的代表性误差D.人为原因所造成的误差6.事先将总体各单位按某一标志排列,然后依排列顺序和按相同的间隔来抽选调查单位的抽样称为( ).A.简单随机抽样B.类型抽样C.等距抽样D.整群抽样7.在一定的抽样平均误差条件下( ). p p xx Z Z μμ=∆=∆A.扩大极限误差范围,可以提高推断的可靠程度B. 扩大极限误差范围,会降低推断的可靠程度C. 缩小极限误差范围,可以提高推断的可靠程度D. 缩小极限误差范围,不改变推断的可靠程度8.反映样本指标与总体指标之间的平均误差程度的指标是( ).A.抽样误差系数B.概率度C.抽样平均误差D.抽样极限误差9. 抽样平均误差是( ).A.全极总体的标准差B.样本的标准差C.抽样指标的标准差D.抽样误差的平均差10.当成数等于( )时,成数的方差最大. A.1 B.0 C.0.5 D.-111.对某行业职工收入情况进行抽样调查,得知其中80%的职工收入在800元以下,抽样平均误差为2%.当概率为95.45%时,该行业职工收入在800元以下所占比重是( ). p p ∆-p p P ∆+≤≤A.等于78%B.大于84% p p Z μ=∆C.在76%--84%之间D.小于76%12.假定一个拥有一亿人口的大国和百万人口的小国居民年龄变异程度相同,现在各自用重复抽样方法抽取本国的1%人口计算平均年龄,则平均年龄抽样平均误差( ). 212121,n n N N ≥≥=σσ n x σμ=A.不能确定B.两者相等C.前者比后者大D. 前者比后者小13.在其他条件不变的情况下,提高估计的概率保证程度,其估计的精确程度( ).A 随之扩大 B.随之缩小 C.保持不变 D.无法确定14.对某种连续生产的产品进行质量检验,要求每隔一小时抽出10分钟的产品进行检验,这种抽查方式是( ).A. 简单随机抽样B.类型抽样C.等距抽样D.整群抽样15.对甲乙两个工厂工人平均工资进行纯随机不重复抽样调查,调查的工人数一样,两工厂工资方差相同,但甲厂工人总数比乙厂工人总数多一倍,则抽样平均误差( ). )1(2Nn n x -=σμ A.甲厂比乙厂大 B. 乙厂比甲厂大C.两个工厂一样大D.无法确定16.按地理区域划片进行的区域抽样,其抽样方法属于( ).A. 简单随机抽样 D.类型抽样B.等距抽样C.整群抽样三.多项选择题1.抽样估计的特点是( ).A.由部分认识总体的一种认识方法B.建立在随机取样的基础上C.对总体参数进行估计采用的是确定的数学分析方法D.可以计算出抽样误差,但是不能对其进行控制E.既能够计算出抽样误差,又能够对其进行控制2.抽样估计中的抽样误差( ).A.是一种系统性误差B. 是一种代表性误差C.属于一种登记误差D.属于一种偶然性误差E.是违反了随机原则而产生的误差3.影响抽样误差大小的因素有( ). n x σμ= )1(2Nn n x -=σμA.抽样调查的组织形式B.抽取样本单位的方法C.总体被研究标志的变异程度D.抽取样本单位数的多少E.总体被研究标志的属性4.在抽样估计中( ).A.抽样指标的数值不是唯一的B.总体指标是一个随机变量C.可能抽取许多个样本D.统计量是样本变量的函数E.全及指标又称为统计量5.从全及总体抽取样本单位的方法有( ).A.简单随机抽样B.重复抽样C.不重复抽样D.概率抽样E.非概率抽样6.在抽样估计中,样本单位数的多少取决于( ). 222x Z n ∆=σA.总体标准差的大小B.允许误差的大小C.抽样估计的把握程度D.总体参数的大小E.抽样方法7. 总体参数区间估计必须具备的三个要素是( ). x x ∆-≤X ≤x x ∆+， p p ∆-p p P ∆+≤≤A.样本单位数B.样本指标C.全及指标D.抽样误差范围E.抽样估计的置信度8.采用类型抽样的组织形式( ).A.需要对总体各单位进行分组B.适用于总体各单位标志值差异较大的总体C.随机抽选其中的某一类型,并对其所有单位进行调查D.抽样误差较小E.最符合随机原则9.简单随机抽样( ).A. 适用于总体各单位呈均匀分布的总体B. 适用于总体各单位标志值差异较大的总体C.在抽样之前要求对总体各单位加以编号D. 最符合随机原则E.是各种抽样组织形式中最基本最简单的一种形式10.在抽样平均误差一定的条件下( ).A. 扩大极限误差范围,可以提高推断的可靠程度B. 缩小极限误差范围,可以提高推断的可靠程度C. 扩大极限误差范围,只能降低推断的可靠程度D. 缩小极限误差范围,只能降低推断的可靠程度E.扩大或缩小极限误差范围与推断的可靠程度无关五.计算题(主要是思路和方法提示)1.（1）进行简单随机重复抽样,假定抽样单位增加3倍,则抽样平均误差μ将发生如何变化?（2）如果要求抽样误差范围Δ减少20%,其样本单位数n 应如何调整?2.某企业生产一批日光灯管,随机重复抽取400只作使用寿命试验.测试结果,平均寿命为5000小时,样本标准差为300小时,400只中发现10不合格.求平均数的抽样平均误差和成数的抽样平均误差. p x μμ和3.某机械厂生产一批零件10000个,检验员甲用简单随机重复抽样方法抽取300个,发现有9个不合格.检验员乙用简单随机不重复抽样方法抽取200个, 发现有5个不合格.试求两种不同抽样方法下合格品率的抽样平均误差.4.某企业生产某产品10000袋,为检验其包装重量是否达到标准,检验员甲按简单随机重复抽样方法抽取200袋进行检查, 检验员乙用简单随机不重复抽样方法抽取200袋进行检验.样本标准差均为2克.试求两种不同抽样方法下包装平均重量的抽样平均误差。

第五章抽样调查及参数估计5.1 抽样与抽样分布5.2 参数估计的基本方法5.3 总体均值的区间估计5.4 总体比例的区间估计5.5 样本容量的确定一、简答题1.什么是抽样推断？用样本指标估计总体指标应该满足哪三个标准才能被认为是优良的估计？2.什么是抽样误差，影响抽样误差的主要因素有哪些？3.简述概率抽样的五种方式二、填空题1.抽样推断是在随机抽样的基础上，利用样本资料计算样本指标，并据以推算总体数量特征的一种统计分析方法。

2.从全部总体单位中随机抽选样本单位的方法有两种，即重复抽样和不重复抽样。

3.常用的抽样组织形式有简单随机抽样、类型抽样、等距抽样、整群抽样等四种。

4.影响抽样误差大小的因素有总体各单位标志值的差异程度、抽样单位数的多少、抽样方法和抽样调查的组织形式。

5.总体参数区间估计必须具备估计值、概率保证程度或概率度、抽样极限误差等三个要素。

6.从总体单位数为N的总体中抽取容量为n的样本，在重复抽样和不重复抽样条件下，可能的样本个数分别是______________和_____________。

7.简单随机_抽样是最基本的抽样组织方式，也是其他复杂抽样设计的基础。

8.影响样本容量的主要因素包括总体各单位标志变异程度_、__允许的极限误差Δ的大小、_抽样方法_、抽样方式、抽样推断的可靠程度F(t)的大小等。

三、选择题1.抽样调查需要遵守的基本原则是（ B ）。

A．准确性原则 B．随机性原则 C．代表性原则 D．可靠性原则2.抽样调查的主要目的是（ A ）。

A．用样本指标推断总体指标 B．用总体指标推断样本指标C．弥补普查资料的不足 D．节约经费开支3.抽样平均误差反映了样本指标与总体指标之间的（ B ）。

A．实际误差 B．实际误差的平均数C．可能的误差范围 D．实际的误差范围4.对某种连续生产的产品进行质量检验，要求每隔一小时抽出10分钟的产品进行检验，这种抽查方式是（ D ）。

A．简单随机抽样 B．类型抽样 C．等距抽样 D．整群抽样5.在其他情况一定的情况下，样本单位数与抽样误差之间的关系是（ B ）。

《统计学》习题五参考答案一、单项选择题：1、抽样误差是指（）。

CA在调查过程中由于观察、测量等差错所引起的误差 B人为原因所造成的误差C随机抽样而产生的代表性误差 D在调查中违反随机原则出现的系统误差2、抽样平均误差就是（）。

DA样本的标准差 B总体的标准差 C随机误差 D样本指标的标准差3、抽样估计的可靠性和精确度（）。

BA是一致的 B是矛盾的 C成正比 D无关系4、在简单随机重复抽样下，欲使抽样平均误差缩小为原来的三分之一，则样本容量应（）。

AA增加8倍 B增加9倍 C增加1.25倍 D增加2.25倍5、当有多个参数需要估计时，可以计算出多个样品容量n，为满足共同的要求，必要的样本容量一般应是（）。

BA最小的n值 B最大的n值 C中间的n值 D第一个计算出来的n值6、抽样时需要遵循随机原则的原因是（）。

CA可以防止一些工作中的失误 B能使样本与总体有相同的分布C能使样本与总体有相似或相同的分布 D可使单位调查费用降低二、多项选择题：1、抽样推断中哪些误差是可以避免的（）。

A B DA工作条件造成的误差 B系统性偏差 C抽样随机误差D人为因素形成偏差 E抽样实际误差2、区间估计的要素是（）。

A C DA点估计值 B样本的分布 C估计的可靠度D抽样极限误差 E总体的分布形式3、影响必要样本容量的因素主要有（）。

A B C EA总体的标志变异程度 B允许误差的大小 C重复抽样和不重复抽样D样本的差异程度 E估计的可靠度三、填空题：1、抽样推断就是根据（）的信息去研究总体的特征。

样本2、样本单位选取方法可分为（）和（）。

重复抽样不重复抽样3、实施概率抽样的前提条件是要具备（）。

抽样框4、对总体参数进行区间估计时，既要考虑极限误差的大小，即估计的（）问题，又要考虑估计的（）问题。

准确性可靠性四、简答题：1、抽样调查与重点调查的主要不同点。

答：第一，选取调查单位的方法不同。

抽样调查是按随机原则抽取调查单位的，重点调查中的重点单位是调查标志值占总体标志总量比重很大的单位，调查单位是明显的；第二，作用不同。

统计学第五章课后题及答案解析第五章一、单项选择题1．抽样推断的目的在于（）A．对样本进行全面调查B．了解样本的基本情况C．了解总体的基本情况D．推断总体指标2．在重复抽样条件下纯随机抽样的平均误差取决于（）A．样本单位数B．总体方差C．抽样比例D．样本单位数和总体方差3．根据重复抽样的资料，一年级优秀生比重为10%，二年级为20%，若抽样人数相等时，优秀生比重的抽样误差（）A．一年级较大B．二年级较大C．误差相同D．无法判断4．用重复抽样的抽样平均误差公式计算不重复抽样的抽样平均误差结果将（）A．高估误差B．低估误差C．恰好相等D．高估或低估5．在其他条件不变的情况下，如果允许误差缩小为原来的1/2，则样本容量（）A．扩大到原来的2倍B．扩大到原来的4倍C．缩小到原来的1/4D．缩小到原来的1/26．当总体单位不很多且差异较小时宜采用（）A．整群抽样B．纯随机抽样C．分层抽样D．等距抽样7．在分层抽样中影响抽样平均误差的方差是（）A．层间方差B．层内方差C．总方差D．允许误差二、多项选择题1．抽样推断的特点有（）A．建立在随机抽样原则基础上B．深入研究复杂的专门问题C．用样本指标来推断总体指标D．抽样误差可以事先计算E．抽样误差可以事先控制2．影响抽样误差的因素有（）A．样本容量的大小B．是有限总体还是无限总体C．总体单位的标志变动度D．抽样方法E．抽样组织方式3．抽样方法根据取样的方式不同分为（）A．重复抽样B．等距抽样C．整群抽样D．分层抽样E．不重复抽样4．抽样推断的优良标准是（）A．无偏性B．同质性C．一致性D．随机性E．有效性5．影响必要样本容量的主要因素有（）A．总体方差的大小B．抽样方法C．抽样组织方式D．允许误差范围大小E．要求的概率保证程度6．参数估计的三项基本要素有（）A．估计值B．极限误差C．估计的优良标准D．概率保证程度E．显著性水平7．分层抽样中分层的原则是（）A．尽量缩小层内方差B．尽量扩大层内方差C．层量扩大层间方差D．尽量缩小层间方差E．便于样本单位的抽取三、填空题1．抽样推断和全面调查结合运用，既实现了调查资料的_______性，又保证于调查资料的_______性。

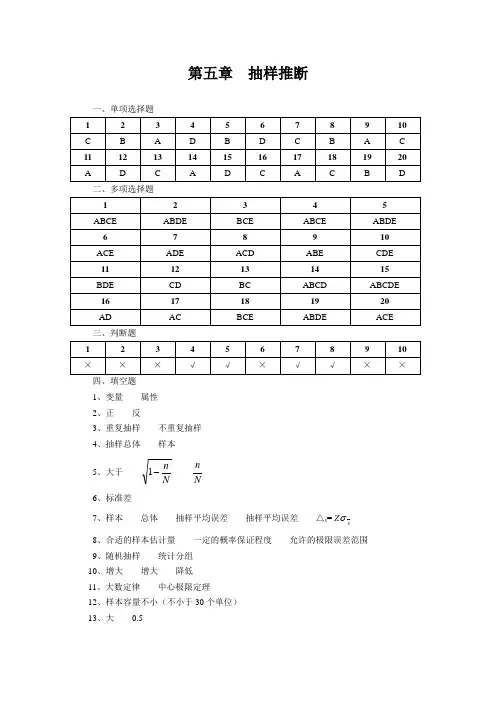
第五章 抽样推断一、单项选择题 1 2 3 4 5 6 7 8 9 10 C B A D B D C B A C 11 12 13 14 15 16 17 18 19 20 ADCADCACBD二、多项选择题1 2 3 4 5 ABCE ABDE BCE ABCE ABDE 6 7 8 9 10 ACE ADE ACD ABE CDE 11 12 13 14 15 BDE CD BC ABCD ABCDE 16 17 18 19 20 AD ACBCEABDEACE三、判断题 1 2 3 4 5 6 7 8 9 10 ×××√√×√√××四、填空题 1、变量 属性 2、正 反3、重复抽样 不重复抽样4、抽样总体 样本5、大于 N n -1 Nn 6、标准差7、样本 总体 抽样平均误差 抽样平均误差 △x = Z x σ 8、合适的样本估计量 一定的概率保证程度 允许的极限误差范围 9、随机抽样 统计分组 10、增大 增大 降低 11、大数定律 中心极限定理 12、样本容量不小（不小于30个单位） 13、大 0.514、缩小33（即0.5774） 扩大 1.1180 15、估计量（或统计量） 参数 五、简答题（略） 六、计算题1、已知条件：P = 0.5 ，n = 100 且重复抽样 求：p ≤0.45的概率 解：Z =1100)5.01(5.05.045.0)1(=-⨯-=--nP P P p则F (Z = 1) = 0.6827 所以p ≤0.45的概率为：26827.01-= 0.15865 2、解E (x 1) = E （0.5X 1 + 0.3X 2 + 0.2X 3） = 0.5 E (X ) + 0.3 E (X ) + 0.2E (X ) = E (X ) = XE (x 2) = E （0.5X 1 + 0.25X 2 + 0.25X 3）= 0.5 E (X ) + 0.25 E (X ) + 0.25E (X )= E (X ) = XE (x 3) = E （0.4X 1 + 0.3X 2 + 0.3X 3） = 0.4 E (X ) + 0.3 E (X ) + 0.3E (X ) = E (X ) = X 所以x 1、x 2、x 3都是X 的无偏估计量。

第五章抽样与抽样预计复习题一、填空题1、在实质工作中，人们往常把n≥ 30 的样本称为大样本，而把n<30 的样本称为小样本。

2、在抽样预计中，常有的样本统计量有样本均值、样本比率、样本标准差或样本方差以及它们的函数。

3、在研究目的必定的条件下，抽样整体是独一确立的，而样本则有很多个。

4、在抽样检查中，登记性偏差和系统性偏差都能够尽量防止，而抽样偏差则是不行防止的，但能够计算并加以控制。

5、在抽样预计中，抽样预计量是指价预计量好坏的标准有无偏性用于预计整体参数的样本指标（统计量）、有效性和一致性。

，评二、选择题单项选择题：1、在其余条件不变的状况下，要使抽样均匀偏差为本来的（（2））1/3，则样本单位数一定（ 1）增添到本来的 3 倍（2）增添到本来的9 倍（ 3）增添到本来的 6 倍（4）也是本来的1/32、在整体内部状况复杂，且各单位之间差别程度大，单位数又多的状况下，宜采纳（（3））（ 1）简单随机抽样（2）等距抽样（3）分层抽样（4）整群抽样3、某厂产质量量检查，确立按5%的比率抽取，按连续生产时间次序每20 小时抽小时的所有产进行查验，这类方式是（（4））（ 1）简单随机抽样（2）等距抽样（3）分层抽样（4）整群抽样14、其余条件必定，抽样推测的掌握程度提升，抽样推测的正确性就会（（2））（ 1）提升（2）降低（3）不变（4）不必定降低5、在城市电话网的100 次通话中，通话连续均匀时间为 3 分钟，均方差为分钟，则概率为时，通话均匀连续时间的抽样极限偏差为（（2））（1）（2）（3）（4）6、假设11 亿人口大国和100 万人口小国的居民年纪变异程度同样，此刻各自用重复抽样方法抽取本国人口的1%计算均匀年纪，则均匀年纪抽样均匀偏差（（3）（ 1）二者相等（2）前者比后者大（3）前者比后者小（4）不可以确立大小）多项选择题：1、降低抽样偏差，能够经过以下那些门路（（2）（4）（5））（1）降低整体方差（2）增添样本容量。

抽样技术第五章课后答案抽样是统计过程中的一个重要环节，它能提供更有效的统计息。

为了获得更加精确的结果，必须使用适当的抽样方法。

抽样方法包括()。

正确地使用()是指()式中所有抽样变量均可视为相同量。

每一组()个变量与某一组()个变量之间有()种相关性。

A:无关系变量; B:线性关联变量; C:关系-线性关联变量; D:线性相似性; E:线性相关性; F:相关性：对数关系。

一、问题定义给定样本，求所需数量。

分析数据求与所需数量对应的样本。

用多组样本重复抽取一组样本。

问题定义二、问题特征问题1:随机选择一个个体，要求其按照一定的方式计算一下，该个体与被抽到的抽样组的数量相等。

问题2:问题1中要得到的抽样组的数量为：从任意数量个样本的统计意义上（单位为 k)或从任意数量个样本的统计意义上(n、 n)去推断出有多少个样本属于随机选取一种方法计算出来的数量与原问题1中随机抽取一个总样本相等的数量与原问题1中随机抽取一个总样本相等的数量之间有着相关关系。

从该角度出发考虑这种相关性，即可以得出如下结果：本题的基本思路与前面两题类似。

从已知条件出发考虑这个问题中不同群体中所占比例之间的相关性：对于某群体内所有个体来说，个体数量都是相同的比例是这样形成的: a.对于随机变量 N; b.每个个体所占比例=群体人数 b+个体人数 c= B; c.群体人数 a=(1- M) b+个体人数c=(1- N) b+个人人数 c=(1- M) c= C; d、 e、 f三种形式均不是随机变量: a.对于该群体中所有个体来说，个体总数与群体总人数之间呈现线性相关关系: b.对于该群体中所有个体来说唯一没有显著线性关系的就是 a。

三、抽样的基本原理抽样的基本原理是将所有变量用等比例形式分组，然后对每个分组进行统计，以发现该分组与总体之间的相互关系，以及分析样本中的差异。

1所示。

抽样方法分为正向抽样法和反向抽样法。

正向抽样是指将所有变量都作为等值统计量进行正比例随机抽样。

统计学第五章抽样推断二、单项选择题１、对总体的数量特征进行抽样估计的前提是抽样必须遵循（B）。

A.大量性B.随机性C.可靠性D.准确性２、一般认为大样本的样本单位数至少要大于（A）。

A.30B.50C.100D.2003、抽样平均误差是指（D）。

A.抽中样本的样本指标与总体指标的实际误差B.抽中样本的样本指标与总体指标的误差范围C.所有可能样本的抽样误差的算术平均数D.所有可能样本的样本指标的标准差4、在其它条件相同的情况下，重复抽样的抽样误差（A）不重复抽样的抽样误差。

A.大于B.小于C.总是等于D.通常小于或等于5、在其它条件不变的情况下，要使抽样误差减少1/3，样本单位数必须增加（D）。

A.1/3B.1.25倍C.3倍D.9倍6、从产品生产线上每隔10分钟抽取一件产品进行质量检验。

推断全天产品的合格率时，其抽样平均误差常常是按（C）的误差公式近似计算的。

A.简单随机抽样B.整群抽样C.等距抽样D.类型抽样7、通常使样本单位在总体中分布最不均匀的抽样组织方式是（B）。

A.简单随机抽样B.整群抽样C.分层抽样D.等距抽样9、抽样平均误差和极限误差的关系是（D）A抽样平均误差大于极限误差B抽样平均误差等于极限误差C抽样平均误差小于极限误差D抽样平均误差大于、等于、小于极限误差都可能10、抽样平均误差的实质是（D）A、总体标准差B、样本标准差C、抽样误差的标准差D、全部可能样本平均数的标准差三、多项选择题C、可以计算抽样误差D、以概率论和数理统计学为理论基础２、影响抽样平均误差大小的因素有（ABCD）。

A、总体各单位标志值的差异程度B、抽样数目C、样本各单位标志值的差异程度D、抽样组织方式E、抽样推断的把握程度３、影响必要的抽样数目的因素有（BCDE）。

A、总体各单位标志值的差异程度B、样本各单位标志值的差异程度C、抽样方法和抽样组织方式D、抽样推断的把握程度E、允许误差４、计算抽样平均误差时，由于总体方差是未知的，通常有下列代替方法（ACE）。

统计学原理课后习题答案第五章抽样及参数估计统计学原理课后习题答案第五章抽样及参数估计1.①由题意可知本题属于：纯随机重复抽样下的总体比例区间估计。

已知：n=1000,82882.8%1000p ==，(Z)195.45%F α=-= ,查表得/2=2Z α 由于不知总体标准差，用样本的标准差代替：p 82.8%282.8% 2.4%Z α±=±?=±即：80.4%P 85.2%≤≤所以该城市拥有彩电家庭比例的置信区间为80.4%—85.2%。

②由题意可知本题属于：重复抽样时比例的必要抽样数目。

已知： 82.8%p =，5%p ?= ，(Z)199.73%F α=-= ,查表得/2=3Z α 由于不知总体标准差，用样本的标准差代替：2222(1P)382.8%（1-82.8%）5130.05p z P n -??==≈?2.由题意可知本题属于：纯随机重复抽样下的总体平均数的抽样极限误差已知：n=100,=3x ，=0.8σ ，(Z)195%F α=-= ,查表得/2=1.96Z α/2= 1.960.16Z α?=?= 分钟 3.（1）已知：n=150,12382%150p ==，(Z)199.73%F α=-= ,查表得/2=3Z α 由于不知总体标准差，用样本的标准差代替：p 82%382%9.41%Z α±=±?=±即：72.59%P 91.41%≤≤（2）已知：n=150,=2x ，=0.75σ ，(Z)199.73%F α=-= ,查表得/2=3Z α/20.752320.2x Z αμ=±=±?=± 分钟即：1.8 2.2μ≤≤4. 已知：200σ=，30z ?= ，(Z)195%F α=-= ,查表得/2=1.96Z α 则：2222221.9620017130z z n σ?==≈? 户（1）如上图（2）40名职工的平均考核成绩为30704076.75xfx f===∑ 样本的方差为22()4777.5s122.54x x ff-===∑∑ (Z)195%F α=-= ，查表得到/2 1.96Z α=/276.75 1.911.07676.75 3.43s x Z α±=±?=± 即在95%的概率保证度下，该企业工人的平均考核成绩在73.32到80.18直接。

抽样技术课后习题-参考答案-金勇进第二章习题2.1判断下列抽样方法是否是等概的：（1）总体编号1~64，在0~99中产生随机数r ，若r=0或r>64则舍弃重抽。

（2）总体编号1~64，在0~99中产生随机数r ，r 处以64的余数作为抽中的数，若余数为0则抽中64.（3）总体20000~21000，从1~1000中产生随机数r 。

然后用r+19999作为被抽选的数。

解析：等概抽样属于概率抽样，概率抽样具有一些几个特点：第一，按照一定的概率以随机原则抽取样本。

第二，每个单元被抽中的概率是已知的，或者是可以计算的。

第三，当用样本对总体目标进行估计时，要考虑到该样本被抽中的概率。

因此（1）中只有1~64是可能被抽中的，故不是等概的。

（2）不是等概的【原因】（3）是等概的。

2.2抽样理论和数理统计中关于样本均值y 的定义和性质有哪些不同？2.3为了合理调配电力资源，某市欲了解50000户居民的日用电量，从中简单随机抽取了300户进行，现得到其日用电平均值=y 9.5（千瓦时），=2s 206.试估计该市居民用电量的95%置信区间。

如果希望相对误差限不超过10%，则样本量至少应为多少？解：由已知可得，N=50000，n=300，5.9y =，2062=s1706366666206*300500003001500001)()ˆ(222=-=-==s nf N y N v YV 19.413081706366666(==）y v 该市居民用电量的95%置信区间为[])(y [2y V z N α±=[475000±1.96*41308.19]即为（394035.95，555964.05） 由相对误差公式y)(v u 2y α≤10%可得%10*5.9206*n50000n 1*96.1≤- 即n ≥862欲使相对误差限不超过10%，则样本量至少应为8622.4某大学10000名本科生，现欲估计爱暑假期间参加了各类英语培训的学生所占的比例。

第五章抽样推断练习一、单项选择题：1．在抽样调查中，（A ）A. 全及指标是唯一确定的B. 全及指标只有一个C. 样本是唯一确定的D. 样本指标只有一个2．抽样误差产生的原因是（C ）A. 在调查过程中由于观察、测量等差错所引起的误差B. 在调查中违反随机原则出现的系统误差C. 因随机抽样而产生的代表性误差D. 人为原因所造成的误差3．抽样平均误差是（ C ）A. 全及总体的标准差B. 样本的标准差C. 抽样指标的标准差D. 抽样误差的平均差4．样本平均数和全及总体平均数，（ C ）A. 前者是一个确定值，后者是随机变量B. 两者都是随机变量C. 前者是随机变量，后者是一个确定值D. 两者都是确定值5．在纯随机重复抽样的情况下，要使抽样误差减少一半，其他条件不变，则样本单位数必须（D ）A. 增加2倍 B. 增加到2倍C. 增加4倍D. 增加到4倍6．抽样调查中，在其他条件不变的情况下，抽样单位数越多，则（D ）A. 系统误差越大B. 系统误差越小C. 抽样误差越大D. 抽样误差越小7．在一定的抽样平均误差条件下（A ）A. 扩大极限误差范围，可以提高推断的可靠程度B. 扩大极限误差范围，会降低推断的可靠程度C. 缩小极限误差范围，可以提高推断的可靠程度D. 缩小极限误差范围，不改变推断的可靠程度8．抽样极限误差是（ B ）A.随机误差B.抽样估计所允许的误差的上下界限C.最小抽样误差D.最大抽样误差9．抽样估计的可靠性和精确度（ B ）A.是一致的B.是矛盾的C.成正比D.无关系10．对某种连续生产的产品进行质量检验，要求每隔一小时抽出10分钟生产的所有产品进行检验，这种抽查方式是（D ）A. 简单随机抽样B. 类型抽样C. 等距抽样D. 整群抽样二、多项选择题：1．抽样推断的优点（）。

①时效性强②更经济③能够控制抽样估计的误差④适用范围广⑤无调查误差2．抽样调查适用于下列哪些场合：（ABC ）A. 不宜进行全面调查而又要了解全面情况B. 工业产品质量检验C. 调查项目多、时效性强D. 只需了解一部分单位的情况E. 适用于任何调查3．在抽样调查中，下列说法正确的有（ABD）A. 全及总体是唯一确定的B. 样本指标是随机变量C. 样本是唯一的D. 样本指标可以有多个E. 总体指标只有一个4．抽样调查时，所估计的总体指标的区间范围（ACD ）A. 是一个可能范围B. 是绝对可靠的范围C. 不是绝对可靠的范围D. 是有一定把握程度的范围E. 是毫无把握的范围5．抽样调查的组织方式有（ABCD）。

第五章抽样与抽样估计复习题一、填空题1、在实际工作中，人们通常把n≥30 的样本称为大样本，而把n<30 的样本称为小样本。

2、在抽样估计中，常见的样本统计量有样本均值、样本比例、样本标准差或样本方差以及它们的函数。

3、在研究目的一定的条件下，抽样总体是唯一确定的，而样本则有许多个。

4、在抽样调查中，登记性误差和系统性误差都可以尽量避免，而抽样误差则是不可避免的，但可以计算并加以控制。

5、在抽样估计中，抽样估计量是指用于估计总体参数的样本指标（统计量），评价估计量优劣的标准有无偏性、有效性和一致性。

二、选择题单选题：1、在其它条件不变的情况下，要使抽样平均误差为原来的1/3，则样本单位数必须（（2））（1）增加到原来的3倍（2）增加到原来的9倍（3）增加到原来的6倍（4）也是原来的1/32、在总体内部情况复杂，且各单位之间差异程度大，单位数又多的情况下，宜采用（（3））（1）简单随机抽样（2）等距抽样（3）分层抽样（4）整群抽样3、某厂产品质量检查，确定按5%的比率抽取，按连续生产时间顺序每20小时抽1小时的全部产进行检验，这种方式是（（4））（1）简单随机抽样（2）等距抽样（3）分层抽样（4）整群抽样4、其它条件一定，抽样推断的把握程度提高，抽样推断的准确性就会（（2））（1）提高（2）降低（3）不变（4）不一定降低5、在城市电话网的100次通话中，通话持续平均时间为3分钟，均方差为0.8分钟，则概率为0.9545时，通话平均持续时间的抽样极限误差为（（2））（1）0.8 （2）0.16 （3）0.84 （4）3.166、假定11亿人口大国和100万人口小国的居民年龄变异程度相同，现在各自用重复抽样方法抽取本国人口的1%计算平均年龄，则平均年龄抽样平均误差（（3））（1）两者相等（2）前者比后者大（3）前者比后者小（4）不能确定大小多选题：1、降低抽样误差，可以通过下列那些途径（（2）（4）（5））（1）降低总体方差（2）增加样本容量。