应用多元统计分析-第八章 列联与对应分析

应用多元统计分析第8章 对应分析- 1-对应分析(Correspondence Analysis)是在因子分析的基础上发展起来的一种视觉化的数据分析方法,目的是通过定位点图直观地揭示样品和变量之间的内在联系。

R型因子分析是对变量（指标）进行因子分析，研究的是变量之间的相互关系；Q型因子分析是对样品作因子分析，研究的是样品之间的相互关系。

但无论是R型或Q型分析都不能很好地揭示变量和样品之间的双重关系。

而在许多领域错综复杂的多维数据分析中，经常需要同时考虑三种关系，即变量之间的关系、样品之间的关系以及变量与样品之间的交互关系。

法国学者苯参次(J.P.Benzecri)于1970年提出了对应分析方法，这个方法对原始数据采用适当的标度化处理，把R型和Q型分析结合起来，通过R型因子分析直接得到Q型因子分析的结果，同时把变量和样品反映到同一因子平面上，从而揭示所研究的样品和变量之间的内在联系。

在因子分析中，R型因子分析和Q型因子分析都是从分析观测数据矩阵出发的，它们是反映一个整体的不同侧面，因而它们之间一定存在内在联系。

对应分析就是通过某种特定的标准化变换后得到的对应变换矩阵Z将两者有机地结合起来。

具体地，就是首先给出变量的R型因子分析的协方差阵 和样品的Q型因子分析的协方差阵 。

由于矩阵 和 有相同的非零特征值，记为 ，如果 的对应于特征值 的标准化特征向量为 ，则容易证明， 的对应于同一特征值的标准化特征向量为当样本容量n很大时，直接计算矩阵 的特征向量会占用相当大的容量，也会大大降低计算速度。

利用上面关系式，很容易从 的特征向量得到 的特征向量。

并且由 的特征值和特征向量即可得到R 型因子分析的因子载荷阵A和Q型因子分析的因子载荷阵B，即有由于 和 具有相同的非零特征值，而这些特征值又是各个公因子的方差，因此设有p个变量的n个样品观测矩阵 ，这里要求所有元素 ，否则对所有数据同时加上一个适当的正数，以使它们满足以上要求。

第八章作业8.10解：首先对数据进行标准化处理，消除不同的度量带来的差异标准化的数据如下表：表1对处理的数据做主成分分析样本相关系数矩阵即为相应的样本协方差矩阵S即相应的协方差矩阵为：表2从表3可以得出，五个主因子解释的总体方差比重表3五个主因子间的协方差矩阵如下表4：表4从表4可以看出，这两个因子之间的相关程度比较低表5从表5可以得出五个主成分的表达式：F1=0.302X1+0.403X2+0.342X3+0.277X4+0.242X5F2=(-0.245)X1+(-0.14)X2+(-0.339)X3+0.46X4+0.492X5F3=1.016X1+(-0.517)X2+(-0.365)X3+0.005X4+0.102X5F4=(-0.163)X1+(-1.058)X2+1.096X3+0.216X4+0.169X5F5=(-0.044)X1+0.056X2+0.1X3+(-1.157)X4+1.144X5(b)五个特征值分别为：λ1，λ2，λ3，λ4，λ5，从表三可以得出： 第一主成分的总方差贡献为：λ1λ1+λ2+λ3+λ4+λ5=39.502% 第二主成分的总方差贡献为：λ2λ1+λ2+λ3+λ4+λ5=30.879% 第三主成分的总方差贡献为：λ3λ1+λ2+λ3+λ4+λ5=13.856%（c ）第一主成分的特征值λ1对应的庞弗罗尼联合置信区间为【0.00106，0.00195】第二主成分的特征值λ2对应的庞弗罗尼联合置信区间为【0.00054，0.001】第三主成分的特征值λ3对应的庞弗罗尼联合置信区间为【0.00019，0.00036】 （d ）从（a ）~（c ）的结果，前三个主成分的方差贡献超过80%，我们可以得出，综合股票回报率数据能在小于五维的空间中得到解释。

8.13（a ）变量的相关系数矩阵如下表：(b)有相应的相关系数表可以求出相应的特征值及特征向量表1从表1可以得出相应的特征值表2从上表可以得出相应的特征向量e1=(0.872,0.903,0.659,0.79,0.977,0.134)ˋe2=(0.361,-0.151,-0.23,-0.128,-0.037,0.955)ˋe3=(-0.382, -0.372,0.576, 0.246,0.044, 0.259)ˋe4=(0.189,0.071,0.423,-0.541,-0.068,-0.033)ˋe5=(-0.016,0.128,0.042,0.065 ,-0.191,0.038)ˋe6=(-0.061,0.049,-0.01,-0.028,0.032,0.026)ˋ第一主成分的总方差贡献为：λ1=58.846%λ1+λ2+λ3+λ4+λ5+λ6=18.925%第二主成分的总方差贡献为：λ2λ1+λ2+λ3+λ4+λ5+λ6=12.433%第三主成分的总方差贡献为：λ3λ1+λ2+λ3+λ4+λ5+λ6第四主成分的总方差贡献为：λ4=8.641%λ1+λ2+λ3+λ4+λ5+λ6=1.010%第五主成分的总方差贡献为：λ5λ1+λ2+λ3+λ4+λ5+λ6=0.145%第六主成分的总方差贡献为：λ6λ1+λ2+λ3+λ4+λ5+λ6（c）从（b）的结果可以看出，第一个主成解释了总方差的58.846%，低于80%，所以用一个指标来反映综合放射法数据是不合理的（d）从（b的结果可以得出，提取前三个主成分比较合适，前三个主成分的的累积方差贡献超过80%，前三个主成分与x1,x2,x3,x4.x5及x6的相关系数表如下：表3第九章作业9.20（a）空气污染变量X1,X2,X5,X6的样本协方差矩阵如表1：表1（a）先求出m=1时的因子矩阵，然后计算响应的主成分得分，再利用公式Xi=∝F1 其中∝为第一主成分的方差贡献，由此可以得到m=1的因子模型的主成分解如表2：表2m=2表3。

第八章 典型相关分析在对经济问题的研究和管理研究中，不仅经常需要考察两个变量之间的相关程度，而且还经常需要考察多个变量与多个变量之间即两组变量之间的相关性。

典型相关分析就是测度两组变量之间相关程度的一种多元统计方法。

第一节 典型相关的基本原理（一）典型相关分析的基本思想 典型相关分析方法(canonical correlation analysis)最早源于荷泰林(H ，Hotelling)于1936年在《生物统计》期刊上发表的一篇论文《两组变式之间的关系》。

他所提出的方法经过多年的应用及发展，逐渐达到完善，在70年代臻于成熟。

由于典型相关分析涉及较大量的矩阵计算，其方法的应用在早期曾受到相当的限制。

但随着当代计算机技术及其软件的迅速发展，弥补了应用典型相关分析中的困难，因此它的应用开始走向普及化。

典型相关分析是研究两组变量之间相关关系的一种统计分析方法。

为了研究两组变量1X ，2X ，…，p X 和1Y ， 2Y ，…，q Y 之间的相关关系，采用类似于主成分分析的方法，在两组变量中，分别选取若干有代表性的变量组成有代表性的综合指标，通过研究这两组综合指标之间的相关关系，来代替这两组变量间的相关关系，这些综合指标称为典型变量。

（二）典型相关分析的数学描述设有两随机变量组=X (1X ，2X ，…，)'pX 和=Y (1Y ， 2Y ，…，qY )'，不妨设p ≤q 。

对于X ，Y ，不妨设第一组变量的均值和协方差为矩阵为 ()X E =1μ Cov ()X =∑11第二组变量的均值和协方差为矩阵为()Y E =2μ Cov ()Y =∑22第一组与第二组变量的协方差为矩阵为Cov ()Y X ,=∑12= ∑21'于是，对于矩阵 Z = ⎥⎦⎤⎢⎣⎡Y X 有 （9—1—1） 均值向量 μ=E ()Z =E ()()⎥⎦⎤⎢⎣⎡Y E X E =⎥⎦⎤⎢⎣⎡21μμ （9—1—2）协方差矩阵()()∑+⨯+q p q p =E ()μ-Z ()'-μZ=()()()()()()()()⎥⎥⎦⎤⎢⎢⎣⎡'--'--'--'--22122111μμμμμμμμY Y E X Y E Y X E X X E =()()()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∑∑∑∑⨯⨯⨯⨯q q p q qp p p 22211211要研究两组变量1X ，2X ，…，p X 和1Y ， 2Y ，…，q Y 之间的相关关系，首先分别作两组变量的线性组合，即p p X a X a X a U +++= 2211=X a 'V =q q Y b Y b Y b +++ 2211=Y b '()'=p a a a a ,,,21 ，()'=q b b b b ,,,21 分别为任意非零常系数向量，则可得，Var ()U =a 'Cov ()a X = a '∑11a Var ()V =b 'Cov ()b Y = b '∑22bCov ()V U ,=a 'Cov ()Y X ,b = a '∑12b则称U 与V 为典型变量，它们之间的相关系数ρ称为典型相关系，即ρ=Corr ()V U ,=bb a a b a ∑∑∑'''221112典型相关分析研究的问题是，如何选取典型变量的最优线性组合。

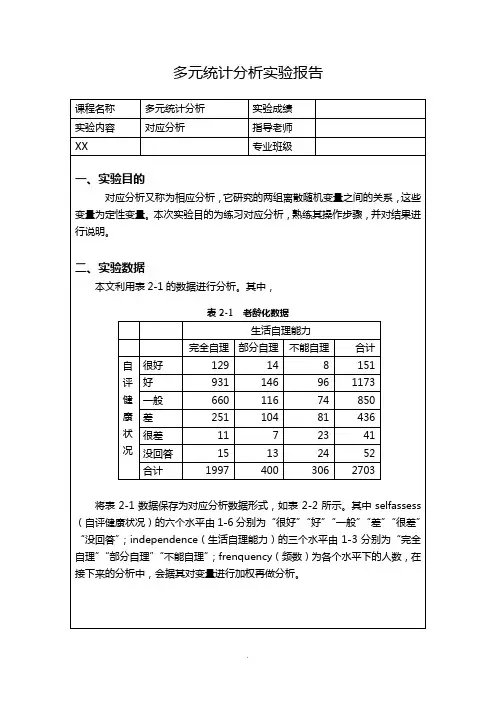
多元统计分析实验报告表2-2 对应分析数据（老龄化数据）三、实验过程在spss16.0软件中，对表2-2数据做对应分析。

首先应对个案进行加权操作。

选择【Date】—【Weight Cases】，出现表3对话框。

选择frequency作为加权，如图3-1所示。

图3-1 加权个案对个案加权后，开始做对应分析。

选择【Analyze】—【Date Reduction】—【Corespondence Analysis】，会出现图3-2对话画框。

图3-2 对应分析对话框接下来对行变量和列变量进行设置。

将selfassess（自评健康状况）选入Row，作为行变量，并选择【Define Range】，填写范围后点击【Update】—【Continue】，如图3-3所示；按同样的步骤，将independence（生活自理能力）选入Column（列变量），并设置列变量，如图3-4所示；最终设置结果如图3-5所示。

图3-3 行变量设置图3-4 列变量设置图3-5 对应分析设置结果点击【OK】，便可得到对应分析结果。

四、实验过程表4-1为对应分析的版本信息。

图中显示为1.1版本。

表4-1 对应分析版本信息表4-2是列联表，列示了在各个水平下的人数。

表4-2 列联表表4-3为对应分析总述表。

表中显示了奇异值（Singular Value），第一个维度的奇异值为0.253，第二个维度的奇异值为0.125；惯量（Inertia）为特征根，就是奇异值的平方；Chi Square 值为212.593，是总样本数除以总的Inertia 觉原假设，认为两个随机变量不是相互独立的，本例中就是自评健康状况和生活自理能力不是相互独立的；贡献率（Accounted for）显示，第一个维度解释了总变异的80.4%，第二个维度解释了19.6%，两个维度解释了所有的变异；接下来依次为累计贡献率（Cumulative）、奇异值的方差（Standard Deviation）、奇异值的相关系数（Correlation）。

第8章 典型相关分析典型相关分析是用来描述两组随机变量（两个随机向量）间关系的统计分析方法。

两组随机向量，各含有许多随机变量，能否用少量随机变量来描述其相关性？例如为了研究饲料与荤菜价格的关系，统计若干年玉米、大豆、稻子、麦子、鱼粉以及猪肉、牛肉、羊肉、鸡肉、鸡蛋、鸭肉、鸭蛋的价格，分析饲料与荤菜价格的关系时，发现单独一种饲料和单独一种肉蛋禽价格关系并不密切(由显著性检验可见)，但饲料的某种综合价格则与肉蛋禽综合价格的关系很密切。

把饲料价格看成一组随机变量，肉蛋禽价格看成另一组随机变量，找这两组随机变量的线性组合，使之相关系数平方最大，从而分析两组随机变量间的关系，判定这两组随机变量是否有关联，这就是典型相关分析。

8.1 典型相关分析数学模型设随机向量)',...(1p x x X =与)',...(1p y y Y =的方差yy xx ∑∑,存在，协方差为xy Y X ∑=),cov(。

b a ,为常数向量。

则1/2(',')'/('')xy xx yy corr a X b Y a b a ab b =∑∑∑，为了计算确定性，限制,1')'(=∑=a a X a D xx 1')'(=∑=b b Y b D yy 。

定义8.1 设11,b b a a ==在条件：,1')'(=∑=a a X a D xx 1')'(=∑=b b Y b D yy下使co v(',')a X b Y 大，则称Y b w X a v ','1111==为第一对典型相关变量，c o v(',')a Xb Y 称为第一典型相关系数。

由定义可见，11,w v 尽可能多地反映原来p 对随机变量相关的信息。

第一对典型相关变量往往不能完全反映随机向量间的关系，必须建立其它典型相关变量,它应当最能反映随机向量间的关系，但是它应当与第一对典型相关变量不相关（不包含第一对典型相关变量的信息）。

第八章 相应分析8.1 什么是相应分析？它与因子分析有何关系？答：相应分析也叫对应分析，通常意义下，是指两个定性变量的多种水平进行相应性研究。

其特点是它所研究的变量可以是定性的。

相应分析与因子分析的关系是： 在进行相应分析过程中，计算出过渡矩阵后，要分别对变量和样本进行因子分析。

因此，因子分析是相应分析的基础。

具体而言，Σr （Zu j ）=λj （Zu j ）式表明Zu j 为相对于特征值λj 的关于因素A 各水平构成的协差阵Σr 的特征向量。

从而建立了相应分析中R 型因子分析和Q 型因子分析的关系。

8.2试述相应分析的基本思想。

答：相应分析，是指对两个定性变量的多种水平进行分析。

设有两组因素A 和B ，其中因素A 包含r 个水平，因素B 包含c 个水平。

对这两组因素作随机抽样调查，得到一个r c ⨯的二维列联表，记为()ij r c k ⨯=K 。

要寻求列联表列因素A 和行因素B 的基本分析特征和最优列联表示。

相应分析即是通过列联表的转换，使得因素A 和因素B 具有对等性，从而用相同的因子轴同时描述两个因素各个水平的情况。

把两个因素的各个水平的状况同时反映到具有相同坐标轴的因子平面上，从而得到因素A 、B 的联系。

8.3 试述相应分析的基本步骤。

答：（1）建立列联表设受制于某个载体总体的两个因素为A 和B ，其中因素A 包含r 个水平，因素B 包含c 个水平。

对这两组因素作随机抽样调查，得到一个r c ⨯的二维列联表，记为()ij r c k ⨯=K 。

（2）将原始的列联资料K =(kij) r ⨯c 变换成矩阵Z =(zij) r ⨯c ，使得zij 对因素A 和列因素B 具有对等性。

通过变换Z ij =k −k i.k .jr k k 。

得c '=ΣZ Z ，r '=ΣZZ 。

（3）对因素B 进行因子分析。

计算出c '=ΣZ Z 的特征向量λ1，λ2⋯，λm 及其相应的特征向量 t 1，t 2，⋯t m 计算出因素B 的因子 U 1,U 2⋯U =( λ1t 1, λ2t 2,⋯ λm t m )（4）对因素A 进行因子分析。

多元统计分析对应分析(总6页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除学生实验报告学院：统计学院课程名称：多元统计分析专业班级：统计123班姓名：叶常青学号： 0124253目的熟悉和掌握对应分析的原理和上机操作方法内容及要求本次操作就父母与孩子的受教育程度的关系进行对应分析，分别对父亲与孩子和母亲与孩子的受教育程度做对应分析，最后再对输出结果进行详细的分析。

打开GSS93 subset .sav数据,对变量Degree与变量padeg和madeg进行对应分析,依次选择分析→降维…进入对应分析对话框，进行进行如下设置，便可输出想要的数据的：四、实验结果与数据处理：按照上述方法和步骤得出以下输出结果.对父亲受教育程度与孩子受教育程度的关系进行分析如下：Highest DegreeLess than HSHighschoolJuniorcollegeBachelorGraduate有效边际LT High School156308294525563 High School27248347937425 Junior College11128325 Bachelor64374718121 Graduate3223271671有效边际19363275206991205第二部分摘要给出了惯量，卡方值以及每一维度所解释的总惯量的百分比信息。

总惯量为0.189，卡方值为228.193，有关系式228.193=0.189*1205，由此可以清楚的看到总惯量和卡方的关系。

Sig.是假设卡方值为0成立的概率，它的值几乎为0说明列联表之间有较强的相关性。

表注表明的自由度为（5-1）*（5-1）=16。

惯量部分是四个公共因子分别解释总惯量的百分比。

表4行简要表 Father's Highest Degree R's Highest Degree Less than HS High school Junior college Bach elor Grad uate 有效边际LT High School.277 .547 .052 .080 .044 1.00High School.064 .584 .080 .186 .087 1.00Junior College.040 .440 .080 .320 .120 1.00Bachelor.050 .355 .058 .388 .149 1.00Graduate.042 .310 .042 .380 .225 1.00质量 .160 .524 .062 .171 .082 表5列简要表 Father's Highest Degree R's Highest Degree Less than HS High school Junior college Bach elor Grad uate质量LT High School .808 .487 .387 .218 .253 .467 High School .140 .392 .453 .383 .374 .353 Junior College .005 .017 .027 .039 .030 .021 Bachelor .031 .068 .093 .228 .182 .100 Graduate .016 .035 .040.131 .162 .059有效边际1.000 1.000 1.000 1.000 1.000第三部分的结果是在对应分析中点击Statistics 按钮，进入Statistics 对话框，选中Row profiles 和Column profiles 交友程序运行所得到的。