分子的平均平动动能
- 格式：ppt
- 大小：1.39 MB
- 文档页数：50
下载文档原格式
合集下载
分子动理论气体分子平均动能
32 103 26 m 5 . 31 10 kg 23 N A 6.02 10 （3）
3 3 k kT 1.38 10 23 ( 27 273) 6.21 10 21 J 2 2
3 – 3 理想气体分子的平均平动动能与温度的关系
第三章气体动理论
子数相等。
分子数 密度
k=R/NA=1.38×10-23J· K-1
称为玻耳斯曼常量
3 – 3 理想气体分子的平均平动动能与温度的关系
第三章气体动理论
二、理想气体分子的平均平动动能与温度的关系
阿伏加德罗定律：
p nkT
2 1 2 理想气体压强公式 p n mv 3 2 1 3 2 k m v kT 分子平均平动动能 2 2
容器内不同气体的温度相同分子的平均平动动能也相同即kknkk?????????????????21而分子数密度满足????inn故压强为??????????????????????????????????????????????ikiikikikpnnnnp????????32323232即容器中混合气体的压强等于在同样温度体积条件下组成混合气体的各成分单独存在时的分压强之和
例 利用理想气体的温度公式说明Dalton 分压定律。
解：容器内不同气体的温度相同，分子的平均平动动能也 相同，即
k1 k 2 kn k
而分子数密度满足
n ni
故压强为 2 2 2 2 P n k ni k ni k ni ki Pi 3 3 3 3 即容器中混合气体的压强等于在同样温度、体积条件下组成 混合气体的各成分单独存在时的分压强之和。这就是Dalton 分压定律。
分子的平均平动动能
F斥
F引 F引
r0
F合
r
F引
r0 平衡距离
F斥
（2）当r＜r0时，随r的减小，F引、F斥都增大，F斥比F引增 大得快，F斥＞F引，分子力表现为斥力，r减小，分子力增大
F
F斥
r＞r0
F斥
F引
F引
F斥
0
r0
F合
r
F引
(3)当r＞r0时，随r 的增加，F引、F斥都减小，F斥 比F引减小得快，F斥＜F引，分子力表现为引力
第四步： 计算N个分子给器壁的平均冲力：
mv m N 2 vx F Fi l x i 1 lx i i 1
该面所受压强
F 1 P S l x l y lz
N
2 x
Nm 1 ( mv V N i
N 2 ix
2 v ix ) nm v i
N
_____
2 x
定义分子速率平均值
v
则
v
i
i
N
；
定义分子速率平方的平均值
vx v y vz ； 2 v i 2
v
2 z
i
N
； v2
v v v ；
2 x 2 y 2 z
则
1 2 v v v v ； v x v y vz v 3
2 2 x 2 y
2
2
2
注意：统计规律有涨落 （fluctuation）， 统计对象的数量越大，涨落越小。
微观理论，从分子热运动观点出发，依赖微 观粒子的力学规律，运用统计方法研究气体 分子热运动的宏观性质和变化规律。寻求宏 观量与微观量之间的关系，揭示气体宏观热 现象及其规律的微观本质。
F引 F引
r0
F合
r
F引
r0 平衡距离
F斥
（2）当r＜r0时，随r的减小，F引、F斥都增大，F斥比F引增 大得快，F斥＞F引，分子力表现为斥力，r减小，分子力增大
F
F斥
r＞r0
F斥
F引
F引
F斥
0
r0
F合
r
F引
(3)当r＞r0时，随r 的增加，F引、F斥都减小，F斥 比F引减小得快，F斥＜F引，分子力表现为引力
第四步： 计算N个分子给器壁的平均冲力：
mv m N 2 vx F Fi l x i 1 lx i i 1
该面所受压强
F 1 P S l x l y lz
N
2 x
Nm 1 ( mv V N i
N 2 ix
2 v ix ) nm v i
N
_____
2 x
定义分子速率平均值
v
则
v
i
i
N
；
定义分子速率平方的平均值
vx v y vz ； 2 v i 2
v
2 z
i
N
； v2
v v v ；
2 x 2 y 2 z
则
1 2 v v v v ； v x v y vz v 3
2 2 x 2 y
2
2
2
注意：统计规律有涨落 （fluctuation）， 统计对象的数量越大，涨落越小。
微观理论，从分子热运动观点出发，依赖微 观粒子的力学规律，运用统计方法研究气体 分子热运动的宏观性质和变化规律。寻求宏 观量与微观量之间的关系，揭示气体宏观热 现象及其规律的微观本质。
分子的平均动能和平均平动动能
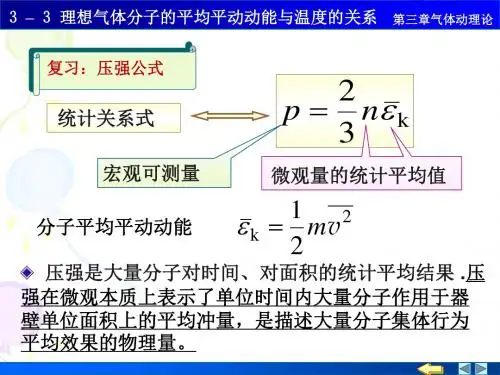
分子的平均动能和平均平动动能分子的平均动能和平均平动动能，听上去像是科学课上的难题，实际上却是我们生活中无处不在的小秘密。
想象一下，空气中那些看不见的小家伙，分子们正像在狂欢派对上，兴奋得乱舞呢。
每个分子都是小小的舞者，它们的动能就像是舞池里的热情，越多越好。
这种动能不是凭空而来的，而是温度的结果，温度越高，分子就越活跃，像是喝了咖啡的小伙伴，嗨得不得了。
我们先说说“平均动能”这回事。
分子们就像一群在操场上玩耍的小朋友，个个都有自己的速度。
有人慢悠悠，有人飞快。
这样一来，要想知道这些小家伙的平均水平，就得把它们的动能加起来，然后除以总数。
想象一下，算得不容易，有点像聚会后算账，喝了多少、吃了多少，最后还得分个清楚。
但是别担心，科学家们早就把这套公式搞定了，简单明了。
再来聊聊“平均平动动能”。
说白了，就是分子在特定方向上的运动能量。
好比你在马路上走路，走得快快的，偶尔停下来看看风景。
分子们也是，虽然它们总是转来转去，但我们关注的，是它们在某个方向上走的速度。
像是赛车，冲刺的时候速度很快，停下来的那一瞬间，动能就降到最低。
换句话说，分子在某个方向上的运动就是它们的平动，动能就是它们的实力。
要知道，温度不仅仅是数字，它是个大角色。
在炎热的夏天，分子的动能像火焰一样旺盛，碰撞得热火朝天，感觉连空气都在冒烟。
而在寒冷的冬天，分子的动能就像缩进了被窝里，懒洋洋的，基本上就是个“冬眠”的状态。
这些分子的表现，就决定了我们周围的温度和状态。
你可别小看这动能，有它在，冰水也能化开，空气也能流动，所有的变化都和这小小的动能息息相关。
想象一下，科学家们通过研究这些分子的动能，揭示了许多自然现象的奥秘。
比如说，水为什么会蒸发，冰为什么会融化，这些背后都藏着动能的秘密。
当分子们的动能达到了一定程度，它们就会开始挣脱束缚，水分子从液态变成气态，像是蝴蝶破茧而出。
科学家们用这些发现推动了许多技术的发展，比如空调、冰箱，甚至是航天科技。
理想气体分子的平均平动动能与温度的关系
大学物理
§12-4 理想气体分子的平均平动动能 与温度的关系
§12-4
理想气体分子的平均平动动能与温度的关系
一、气体温度和平均平动动能的关系
根据理想气体状态方程，可得：
PV vRT
2 P n nkT 3
2019年3月20日星期三
vRT vN A kT P nkT V V
3 kT 2
2019年3月20日星期三
理学院 物理系
2019年3月20日星期三
理学院 物理系
大学物理
§12-4
理想气体分子的平均平动动能与温度的关系来自三、气体分子的方均根速率
3 1 2 kT m v 2 2
3kT 3 RT v m
2
00C时气体分子的方均根速率 气体种类 方均根速率(m/s) O2 4.61×102 N2 4.93×102 H2 1.84×103 CO2 3.93×102 H2O 6.15×102
理学院 物理系
大学物理
§12-4
理想气体分子的平均平动动能与温度的关系
3 二、 2 kT
的物理意义
1.平均平动动能只与温度有关。 2.温度具有统计的意义，只能用于大量分子，对单个 分子谈温度是无意义的。 3.当两种气体具有相同的温度时，它们相应的平均平 动动能相等。 若使这两种气相接触,两种气体间将没有宏观的能量 传递,它们各自处于热平衡状态。即温度是表征气体 处于热平衡状态的物理量。这也就是热力学第零定 律的微观解释。
§12-4 理想气体分子的平均平动动能 与温度的关系
§12-4
理想气体分子的平均平动动能与温度的关系
一、气体温度和平均平动动能的关系
根据理想气体状态方程，可得：
PV vRT
2 P n nkT 3
2019年3月20日星期三
vRT vN A kT P nkT V V
3 kT 2
2019年3月20日星期三
理学院 物理系
2019年3月20日星期三
理学院 物理系
大学物理
§12-4
理想气体分子的平均平动动能与温度的关系来自三、气体分子的方均根速率
3 1 2 kT m v 2 2
3kT 3 RT v m
2
00C时气体分子的方均根速率 气体种类 方均根速率(m/s) O2 4.61×102 N2 4.93×102 H2 1.84×103 CO2 3.93×102 H2O 6.15×102
理学院 物理系
大学物理
§12-4
理想气体分子的平均平动动能与温度的关系
3 二、 2 kT
的物理意义
1.平均平动动能只与温度有关。 2.温度具有统计的意义，只能用于大量分子，对单个 分子谈温度是无意义的。 3.当两种气体具有相同的温度时，它们相应的平均平 动动能相等。 若使这两种气相接触,两种气体间将没有宏观的能量 传递,它们各自处于热平衡状态。即温度是表征气体 处于热平衡状态的物理量。这也就是热力学第零定 律的微观解释。
分子平均平动动能-精品
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
理想气体压强公式
p
2 3
n k
理想气体物态方程 p nkT
分子平均平动动能：
k
1mv2 2
3kT 2
微观量的统计平均 宏观可测量量
第十二章 气体动理论
1
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
温度 T 的物理意义
第十二章 气体动理论
4
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
2 理想气体体积为 V ，压强为 p ，温度为 T . 一个分子 的质量为 m ，k 为玻耳兹曼常 量，R 为摩尔气体常量，则该理想气体的分 子数为：
（A） pV m （B） pV(kT)
（C） pV(RT) （D） pV(mT)
k
1mv2 2
3kT 2
（1）温度是分子平均平动动能的量度.
k T
（2）温度是大量分子的集体表现.
（3）在同一温度下各种气体分子平均平 动动能均相等.
第十二章 气体动理论
2
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
注意
热运动与宏观运动的区别：温度所 反映的是分子的无规则运动，它和物体 的整体运动无关，物体的整体运动是其 所有分子的一种有规则运动的表现.
解 p nkT
N nV pV kT
第十二章 气体动理论
5
第十二章 气体动理论
3
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
讨论
1 一瓶氦气和一瓶氮气质量密度相同，分子 平均平动动能相同，且都处于平衡状态，则：
12-4 理想气体分子平均平动动能与温度的关系
第五版
理想气体压强公式
p
2 3
n k
理想气体物态方程 p nkT
分子平均平动动能：
k
1mv2 2
3kT 2
微观量的统计平均 宏观可测量量
第十二章 气体动理论
1
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
温度 T 的物理意义
第十二章 气体动理论
4
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
2 理想气体体积为 V ，压强为 p ，温度为 T . 一个分子 的质量为 m ，k 为玻耳兹曼常 量，R 为摩尔气体常量，则该理想气体的分 子数为：
（A） pV m （B） pV(kT)
（C） pV(RT) （D） pV(mT)
k
1mv2 2
3kT 2
（1）温度是分子平均平动动能的量度.
k T
（2）温度是大量分子的集体表现.
（3）在同一温度下各种气体分子平均平 动动能均相等.
第十二章 气体动理论
2
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
注意
热运动与宏观运动的区别：温度所 反映的是分子的无规则运动，它和物体 的整体运动无关，物体的整体运动是其 所有分子的一种有规则运动的表现.
解 p nkT
N nV pV kT
第十二章 气体动理论
5
第十二章 气体动理论
3
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
讨论
1 一瓶氦气和一瓶氮气质量密度相同，分子 平均平动动能相同，且都处于平衡状态，则：
7-3 理想气体分子的平均平动动能与温度的关系
t 2 0 C时气体分
0
3 3 23 kT1 1.38 10 1273 J 2 2 2.64 1020 J T2 273K 3 3 kT 2 1.38 10 23 273 J 2 2 5.65 1021 J
第7章 气体动理论
第7章 气体动理论
返回
7
南通大学
Nantong University
7-3 理想气体分子的平均平动动能与温度的关系
0
[例7-6] 试计算 0 C 时氧分子的方均根速率.
解 已知 T 273 K ，氧气的摩尔质量
M mol 32103 kg mol1
可求得
vrms 3RT 3 8.31 273 1 1 m s 461 ms 3 M mol 32 10
第7章 气体动理论
返回
8
南通大学
Nantong University
7-3 理想气体分子的平均平动动能与温度的关系
讨论
1 一瓶氦气和一瓶氮气密度相同，分子平均 平动动能相同，而且都处于平衡状态，则：
（A）温度相同、压强相同. （B）温度、压强都不同. （C）温度相同，氦气压强大于氮气压强. （D）温度相同，氦气压强小于氮气压强. N k 解 p nkT kT T V m
（C） pV ( RT ) 解 （D） pV (m T )
pV N nV kT
第7章 气体动理论
返回
10
p nkT
返回
5
南通大学
Nantong University
7-3 理想气体分子的平均平动动能与温度的关系
[例7-5] 在多高温度下，气体分子的平均平 动能等于一个电子伏特？ 解 电子伏特（eV）是一种能量单位，它指 的是，一个电子在电场中通过电位差为lv(伏 特 ) 的区间时，由于电场力做功所获得的能 量．
12-4理想气体分子的平均平动动能与温度的关系
1 2
m 1 v12
1 2
m2
v22
v12 m2
v22
m1
•当温度T=0时，气体的平均平动动能为零，这时气体
分子的热运动将停止。然而事实上是绝对零度是不可 到达的(热力学第三定律)，因而分子的运动是用不停 息的。
第十二章 气体动理论
3
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
注意
（A） pV m （B） pV (kT )
（C） pV (RT ) （D） pV (mT )
解 p nkT
N nV pV kT
第十二章 气体动理论
6
分子平均平动动能：
k
1 2
mv2
3 2
kT
微观量的统计平均 宏观可测量量
第十二章 气体动理论
1
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
温度 T 的物理意义
k
1 mv2 2
3 kT 2
(1)温度的微观本质：温度是分子平均平动动能的量度.
k T
(2)温度是大量分子的集体表现.单个分子的温度无意义。
大学物理124理想气体分子的平均平动动能与温度的关系理学院物理系2019323方均根速率ms气体种类第十二章气体动理论124理想气体分子平均平动动能与温度的关系物理学第五版a温度相同压强相同
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
理想气体压强公式
p
2 3
n k
理想气体物态方程 p nkT
(3)同一温度下各种气体分子平均平动动能均相等.
(4)温度的实质：分子热运动剧烈程度的宏观表现。
理想气体分子的平均平动动能与温度的关系
V
m
第十二章 气体动理论
4
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
2 理想气体体积为 V ，压强为 p ，温度为 T . 一个分子 的质量为 m ，k 为玻耳兹曼常 量，R 为摩尔气体常量，则该理想气体的分 子数为：
（A） pV m （B） pV (kT )
（C） pV (RT ) （D） pV (mT )
第十二章 气体动理论
3
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
讨论
1 一瓶氦气和一瓶氮气密度相同，分子平均 平动动能相同，而且都处于平衡状态，则：
（A）温度相同、压强相同.
（B）温度、压强都不同.
（C）温度相同，氦气压强大于氮气压强.
（D）温度相同，氦气压强小于氮气压强.
解 p nkT N kT k T
解 p nkT
N nV pV kT
第十二章 气体动理论
5
k
1 mv2 2
ห้องสมุดไป่ตู้
3 kT 2
（1）温度是分子平均平动动能的量度.
k T
（2）温度是大量分子的集体表现.
（3）在同一温度下各种气体分子平均平 动动能均相等.
第十二章 气体动理论
2
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
注意
热运动与宏观运动的区别：温度所 反映的是分子的无规则运动，它和物体 的整体运动无关，物体的整体运动是其 中所有分子的一种有规则运动的表现.
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
理想气体压强公式
分子平均平动动能：
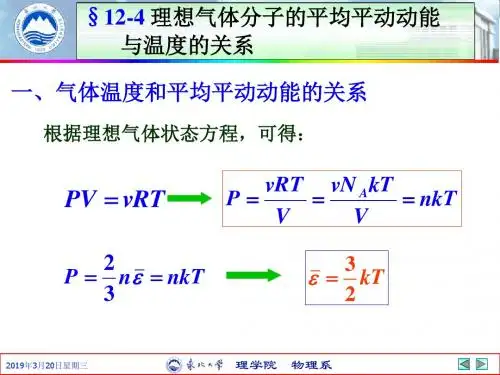
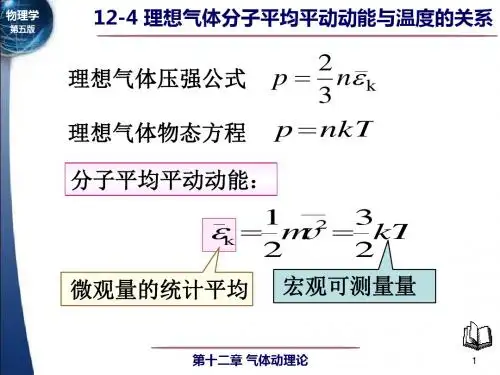
分子平均平动动能：分子平均平动动能是描述分子热运动的一种物理量，它揭示了分子在热运动过程中的平均运动情况。
在我们日常生活中，热能是无处不在的，分子的平动动能是构成热能的基本要素之一。
本文将从定义、计算方法以及一些实际应用等方面来详细介绍分子平均平动动能。
首先，我们来看一下分子平均平动动能的定义。
分子平均平动动能是指一个系统中所有分子平动动能的平均值。
根据动能的定义，分子平均平动动能可以用公式K_avg = (1/2) mv^2 来表示，其中m是分子的质量，v是其速度。
这个公式表明，分子的运动速度越大，分子的平动动能也就越大。
那么如何计算分子平均平动动能呢？我们需要用到统计物理学中的一些基本概念和理论。
首先，我们需要知道系统中分子的数目N和总的平动动能E，那么分子平均平动动能K_avg =E/N。
在理论计算中，可以采用玻尔兹曼分布定律来确定分子速度的分布概率，进而计算出分子平均平动动能。
实际上，分子平均平动动能不仅仅是一个理论概念，它在很多实际应用领域都有很大的作用。
首先，分子平均平动动能是理解物质的热性质和热传导的基础。
在热力学中，平动动能的增加意味着系统的温度升高，而热传导则是分子平均平动动能在不同物体之间的传递。
此外，分子平均平动动能还在研究化学反应动力学和速率论方面具有重要意义。
在化学反应中，分子发生碰撞并因此发生反应。
分子平均平动动能的高低会对化学反应的速率和动力学过程产生影响。
分子平均平动动能还与气体的压力有密切关系。
根据理想气体状态方程，P V = N k T，其中P是气体的压力，V是气体的体积，N是气体的分子数，k是玻尔兹曼常量，T是气体的温度。
由此可见，温度升高和分子平均平动动能的增加，会导致气体的压强增加。
最后需要注意的是，分子平均平动动能只是热能的一部分，还有分子的转动动能和振动动能等。
这些能量组成了分子的总动能。
而热能是分子或粒子的总动能的表现形式，它包括热力学性质（如温度、热容等）和能量传递机制的研究。
12-4理想气体分子的平均平动动能与温度的关系讲解
玻尔兹曼常数 k R 1.381023 J K1 NA
则 pV NkT 或 p nkT
温度的微观本质
p
nkT 与压强公式
P
2 3
n k
比较
得
k
1 2
v2
3 2
kT
处于平衡态的理想气体，分子的平均平 动动能与气体的温度成正比。
例1 计算标准状态下，任何气体在1cm3体积中 含有的分子数 。
1 2 3
若各种气体的分子数密度分别为 n1，n2，n3，…
则混合气体的分子数密度为
n=n1+n2+n3+…
将n代入 p 2n / 3 ，得
p
2 3
n
2 3
(n1
n2
n3
)
p
2 3
n11
2 3
n2 2
2 3
n3 3
即 p p1 p2 p3
—— 道尔顿分压定律。
其中
p1
2 3
n11,
p2
2 3
n2 2 ,
p3
2 3
n3 3 ,
例3 有一容积为 10 cm3 的电子管，当温度为
300 K时用真空泵抽成高真空，使管内压强为 5×10-6 mmHg。求 (1) 此时管内气体分子的
数目； (2) 这些分子的总平动动能。
解 (1) 由理想气体状态方程得
N
pV kT
5106 133.3105 1.381023 300
12.4 温度的微观本质
一、理想气体温度与分子平均平动动能的关系
理想气体分子的平均平动动能为
1 v2 1 3kT
2
2
3 kT
2
则 pV NkT 或 p nkT
温度的微观本质
p
nkT 与压强公式
P
2 3
n k
比较
得
k
1 2
v2
3 2
kT
处于平衡态的理想气体，分子的平均平 动动能与气体的温度成正比。
例1 计算标准状态下，任何气体在1cm3体积中 含有的分子数 。
1 2 3
若各种气体的分子数密度分别为 n1，n2，n3，…
则混合气体的分子数密度为
n=n1+n2+n3+…
将n代入 p 2n / 3 ，得
p
2 3
n
2 3
(n1
n2
n3
)
p
2 3
n11
2 3
n2 2
2 3
n3 3
即 p p1 p2 p3
—— 道尔顿分压定律。
其中
p1
2 3
n11,
p2
2 3
n2 2 ,
p3
2 3
n3 3 ,
例3 有一容积为 10 cm3 的电子管，当温度为
300 K时用真空泵抽成高真空，使管内压强为 5×10-6 mmHg。求 (1) 此时管内气体分子的
数目； (2) 这些分子的总平动动能。
解 (1) 由理想气体状态方程得
N
pV kT
5106 133.3105 1.381023 300
12.4 温度的微观本质
一、理想气体温度与分子平均平动动能的关系
理想气体分子的平均平动动能为
1 v2 1 3kT
2
2
3 kT
2
理想气体分子平均平动动能与温度的关系
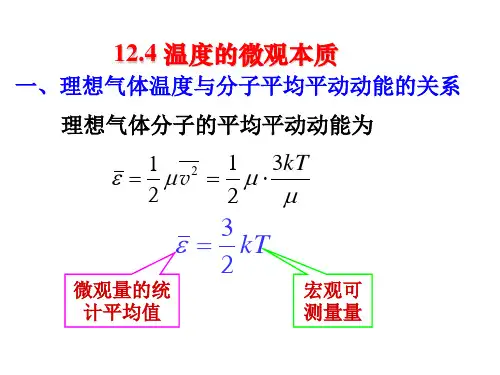
四、理想气体分子平均平动动能与温度的关系（可以用一个公式加以概括）k ε=kT v m 23212=1.简单推导：理想气体的物态方程：RT m N m N RT M m PV A ''== 而⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=2221322132v m V N v m n P n=N/V 为单位体积内的分子数，即分子数密度， k =R /N A =1.38×10-23J·K -1称为玻尔斯曼常量。
所以：kT v m 23212= 这就是理想气体分子的平均平动动能与温度的关系，是气体动理论的另一个基本公式。
它表明分子的平均平动动能与气体的温度成正比。
气体的温度越高，分子的平均平动动能越大；分子的平均平动动能越大，分子热运动的程度越剧烈。
因此，温度是表征大量分子热运动剧烈程度的宏观物理量，是大量分子热运动的集体表现。
对个别分子，说它有多少温度，是没有意义的。
从这个式子中我们可以看出2．温度的统计意义该公式把宏观量温度和微观量的统计平均值(分子的平均平动动能)联系起来，从而揭示了温度的微观本质。
关于温度的几点说明1．由kT v m 23212=得021 02=v m T ＝，＝ε，气体分子的热运动将停止。
然而事实上是绝对零度是不可到达的(热力学第三定律)，因而分子的运动是用不停息的。
2．气体分子的平均平动动能是非常小的。
J K T 2110,300-==ε J K T 15810 ,10-==ε例1． 一容器内贮有氧气，压强为P=1.013×105Pa ，温度t=27℃，求（1）单位体积内的分子数；（2）氧分子的质量；（3）分子的平均平动动能。
解：（1）有P=nkT得 ()3252351045.2273271038.110013.1--⨯=+⨯⨯⨯==m kT P n （2）kg N M m A 262331031.51002.61032--⨯=⨯⨯==（3）J kT k 21231021.6)27327(1038.12323--⨯=+⨯⨯⨯==ε例2． 利用理想气体的温度公式说明Dalton 分压定律。
分子的平均平动动能
微观理论，从分子热运动观点出发，依赖微 观粒子的力学规律，运用统计方法研究气体 分子热运动的宏观性质和变化规律。寻求宏 观量与微观量之间的关系，揭示气体宏观热 现象及其规律的微观本质。
第二章 气体动理论主要内容
• 气体的微观图像
• 理想气体的压强与温度
• 麦克斯韦速率分布律 • 能量按自由度均分定理
•实验表明，标态下，气体分子间的距离约为分子直径的10倍 •每个分子所占有的体积约为分子本身的体积的1000倍。 •因而气体分子可看成是大小可以忽略不计的质点。
18世纪中期，瓦特制成了蒸汽机，引发了第一次工业革命，蒸汽机 被广泛应用于纺织、火车、轮船、机械加工等行业。 随着蒸汽机在生产上被广泛地利用，提高效率便成为首要任务，因 为当时的热机效率只有5％～8％，改进蒸汽机，提高其热效率，就成为 许多科学家和工程师毕生追求的目标。 对提高热机效率的思考导致了1824年卡诺定理的产生。卡诺定理指 出了提高热机效率的方向，成为热机研究的理论依据。
2、分子的数密度和线度
•实验表明：任何物质1摩尔所含有的微观粒子——分子或原子的 数目均相等，为阿伏加德罗常数，用NA表示 计算中，一般取NA=6.02×1023mol-1
NA=6.022 136 7(36)×1023mol-1
分子数密度n：
单位体积内的分子数：n=N/V
分子的线度：
线度直观上说基本上就是大小的意思。线度一般指物体从各个方向来测量时 的最大的长（宽）度，并且往往只精确到数量级。
热学的研究方法：
1.宏观法 Macroscopic method 宏观理论，从能量观点出发，研究热现象的 宏观规律——称为热力学 Thermodynamics。
优点：具有高度的可靠性和普遍性。 缺点：未揭示微观本质，一些宏观现象（如 涨落）不能解释。
第二章 气体动理论主要内容
• 气体的微观图像
• 理想气体的压强与温度
• 麦克斯韦速率分布律 • 能量按自由度均分定理
•实验表明，标态下，气体分子间的距离约为分子直径的10倍 •每个分子所占有的体积约为分子本身的体积的1000倍。 •因而气体分子可看成是大小可以忽略不计的质点。
18世纪中期，瓦特制成了蒸汽机，引发了第一次工业革命，蒸汽机 被广泛应用于纺织、火车、轮船、机械加工等行业。 随着蒸汽机在生产上被广泛地利用，提高效率便成为首要任务，因 为当时的热机效率只有5％～8％，改进蒸汽机，提高其热效率，就成为 许多科学家和工程师毕生追求的目标。 对提高热机效率的思考导致了1824年卡诺定理的产生。卡诺定理指 出了提高热机效率的方向，成为热机研究的理论依据。
2、分子的数密度和线度
•实验表明：任何物质1摩尔所含有的微观粒子——分子或原子的 数目均相等，为阿伏加德罗常数，用NA表示 计算中，一般取NA=6.02×1023mol-1
NA=6.022 136 7(36)×1023mol-1
分子数密度n：
单位体积内的分子数：n=N/V
分子的线度：
线度直观上说基本上就是大小的意思。线度一般指物体从各个方向来测量时 的最大的长（宽）度，并且往往只精确到数量级。
热学的研究方法：
1.宏观法 Macroscopic method 宏观理论，从能量观点出发，研究热现象的 宏观规律——称为热力学 Thermodynamics。
优点：具有高度的可靠性和普遍性。 缺点：未揭示微观本质，一些宏观现象（如 涨落）不能解释。
分子的平均平动动能
分子的平均平动动能分子的平均平动动能是指分子在三维空间内做自由运动时，其平均动能的大小。
分子的平均平动动能与温度密切相关，当温度升高时，分子的平均平动动能也会增加。
下面将对分子的平均平动动能进行详细解释：一、分子平均平动动能的定义分子的平均平动动能是指在某个温度下，各个分子在空间中做自由运动时，其动能的平均值。
由于气体分子随机运动，因此各个分子的动能大小不同，但在一个温度下，所有分子的平均动能是相同的。
二、分子平均平动动能的计算公式分子的平均平动动能可以用下面的公式进行计算：E_k = 1/2 * m * v^2其中，E_k表示平均平动动能，m表示分子的质量，v表示分子的速度。
由此可见，分子的动能与其质量和速度有关，质量越大、速度越快的分子，其动能也就越大。
三、分子平均平动动能与温度的关系在同一体积的气体中，温度越高，分子的平均平动动能也就越大，因为分子的能量是由其速度和质量共同决定的，而温度提高会导致分子的速度增加。
根据分子的平均平动动能和温度的关系，可以得出一个公式：E_k = 3/2 * k_b * T其中，k_b表示玻尔兹曼常数，T表示温度。
这个公式说明，分子的平均平动动能与温度成正比，温度升高，分子的平均平动动能也会增加。
四、应用举例气温的测量：根据气体分子的平均平动动能与温度的关系，可以设计出一些测量气温的方法。
例如，可以测量气体分子的速度，从而计算出气体的温度。
材料科学：研究材料的热学性质时，需要考虑分子的平均平动动能，因为分子的动能会影响材料的热膨胀、热导率等性质。
总之，分子的平均平动动能是一个非常重要的物理量，对于研究和应用都具有重要意义。
分子的平均平动动能公式
分子的平均平动动能公式首先，我们需要了解一些基本概念和假设：1. 分子速度分布函数：它描述了理想气体中分子速度的分布情况。
一般来说，分子速度分布服从麦克斯韦-玻尔兹曼分布，表示为f(v) =4πv^2 * (m/(2πkT))^1.5 * e^(-mv^2/(2kT))，其中v是分子速度，m 是分子质量，k是玻尔兹曼常数，T是气体温度。
2. Maxwell-Boltzmann分布定律：根据这个定律，理想气体中分子的速度分布可以用麦克斯韦-玻尔兹曼分布函数来描述。
3. 分子平动动能的定义：根据动能定理，分子的平动动能E_kin等于分子的质量m乘以速度v的平方再除以2，即E_kin = 1/2 * m * v^2我们现在开始推导分子的平均平动动能公式：1.首先我们假设分子速度在其中一方向上的分布为麦克斯韦-玻尔兹曼分布。
2.为了计算平均平动动能，我们需要对分子速度的分布进行积分。
由于麦克斯韦-玻尔兹曼分布在速度的全部区间上都有定义，所以我们将积分区间确定为从0到无穷大。
3. 我们用E_kin表示分子平动动能的平均值，根据定义，有E_kin = ∫(1/2 * m * v^2 * f(v))dv。
根据麦克斯韦-玻尔兹曼分布函数的表达式，代入并进行积分运算，可以得到E_kin = (3/2) * kT。
4. 由于我们的假设是分子速度在其中一方向上的分布，而分子的运动是三维的，所以我们需要将结果乘以3，即E_total = (3/2) * 3 * kT = 3kT。
所以，分子的平均平动动能公式为E_total = 3kT，其中E_total是分子的总平动动能，k是玻尔兹曼常数，T是气体温度。
这个公式说明了分子平动动能与温度之间的线性关系，说明了当温度升高时，分子的平动动能也会增加。
此外，公式还表明了当温度接近绝对零度时，分子的平动动能接近零，符合经典平衡态的预期。
6-4 理想气体分子的平均平动动能与温度的关系
温度 T 的物理意义
k
1 2
mv2
3 2
kT
（1）温度是分子平均平动动能的量度.
k T
（2）温度是大量分子的集体表现.
（3）在同一温度下各种气体分子平均平 动动能均相等.
第六章 气体动理论
2
6-4 理想气体分子平均平动动能与温度的关系
注意
热运动与宏观运动的区别：温度所 反映的是分子的无规则运动，它和物体 的整体运动无关，物体的整体运动是其 中所有分子的一种有规则运动的表现.
第六章 气体动理论
3
6-4 理想气体分子平均平动动能与温度的关系
理想气体压强公式
p
2 3
n k
理想气体物态方程 p nkT
分子平均平动动能：
k
1 2
mv2
3 2
kT
微观量的统计平均 宏观可测量量
பைடு நூலகம்
方均根速率： v2 3kT m
第六章 气体动理论
3RT M
1
6-4 理想气体分子平均平动动能与温度的关系
高二物理竞赛理想气体的温度和分子平均平动动能课件
(1) 理想气体的内能只取决于分子运动的自由度 如质点被限制在平面或曲面上运动，则 i= 2；
试证：室温由 T1 升高到 T2，房间内气体的内能不变。
i
和热力
学温度T，或者说理想气体的内能只是温度T的单值函数， 如静止于地面的物体，相对于地面，它的机械能（包括动能和重力势能）等于零；
实验和理论证明，分子速率分布函数 f (v) 的具体形式依赖于系统的性质和宏观条件。
1、 理想气体的温度和分子平均平动动能
由
p
nkT
2 3
n t
t
3 2
kT
平均平动动能只与温度有关
理想气体温标或热力学温标
说明了温度的微观意义，即热力学温度是分子平均平动动 能的量度，气体的温度越高，分子的平均平动动能就越大； 分子的平均平动动能越大，分子热运动的程度越激烈。因 此， 可以说温度反映了物体内部分子无规运动的剧烈程度。
设总分子数N，其中速率分布在v ~ v+dv速率区间内的分
子数 dNv
速率分布函数
则
dNv = f (v) dv
N
速率 在v 附近的单位速率区间内的分子数占总分子数的百 分比。
用“概率”来解释
dNv
一个分子的速率在 v 附近 dv 区间内的概率
N
f (v)
一个分子的速率在 v 附近单位速率区间内的概率
单原子分子 经典励志短句(二)
不要志气高大，倒要俯就卑微的人。不要自以为聪明。
刚性双原子分子 刚性双多原子分子
与其当一辈子乌鸦，莫如当一次鹰。
k
3 kT 2
k
5 kT 2
k 3kT
理想气体的内能
气体的内能是指它的内动能，即它所包含的所有分子的动 能（相对于质心参考系）和分子间的相互作用势能的总和。
能量按自由度均分原理理想气体的内能
理想气体内能：所有分子的动能总和。
理想气体：
1.一个分子的能量为:
k
i kT 2
9
1.一个分子的能量为:
k
i 2
2. 1 mol气体分子的能量为:
kT E
i 2
N0kT
i 2
RT
3.M 千克气体的内能为：E M i RT i RT
单原子分子气体 E 3RT
M mol 2
2
对于一定量的理
2 刚性双原子分子气体
1 2
kT。
由此可知，分子有 i 个自由度，其平均动能就有i
份 kT/2 的能量。
分子平均总动能：
说明：
k
i kT 2
1）该定理是统计规律，只适用于大量分子组成的系统。
2）是由于大量分子无规则碰撞的结果。
由于分子的激烈碰撞（几亿次/秒），使平动动能 与转动动能不断转换，
平动动能
转动动能
使平动动能与转动动能达到相同，即每个自由度上也
1.单原子分子气体 例如：He、Ne、Ar。其模型可用一个质点来代替。
平动自由度 t 3 转动自由度 r 0
总自由度 i t r 3 0 3
2.双原子分子气体 例如：氢气（H2）、氧气（O2）等为双原子分子气 体。其模型可用两个刚性质点模型来代替。
平动自由度 t 3 转动自由度 r 2
同理：1 2
m
v
2 y
1 2
m
v
2 z
1 2
kT
在x 、y、z方向上均分 配了一份kT/2的能量，
2
将理想气体模型稍作修改，即将气体分为单原子分 子气体，双原子分子气体，多原子分子气体。这样， 气体分子除平动外，还有转动和分子内原子之间的振 动。考虑分子的能量时，要考虑分子各种运动的能量。
平均平动动能和平均动能的公式
平均平动动能和平均动能的公式
1.平均平动动能的定义与公式。
平均平动动能的计算公式为E_k=3/2某k某T，其中E_k为平均平动
动能、k为玻尔兹曼常数、T为温度。
这个公式的含义是，当温度恒定时，不同物体的分子或原子的平均平动动能是相等的。
这个公式也可以帮助我
们了解热量与动能之间的关系，即温度越高，分子的动能越大，物体的热
量也越大。
2.平均动能的定义与公式。
平均动能指的是物体所有粒子的运动动能平均值。
在物理学中，动能
指的是物体由于运动而具有的能量，它与物体的质量和速度有关。
物体的
运动状态可以由它的动能来衡量，其中平均动能是物体所有粒子动能的平
均值。
平均动能的计算公式为E_k=1/2某m某v^2，其中E_k为平均动能、
m为物体的质量、v为物体的速度。
在这个公式中，平均动能与物体的质
量和速度平方有关，速度越大、质量越大，平均动能也就越大。
在物理学中，这个公式被广泛应用于研究物体的动态性能和能量转换的过程。
总之，平均平动动能和平均动能是热力学和动力学领域中基础的物理
概念，它们可以帮助我们了解物体的运动状态和能量状况。
在实际应用中，这些概念被广泛运用于工程设计、物理实验和科学研究等各个领域中。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解 根据题给初始条件得氧气的物质的量为
n m / M P1V1 / RT1 4.41102 mol
查表知氧气的定压摩尔热容
Cp,m 29.44J mol-1 K-1
定体摩尔热容
CV ,m 21.12J mol-1 K-1
（1）等压过程中氧气（系统）吸热
QP pdV E nCp,m (T2 T1) 129.8J
S 2v0 N f (v)dv = N 0
即曲线下面积表示系统分子总数N
（2）从图中可知，在0到 v0 区间内， Nf (v) = av/v0 而在 v0 到 2v0 区间，Nf (v) = a 则利用归一化条件有
N v0 avdv + 2v0 adv
0 v0
v0
a = 2N / 3v0
v0 av3 dv + 0 Nv0
2v0 v0
av2 dv) N
=
31 36
mv02
18 目前实验室获得的极限真空约为1.33×10-11Pa， 这与距地球表面1.0×104km处的压强大致相等。试求在 27oC时单位体积中的分子数及分子的平均自由程。（设 气体分子的有效直径d=3.0×10-8cm）
解：由分析知 Z p ，当压强由 p0 降为 p0 / 2时
平均碰撞频率为
Z
Z0
p0 / 2 p0
Z0 / 2
又因1 / p ，故当压强减半时，平均自由程为
0
p0 / 2 p0
20
6-10 一压强为1.010 5pa，体积为1.010－3m3的 氧气自0℃加热到100℃，问：（1）当压强不变时， 需要多少热量？当体积不变时，需要多少热量？（2） 在等压或等体过程中各作了多少功？
式中符号表示系统向外放热252J
6-16 如图所示，使1mol氧气（1）由A等温 地变到B；（2）由A等体地变到C，再由C等压地 变到B. 试分别计算氧气所作的功和吸收的热量.
解 （1）沿AB作等温膨胀的过程中，系统作功
WAB
m M
RT
ln(VB ) VA
PAVA
ln(VB VA
)
2.77 103 J
可知在等温过程中，氧气吸收的热量为
QAB WAB 2.77 103 J
（2）沿A到C再到B的过程中系统做功和吸热分别为
WACB WAC WCB WCB PC (VB VC ) 2.0 103 J
QACB WACB 2.0 103 J
P(105Pa) A
13.18 马文蔚（5版）P257
C
B
V（10-3m3）
2
解：（2）由A到C为等体过程，则：
QAC=μCV(TC-TA)=μ·5/2·（PCVC-PAVA） =2.5×（1×1×2-2×1×2）×103 = -5000J
WAC=0 由C到B为等压过程，有
QCB= μCP(TB-TC)=μ·7/2·（PBV-BPCVC） =……=7000J
（3）速率在 v0 / 2 到 3v0 / 2 间隔内的分子数为
N
v0
avdv +
3v0
/2
adv
=
7N
/
12
v v0 / 2 0
v0
（4）分子速率平方的平均值按定义为
v2
N v2dN
0
v2 f (v)dv
N
0
故分子的平均平动动能为
k
1 mv2 2
1 m( 2
14 有N个质量均为m的同种气体分子，它们的速率 分布如图所示. （1）说明曲线与横坐标所包围面积的
含义（2）由N和 v0求a值；（3）求在速率v0 / 2 到v0 / 3
间隔内的分子数；（4）求分子的平均平动动能.
解（1）由于分子所允许的速率在0到 2v0 的范围内， 由归一化条件可知图中曲线下的面积
WBC=0 由C到D为等压过程，有
QCD= μCP(TD-TC)=μ·7/2·（PDVD-PCVC）
QDA=μCV(TD-TA)=250J WDA=0 由A到B为等压过程，有
QAB= μCP(TB-TA)=700J WAB=P（VB-VA）=200J
=……= -350J
WCD=P（VD-VC）=……=-100J
解 系统经ABC过程所吸收的热量及对外所作的功分别为
QABC 326J
WABC 126J
则由热力学第一定律可得由A到C过程中系统内能的增量
EAC QABC WABC 200J
由此可得从C到A系统内能的增量为
ECA 200J
从C到A，系统所吸收的热量为
QCA ECA WCA 252J
WCB=P（VB-VC）=……=2000J
或者：
由热力学第二定律： QACB=WACB+△EACB=2000J
P(105Pa)
A
B
D
C
1
2
解：由B到C为等体过程，则：
V（10-3m3） 同理，由D到A为等体过程，则：
QBC=μCV(TC-TB)=μ·5/2·（PCVC-PBVB） =2.5×（2×1-2×2）×102 = -500J
6-19 0.32kg的氧气作图中所示循环ABCDA，设V2=2V1， T1=300K，T2=200K，求循环效率. （已知氧气的定体摩 尔热容的实验值Cv, m=21.1 J·mol－1·K－1）
解：由理想气体物态方程 p nkT 得分子数密度为
n p / kT 3.21109 m3
分子的平均自由程为 kT 7.8 108 m
2 πd2p
可见分子间几乎不发生碰撞
20 如果理想气体的温度保持不变，当压强降 为原值的一半，分子的平均碰撞频率和平均自由 程如何变化？
等体过程中氧气（系统）吸热
QV E nCV ,m (T2 T1) 93.1J
m
dW PdV RdT
（2）在等压过程中 m T2
M
W dW RdT 36.6J M T1
而在等体过程中，因气体的体积不变，故做功为
WV p(V )dV 0
6-11 如图所示，系统从状态A沿ABC变化到状态C 的过程中，外界有326J的热量传递给系统，同时系统 对外作功126J. 如果系统从状态C沿另一曲线CA回到 状态A，外界对系统作功为52J，则此过程中系统是吸 热还是放热？传递热量是多少？
n m / M P1V1 / RT1 4.41102 mol
查表知氧气的定压摩尔热容
Cp,m 29.44J mol-1 K-1
定体摩尔热容
CV ,m 21.12J mol-1 K-1
（1）等压过程中氧气（系统）吸热
QP pdV E nCp,m (T2 T1) 129.8J
S 2v0 N f (v)dv = N 0
即曲线下面积表示系统分子总数N
（2）从图中可知，在0到 v0 区间内， Nf (v) = av/v0 而在 v0 到 2v0 区间，Nf (v) = a 则利用归一化条件有
N v0 avdv + 2v0 adv
0 v0
v0
a = 2N / 3v0
v0 av3 dv + 0 Nv0
2v0 v0
av2 dv) N
=
31 36
mv02
18 目前实验室获得的极限真空约为1.33×10-11Pa， 这与距地球表面1.0×104km处的压强大致相等。试求在 27oC时单位体积中的分子数及分子的平均自由程。（设 气体分子的有效直径d=3.0×10-8cm）
解：由分析知 Z p ，当压强由 p0 降为 p0 / 2时
平均碰撞频率为
Z
Z0
p0 / 2 p0
Z0 / 2
又因1 / p ，故当压强减半时，平均自由程为
0
p0 / 2 p0
20
6-10 一压强为1.010 5pa，体积为1.010－3m3的 氧气自0℃加热到100℃，问：（1）当压强不变时， 需要多少热量？当体积不变时，需要多少热量？（2） 在等压或等体过程中各作了多少功？
式中符号表示系统向外放热252J
6-16 如图所示，使1mol氧气（1）由A等温 地变到B；（2）由A等体地变到C，再由C等压地 变到B. 试分别计算氧气所作的功和吸收的热量.
解 （1）沿AB作等温膨胀的过程中，系统作功
WAB
m M
RT
ln(VB ) VA
PAVA
ln(VB VA
)
2.77 103 J
可知在等温过程中，氧气吸收的热量为
QAB WAB 2.77 103 J
（2）沿A到C再到B的过程中系统做功和吸热分别为
WACB WAC WCB WCB PC (VB VC ) 2.0 103 J
QACB WACB 2.0 103 J
P(105Pa) A
13.18 马文蔚（5版）P257
C
B
V（10-3m3）
2
解：（2）由A到C为等体过程，则：
QAC=μCV(TC-TA)=μ·5/2·（PCVC-PAVA） =2.5×（1×1×2-2×1×2）×103 = -5000J
WAC=0 由C到B为等压过程，有
QCB= μCP(TB-TC)=μ·7/2·（PBV-BPCVC） =……=7000J
（3）速率在 v0 / 2 到 3v0 / 2 间隔内的分子数为
N
v0
avdv +
3v0
/2
adv
=
7N
/
12
v v0 / 2 0
v0
（4）分子速率平方的平均值按定义为
v2
N v2dN
0
v2 f (v)dv
N
0
故分子的平均平动动能为
k
1 mv2 2
1 m( 2
14 有N个质量均为m的同种气体分子，它们的速率 分布如图所示. （1）说明曲线与横坐标所包围面积的
含义（2）由N和 v0求a值；（3）求在速率v0 / 2 到v0 / 3
间隔内的分子数；（4）求分子的平均平动动能.
解（1）由于分子所允许的速率在0到 2v0 的范围内， 由归一化条件可知图中曲线下的面积
WBC=0 由C到D为等压过程，有
QCD= μCP(TD-TC)=μ·7/2·（PDVD-PCVC）
QDA=μCV(TD-TA)=250J WDA=0 由A到B为等压过程，有
QAB= μCP(TB-TA)=700J WAB=P（VB-VA）=200J
=……= -350J
WCD=P（VD-VC）=……=-100J
解 系统经ABC过程所吸收的热量及对外所作的功分别为
QABC 326J
WABC 126J
则由热力学第一定律可得由A到C过程中系统内能的增量
EAC QABC WABC 200J
由此可得从C到A系统内能的增量为
ECA 200J
从C到A，系统所吸收的热量为
QCA ECA WCA 252J
WCB=P（VB-VC）=……=2000J
或者：
由热力学第二定律： QACB=WACB+△EACB=2000J
P(105Pa)
A
B
D
C
1
2
解：由B到C为等体过程，则：
V（10-3m3） 同理，由D到A为等体过程，则：
QBC=μCV(TC-TB)=μ·5/2·（PCVC-PBVB） =2.5×（2×1-2×2）×102 = -500J
6-19 0.32kg的氧气作图中所示循环ABCDA，设V2=2V1， T1=300K，T2=200K，求循环效率. （已知氧气的定体摩 尔热容的实验值Cv, m=21.1 J·mol－1·K－1）
解：由理想气体物态方程 p nkT 得分子数密度为
n p / kT 3.21109 m3
分子的平均自由程为 kT 7.8 108 m
2 πd2p
可见分子间几乎不发生碰撞
20 如果理想气体的温度保持不变，当压强降 为原值的一半，分子的平均碰撞频率和平均自由 程如何变化？
等体过程中氧气（系统）吸热
QV E nCV ,m (T2 T1) 93.1J
m
dW PdV RdT
（2）在等压过程中 m T2
M
W dW RdT 36.6J M T1
而在等体过程中，因气体的体积不变，故做功为
WV p(V )dV 0
6-11 如图所示，系统从状态A沿ABC变化到状态C 的过程中，外界有326J的热量传递给系统，同时系统 对外作功126J. 如果系统从状态C沿另一曲线CA回到 状态A，外界对系统作功为52J，则此过程中系统是吸 热还是放热？传递热量是多少？