最新电阻的串并联等效变换

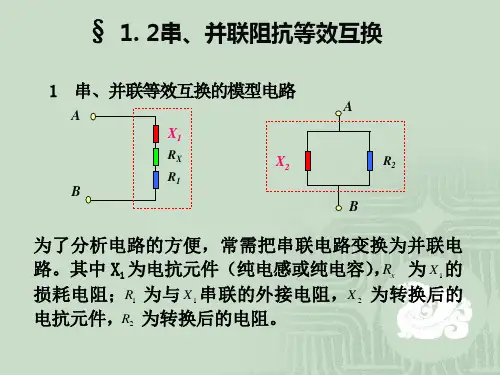
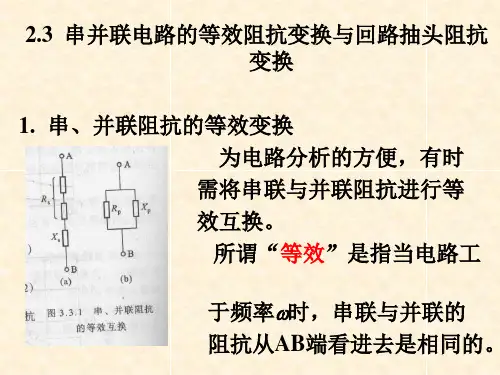
串并联转换公式1首先，我们需要明确一下串并联转换公式是什么。

串并联转换是电路中常见的一种转换方式，用于简化复杂电路的分析和计算。

在电路中，元件的串联意味着它们依次连接在一起，电流从一个元件流向另一个元件。

而元件的并联则意味着它们共享相同的电压，电流在各个元件之间分流。

下面，我们将介绍串并联转换公式1，该公式用于计算电阻在串并联转换下的等效值。

假设有两个电阻R1和R2，它们分别与电源相连。

当R1和R2串联连接时，它们的等效电阻为Req。

当R1和R2并联连接时，它们的等效电阻为Rpar。

串并联转换公式1如下：1/Req = 1/R1 + 1/R2Rpar = R1 * R2 / (R1 + R2)在上述公式中，Req代表串联连接下的等效电阻，Rpar代表并联连接下的等效电阻。

通过使用这个公式，我们可以根据给定的电阻值计算串并联连接下的等效电阻。

这在电路分析和设计中非常有用，因为可以简化复杂电路的计算。

接下来，让我们来看一个实际的例子，以更好地理解和应用串并联转换公式1。

假设有一个电路，其中有三个电阻R1、R2和R3，如图所示：```--- R1 --| |V1 R2| |--- R3 --```我们的目标是计算这三个电阻的等效电阻。

首先，我们将R1和R2并联，得到R12：R12 = R1 * R2 / (R1 + R2)然后，将R12和R3串联，得到Req：1/Req = 1/R12 + 1/R3求解上述方程，即可得到Req的值。

通过这种方式，我们可以使用串并联转换公式1来计算更复杂电路的等效电阻。

在实际应用中，除了电阻，电容和电感等元件也存在串并联转换公式。

不同的元件有不同的转换公式，但基本的原理和思想是相似的。

总结一下，串并联转换公式1是用于计算电路中电阻在串并联转换下的等效值的公式。

它在电路分析和设计中起到了重要的作用，可以简化复杂电路的计算。

希望本文对你有所帮助，理解串并联转换公式1的原理和应用。

电阻的串联和并联等效变换1.电阻串联(1)电流：各电阻顺序连接，流过同一电流(2)电压：总电压等于各串联电阻的电压之代数和nk u u u u +⋅⋅⋅++⋅⋅⋅+=1+_R 1R n +_u k i+_u 1+_u n uR k R 2+_u 2i 1i 2由欧姆定律串联电路的总电阻等于各分电阻之和iR R i R i R i R u n n k )(11++=++++= ∑==++++==nk k n k R R R R i uR 11 eq R eq i +_u(3)等效电阻等效nku u u u +⋅⋅⋅++⋅⋅⋅+=1+_R 1R n +_u k i+_u 1+_u n u R kR 2+_u 2kR >(4)电压分配i R u k k =分压公式电压与电阻成正比21eq2eq121R R u R R uR R u u ==R eq i +_u等效u u R R R uR k k <==eqeq +_R 1R n +_u k i+_u 1+_u n u R kR 2+_u 2(5)功率eq eq eq p p R R i R p k k k <==2各电阻消耗的功率与电阻大小成正比2121R R p p =总功率等于各串联电阻消耗功率的和()n n k PP i R R R i R p ++=++++== 1212eq eq R eqi +_u等效+_R 1R n +_u ki +_u 1+_u nu R k R 2+_u 22.电阻并联(1)电压：各电阻两端为同一电压(2)电流：总电流等于各并联电阻的电流之代数和nk i i i i +⋅⋅⋅++⋅⋅⋅+=1i i nR 1R kR n+u i 1i k _R 2i 2并联电路的等效电导等于并联的各电导之和等效R eqi +_u(3)等效电阻∑==+++==nk k n G G G G u iG 121 eq )(11n n G G G u uG uG uG i +⋅⋅⋅++=+⋅⋅⋅++=22kR G R <=eqeq 1nk i i i i +⋅⋅⋅++⋅⋅⋅+=1i i n R 1R kR n+u i 1i k _R 2i 2kG >(4)电流分配电流与电导成正比eqeq G G R u R u i i kk k ==//i G G i kk eq=分流公式21eq2eq 121G G i G G iG G i i ==等效R eqi +_ui i n R 1R kR n+u i 1i k _R 2i 2(5)功率eqeq eqp p G G u G p k k k <==2各电阻消耗的功率与电阻大小成反比122121R R G G p p ==总功率等于各并联电阻消耗功率的和()n n k PP u G G G u G p ++=++++== 1212eq eq 等效R eqi +_uii n R 1R kR n+u i 1i k _R 2i 2有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）3.电阻的串并联电路中有电阻的串联，又有电阻的并联，这种连接方式称电阻的串并联。

第二章-电阻电路的等效变第二章 电阻电路的等效变换2.1 学习要点1. 电阻的等效变换：电阻的串并联， Y 与△的等效变换。

2. 电源的串联、并联及等效变换。

3. “实际电源”的等效变换。

4. 输入电阻的求法。

2.2 内容提要 2.2.1 电阻的等效变换1. 电阻的串联：等效电阻： R eq ＝∑1=k nk R ；分压公式：u k ＝eqkeq ×R R u ； 2. 电阻的并联：等效电导：G eq ＝∑1=k nk G ；分流公式：qe G G i i keqk ×=；2.2.2. 电阻的Y 与△的等效变换1. △→Y ：一般公式：Y 形电阻＝形电阻之和形相邻电阻的乘积∆∆；即31232331*********231231212311++=++=++R R R R R R R R R R R R R R R R R R 2312＝2. Y →△：一般公式：形不相邻电阻形电阻两两乘积之和形电阻＝Y Y ∆；即：213322131113322123313322112++=++=++=R R R R R R R RR R R R R R R R R R R R R R R R2.2.3 电源的串联、并联等效变换 电源的串联、并联等效变换见表2.1。

表2.1 电源的串联、并联等效变换图2.2.4 “实际电源”的等效变换 1. “实际电压源”→“实际电流源” R i ＝R u 或 G i ＝1/R u i s ＝u s /R u 2. “实际电流源”→“实际电压源”R u ＝R i ＝1/G i u s ＝i s R i ＝i s /G i两者等效互换的原则是保持其端口的V AR 不变。

2.2.5 输入电阻的求法一端口无源网络输入电阻的定义（见图2.2）：R in ＝u/ i1. 当一端口无源网络由纯电阻构成时，可用电阻的 串并联、Y 形与△形等效变换化简求得。

2. 当一端口无源网络内含有受控源时，可采用外加电压法或外加电流法求得： 即输入电阻R in ＝u s /i 或 R in ＝u/ i s方法是：在端口处加一电压源u s （或电流源i s ）, 再求比值u s /i 或u/ i s ，该比值即是一端口无源网络的输入电阻。

电阻的等效变换1并联的等效电导等于各支路电导之和。

2线路合并即求等效电阻方法。

（1）线路间无电器元件时，等电位可以合并。

（2）对称电路可以等电位。

3星型与三角形的转换：星型电阻等于相邻电阻的乘积除以三个电阻的和，三角形电导等于相邻电导的乘积除以三个电导的和。

4只有相同的电压源才可以并联，同理只有相同的电流源才可以串联。

5一个好的电压源内阻趋向于0，一个好的电流源并联的内阻趋向于无穷大。

6电压源与电流源可以等效转换，其实就是戴维南定理和诺顿定理的转换。

7输入电阻的求法：（1）纯电阻可以用星型与三角形变换。

（2）含有受控源的电路可以用外加电源法。

例如加压求流或者加流求压。

这可以为以后戴维南定理打下基础。

8注意在求等效电阻的时候，第一步电源置零，第二步看是否有受控源，若无则采用合并等等效变换，若有则采用外加电源法求解。

电阻电路的基本分析1基本回路又称为单连支回路，且网孔数就是单连支回路数，所以网孔是基本回路。

连支数是与树有关系的，树是指所有节点都要包含且没有闭合回路。

连支数=节点数-12KCL与KVL方程的数目：KCL列式比节点数少一个，因为选一个为参考点。

KVL列式直接就是网孔数。

3支路电流法，就是KCL和KVL方程法，之所以用电流二不用电压，那是因为电压表示电流要复杂一点点，注意特殊情况，比如理想电流源和含有受控电源，正常列式最后再加上增补方程即可。

4网孔电流法：最本质还是KVL方程，首先以网孔电流为标准，由自电阻，互电阻列式，右侧为电压。

5回路电流法：本质上就是网孔电流法，只是这个网孔可以任意选择罢了，对于理想电流源的处理有两种方法，至于受控电源的处理，先将它们看做独立源，然后在对控制量列些增补方程即可。

6节点电压法：以节点电压为为变量，列KCL方程，自电导为正，互电导是负的，注意电源的转换，还有理想电压源的处理，可以加电流，在增补一个已知量方程，或者节点的选取以减少方程的数量。

同样受控源按照独立源处理，再加上控制量增补方程即可。