电力系统经济学原理第三章
- 格式:ppt
- 大小:912.50 KB
- 文档页数:44


电力系统经济学原理课后习题及答案第二章 经济学基础 2-1 解:1) 边际生产成本表达式:()502000dc q q dq=+ 2)按边际成本出售产品时,收入: 2()502000dc q q q q dq⨯=+ 利润=收入-成本222502000(252000)25q q q q q =+-+= 2-2 解:1)根据反需求函数:102000q π=-+,画出反需求函数曲线:当价格为零时,最大消费需求:max 200q =。
2)根据1)所示的反需求函数曲线,最高购买价格:max 2000π= 美元/件3)由1)的反需求函数曲线可知最大消费者剩余即为反需求函数曲线、价格坐标轴、数量坐标所围三角形的面积。
最大消费者剩余:120002002000002⨯⨯=美元但是生产者生产了产品,不可能什么都不卖,因此该最大消费者剩余不可能实现。
4)当价格π=1000美元/单位产量反需求函数曲线如下: 消费量:200010010q π-==总消费者剩余:1(10002000)1001500002⨯+⨯=美元 生产者收入:1000100100000q π=⨯=美元净消费者剩余:净消费者剩余=总消费者剩余-生产者收入 =15000010000050000-=美元 5)如果价格增加20%,则1000(120%)1200π=⨯+=美元/单位产量, 消费量:20008010q π-== 生产者收入:12008096000q π=⨯=美元 6)当1000π=美元/单位产量时,100q =需求价格弹性:110()110dqdq q d q d πεπππ===⨯-=- 7)如下图所示以需求为变量的反需求函数曲线:知总消费者剩余为一梯形,所以 总消费者剩余为:211111111(2000)(104000)5200022q q q q q π+⋅=-+⋅=-+ 总消费者剩余函数为:252000q q -+ 净消费者剩余为一三角形,所以净消费者剩余为:21111111(2000)(2000102000)522q q q q π-⋅=+-⋅= 净消费者剩余函数为:25q 以4)中当需求为100q =时检验,总消费者剩余:225200051002000100150000q q -+=-⨯+⨯=美元 净消费者剩余:225510050000q =⨯=美元 结果一样。

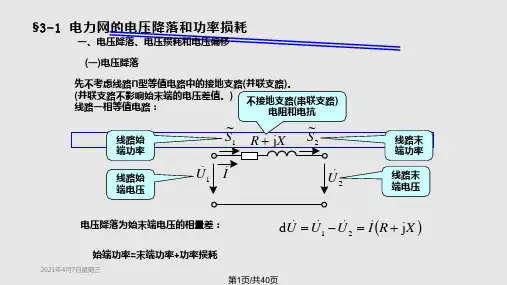
3 简单电力系统潮流计算3.1 思考题、习题1)电力线路阻抗中的功率损耗表达式是什么?电力线路始、末端的电容功率表达式是什么?上述表达式均是以单相形式推导的,是否适合于三相形式?为什么?2)电力线路阻抗中电压降落的纵分量和横分量的表达式是什么?其电压降落的计算公式是以相电压推导的,是否适合于线电压?为什么?3)什么叫电压降落、电压损耗、电压偏移、电压调整及输电效率?4)什么叫运算功率?什么叫运算负荷?一个变电所的运算负荷如何计算?5)对简单开式网络、变电所较多的开式网络和环形网络潮流计算的内容及步骤是什么?6)变压器在额定状况下,其功率损耗的简单表达式是什么?7)求环形网络中功率分布的力矩法计算公式是什么?用力矩法求出的功率分布是否考虑了网络中的功率损耗和电压降落?8)力矩法计算公式在什么情况下可以简化?如何简化?9)为什么要对电力网络的潮流进行调整控制?调整控制潮流的手段主要有哪些?10)欲改变电力网络的有功功率和无功功率分布,分别需要调整网络的什么参数?11)超高压远距离交流输电的作用和特点分别是什么?12)什么是传播常数、衰减常数、相位常数、波阻抗、波长、相位速度?13)什么是自然功率?当远距离交流输电线路输送自然功率时,会有什么有趣的现象?14)何为半波长电力线路、全波长电力线路?半波长电力线路的运行会有什么缺点?15)怎样提高远距离交流输电线路的功率极限,改善其运行特性?原理是什么?16)110kV双回架空线路,长度为150kM,导线型号为LGJ-120,导线计算外径为15。
2mm,三相导线几何平均距离为5m.已知电力线路末端负荷为30+j15MVA,末端电压为106kV,求始端电压、功率,并作出电压向量图。
17)220kV单回架空线路,长度为200kM,导线型号为LGJ—300,导线计算外径为24.2mm,三相导线几何平均距离为7。
5m。
已知电力线路始端输入功率为120+j50MVA,始端电压为240kV,求末端电压、功率,并作出电压向量图。


第三节 电力系统的经济调度与自动调频1)经济调度控制(EDC )的任务是使电力系统运行具有良好的经济性 2)有人称EDC 为三次经济调整。
一、等微增率分配负荷的基本概念 1)微增率定义输入耗量微增率与输出功率微增率的比值。
PF b ∆∆=(a ) 锅炉耗量特性 (d )锅炉耗量微增率 (b ) 汽轮机耗量特性 (e )汽轮机耗量微增率 (c ) 发电机耗量特性 (f )发电机耗量微增率由于汽轮机的微增率变化不大和发电机的效率接近1,所以整个机组的耗量特性和微增率可以认为如图3-15(a )和图3-15(d )的形状。
耗量微增率随输出功率的增加而增大。
2)等微增率法则运行的发电机组按微增率相等的原则来分配负荷,这样就可使系统总的燃料消耗(或费用)为最小,从而是最经济的。
两台机组并联运行为例:机组1为P 1,微增率为b 1机组2为P 1,微增率为b 2 且b 1>b 2 总的负荷不变的前提下调整一下负荷分配:机组1的功率减小P ∆,即功率变为'1P ,微增率减小到'1b ,减小的燃料消耗P 1、1b 、1b '、1P '所围的面积)(b )(a )(c )(d )(e )(f FP FP FPbPbP bP oooooo图3-15 三种典型的耗量特性及其微增率曲线机组2增加相同的P ∆,其功率变为'2P ,微增率增至'2b ,增加的燃料消耗P 2、2b 、、'2b '2P 所围的面积两个面积的差即为减少的燃料消耗 3)等微增率准则数学证明设有n 台机组,每台机组承担的负荷为P 1,P 2,…,P n ,对应的燃料消耗为F 1,F 2,…,F n ,则总的燃料消耗为∑=-n i i F F 1(3-29)而总负荷功率P L 为∑==n i i L p P 1(3-30)现在要使发电机组总的输出在满足负荷的条件下,总的燃料消耗为最小,即使F F min =。

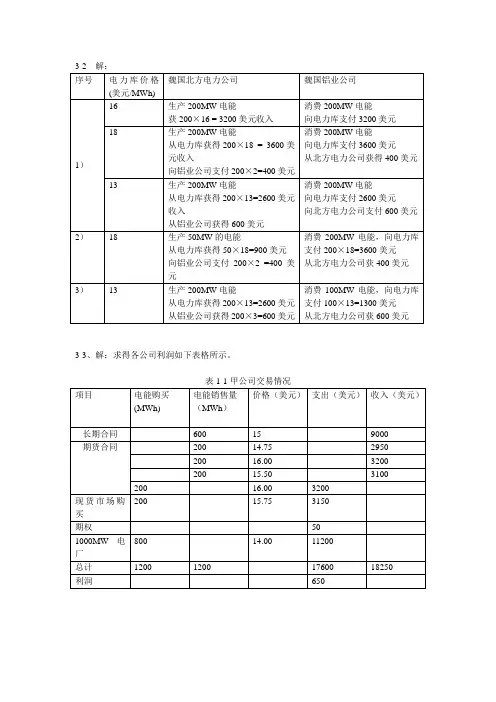
3-2 解:序号电力库价格(美元/MWh)魏国北方电力公司魏国铝业公司1)16 生产200MW电能获200×16 = 3200美元收入消费200MW电能向电力库支付3200美元18 生产200MW电能从电力库获得200×18 = 3600美元收入向铝业公司支付200×2=400美元消费200MW电能向电力库支付3600美元从北方电力公司获得400美元13 生产200MW电能从电力库获得200×13=2600美元收入从铝业公司获得600美元消费200MW电能向电力库支付2600美元向北方电力公司支付600美元2)18 生产50MW的电能从电力库获得50×18=900美元向铝业公司支付200×2 =400美元消费200MW电能,向电力库支付200×18=3600美元从北方电力公司获400美元3)13 生产200MW电能从电力库获得200×13=2600美元从铝业公司获得200×3=600美元消费100MW电能,向电力库支付100×13=1300美元从北方电力公司获600美元3-3、解:求得各公司利润如下表格所示。
表1-1甲公司交易情况项目电能购买(MWh) 电能销售量(MWh)价格(美元)支出(美元)收入(美元)长期合同600 15 9000 期货合同200 14.75 2950200 16.00 3200200 15.50 3100 200 16.00 3200现货市场购买200 15.75 3150期权501000MW电厂800 14.00 11200总计1200 1200 17600 18250 利润650项目电能购买(MWh) 电能销售量(MWh)价格(美元)支出(美元)收入(美元)长期合同500 16.00 8000 期货合同250 15.75 3937.5 现货市场购买20 15.75 315 800MW电厂770 14.25 10972.5 总计770 770 10972.5 12252.5 利润1280表1-3丙公司交易情况项目电能购买(MWh)电能销售量(MWh)价格(美元)支出(美元)收入(美元)长期合同700 15.50 10850期货合同250 15.75 3937.5300 15.00 450050 15.50 775 现货市场购买50 15.75 787.5电力需求1250 16.50 20625 总计1300 1300 20075 21400 利润1325表1-4丁公司交易情况项目电能购买(MWh)电能销售量(MWh)价格(美元)支出(美元)收入(美元)长期合同550 16.25 8937.5期货合同200 15.00 3000200 14.75 295050 14.50 725100 14.00 1400 期权100 15.50 1550+25现货市场150 15.75 2362.5 电力需求850 16.40 13940 总计1100 1100 17187.5 17702.5 利润515项目 电能购买(MWh )电能销售量(MWh )价格(美元) 支出(美元) 收入(美元)期货合同50 14.50 725 100 15.00 1500 100 15.25 1525 50 14.25 712.5100 17.00 1700 总计 200 200 2937.5 3225 利润287.5表1-6戊公司交易情况项目 电能购买(MWh )电能销售量(MWh )价格(美元) 支出(美元) 收入(美元)期货合同100 14.50 1475 50 15.00 750 200 14.5 2900 25014.00 3500 总计 300 300 4250 4375 利润1253-4解:表1-7 400MW 、600MW 、875MW 的供应曲线(2)表1-8 400MW 、600MW 、875MW 的负荷针对市场价格、各公司情况负荷预测(MW ) 需求(M W ) 价格(美元/MWh ) 甲生产量(MWh) 甲收入(美元) 乙生产量(MWh) 乙收入(美元) 丙生产量(MWh) 丙收入(美元) 400 400 13.00 100 1300 0 0 300 3900 600 600 14.00 150 2100 50 700 400 5600 87587518.00225405015027005009000(3)解:当负荷需求的关系式为:D = L -4.0π当L = 400时,由表7-1读出价格π = 13,计算出D = 346,该价格与需求符合表7-1中的对应关系;当L = 600时,读出π = 14,计算出D = 544,而供应曲线中需求为544对应的价格为13.5,再计算此价格π = 13.5下对应的需求D=546,此时的价格与需求符合表7-1中的对应关系;当L=875时,情况与L=600类似,计算出需求D=813,价格π=15.5。

电力系统经济学原理课后习题及答案第二章 经济学基础 2-1 解:1) 边际生产成本表达式:()502000dc q q dq=+ 2)按边际成本出售产品时,收入: 2()502000dc q q q q dq⨯=+ 利润=收入-成本222502000(252000)25q q q q q =+-+= 2-2 解:1)根据反需求函数:102000q π=-+,画出反需求函数曲线:当价格为零时,最大消费需求:max 200q =。
2)根据1)所示的反需求函数曲线,最高购买价格:max 2000π= 美元/件3)由1)的反需求函数曲线可知最大消费者剩余即为反需求函数曲线、价格坐标轴、数量坐标所围三角形的面积。
最大消费者剩余:120002002000002⨯⨯=美元但是生产者生产了产品,不可能什么都不卖,因此该最大消费者剩余不可能实现。
4)当价格π=1000美元/单位产量反需求函数曲线如下: 消费量:200010010q π-==总消费者剩余:1(10002000)1001500002⨯+⨯=美元 生产者收入:1000100100000q π=⨯=美元净消费者剩余:净消费者剩余=总消费者剩余-生产者收入 =15000010000050000-=美元 5)如果价格增加20%,则1000(120%)1200π=⨯+=美元/单位产量, 消费量:20008010q π-== 生产者收入:12008096000q π=⨯=美元 6)当1000π=美元/单位产量时,100q =需求价格弹性:110()110dqdq q d q d πεπππ===⨯-=- 7)如下图所示以需求为变量的反需求函数曲线:知总消费者剩余为一梯形,所以 总消费者剩余为:211111111(2000)(104000)5200022q q q q q π+⋅=-+⋅=-+ 总消费者剩余函数为:252000q q -+ 净消费者剩余为一三角形,所以净消费者剩余为:21111111(2000)(2000102000)522q q q q π-⋅=+-⋅= 净消费者剩余函数为:25q 以4)中当需求为100q =时检验,总消费者剩余:225200051002000100150000q q -+=-⨯+⨯=美元 净消费者剩余:225510050000q =⨯=美元 结果一样。


.电力系统经济学原理[英]Daniel S.Kirschen, Goran Strbac 著朱治中译课后习题答案第二章 经济学基础 2-1 解:1) 边际生产成本表达式:()502000dc q q dq=+ 2)按边际成本出售产品时,收入: 2()502000dc q q q q dq⨯=+ 利润=收入-成本222502000(252000)25q q q q q =+-+=2-2 解:1)根据反需求函数:102000q π=-+,画出反需求函数曲线:2002000π当价格为零时,最大消费需求:max200q =。
2)根据1)所示的反需求函数曲线,最高购买价格:max2000π= 美元/件3)由1)的反需求函数曲线可知最大消费者剩余即为反需求函数曲线、价格坐标轴、数量坐标所围三角形的面积。
最大消费者剩余:120002002000002⨯⨯=美元 但是生产者生产了产品,不可能什么都不卖,因此该最大消费者剩余不可能实现。
4)当价格π=1000美元/单位产量反需求函数曲线如下:200消费量:200010010q π-== 总消费者剩余:1(10002000)1001500002⨯+⨯=美元生产者收入:1000100100000q π=⨯=美元净消费者剩余:净消费者剩余=总消费者剩余-生产者收入 =15000010000050000-=美元 5)如果价格增加20%,则1000(120%)1200π=⨯+=美元/单位产量, 消费量:20008010q π-== 生产者收入:12008096000q π=⨯=美元 6)当1000π=美元/单位产量时,100q =需求价格弹性:110()110dqdq qd q d πεπππ===⨯-=-7)如下图所示以需求为变量的反需求函数曲线:2002000π1π知总消费者剩余为一梯形,所以 总消费者剩余为:211111111(2000)(104000)5200022q q q q q π+⋅=-+⋅=-+ 总消费者剩余函数为:252000q q -+ 净消费者剩余为一三角形,所以 净消费者剩余为:21111111(2000)(2000102000)522q q q q π-⋅=+-⋅= 净消费者剩余函数为:25q 以4)中当需求为100q =时检验,总消费者剩余:225200051002000100150000q q -+=-⨯+⨯=美元净消费者剩余:225510050000q =⨯=美元 结果一样。
电力系统经济学原理习题-全————————————————————————————————作者:————————————————————————————————日期:电力系统经济学原理[英]Daniel S.Kirschen, Goran Strbac 著朱治中译课后习题答案第二章 经济学基础 2-1 解:1) 边际生产成本表达式:()502000dc q q dq=+ 2)按边际成本出售产品时,收入: 2()502000dc q q q q dq⨯=+ 利润=收入-成本222502000(252000)25q q q q q =+-+=2-2 解:1)根据反需求函数:102000q π=-+,画出反需求函数曲线:2002000πq当价格为零时,最大消费需求:max200q=。
2)根据1)所示的反需求函数曲线,最高购买价格:max2000π= 美元/件3)由1)的反需求函数曲线可知最大消费者剩余即为反需求函数曲线、价格坐标轴、数量坐标所围三角形的面积。
最大消费者剩余:120002002000002⨯⨯=美元 但是生产者生产了产品,不可能什么都不卖,因此该最大消费者剩余不可能实现。
4)当价格π=1000美元/单位产量反需求函数曲线如下:2002000πq净消费者剩余生产者收入总消费者剩余1000q消费量:200010010q π-== 总消费者剩余:1(10002000)1001500002⨯+⨯=美元生产者收入:1000100100000q π=⨯=美元净消费者剩余:净消费者剩余=总消费者剩余-生产者收入=15000010000050000-=美元 5)如果价格增加20%,则1000(120%)1200π=⨯+=美元/单位产量,消费量:20008010q π-== 生产者收入:12008096000q π=⨯=美元 6)当1000π=美元/单位产量时,100q =需求价格弹性:110()110dqdq qd q d πεπππ===⨯-=-7)如下图所示以需求为变量的反需求函数曲线:2002000πq净消费者剩余总消费者剩余1q 1π知总消费者剩余为一梯形,所以 总消费者剩余为:211111111(2000)(104000)5200022q q q q q π+⋅=-+⋅=-+ 总消费者剩余函数为:252000q q -+ 净消费者剩余为一三角形,所以 净消费者剩余为:21111111(2000)(2000102000)522q q q q π-⋅=+-⋅= 净消费者剩余函数为:25q 以4)中当需求为100q =时检验,总消费者剩余:225200051002000100150000q q -+=-⨯+⨯=美元净消费者剩余:225510050000q =⨯=美元 结果一样。