当前位置：文档之家 › 电力系统经济学原理第六章.

电力系统经济学原理第六章.

  • 格式：ppt
  • 大小：2.34 MB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

电力系统分析第6章

电力系统分析第6章

即：
I a ,b ,c = P −1 ⋅ I d ,q ,o
α是d轴领先 相磁轴间的角度 是 轴领先 轴领先a相磁轴间的角度
第六章 同步电机的数学模型
ia，ib，ic三相不平衡时，每相中都含有相同的零轴电 三相不平衡时， 三相零轴电流大小一样，空间互差120°，其在气 流i0。三相零轴电流大小一样，空间互差 ° 隙中的合成磁势为零，只产生与定子绕组相交链的磁通， 隙中的合成磁势为零，只产生与定子绕组相交链的磁通， 不产生与转子绕组交链的磁通。 不产生与转子绕组交链的磁通。 a,b,c系统中的直流分量和倍频交流分量对应于 系统中的直流分量和倍频交流分量对应于d,q,0 系统中的直流分量和倍频交流分量对应于 系统的基频分量， 系统的基频分量， a,b,c系统中的基频交流分量对应于 系统中的基频交流分量对应于 d,q,0系统的直流分量。 系统的直流分量。 系统的直流分量 派克变换不仅可用于电流，也可用于电压和磁链。 派克变换不仅可用于电流，也可用于电压和磁链。
第六章 同步电机的数学模型
ψ L a aa ψ b M ba ψ M c ca ψ f = M fa ψ D M Da ψ M ga g ψ Q M Qa
M ab Lbb M cb M fb M Db M gb M Qb
第六章 同步电机的数学模型
派克变换的物理意义
• 在任一时刻，三相绕组a、b、c流过电流 a、 ib 、ic在气 在任一时刻，三相绕组 、 、 流过电流i 流过电流 隙中所产生的合成磁动势分布，可以用等值绕组 、 中 隙中所产生的合成磁动势分布，可以用等值绕组d、q中 流过的电流i 所产生的合成磁动势分布来代替。 流过的电流 d 、iq所产生的合成磁动势分布来代替。 • d、q绕组磁轴分别为转子的 轴和 轴，并且随转子一起 、 绕组磁轴分别为转子的 轴和q轴 绕组磁轴分别为转子的d轴和 旋转，其匝数为相绕组的 倍 其电流满足下式： 旋转，其匝数为相绕组的3/2倍，其电流满足下式：

电力系统分析第六章

电力系统分析第六章

Northeastern University
第六章 电力系统的无功功率平衡和电压调整
据此相量图作出了发电机的运行极 限图。运行极限图表明在不同功率因数 下，受发电机定子额定电流(额定视在功 率)、转子额定电流(空载电势)、原动机 出力(额定有功功率)等的限制，发电机 应发有功功率和无功功率的限额。 图中，以A为圆心，以AC为半径的 圆弧表示定子额定电流的限制；以O为 圆心，OC为半径的圆弧表示转子额定 电流的限制；水平线DC表示原动机出力 的限制。此外，曲线DF表示当发电机超 前功率因数运行即进相运行时，发电机 静态稳定性和定子端部温升的限制。发 电机应发有功功率、无功功率的限额在 图中体现为曲线段AB、BC、CD、DF 包围的面积。
Qc U 2 / X c
Northeastern University
第六章 电力系统的无功功率平衡和电压调整
缺点：电容器的无功功率调节性能比较差。 优点：静电电容器的装设容量可大可小，既可集中使用，又可以分散安 装。且电容器每单位容量的投资费用较小，运行时功率损耗亦较小，维 护也较方便。 4.静止补偿器 静止补偿器是20世纪60年代起发展起来的一种新型可控的静止无功补偿 装置，它简称为SVC。其特点是：利用晶闸管电力电子元件所组成的电 子开关来分别控制电容器组与电抗器的投切，这样它的性能完全可以做 到和同步补偿机一样，既可发出感性无功，又可发出容性无功，并能依 靠自身装置实现快速调节，从而可以作为系统的一种动态无功电源，对 稳定电压、提高系统的暂态稳定性以及减弱动态电压闪变等均能起着较 大的作用。
Northeastern University
第六章 电力系统的无功功率平衡和电压调整
对应的负荷的无功功率--电压特性如图6-2所示。 图中， 为电动机的受载系数(实际负荷与额定负荷之比)。由图可见， 在额定电压附近，电动机的无功功率随电压的升高或降低而增大或减小； Q 当电压明显低于额定值时，无功功率随电压的下降而增大( 起主要作 用)。

电力系统经济学原理课后习题及答案

电力系统经济学原理课后习题及答案

电力系统经济学原理课后习题及答案第二章 经济学基础 2-1 解：1) 边际生产成本表达式：()502000dc q q dq=+ 2）按边际成本出售产品时，收入： 2()502000dc q q q q dq⨯=+ 利润＝收入－成本222502000(252000)25q q q q q =+-+= 2-2 解：1）根据反需求函数：102000q π=-+，画出反需求函数曲线：当价格为零时，最大消费需求：max 200q =。

2）根据1）所示的反需求函数曲线，最高购买价格：max 2000π= 美元/件3）由1）的反需求函数曲线可知最大消费者剩余即为反需求函数曲线、价格坐标轴、数量坐标所围三角形的面积。

最大消费者剩余：120002002000002⨯⨯=美元但是生产者生产了产品，不可能什么都不卖，因此该最大消费者剩余不可能实现。

4）当价格π=1000美元/单位产量反需求函数曲线如下： 消费量：200010010q π-==总消费者剩余：1(10002000)1001500002⨯+⨯=美元 生产者收入：1000100100000q π=⨯=美元净消费者剩余：净消费者剩余＝总消费者剩余－生产者收入 ＝15000010000050000-=美元 5）如果价格增加20%，则1000(120%)1200π=⨯+=美元/单位产量， 消费量：20008010q π-== 生产者收入：12008096000q π=⨯=美元 6）当1000π=美元/单位产量时，100q =需求价格弹性：110()110dqdq q d q d πεπππ===⨯-=- 7）如下图所示以需求为变量的反需求函数曲线：知总消费者剩余为一梯形，所以 总消费者剩余为：211111111(2000)(104000)5200022q q q q q π+⋅=-+⋅=-+ 总消费者剩余函数为：252000q q -+ 净消费者剩余为一三角形，所以净消费者剩余为：21111111(2000)(2000102000)522q q q q π-⋅=+-⋅= 净消费者剩余函数为：25q 以4）中当需求为100q =时检验，总消费者剩余：225200051002000100150000q q -+=-⨯+⨯=美元 净消费者剩余：225510050000q =⨯=美元 结果一样。

电力系统分析第六章新 72页PPT文档

电力系统分析第六章新 72页PPT文档
3、什么是冲击电流?什么是冲击系数？ 4、什么是无限大容量电源供电系统短路电流最大有效值？
如何计算？
6.2 同步发电机的基本方程和等值电路
一、同步发电机绕组等效电路
1、同步发电机的6个绕组： ♦ 有阻尼绕组的凸极式发电机
定子：有静止的三相绕组abc ， 通过该三相绕组与外电 路连接，向系统供电；
转子：有与转子一起旋转的一 个励磁绕组 f、d 轴等效阻尼绕组 D 和 q 轴等效阻 尼绕组Q 。
旋转的矢量 F
来表示；如果定子电
a
流用一个同步旋转的通用相量 I 表
示，那么，F a 与 I 在任何时刻都同
相位，而且在数值上成比例，如图所示：
6.2 同步发电机的基本方程和等值电路
ia = I cosθ

ib
=
I
cos(θ
－120 o
)

ic = I cos(θ + 120 o )
根据三相线路的对称性：
ib= Im s in (ω t+ α --1 2 0 o)+
-t
Im 0 s in (α -0-1 2 0 0)-Im s in (α --1 2 0 0) eT a
ic= Im s in (ω t+ α -+ 1 2 0 o)+
-t
Im 0 s in (α -0+ 1 2 0 0)-Im s in (α -+ 1 2 0 0) eT a
6.1 概述
二、无限大功率电源供电的三相短路电流分析
1、无限大功率电源（又称恒定电势源）：是指端电压幅值和 频率都保持恒定的电源，其内阻抗为零。 理解：1）电源功率为无限大时，外电路发生短路引起的 功率改变对于电源来说是微不足道的，因而电源的电压 和频率保持恒定（对应于同步电机的转速）； 2）无限大功率电源可以看作是由无限多个有限功 率电源并联而成，因而其内阻抗为零。

电力系统分析第六章

电力系统分析第六章

双绕组变压器有载调压：
当无载调压不论怎样选择分接头，低压母线的实 际电压总不能满足要求时，这时可使用有载调压变压 器．它不仅可在有载情况下更改分接头，而且调节范 围也较大，只是经济性稍差一些．
３.利用无功补偿调压：
并联补偿
原理: 减少无功流动，直接减少线路有功损耗，减少电压损耗， 从而提高电压 补偿容量的计算 设有下图所示模型:
第三节 电力系统电压调整
一.调压的必要性
1.电压偏移对负荷的影响
照明、电热、电动机、家用电器
2.电压偏移对电力系统的影响
功率损耗、电能损耗、设备绝缘、运行稳定 性、电晕损耗
二、调压的整体思想

1.什么是电压中枢点 中枢点: 大型发电厂的高压母线、大型变电 所的二次母线、有大量地方负荷的发电厂母 线 负荷点A 如下图所示:
QG1
P 1 QG1 1 Q

Q 1 QG2 1 Q
QG2

i n i 1
QGi
i n
P 1 QGn 1 Q QGn
QLi Q 0
i 1
确立了最优分布的等网损微增率准则然后由条件 列出方程组，解出各解，就可得到电源的最优分 布 3.注意: 当某点求出的无功容量超过了不等式的约束条 件时，应取这点的无功即为它的极限，然后由其 他点继续做计算求出无功功率
2 ．调整变比K1、K2；

怎 么 实 现

3．改变功率分布(以Q为主)；
4．改变网络参数R+jX(以X为主);
？

五．调压措施：

１.利用发电机调压 ２.改变变压器变比调压
３.利用无功补偿调压


１.利用发电机调压

电力系统经济学原理第六单元习题答案

电力系统经济学原理第六单元习题答案

(1)母线A与B之间的线路断开P A = 2000AHP 严=1000』/VJ\IC A = 20 + 0.03P A = 20 + 0.03 x 2000 = SO美元/MWhMC B = 15 + 0.02R = 15 + 0.02 x 1000 = 35美元/MWh线路上的潮流用3 = O.Vir, A母线电价为80美元/MWh, B母线电价为35美元。

(2)母线A与B之间的线路处于投运状态，并且不会岀现输电容量约束限制。

由题意得：MC A =MC B⑴P A^P B = 3000A/n7(2)由(1) (2)式解得Pa = 1100iVir.P5 = 1900J/H\ 此时= 7T3 = 20 + 0.03 x 1100 = 53美元/MWh。

线路上潮流F AS = -900MJV, 负号表示从母线B传到母线A电能为900MW. (3)母线A与B之间的线路处于投运状态，并且不会出现输电容量约束限制。

但发电机B 的最大出力只有1500MW. P A +P B = 3000MW.P B = 1500J/F贝丹=lo003/II\ 可知：mi = MC A = 20 + 0.03 x 1500 = 65美元/MWh。

7TB =MC B = 15 + 0.02 x 1500 = 45美元/MWho则E E = -(1500 -1000) = 一500卜[\匕从母线B到A母线输送500MW的电能。

(4)母线A与B之间的线路处于投运状态，并且不会出现输电容量约朿限制。

但发电机A的最大出力只有900MW。

P A+P B=3000.UH\P A = 900MV,则刊=2100MIF。

TTA =]\IC A = 20 + 0.03 x 900 = 47美元/MWh。

7T B=》1C B = 15 + 0.02 x 2100 = 57美元/MWh o Fab = ~<Pb - Db) = -(2100 - 900) = -1200MW O从母线B到 A 母线输送1200MW的电能。

电力市场与电力经济第六章 电力市场中的电价

电力市场与电力经济第六章 电力市场中的电价
电力市场
第六章 电力市场中的电价
第一节 第二节 第三节 第四节 制订电价的基本原则 制定电价的理论方法 电价的计算方法 实时电价理论
第一节 制订电价的基本原则
《电力法》规定：合理补偿成本，合理确定 合理补偿成本， 合理补偿成本 收益，依法计入税金，公平负担； 收益，依法计入税金，公平负担；有利于促 进合理用电和合理利用资源。 进合理用电和合理利用资源 在公平基础上，电价等于成本、利润、税金 电价等于成本、 电价等于成本 利润、 之和
表4 A、B、C厂避峰前后各时段的用电量情况
避峰前 用户 高峰 平峰 低谷 高峰 平峰 低谷 避峰后
A厂 厂
1.79
1.10
0.00
0.00
1.10
1.79
B厂 厂
4.66
0.26
1.84
0.00
1.46
5.30
C厂 厂
16.12
14.02
2.73
13.39
14.02
5.46
表 各厂避峰前后平均电价水平 （分/kW.h)
第二节 制定电价的理论方法
3、调节电价结构 （2）功率因数调整电价。 功率因数标准共分三档：0.9，0.85，0.8， 适用于不同的用电对象。这一电价政策在技 术上要求单独加装有功电度表和无功电度表， 计算月平均功率因数cosθ。根据cosθ高于 或低于标准的情况，按照电费调整表的要求 调节电价。
第二节 制定电价的理论方法
3、调节电价结构-供电、用电、调节 供电、 供电 用电、 （1）峰谷分时电价和丰枯分季节电价。 峰谷分时电价：将日负荷曲线按时间划分为
高峰、平段、低谷三个时段，或仅划分高峰、 低谷两个时段，实行高峰高价、低谷低价的政 策。国内的峰谷电价大多相差3-4倍。

第6章电力系统经济运行

第6章电力系统经济运行
❖ 的计算乃是一个工程中的统计问题，可以有解
的方法，不要求深入探究 。
8
I
➢ 2、等值功率法
R
P
仍以此图为例，在给定的时
cos
间T 内的能量损耗：
A T S 2 R 103 dt
0 V
--- (1)
简单供电网
Pe2q
Qe2q
1 T
T S 2dt
o
--- (2)
Peq ：有功功率等效值 Qeq ：无功功率等效值
Pg 2
两台机组并联运行
如何确定负荷功率在两机组间的 分配，使总的燃料消耗最小？
约束条件： 已知， 耗量特性：
Pg1 Pg2 PLD
F1 F1( Pg1 ) F2 F2 ( Pg2 )
求解， 目标函数： min(F1 F2 )
21
2、双机运行时的有功分配
采用拉格朗日乘数法求条件极值：
Pg1
12
如图所示
V R1 jX1 S1
P jQ
R2 jX 2 S2
将上式分别对 P1 和 Q1 取偏导数，
并令其等于零
网络的功率损耗为：
PL
S12 V2
R1
S
2 2
V2
R 2
P12 Q12 V2
R1
P22 Q22 V2
R2
P12 Q12 V2
R1
(P
P1
)2 (Q Q1 )2 V22
第6章 电力系统经济运行
研究内容： 在供应相同负荷和满足相同约束的条件
下，采用优化系统中可能的所有手段使运 行费用最小。
1
§6.1 电力网中的能量损耗
一、基本概念
供电量
在给定的时间内，系统中所有发电 厂的总发电量同厂用电量之差。

电力系统经济学原理第六章

电力系统经济学原理第六章
• 由于此类输电权是在一个公共拍卖平台上购买的 ，因此交易方将可以方便地判断这一输电权附加 成本是否合理。
输电网络与电力市场 7
物理输电权
举例来说，可以假设图6-1中的发电机G1和负荷 L1商定的交易价格是30美元/MWh，而发电机G2 和负荷L2商定的交易价格是32美元/MWh 。同时 发电机G3所提供电能的价格是35美元/MWh 。 • 很明显，负荷L2将愿意支付的输电权购买价格不 会超过3美元/MW。当输电权的价格超过5美元 /MW 时，负荷L1也会得出同样的结论。 • 输电权成本帮助与发电商进行讨价还价，从而降 低交易价格。 • 输电权赋予持有者实际使用某条给定线路一部分 输电容量的权利，通常被称为物理输电权。
输电网络与电力市场 16
基本内容
6.1 简介
6.2 基于输电网络的分散式交易 6.3 基于输电网络的集中式交易
6.4 推荐阅读材料
输电网络与电力市场
17
基于输电网络的集中式交易
• 采用集中式或电力库交易机制时，系统运营商同 时也是巿场运营商，生产者和用户需要向系统运 营商提交各自的投标和报价。系统运营商独立于 其他所有市场成员，他会在计及输电网络安全约 束的前提下，按照最优经济效率原则确定中标的 投标和报价，实现市场出清。 • 在同一交易时段内，对于连接在同一母线上的所 有市场交易者而言，无论是用户还是生产者，他 们所面临的价格完全一样。 • 在集中交易机制条件下，系统运营商能发挥更为 积极的作用，电力市场的经济效率才有可能达到 最优。
p = pS = pW = 24.3美元/ MWh
PS = 1433 MWh PW = 567 MWh
输电网络与电力市场 24
无约束输电
• 互联线路上的潮流数量等于蜀国系统的发电减去

电力系统经济学原理第六单元习题答案

电力系统经济学原理第六单元习题答案

(1)母线A 与B 之间的线路断开2000,1000ABP MW P MW200.03200.03200080A A MC P 美元/MWh 150.02150.02100035BB MC P 美元/MWh线路上的潮流0ABF MW ，A 母线电价为80美元/MWh ，B 母线电价为35美元。

（2）母线A 与B 之间的线路处于投运状态，并且不会出现输电容量约束限制。

由题意得：(1)AB MC MC 3000(2)ABP P MW由（1）（2）式解得1100,1900ABP MW P MW ,此时200.03110053AB 美元/MWh 。

线路上潮流900AB F MW ,负号表示从母线B 传到母线A 电能为900MW 。

（3）母线A 与B 之间的线路处于投运状态，并且不会出现输电容量约束限制。

但发电机B的最大出力只有1500MW 。

3000,1500A BB P P MW P MW ,则1500A P MW 。

可知：200.03150065AA MC 美元/MWh 。

150.02150045B B MC 美元/MWh 。

则(15001000)500ABF MW 。

从母线B 到A 母线输送500MW 的电能。

(4)母线A 与B 之间的线路处于投运状态，并且不会出现输电容量约束限制。

但发电机A 的最大出力只有900MW 。

3000,900AB AP P MW P MW ,则2100B P MW 。

200.0390047AA MC 美元/MWh 。

150.02210057B B MC 美元/MWh 。

()(2100900)1200ABB B F P D MW 。

从母线B 到A 母线输送1200MW 的电能。

（5）母线A 与B 之间的线路处于投运状态，但它的最大输电容量只有600MW ，发电机的出力不受限制。

600ABF MW 。

则1600B B AB P D F MW ，因为3000,A B P P MW 则1400A P MW 。

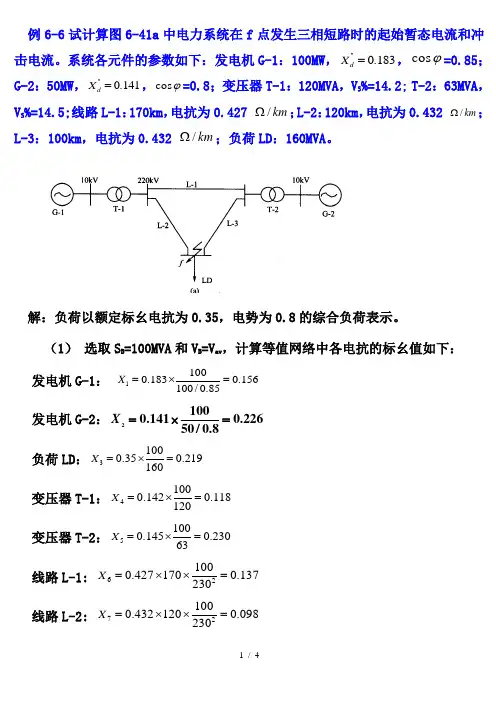
电力系统分析理论第六章例6-5

电力系统分析理论第六章例6-5

例6-6试计算图6-41a 中电力系统在f 点发生三相短路时的起始暂态电流和冲击电流。

系统各元件的参数如下：发电机G-1：100MW ，''0.183dX =，cos ϕ=0.85；G-2：50MW ，''0.141d X =，cos ϕ=0.8；变压器T-1：120MVA ，V S %=14.2; T-2：63MVA ，V S %=14.5;线路L-1：170km ，电抗为0.427 /km Ω；L-2：120km ，电抗为0.432 /km Ω；L-3：100km ，电抗为0.432 /km Ω；负荷LD ：160MVA 。

解：负荷以额定标幺电抗为0.35，电势为0.8的综合负荷表示。

（1） 选取S B =100MVA 和V B =V av ，计算等值网络中各电抗的标幺值如下： 发电机G-1： 11000.1830.156100/0.85X =⨯= 发电机G-2：226.08.0/50100141.02=⨯=X 负荷LD ：31000.350.219160X =⨯= 变压器T-1：41000.1420.118120X =⨯= 变压器T-2：51000.1450.23063X =⨯= 线路L-1: 621000.4271700.137230X =⨯⨯= 线路L-2: 721000.4321200.098230X =⨯⨯=线路L-3: 821000.4321000.082230X =⨯⨯= 取发电机的次暂态电势E 1=E 2=1.08。

简化网络。

X9=X1+X4=0.156+0.118=0.274X10=X2+X5=0.226+0.230=0.456将X6，X7，X8构成的三角形化为星形67116780.1370.0980.0420.1370.0980.082X X X X X X ⨯===++++68126780.1370.0820.0350.1370.0980.082X X X X X X ⨯===++++025.08768713=++=X X X X X X化简后的网络如图6-41（c ）所示。

电力系统原理——第六章1

电力系统原理——第六章1
115 .5
U 2.min
U 1.minU T .min U 2N U 1t
115 2.311 10.73kV 11kV
115 .5
均未超出允许电压范围10~11kV，因此所选分接头 能满足调压要求。
2020/5/26
30
升压变压器分接头的选择
升压变压器分接头的选择方法与降压变压器基本相 同，但是，由于升压变压器中功率方向是从低压侧送往 高压侧的，故公式中 U T前的符号应相反，即有
U 1t. m ax
(U 1. max
U T . max )U 2N U 2. max
U 1t m in
(U 1. min
U T . min )U 2N U 2. min
U2
~
P+jQ
RT ＋jXT
高压侧
U1
则变压器的分接头电压为：
U1t
1 2
U1t.max U1t.min
2020/5/26
➢枢纽变电所大型的二次母线；
2020/5/26
19
➢有大量地方负荷的发电厂母线；
➢城市直降变电所的二次母线。 2. 中枢点的调压方式
➢逆调压： 最大负荷时升高中枢点电压，但不超过线路 额定电压的105%，最小负荷时降低中枢点电压，但不低 于线路的额定电压。适用于供电线路较长、负荷变化较 大的中枢点。
✓并联电纳中的无功损耗：又称充电功率，与线路电 压的平方成正比，呈容性。
✓串联电抗中的损耗：与负荷电流的平方成正比，
呈感性。
.
.
U1
R jX U2
QZ I 2 X
Q yl
jB 2
2
Q yl
jB 2
2
Qyl

【国网电力系统】电力系统分析第六章.1030

【国网电力系统】电力系统分析第六章.1030

2．变压器的无功损耗
QLT
Q0
QT
U2BT
S U
2
XT
I0% 100
SN
Uk %S 2 100SN
UN U
2
假定一台变压器的空载电流I0%=2.5，短路电压Uk%=10.5，
在额定满载下运行时，无功功率的消耗将达额定容量的13%。 如果从电源到用户需要经过好几级变压，则变压器中无功 功率损耗的数值是相当可观的。
额定值，使其容量得到最充分的利用。
2. 同步调相机
•同步调相机相当于空载运行的同步电动机。 •在过励磁运行时，它向系统供给感性无功功率而起无功 电源的作用，能提高系统电压； •在欠励磁运行时（欠励磁最大容量只有过励磁容量的 （50% ～65%）)，它从系统吸取感性无功功率而起无功负 荷作用，可降低系统电压。 •它能根据装设地点电压的数值平滑改变输出（或吸取） 的无功功率，进行电压调节。因而调节性能较好。
二、无功功率电源
•电力系统的无功功率电源有发电机、同步调相机、静 电电容器及静止补偿器，后三种装置又称为无功补偿 装置。
1. 发电机
发电机在额定状态下运行时，可发出无功功率：
QGN SGN sin N PGN tg N
发电机在非额定功率因数下运行时可能发出的无功 功率。
图6-4 发电机的P-Q极限
一、无功功率负荷和无功功率损耗
1．无功功率负荷
•异步电动机
QM
Qm
Q
U2 Xm
I 2 X
jX
电压下降,转差 增大,定子电流 增大.
图6-1 异步电动机的简化等值电路
受载系数:实际负载和额定负载之比.
在额定电压附近，电动 机的无功功率随电压的 升降而增减

电力系统分析第六章

电力系统分析第六章

调相机供应QC1、并联电容器供应QC2和静止补偿器供应的Q C3
16
定期作无功功率平衡计算的内容：
1 参考累计的运行资料来确定未来的、有代表性的预 想有功功率日负荷曲线 2 确定出现无功功率日最大负荷时系统中有功功率符 合的分配。 3 假设各无功功率电源的容量与配置情况以及某些枢 纽的电压水平 4 计算系统中的潮流分布 5 根据潮流分布情况，统计出平衡关系中各项数据， 判断系统中无功功率能否平衡 6 如统计结果表明系统中无功功率一缺额，则应变更 上述条件，重作潮流计算，如始综无法平衡，则考虑 增设无功电源的方案
71
4
2 变压器中的无功功率损耗
变压器中的无功功率损耗分两部分，即 励磁支路损耗和绕组漏抗中损耗。 1励磁支路损耗的百分值基本上等于漏抗中损耗，在变压器满载时，基 本上等于短路电压U k ，约为10%，
5
3 电力线路上的无功功率损耗
电力线路上的无功功率损耗也分两部分，即并 联电纳和串联电抗中的无功功率损耗。 1 并联电纳中的这种损耗又称充电损耗，与线 路电压的平方成正比，呈容性。 2 串联电抗中的这种损耗与负荷电流的平方成 正比，呈感性。 当通过线路输送的有功功率大于自然功率时， 线路将消耗感性无功功率；当通过线路输送的 有功功率小于自然功率时，线路将消耗容性无 功功率。
31
32
33
综上可见，在保证系统中无功功率平衡的基础上， 如同调整控制频率一样．调整控制电压，使其偏移 和波动保持在允许范围内，是系统运行的又一重要 问题。
34
3-2 电力系统的电压管理
35
36
37
38
39
40
41
42
43
44
45
46

电力系统分析第6章(电力系统的经济运行)

电力系统分析第6章(电力系统的经济运行)

1500～2200
二班制企业
3000～4500
三班制企业
6000～7000
农业用电
1000～1500
6.2 电力系统有功功率负荷的经济分配
6.2.1 发电机组的耗量特性 6.2.2 等微增率准则 6.2.3 火电厂间有功功率负荷的经济分配 6.2.4 计及网损时水、火电厂间有功功率
负荷的经济分配
6.2 电力系统有功功率负荷的经济分配
式中，S的单位为KVA，U的单位为KV。
若时间 t 24h, 则 W 为一天的电能损耗； 若 t 8760h, 则W 为全年的电能损耗。
最大负荷损耗时间法
线路向一个集中负荷供电.
设如果面积 S0abc 与一矩形
面积相等，并令矩形的高
等于
பைடு நூலகம்
S
2 max
，则矩形的底用
表示，电能损耗可表示
为
6.3电力网中的电能损耗
综合用电负荷：指工业、农业、交通运输、市政 生活等各方面消耗的功率之和。
供电负荷：电力系统的综合用电负荷加上网损，即 发电厂供出的负荷，称为电力系统的供电负荷。
发电负荷：供电负荷再加上发电厂厂用电就是发电 机应发出的功率，称为发电负荷。
6.1 电力系统的负荷和负荷曲线
6.1.2 负荷曲线
负荷曲线： 表示电力系统的负荷随时间变化的规律的曲线。
•
16、我总是站在顾客的角度看待即将推出的产品或服务，因为我就是顾客。2021年10月20日星期三9时3分43秒21:03:4320 October 2021
•
17、当有机会获利时，千万不要畏缩不前。当你对一笔交易有把握时，给对方致命一击，即做对还不够，要尽可能多地获取。下午9时3分43秒下午9时3分21:03:4321.10.20

电力系统原理——第六章(2)

电力系统原理——第六章(2)

多，且中枢点到负荷处线路上的电压损耗的大小和变化 规律的差别可能很大，完全可能出现在某些时段内，中 枢点电压取任何值均不能满足要求，这时须采取其他措 施（如在负荷处进行无功补偿，改变变压器变比等）。
（2）中枢点电压的调整方式
逆调压： 最大负荷时升高中枢点电压，但不超过线路 额定电压的105%，最小负荷时降低中枢点电压，但不低 于线路的额定电压（100 %） 。适用于供电线路较长、 负荷变化较大的中枢点。
U j U j
四. 借改变变压器变比调压 （1）对于双绕组降压变压器i
U I
U i
i
U i
U I
U i
Ui
给定U Im ax , Smax ,U Im in , Smin , 低压侧期望实际电压U imax，U imin， 要求选择U t Im ax，U t Im in。
四. 借改变变压器变比调压 双绕组变压器的高压绕组和三绕组的高、中压绕组有3-5个 分接头可供选择，如有UN±5％、 UN±2×2.5％ 。其中对应于 UN的分接头常称主接头或主抽头。 合理选择变压器的分接头也可调压。
g
G
U g U g
U G
i
U I
U J
j
U分接头电压分别为：
U1t .max
U1.max U T .max U 2 N 113 5.5611 118.2kV
.max U2 10
U1t .min
U1.min UT .min U 2 N 115 2.311 112.7kV
U tJ kj U Nj
U jc Uj 2 QC U jc kj xij k j U jc 2 QC U U k jc j j xij

电力系统经济学原理复习提纲

电力系统经济学原理复习提纲

3. 什么是商业剩余？ 所有母线上用户的支出与发电商收入的差值即为商业剩余。 4. 三节点系统中集中式交易的经济调度方案及经济调度调整 5. 输电网络的损耗有哪几种类型？分别是什么？ • • • 变动损耗 固定损耗 非技术损耗
6． ，何为反经济潮流现象？ 7. 何为金融输电权？何为关口权？ 输电权的定义还可以依附于网络中的某条支路或关口， 因此通常称它们为关口 权。
第七章 发电投资 1. 如何进行新建发电厂投资决策？ • • • • 为了做出发电投资决策， 资本所有者必须计算电厂的长期边际成本（包含 期望回报率） ，并预测电厂发电出力可能面临的销售价格。 只有当预测价格超过电厂的长期边际成本时， 电厂的新建决策才有可能是 合理的。 在电力巿场上建立“商业性发电扩容”机制。 非常多的不确定因素可能会影响长期边际成本与价格预测值， 例如建造工 期延长、燃料价格波动等问题均有可能会影响长期边际成本。 2. 发电厂在什么情况下会退役？ • • • 一旦发电厂投产运行，它的设计寿命期就只具有理论参考意义， 实际的使 用寿命可能会与设计值之间有很大的偏离。 真实的市场状况也可能会出现很大的变化， 发电厂收入有可能很难回收它 的运行成本。 在上述条件下，除非有充足的证据表明未来市场状况可能会有所好转， 否 则该电厂就不得不退役。
2. 何为无功支持服务？ 电压控制服务的定义不仅需要考虑系统在正常状态下的运行情况， 还应当考 虑那些难以预测的停运可能产生的影响。 电压控制服务反映的不仅仅是正常运行 状态下的电压调整能力，同时它还需要能在紧急状态下提供足够的无功。电压控 制服务常常被称为无功支持服务 3. 系统运行人员获取服务的方式有哪些？ • • 强制要求其他行业成员提供一部分辅助服务； 将辅助服务的供应市场化。
3. 什么是价格需求弹性？ 需求相对变化与价格相对变化两者之间的比率。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

输电网络与电力市场
2
基本内容
6.1 简介
6.2 基于输电网络的分散式交易 6.3 基于输电网络的集中式交易
6.4 推荐阅读材料
输电网络与电力市场
3
6.2基于输电网络的分散式交易
在分散式或双边交易机制中，所有的电能交易只涉 及两个主体：一个购电者和一个售电者。购售双方 需要就以下内容达成一致，即交易数量、价格和他 们可能希望的其他附加合同条款。
• 由于此类输电权是在一个公共拍卖平台上购买的 ，因此交易方将可以方便地判断这一输电权附加 成本是否合理。
输电网络与电力市场 7
物理输电权
举例来说，可以假设图 6-1 中的发电机 G1 和负荷 L1 商定的交易价格是 30 美元 /MWh ，而发电机 G2 和负荷L2商定的交易价格是 32美元/MWh 。同时 发电机G3所提供电能的价格是35美元/MWh 。 • 很明显，负荷L2将愿意支付的输电权购买价格不 会超过 3 美元 /MW 。当输电权的价格超过 5 美元 /MW 时，负荷L1也会得出同样的结论。 • 输电权成本帮助与发电商进行讨价还价，从而降 低交易价格。 • 输电权赋予持有者实际使用某条给定线路一部分 输电容量的权利，通常被称为物理输电权。
因为是双边合同，所以交易价格均由交易双方私下商 定。他们有必要向系统运营商报告合同涉及的电能传 输数量。 系统运行商要进行效验，如果A、B之间的可以输送的 功率数量少于500MW，系统运行商必须进行干预。
输电网络与电力市场 5
6.2.1 物理输电权
• 为了保证系统的安全水平，系统运行人员需要选 择削减一些交易，然而这一问题非常复杂。 输电负荷减载程序应当考虑的因素的影响有：
输电网络与电力市场
9
并联支路
• I 可以沿着两条并联支路从 母线1 流向母线2，支路的 阻抗分 别是 zA 和 zB 。两节 点之间的电压差为： U12 = zA IA=zB IB 由于 I = IA+ IB ，得：
zB IA I z A zB zA IB I z A zB
并联支路中通过的电流与各条 支路的阻抗成反比。
13
输电网络与电力市场
示例
• 为了确保上述交易能够完全实现，交易者需要在线路 1-3 上获得 240MW 的输电权，在线路 1-2 和 2-3 上均取 得160MW的输电权。 • 在 线 路 1-2 和 2-3 的 线 路 容 量 分 别 只 有 126MW 和 130MW。由于约束主要是线路1-2的容量不足造成的 ，即使在没有其他交易的情况下， A 和 Y 所能签订的 合同数量最大也只能是：
Pmax = 0.5/0.2×126=315MW
理论上，如果市场是充分竞争的，经过数次循环往复 ，交易者总可以找到双边电能交易与双边输电权交易 的最佳组合。但实际上，电力系统的约束远不止容量 约朿一种，双边交易需要交换信息的数量十分巨大。
输电网络与电力市场 11
示例
• 图显示了一个包含三条母 线的闭环系统。 • 为了简化分析，假设略线路电阻的影响。 • 下表显示了该系统的相关 参数。
支路 1-2 1-3 2-3 电抗(p.u.) 0.2 0.2 0.1
输电网络与电力市场
容量(MW) 126 250 130
第六章 输电网络与电力市场
输电网络与电力市场
0
基本内容
6.1 简介
6.2 基于输电网络的分散式交易 6.3 基于输电网络的集中式交易
6.4 推荐阅读材料
输电网络与电力市场
1
6.1 简介
• 研究输电网络对电能交易的影响 • 寻找出一套行之有效的机制，规避输电网络引 起的交易限制与价格波动风险 • 简单地考察双边或分散交易 • 随后将转而深人研究集中交易或电力库交易
系统运营商要保证系统的平衡和安全，其职能有： • 通过电能购售平衡负荷与发电。在一般情况下， 这些平衡交易涉及的电能数量是很少的。 • 在无法通过其他手段保证系统安全时，限制系统 中某些节点的发电出力。
输电网络与电力市场 4
两节点系统中的双边交易
假设该系统中的电能均通过双边合同实现交易。
• 假设发电机 G1 与负荷 L1 之 间签订了一笔双边合同，由 G1向L1输送300MW电能； • 发电机 G2 与负荷 L2 之间也 签定了一笔电能数量为 200MW的双边合同。
输电网络与电力市场 10
并联支路
• 假设所有支路的电阻均远小 于它的电抗，得到： Z = R + j X ≈ jX • 同时忽略网络中的无功潮流 和网损。 • 并行电路中的有功潮流为：
xB F P x A xB
A
xA F P x A xB
B
反映有功注人量与支路潮流之 间关系的因子叫做功率转移分 布系数。
12
示例
• 假定发电机 B 希望和负荷 Y签订一笔数量为 400MW 的双边交易。 • 如果发电机B通过母线1将 400MW 的 电 力 注 入 系 统 ，而负荷Y从节点母线3处 获得同样数量的电力，那 么系统中两条路径I和II的 潮流为：
0.2 FI 400 160 MW 0.2 0.3 0.3 FII 400 240 MW 0.2 0.3
输电网络与电力市场 8
6.2.2 物理输电权存在的问题
并联支路 电网中的电流和潮流分布受基尔霍夫电流和电压定 律的约束。 • 基尔霍夫电流定律：流入某一节点的所有电流之 和等于流出该节点的所有电流之和；它同时也意 味着每个节点应同时保持有功和无功平衡。 • 基尔霍夫电压定律：任一闭合回路所有组成支路 上的电压降之和一定等于零；或者换句话说，并 联支路上的电压降相等。
• 交易性质(固定或非固定) • 交易向系统运营商申报的顺序 • 甚至可能是一些历史因素 但分散式交易机制并没有提供一个可以对经济效益
进行评估的框架，输电负荷减载程序因此无法权衡
各类交易的相对经济效益。
输电网络与电力市场 6
物理输电权
• 分散式电力交易的支持者认为，最好能提供这样 一种办法，它可以让电能交易方明确他自身是否 愿意使用输电网络。 • 以母线A处的生产者和母线B处的用户为例，在签 订合同时，如果他们不想看到自己的双边交易因 为阻塞而中断，购售双方就应当为该交易购买输 电系统使用权。