应用弹塑性力学 李同林 第四章

应用弹塑性力学李同林第四章这是变形理论。

这个理论首先由亨斯基提出，然后由前苏联的伊留申进一步完善。

问题提出得更清楚了，并且给出了使用条件。

因此，这个理论也被称为亨奇-伊柳辛理论。

伊柳欣的变形理论应该满足几个条件:(1)外载荷(包括体力)成比例增加，变形体处于主动变形过程中(即应力强度无中间卸载)；(2)材料所用体积不可压缩，采用泊松比μ = 1/2进行计算；(3)材料的应力-应变曲线具有幂强化形式，即或者；在变形过程中(4)满足小弹塑性变形的各种条件，塑性变形和弹性变形大小相同。

满足上述条件后，变形理论将给出正确的结果。

如果负载没有成比例地增加，则外部负载成比例地增加是简单负载的必要条件。

这样不仅不能保证物体内部的简单加载状态，而且物体表面也不能满足简单加载条件。

体积不可压缩性和泊松比μ=1/2的假设不仅简化了具体计算，而且与实验结果基本一致，因此变形理论的物理关系主要表现为应力挠度和应变挠度之间的关系，这是令人满意的。

法律。

使用幂强化模型可以避免区分弹性区和塑性区，但实际上该模型对不同材料的限制很小，因为各种材料都可以通过选择公式中常数a的指数m来拟合拉伸曲线。

采用小变形条件是因为平衡方程和几何方程是在小变形条件下推导出来的，物理关系也是小变形条件下的关系。

伊柳辛不仅明确规定了亨奇变形理论的适用条件，而且证明了简单加载定理。

他提出，在小的弹塑性变形条件下，总应变与应力挠度成正比，即:如果使用主应力，有等效应变的表达式为:从这里因此，Hench-Ilyushin理论的应力-应变关系可以写成如下:展开等式(4-84):根据胡克定律(4-33)，弹性应变为:因为塑性应变是总应变和弹性应变之间的差，所以它由方程(4-85)和(1)获得:公式(4-86)可以缩写为:实施例4-3众所周知，具有封闭端的薄壁圆筒的平均半径为R，平均直径为D，壁厚为T，圆筒长度为L，并且承受内压P以产生塑性变形。

材料是各向同性的。

应用弹塑性力学李同林第四章应用弹塑性力学李同林第四章第四章弹性变形和塑性变形本构方程当我们要确定物体变形时其内部的应力分布和变形规律时，单从静力平衡条件去研究是解决不了问题的。

因此，弹塑性力学研究的问题大多是静不定问题。

要使静不定问题得到解答，就必须从静力平衡、几何变形和物性关系三个方面来进行研究。

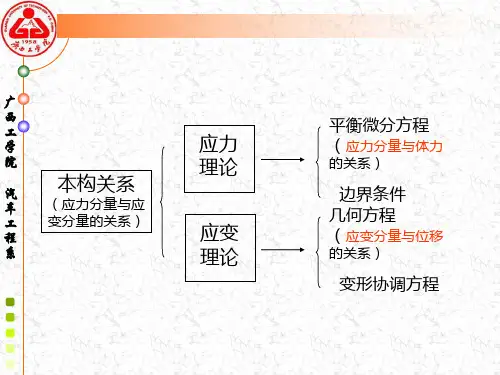
考虑这三个方面，就可以构成三类方程，即力学方程、几何方程和物性方程。

综合求解这三类方程，同时再满足具体问题的边界条件，从理论上讲就可使问题得到解答。

在第二章和第三章中，我们从静力学和几何学两个方面研究了受力物体应满足的各种方程，即平衡微分方程（2-44）和几何方程（3-2）。

因此，现在的问题是，我们必须考虑物体的物理性质，即物体变形时的应力和应变之间的关系。

在力学中，应力应变关系通常被称为本构关系或本构方程。

本章将介绍物体变形时的弹性和塑性应力应变关系。

大量实验证实，应力和应变之间的关系是相辅相成的，有应力就会有应变，而有应变就会有应力。

对于每一种具体的固体材料，在一定条件下，应力和应变之间有着确定的关系，这种关系反映了材料客观固有的特性。

下面我们以在材料力学所熟知的典型塑性金属材料低碳钢轴向拉伸试验所得的应力应变曲线(如图4-1所示)为例来说明和总结固体材料产生弹性变形和塑性变形的特点，并由此说明塑性应力应变关系比弹性应力应变关系要复杂的多。

在图4-1中，OA段是一个成比例的变形阶段。

在这个阶段，应力和应变之间的关系是线性的，可以用胡克定律来表示：ζ=eε(4-1)其中e是弹性模量，e是弹性变形期间的常数。

对应于a点的应力称为比例极限，并记录为ζp。

从a点到B点，它不再由线性关系表示，但变形仍然是弹性的。

对应于点B的应力称为弹性极限，并记录为ζr。

对于许多材料，从点a到点B的距离非常小，即ζP和ζ，r的值非常接近，通常不区分，但在ζr中表示，当应力小于ζr时，应力和应变之间的关系满足方程（4-1）。

弹塑性力学引言一、固体力学在工程中的作用工程中的各种机械都是用固体材料制造而成的、各种结构物也都是用固体材料建造的。

为了使机械结构正常使用、实现其设计的功能，首先要保证它们在工作载荷与环境作用下不发生材料的破坏或影响使用的过大的变形，即保证它们具有足够的强度、刚度和稳定性。

在设计阶段，要根据要求实现的功能，对于设计的机械结构的形式按强度要求确定其各部分的形状和尺寸，以及所需选择的材料。

要完成这样的任务，首先要解决如下基本问题：在给定形状尺寸与材料的机械结构在设计规定载荷与环境（如温度）作用下所产生的变形与应力。

对于柔性结构，如细长梁、薄板、薄壳，以及它们的组合结构，还要分析其是否会丧失稳定性。

这些都是固体力学的基本问题。

如果机械结构所受载荷或环境的作用是随时间变化的，那么，它们的振动特性也对其性能有重要的影响。

在设计时往往要对其进行模态分析，求出影响最大的各个低阶固有频率与相应的振型，以确保不会与主要的激振载荷产生共振，导致过大的交变应力与变形，影响强度和舒适性。

有些情况下还要考虑它们在瞬态或冲击载荷作用下的瞬态响应。

这些也是固体力学的基本问题。

此外、许多机械零件和结构元件在制造工程中，采用各种成型工艺，材料要产生很大的塑性变形。

如何保证加工质量，提高形状准确性、减少残余应力、避免产生裂纹、皱曲等缺陷？如何设计加工用的各种模具，加工的压力，以及整个工艺流程，这里也都有固体力学问题。

正因为工程中提出了各种各样的固体力学问题，有时还有流体力学问题，在19世纪产生了弹性力学和流体力学，才导致力学逐渐从物理学中独立出来。

工程技术发展的要求是工程力学，包括固体力学、流体力学等发展的最重要的推动力。

而工程力学的发展则大大推动了许多工程技术的飞速发展。

因此，力学是许多工程部门设计研究人员的基本素质之一。

二、力学发展概况力学曾经是物理学的一个部分，最初也是物理学中最重要的组成部分。

力学知识最早起源于人们对自然现象的观察和在生产劳动中积累的经验。

~弹塑性力学习题集[殷绥域李同林编!)~中国地质大学·力学教研室二○○三年九月》目录弹塑性力学习题 (1)第二章应力理论.应变理论 (1)；第三章弹性变形.塑性变形.本构方程 (6)第四章弹塑性力学基础理论的建立及基本解法 (8)第五章平面问题的直角坐标解答 (9)第六章平面问题的极坐标解答 (11)第七章柱体的扭转 (13)]第八章弹性力学问题一般解.空间轴对称问题 (14)第九章* 加载曲面.材料稳定性假设.塑性势能理论 (15)第十章弹性力学变分法及近似解法 (16)第十一章* 塑性力学极限分析定理与塑性分析 (18)第十二章* 平面应变问题的滑移线场理论解 (19)`附录一张量概念及其基本运算.下标记号法.求和约定 (21)习题参考答案及解题提示 (22)>前言弹塑性力学是一门理论性较强的技术基础课程，它与许多工程技术问题都有着十分密切地联系。

应用这门课程的知识，能较真实地反映出物体受载时其内部的应力和应变的分布规律，能为工程结构和构件的设计提供可靠的理论依据，因而受到工程类各专业的重视。

·《弹塑性力学习题集》是专为《弹塑性力学》（中国地质大学李同林、殷绥域编，研究生教学用书。

）教材的教学使用而编写的配套教材。

本习题集紧扣教材内容，选编了170余道习题。

作者期望通过不同类型习题的训练能有助于读者理解和掌握弹塑性力学的基本概念、基础理论和基本技能，并培养和提高其分析问题和解决问题的能力。

鉴于弹塑性力学课程理论性强、内容抽象、解题困难等特点，本书对所编习题均给出了参考答案，并对难度较大的习题给出了解题提示或解答。

本习题集的编写基本取材于殷绥域老师编写的弹塑性力学习题集，由李同林老师重新修编，进一步充实而成。

书中大部分内容都经过了多届教学使用。

为保证教学基本内容的学习，习题中带“*”号的题目可酌情选做。

由于编者水平所限，错误和不妥之处仍在所难免，敬请读者指正。

<编者2003年9月@弹塑性力学习题"第二章 应力理论·应变理论2—1 试用材料力学公式计算：直径为1cm 的圆杆，在轴向拉力P = 10KN 的作用下杆横截面上的正应力σ及与横截面夹角︒=30α的斜截面上的总应力αP 、正应力ασ和剪应力ατ，并按弹塑性力学应力符号规则说明其不同点。

应用弹塑性力学习题解答张宏编写西北工业大学出版社目录第二章习题答案 ..... 错误!未定义书签。

第三章习题答案 ..... 错误!未定义书签。

第四章习题答案 ..... 错误!未定义书签。

第五章习题答案 ..... 错误!未定义书签。

第六章习题答案 ..... 错误!未定义书签。

第七章习题答案 ..... 错误!未定义书签。

第八章习题答案 ..... 错误!未定义书签。

第九章习题答案 ..... 错误!未定义书签。

第十章习题答案 ..... 错误!未定义书签。

第十一章习题答案 ... 错误!未定义书签。

第二章 习题答案设某点应力张量ijσ的分量值已知，求作用在过此点平面ax by cz d ++=上的应力矢量(,,)n nx ny nz p p p p ，并求该应力矢量的法向分量n σ。

解 该平面的法线方向的方向余弦为l a d m b d n c d d ====，，，而应力矢量的三个分量满足关系nx x xy xz ny xy y yz nz xz yz z p l m n p l m n p l m nστττστττσ⎧=++⎪=++⎨⎪=++⎩ 而法向分量n σ满足关系n nx ny nx p l p m p n σ=++最后结果为()()()()22222222222nx x xy xz ny xy y yz nx xz yz z n x y z xy yz zx p a b c d p a b c a p a b c da b c ab bc ca d d a b c στττστττσσσσστττ=++=++=++=+++++=++利用上题结果求应力分量为0,2,1,1,2,0x y z xy xz yz σσστττ======时，过平面31x y z ++=处的应力矢量n p ，及该矢量的法向分量n σ及切向分量n τ。

解求出l m n ===,,nx ny nz p p p 及n σ，再利用关系222222n nx ny nz n np p p p στ=++=+可求得n τ。

弹塑性力学第四章 弹性力学的基本方程与解法一、线性弹性理论适定问题的基本方程和边界条件对于在空间占有体积域V 的线弹性体在外加恒定载荷和固定几何约束条件下引起的小变形问题，若以, ,u εσ作为求解变量，则可以建立如下偏微分方程边值问题： 几何方程()1,,2ij i j j i u u ε=+ ()12∇+∇u u ε= (1a)广义胡克定律 ij ijkl kl E σε= :E σ=ε(1b)平衡方程 ,0ij j i f σ+= ∇⋅+=f 0σ V∀∈x (1c)以上方程均要求在域内各点均满足。

边界条件 u u i i = ∀∈x S ui (2a)n t j ji i σ= ∀∈x S ti(2b)对于适定问题，即不仅要求保证解存在唯一，而且有较好的稳定性。

当载荷或边界条件给定值有微小摄动时，应能保证问题解的变化也是微小的。

对于边界条件的提法就有严格的要求。

即要求：S S S S S ui ti ui ti U I ==∅(2c)对于各向同性材料，其广义胡克定律可具体写成 σλεδεij kk ij ij G =+2 ()tr 2G λ+I σ=εε (3a)()11ij ij kk ij E ενσνσδ⎡⎤=+−⎣⎦ ()()1tr Eνν=⎡⎤⎣⎦I ε1+σ−σ (3b)以上就域内方程来说，一共是对于u ,,σ ε的15个独立分量u i ij ij ,, σε的15个方程。

对于边界条件来说，三维问题每点有三个边界条件，而且是在三个正交方向上每个方向有一个边界条件，这个边界条件或者给定位移、或者给定面力。

这三个正交第四章 弹性力学的基本方程与解法方向可以是整体笛卡儿坐标系的三个方向，也可以是边界自然坐标系的三个方向（即法向和两个切向）。

从更一般来说，除去给定位移或面力外，还有另一种线性的边界条件t K u c i ij j i +=(4)这是一种弹性约束条件。

用这个条件可以取代给定位移或给定面力的条件。

附录Ⅱ习题解答提示与参考答案第二章应力理论2-1 ζn=ζ1l2+ζ2m2,；式中l、m、n为斜截面外法线的方向余弦。

2-2 p=111.5A；ζn=26A；ηn=108.5A2-3 提示：平面Ax+By+C z+D=0的外法线的方向余弦为：(式中i=1，2，3或A，B，C)答案：2-4 略2-5 (a)ζ1=738.5；ζ2=600；ζ3=-338.5；ηmax=538.5；应力单位为MPa。

(b)ζ1=700；ζ2=600；ζ3=-600；ηmax=650；应力单位为MPa。

2-6 ζ1=3.732η0；ζ2=-0.268η0；α=15º。

2-7 (材料力学解) 应力单位为MPa。

(弹塑性力学解) 应力单位为MPa。

2-8 ζ1=107.3a；ζ2=44.1a；ζ3=-91.4a；ζ1主方向：(±0.314，0.900，0.305)；ζ2主方向：(±0.948，±0.282，±0.146)；ζ3主方向：(0.048，±0.337，0.940)。

2-9；ζ2=0；ζ3=-ζ1。

2-10、2-11 略2-12 (1)略；(2)ζ8=ζm=5.333MPa；η8=8.654MPa。

2-13 p8=59.5；ζ8=25.0a；η8=54.1a。

2-14上式中S为静矩。

材料力学解不满足平衡微分方程和边界条件。

2-15，Q为梁横截面上的剪力。

提示：利用平衡微分方程求解。

2-16 ζ1=17.083×103Pa；ζ2=4.917×103Pa；ζ3=0,∂=40º16′。

2-17 略2-18 2。

2-19 提示：将三个主方向的三组方向余弦分别两两一组代人式(2-12)证之。

2-20 。

2-21 在AA′上：ζx=-γy，ηxy=0；在AB上：ηxy=0，ζy=-γh；在BB′上：l1=cosα，l2=-sinα，l3=0；则应力分量满足关系式：2-22 。

第八章 能量原理及其应用弹塑性力学问题实质上是边值问题，即求解满足一定边界条件的偏微分方程组。

然而只有对一些特殊的结构在特定加载条件下才能找到精确解，而对于一般的力学问题，如空间问题，泛定方程为含有15个未知量的6个偏微分方程，在给定边界条件时．求解是极其困难的，而且往往足小对能的。

因此，为了解决具体的工程结构力学问题，目前都广泛应用数值方法，如有限元法、无限元法、边界元法、无网格化法及样条元法等等。

这些解法的依据都是能量原理。

本章将讨论利用能量原理和极值原理求解弹塑性力学问题的近似解法。

本章共讨论五个能量原理。

首先是虚位移原理，由虚位移原理推导出最小势能原理，其次介绍虚应力原理，和由虚应力原理推导出最小余能原理。

另外，还简单介绍最大耗散能原理。

本章还讲述了根据上述的能量原理建立的有关弹性力学问题的数值解法。

8.1 基本概念1.1 物体变形的热力学过程由第四章知，物体在外界因素影响下的变形过程，严格来说都是一个热力学过程。

因此研究物体的状态，不仅要知道物体的变形状态，而且还要知道物体中每一点的温度。

如果物体在变形过程中，各点的温度与其周围介质的温度保持平衡，则称这一过程为等温过程；若在变形过程中，物体的温度没有改变，即既没有热量损失也没有热量增加，则称这一过程为绝热过程。

物体的瞬态高频振动，高速变形过程都可视为绝热过程。

令物体在变形过程中的动能为E ，应变能为U ，则在微小的t δ时间间隔内，物体从一种状态过渡到另一种状态时，根据热力学第一定律，总能量的变化为 Q W U E δδδδ+=+ (a) 其中，W δ为作用于物体上的体力和面力所完成的功；Q δ是物体由其周围介质所吸收(或向外发散)的热量，并以等量的功度量。

假定弹性变形过程是绝热的，则对于静力平衡问题有00==Q ，E δδ (b)将式(b)代入式(a)，则有W U δδ= (8.1-1)1.2 应变能由第四章的式(4.1-5b)知，在线弹性情况下，单位体积的应变能为ik ij ij ij ij d U εσεσε2100==⎰ (8.1-2)对于一维应力状态，在x x εσ-平面内，则0U 实际上就是应力应变曲线与x ε轴和'xx εε=所 围成的面积(图8.1)，即⎰='0Xx x d U εεσ (8.1-3)其中'x ε是物体变形过程某一指定时刻的应变，应 图8.1 应变能与应变余能变能0U 表示物体在变形过程中所储存的能量。

第四章本构方程在前面的章节中，已经建立了变形体的平衡微分方程和几何方程，分别是从静力学方面和从几何学方面考察了变形体的受力和变形。

但是只有这些方程还不足以解决变形体内的应力和变形问题。

对于变形体，未知变量包括6个应力分量，6个应变分量和3个位移分量，一共有15个未知函数，而平衡方程和几何方程一共是9个，未知函数的个数多于方程数。

因此还必须研究物体的物理性质，即应力与应变之间的关系。

通常称这种关系为变形体的本构方程，或称为物性方程。

塑性本构包括三个方面：1、屈服条件，2、流动法则，3、硬化关系；其中屈服条件：判断何时达到屈服，流动法则：屈服后塑性应变增量的方向，也即各分量的比值，硬化规律：决定给定的应力增量引起的塑性应变增量大小。

以上构成塑性本构关系。

4.1弹性应变能函数变形固体的平衡问题不仅需要运动微分方程、应变—位移方程(即变形几何方程)还需要将应变分量和应力张量分量联系起来，方能给定物体的材料抵抗各种形式变形的规律。

该规律的理论解释需要对分子间力的本质有深入的认识，该分子力力图使固体粒子间保持—定的距离，也就是需要对固体中应力分量和应变分量有深入的认识。

这种作用机理在非常接近稳定状态的气体中己弄清楚，但对于弹性体情况，目前科学技术发展水平还不能解决这一难题。

如要通过实验探求物体内部的应力和应变的关系，则总是从一些量的测量来推理得到，在一般情况下，这些量并非应力或应变的分量(例如平均应变、体积压缩、物体表面一线元的伸长等等)．因此，在现时应力与应变关系主要是通过直接实验建立。

然而该关系中的某些固有的一般特性可以在理沦上加以说朋，如能量守恒定律为应力-应变关系的理论研究提供了基础。

1.1应变能密度假设变形的过程是绝热的，也就是在变形过程中系统没有热的损失，而且假设物体中任意无穷小单元改变其体积和形状所消耗的功与其从未变形状态到最终变形状态的转换方式无关。

这个条件是弹性的另一种定义。

换句话说，就是假设物体粒子互相作用过程中的耗散(非保守)力的作用与保守力的作用相比是可以忽略的。