第四章弹塑性波的相互作用
- 格式:ppt
- 大小:8.53 MB
- 文档页数:110

第一题:推导波动方程,简述弹性波和塑性波的主要区别?要求给出主要的推导步骤,主要的方程,以及弹性波和塑性波的本质区别。
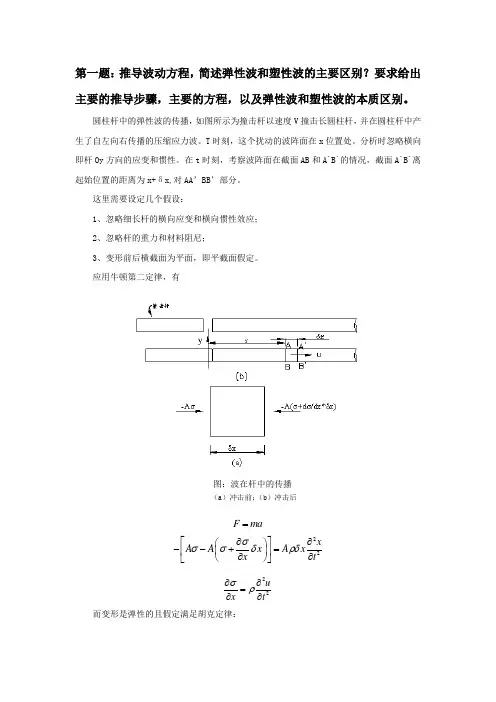
圆柱杆中的弹性波的传播,如图所示为撞击杆以速度V 撞击长圆柱杆,并在圆柱杆中产生了自左向右传播的压缩应力波。
T 时刻,这个扰动的波阵面在x 位置处。
分析时忽略横向即杆Oy 方向的应变和惯性。
在t 时刻,考察波阵面在截面AB 和A`B`的情况,截面A`B`离起始位置的距离为x+δx,对AA ’BB ’部分。
这里需要设定几个假设:1、忽略细长杆的横向应变和横向惯性效应;2、忽略杆的重力和材料阻尼;3、变形前后横截面为平面,即平截面假定。
应用牛顿第二定律,有图:波在杆中的传播(a )冲击前;(b )冲击后F ma =22x A A x A x x t σσσδρδ⎡∂⎤∂⎛⎫--+= ⎪⎢⎥∂∂⎝⎭⎣⎦ 22u x tσρ∂∂=∂∂ 而变形是弹性的且假定满足胡克定律:=E σε其中ε为应变,定义为/u x ∂∂,负号表示压应变,因此有22u u E x x tρ∂∂∂⎡⎤=⎢⎥∂∂∂⎣⎦ 和2222u E u t xρ∂∂=∂∂ 上式即为弹性波的波动方程,其中0EC ρ=为波速。
二、弹性波和塑性波的区别当物体某部分突然受力时,该处将产生弹性变形,并以波的形式向周围传播,使整个物体产生弹性变形,这种波称为弹性波。
当物体受到超过弹性极限的冲击应力扰动后产生的应力和应变的传播、反射,并使得物体产生塑性变形,这种波称为塑性波。
由于固体材料弹性性质和塑性性质的不同,因此在均匀的弹塑性介质中传播的塑性波和弹性波是有区别的,主要表现在:1、塑性波波速与应力有关,它随着应力的增大而减小,较大的变形将以较小的速度传播,而弹性波的波速与应力大小无关;2、在应力σ和应变ε的关系满足()σσε=时,塑性波波速总比弹性波波速小;3、塑性波在传播的过程中波形会发生变化,而弹性波则保持波形不变。
弹性波和塑性波的这些本质区别可以从波动方程中看出,在波动方程中的C 表示的就是应力波的传播速度,其中 弹性波的波速为:001d C C d σερ==,,Y d d E σσε≤= 塑性波的波速为:001d C C d σερ=<,,Y d d E σσε>< 其中Y 表示材料的屈服强度,E 表示材料的弹性模量。





第一题:推导波动方程,简述弹性波和塑性波的主要区别?要求给出主要的推导步骤,主要的方程,以及弹性波和塑性波的本质区别。
圆柱杆中的弹性波的传播,如图所示为撞击杆以速度V 撞击长圆柱杆,并在圆柱杆中产生了自左向右传播的压缩应力波。
T 时刻,这个扰动的波阵面在x 位置处。
分析时忽略横向即杆Oy 方向的应变和惯性。
在t 时刻,考察波阵面在截面AB 和A`B`的情况,截面A`B`离起始位置的距离为x+δx,对AA ’BB ’部分。
这里需要设定几个假设:1、忽略细长杆的横向应变和横向惯性效应;2、忽略杆的重力和材料阻尼;3、变形前后横截面为平面,即平截面假定。
应用牛顿第二定律,有图:波在杆中的传播(a )冲击前;(b )冲击后F ma =22x A A x A x x t σσσδρδ⎡∂⎤∂⎛⎫--+= ⎪⎢⎥∂∂⎝⎭⎣⎦ 22u x tσρ∂∂=∂∂ 而变形是弹性的且假定满足胡克定律:=E σε其中ε为应变,定义为/u x ∂∂,负号表示压应变,因此有22u u E x x tρ∂∂∂⎡⎤=⎢⎥∂∂∂⎣⎦ 和2222u E u t xρ∂∂=∂∂ 上式即为弹性波的波动方程,其中0EC ρ=为波速。
二、弹性波和塑性波的区别当物体某部分突然受力时,该处将产生弹性变形,并以波的形式向周围传播,使整个物体产生弹性变形,这种波称为弹性波。
当物体受到超过弹性极限的冲击应力扰动后产生的应力和应变的传播、反射,并使得物体产生塑性变形,这种波称为塑性波。
由于固体材料弹性性质和塑性性质的不同,因此在均匀的弹塑性介质中传播的塑性波和弹性波是有区别的,主要表现在:1、塑性波波速与应力有关,它随着应力的增大而减小,较大的变形将以较小的速度传播,而弹性波的波速与应力大小无关;2、在应力σ和应变ε的关系满足()σσε=时,塑性波波速总比弹性波波速小;3、塑性波在传播的过程中波形会发生变化,而弹性波则保持波形不变。
弹性波和塑性波的这些本质区别可以从波动方程中看出,在波动方程中的C 表示的就是应力波的传播速度,其中 弹性波的波速为:001d C C d σερ==,,Y d d E σσε≤= 塑性波的波速为:001d C C d σερ=<,,Y d d E σσε>< 其中Y 表示材料的屈服强度,E 表示材料的弹性模量。



水平地震作用下桩—土—上部结构弹塑性动力相互作用分析一、本文概述《水平地震作用下桩—土—上部结构弹塑性动力相互作用分析》这篇文章主要探讨了水平地震作用对桩—土—上部结构体系的影响,并详细分析了这一复杂系统在地震作用下的弹塑性动力相互作用。
本文旨在深入理解地震时桩—土—上部结构体系的动态行为,为工程实践提供理论依据和指导,以提高结构的抗震性能。
本文首先介绍了地震作用下桩—土—上部结构体系的研究背景和意义,阐述了国内外在该领域的研究现状和发展趋势。
接着,文章对桩—土—上部结构体系的弹塑性动力相互作用进行了理论分析,包括桩土相互作用、地震波的传播与散射、结构的动力响应等方面。
在理论分析的基础上,本文进行了数值模拟和实验研究。
通过建立合理的数值模型,模拟了不同地震波作用下的桩—土—上部结构体系的动态响应过程,得到了结构的地震反应特性和破坏模式。
同时,结合实验数据,验证了数值模拟的有效性,并对模拟结果进行了深入分析。
本文总结了地震作用下桩—土—上部结构弹塑性动力相互作用的研究成果,指出了现有研究的不足和未来研究方向。
文章强调了在实际工程中应考虑桩土相互作用的影响,合理设计抗震结构,以提高结构的整体抗震性能。
通过本文的研究,可以为工程师和科研人员提供有益的参考,推动桩—土—上部结构体系抗震设计方法的改进和完善,为保障人民生命财产安全和提高建筑行业的可持续发展水平做出贡献。
二、桩—土—上部结构相互作用的基本理论桩—土—上部结构的相互作用是一个复杂且关键的动力学问题,涉及到地震波传播、土壤动力学、结构动力学等多个领域。
在水平地震作用下,土壤对桩的约束和桩对土壤的支撑形成了相互作用力,这些力通过桩传递到上部结构,进而影响整个系统的动力响应。
桩—土相互作用的理论基础主要是基于土的动力学特性和桩土之间的接触关系。
土壤在地震作用下的行为受到其本身的物理特性(如密度、弹性模量、泊松比等)和动力特性(如阻尼比、剪切波速等)的影响。
声波调控下弹塑性形变现象分析引言:声波调控是一种新兴的技术手段,通过声波对物质的影响和控制,可以实现许多独特的现象和效应。
弹塑性形变是固体材料在外力作用下发生的一种形变过程,既具有弹性回复的特点,又伴随着一定程度的塑性变形。
本文将讨论声波调控对材料弹塑性形变现象的影响及其机理。
一、声波调控下弹性形变现象分析声波是一种机械波,将物质中的粒子进行周期性的振动。
当声波传播到固体材料中时,声波的压力波将作用于材料表面,使材料发生弹性形变。
这种形变是临时的,一旦声波停止,材料将恢复到原来的形状。
因此,声波调控下的弹性形变现象主要体现为材料的压缩、拉伸和扭转等。
在声波场的作用下,材料会产生压力变化。
当声波作用于材料表面时,声波的压力波将引起表面的局部压缩或拉伸,从而导致形变。
这种形变可以通过弹性模量来描述,即形变的比例与应力的比值。
根据胡克定律,压力与形变成正比,且成反比于材料的弹性模量。
因此,弹性形变可以通过调整声波的振幅和频率来控制。
二、声波调控下塑性形变现象分析塑性形变是固体材料在外力作用下,超过其弹性限度后发生的不可逆形变。
声波调控下的塑性形变现象主要体现为材料的滑移、扩散和晶格变形等。
声波可以通过激活材料中的位错,引起位错运动和扩散,从而促进塑性变形。
位错是材料中的晶格缺陷,是材料塑性变形的重要因素。
当声波作用于材料中时,它会给位错施加额外的力,促使位错进行滑移和扩散。
这将导致材料的局部塑性变形,形成塑性形变。
通过调控声波的频率和振幅,可以改变位错的密度和活动能力,从而控制材料的塑性形变。
较高的声波频率和振幅使材料中的位错活动增加,导致更大的塑性形变。
而较低的频率和振幅则减少位错的活动能力,限制了材料的塑性变形。
三、声波调控下弹塑性形变的机理分析声波调控下材料的弹塑性形变机理主要涉及声波的作用原理和材料的力学特性。
首先,声波作用于材料表面的压力波会引起材料分子的振动和位移。
这种振动和位移会产生应力和形变,使材料发生弹性变形。
弹塑性⼒学定理和公式应⼒应变关系弹性模量||⼴义虎克定律1.弹性模量对于应⼒分量与应变分量成线性关系的各向同性弹性体,常⽤的弹性常数包括:a弹性模量单向拉伸或压缩时正应⼒与线应变之⽐,即b切变模量切应⼒与相应的切应变之⽐,即c体积弹性模量三向平均应⼒与体积应变θ(=εx+εy+εz)之⽐,即d泊松⽐单向正应⼒引起的横向线应变ε1的绝对值与轴向线应变ε的绝对值之⽐,即此外还有拉梅常数λ。
对于各向同性材料,这五个常数中只有两个是独⽴的。
常⽤弹性常数之间的关系见表3-1 弹性常数间的关系。
室温下弹性常数的典型值见表3-2 弹性常数的典型值。
2.⼴义虎克定律线弹性材料在复杂应⼒状态下的应⼒应变关系称为⼴义虎克定律。
它是由实验确定,通常称为物性⽅程,反映弹性体变形的物理本质。
A各向同性材料的⼴义虎克定律表达式(见表3-3 ⼴义胡克定律表达式)对于圆柱坐标和球坐标,表中三向应⼒公式中的x 、y、z分别⽤r、θ、z和r、θ、φ代替。
对于平⾯极坐标,表中平⾯应⼒和平⾯应变公式中的x、y、z⽤r、θ、z代替。
B⽤偏量形式和体积弹性定律表⽰的⼴义虎克定律应⼒和应变量分解为球量和偏量两部分时,虎克定律可写成更简单的形式,即体积弹性定律应⼒偏量与应变偏量关系式在直⾓坐标中,i,j=x,y,z;在圆柱坐标中,i,j=r,θ,z,在球坐标中i,j=r,θ,φ。
弹性⼒学基本⽅程及其解法弹性⼒学基本⽅程|| 边界条件|| 按位移求解的弹性⼒学基本⽅法|| 按应⼒求解的弹性⼒学基本⽅程|| 平⾯问题的基本⽅程|| 基本⽅程的解法|| ⼆维和三维问题常⽤的应⼒、位移公式1.弹性⼒学基本⽅程在弹性⼒学⼀般问题中,需要确定15个未知量,即6个应⼒分量,6个应变分量和3个位移分量。
这15个未知量可由15个线性⽅程确定,即(1)3个平衡⽅程[式(2-1-22)],或⽤脚标形式简写为(2)6个变形⼏何⽅程[式(2-1-29)],或简写为(3)6个物性⽅程[式(3-5)或式(3-6)],简写为或2.边界条件弹性⼒学⼀般问题的解,在物体部满⾜上述线性⽅程组,在边界上必须满⾜给定的边界条件。
第四章本构方程在前面的章节中,已经建立了变形体的平衡微分方程和几何方程,分别是从静力学方面和从几何学方面考察了变形体的受力和变形。
但是只有这些方程还不足以解决变形体内的应力和变形问题。
对于变形体,未知变量包括6个应力分量,6个应变分量和3个位移分量,一共有15个未知函数,而平衡方程和几何方程一共是9个,未知函数的个数多于方程数。
因此还必须研究物体的物理性质,即应力与应变之间的关系。
通常称这种关系为变形体的本构方程,或称为物性方程。
塑性本构包括三个方面:1、屈服条件,2、流动法则,3、硬化关系;其中屈服条件:判断何时达到屈服,流动法则:屈服后塑性应变增量的方向,也即各分量的比值,硬化规律:决定给定的应力增量引起的塑性应变增量大小。
以上构成塑性本构关系。
4.1弹性应变能函数变形固体的平衡问题不仅需要运动微分方程、应变—位移方程(即变形几何方程)还需要将应变分量和应力张量分量联系起来,方能给定物体的材料抵抗各种形式变形的规律。
该规律的理论解释需要对分子间力的本质有深入的认识,该分子力力图使固体粒子间保持—定的距离,也就是需要对固体中应力分量和应变分量有深入的认识。
这种作用机理在非常接近稳定状态的气体中己弄清楚,但对于弹性体情况,目前科学技术发展水平还不能解决这一难题。
如要通过实验探求物体内部的应力和应变的关系,则总是从一些量的测量来推理得到,在一般情况下,这些量并非应力或应变的分量(例如平均应变、体积压缩、物体表面一线元的伸长等等).因此,在现时应力与应变关系主要是通过直接实验建立。
然而该关系中的某些固有的一般特性可以在理沦上加以说朋,如能量守恒定律为应力-应变关系的理论研究提供了基础。
1.1应变能密度假设变形的过程是绝热的,也就是在变形过程中系统没有热的损失,而且假设物体中任意无穷小单元改变其体积和形状所消耗的功与其从未变形状态到最终变形状态的转换方式无关。
这个条件是弹性的另一种定义。
换句话说,就是假设物体粒子互相作用过程中的耗散(非保守)力的作用与保守力的作用相比是可以忽略的。