下载文档原格式
《中级计量经济学》课程简介课程号：课程名称(含英文主)：研究生《中级计量经济学》（Intermediate Econometrics）学分：2周学时：4预修课程：经济学、高等数学、概率论和数理统计内容简介：首先介绍计量经济学中必须具备的数学知识如高等代数中矩阵、概率论与数理统计中点估计、有效估计、一致估计、区间估计、假设检验、大样本与极限理论等。
而后介绍古典线性回归模型、多元线性回归模型、带有线性约束的多元线性回归模型及其假设检验、正态线性统计模型的最大似然估计、古典线性的大样本理论、非球形扰动与广义最小二乘、异方差性、非线性回归模型等。
选用教材或参考书：教材：William H. Greene，Econometrics Analysis, fourth edition。
参考书：1．William H. Greene，经济计量分析，Econometrics Analysis 的翻译, 中国社会科学出版社。
2．课件。
教学大纲课程号：课程名称(含英文主)：研究生《中级计量经济学》（Intermediate Econometrics）学分：2周学时：4预修课程：经济学、高等数学、概率论和数理统计一、课程的教学目的和基本要求：本课程为已具备经济学，概率论和数理统计以及初级计量经济学的研究生开设的《中级计量经济学》。
目的是为他们今后在经济和金融领域能够独立开展科学研究和调查提供坚实的统计与计量经济学的方法与技巧。
本课程的重点是使学生充分掌握和理解以下三个方面的知识与技能：1．计量经济学的理论与原理；2．计量经济学中广泛使用的统计推断知识，方法与技巧；3．掌握各种模型需要的条件与模型的局限性和适用性。
二、课程内容与学时分配第一章引言…………………………………………………………………..1学时 计量经济学概念为什么学计量经济学计量经济学模型第二章矩阵的基础知识……………………………………………………..4学时 矩阵的概念与运算矩阵的特征根与特征向量矩阵的二次型与二项式矩阵的微分第三章概率论与数理统计……………………………………………………..4学时 随机变量与概率分布函数与中心极限定理二元态分布与多元正态分布样本与样本的分布函数统计量及其分布点估计有效估计一致估计区间估计假设检验第四章古典线性回归模型…………………………………………………..4学时 古典线性回归模型与其假设条件最小二乘回归方差分析最小二乘统计量的有限样本性质预测第五章多元线性回归模型…………………………………………………..4学时 多元线性回归模型与其假设条件最小二乘回归方差分析最小二乘统计量的有限样本性质预测第六章带有线性约束的多元线性回归模型及其假设检验…………………4学时带有线性约束的多元线性回归模型与其假设条件线性约束的检验参数带有约束的最小二乘回归Wald检验实例第七章正态线性统计模型的最大似然估计………………………………..4学时 模型及其假设条件模型求解与最小二乘估计量的比较第八章古典线性回归的大样本理论………………………………..4学时 最小二乘统计量的有限样本性质古典回归模型的渐近分布理论最小二乘估计量的渐近正态性标准检验统计量的渐近行为第九章非线性回归模型………………………………..2学时非线性回归模型可供选择的几个统计量假设检验与参数约束Box-Cox 变换第十章异方差性………………………………..2学时OLS估计的探讨异方差性的检验GLS估计二阶段估计第一章引言1.1什么是计量经济学？计量经济学是由挪威经济学家R.Fisher在三十年代首先创立的一门学科，是关于运用统计方法测量经济关系的艺术与科学，已经成为现代经济学的重要组成部分之一。
计量经济学讲义第六讲（共⼗讲）第六讲多重共线⼀、 FWL 定理及其应⽤考虑模型：112233i i i i i y a b x b x b x ε=++++ （1）假如我们只关注1b，则通过如下步骤可以获得之。
第1步：把1x 对其他解释变量进⾏回归（请注意，截距所对应的解释变量为1），即有： 101223i i i ix x x v βββ=+++ （2）第2步：把y 也对（2）中的解释变量进⾏回归，即有：01223i i i i y x x w ???=+++ （3）第3步：把w 对?v 进⾏回归（不含截距，当然你可以包含截距，但你会发现，截距的估计结果是零，这是因为?w 与?v 其均值都为零），即有模型：i i i ve w η=+ （4）则有：2i i iw v v η=∑∑，可以验证，1??b η=，且残差?i e 等于初始的残差?i ε。
此即著名的FWL 定理（Frisch-Waugh-Lovell theorem ）。
关于FWL 定理的⼀个简单证明见附录1。
思考题：利⽤关于“偏导数”的直觉，你能够理解1b η=吗？考察2i i iw v v η=∑∑，把01223i i i i y x x w ?=---代⼊，现在分⼦是：2012230123()?i i i i i i i ii i i v x i i y x x y v x v v v wv ------∑∑∑==∑∑∑应该注意到，在进⾏第⼀步回归时，OLS 法保证了203i i i i i v x x vv ===∑∑∑ 因此，22i i i i i iw v y v v v η==∑∑∑∑ 显然，如果把y 对?v 直接进⾏⽆截距回归：*?iiiy v η?=+ （5）我们也可以得到：*122i i i i i i y v w v b v vηη====∑∑∑∑。
因此，如果只关注如何获得1b ，我们可以把FWL 定理中第⼆步与第三步合并为把y 对v 直接进⾏⽆截距回归。
第6章 多重共线性6.1 多重共线性及其产生的原因6.1.1 多重共线性(Multicollinearity)的定义从数学意义上去解释变量之间存在共线性，就是对于变量k x x x ,,21，如果存在不全为零的常数k λλλ ,,21，使得下式成立02211=+++k k x x x λλλ （6.1.1）则称变量k x x x ,,21之间存在完全共线性。
在计量经济学中，一个具有两个以上解释变量的线性回归模型里，如果解释变量之间存在式（6.1.1）那样的关系，则称这些解释变量之间存在完全的多重共线性。
完全多重共线性还可以用矩阵形式加以描述。
设解释变量矩阵X 为X = ⎪⎪⎪⎪⎪⎭⎫⎝⎛kn k k n n x x x x x x x x x 212222*********所谓完全的多重共线性，就是0='X X 。
或者rank (X )k 〈+1，表明在矩阵X 中，至少有一个列向量可以由其余的列向量线性表示。
所谓近似共线性或不完全多重共线性是指对于k 个解释变量t x (t =1,2,3,…k)，如果存在不全为零的数k λλλ ,,21使得02211=++++u x x x k k λλλ （6.1.2）成立，其中u 为随机误差项。
如果k 个解释变量之间不存在上述完全或不完全的线性关系式，则称无多重共线性。
如果用矩阵表示，这时X 为满秩矩阵，即rank (X )=k +1。
6.1.2 多重共线性产生的原因根据经验，多重共线性产生的经济背景和原因有以下几个方面：1．经济变量之间往往存在同方向的变化趋势 2．经济变量之间往往存在着密切的关联度 3．在模型中引入滞后变量也容易产生多重共线性4．在建模过程中由于解释变量选择不当，引起了变量之间的多重共线性6.2 多重共线性造成的影响6.2.1 完全共线性下参数估计量不存在多元线性回归模型U XB Y +=的普通最小二乘估计量为Y X X X B ''=-1)(ˆ如果解释变量之间存在完全多重共线性，由于X 矩阵的系数行列式0='X X ，逆矩阵1)(-'X X 不存在，无法得到参数估计式Bˆ。
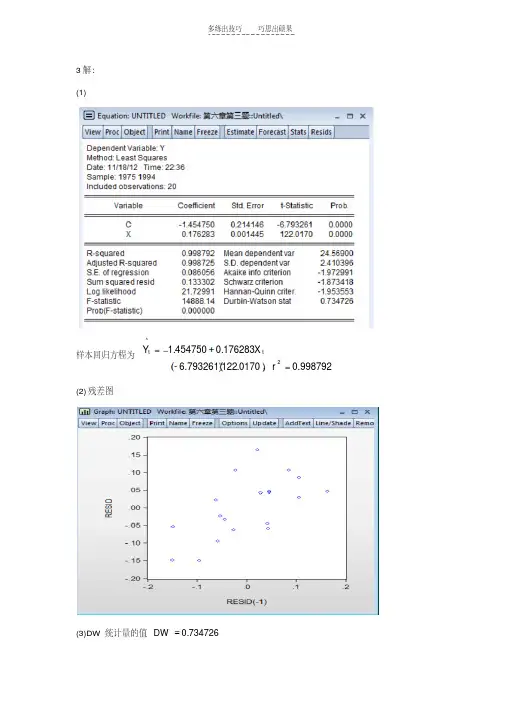
3解:(1)样本回归方程为998792.00170.1226.793261-176283.0454750.12^t r X Y t，(2)残差图(3)DW 统计量的值734726.0DW(4)BG LM 自相关检验辅助回归式估计结果是t t t tX e e 000420.0060923.0638831.01因为84.3998223.7,84.31205.0LM ,所以LM 检验量也说明样本回归方程的误差项存在一阶正自相关。
首先估计自相关系数^，得632637.02734726.0121^DW 对原变量做广义差分变换。
令1t 632637.0t t Y Y GDY ，1t 632637.0t t X X GDX 以年1994~1975,,t t GDX GDY 为样本再次回归，得tGDX GDY 173740.0391490.0t 回归方程拟合的效果仍然比较好,651914.1DW 对于给定05.0，查表得，。
43.1,24.1U L d d 因为75.243.11651914.1DW ,依据判别规则，误差项已消除自相关。
由391490.0^*0，得06568.1632637.01/391490.01/^^*0^0则原模型的广义最小二乘估计结果是t X Y 173470.006568.1^t 。
4解：（1）样本回归方程为tGDP Y 694454.0674.2816^t（2）残差图(3)3397.0DW(4)BG LM 自相关检验辅助回归式估计结果是t t t tGDP e e 029062.07871.334985257.01因为84.309615.30,84.31205.0LM ,所以LM 检验量也说明样本回归方程的误差项存在一阶正自相关。
首先估计自相关系数^，得83015.023397.0121^DW对原变量做广义差分变换。
令1t 83015.0t t Y Y GDY ，183015.0t t tGDGDP GDP GDGDP ，以年1994~1975,,t t GDGDP GDY 为样本再次回归，得。
第六讲 多重共线一、 数学准备：FWL 定理对于多元线性回归模型：112233i i i i i y a b x b x b x ε=++++ （1）在OLS 法下，各系数估计通过求解四个正规方程而获得。
事实上，如果只关注某一个斜率系数的估计结果，则通过构造一系列简单线性回归模型就能获得所关注的斜率系数的估计。
假设我们现在关注1ˆb ，那么构造系列简单线性回归模型的过程是：第一步：把1x 对其他解释变量进行回归（请注意，截距所对应的解释变量为1），即有：101223ˆˆˆˆi i i i x x x v βββ=+++ （2） 第二步：把y 也对（2）中的解释变量进行回归，即有：01223ˆˆˆˆi i i i y x x w ϕϕϕ=+++ （3）第三步：把ˆw 对ˆv 进行回归（因为ˆw 与ˆv 其均值都为零，所以该回归模型不必带有截距项），即有：ˆˆˆˆi i i v e w η=+ （4） 现在有两个结论，即，结论一：21ˆˆˆˆˆi i i wv v b η==∑∑；结论二：残差ˆi e 等于多元回归中的残差ˆi ε。
这两个结论就是著名的FWL 定理（Frisch-Waugh-Lovell theorem ）。
关于FWL 定理的一个简单证明见附录1。
附录2涉及到该定理的应用。
笔记：1b 所反映的是，在控制其他因素后1x 对y 的影响（与“偏导数”概念对应）。
1x 与y 的相关关系可能是由于它们共同的“亲戚”—— 2x 与3x 所带来的。
在控制共同“亲戚”对1x 及其y 的影响后，我们所发现的1x 与y 的相关关系被称为偏相关关系。
在前述步骤中，第一步与第二步实际上是在剔除共同“亲戚”的影响。
练习：基于简单线性回归模型：i i i y a bx ε=++验证FWL 定理。
如果我们只需要结论一，则上述三步骤可以被简化为两步骤：首先把1x 对其他解释变量进行回归，得到残差ˆi v ，其次把y 对ˆv 进行回归：ˆˆ*ˆi i iv y ηξ=+ 可以验证：122ˆˆˆˆˆˆ*ˆˆi i i i i iy v wv b v v ηη====∑∑∑∑，但应该注意此时并不能保证ˆˆi i ξε=成立。
