stata中级计量经济学多元线性模型设定和估计

多元线性回归模型的估计与解释多元线性回归是一种广泛应用于统计学和机器学习领域的预测模型。

与简单线性回归模型相比，多元线性回归模型允许我们将多个自变量引入到模型中，以更准确地解释因变量的变化。

一、多元线性回归模型的基本原理多元线性回归模型的基本原理是建立一个包含多个自变量的线性方程，通过对样本数据进行参数估计，求解出各个自变量的系数，从而得到一个可以预测因变量的模型。

其数学表达形式为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中，Y为因变量，X1、X2、...、Xn为自变量，β0、β1、β2、...、βn为模型的系数，ε为误差项。

二、多元线性回归模型的估计方法1. 最小二乘法估计最小二乘法是最常用的多元线性回归模型估计方法。

它通过使残差平方和最小化来确定模型的系数。

残差即观测值与预测值之间的差异，最小二乘法通过找到使残差平方和最小的系数组合来拟合数据。

2. 矩阵求解方法多元线性回归模型也可以通过矩阵求解方法进行参数估计。

将自变量和因变量分别构成矩阵，利用矩阵运算，可以直接求解出模型的系数。

三、多元线性回归模型的解释多元线性回归模型可以通过系数估计来解释自变量与因变量之间的关系。

系数的符号表示了自变量对因变量的影响方向，而系数的大小则表示了自变量对因变量的影响程度。

此外，多元线性回归模型还可以通过假设检验来验证模型的显著性。

假设检验包括对模型整体的显著性检验和对各个自变量的显著性检验。

对于整体的显著性检验，一般采用F检验或R方检验。

F检验通过比较回归平方和和残差平方和的比值来判断模型是否显著。

对于各个自变量的显著性检验，一般采用t检验，通过检验系数的置信区间与预先设定的显著性水平进行比较，来判断自变量的系数是否显著不为零。

通过解释模型的系数和做假设检验，我们可以对多元线性回归模型进行全面的解释和评估。

四、多元线性回归模型的应用多元线性回归模型在实际应用中具有广泛的应用价值。

一、邹式检验（突变点检验、稳定性检验）1.突变点检验1985—2002年中国家用汽车拥有量（t y ，万辆）与城镇居民家庭人均可支配收入（t x ，元），数据见表。

表 中国家用汽车拥有量（t y ）与城镇居民家庭人均可支配收入（t x ）数据年份 t y （万辆） t x （元）年份 t y （万辆） t x （元）1985 1994 1986 1995 4283 1987 1996 1988 1997 1989 1998 1990 1999 5854 1991 2000 6280 1992 2001 19932002下图是关于t y 和t x 的散点图：从上图可以看出，1996年是一个突变点，当城镇居民家庭人均可支配收入突破元之后，城镇居民家庭购买家用汽车的能力大大提高。

现在用邹突变点检验法检验1996年是不是一个突变点。

：两个字样本（1985—1995年，1996—2002年）相对应的模型回归参数相等HH：备择假设是两个子样本对应的回归参数不等。

1在1985—2002年样本范围内做回归。

在回归结果中作如下步骤(邹氏检验)：1、 Chow 模型稳定性检验（lrtest）用似然比作chow检验，chow检验的零假设：无结构变化，小概率发生结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用似然比检验检验结构没有发生变化的约束得到结果如下;(如何解释)2.稳定性检验（邹氏稳定性检验）以表为例，在用1985—1999年数据建立的模型基础上，检验当把2000—2002年数据加入样本后，模型的回归参数时候出现显著性变化。

* 用F-test作chow间断点检验检验模型稳定性* chow检验的零假设：无结构变化，小概率发生结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用F 检验检验结构没有发生变化的约束*计算和显示 F 检验统计量公式，零假设：无结构变化然后 dis f_test 则 得到结果;* F 统计量的临界概率然后 得到结果* F 统计量的临界值然后 得到结果(如何解释)二、似然比（LR ）检验有中国国债发行总量（t DEBT ，亿元）模型如下：0123t t t t t DEBT GDP DEF REPAY u ββββ=++++其中t GDP 表示国内生产总值（百亿元），t DEF 表示年财政赤字额（亿元），t REPAY 表示年还本付息额（亿元）。

多元线性回归模型及其参数估计多元线性回归的显著性Y=β0+β1X1+β2X2+...+βnXn+ε其中，Y表示因变量（被预测或解释的变量），X1,X2,...,Xn表示自变量（用于预测或解释因变量的变量），β0,β1,β2,...,βn表示模型的参数，ε表示误差项。

参数估计就是指通过样本数据来估计模型中的参数。

在多元线性回归中，常用的参数估计方法是最小二乘法。

最小二乘法的目标是最小化实际观测值与回归方程所预测值之间的残差平方和。

为了评估多元线性回归模型的显著性，可以进行假设检验。

最常用的假设检验是利用F检验来检验整个回归模型的显著性。

F检验的原假设是回归模型中所有自变量的系数都等于零，即H0:β1=β2=...=βn=0，备择假设是至少存在一个自变量的系数不等于零，即H1:β1≠β2≠...≠βn≠0。

F统计量的计算公式为：F=(SSR/k)/(SSE/(n-k-1))其中，SSR表示回归平方和，即实际观测值与回归方程所预测值之间的残差平方和，k表示自变量的个数，SSE表示误差平方和，即实际观测值与回归方程所预测值之间的残差平方和，n表示样本容量。

根据F统计量的分布特性，可以计算得出拒绝原假设的临界值，若计算出来的F统计量大于临界值，则可以拒绝原假设，认为回归模型是显著的，即至少存在一个自变量对因变量有显著影响。

除了整体的回归模型显著性检验，我们还可以进行各个自变量的显著性检验。

每一个自变量的显著性检验都是基于t检验。

t检验的原假设是自变量的系数等于零，即H0:βi=0，备择假设是自变量的系数不等于零，即H1:βi≠0。

t统计量的计算公式为：t = (βi - bi) / (SE(βi))其中，βi表示模型中第i个自变量的系数估计值，bi表示模型中第i个自变量的理论值（一般为零），SE(βi)表示第i个自变量的系数的标准误。

根据t统计量的分布特性，可以计算得出对应自由度和置信水平的临界值，若计算出来的t统计量的绝对值大于临界值，则可以拒绝原假设，认为该自变量是显著的，即对因变量有显著影响。

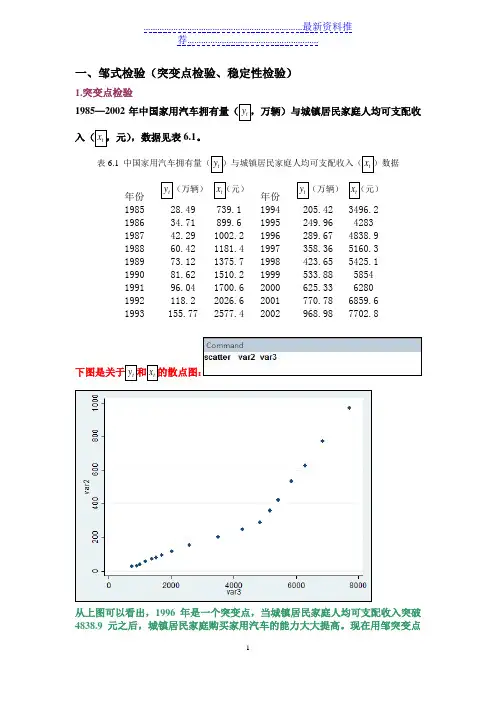
一、邹式检验（突变点检验、稳定性检验）1.突变点检验1985—2002年中国家用汽车拥有量（t y ，万辆）与城镇居民家庭人均可支配收入（t x ，元），数据见表6.1。

表6.1 中国家用汽车拥有量（t y ）与城镇居民家庭人均可支配收入（t x ）数据年份 t y （万辆） t x （元）年份 t y （万辆） t x （元）1985 28.49 739.1 1994 205.42 3496.2 1986 34.71 899.6 1995 249.96 4283 1987 42.29 1002.2 1996 289.67 4838.9 1988 60.42 1181.4 1997 358.36 5160.3 1989 73.12 1375.7 1998 423.65 5425.1 1990 81.62 1510.2 1999 533.88 5854 1991 96.04 1700.6 2000 625.33 6280 1992 118.2 2026.6 2001 770.78 6859.6 1993155.77 2577.42002968.98 7702.8下图是关于t y 和t x 的散点图：从上图可以看出，1996年是一个突变点，当城镇居民家庭人均可支配收入突破4838.9元之后，城镇居民家庭购买家用汽车的能力大大提高。

现在用邹突变点检验法检验1996年是不是一个突变点。

H0：两个字样本（1985—1995年，1996—2002年）相对应的模型回归参数相等H1：备择假设是两个子样本对应的回归参数不等。

在1985—2002年样本范围内做回归。

在回归结果中作如下步骤(邹氏检验)：1、Chow 模型稳定性检验（lrtest）用似然比作chow检验，chow检验的零假设：无结构变化，小概率发生结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用似然比检验检验结构没有发生变化的约束得到结果如下;(如何解释？)2.稳定性检验（邹氏稳定性检验）以表6.1为例，在用1985—1999年数据建立的模型基础上，检验当把2000—2002 * 用F-test作chow间断点检验检验模型稳定性* chow检验的零假设：无结构变化，小概率发生结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用F 检验检验结构没有发生变化的约束*计算和显示 F 检验统计量公式，零假设：无结构变化然后dis f_test 则得到结果;* F 统计量的临界概率然后 得到结果* F 统计量的临界值然后 得到结果(如何解释？)二、似然比（LR ）检验有中国国债发行总量（t DEBT ，亿元）模型如下：0123t t t t t DEBT GDP DEF REPAY u ββββ=++++其中t GDP 表示国内生产总值（百亿元），t DEF 表示年财政赤字额（亿元），t REPAY 表示年还本付息额（亿元）。

计量经济学实验报告stata计量经济学实验报告导言计量经济学是经济学中的一个重要分支，通过运用统计学和数学工具来研究经济现象和经济理论的有效性。

其中，实证研究是计量经济学的核心内容之一，而stata作为一款强大的统计分析软件，被广泛应用于计量经济学实证研究中。

本文将结合实例，介绍如何使用stata进行计量经济学实验研究。

实证研究的背景和目的实证研究是通过收集实际数据，运用统计学方法对经济理论进行检验和验证的过程。

实证研究的目的在于揭示经济现象的本质规律，为政策制定和经济决策提供科学依据。

在本次实证研究中，我们将以某国家的GDP增长率作为主要研究对象，探讨GDP增长率与人口增长率、投资率以及出口增长率之间的关系。

数据收集和处理首先，我们需要收集相关数据，包括GDP增长率、人口增长率、投资率和出口增长率。

这些数据可以从国家统计局或其他相关机构获取。

在收集到数据后，我们需要对数据进行处理，确保数据的准确性和一致性。

在stata中，可以使用命令load或import将数据导入软件中，并利用命令describe对数据进行描述性统计。

模型设定和估计在数据处理完成后，我们需要建立经济模型，并对模型进行估计。

在本次实证研究中，我们将采用多元线性回归模型来探究GDP增长率与人口增长率、投资率和出口增长率之间的关系。

模型设定如下：GDP增长率= β0 + β1 * 人口增长率+ β2 * 投资率+ β3 * 出口增长率+ ε其中，β0、β1、β2和β3为待估参数，ε为误差项。

在stata中，可以使用命令regress来进行回归分析，估计模型中的参数。

同时，还可以使用命令summary 对回归结果进行统计学检验，判断模型的显著性和拟合优度。

结果分析和讨论在完成模型估计后，我们需要对结果进行分析和讨论。

首先，可以通过回归结果中的系数估计值来判断变量之间的关系。

如果系数为正，表示变量之间存在正向关系；如果系数为负，表示变量之间存在负向关系。

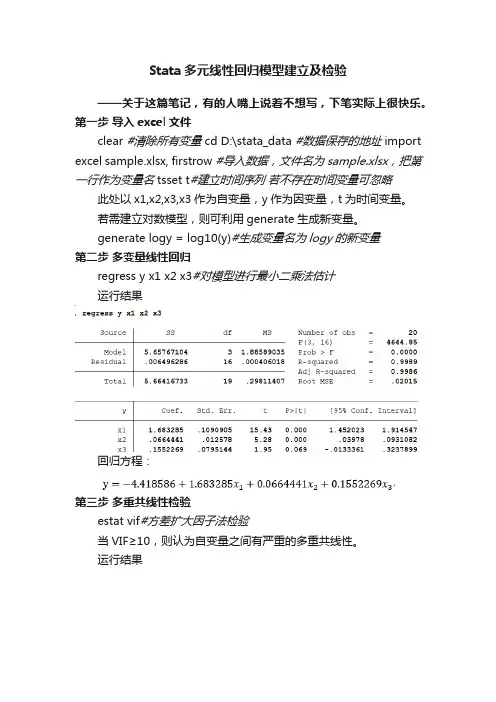
Stata多元线性回归模型建立及检验——关于这篇笔记，有的人嘴上说着不想写，下笔实际上很快乐。

第一步导入excel文件clear #清除所有变量 cd D:\stata_data #数据保存的地址 import excel sample.xlsx, firstrow #导入数据，文件名为sample.xlsx，把第一行作为变量名 tsset t#建立时间序列若不存在时间变量可忽略此处以x1,x2,x3,x3作为自变量，y作为因变量，t为时间变量。

若需建立对数模型，则可利用generate生成新变量。

generate logy = log10(y)#生成变量名为logy的新变量第二步多变量线性回归regress y x1 x2 x3#对模型进行最小二乘法估计运行结果回归方程：第三步多重共线性检验estat vif#方差扩大因子法检验当VIF≥10，则认为自变量之间有严重的多重共线性。

运行结果若模型出现多重共线性，可以剔除一些不重要的解释变量，或增大样本量。

第四步异方差检验imtest,white#White检验如果输出的P-Value显著小于0.05，则拒绝原假设，认为存在异方差性。

运行结果若模型出现异方差性，则不能用普通的最小二乘法进行估计，需要对原模型进行变换，使之满足同方差性假设，然后进行模型参数估计。

通常可以采用加权最小二乘法（weighted least square,WLS）或BOX-COX变换法。

第五步序列相关性检验首先保证所用的数据必须为时间序列数据。

如果原数据不是时间序列数据，则需要自行定义一个：gen n=_n #生成一个时间序列的标志变量ntsset n #将这个数据集定义为依据时间序列标志变量n定义的时间序列数据接下来介绍三种检验方法（一）残差图检验predict e,r#生成残差值e scatter eLe#生成残差散点图运行结果（二）DW检验（一阶自相关问题的常用检验法）estat dwatson#DW检验经验上，DW值在1.8-2.2之间时接受原假设，说明模型不存在一阶自相关，若DW值接近0或4，则拒绝原假设，认为存在一阶自相关。

第三章 多元线性回归模型第一节 多元线性回归模型及基本假定问题：只有一个解释变量的线性回归模型能否满足分析经济问题的需要？简单线性回归模型的主要缺陷是：把被解释变量Y 看成是解释变量X 的函数是前提是，在其它条件不变的情况下，并且，所有其它影响Y 的因素都应与X 不相关，但这在实际情况中很难满足。

怎样在一元线性回归的基础上引入多元变量的回归？ 看教科书第72—73页关于汽车销售量的影响因素的讨论。

一、多元线性回归模型的意义1、建立多元线性回归模型的意义，即一元线性回归模型的缺陷，多个主要影响因素的缺失对模型的不利影响。

在一元线性回归模型中，如果总体回归函数的设定是正确的，那么，根据样本数据得到的样本回归模型就应该有较好的拟合效果，这时，可决系数就应该较大。

相反，如果在模型设定时忽略了影响被解释变量的某些重要因素，拟合效果可能就会较差，此时可决系数会偏低，并且由于忽略了一些重要变量而对误差项的影响会加大，这时误差项会表现出一些违背假定的情况。

2、从一个解释变量到多个解释变量的演变。

一个生产函数的例子，一个商品需求函数的例子，（教材第74页）。

二、多元线性回归模型及其矩阵表示1、一般线性回归模型的数学表达式。

设 12233i ii k k ii Y XXXu ββββ=+++++i=1，2，3，…，n在模型表达式里，1β仍是截距项，它反映的是当所有解释变量取值为零时，被解释变量Y 的取值；j β（j=2，3，…，k ）为斜率系数，它的经济含义：在其它变量不变的情况下，第j 个解释变量每变动一个单位，Y 平均增加（或减少）j β个单位，这就是所谓的运用边际分析法对多元变量意义下回归参数的解释。

因此，称j β为偏回归系数，它反映了第j 个解释变量对Y 的边际影响程度。

4、2、总体回归函数，即12233(|)i i i k ki E Y X X X X ββββ=++++3、样本回归函数，即12233ˆˆˆˆˆi i k k iY X X Xββββ=++++ 4、将n 个样本观测值代入上述表达式，可得到从形式上看，像似方程组的形式。

多元线性回归模型的参数估计与显著性检验多元线性回归模型是一种常用的统计分析方法，用于研究多个自变量与一个因变量之间的关系。

在进行多元线性回归时，我们希望通过估计模型的参数来描述自变量与因变量之间的关系，并通过显著性检验来确定这种关系是否存在。

一、多元线性回归模型多元线性回归模型可以用如下的数学表达式表示：Y = β0 + β1*X1 + β2*X2 + ... + βn*Xn + ε其中，Y表示因变量（被解释变量），X1、X2、...、Xn表示自变量（解释变量），β0、β1、β2、...、βn表示回归方程的参数，ε表示误差项。

二、参数估计在多元线性回归中，我们需要通过样本数据来估计回归方程的参数。

最常用的估计方法是最小二乘法（Ordinary Least Squares，OLS），它通过最小化观测值与回归方程预测值之间的残差平方和来确定参数的估计值。

具体而言，最小二乘法的目标是选择参数的估计值，使得残差平方和最小化。

为了得到参数的估计值，可以使用矩阵形式的正规方程来求解，即：β = (X'X)-1X'Y其中，β是参数的估计值，X是自变量矩阵，Y是因变量向量，X'表示X的转置，-1表示逆矩阵。

三、显著性检验在进行多元线性回归时，我们通常希望确定自变量与因变量之间的关系是否显著存在。

为了进行显著性检验，我们需要计算模型的显著性水平（p-value）。

常见的显著性检验方法包括F检验和t检验。

F检验用于判断整体回归模型的显著性，而t检验用于判断单个自变量对因变量的显著性影响。

F检验的假设为：H0：模型中所有自变量的系数均为零（即自变量对因变量没有显著影响）H1：模型中至少存在一个自变量的系数不为零在进行F检验时，我们计算模型的F统计量，然后与临界值进行比较。

若F统计量大于临界值，则拒绝原假设，认为回归模型显著。

而t检验的假设为：H0：自变量的系数为零（即自变量对因变量没有显著影响）H1：自变量的系数不为零在进行t检验时，我们计算各个自变量系数的t统计量，然后与临界值进行比较。