最新回弹模量计算(试内)
- 格式:xls
- 大小:50.50 KB
- 文档页数:1

地基回弹模量试验方法1. 什么是地基回弹模量?大家好,今天咱们聊聊一个听起来有点儿“高大上”的话题——地基回弹模量试验方法。
听名字似乎有点儿深奥,但其实它关乎我们脚下的土地,跟每一栋建筑的安全密切相关。
别担心,咱们一步一步来,就像在街边小摊上吃糖葫芦一样,慢慢来,乐趣多多!1.1 地基回弹模量的含义首先,咱得弄清楚“地基回弹模量”到底是个啥。
简单来说,地基回弹模量就是土壤在受到压力后,能否恢复原来的形状,换句话说,就是“弹性”。
如果地基像个弹簧,受了力之后能恢复,那它的回弹模量就高;要是像个老软蛋,受力后就变形不堪,那回弹模量就低了。
这关系到建筑物的稳定性,毕竟谁都不想自家的房子晃晃悠悠的,对吧?1.2 为什么要做这个试验?那么,既然知道了回弹模量的重要性,咱们就得问了,为什么要特地去做这个试验呢?想象一下,如果不测一下,建筑工人在地基上开工,结果发现这块地像泥巴一样,连个小雨都能把它泡软,那可就麻烦了!试验的目的是为了了解土壤的特性,确保建筑安全。
你看,防患于未然,真是一句老话。
2. 地基回弹模量试验的方法接下来,让我们看看这试验到底是怎么个过程,简直就像一场土壤的“体检”!2.1 准备工作首先,准备工作是相当重要的。
得选一个合适的地点进行试验,保证这个地方的土壤代表性。
就像你去医院体检,医生得找个适合的地方抽血,才靠谱嘛!然后呢,咱们需要一些设备,比如回弹仪、测量工具,还有那些让人头疼的计算器。
哦,对了,别忘了请上几位经验丰富的技术人员,毕竟“人多力量大”不是没道理的。
2.2 试验过程试验正式开始啦!首先,技术人员会在土壤上施加一定的压力,看看土壤是怎么反应的。
接着,他们会记录下土壤在压力下的变形情况。
然后,慢慢减轻压力,观察土壤能否恢复到原来的样子。
这一过程就像在给土壤“量身定做”一样,记录下它的每一个反应。
最后,通过公式计算,得出回弹模量的数值,大家可以想象一下,数据像小鸟一样在计算器上飞舞!3. 地基回弹模量的重要性聊完了试验的方法,咱们再来说说地基回弹模量的重要性。

路基顶面回弹模量确定的新方法-CAL-FENGHAI.-(YICAI)-Company One1路基顶面回弹模量确定的新方法——学习新的《公路沥青路面设计规范》征求意见稿笔记吴祖德(常州市建设工程施工图设计审查中心,江苏常州 213002)内容提要新的《公路沥青路面设计规范》征求意见稿,对路基顶面回弹模量值的确定,改变了现有规范采用的方法,提出了新方法。
本文详细介绍了新的规范征求意见稿中,对路基顶面回弹模量值的确定方法,并与现规范的方法进行比较,供技术人员在学习中参考。
关键词征求意见稿路基顶面回弹模量的确定0 前言路基土的回弹模量是沥青路面结构力学响应分析的重要参数之一。
现规范与新规范征求意见稿对路基顶面回弹模量的要求、测试及有关规定的区别,列表如下:表1 现规范与新规范征求意见稿对路基顶面回弹模量的要求、测试及有关规定的区1 三轴试验测试路基土的回弹模量路基土回弹模量主要受其应力状况、物理状况(含水量与密实度)和材料性质三方面的因素的影响。
对于处于特定状态(一定含水量和密实度值)的各类路基土来说,影响其模量的主要因素便是应力状况。
在不同的交通等级下,以及不同的路面类型和结构组合中,路基土的应力状况是不相同的,故其模量值也是不一样的。
因而,路基土的模量参数的测试方法和指标值取用,一方面要遵循反映材料基本特性的要求,另一方面则要与结构应力—应变分析时所选用的方法和条件相一致。
我国现行沥青路面设计规范中,采用“室内试验法(小承载板法)”及“现场实测法(承载板法或贝克曼梁法)”来确定路基模量,而室内小承载板试验中试件的受力状况与现场路基上的应力状况并不一致,并且这种测试方法仅适用于静态模量标定,这些都影响了路基回弹模量取值的科学性和合理性。
所以经过对我国各种路面结构中路基土的受力水平进行分析,制定出了更加合理的室内三轴重复加载测试回弹模量的方法与取值标准。
(注:①可参阅附后的“粒料与路基土室内回弹模量试验测试方法草案”;②该试验方法:对圆柱体试件施加一个固定幅度、加载试件(路基—,粒料基层/底基层—)和循环周期(一般取)的轴向重复荷载。
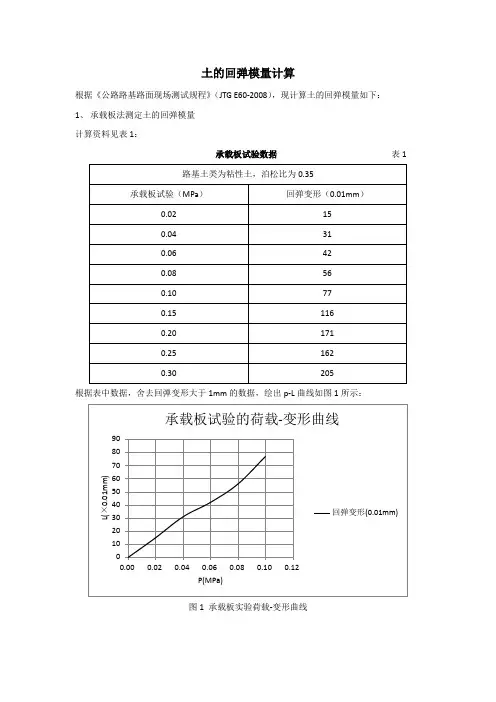
土的回弹模量计算根据《公路路基路面现场测试规程》(JTG E60-2008),现计算土的回弹模量如下:1、承载板法测定土的回弹模量计算资料见表1:承载板试验数据表1根据表中数据,舍去回弹变形大于1mm的数据,绘出p-L曲线如图1所示:图1 承载板实验荷载-变形曲线根据规范,由于曲线起始部分出现反弯,故应进行原点修正,并进行直线拟合,如图2所示:图2 原点修正图由图2读的各级荷载作用下图的回弹变形值如表2所示:各级荷载对应的土的回弹变形值表2由公式E0=πD4(1−μ02)∑p i∑L i计算得:E0=π×3004×(1−0.352)×(0.02+0.04+0.06+0.08+0.10)(17+31+43+58+73)×10−2=27.93(MPa)式中:E0——土基回弹模量D——刚性承载板直径,规定为30cmμ0——土基泊松比,取为0.35∑p i——回弹变形小于1mm的各级荷载单位压力总和∑L i——各级荷载单位压力作用下,回弹变形小于1mm的回弹变形总和2、 贝克曼梁弯沉试验法测定土的回弹模量 2.1计算资料见表3:贝克曼梁弯沉试验数据 表32.2计算全部测定值得算术平均值L̅、单次测量的标准差S 0和自然误差r 0 L̅=∑L iN=172 S 0=√∑(L i −L̅)2N −1=23.31r 0=0.675S 0=0.675×23.31=15.73式中: L̅——回弹弯沉的平均值(0.01mm ) S 0——回弹弯沉测定值的标准差(0.01mm ) r 0——回弹弯沉测定值的自然误差(0.01mm ) L i ——各测点的回弹弯沉值(0.01mm ) N——测点总数2.3计算各测点的测定值与算术平均值的偏差值d i =L i −L̅,并计算较大的偏差值与自然误差值之比d i r 0⁄,计算值如表3所示,由表可知:max (di r 0⁄)=2.73<3.2,故所有测点数据均有效。

回弹模量计算公式回弹模量(YoungModulus,缩写为YM)是材料力学中一个重要的参数,表征材料的弹性变形特性。
它是指当外力的大小趋于零时,材料的平衡形状和尺寸变化和外力之前线性变化的比例,也称为材料变形系数。
回弹模量是材料力学实验中测量和确定最常用的参数,它也是用来预测材料力学性能的唯一参数之一。
一般来说,回弹模量是指材料受到外力作用,在回复外力平衡状态时,其延伸量与外力之比例关系,用回弹模量YM表示。
它等于有限的变形和有限的外力之间的比值,可用下式表示:YM =σ/ε其中,σ表示外力的大小,ε表示变形的大小。
位移的大小根据变形量的大小计算,其计算公式为:Δs =s * L其中,εs表示变形量在恢复平衡状态时的变化量,L表示受力前的原始长度。
可以根据上面的公式得出回弹模量的计算公式:YM =σ*L/Δs为精确测定回弹模量,需要进行多遍试验,以确定外力σ和变形量εs之间的关系,然后根据试验结果,按以上公式算出材料的回弹模量。
实际测量过程中,应尽量确保外动力作用的方向与材料的轴向平行,以保证测量结果的准确性。
此外,实验中要注意材料的温度,并定期检查机械设备的工作情况,以确保实验结果的准确性。
回弹模量是材料力学中重要的参数,它能够反映材料弹性性能的好坏,也可以用来衡量材料的抗变形性能。
因此,广泛应用于材料力学研究、机械设计分析等领域,对于材料的实用性能和利用性有着重要意义。
回弹模量是比较容易测量的参数,但其准确性却不容小视。
正确的实验操作、准确的测量结果、合理的计算公式,都是测定回弹模量的关键所在。
因此,测量实验前应仔细准备,在实验测量过程中应更加谨慎,以期在测量中取得满意的结果。

水稳试件回弹模量计算公式水稳试件回弹模量是指在水稳材料的施工过程中,用来评价材料的弹性变形能力的一个重要指标。
回弹模量的大小直接影响到水稳材料的使用性能和工程质量,因此对其进行准确计算和评价具有重要意义。
水稳试件回弹模量计算公式是通过实验测定水稳试件的回弹值和压实应力,然后根据回弹值和压实应力的关系来计算得出的。
下面将详细介绍水稳试件回弹模量的计算公式及其相关内容。
1. 水稳试件回弹模量的定义。
水稳试件回弹模量是指在水稳试件受到一定压实应力后,恢复到原始形状所需的弹性模量。
它反映了水稳试件在受到压实应力后的变形能力,是评价水稳材料抗压性能的重要指标之一。
2. 水稳试件回弹模量的计算公式。
水稳试件回弹模量的计算公式为:E = (1 (H1/H0)) σ。
其中,E为水稳试件的回弹模量,H1为水稳试件受到压实应力后的回弹值,H0为水稳试件未受到压实应力前的初始高度,σ为水稳试件的压实应力。
3. 水稳试件回弹模量的实验测定方法。
为了计算水稳试件的回弹模量,需要进行实验测定。
具体的实验测定方法如下:(1)制备水稳试件,首先需要按照相关标准和规范要求,制备水稳试件。
通常情况下,水稳试件的尺寸为直径150mm,高度300mm。
(2)施加压实应力,将制备好的水稳试件放置在压实设备上,施加一定的压实应力。
在施加压实应力的过程中,需要记录下水稳试件的初始高度H0和受到压实应力后的高度H1。
(3)测定回弹值,在施加完压实应力后,松开压实设备,让水稳试件恢复到原始形状。
然后测定试件的回弹值H1。
(4)计算回弹模量,根据测定得到的回弹值H1、初始高度H0和施加的压实应力σ,利用上述的计算公式可以得到水稳试件的回弹模量E。
4. 水稳试件回弹模量的影响因素。
水稳试件回弹模量受到多种因素的影响,主要包括水稳试件的材料性质、压实应力的大小和试件的形状尺寸等。
(1)材料性质,不同类型的水稳材料具有不同的回弹模量。
一般来说,材料的密实性和弹性模量越大,回弹模量也会相应增大。

土体回弹模量土工材料的力学性能参数是土工工程设计的重要依据。
土体回弹模量是评价土工材料稳定性和变形能力的重要指标之一,与土工工程的安全性和使用寿命密切相关。
本文将从定义、测定方法和应用等方面详细阐述土体回弹模量。
一、定义土体回弹模量(rebound modulus)是指刚体撞击土体后,土体恢复弹性形变的能力与原形变大小之间的比值,也称回弹式混凝土模量。
该模量的计算方式为E = ρgH2r2/[3(h+r)Δh],其中ρ为土体的密度,g为重力加速度,H为撞击锤重,r为锤头半径,h为试件厚度,Δh为试件弹性压缩量。
土体回弹模量越大,土体弹性回复能力越强,抗压强度和变形能力越好。
二、测定方法1.回弹法回弹法是根据土体受重物打击后的反弹程度和打击能量之间的关系,来计算土体回弹模量。
这种方法比较简便,适用于较各种类型的土体。
2.压缩-回弹法压缩-回弹法是将土体在标准条件下进行压缩后,记下其压缩量和回弹量,通过对比得出土体回弹模量。
该方法在较高的应变范围内可以获得较精确的结果。
3.剪切-回弹法剪切-回弹法在测定泥土回弹模量时比较常用。
通过双镜头摄像记录土体在受力情况下的变形,进而计算回弹模量或者采用类似压缩回弹法的方式进行计算。
三、应用1.土工工程中的应用土体回弹模量是判断土工材料和结构性能的重要指标之一。
在土工工程中,土体回弹模量可以作为边坡稳定性和土工结构变形能力的评价指标,来选取适合的土工材料进行实际工程使用。
2.材料研究领域的应用土体回弹模量可以在材料研究领域中应用。
通过分析材料显著的回弹行为,评估材料的耐用性和吸震性能。
3.道路工程中的应用在道路工程中,设施的稳定性决定了安全和使用的寿命。
土体回弹模量的测定可以为道路工程提供更多的结构性能参数信息,为道路设计和维修提供支持。
四、结论土体回弹模量是土工工程和材料研究中的一个重要参数,对研究和评价土工材料和结构性能有着较大的意义。
各种测定方法不同,因此测定结果也存在一定的误差。



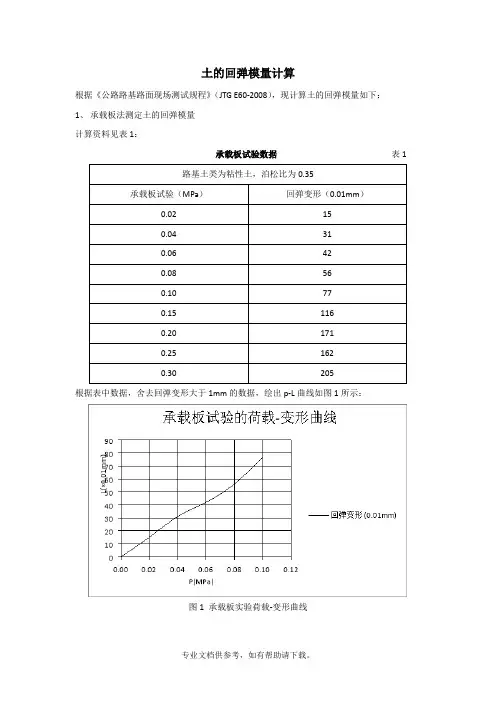
土的回弹模量计算根据《公路路基路面现场测试规程》(JTG E60-2008),现计算土的回弹模量如下:1、承载板法测定土的回弹模量计算资料见表1:承载板试验数据表1路基土类为粘性土,泊松比为0.35承载板试验(MPa)回弹变形(0.01mm)0.02 150.04 310.06 420.08 560.10 770.15 1160.20 1710.25 1620.30 205根据表中数据,舍去回弹变形大于1mm的数据,绘出p-L曲线如图1所示:图1 承载板实验荷载-变形曲线根据规范,由于曲线起始部分出现反弯,故应进行原点修正,并进行直线拟合,如图2所示:图2 原点修正图由图2读的各级荷载作用下图的回弹变形值如表2所示:各级荷载对应的土的回弹变形值表20.02 0.04 0.06 0.08 0.1017 31 43 58 73由公式计算得:式中:土基回弹模量刚性承载板直径,规定为30cm土基泊松比,取为0.35回弹变形小于1mm的各级荷载单位压力总和各级荷载单位压力作用下,回弹变形小于1mm的回弹变形总和2、贝克曼梁弯沉试验法测定土的回弹模量2.1计算资料见表3:贝克曼梁弯沉试验数据表3 测点回弹弯沉(0.01mm) di=Li-L(mm) di/r01 177 5 0.322 151 -21 -1.343 193 21 1.344 159 -13 -0.835 1786 0.386 144 -28 -1.787 152 -20 -1.278 158 -14 -0.899 198 26 1.6510 171 -1 -0.0611 147 -25 -1.5912 215 43 2.7313 207 35 2.2314 158 -14 -0.892.2计算全部测定值得算术平均值、单次测量的标准差和自然误差式中:——回弹弯沉的平均值(0.01mm)——回弹弯沉测定值的标准差(0.01mm)回弹弯沉测定值的自然误差(0.01mm)各测点的回弹弯沉值(0.01mm)测点总数2.3计算各测点的测定值与算术平均值的偏差值,并计算较大的偏差值与自然误差值之比,计算值如表3所示,由表可知:,故所有测点数据均有效。

回弹模量计算公式回弹模量,又称为弹性模量或Young's Modulus,是材料在受力后回复到原始形状的能力的度量。
它代表了材料的刚度和弹性特性,是评估材料在弹性变形中的表现的重要指标。
回弹模量的计算公式取决于材料的形状和应力的方向。
回弹模量的计算可以根据应力与应变的关系进行。
在弹性变形下,应力和应变的关系遵循胡克定律:应力(σ)等于材料的弹性模量(E)乘以应变(ε),即σ=Eε。
其中,应变是指材料在受到力作用时发生的相对变形。
回弹模量的计算公式如下:E=(1+e)*(1-2v)/e其中,E表示回弹模量,e表示侧向收缩系数,v表示泊松比。
对于材料的大部分工程应用,可以忽略侧向收缩系数e,即e≈0。
在此情况下,回弹模量的计算公式简化为:E=2*(1+v)*σ/ε其中,σ表示应力,ε表示应变,v表示泊松比。
泊松比(Poison's Ratio)是为了描述材料在沿一个方向受拉伸时在另一个方向上收缩的变形程度而引入的一个参数。
泊松比是一个无量纲数,其计算公式为:v=-ε横/ε纵其中,ε横表示材料在垂直于拉伸方向的纵向应变,ε纵表示材料在拉伸方向的纵向应变。
回弹模量常用于描述金属材料的力学性能,可以通过各种实验方法进行测量,如拉伸试验、弯曲试验和压缩试验等。
实际应用中,通常使用标准试样进行实验,并测量在不同应力下的应变,据此可以计算出回弹模量。
需要注意的是,回弹模量是一个各向同性的材料性质。
在计算中需要考虑材料的各向异性对结果的影响。
对于非各向同性材料,需要根据不同的应力方向和应变方向使用相应的计算公式。
Open Journal of Transportation Technologies 交通技术, 2023, 12(5), 438-448 Published Online September 2023 in Hans. https:///journal/ojtt https:///10.12677/ojtt.2023.125048基于室内试验的动态回弹模量与变形模量的 比较与公式修正研究纪厚强1,冯元正1,郭超宇2,王建立1,束冬林3,方明镜21安徽省交通控股集团有限公司,安徽 合肥 2武汉理工大学土木工程与建筑学院,湖北 武汉3安徽省高速公路试验检测科研中心有限公司,安徽 合肥收稿日期:2023年8月17日;录用日期:2023年9月14日;发布日期:2023年9月25日摘 要动态回弹模量测试仪(DEMT)是在动态变形模量Evd 测试仪(PFWD)与车载式落锤弯沉仪(FWD)检测原理基础上研制而成。
本研究旨在探究公路路基DEMT 现场检测中动态回弹模量的真实值,比较分析PFWD 动态变形模量与DEMT 动态回弹模量定义上以及公式计算的差异,修正采用DEMT 进行动态回弹模量检测时塑性变形对结果的影响。
通过定制钢模制备不同掺灰量与不同压实度的土样试件,并使用高精度游标卡尺测量DEMT 测试前后试件高度差。
试验结果表明,掺灰条件下,压实度越低,试件可被压缩区间越大,受到冲击荷载时产生的塑性变形越大,压实度为90%,测试回弹模量值时初始塑性变形最大,为0.0532 mm ,压实度为96%时,总变形中初始塑性变形最小,为0.0201 mm 。
由此可见,路基土试样进行动态回弹模量测试时塑性变形在总变形中的占比随压实度的增加而减小,且同一压实度试件随回弹模量测试次数的增加塑性变形占比逐渐减小。
关键词动态回弹模量,塑性修正,模拟现场试验,细粒土路基Indoor Test-Based Comparison and Formula Correction of Dynamic Resilient and Deformation ModulusHouqiang Ji 1, Yuanzheng Feng 1, Chaoyu Guo 2, Jianli Wang 1, Donglin Shu 3, Mingjing Fang 2 1Anhui Transportation Holding Group Co., Ltd., Hefei Anhui 2School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan Hubei 3Anhui Expressway Test and Inspection Research Center Co., Ltd., Hefei Anhui Received: Aug. 17th , 2023; accepted: Sep. 14th , 2023; published: Sep. 25th , 2023纪厚强 等Abstract The Resilience modulus Tester (DEMT) is developed based on the principles of the Dynamic De-formation Modulus Evd Tester (PFWD) and the Falling Weight Deflectometer (FWD). This study aims to explore the true values of the Resilience modulus (DEMT) in on-site testing of highway subgrade. A comparative analysis is conducted between the dynamic deformation modulus meas-ured by PFWD and the Resilience modulus measured by DEMT. The differences in modulus defini-tions and formula calculations are analyzed, and the influence of plastic deformation on the re-sults when using DEMT for Resilience modulus testing is corrected. Custom steel molds were used to prepare soil specimens with different fly ash contents and compaction degrees. The height dif-ference of the specimens before and after DEMT testing was measured using a high-precision ver-nier caliper. The experimental results show that under fly ash conditions, the lower the compac-tion degree, the larger the compressible range of the specimen, and the greater the plastic defor-mation induced by the impact load. When the compaction degree is 90%, the initial plastic defor-mation is the largest, measuring 0.0532 mm. When the compaction degree is 96%, the initial plas-tic deformation is the smallest, measuring 0.0201 mm in the total deformation. Therefore, it can be observed that the proportion of plastic deformation in the total deformation during Resilience modulus testing of subgrade soil samples decreases with the increase of compaction degree. Moreover, for specimens with the same compaction degree, the proportion of plastic deformation decreases gradually with an increase in the number of rebound modulus tests. KeywordsResilience Modulus, Plastic Correction, Simulated Field Test, Fine-Grained Soil SubgradeCopyright © 2023 by author(s) and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY 4.0). /licenses/by/4.0/1. 引言高速公路路基压实质量能够直接影响路基的服役能力、路面荷载、抗车辙能力、抗病害能力 [1]等。
道路路床回弹模量计算公式道路路床回弹模量是评价道路路基材料抗变形能力的重要指标之一。
它是指在一定试验条件下,用回弹式动力触探仪测得的路基材料的回弹值,通过回弹值与试验条件的关系,计算出路基材料的回弹模量。
回弹模量的大小直接影响着路基材料的变形性能和承载能力,因此对于道路工程设计和施工来说具有重要的意义。
回弹模量计算公式是通过试验数据和理论分析得出的,它是根据路基材料的物理性质和试验条件来确定的。
一般来说,回弹模量计算公式包括材料参数、试验条件和回弹值之间的关系,通过这些参数的相互作用,可以准确地计算出路基材料的回弹模量。
在道路工程中,回弹模量的计算公式通常采用以下形式:E = K × (h/D)^n。
其中,E为回弹模量,单位为兆帕(MPa);K为材料参数,与路基材料的类型和性质有关;h为试验荷载的压实深度,单位为毫米(mm);D为试验荷载的直径,单位为毫米(mm);n为试验条件参数,与试验设备和试验方法有关。
在这个公式中,材料参数K是反映路基材料抗变形能力的重要参数之一,它与路基材料的类型、密实度、含水量等因素密切相关。
一般来说,K值越大,表示路基材料的抗变形能力越强;反之,K值越小,表示路基材料的抗变形能力越弱。
因此,在设计和施工中,需要根据路基材料的实际情况来确定K值,以保证路基材料的变形性能和承载能力。
试验荷载的压实深度h和直径D是影响回弹模量的重要试验条件参数。
一般来说,试验荷载的压实深度越大,回弹模量越小;试验荷载的直径越大,回弹模量也越小。
因此,在进行回弹模量试验时,需要合理选择试验荷载的压实深度和直径,以保证试验结果的准确性和可靠性。
除了上述计算公式外,还有一些修正公式用于修正回弹模量的计算结果。
这些修正公式通常是根据试验数据和理论分析得出的,用于考虑一些特殊情况下的影响因素,如试验条件的变化、路基材料的特殊性质等。
通过这些修正公式,可以更准确地计算出路基材料的回弹模量,为道路工程设计和施工提供更可靠的依据。
回弹模量计算公式回弹模量是材料力学性质的一种参数,用于描述材料在受到外力作用后恢复原状的能力。
回弹模量的计算公式主要有以下几种:1. 弹性体的回弹模量(Young's modulus, E):回弹模量是材料在受到外力作用时,从开始变形到力消失时,所经历的应力和应变关系的常数比值。
在弹性阶段,材料的应力与应变成线性关系。
回弹模量的计算公式为:E=σ/ε其中,E为回弹模量,σ为材料的应力,ε为材料的应变。
2. 剪切模量(Shear modulus, G):剪切模量是材料在受到剪切应力时,发生剪切变形的能力。
剪切模量描述了材料在剪切应力作用下的弹性恢复能力。
剪切模量的计算公式为:G=τ/γ其中,G为剪切模量,τ为材料的剪切应力,γ为材料的剪切应变。
3. 体积模量(Bulk modulus, K):体积模量是材料在受到体积应力时,发生体积变形的能力。
体积模量描述了材料在受到压缩或膨胀应力时的弹性恢复能力。
体积模量的计算公式为:K=-P/ΔV/V其中,K为体积模量,P为施加的压力,ΔV为体积的变化量,V为初始体积。
4. 杨氏模量(Modulus of elasticity, E):杨氏模量和回弹模量实质上是同一概念,表示了材料单位面积内的应力和应变关系的常数比值。
杨氏模量常用于描述纵向受力下的材料弹性恢复性能。
杨氏模量的计算公式为:E=σ/ε其中,E为杨氏模量,σ为材料的纵向应力,ε为材料的纵向应变。
以上公式是常用的回弹模量计算公式,根据材料的特性和受力情况,选择适当的公式进行计算。
测定土的回弹模量的两种室内试验方法的探讨田丽霞杨斌娟吴英印文东摘要:本文根据大量的土工室内试验数据,对土体回弹模量两种试验方法获得的数据进行了综合比较分析,并结合相关工程基坑坑底隆起量的估算与实测数据的对比,提出了室内土体回弹模量试验方法的建议。
关键词:回弹模量常规固结试验静止侧压力试验1前言随着城市建设的高速发展,地下空间开发和应用也进入快速发展阶段,由此伴生了大量的基坑工程,尤其是随着地下空间开发应用的规模和开挖深度不断加大,基坑实施过程中对环境的影响也越来越引起人们的重视,其中基坑开挖过程中的坑底隆起对基坑变形和安全的控制尤为重要。
在深大基坑开挖过程中,由于基坑土体的卸载以及周边围护体的挤压变形等作用,导致底部土体产生较大的回弹,如何准确便捷的估算基坑坑底土体的隆起量十分重要。
土体回弹模量是较合理估算基坑坑底土体回弹量的重要参数之一,目前在室内试验方面获得土体回弹参数主要是采用高压固结试验和常规的固结试验后继续做回弹再压缩试验两种试验方法,而常规的固结后再回弹试验是模拟基坑开挖坑底土体的卸荷应力路径,所得的回弹模量对估算基坑坑底土体回弹量更具有实际意义。
本文利用土工试验中的普通固结仪和K0固结仪,模拟深基坑开挖坑底土体的卸荷应力路径进行试验,通过比较采用两种方法求得的回弹模量,得出更合理的室内试验方法。
同时,对土体固结(恢复土体天然应力状态)稳定时间长短对回弹模量的影响进行了试验比较。
2. 常规固结仪和K0固结仪试验确定回弹模量2.1试验方法2.1.1常规固结仪试验方法首先用环刀制取样品,样品尺寸高2cm、直径6.18cm,将样品装入常规固结仪容器内,按土体的天然固结压力,在有侧向限制的条件下对土样进行固结,使土样的竖向应力达到基坑开挖前土体的自重应力状态,固结稳定后(一般24小时以上),模拟基坑的开挖逐级卸荷,每一级卸荷达到稳定后,记录土体竖向变形及相关的数据,并进行下一级卸荷,根据土体深度不同,直至卸荷到规定卸荷荷重。
混凝土路基回弹模量试验标准一、前言混凝土路基回弹模量试验是一项重要的工程试验,用于评估混凝土路基的强度和稳定性。
本文将详细介绍混凝土路基回弹模量试验的标准,包括试验设备、试验方法、试验数据处理等方面的内容。
二、试验设备1.回弹仪回弹仪是进行混凝土路基回弹模量试验的主要设备,其结构应符合GB/T50315-2010《混凝土路面工程施工质量验收规范》的要求。
回弹仪应具备以下技术指标:(1)回弹锤重量:2.25kg;(2)回弹锤下落高度:20mm;(3)回弹针锥角:60度;(4)回弹仪示值误差:±1.5%。
2.量具进行混凝土路基回弹模量试验时,还需要使用以下量具:(1)0.5mm游标卡尺:用于测量混凝土路基的厚度;(2)直角尺:用于检查混凝土路基表面的平整度;(3)六分尺:用于测量混凝土路基的长度和宽度。
3.其他设备在进行混凝土路基回弹模量试验时,还需要使用以下设备:(1)锤子:用于敲击回弹锤,使其落下;(2)标志线:用于标记混凝土路基的试验点。
三、试验方法1.试验前准备(1)检查回弹仪是否正常工作;(2)根据设计要求,确定混凝土路基的试验点;(3)清理试验点,保证混凝土路基表面干净平整;(4)用游标卡尺测量混凝土路基的厚度,并记录数据。
2.试验操作(1)将回弹仪放置在混凝土路基试验点上,使回弹针与混凝土路基表面垂直,并用直角尺检查回弹仪是否水平;(2)将回弹锤从20mm高度敲击混凝土路基表面,记录回弹仪显示的回弹模量;(3)在同一试验点进行3次试验,取平均值作为该点的回弹模量。
(4)在每个试验点进行3次试验,取平均值作为该点的回弹模量,记录数据。
3.试验要求(1)混凝土路基表面应干净平整,无大坑大洼和明显的破损;(2)回弹仪应放置平稳,回弹针应与混凝土路基表面垂直;(3)每个试验点应进行3次试验,取平均值作为该点的回弹模量;(4)试验过程中应注意安全,避免造成设备和人员损伤。
四、试验数据处理1.数据计算计算每个试验点的平均回弹模量的公式为:Em = (E1+E2+E3)/3其中,Em为平均回弹模量,E1、E2、E3为同一试验点的3次回弹模量。