下载文档原格式
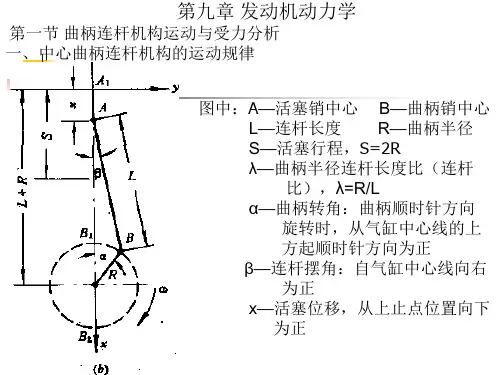
游梁式抽油机是以游梁支点和曲柄轴中心的连线做固定杆，以曲柄，连杆和游梁后臂为三个活动杆所构成的四连结构。
1.1四连杆机构运动分析：图1复数矢量法： 为了对机构进行运动分析，先建立坐标系，并将各构件表示为杆矢量。
结构封闭矢量方程式的复数矢量形式：3121234i i i l e l e l e l ϕϕϕ+=+ (1)应用欧拉公式cos sin i e i θθθ=+将(1)的实部、虚部分离，得1122433112233cos cos cos sin sin sin l l l l l l l ϕϕϕϕϕϕ+=+⎫⎬+=⎭(2)由此方程组可求得两个未知方位角23,ϕϕ。
当要求解3ϕ时，应将2ϕ消去可得2222234134313311412cos 2cos()2cos l l l l l l l l l l ϕϕϕϕ=++---- (3)解得2223tan(/2)()/()B A B C A C ϕ=+-- (4)33233sin arctancos B l A l ϕϕϕ+=+ (5)其中：411112222323cos sin 2A l l B l A B l l C l ϕϕ=-=-++-=(4)式中负号对应的四连杆机构的图形如图2所示，在求得3ϕ之后，可利用(5)求得2ϕ。
图2由于初始状态1ϕ有个初始角度，定义为01ϕ，因此，我们可以得到关于011t ϕϕω=+，ω是曲柄的角速度。
而通过图形3分析，我们得到OA 的角度0312πθϕϕ=--。
因此悬点E 的位移公式为||s OA θ=⨯，速度||ds d v OA dt dtθ==，加速度2222||dv d s d a OA dt dt dtθ===。
图3已知附录4给出四连杆各段尺寸，前臂AO=4315mm ，后臂BO=2495mm ，连杆BD=3675mm ，曲柄半径O ’D=R=950mm ，根据已知条件我们推出''||||||||OO O D OB BD +>+违背了抽油系统的四连结构基本原则。
牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是关于结构型式及尺寸参数已定的具体机构，按主动件的位置、速度和加速度来确信从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量，运动参数又是机械动力学分析的依据，因此机构的运动分析是机械设计进程中必不可少的重要环节。
以运算机为手腕的解析方式，由于解算速度快，精准度高，程序有必然的通用性，已成为机构运动分析的要紧方式。
连杆机构作为在机械制造专门是在加工机械制造中要紧用作传动的机构型式，同其他型式机构专门是凸轮机构相较具有很多优势。
连杆机构采纳低副连接，结构简单，易于加工、安装并能保证精度要求。
连杆机构能够将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件，实现间歇运动，知足给定的运动要求，完成机械的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动，实现工件的切削。
工作台的横向运动即是进给运动，实现对切削精度的操纵。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成，其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时，通过六杆机构驱动刨刀作往复移动。
刨刀右行时，当刨刀处于工作行程时;要求刨刀的速度较低且平稳，以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时，刨刀不工作，称为空行程，现在要求刨刀的速度较高以提高生产率。
由此可见，牛头刨床的纵向运动特性对机床的性能有决定性的阻碍。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成，其中实现刨头切削运动的六杆机构是一个关键机构。
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件，刨刀装在C点上。
假设已知各构件的尺寸如表1所示，原动件1以等角速度ω1=1rad/s沿着逆时针方向回转，要求分析各从动件的角位移、角速度和角加速度和刨刀C点的位移、速度和加速度的转变情形。
多连杆机构的运动学分析与合理设计多连杆机构作为机械系统中常见的一种形式，广泛应用于各种工程领域。
它由多个连杆和铰接连接的节点构成，能够实现复杂的运动路径。
在机器人技术、汽车工程和航天领域等众多应用中，多连杆机构的运动学分析和合理设计是至关重要的。
在进行多连杆机构的运动学分析时，需要首先确定各个连杆的长度、连杆的连接方式以及铰接的位置等。
通过这些参数的确定，可以进一步推导出机构的运动方程和运动学限制条件。
常见的多连杆机构包括摇杆机构、曲柄滑块机构和平面四杆机构等。
以摇杆机构为例，它由一个直杆和两个转轴构成。
当一个转动的驱动件作用于摇杆机构时，整个机构的运动路径可以被描述为抛物线形状。
通过分析抛物线的特性，可以确定驱动件的转速和转动角度对机构运动轨迹的影响，从而实现对机构运动的控制。
曲柄滑块机构是另一种常见的多连杆机构，它由一个转动的曲柄和一个滑块构成。
曲柄滑块机构的运动轨迹通常是椭圆形状，可以通过改变曲柄的转动角度和滑块位置来实现不同的运动路径。
在实际应用中，曲柄滑块机构常被用于发动机和机械传动系统中，其运动学分析对于提高机构的效率和可靠性至关重要。
平面四杆机构是一种更为复杂的多连杆机构，它由四个连杆和四个铰接节点组成。
平面四杆机构的运动学分析涉及到大量的几何关系和运动学方程的推导，需要利用刚体座标系和几何约束条件进行求解。
通过解析解或数值解的方法，可以求得平面四杆机构的运动轨迹、速度和加速度等运动学参数，为机构的合理设计提供了重要依据。
在多连杆机构的合理设计中，除了运动学分析以外，还需要考虑机构的结构刚度、平衡性和可靠性等因素。
合理的机构设计可以提高机构的性能，并确保机构能够承受预期的载荷和工作环境。
此外，还需要考虑机构的制造成本和装配难度等实际因素，以实现设计与制造的良好平衡。
总之，多连杆机构的运动学分析和合理设计是一项复杂而重要的任务。
通过分析机构的运动学特性和设计要求，可以实现对机构运动路径和性能的优化控制。
实验二平面连杆机构设计分析及运动分析综合实验一、实验目的：1、掌握机构运动参数测试的原理和方法。
了解利用测试结果，重新调整、设计机构的原理。
2、体验机构的结构参数及几何参数对机构运动性能的影响，进一步了解机构运动学和机构的真实运动规律。
3、熟悉计算机多媒体的交互式设计方法，实验台操作及虚拟仿真。
独立自主地进行实验内容的选择，学会综合分析能力及独立解决工程实际问题的能力，了解现代实验设备和现代测试手段。
二、实验内容1、曲柄滑块机构及曲柄摇杆机构类型的选取。
2、机构设计，既各杆长度的选取。
（包括数据的填写和调整好与“填写的数据”相对应的试验台上的杆机构的各杆长度。
）3、动分析（包括动态仿真和实际测试）。
4、分析动态仿真和实测的结果，重新调整数据最后完成设计。
三、实验设备：平面机构动态分析和设计分析综合实验台，包括：曲柄滑块机构实验台、曲柄摇杆机构实验台，测试控制箱，配套的测试分析及运动仿真软件，计算机。
四、实验原理和内容：1、曲柄摇杆机构综合试验台①曲柄摇杆机构动态参数测试分析：该机构活动构件杆长可调、平衡质量及位置可调。
该机构的动态参数测试包括：用角速度传感器采集曲柄及摇杆的运动参数，用加速度传感器采集整机振动参数，并通过A/D板进行数据处理和传输，最后输入计算机绘制各实测动态参数曲线。
可清楚地了解该机构的结构参数及几何参数对机构运动及动力性能的影响。
②曲柄摇杆机构真实运动仿真分析：本试验台配置的计算机软件，通过建模可对该机构进行运动模拟，对曲柄摇杆及整机进行运动仿真，并做出相应的动态参数曲线，可与实测曲线进行比较分析，同时得出速度波动调节的飞轮转动惯量及平衡质量，从而使学生对机械运动学和动力学，机构真实运动规律，速度波动调节有一个完整的认识。
③曲柄摇杆机构的设计分析：本试验台配置的计算机软件，还可用三种不同的设计方法，根据基本要求，设计符合预定运动性能和动力性能要求的曲柄摇杆机构。
另外还提供了连杆运动轨迹仿真，可做出不同杆长，连杆上不同点的运动轨迹，为平面连杆机构按运动轨迹设计提供了方便快捷的虚拟实验方法。
曲柄连杆机构运动分析四缸发动机曲轴、连杆和活塞的运动是较复杂的机械运动。
曲轴做旋转运动，连杆做平动，活塞是直线往复运动。
在用Pro/Engineer做曲轴、连杆和活塞的运动分析的步骤如下所示[20]:（1）设置曲轴、连杆和活塞的连接。
为使机构能够按照预定的方式运动，须分别在曲轴与机体之间、连杆与曲轴之间、活塞与连杆之间添加销钉。
在活塞与机体之间添加滑动杆连接。
（2）定义伺服电动机。
利用伺服电动机驱动曲轴转动。
（3）建立运动分析。
（4）干涉检验与视频制作。
（5）获取分析结果。
7.1 活塞及连杆的装配7.1.1 组件装配的分析与思路活塞组件主要包括活塞、活塞销和活塞销卡环，连杆由连杆体和连杆盖两部分组成，将活塞组与连杆组分别组装，工作时用螺栓和螺母将连杆体、连杆盖和曲轴装配在一起，用活塞销将连杆小头和活塞装配在一起[21]。
7.1.2 活塞组件装配步骤1、向组件中添加活塞新建组件文件，运用【添加元件】，将活塞在缺省位置，完成装配。
2、向组件中添加活塞销卡环（1）在“约束类型”中选择“对齐”选项，将卡环中心轴与活塞销孔中心轴对齐；（2）选择“匹配”选项，将卡环外圆曲面与卡环槽曲面相匹配，完成两个活塞销卡环的装配。
3、向组件中添加活塞销（1）选择“对齐”选项，将活塞销中心轴与活塞销座孔的中心轴对齐；（2）选择“匹配”选项，将活塞销端面与卡环端面相匹配，完成活塞销的装配。
装配结果如图7.1所示：图7-1 活塞组装配结果Figure7-1Piston assembly results7.1.3 连杆组件的装配步骤1、向组件中添加连杆体新建组件文件，运用【添加元件】，将连杆体添加在“缺省”位置，完成连杆体的装配。
2、向组件中添加连杆衬套（1）选择“插入”选项，将连杆衬套的外侧圆柱面与连杆小头孔内侧圆柱面以插入的方式相配合。
（2）选择“对齐”选项，将连杆衬套的中心轴和连杆小头孔的中心轴对齐，完成连杆衬套的装配。
基于SolidWorks的连杆机构的运动分析与仿真共3篇基于SolidWorks的连杆机构的运动分析与仿真1基于SolidWorks的连杆机构的运动分析与仿真引言机械工程是一门涵盖广泛领域的学科，而其核心是机械设计。
机械设计在现代化社会中具有举足轻重的地位，是实现生产自动化、机械化和数字化的必不可少的手段。
在机械设计中，连杆机构是一种非常重要的机械构件，因其能够将单向的直线运动转换为复杂的曲线运动。
因此，了解和掌握连杆机构的运动特点对于机械工程师和设计师具有非常大的实用价值。
本文将介绍基于SolidWorks的连杆机构的运动分析与仿真。
正文SolidWorks是目前应用最广泛的三维计算机辅助设计(CAD)软件之一，其主要功能是建立三维模型和进行工程分析。
在SolidWorks中，连杆机构是一种常用的机构，在机械设计中有着广泛的应用。
通过 SolidWorks 可以进行连杆机构的建模、运动分析和仿真等全过程，以便更好地理解该机构的运动特点，为机械设计提供便利。
连杆机构是一种具有连杆、销轴和铰链等构件相互连接而成的复杂机械结构。
通过连杆机构可以将旋转运动和直线运动相互转换，实现有效的动力传递和力量转换。
对于机械设计师而言，了解连杆机构的运动特点是非常重要的。
在SolidWorks中，连杆机构的建模首先需要考虑构件的建立。
构件的建立应符合物理规律和机械原理，并使得机构具有合适的运动特性。
比如，在连杆机构中，需要考虑杆件的长度、销轴的直径、铰链的设计等因素。
在建模过程中，需要给予合适的参数设定，从而实现模型的运动模拟。
模型建立完毕后，可进行三维建模、组装和运动仿真。
通过连杆机构的仿真，可以深入地理解机械运动规律和性能特点，为机械设计提供便利。
此外，连杆机构的运动分析也是非常重要的一步。
通过对运动分析的深入研究，可以了解动力学和运动学的相关规律，为机械设计提供依据。
具体地，运动分析包括以下几个方面：速度和加速度分析、运动轨迹分析、力学分析等。
构件上点的运动分析函数文件（m文件）格式：function [ 输出参数] = 函数名（输入参数）p_crank.m function [p_Nx,p_Ny]=p_crank(Ax,Ay,theta,phi,l1)v_crank.m function [v_Nx,v_Ny]=v_crank(l1,v_Ax,v_Ay,omiga,theta,phi)a_crank.m function [a_Nx,a_Ny]=a_crank(l1,a_Ax,a_Ay,alpha,omiga,theta,phi)函数中的符号说明函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）p_RRR.m function [cx,cy,theta2,theta3]=p_RRR(bx,by,dx,dy,l2,l3,m)v_RRR.m function [vcx,vcy,omiga2,omiga3]=v_RRR(vbx,vby,vdx,vdy,cx,cy,bx,by,dx,dy)a_RRR.m function [acx,acy,alpha2,alpha3]=a_RRR(abx,aby,adx,ady,cx,cy,bx,by,dx,dy,omiga2,omiga3)函数中的符号说明m =1 m = -1RRR Ⅱ级杆组运动分析函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）p_RRP.m function [cx,cy,sr,theta2]=p_RRP(bx,by,px,py,theta3,l2,m)v_RRP.m function [vcx,vcy,vr,omiga2]=v_RRP(bx,by,cx,cy,vbx,vby,vpx,vpy,theta2,theta3,l2,sr,omiga3) a_RRP.m function [acx,acy,ar,alpha2]=a_RRP(bx,by,cx,cy,px,py,abx,aby,apx,apy,theta3,vr,omiga2,omiga3,alpha3)函数中的符号说明1 1∠BCP < 90︒，∠BC 'P > 90︒，m =1RRP Ⅱ级杆组运动分析函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）p_RPR.m function [dx,dy,sr,theta3]=p_RPR(bx,by,cx,cy,e,l3,m)v_RPR.m function [vdx,vdy,omiga3,vr]=v_RPR(bx,by,cx,cy,dx,dy,vcx,vcy,vbx,vby,theta3) a_RPR.m function [adx,ady,alpha3,ar]=a_RPR(bx,by,cx,cy,dx,dy,acx,acy,abx,aby,vr,omiga3,theta3)函数中的符号说明RRP Ⅱ级杆组运动分析实线位置，m =1 虚线位置，m = -1函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）F_RRR.m function [R12x,R12y,R23x,R23y,R34x,R34y]=F_RRR(bxy,cxy,dxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,as2,as3,alpha2,alpha3)RRR Ⅱ级杆组力分析R 23xF 2R F 3xR 23函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）F_RRP.m function [R12x,R12y,R23x,R23y,R34x,R34y,lcn]=F_RRP(bxy,cxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,theta3,as2,as3,alpha2,alph3)RRP Ⅱ级杆组力分析R 34函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）F_RPR.m function [R12x,R12y,R23x,R23y,R35x,R35y,lcn]=F_RRP(bxy,cxy,dxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,R34,theta3,as2,as3,alpha3)RPR Ⅱ级杆组力分析238. 作用有平衡力的构件力分析作用有平衡力的构件力分析函数文件（m文件）格式：function [ 输出参数] = 函数名（输入参数）F_Bar.m function [R01x,R01y,Mb]=F_Bar(axy,bxy,s1,m1,Js1,M1,F1,R12,as1,alpha1)函数中的符号说明9. 平面连杆机构运动分析算例例1图示曲柄摇杆机构，已知l 1=150mm ，l 2=220mm ，l 3=250mm ，l 4=300mm ，曲柄以n 1=100r/min 逆时针匀速转动，分析该机构的运动。
主程序% 曲柄摇杆机构运动分析 clc,clearl1=150;% 曲柄长度 l2=220;% 连杆长度 l3=250;% 摇杆长度 l4=300;% 机架长度 n=100;% 曲柄转速m=1;% RRR II 级杆组装配模式系数omiga1=2*pi*n/60;alpha1=0;% 曲柄角速度、角加速度ax=0;ay=0;vax=0;vay=0;aax=0;aay=0;% A 点位置、速度、加速度 dx=l4;dy=0;vdx=0;vdy=0;adx=0;ady=0;% D 点位置、速度、加速度 phi=0;% 曲柄的结构参数theta1=0:10:360;% 曲柄转角(每隔10°计算一次) theta1=theta1*pi/180;% 调用crank 函数，计算B 点运动参数 [bx,by]=p_crank(ax,ay,theta1,phi,l1);[vbx,vby]=v_crank(l1,vax,vay,omiga1,theta1,phi); [abx,aby]=a_crank(l1,aax,aay,alpha1,omiga1,theta1,phi); % 调用RRR 函数，计算BC 杆和CD 杆以及C 点运动参数 [cx,cy,theta2,theta3]=p_RRR(bx,by,dx,dy,l2,l3,m);[vcx,vcy,omiga2,omiga3]=v_RRR(vbx,vby,vdx,vdy,cx,cy,bx,by,dx,dy);[acx,acy,alpha2,alpha3]=a_RRR(abx,aby,adx,ady,cx,cy,bx,by,dx,dy,omiga2,omiga3); % 绘制运动线图 theta1=theta1*180/pi; figure(1) subplot(3,1,1);plot(theta1,cx,'-',theta1,cy,':r'),grid on xlabel('曲柄转角( ° )');ylabel('位移(mm/s)'); legend('C 点x 方向位移','C 点y 方向位移');曲柄摇杆机构subplot(3,1,2);plot(theta1,vcx,'-',theta1,vcy,':r'),grid onxlabel('曲柄转角( ° )');ylabel('速度(mm/s)');legend('C点x方向速度','C点y方向速度');subplot(3,1,3);plot(theta1,acx,'-',theta1,acy,':r'),grid onxlabel('曲柄转角( ° )');ylabel('加速度(mm/s^2)'); legend('C点x方向加速度','C点y方向加速度'); figure(2)subplot(2,1,1);plot(theta1,theta3*180/pi),grid onxlabel('曲柄转角( ° )');ylabel('摇杆角位移( ° )'); subplot(2,1,2);plot(theta1,omiga3),grid onxlabel('曲柄转角( ° )');ylabel('摇杆角速度(rad/s)'); subplot(2,1,3);plot(theta1,alpha3),grid onxlabel('曲柄转角( ° )');ylabel('摇杆角加速度(/rad/s^2)');例2 图示曲柄滑块机构，已知l 1=150mm ，l 2=150mm ，e =25mm ，曲柄以n 1=955r/min 逆时针匀速转动，分析该机构的运动。
主程序% 曲柄滑块机构运动分析 clc,clearl1=50;% 曲柄长度 l2=150;% 连杆长度 e=25;% 偏距 n=955;% 曲柄转速m=1;% RRP II 级杆组装配模式系数omiga1=2*pi*n/60;alpha1=0;% 曲柄角速度、角加速度ax=0;ay=e;vax=0;vay=0;aax=0;aay=0;% A 点位置、速度、及速度 px=0;py=0;% 滑块导路上一定点（选为O 点）的坐标 vpx=0;vpy=0;apx=0;apy=0;% 滑块导路上一定点的速度、加速度 theta3=0;omiga3=0;alpha3=0;% 滑块导路角位置、角速度、角加速度 phi=0;% 曲柄的结构参数theta1=0:30:360;% 曲柄转角(每隔10°计算一次) theta1=theta1*pi/180;% 调用crank 函数，计算B 点运动参数 [bx,by]=p_crank(ax,ay,theta1,phi,l1);[vbx,vby]=v_crank(l1,vax,vay,omiga1,theta1,phi); [abx,aby]=a_crank(l1,aax,aay,alpha1,omiga1,theta1,phi); % 调用RRP 函数，计算BC 杆和滑块的运动参数 [cx,cy,sr,theta2]=p_RRP(bx,by,px,py,theta3,l2,m);[vcx,vcy,vr,omiga2]=v_RRP(bx,by,cx,cy,vbx,vby,vpx,vpy,theta2,theta3,l2,sr,omiga3); [acx,acy,ar,alpha2]=a_RRP(bx,by,cx,cy,px,py,abx,aby,apx,apy,theta3,vr,omiga2,omiga3,alpha3); % 绘制运动线图crankx=l1.*cos(theta1);cranky=e+l1.*sin(theta1); theta1=theta1*180/pi; figure(1) subplot(3,1,1); plot(theta1,cx,'r'),grid onxlabel('曲柄转角( ° )');ylabel('滑块位移(mm/s)');曲柄滑块机构subplot(3,1,2);plot(theta1,vcx,'r'),grid onxlabel('曲柄转角( °)');ylabel('滑块速度(mm/s)'); subplot(3,1,3);plot(theta1,acx,'r'),grid onxlabel('曲柄转角( °)');ylabel('滑块加速度(mm/s^2)');例3 图示摆动导杆机构，已知l 1=280mm ，h =380mm ，l CD =840mm ，曲柄1以ω1=18.012rad/逆时针匀速转动，分析该机构的运动。
