届高三数学第二轮复习空间角与距离

2021年高考数学二轮复习难点.7立体几何中的空间角与距离教学案理2021年高考数学二轮复习难点2.7 立体几何中的空间角与距离教学案理立体几何中的“角”与“距离”是定量分析空间几何元素（点、线、面）间位置关系的两个重要的几何量,在研究这些“角”和“距离”时,常将空间问题转化为平面问题来处理,这是化归思想在立体几何中的具体应用. 空间角是考查学生对立体几何中的视图、空间想象能力、逻辑推理能力以及运算能力的一个综合知识点;空间距离既能考查学生的空间想象能力和逻辑推理能力,又能考查学生的转化思想及运算能力,空间距离的计算也是学生感觉较难的部分.在求解空间的角与距离的问题时,一般应包括三个部分:求作、论证和计算,这三部分是一个统一的整体.求空间中的角或距离的常用方法注意根据定义找出或作出所求的角或距离，给出证明，一般情况下，力求明确所求角或距离的位置.求角与距离的关键是将空间的角与距离灵活地转化为平面上的角与距离，然后将所求量置于一个三角形中，通过解三角形最终求得所需的角与距离. 空间向量是高中数学立体几何中新增加的内容 .借助于空间向量工具，可以对一些传统解法中较为繁琐的问题加以定量化,从而降低了思维难度 ,增强了可操作性 ,使学生对立体几何更容易产生兴趣 .空间向量在角和距离的处理上有着独特的优势,它最大限度地避开了思维的高强度转换 ,避开了各种辅助线添加的难处 ,代之以空间向量的计算 ,有利于我们较好地解决问题 .1 异面直线所成的角异面直线所成角的大小，是由空间一点分别引它们的平行线所成的锐角（或直角）来定义的.因此，通常我们要求异面直线所成的角会要求学生通过平移直线，形成角，然后在某个三角形中求出角的方法来得到异面直线所成角的大小.在这一方法中，平移直线是求异面直线所成角的关键，而如何平移直线要求学生有良好的空间观和作图能力.新教材对立体几何的处理有了一些新的变化，淡化了对学生作图能力的要求，引进了空间向量的方法（实际上是把空间问题代数化），避开了一些繁杂的作图，其中在求异面直线所成的角中运用空间向量的方法有很大的优点.另外，对异面直线所成的角的求法我们还可以借用一些固定的模型，引用一些已知的公式来求出角的大小.例１在直三棱柱中，底面是直角三角形，，为侧棱的中点.（1）求异面直线、所成角的余弦值；（2）求二面角的平面角的余弦值.思路分析：建立空间直角坐标系，由题意写出相关点的坐标；（1）求出异面直线所在的方向向量，直接计算即可；（2）求出平面与平面的法向量，计算即可.（2）因为，，，所以，，所以为平面的一个法向量.因为，，设平面的一个法向量为， .由得令，则，.所以42cos(,).323||||n CBn CBn CB===所以二面角的余弦值为点评：本题考查空间向量的应用，属中档题；在空间求线线角、线面角、二面角，是通过建立恰当的空间直角坐标系,正确写出各点的坐标，则通直线所在的方向向量、平面的法向量，通过向量的夹角间接求解，准确运算是解决这类问题的关键.2 直线与平面所成的角直线与平面所成角是空间三大角之一,它既是教与学的难点,又是高考的热点,求直线与平面所成角的常用方法.一、直接法直接法就是根据斜线与平面所成角的定义,直接作出斜线在平面内的射影,则斜线与射影所成角就是斜线与平面所成角,这是解题时首先要考虑的方法,直接法的关键是确定斜线在平面内的射影,下列结论常作为找斜线在平面内射影的依据.(1)(两平面垂直的性质定理)如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.(2)如果一个角所在平面外一点到角的两边的距离相等,那么这个点在平面内的射影在这个角的平分线上.(3)经过一个角的顶点引这个角所在平面的斜线,设它和已知角的两边的夹角为锐角且相等,则这条斜线在平面的射影是这个角的平分线.(4)若三棱锥的三条侧棱相等,则其顶点在底面上的射影是底面三角形的外心. 二、借助于空间向量工具，利用直线的方向向量与平面的法向量的夹角来转化，当直线的方向向量与平面的法向量夹角为锐角时，通过直角三角形可以知道，直线与平面所成的角与直线的方向向量与平面的法向量夹角互余，因此直线与平面所成的角的正弦就等于直线的方向向量与平面的法向量夹角的余弦，当直线的方向向量与平面的法向量夹角为钝角时，其补角跟直线与平面所成的角互余，因此因此直线与平面所成的角的正弦就等于直线的方向向量与平面的法向量夹角的余弦的相反数.例2【西南名校联盟高三xx年元月】如图，在等腰梯形中，，上底，下底，点为下底的中点，现将该梯形中的三角形沿线段折起，形成四棱锥.（1）在四棱锥中，求证：；（2）若平面与平面所成二面角的平面角为，求直线与平面所成角的正弦值.思路分析：（1）由，，，点为的中点，得三角形沿线段折起后可得四边形为菱形，边长为，，取的中点，连接，，，可证，，即可证平面，从而平面，即可得证；（2）以为坐标原点，建立空间直角坐标系，由（1）可证为平面与平面所成二面角的平面角，从而求出，，，，再求出平面的一个法向量，即可求出直线与平面所成角的正弦值.∴，而，∴且，得点的横坐标为，点的竖坐标为，则，，，，故，，，设平面的一个法向量为，∴()()()333·0?022{ ·020?0BD n x y z AD n x y z ??=-= ? ???=-=，，，，，，，，，，得3330 220x z y -=-=，，点评：直线与平面所成的角解题的一般思路为：首先建立适当的空间直角坐标系并正确写出各点的空间坐标，并求出平面的法向量，最后运用公式即可得出结果. 利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.3 二面角二面角及其平面角的概念是立体几何最重要的概念之一，在历年高考中几乎都要涉及.尤其是在数学新课改的大环境下，要求对二面角求法的掌握变得更加灵活，二面角的概念发展、完善了空间角的概念；而二面角的平面角不但定量描述了两相交平面的相对位置，同时它也是空间中线线、线面、面面位置关系的一个汇集点.研究二面角的求法，可以进一步培养学生的空间想象能力和逻辑思维能力，为培养学生的创新意识和创新能力提供了一个良好的契机. 在求解二面角的问题中，通常首先要定位出二面角的平面角，而这也是学生在解题中感到最为陌生和棘手的问题.特别是若二面角的棱隐而不露其解题的难度又会增大.求解二面角是立体几何中最基本、最重要的题型，也是各地高考中的“热点”问题，虽然对此可说是“千锤百炼”，但我们必须面对新的情境、新的变化，如何以基本方法的“不变”去应对题目中的“万变”就是我们研究的中心话题. 总的来说，求解二面角的大体步骤为：“作、证、求”.其中“作、证”是关键也是难点，“求”依靠的计算，也决不能忽视，否则因小失大，功亏一篑，也是十分遗憾之事.例3【北京市朝阳区xx届期末】如图，在三棱柱中，，是线段的中点，且平面．（Ⅰ）求证：平面平面；（Ⅱ）求证：平面；。

EA BC D A1B1C1D1FGH IJ高考数学第二轮复习教案空间角与距离的计算考点核心整合一．空间角计算空间角，其一般方法是根据定义通过作辅助线或辅助面构造出要求的角θ并作出含有角θ的三角形，从而通过解三角形得角θ的值．1．求异面直线所成角的常用方法（1）平移法（定义法）：即根据定义找出或作出有关角的图形并证明它符合定义，进而求出角的大小．（2）补形法：有时在原几何体上补一个类似的几何体．2．求直线与平面所成角的常用方法（1）定义法：关键是作出斜线在平面内的射影，即关键是判断射影在平面内的位置．（2）公式法：cosθ= cosθ1cosθ2（其中θ1为所求线面角，θ为斜线与平面内任一直线所成的角，θ2为射影与该直线所成的角）．3．二面角的定义从一条直线出发的两个半平面所组成的图形叫做二面角．（1）二面角定量地反映了两个平面相交的位置关系，它是转化成平面内两条相交直线所成的角（二面角的平面角）度量的，与顶点在棱上的位置无关．（2）求二面角大小的三个步骤：①找出或作出二面角的平面角（本着先找后作的原则）；②证明符合定义；③指出某角即为二面角的平面角并计算（往往把该平面角放置到一个三角形中去求）．简单地表述为：一作，二证，三计算．二面角的大小，课本中给出了具体范围，即为[0，π]．（3）求作二面角的平面角的方法：①定义法：在棱上找一点O，在二面角的两个面内分别作棱的垂线AO、BO，则∠AOB即为二面角的平面角．②用三垂线定理（或逆定理）作二面角的平面角：从二面角的一个面内选一个特殊点A，由A向另一个平面作垂线，垂足为B，再由B向棱作垂线交于点C，则∠ACB即为二面角的平面角．③作棱的垂面：作垂直于二面角的棱或二面角两个半平面的垂面，则该垂面与两个半平面交线所成的角就是二面角的平面角．④面积法：如果一个多边形在一个平面内的射影是一个多边形，且这两个多边形所在平面所成的二面角为θ，则cosθ=S射影多边形S斜多边形．⑤对于未给棱的二面角的求法，一般情况下首先作棱或在有利条件下利用射影公式求更方便．二、空间的距离立体几何中涉及到的距离有八种：两点间距离、点到直线距离、点到平面距离、两平行线间距离、异面直线间距离、与平面平行的直线到平面的距离、两平行平面间的距离以及求球面上两点间距离．这八种距离都归结到求点到点、点到直线、点到面这三种距离．求距离问题的解题步骤是找到表示该距离的线段，证明该线段合题意，得到该线段所在三角形，解这个三角形，求出距离．1．求异面直线间距离大体有如下的解法：（1）作出两条异面直线的公垂线段然后求之；（2）将异面直线间距离转化为线面之间的距离；（3）将异面直线间距离转化为面面之间的距离；（4）运用“两条异面直线间距离，是分别在两条异面直线上的两点间距离的最小值”这一概念求之；（5）利用体积法（主要是指三棱锥的体积）求之．2．点到直线或平面的距离是空间最常见的，求解的关键是正确作出图形，其中确定垂足位置最重要，应充分利用图形性质，注意各种距离之间的相互转化，等积求法及“平行移动”的思想方法．3．求距离的方法大致有两种：（1）直接法：步骤是“一作，二证，三计算”，即先作出表示该距离的线段，再证明该线段即为所求距离，然后再计算，不能忽视第二步的证明．（2）间接法：包括等积法和转化法，转化法即不断地进行点面、线面、面面距离之间的转化，直到求出为止．考题名师诠释【例1】已知正方体ABCD—A1B1C1D1的棱长为1，在正方体表面上与点A距离为233的点的集合形成一条曲线，则这条曲线的长度为．解析如右图，题目即以A为球心，233为半径的球面与正方体六个面交线的长度，而这条交线有六条弧构成，即EFGHIJ．由对称性知EF = GH = IJ，FG = HI = JE，所以，所求曲线长l = 3(EF⌒+ FG⌒)．由AE =233，AA1 = 1，ABCDEOFG则AF = AE = 233，A 1E = AE 2 - AA 12= 33，A 1F = A 1E = 33，∠A 1AE = ∠A 1AF = π6．由对称性∠FAG = π2 -∠A 1AE = π2 - 2×π6 = π6．因此EF ⌒为以A 1为圆心、33为半径、π2为圆心角的一段弧，故EF ⌒= A 1E × π2 = 3π6．同理，FG 为以A 为圆心，233为半径、π6为圆心角的一段圆弧．故FG ⌒= AF × π6 = 3π9．所以，所求曲线的长l = 3(3π6+ 3π9) = 53π6． 答案 53π6．评叙 本题以正方体各侧面截球面求交线为背景，全面考查空间想象能力和分析解决问题的能力．考虑正方体各面与球面的交线时，应知道截线都是圆弧，但不过球心A 的面截球面所的截线是小圆的圆弧，而经过球心A 的面截球面所得的是大圆的圆弧．【例2】（2005年福建卷，20）如图，直二面角D -AB -E 中，四边形ABCD 是边长为2的正方形，AE = EB ，F 为CE 上的点，且BF ⊥平面ACE ．（1）求证：AE ⊥平面BCE ； （2）求二面角B -AC -E 的大小；（3）求点D 到平面ACE 的距离． （1）证明：∵BF ⊥平面ACE ，∴BF ⊥AE ．∵二面角D -AB -E 为直二面角，且CB ⊥AB ，∴CB ⊥平面ABE ．∴CB ⊥AE ． ∴AE ⊥平面BCE ．（2）解：连结BD 交AC 于点G ，，连结FG ． ∵正方形ABCD 的边长为2，∴BG ⊥AC ，BG = 2． ∵BF ⊥平面ACE ，由三垂线定理的逆定理，得FG ⊥AC ． ∴∠BGF 是二面角B -AC -E 的平面角． 由（1）AE ⊥平面BCE ，∴AE ⊥EB ．又∵AE = EB ，∴在等腰直角△AEB 中，BE = 2．又∵直角△BCE 中，EC = BC 2 + BE 2= 6，BF =BC ·BE EC = 2×26= 233， ∴Rt △BFG 中，sin ∠BGF = BF BG = 2332 = 63．∴二面角B -AC -E 等于arcsin63． （3）解：过E 作EO ⊥AB 交AB 于点O ，OE = 1． ∵二面角D -AB -E 为直二面角，∴EO ⊥平面ABCD ． 设D 到平面ACE 的距离为h ，∵V D —ACE = V E —ACD ， ∴13S △ACE ·h = 13S △ACD ·EO ．∵AE ⊥平面BCE ，∴AE ⊥EC ．∴h = 12AD ·DC ·EO 12AE ·EC = 12×2×2×112×2×6 = 233．∴点D 到平面ACE 的距离为233．评叙 本题主要考查直线、直线与平面、二面角及点到平面的距离等基础知识，考查空间想象能力、逻辑思维能力与运算能力．【例3】（2005年北京卷，理16）如图，在直四棱柱ABCD -A 1B 1C 1D 1中，AB = AD = 2，DC = 23，AA 1 = 3，AD ⊥DC ，AC ⊥BD ，垂足为E ．（1）求证：BD ⊥A 1C ；（2）求二面角A 1- BD –C 1的大小；（3）求异面直线AD 与BC 1所成的角的大小． （1）证明： 在直四棱柱ABCD -A 1B 1C 1D 1中，∵A 1A ⊥底面ABCD ．∴AC 是A 1C 在平面ABCD 上的射影．∵BD ⊥AC ，∴BD ∥A 1C ． （2）解：连结A 1E 、C 1E 、A 1C 1．与（1）同理可证BD ⊥A 1E ，BD ⊥C 1E ，∴∠A 1EC 1为二面角A 1- BD –C 1的平面角． ∵AD ⊥DC ，∴∠A 1D 1C 1 = ∠ADC = 90º．又A 1D 1 = AD = 2，D 1C 1 = DC = 23，AA 1 = 3，且AC ⊥BD ，∴A 1C 1 = 4， AE = 1，EC = 3．∴A 1E = 2，C 1E = 23． 在△A 1EC 1中，A 1C 12= A 1E 2+ C 1E 2，∴∠A 1EC 1 = 90º，即二面角A 1- BD –C 1的大小为90º．BA CD E FABCD（3）解：过B 作BF ∥AD 交AC 于点F ，连结FC 1， 则∠C 1BF 就是AD 与BC 1所成的角． ∵AB = AD = 2，AC ⊥BD ，AE = 1， ∴BF = 2，EF = 1，FC = 2，BC = DC ． ∴FC 1 = 7，BC 1 = 15．在△BFC 1中，cos ∠C 1BF = 15 + 4 - 72×2×15 = 155．∴∠C 1BF = arccos155，即异面直线AD 与BC 1所成的角的大小为arccos 155． 【例4】（2004年全国卷Ⅰ，20）如图，已知四棱锥P —ABCD ，PB ⊥AD ，侧面PAD 为边长等于2的正三角形，底面ABCD 为菱形，侧面PAD 与底面ABCD 所成的二面角为120º． （1）求点P 到平面ABCD 的距离；（2）求面APB 与面CPB 所成的二面角的大小． 解（1）：如图，作PO ⊥平面ABCD ，垂足为点O ． 连结OB 、OA 、OD ，OB 与AD 交于点E ，连结PE ． ∵AD ⊥PB ，∴AD ⊥OB ．∵PA = PD ，∴OA = OD ． 于是OB 平分AD ，点E 为AD 的中点，∴PE ⊥AD ．由此知∠PEB 为面PAD 与面ABCD 所成二面角的平面角，∴∠PEB = 120º，∠PEO = 60º． 由已知可求得PE = 3．∴PO = PE ·sin60º = 3×32 = 32．即点P 到平面ABCD 的距离为32．（2）如图，取PB 的中点G ，PC 的中点F ， 连结EG 、AG 、GF ，则AG ⊥PB ，FG ∥BC ，FG = 12BC ．∵AD ⊥PB ，∴BC ⊥PB ，FG ⊥PB ．∴∠AGF 是所求二面角的平面角． ∵AD ⊥面POB ，∴AD ⊥EG ．又∵PE = BE ，∴EG ⊥PB ，且∠PEG = 60º． 在Rt △PEG 中，EG = PE ·cos60º = 32．在Rt △PEG 中，EG = 12AD = 1．于是tan ∠GAE = EG AE =32．又∠AGF = π - ∠GAE ， ∴所求二面角的大小为π - arctan32． 评叙 本题主要考查棱锥、二面角和线面关系等基本知识，同时考查空间想象能力和推理、运算能力． 特别提示1．求二面角的平面角的步骤：（1）先作出二面角的平面角，其作法有定义法、根据三垂线定理及其逆定理、垂面法；（2）根据作法构造三角形，在直角三角形中，用解直角三角形的方法；在斜三角形中，利用正、余弦定理求二面角的平面角．2．二面角的计算方法常用的还有：射影面积法，向量法．利用这些方法可在不作出二面角的平面角的情况下求出二面角的平面角．考能提升训练一、选择题1．（2005年湖南卷，5）如图，正方体ABCD -A 1B 1C 1D 1的棱长为1，O 是底面的中心，则O 到平面ABC 1D 1的距离为 ………（ ）A ．12B ．24C ．22D ．322．对于已知直线a ，如果直线b 同时满足下列三个条件：①与a 是异面直线；②与a 所成的角为定值 ；③与a 的距离为定值d ．那么这样的直线b 有 ……………………………（ ） A ．1条B ．2条C ．3条D ．无数条3．如图，在正三棱锥P -ABC 中，M 、N 分别是侧棱PB 、PC 的中点，若截面AMN ⊥侧面PBC ，则此三棱锥的侧棱与底面所成角的正切值 是…………………………………………… （ ）A ．32B ． 2C ．52D ．634．如图，ABC -A 1B 1C 1是直三棱柱，∠BCA = 90º，点D 1、F 1分别是A 1B 1、A 1C 1的中点，若BC = CA = CC 1，则BD 1与AF 1所成角的余弦值是………………………………………………………………（ ）A ．3010B ．12C ．3015D ．15105．正方形ABCD 的边长是2，E 、F 分别是AB 和CD 的中点，将正方形沿EF 折成直二面角（如图所示）．M 为矩形AEFD 内一点，如果ABCDPABCD PE OABCDPE OG F ABD OA 1B 1C 1D 1ABCPMNABCA 1B 1C 1D 1 F 1DMB CF∠MBE = ∠MBC ，MB 和平面BCE 所成角的正切值为12，那么点M到直线EF 的距离为………………………………… （ ） A ．22B ．1C ．32D ．12二、填空题6．长方体的一条对角线与交于一点的三个面所成的角分别为α、β、γ，那么下列命题： ①sin 2α+ sin 2β+ sin2γ= 1；②sin 2α+ sin 2β+ sin 2γ= 2；③cos 2α+ cos 2β+ cos 2γ= 1；④cos 2α+ cos 2β+ cos 2γ= 2．其中正确命题的序号是 ．7．（2005年江西卷，理15）如图，在直三棱柱ABC -A 1B 1C 1中，AB = BC = 2，BB 1 = 2，∠ABC = 90º，E 、F 分别为AA 1、 C 1B 1的中点，沿棱柱的表面从E 到F 两点的最短路径的长度为 ． 三、解答题8．（2004年春季北京卷，17）如图，四棱锥S -ABCD 的底面是边长为1的正方形，SD ⊥底面ABCD ，SB = 3．（1）求证：BC ⊥SC ；（2）求面ASD 与面BSC 所成二面角的大小；（3）设棱SA 的中点为M ，求异面直线DM 与SB 所成角的大小．9．（2005年湖北卷，理20）如图，在四棱锥P -ABCD 中，底面ABCD 为矩形，侧棱PA ⊥底面ABCD ，AB = 3，BC = 1，PA = 2，E 为PD 的中点．（1）求直线AC 与PB 所成角的余弦值；（2）在侧面PAB 内找一点N ，使NE ⊥面PAC ，并求出N 点到AB 和AP 的距离．B A 1BCA DSMBA10．如图所示，在矩形ABCD 中，AB = 1，BC = a ，PA ⊥平面ABCD ，PA = 1． （1）在BC 边上是否存在点Q ，使得PQ ⊥QD ？说明理由．（2）若BC 边上有且仅有一个点Q ，使PQ ⊥QD ，求AD 与平面PDQ 所成的角的正弦值． （3）在（2）的条件下，能求出平面PQD 与平面PAB 所成的角的大小吗？训练参考答案一、1．B 2．D 3．C 4．A 5．A 二、6．①④ 7．322三、8．（1）略；（2）45º；（3）90º．9．（1）3714（2）在面ABCD 内过点D 作AC 的垂线交AB 于点F ，连结PF ，N 为PF 的中点，N 点到AB 的距离为1，N 点到AP的距离为36． 10．（1）a ≥2时，BC 边上存在存在点Q ，使得PQ ⊥QD ；a ＜2时，不存在点Q ，使得PQ ⊥QD ；（2）66；（3）能，大小为arctan 5． BCA DP Q。

空间角与空间距离本部分知识主要包括异面直线所成角、线线角、线面角、点到面的距离，是新课标考查的重点，其考查题型多为一道客观题加一道解答题，客观题主要考查简单的距离和角的求法，以中档题为主，解答题考查一般以考查空间向量在立体几何中的应用，题目常常为中高档题。

【2010年高考预测】从近几年对这部分知识的考查来看，2010年仍是考查热点，应该是一道客观题加一道解答题，分值应该在15分左右，主要考查空间的各种角和各种距离的求解，同时与探索性、存在性问题相结合的可能性很大。

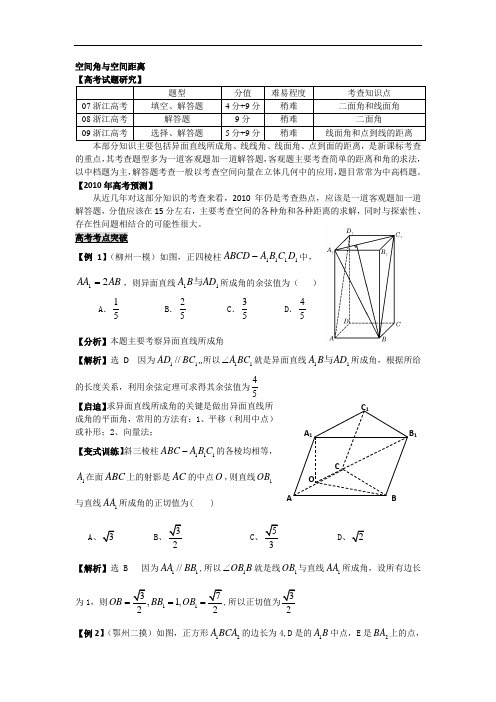
【例1】（柳州一模）如图，正四棱柱1111D C BA ABCD -中，AB AA 21=，则异面直线11AD B A 与所成角的余弦值为（）A ．51 B ．52 C ．53 D ．54【分析】本题主要考察异面直线所成角【解析】选D 因为11//AD BC ,,所以11A BC ∠就是异面直线11AD B A 与所成角，根据所给的长度关系，利用余弦定理可求得其余弦值为45【启迪】求异面直线所成角的关键是做出异面直线所成角的平面角，常用的方法有：1、平移（利用中点）或补形；2、向量法；【变式训练】斜三棱柱111ABC A B C -的各棱均相等，1A 在面ABC 上的射影是AC 的中点O，则直线1OB 与直线1AA 所成角的正切值为( ) A B C D 【解析】选 B 因为11//AA BB ,所以1OB B ∠就是线1OB 与直线1AA 所成角，设所有边长为1，则111,OB BB OB === 【例2】（鄂州二摸）如图，正方形12A BCA 的边长为4,D 是的1A B 中点，E 是2BA 上的点，ABCA 1B 1C 1O将△A 1DC 及△A 2EC 分别沿DC 和EC 折起，使A 1A 2重合于A ，且二面角A —DC —E 为直二面角。

（1）求BE 的长；（2）求AD 与平面AEC 所成角的正弦值。

【分析】本题主要考查在翻折问题中求线面角【解析】(1)∵A 1、A 2重合于A ∴AC ⊥AD ，AC ⊥AE ，故AC ⊥面ADE ∴AC ⊥DE ∵A-DC-E 为直二面角， ∴过A 作AF ⊥CD 于F ，则AF ⊥面CDE ， 故CD 为AC 在面CDE 上的射影，由三垂线定理的逆定理有：CD ⊥DE.在Rt △CAD 中，AD=2，AC=4，∴DC=25，AF=54，又∵CD ⊥DE ，∴在正方体A 1BA 2C 中，△DBE ～△CA 1D 故111=⇒=BE BEBDD A C A .(2)法一：设D 到面AEC 的距离为d ，则由V D —AEC =V A —DEC 有：AF DE CD d AC AE ⋅⋅⋅⋅=⋅⋅⋅21312131 ∴3×4d=25455⋅⋅ 故352=d ，即点D 到平面AEC 的距离为352.设AD 与平面AEC 所成角为θ，则35sin =θ 法二：由于AC ⊥面ADE ，所以平面AEC ⊥平面ADE ，所以点D 在平面AEC 上的射影在AE 上，所以DAE ∠就是DA 与平面AEC 所成的角。

第二讲空间位置关系、空间角与空间距离——小题备考微专题1空间位置关系常考常用结论1．直线、平面平行的判定及其性质(1)线面平行的判定定理：a⊄α，b⊂α，a∥b⇒a∥α.(2)线面平行的性质定理：a∥α，a⊂β，α∩β＝b⇒a∥b.(3)面面平行的判定定理：a⊂β，b⊂β，a∩b＝P，a∥α，b∥α⇒α∥β.(4)面面平行的性质定理：α∥β，α∩γ＝a，β∩γ＝b⇒a∥b.2．直线、平面垂直的判定及其性质(1)线面垂直的判定定理：m⊂α，n⊂α，m∩n＝P，l⊥m，l⊥n⇒l⊥α.(2)线面垂直的性质定理：a⊥α，b⊥α⇒a∥b.(3)面面垂直的判定定理：a⊂β，a⊥α⇒α⊥β.(4)面面垂直的性质定理：α⊥β，α∩β＝l，a⊂α，a⊥l⇒a⊥β.保分题1.[2022·山东烟台三模]若a和α分别为空间中的直线和平面，则“a⊥α”是“a垂直α内无数条直线”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件2．[2022·北京东城三模]如图，在正方体ABCD-A1B1C1D1中，E，F分别为CC1，D1C1的中点，则下列直线中与直线BE相交的是()A．直线A1F B．直线AD1C．直线C1D1D．直线AA13．[2022·福建福州三模]在底面半径为1的圆柱OO1中，过旋转轴OO1作圆柱的轴截面ABCD，其中母线AB＝2，E是BĈ的中点，F是AB的中点，则()A．AE＝CF，AC与EF是共面直线B．AE≠CF，AC与EF是共面直线C．AE＝CF，AC与EF是异面直线D．AE≠CF，AC与EF是异面直线提分题例1 (1)[2022·山东淄博一模](多选)若m，n是两条不同的直线，α，β是两个不同的平面，则下列说法正确的有()A．若α∥β，m⊂α，则m∥βB．若α⊥β，m⊥α，则m∥βC．若m∥n，m⊥α，则n⊥αD．若m⊥n，m∥α，则n∥α(2)[2022·全国乙卷]在正方体ABCD-A1B1C1D1中，E，F分别为AB，BC的中点，则()A．平面B1EF⊥平面BDD1B．平面B1EF⊥平面A1BDC．平面B1EF∥平面A1ACD．平面B1EF∥平面A1C1D听课笔记：【技法领悟】1．根据空间线面平行、垂直关系的判定定理和性质定理逐项判断来解决问题；2．必要时可以借助空间几何模型，如从长方体、四面体等模型中观察线面位置关系，并结合有关定理来进行判断．巩固训练11.[2022·湖南衡阳二模]设m、n是空间中两条不同的直线，α、β是两个不同的平面，则下列说法正确的是()A．若m⊥α，n⊥β，m⊥n，则α⊥βB．若m⊂α，n⊂β，α∥β，则m∥nC．若m∥α，n∥β，α⊥β，则m⊥nD．若m⊂α，n⊂β，m∥β，n∥α，则α∥β2．[2022·广东广州三模]一几何体的平面展开图如图所示，其中四边形ABCD为正方形，E、F分别为PB、PC的中点，在此几何体中，下面结论错误的是()A．直线AE与直线BF异面B．直线AE与直线DF异面C．直线EF∥平面P ADD．直线EF∥平面ABCD微专题2 空间角与距离常考常用结论1．直线与直线的夹角若n 1，n 2分别为直线l 1，l 2的方向向量，θ为直线l 1，l 2的夹角，则cos θ＝|cos 〈n 1，n 2〉|＝|n 1·n 2|n 1||n 2||. 2．直线与平面的夹角设n 1是直线l 的方向向量，n 2是平面α的法向量，直线与平面的夹角为θ.则sin θ＝|cos 〈n 1，n 2〉|＝|n 1·n2|n 1||n 2||.3．平面与平面的夹角若n 1，n 2分别为平面α，β的法向量，θ为平面α，β的夹角，则cos θ＝|cos 〈n 1，n 2〉|＝|n 1·n2|n 1||n 2||.4．点到直线的距离：已知A ，B 是直线l 上任意两点， P 是l 外一点，PQ ⊥l ，则点P 到直线l 的距离为PQ ＝ √|AP ⃗⃗⃗⃗⃗ |2−|AQ ⃗⃗⃗⃗⃗ |2＝√|AP ⃗⃗⃗⃗⃗ |2−|AP ⃗⃗⃗⃗⃗ ·AB ⃗⃗⃗⃗⃗⃗ |AB ⃗⃗⃗⃗⃗⃗||2. 5．求点到平面的距离已知平面α的法向量为n , A 是平面α内的任一点，P 是平面α外一点，过点P 作平面α的垂线l ，交平面α于点Q ，则点P 到平面α的距离为|PQ |＝|AP⃗⃗⃗⃗⃗ ·n |n ||.保 分 题1.[2022·辽宁辽阳二模]在四棱锥P - ABCD 中，底面ABCD 是矩形，P A ⊥底面ABCD ，且P A ＝AB ，AD ＝3AB ，则PC 与底面ABCD 所成角的正切值为( )A ．13 B ．3 C ．√1010D ．√102．[2022·广东茂名二模]正三棱锥S - ABC 的底面边长为4，侧棱长为2√3，D 为棱AC 的中点，则异面直线SD 与AB 所成角的余弦值为________.3．已知正方体ABCD - A 1B 1C 1D 1的棱长为2，点E 是A 1B 1的中点，则点A 到直线BE 的距离是________．提 分 题例2 (1)若正四棱柱ABCD - A 1B 1C 1D 1的底边长为2，∠B 1AB ＝π3，E 是D 1D 的中点，则A 1C 1到平面EAC 的距离为( )A．√5B．2√5C．2√305D．2√303(2)[2022·全国甲卷]在长方体ABCD-A1B1C1D1中，已知B1D与平面ABCD和平面AA1B1B 所成的角均为30°，则()A．AB＝2ADB．AB与平面AB1C1D所成的角为30°C．AC＝CB1D．B1D与平面BB1C1C所成的角为45°听课笔记：【技法领悟】1．用几何法求空间角时，关键要找出空间角，再在三角形中求解．2．用向量法求空间角和空间距离时，要熟记公式，还要正确建立空间直角坐标系．巩固训练21.在四棱锥P-ABCD中，P A⊥平面ABCD，ABCD是矩形，且AB＝3，AD＝4，P A＝4√35，则平面ABD与平面PBD的夹角为()A．30° B．45°C．60° D．75°2．如图，在长方体中，AD＝AA1＝2，AB＝3，若E为AB中点，则点B1到平面D1EC 的距离为________.第二讲空间位置关系、空间角与空间距离微专题1空间位置关系保分题1．解析：若a⊥α，则a垂直α内所有直线，因此，命题“若a⊥α，则a垂直α内无数条直线”正确，a垂直α内无数条直线，若这无数条直线中无任何两条直线相交，此时直线a可以在平面α内，即不能推出a⊥α，所以“a⊥α”是“a垂直α内无数条直线”的充分不必要条件．答案：ACD1，2．解析：连接EF，CD1，A1B，则EF∥CD1，EF＝12由A1D1∥BC，A1D1＝BC，可得四边形A1D1CB为平行四边形，∴A1B∥CD1，A1B＝CD1，A1B，即四边形EF A1B为梯形，所以EF∥A1B，EF＝12故直线A1F与直线BE相交，直线AD1与直线BE为异面直线，直线C1D1与直线BE为异面直线，直线AA1与直线BE为异面直线．答案：A3．解析：由题意，圆柱的轴截面ABCD为边长为2的正方形，E是BĈ的中点，F是AB的中点，所以AC⊂平面ABC，EF与平面ABC相交，且与AC无交点，所以AC与EF是异面直线；又CF＝√12+22＝√5，AE＝√22+(√2)2＝√6，所以AE≠CF.答案：D提分题[例1]解析：(1)对于A，由面面平行性质：两平面平行，在一平面内的任意直线与另一平面平行．而α∥β，m⊂α，故m∥β，A正确；对于B，α⊥β，m⊥α，此时m有可能在平面β内，故不能得到m∥β，B错误；对于C，由于m∥n，则n可经平移到与m重合的位置而平移不改变直线与平面是否垂直，m⊥α，故n⊥α，C正确；对于D，当m∥α，m⊄α，过m上一点作直线n⊥α，此时m⊥n，不能得到n∥α，D错误．综上，AC正确．(2)如图，在正方体ABCD-A1B1C1D1中，易知BD⊥AC.又E，F分别为AB，BC的中点，所以EF∥AC，所以BD⊥EF.由正方体的性质，知DD1⊥平面ABCD.又EF⊂平面ABCD，所以DD1⊥EF.因为BD∩DD1＝D，所以EF⊥平面BDD1.因为EF⊂平面B1EF，所以平面B1EF⊥平面BDD1，A正确．假设平面B1EF⊥平面A1BD.因为平面B1EF⊥平面BDD1，且平面A1BD∩平面BDD1＝BD，所以BD⊥平面B1EF.在正方体ABCD－A1B1C1D1中，显然BD与平面B1EF 不垂直，B错误．设A1A与B1E的延长线相交于点P，所以平面B1EF与平面A1AC不平行，C错误．连接AB1，B1C，易证平面ACB1∥平面A1C1D.因为平面ACB1与平面B1EF相交，所以平面B1EF与平面A1C1D不可能平行，D错误．故选A.答案：(1)AC(2)A[巩固训练1]1．解析：对于A 选项，设直线m 、n 的方向向量分别为u 、v ，因为m ⊥α，n ⊥β，则平面α的一个法向量为u ，平面β的一个法向量为v ， 因为m ⊥n ，则u ⊥v ，故α⊥β，A 对；对于B 选项，若m ⊂α，n ⊂β，α∥β，则m 、n 平行或异面，B 错； 对于C 选项，若m ∥α，n ∥β，α⊥β，则m 、n 的位置关系不确定，C 错； 对于D 选项，若m ⊂α，n ⊂β，m ∥β，n ∥α，则α、β平行或相交，D 错． 答案：A 2.解析：由题意知：该几何体是底面为正方形的四棱锥，如图所示，连接AE ，EF ，BF ，DF ，易得EF ∥BC ，BC ∥AD ，则EF ∥AD ，故EF ，AD 共面，则AE ，DF 共面，故B 错误；又F ∈平面AEFD ，B ∉平面AEFD ，F 不在直线AE 上，则直线AE 与直线BF 异面，A 正确；由EF ∥AD ，EF ⊄平面P AD ，AD ⊂平面P AD ，则直线EF ∥平面P AD ，C 正确；EF ⊄平面ABCD ，AD ⊂平面ABCD ，则直线EF ∥平面ABCD ，D 正确．答案：B微专题2 空间角与距离保分题1．解析：因为P A ⊥底面ABCD ，AC ⊂底面ABCD ， 所以P A ⊥AC ，则PC 与底面ABCD 所成角为∠PCA .设AB ＝1，则P A ＝1，AD ＝3，AC ＝√10. 所以tan ∠PCA ＝PAAC ＝√1010. 答案：C2．解析：取BC 的中点E ，连接SE ，DE ，则∠SDE (或其补角)为异面直线SD 与AB 所成的角，由题意知SE ＝SD ＝√12−4＝2√2，DE ＝2， 所以cos ∠SDE ＝2×2√2×2＝√24. 答案：√243．解析：建立如图所示空间直角坐标系，则BA⃗⃗⃗⃗⃗ ＝(0，2，0)，BE ⃗⃗⃗⃗⃗ ＝(0，1，2)．∴cos θ＝|BA ⃗⃗⃗⃗⃗⃗ ·BE ⃗⃗⃗⃗⃗ ||BA ⃗⃗⃗⃗⃗⃗|·|BE⃗⃗⃗⃗⃗ |＝2√5＝√55.∴sin θ＝√1−cos 2θ＝2√55. 故点A 到直线BE 的距离d ＝|AB⃗⃗⃗⃗⃗ |sin θ＝2×2√55＝4√55. 答案：4√55提分题[例2] 解析：(1)由棱柱的几何性质可知，A 1C 1∥AC ， 又A 1C 1⊄平面EAC ，AC ⊂平面EAC ， 则A 1C 1∥平面EAC ，所以点A 1到平面EAC 的距离即为直线A 1C 1到平面EAC 的距离， 因为正四棱柱ABCD - A 1B 1C 1D 1的底边长为2，∠B 1AB ＝π3， 则AA 1＝2√3，以点A 为坐标原点建立空间直角坐标系如图所示，则A (0，0，0)，A 1(0，0，2√3)，C (2，2，0)，E (0，2，√3)，所以AE ⃗⃗⃗⃗⃗ ＝(0，2，√3)，AC ⃗⃗⃗⃗⃗ ＝(2，2，0)，AA 1⃗⃗⃗⃗⃗⃗⃗ ＝(0，0，2√3)， 设平面AEC 的法向量为n ＝(x ，y ，z )， 则{n ·AE ⃗⃗⃗⃗⃗ =0n ·AC ⃗⃗⃗⃗⃗ =0，即{2y +√3z =02x +2y =0，令x ＝√3，则y ＝－√3，z ＝2， 故n ＝(√3，－√3，2)， 所以点A 1到平面EAC 的距离d ＝|AA 1⃗⃗⃗⃗⃗⃗⃗⃗ ·n||n |＝√3√3+3+4＝2√305，故A 1C 1到平面EAC 的距离为2√305.(2)连接BD ，则∠B 1DB ，∠DB 1A 分别是B 1D 与平面ABCD 和平面AA 1B 1B 所成的角，所以∠B 1DB ＝∠DB 1A ＝30°.所以BB 1＝12DB 1，BD ＝√32DB 1，AD ＝12DB 1.设BB 1＝a ，则DB 1＝2a ，AD ＝BC ＝a ，BD ＝√3a ，所以AB ＝√BD 2−AD 2＝√2a ，AC ＝BD ＝√3a ，CB 1＝√BB 12+BC 2＝√2a .所以AB ＝√2AD ，AC ≠CB 1 ，因此A ，C 项错误．易知∠DB 1C 是B 1D与平面BB 1C 1C 所成的角，且为锐角．因为DC ＝√2a ，DB 1＝2a ，CB 1＝√2a ，所以DC 2+CB 12＝DB 12，所以DC ⊥CB 1.在Rt △DCB 1中，sin ∠DB 1C ＝DC DB 1＝√22，所以∠DB 1C ＝45°，即B 1D与平面BB 1C 1C 所成的角为45°，因此D 项正确．因为AD ⊥平面ABB 1A 1，AD ⊂平面AB 1C 1D ，所以平面AB 1C 1D ⊥平面ABB 1A 1，所以∠B 1AB 是AB 与平面AB 1C 1D 所成的角．在Rt △ABB 1中，AB ＝√2a ，BB 1＝a ，所以tan ∠B 1AB ＝BB1AB ＝√22≠√33，所以∠B 1AB ≠30°，即AB 与平面AB 1C 1D 所成的角不是30°，因此B 项错误．故选D.答案：(1)C (2)D [巩固训练2]1．解析：因为P A ⊥平面ABCD ，ABCD 是矩形，所以AB ，AD ，AP 两两垂直，故以A 为坐标原点，AB ，AD ，AP 为x 轴，y 轴，z 轴建立空间直角坐标系， 又AB ＝3，AD ＝4，P A ＝4√35， 所以A (0，0，0)，B (3，0，0)，D (0，4，0)，P (0，0，4√35)， 因为P A ⊥平面ABCD ，所以平面ABD 的一个法向量为n ＝(0，0，1)， 而PB⃗⃗⃗⃗⃗ ＝(3，0，－4√35)，BD ⃗⃗⃗⃗⃗ ＝(－3，4，0)， 设平面PBD 的法向量为m ＝(x ，y ，z )，则{m ·PB ⃗⃗⃗⃗⃗ =3x −4√35z =0m ·BD ⃗⃗⃗⃗⃗ =−3x +4y =0，取x ＝4，则平面PBD 的法向量m ＝(4，3，5√3)，cos 〈n ，m 〉＝n·m |n |·|m |＝√31×√42+32+(5√3)＝√32，所以〈n ，m 〉＝30°， 由图可知平面ABD 与平面PBD 的夹角为锐角，所以平面ABD 与平面PBD 的夹角为30°.答案：A 2.解析：以D 为坐标原点，DA ，DC ，DD 1所在直线分别为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系，连接CB 1，由题意得C (0，3，0)，E (2，32，0)，D 1(0，0，2)，B 1(2，3，2)，∴ CE ⃗⃗⃗⃗ ＝(2，−32，0)，CD 1⃗⃗⃗⃗⃗⃗⃗ ＝(0，−3，2)，CB 1⃗⃗⃗⃗⃗⃗⃗ ＝(2，0，2)， 设平面D 1EC 的法向量为n ＝(x ，y ，z )，则{CE⃗⃗⃗⃗ ·n =0CD 1⃗⃗⃗⃗⃗⃗⃗ ·n =0，即{2x −32y =0−3y +2z =0， 令z ＝6，得n ＝(3，4，6)， ∴点B 1到平面D 1EC 的距离d ＝|n· CB 1⃗⃗⃗⃗⃗⃗⃗⃗ ||n |＝18√6161.答案：18√6161。

沪教版（上海）高中数学度高三数学二轮复习立体几何专题之空间的角与距离①教学目标1、理解点到平面、直线和直线、直线和平面、平面和平面距离的概念；会用求距离的常用方法（如：直接法、转化法、向量法）2、理解线线角、线面角、面面角的概念定义和取值范围；会用求角的方法“一作二证三计算”。

知识梳理1、空间角：（1）空间角的计算步骤一作、二证、三算。

（2）异面直线所成角：1>范围：___________ (0°，90°]；2>计算方法:<1>平移法：一般情况下应用平行四边形的对边、梯形的平行对边、三角形的中位线进行平移;<2>补体法；（3）直线与平面所成的角：1>定义：平面的一条斜线和它在这个平面内的射影所成的锐角，叫做这条直线和这个平面所成的角；一条直线垂直于平面，我们说它们所成的角是直角；2>范围：_____________ [0°，90°]；3>斜线与平面所成角的计算：<1>直接法：关键是作垂线，找射影可利用面面垂直的性质；<2>平移法：通过三角形的中位线或平行四边形的对边平移，计算其平行线与平面所成的角（也可平移平面）。

<3>通过等体积法求出斜线任一点到平面的距离d，计算这点与斜足之间的线段长l，则sindl θ=.(6)二面角：1>定义：平面内的一条直线把平面分为两部分，其中的每一部分叫做半平面.从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，每个半平面叫做二面角的面。

二面角的平面角：以二面角的棱上任一点为端点，在两个半平面内分别作垂直于棱的两条射线，这两条射线所成的角，叫做这个二面角的平面角.规定：二面角的两个半平面重合时，二面角为0，当两个半平面合成一个平面时，二面角为π，因此，二面角的大小范围为_______ [0°，180°]；2>确定二面角的方法：<1>定义法；<2>垂面法；注：空间角的计算步骤：一作、二证、三算2、空间距离（1）七种距离：点与点、点到直线、两条平行直线、两条异面直线、点到平面、平行于平面的直线与该平面、两个平行平面之间的距离，其中点与点、点与直线、点到平面的距离是基础，求其它几种距离一般化归为求这三种距离； （2）点与点的距离： 1>解三角形及多边形；2>空间任意两点A 、B 间的距离即线段AB 的长度： 设()111,,A x y z 、()222,,B x y z ，则()()()222121212AB x x y y z z =-+-+-（3）两条异面两条异面直线的距离：直线的公垂线段的长度；说明：两条异面直线的距离等于其中一条直线到过另一条直线且与这条直线平行的平面的距离。