雅可比迭代法预处理
- 格式:docx
- 大小:12.69 KB
- 文档页数:1

jacobi迭代法matlabJacobi迭代法是一种常用的线性方程组求解方法,它是一种迭代法,通过不断迭代来逼近线性方程组的解。
Jacobi迭代法的基本思想是将线性方程组的系数矩阵分解为一个对角矩阵和一个非对角矩阵的和,然后通过迭代求解对角矩阵和非对角矩阵的乘积,最终得到线性方程组的解。
Jacobi迭代法的具体步骤如下:1. 将线性方程组的系数矩阵A分解为一个对角矩阵D和一个非对角矩阵R的和,即A=D+R。
2. 将线性方程组的右端向量b分解为一个对角矩阵D和一个非对角矩阵N的乘积,即b=Dx。
3. 对于任意的初始解向量x0,计算下一次迭代的解向量x1,即x1=D^(-1)(b-Rx0)。
4. 重复步骤3,直到达到预定的精度或迭代次数。
Jacobi迭代法的优点是简单易懂,易于实现,收敛速度较快。
但是,它的缺点也很明显,即收敛速度较慢,需要进行大量的迭代才能达到较高的精度。
在Matlab中,可以使用以下代码实现Jacobi迭代法:function [x,k]=jacobi(A,b,x0,tol,maxit)% Jacobi迭代法求解线性方程组Ax=b% 输入:系数矩阵A,右端向量b,初始解向量x0,精度tol,最大迭代次数maxit% 输出:解向量x,迭代次数kn=length(b); % 系数矩阵A的阶数D=diag(diag(A)); % 对角矩阵DR=A-D; % 非对角矩阵Rx=x0; % 初始解向量for k=1:maxitx1=D\(b-R*x); % 计算下一次迭代的解向量if norm(x1-x)<tol % 判断是否达到精度要求break;endx=x1; % 更新解向量end输出结果可以使用以下代码实现:A=[4 -1 0; -1 4 -1; 0 -1 4]; % 系数矩阵b=[15; 10; 10]; % 右端向量x0=[0; 0; 0]; % 初始解向量tol=1e-6; % 精度要求maxit=1000; % 最大迭代次数[x,k]=jacobi(A,b,x0,tol,maxit); % Jacobi迭代法求解线性方程组fprintf('解向量x=[%f; %f; %f]\n',x(1),x(2),x(3)); % 输出解向量fprintf('迭代次数k=%d\n',k); % 输出迭代次数以上就是Jacobi迭代法的主要内容,通过Matlab实现Jacobi迭代法可以更好地理解其基本思想和具体步骤。


一、简介Matlab中jacobi迭代法是一种用于求解线性方程组的迭代方法,适用于系数矩阵为对称、正定矩阵的情况。
该迭代方法通过将系数矩阵分解为对角矩阵、上三角矩阵和下三角矩阵的形式,然后通过迭代计算得到方程组的解。
在Matlab中,可以利用矩阵运算和迭代循环来实现jacobi迭代法。
二、 jacobi迭代法原理1. 基本思想jacobi迭代法的基本思想是将系数矩阵分解为对角矩阵D、上三角矩阵U和下三角矩阵L的形式,即A=D+L+U,其中D为系数矩阵A 的对角线元素组成的对角矩阵,L为系数矩阵A的下三角部分,U为系数矩阵A的上三角部分。
令x为方程组的解向量,b为方程组的右端向量,则方程组可表示为Ax=b。
根据方程组的性质,可将方程组表示为(D+L+U)x=b,然后利用迭代的方式逐步逼近方程组的解。
2. 迭代公式假设迭代到第k次,方程组可表示为(D+L+U)x=b,将其转化为迭代形式x(k+1)=(D+L)^(-1)(b-Ux(k)),利用迭代公式可以逐步计算出方程组的解。
3. 收敛条件对于jacobi迭代法,收敛条件为系数矩阵A为对角占优矩阵或正定矩阵。
如果满足这一条件,迭代计算会逐步收敛于方程组的解。
三、 Matlab中jacobi迭代法实现在Matlab中,可以利用矩阵运算和迭代循环来实现jacobi迭代法。
具体步骤如下:1. 对系数矩阵进行分解将系数矩阵A分解为对角矩阵D、上三角矩阵U和下三角矩阵L的形式。
2. 初始化迭代变量初始化迭代的初始值x0、迭代次数k、逐次逼近解向量x(k+1)。
3. 迭代计算利用迭代公式x(k+1)=(D+L)^(-1)(b-Ux(k))来逐步计算出方程组的解。
4. 判断收敛条件在迭代计算过程中,需要实时判断迭代计算是否满足收敛条件,如果满足则停止迭代计算,得到方程组的解。
四、实例分析假设有如下方程组:2x1 + x2 + 4x3 = 103x1 + 4x2 - x3 = 10x1 + 2x2 + 3x3 = 0可以利用jacobi迭代法来求解该方程组,在Matlab中可以通过编程实现迭代计算过程。


雅克比迭代法和高斯赛德尔迭代法的算法描述一. 雅克比迭代法雅克比迭代法(Jacobi Iteration)是计算数值解的一种迭代方法,它遵循一个简单的步骤:给定问题的初始值,按照一定的规则,用求出某一个矩阵元素,替换当前值,得到下一个矩阵值,重复这个步骤,直到满足某一个条件,即为所求解的结果。
雅克比迭代法求解矩阵问题的一般步骤为:(1)给定初始矩阵A和右端值矩阵B,将第i行第j列的元素表示为aij,bi;(2)第i行其它元素之和定义为s(i) =∑(j≠i)|a(i, j)|,亦即∑|aij|;(3)如果s(i)不等于0,则第i行第i列元素的值更新为xi=1 (b(i) ∑(j≠i)[a(i, j)x(j)])/a(i, i)(4)重复步骤3,直到满足|X(i)X(i)|<ε(ε为设定的误差),此时x即为所求解的结果。
二. 高斯-赛德尔迭代法高斯-赛德尔迭代法(Gauss-Seidel Iteration)是另一种迭代方法,算法的基本思想也是:通过迭代,计算出当前矩阵的第i行第j列的元素xi;然后更新第i行第j列元素的值,继续迭代,直到某种条件满足,即可求出矩阵的解。
高斯-赛德尔迭代法的基本步骤为:(1)给定初始矩阵A和右端值矩阵B,将第i行第j列的元素表示为aij,bi;(2)第i行其它元素之和定义为s(i) =∑(j≠i)|a(i, j)|,亦即∑|aij|;(3)如果s(i)不等于0,则第i行第i列元素的值更新为xi=1 (b(i) ∑(j<i)[a(i, j)x(j)]∑(j>i)[a(i,j)x(j)] )/a(i, i)(4)重复步骤3,直到满足|X(i)X(i)|<ε(ε为设定的误差),此时x即为所求解的结果。
总结从上面的对比来看,雅克比迭代法和高斯赛德尔迭代法的步骤基本一致,均采用迭代的方式求解矩阵A的解X,不同的是,高斯赛德尔迭代法在更新矩阵A的第i行第i列元素时,采用把小于i的j元素的值替换成当前迭代求得的值来计算,而雅克比迭代法采用把全部j元素的值替换成当前迭代求得的值来计算。

雅克比迭代法马来西亚雅克比迭代法(Marey Jacobs Iterative Method)是一种功能最优化的数值分析方法,又称无约束最优化算法,其目的是找到函数最优值,这是一种全局最优解法,可以有效求解多变量非线性方程和非凸优化问题。
1. 雅克比迭代法的概念雅克比迭代法是数值分析方法的一种,他可以搜索多变量非线性函数的最优值。
该方法的核心思想是:在每次迭代中,通过计算函数的梯度(或偏导数)来找到新的最优值,以及搜索方向。
它基于雅克比矩阵求解多元非线性方程组,需要迭代计算,来自动找到变量最优值点,比如从一个初始点开始,沿着局部函数增加最快的方向,一直搜索到某一程度,就可以得到全局最优结果。
2. 雅克比迭代法的特点①雅克比迭代法可以基于非凸优化,这就使得在多元变量函数中找到最优解更加容易。
②它的收敛速度极快,一般只需一定的迭代周期就可以解出比较精确的解。
③雅克比迭代法具有很大的数值稳定性,它可以适应多元函数的各种变化而取得精确的结果。
3. 雅克比迭代法的应用(1)雅克比迭代法可以用于非线性最优化,用于非线性方程组和非凸优化问题。
(2)它可以用于解决多元、非线性优化问题,特别是在功能最优化技术中经常应用。
(3)它广泛应用于多目标最优化,在这种问题中,可以使用雅可比迭代法来求解最优值。
(4)它可以有效地解决期望、约束类优化问题,其中,约束可以通过增加惩罚函数的系数来改变。
4. 雅克比迭代法的缺点(1)雅可比迭代法的最佳初值特征和求解准确度有较大的依赖,这意味着对于不同的情况,要使用不同的参数,这就耗费了较多的时间;(2)雅可比迭代法因为受函数从原点出发的假定条件,所以只能较不理想的收敛到局部最优解,而不能较好的收敛到全局最优解;(3)雅可比迭代法实现起来较为复杂,对于复杂的非凸优化问题,往往可能导致求解的困难;(4)雅可比迭代法有一定的假定条件,一旦这些假定发生变化,那么最终计算出的结果就可能发生改变。
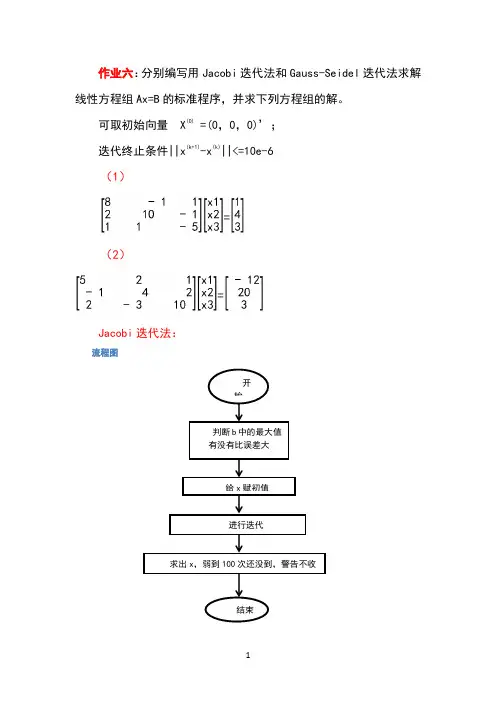

jacobi迭代法
Jacobi迭代法是常见的数值计算中解线性方程组的方法之一,它是一种迭代式方法。
Jacobi迭代法主要用于近似解决线性方程组,它是以变步长的简单迭代方法,以求解高维空间的线性方程组。
Jacobi迭代法的基本思想是,使用当前近似解求解未知数,其数学模型为Ax=b,将x分解为x=x0+dx,其中dx为增量,前面先确定x0,求解dx,新近似解为x0+dx。
Jacobi迭代法的具体步骤是:给定问题的数学模型Ax=b,确定初值xi(0)(i=1,2,…,n),用Aijxj(k)=bi-Σ(i≠j)Aijxj (k)计算第i个未知数的新近似解xi (k+1),代入上一次的新近似解作为右边的初值,重复上述过程,即可以得到新的xi(k+1)。
Jacobi迭代法的主要优点是计算简单,实现容易,需要的存储空间少,因此被广泛应用于解线性方程组。
但是,Jacobi迭代法的收敛性能较差,如果迭代次数太多,会使计算效率降低。
因此,Jacobi迭代法在数值计算中由其算法本身的简单性及其低纬度和低存储量得以广泛使用,其计算过程也由此得到优化。
但是,该迭代法局限于其较差的收敛性能,必须谨慎使用以防超过预定的最大迭代数。

数值分析-雅克⽐迭代法雅克⽐迭代法雅克⽐迭代法就是众多迭代法中⽐较早且较简单的⼀种,其命名也是为纪念普鲁⼠著名数学家雅可⽐。
雅克⽐迭代法的计算公式简单,每迭代⼀次只需计算⼀次矩阵和向量的乘法,且计算过程中原始矩阵A始终不变,⽐较容易并⾏计算。
迭代过程⾸先将⽅程组中的系数矩阵A分解成三部分,即:A = L+D+U,如图1所⽰,其中D为对⾓阵,L为下三⾓矩阵,U为上三⾓矩阵。
之后确定迭代格式,X^(k+1) = B*X^(k) +f ,(这⾥^表⽰的是上标,括号内数字即迭代次数),如图1所⽰,其中B称为迭代矩阵,雅克⽐迭代法中⼀般记为J。
(k = 0,1,…)再选取初始迭代向量X^(0),开始逐次迭代。
收敛性设Ax= b,其中A=D+L+U为⾮奇异矩阵,且对⾓阵D也⾮奇异,则当迭代矩阵J的谱半径ρ(J)<1时,雅克⽐迭代法收敛优缺点雅克⽐迭代法的优点明显,计算公式简单,每迭代⼀次只需计算⼀次矩阵和向量的乘法,且计算过程中原始矩阵A始终不变,⽐较容易并⾏计算。
然⽽这种迭代⽅式收敛速度较慢,⽽且占据的存储空间较⼤例题程序算法#include<math.h>#include<stdio.h>#include <stdlib.h>int main(){float e =0.001, z, m, y[3]; float b[3]={-12, 20, 3};float x[3]={0);float a[3][3]={{5, 2, 1},{-1, 4, 2},{2, -3, 10}};int n =3, j, i, k =1;while(1){for(i=0;i<3;i++){for(j=0;j<3;j++)m=m+a[i][j]*x[j];m = m - x[i] * a[i][i]; y[i]=(b[i] - m) / a[i][i]; m =0;}i =0;while(i <3){z = fabs(x[i] - y[i]);if(z > e)break;i++;}if(i !=3){for(i =0; i <3; i++)x[i]= y[i];k++;}else if(i ==3)break;}printf("%f\n%f\n%f\n", y[0], y[1], y[2]);return0;}1求解⽅程:8 * x1 - 3 * x2 + 2 * x3 =204 * x1 - 11 * x2 - x3 =336 * x1 + 3 * x2 + 12 * x3 =36精确解:x1 =0.411817, x2 = -3.176429, x3 =3.588173 --->迭代公式:x1^(k+1)=(3 * x2^(k) - 2 * x3^(k) + 20) / 8;x2^(k+1)=(-4 * x1^(k) + 1 * x3^(k) + 33) / (-11); x2^(k+1)=(-6 * x1^(k) - 3 * x2^(k) + 36) / 12; */#include <stdio.h>#include <stdlib.h>struct X {float x1;float x2;float x3;};X jcobi(X&v){X r;r.x1 =(3 * v.x2 - 2 * v.x3 + 20) / 8;r.x2 =(-4 * v.x1 + v.x3 + 33) / (-11);r.x3 =(-6 * v.x1 - 3 * v.x2 + 36) / 12;return r;}void main(){X v={0,0,0};int iteration =20;while(iteration-- >0){v= jcobi(v);v= jcobi(v);}printf("%f\n%f\n%f\n", v.x1, v.x2, v.x3); }。

Jacobi-Davidson迭代方法是一种用于求解对称或非对称特征值问题的迭代方法。
它结合了Jacobi方法和Davidson方法的优点,能够在较短的时间内快速收敛到特征值和特征向量。
本文将从原理、算法流程、收敛性等几个方面介绍Jacobi-Davidson迭代方法的相关内容。
1. 原理Jacobi-Davidson迭代方法的原理基于对称或非对称特征值问题的特征值分解。
在实际问题中,许多矩阵是大规模的、稀疏的,因此直接对其进行特征值分解是非常困难的。
Jacobi-Davidson迭代方法通过迭代的方式,逐步逼近矩阵的特征值和特征向量。
2. 算法流程Jacobi-Davidson迭代方法的算法流程如下:(1) 初始化:选择合适的初始特征向量和雅可比矩阵;(2) 迭代计算:通过迭代计算,逐步逼近特征值和特征向量;(3) 收敛判定:判断迭代过程是否收敛,若收敛则停止计算,否则继续迭代;(4) 输出结果:输出计算得到的特征值和特征向量。
3. 收敛性Jacobi-Davidson迭代方法具有较好的收敛性,尤其适用于对称或近似对称的矩阵。
通过合理的初始化和迭代计算,通常可以在较短的时间内获得较为精确的特征值和特征向量。
然而,由于不同问题的特点不同,有时也需要根据具体情况对算法进行调整,以提高收敛速度和精度。
4. 应用领域Jacobi-Davidson迭代方法在科学计算、物理学、化学、工程学等领域广泛应用。
在材料科学中,通过Jacobi-Davidson迭代方法可以快速求解材料的电子结构和能带结构;在计算流体力学中,可以用于求解流体的稳定性和振动特性等问题。
Jacobi-Davidson迭代方法是一种强大的求解特征值问题的数值方法,它通过结合Jacobi方法和Davidson方法的优点,具有较好的收敛性,适用于大规模、稀疏矩阵的特征值计算。
随着计算机技术的发展和应用需求的不断提高,Jacobi-Davidson迭代方法将在更多的领域得到广泛应用,并为解决实际问题提供重要的数值计算工具。

第八节 雅可比迭代法与高斯—塞德尔迭代法一 雅可比迭代法设线性方程组b Ax = (1) 的系数矩阵A 可逆且主对角元素nn a ,...,a ,a 2211均不为零,令()nna ,...,a ,a diag D 2211=并将A 分解成()D D A A +-= (2)从而(1)可写成 ()b x A D Dx +-=令11f x B x +=其中b D f ,A D I B 1111--=-=. (3) 以1B 为迭代矩阵的迭代法(公式)()()111f x B x k k +=+ (4)称为雅可比(Jacobi)迭代法(公式),用向量的分量来表示,(4)为⎩⎨⎧[],...,,k ,n ,...,i x a ba xnij j )k (j j i iii)k (i21021111==∑-=≠=+ (5)其中()()()()()Tn x ,...x ,x x 002010=为初始向量.由此看出,雅可比迭代法公式简单,每迭代一次只需计算一次矩阵和向量的乘法.在电算时需要两组存储单元,以存放()k x 及()1+k x . 例1 例1 用雅可比迭代法求解下列方程组⎪⎩⎪⎨⎧=+--=-+-=--2453821027210321321321.x x x .x x x .x x x解 将方程组按雅可比方法写成⎪⎪⎩⎪⎪⎨⎧++=++=++=8402020830201072020*******2321.x .x .x .x .x .x .x .x .x取初始值()()()()()()T T ,,,x ,x ,x x 0000302010==按迭代公式()()()()()()()()()⎪⎪⎩⎪⎪⎨⎧++=++=++=+++840202083020107202010211331123211.x .x .x .x .x .x .x .x .x k k k k k k k k k进行迭代,其计算结果如表1所示表1二 高斯—塞德尔迭代法由雅可比迭代公式可知,在迭代的每一步计算过程中是用()k x的全部分量来计算()1+k x的所有分量,显然在计算第i 个分量()1+k i x 时,已经计算出的最新分量()()1111+-+k i k x ,...,x 没有被利用,从直观上看,最新计算出的分量可能比旧的分量要好些.因此,对这些最新计算出来的第1+k 次近似()1+k x的分量()1+k jx 加以利用,就得到所谓解方程组的高斯—塞德(Gauss-Seidel )迭代法.把矩阵A 分解成U L D A --= (6)其中()nn a ,...,a ,a diag D 2211=,U ,L --分别为A 的主对角元除外的下三角和上三角部分,于是,方程组(1)便可以写成 ()b Ux x L D +=-即 22f x B x +=其中()()b L D f ,U L D B 1212---=-= (7)以2B 为迭代矩阵构成的迭代法(公式)()()221f x B x k k +=+ (8)称为高斯—塞德尔迭代法(公式),用 量表示的形式为⎩⎨⎧[],...,,k ,n ,,i x a x a b a xi j n i j )k (j ij )k (j ij i ii)k (i21021111111==∑∑--=-=+=++ (9)由此看出,高斯—塞德尔迭代法的一个明显的优点是,在电算时,只需一组存储单元(计算出()1+k ix 后()k ix 不再使用,所以用()1+k i x 冲掉()k ix ,以便存放近似解.例2 例2 用高斯——塞德尔迭代法求解例1.解 取初始值()()()()()()TT,,,x ,x ,x x 0000302010==,按迭代公式()()()()()()()()()⎪⎩⎪⎨⎧++=++=++=++++++840202083020107202010121113311123211.x .x .x .x .x .x .x .x .x k k k k k k k k k进行迭代,其计算结果如下表2从此例看出,高斯—塞德尔迭代法比雅可比迭代法收敛快(达到同样的精度所需迭代次数少),但这个结论,在一定条件下才是对的,甚至有这样的方程组,雅可比方法收敛,而高斯—塞德尔迭代法却是发散的.三 迭代收敛的充分条件定理1 在下列任一条件下,雅可比迭代法(5)收敛.①111<∑=≠=∞nij j iiij ia a max B ;②1111<∑=≠=nij i iiij ja a max B ;③ 111<∑=-≠=∞-nji i jjij jTa a max AD I定理2 设21B B ,分别为雅可比迭代矩阵与高斯—塞德尔迭代矩阵,则∞∞≤12B B (10)从而,当111<∑=≠=∞nij j iiij ia a max B时,高斯—塞德尔迭代法(8)收敛. 证明 由21B B ,的定义,它们可表示成()U L D B +=-11()()U D L D I U L D B 11112-----=-=用e 表示n 维向量()T,...,,e 111=,则有不等式eB e B ∞≤11UD L D B 111--+=这里,记号|·|表示其中矩阵的元素都取绝对值,而不等式是对相应元素来考虑的,于是()()()Ie B L D I eL D B e U D ∞------≤-=111111容易验证()11==--nnL D L D所以,L D I 1--及L D I 1--可逆,且()()()1111111111-----------=++≤+++=-L D I LD ...L D I L D ...L D I LD I n n()I L D I ≥---11从而有()()((){}e I B L D I L D I eU D LD I e B ∞----------≤⋅-≤111111121{()()}eB eL D I I B I ∞--∞≤-⋅--=11111因此必有∞∞≤12B B因为已知11<∞B 所以12<∞B .即高斯—塞德尔迭代法收敛.若矩阵A 为对称,我们有定理3 若矩阵A 正定,则高斯—塞德尔迭代法收敛.证明 把实正定对称矩阵A 分解为T L L D A --=()TL U =,则D 为正定的,迭代矩阵()T L L D B 12--=设λ是2B 的任一特征值,x 为相应的特征向量,则()()x x L L D T λ=--1以L D -左乘上式两端,并由T L L D A --=有()Ax x L T λλ=-1用向量x 的共轭转置左乘上式两端,得()Ax x x L xTTT--=-λλ1 (11)求上式左右两端的共轭转置,得Ax x x L x T T ----=⎪⎭⎫ ⎝⎛-λλ1以λ--1和λ-1分别乘以上二式然后相加,得()()Axx x L L x T T T -----⎪⎭⎫ ⎝⎛-+=+⎪⎭⎫ ⎝⎛--λλλλλλ211 由TL L D A --=,得()()Axx x A D x T T -----⎪⎭⎫ ⎝⎛-+=-⎪⎭⎫ ⎝⎛--λλλλλλ211即()Ax x x L x TT---=-λλλ2211 (12)因为A 和D 都是正定的,且x 不是零向量,所以由(11)式得1≠λ,而由(12)式得012>-λ, 即1<λ,从而()12<B ρ,因而高斯—塞德尔迭代法收敛.定义1 设()nn ij a A ⨯=为n 阶矩阵.① ①如果n,...,i ,a a nij i j ij ii 21=∑>≠= (13)即A 的每一行对角元素的绝对值都严格大于同行其他元素绝对值之和,则称A 为严格对角优势矩阵.② ②如果n,...,i ,a a nij i j ij ii 21=∑≥≠=且至少有一个不等式严格成立,则称A 为弱对角优势矩阵.例如⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-310131012是严格对角优势矩阵,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--310121011是弱对角优势矩阵. 定义2 设()nn ij a A ⨯=是n 阶矩阵,如果经过行的互换及相应列的互换可化为⎥⎦⎤⎢⎣⎡2212110A A A ,即存在n 阶排列矩阵P,使⎥⎦⎤⎢⎣⎡=2212110A A A AP P T其中2211A ,A 为方阵,则称A 是可约的,否则称A 为不可约的.A 是可约矩阵,意味着b Ax =可经过若干次行列重排,化为两个低阶方程组,事实上,b Ax =可化为 ()b P x P AP P TT T =,记()()()()⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡==2121d d d b P ,y y y x P TT于是,求解b Ax =化为求解()()()()()⎪⎩⎪⎨⎧=+=+22221212111d y A d y A y A可以证明,如果A 为严格对角优势矩阵或为不可约弱对角优势矩阵,则A 是非奇异的.定理4 如果A 为严格对角优势矩阵或为不可约弱对角优势矩阵,则对任意()0x ,雅可比迭代法(4)与高斯—塞德尔迭代法(8)均为收敛的.证明 下面我们以A 为不可约弱对角优势矩阵为例,证明雅可比迭代法收敛,其他证明留给读者.要证明雅可比迭代法收敛,只要证()11<B ρ,1B 是迭代矩阵.用反证法,设矩阵1B 有某个特征值μ,使得1≥μ,则()01=-B I det μ,由于A 不可约,且具有弱对角优势,所以1-D 存在,且 ()()D A D D A D I I B I -+=--=---μμμ111从而()0=-+D A D detμ另一方面,矩阵()D A D -+μ与矩阵A 的非零元素的位置是完全相同的,所以()D A D -+μ也是不可约的,又由于1≥μ,且A 弱对角优势,所以n,...,i ,a a a nij i j ij ii ii 21=∑≥≥≠=μ并且至少有一个i 使不等号严格成立.因此,矩阵()D A D -+μ弱对角优势,故()D A D -+μ为不可约弱对角优势矩阵.从而()0≠-+D A D det μ矛盾,故1B 的特征值不能大于等于1,定理得证.。
1.Jacobi迭代法例1 用jacobi迭代法求解代数线性代数方程组,保留四位有效数字(err=1e-4)其中A=[8 -1 1;2 10 -1;1 1 -5];b=[1 ;4; 3]。
解:编写jacobi迭代法的函数文件,保存为jacobi.mfunction [x,k]=jacobi(A,b,x0,eps,N)% 求解Ax=b;x0为初始列向量;eps为误差容限;N为最大迭代次数% 输出x为近似解;k为迭代次数n=length(A);x=zeros(n,1);for k=1:Nfor i=1:n―――――――endif norm(x-x0,inf)<eps % 迭代终止条件% if (max(abs(x-x0)))<epsbreak;endx0=x;end编写主程序如下format longclearA=[8 -1 1;2 10 -1;1 1 -5];b=[1 ;4; 3];x0=[0.125; 0.4 ;-0.6 ]; % x0为初始列向量N为最大迭代次数err=1e-4; % err为误差容限N=25; % N为最大迭代次数[x,k]=jacobi(A,b,x0,err,N)得到结果如下x =0.224923156250000.30561995000000-0.49388680000000k =62.Gauss-seidel迭代法例2 用Gauss-seidel迭代法求解代数线性代数方程组,保留四位有效数字(err=1e-4) 其中A=[8 -1 1;2 10 -1;1 1 -5];b=[1 ;4; 3]。
解:编写Gauss-seidel迭代法的函数文件,保存为gaus.mfunction [x,k]=gaus(A,b,x0,eps,N)% 求解Ax=b;x0为初始列向量;eps为误差容限;N为最大迭代次数% 输出x为近似解;k为迭代次数n=length(A);x=zeros(n,1);for k=1:Nfor i=1:n――――――endif norm(x-x0,inf)<eps % 迭代终止条件% if (max(abs(x-x0)))<epsbreak;endx0=x;end编写主程序如下format longclearA=[8 -1 1;2 10 -1;1 1 -5];b=[1 ;4; 3];x0=[0.125; 0.4 ;-0.6 ]; % x0为初始列向量N为最大迭代次数err=1e-4; % err为误差容限N=25; % N为最大迭代次数[x,k]=gaus(A,b,x0,err,N)输出结果为x =0.224939378906250.30562326171875-0.49388747187500k =53.SOR迭代法例3 用SOR迭代法求解代数线性代数方程组,松驰因子w=1.005,其中A=[8 -1 1;2 10 -1;1 1 -5];b=[1 ;4; 3]。
雅可比迭代法是一种常用于求解线性方程组的迭代方法。
它通过不断迭代来求解方程组的解。
在使用雅可比迭代法之前,我们需要对方程组进行一些预处理,以便使用这种方法求解。
首先,我们需要将方程组化为如下的形式:
Ax = b
其中A 是系数矩阵,x 是未知向量,b 是常数向量。
然后,我们需要确定一个初始猜测解x0,作为迭代的起点。
这个初始猜测解可以是任意的,但是如果能够选择一个较好的初始猜测解,则可能会使迭代收敛得更快。
最后,我们需要选择一个迭代系数,这个系数决定了新的猜测解与旧的猜测解之间的关系。
一般来说,如果选择的迭代系数越小,则迭代收敛得越慢,但是收敛得更稳定;如果选择的迭代系数越大,则迭代收敛得越快,但是收敛得更不稳定。
这就是雅可比迭代法的预处理过程。