数学总复习知识点.docx

初中数学复习提纲第一章 实数★重点★ 实数的有关概念及性质，实数的运算 ☆内容提要☆一、 重要概念 1．数的分类及概念 数系表：说明：“分类”的原则：1）相称（不重、不漏）2）有标准实数无理数(无限不循环小数)正分数 负分数 正整数0 负整数 (有限或无限循环性数) 整数分数正无理数负无理数0 实数负数整数分数无理数有理数正数整数分数无理数有理数2．非负数：正实数与零的统称。

（表为：x ≥0） 常见的非负数有：性质：若干个非负数的和为0，则每个非负担数均为0。

3．倒数： ①定义及表示法②性质：A.a ≠1/a （a ≠±1）;B.1/a 中，a ≠0;C.0＜a ＜1时1/a ＞1;a ＞1时，1/a ＜1;D.积为1。

4．相反数： ①定义及表示法②性质：A.a ≠0时，a ≠-a;B.a 与-a 在数轴上的位置;C.和为0,商为-1。

5．数轴：①定义（“三要素”）②作用：A.直观地比较实数的大小;B.明确体现绝对值意义;C.建立点与实数的一一对应关系。

6．奇数、偶数、质数、合数（正整数—自然数）定义及表示：│a │2aa (a ≥0)(a 为一切实数)奇数：2n-1偶数：2n （n 为自然数）7．绝对值：①定义（两种）： 代数定义：几何定义：数a 的绝对值顶的几何意义是实数a 在数轴上所对应的点到原点的距离。

②│a │≥0,符号“││”是“非负数”的标志;③数a 的绝对值只有一个;④处理任何类型的题目，只要其中有“││”出现，其关键一步是去掉“││”符号。

二、 实数的运算 1． 运算法则（加、减、乘、除、乘方、开方） 2．运算定律（五个—加法[乘法]交换律、结合律;[乘法对加法的] 分配律） 3．运算顺序：A.高级运算到低级运算;B.（同级运算）从“左”到“右”（如5÷51×5）;C.(有括号时)由“小”到“中”到“大”。

a(a≥0) -a(a<0)│a │=三、 应用举例（略）附：典型例题1．已知：a 、b 、x 在数轴上的位置如下图，求证：│x-a │+│x-b │ =b-a.2.已知：a-b=-2且ab<0，（a ≠0，b ≠0），判断a 、b 的符号。

一寸光阴不可轻总复习小学数学复习资料第一章数和数的运算一概念（一）整数1 .整数的意义自然数和0都是整数。

2 .自然数我们在数物体的时候，用来表示物体个数的1，2，3……叫做自然数。

一个物体也没有，用0表示。

0也是自然数。

3.计数单位：一（个）、十、百、千、万、十万、百万、千万、亿……都是计数单位。

每相邻两个计数单位之间的进率都是10。

这样的计数法叫做十进制计数法。

4. 数位计数单位按照一定的顺序排列起来，它们所占的位置叫做数位。

5.数的整除整数a除以整数b(b ≠0），除得的商是整数而没有余数，我们就说a能被b整除，或者说b能整除a 。

如果数a能被数b（b ≠0）整除，a就叫做b的倍数，b就叫做a的约数（或a的因数）。

倍数和约数是相互依存的。

因为35能被7整除，所以35是7的倍数，7是35的约数。

一个数的约数的个数是有限的，其中最小的约数是1，最大的约数是它本身。

例如：10的约数有1、2、5、10，其中最小的约数是1，最大的约数是10。

一个数的倍数的个数是无限的，其中最小的倍数是它本身。

3的倍数有：3、6、9、12……其中最小的倍数是3 ，没有最大的倍数。

个位上是0、2、4、6、8的数，都能被2整除，例如：202、480、304，都能被2整除。

个位上是0或5的数，都能被5整除，例如：5、30、405都能被5整除。

一个数的各位上的数的和能被3整除，这个数就能被3整除，例如：12、108、204都能被3整除。

一个数各位数上的和能被9整除，这个数就能被9整除。

能被3整除的数不一定能被9整除，但是能被9整除的数一定能被3整除。

一个数的末两位数能被4（或25）整除，这个数就能被4（或25）整除。

例如：16、404、1256都能被4整除，50、325、500、1675都能被25整除。

一个数的末三位数能被8（或125）整除，这个数就能被8（或125）整除。

例如：1168、4600、5000、12344都能被8整除，1125、13375、5000都能被125整除。

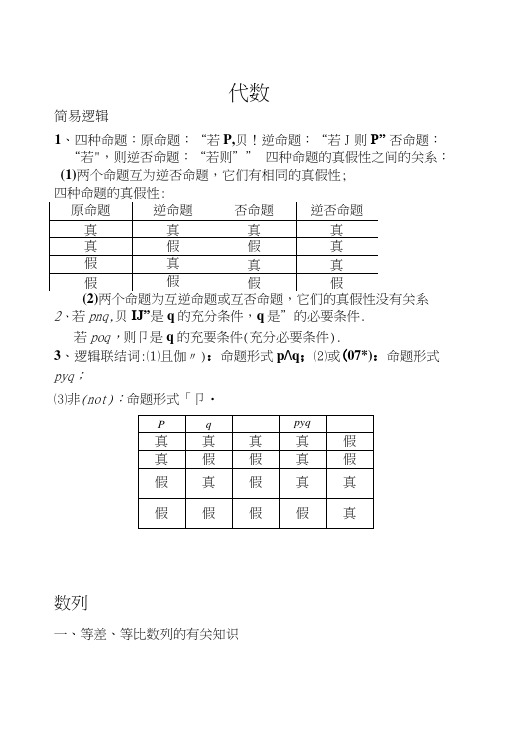
代数简易逻辑1、四种命题：原命题：“若P,贝！逆命题：“若J则P” 否命题：“若"，则逆否命题：“若则”” 四种命题的真假性之间的关系：(1)两个命题互为逆否命题，它们有相同的真假性;四种命题的真假性:两个命题为互逆命题或互否命题，它们的真假性没有关系2、若pnq,贝IJ”是q的充分条件，q是”的必要条件.若poq，则卩是q的充要条件(充分必要条件).3、逻辑联结词:⑴且伽〃)：命题形式p/\q；⑵或(07*)：命题形式pyq；⑶非(not)：命题形式「卩・数列一、等差、等比数列的有关知识1、若仏｝是等差数列, 且加 + 斤=〃 + g ( n?、n > p > g w N * ),贝|J佥+%=你+爲；若仏｝是等差数列,且2n = p + q 5、p、gwN) 则2% = Qp + a q・2、若｛〜｝是等比数列，且m + n = p + q ( m、斤、八q w N)则4” “ =知"；若｛%｝是等比数列，且2n = p + q ( n > p、gwN”),则cr n = a p - a(｛.不等式1> a-h>0<^> a>h ; a-h = O<^> a=h ; a-h <0<^> a <h .2、不等式的性质：①a > b U> b < ci ;②a> b、b > c^> a>c ;③a >b^>a + c>b + c;④ a>b,c>Sc, a>b, c < 0 => < be ; ⑤ a > b, c > d => d + c > b + d ;'a + b' =)2(a > 0,b > 0); ④宀2© a > b > 0,c > d > 0 ac > bd ;⑦ d > b 〉0 => a" > b n (n e N,/i > 1);⑧ a 〉b >0=>> y/b (n e N,n > 1)・3、二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系:为正数八b 的几何平均数.5、均值不等式定理：若a 〉0, b>0 9 则 a +方 2 2\[ah ,即 ° 十">\[ab6、常用的基本不等式:①a 1 +b 2 > lab (a,Z? e /?);②ab 5" ；" (a,b w R);判别式A =戻-4ac A>0二次函数y = ax 2+bx + c （d 〉0）的图象A<0一元二次方程有两个相异实数根有两个相等实ax 2 + bx+c = 0 (tz >0)的根(心)没有实数根ax 1 + bx +次不等 (a > 0) 式的解ax 1 + bx+集(a > 0)X X<兀]或兀 > 兀2 } bx ---------2d喘两个正数’则字称为正数八b 的算术平均数，亦称7、极值定理：设八y 都为正数，则有2⑴若x + y = 5 （和为定值），则当兀=y 时，积xy 取得最大值〒.4（2）若xy = p （积为定值），则当x = y 时，和兀+ y 取得最小值2仆・导数及其应用1、函数/⑴从州到兀2的平均变化率:3.函数y = f （x ）在点处的导数的几何意义是曲线『可⑴在点 卩（心，/仇））处的切线的斜率.4、常见函数的导数公式:① C = 0;②(x n ) = nx n ~l ;③(sinx) = cosx ;④(cosx) = -sinx ;⑤(a x ) =a x \na; ©(e x ) =e x ;⑦(log“ x) = ——;⑧(In x)=-xlnax5、导数运算法则:(I) ［/(x)士g(x)］'=广(x)土g©).⑵［.().g(x)］、广⑴ g(x) + .f(x)g©)・6、在某个区间仏b ）内，若广⑴＞0,则函数y = f （x ）在这个区间内单调递增；2、导数定义/（%）在点兀。

《初一到初三的数学知识点总结.doc》(优选3篇)《初一到初三的数学知识点总结.doc》第1篇（一）概率1.随机事件：在一定的条件下可能发生也可能不发生的事件，叫做随机事件。

2.互斥事件：不可能同时发生的两个事件叫做互斥事件。

3.对立事件：即必有一个发生的互斥事件叫做对立事件。

4.必然事件:那些无需通过实验就能够预先确定它们在每一次实验中都一定会发生的事件称为必然事件。

5.不可能事件：那些在每一次实验中都一定不会发生的事件称为不可能事件。

（二）有理数1.定义：由整数和分数组成的数。

包括：正整数、0、负整数，正分数、负分数。

可以写成两个整之比的形式。

2.相反数：指绝对值相等，正负号相反的两个数互为相反数。

3.绝对值：绝对值是指一个数在数轴上所对应点到原点的距离。

4.有理数的加减法：同号相加，把绝对值相加。

异号相加，取绝对值大的加数的符号，并用较大的绝对值减去较小的绝对值。

5.有理数的乘法：两数相乘，同号得正，异号得负，并把绝对值相乘。

6.有理数的除法：两数相除，同号得正，异号得负，并把绝对值相除。

0除以任何一个不为0的数，都得0。

《初一到初三的数学知识点总结.doc》第2篇第一章丰富的图形世界1、几何图形从实物中抽象出来的各种图形，包括立体图形和平面图形。

2点、线、面、体(1)几何图形的组成点：线和线相交的地方是点，它是几何图形中最基本的图形。

：面和面相交的地方是线，分为直线和曲线。

面：包围着体的是面，分为平面和曲面。

体：几何体也简称体。

(2)点动成线，线动成面，面动成体。

3、生活中的立体图形生活中的立体图形柱:棱柱：三棱柱、四棱柱(长方体、正方体)、五棱柱、……2、相反数：只有符号不同的两个数叫做互为相反数，零的相反数是零3、数轴：规定了原点、正方向和单位长度的直线叫做数轴(画数轴时，三要素缺一不可)。

任何一个有理数都可以用数轴上的一个点来表示。

4、倒数：如果a与b互为倒数，则有ab=1，反之亦成立。

四年级下册数学各单元知识点整理姓名★数学考试应注意：1、用手指着认真读题至少两遍。

2、遇到不会的题不要停留太长时间，可在题目的前面做记号。

（如：“？”）3、画图、连线时必须用尺子。

4、检查时，要注意是否有漏写、少写的情况。

第一单元：四则运算1、加、减的意义和各部分间的关系（1）把两个数合并成一个数的运算，叫做加法。

（2）已知两个数的积与其中的一个加数，求另一个加数的运算，叫做减法。

（3）减法是加法的逆运算。

（4）加法各部分间的关系：和=加数＋加数加数=和－另一个加数（5）减法各部分间的关系：差=被减数－减数减数=被减数－差被减数=减数＋差2、乘、除法的意义和各部分间的关系（1）求几个相同加数的和的简便运算，叫做乘法。

（2）已知两个因数的积与其中一个因数，求另一个因数的运算，叫做除法。

（3）除法是乘法的逆运算。

（4）乘法各部分间的关系：积=因数×因数因数=积÷另一个因数（5）除法各部分间的关系：商=被除数÷除数除数=被除数×商被除数=商×除数（6）有余数的除法，被除数=商×除数 +余数3、加法、减法、乘法、除法统称为四则运算。

4、四则混和运算的顺序（1）在没有括号的算式里，如果只有加、减法，或者只有乘、除法，都要按（从左往右）的顺序计算；（2）在没有括号的算式里，如果既有乘、除法，又有加、减法，要先算（乘、除法），后算（加、减法）；（3）在有括号的算式里，要先算括号里面的，后算括号外面的，括号里面的算式计算顺序遵循以上的计算顺序。

4、有关0 的计算①一个数和0 相加，结果还得原数： a + 0 = a0 + a = a②一个数减去0，结果还得这个数： a －0 = a③一个数减去它本身，结果得零： a － a = 0④一个数和0 相乘，结果得0：a×0 = 00 × a = 0⑤0 除以一个非0 的数，结果得0：0÷a = 0⑥0不能做除数：a÷0 =（无意义）第二单元：观察物体（二）1、正确辨认从上面、前面、左面观察到物体的形状。

数学总复习复习资料数学总复习复习资料(一)整数和小数1、整数和自然数像…，-3，-2，-1，0，1，2，3，…这样的数统称为(整数)。

整数的个数是(无限)的。

数物体的时候,用来表示物体个数的0,1,2,3…叫做(自然数)。

自然数整数的(一部分)。

(“1”)是自然数的单位。

最小的自然数是( 0 )。

2、小数小数表示的就是十分之几，百分之几，千分之几……的数，一位小数可表示为十分之几的数，两位小数可表示为百分之几的数，三位小数可表示为千分之几的数……熟记： =0.2 = 0.4 = 0.6 =0.8=0.25 = 0.75 = 0.125 =0.375 =0.625 =0.875小数点右边第一位是(十分位),计数单位是(十分之一);第二位是(百分位),计数单位是(百分之一)……小数部分有几个数位,就叫做几位小数。

如3.305是( 三 )位小数3、整数、小数的读法和写法：读整数时注意先分级再读数。

28302006000 读作：读小数时注意小数部分顺次读出每个数位上的数。

27.036 读作：写数时注意写好后，一定要读一读仔细校对。

五亿零8千写作：三百八十点零三六写作：为了读写方便,常常把较大的数改写成用“万”或“亿”作单位的数。

如只要求“改写”，结果应是准确数。

768000000 =( )亿如要求“省略”万(亿)后面的尾数，结果应是近似数。

768000000≈( )亿4、小数的性质：小数的末尾添上0或者去掉0,小数的大小不变.5、小数点向右(左)移动一位、两位、三位……原来的数就扩大(缩小)10倍、100倍、1000倍……6、正数、负数0既不是正数也不是负数，0是正数和负数的分界点。

负数<0<正数两个负数比较，负号后面的数越大这个数反而越小。

-6.8<-0.4 -2="">-10(二)因数和倍数1、因数和倍数一个数的最小因数是1，最大的因数是它本身。

一个数的因数的个数是有限的。

小学数学基础知识总复习一、概念姓名：自然数:表示物体个数的数叫自然数.一个物体也没有用0表示,0也是自然数.自然数都是整数.分数:把单位“1”平均分成若干份,表示这样一份或几份的数, 叫分数.表示其中一份的数，是这个分数的分数单位.小数:把单位“I”平均分成10份、100份、1000份……，这样的一份或几份是十分之几、百分之几、千分之几、可以用小数表示，一位小数表示十分之几、两位小数表示百分之几、三位小数表示千分之几……纯小数、混小数（带小数）：整数部分为0的小数叫纯小数;整数部分不为0的小数叫混小数（或叫带小数）.有限小数、无限小数:小数位数是有限的小数叫有限小数;小数位数是无限的小数叫无限小数.循环小数、纯循环小数、混循环小数:从小数部分某一位开始, 一个数字或几个数字依次不断重复出现，这样的小数叫循环小数;如果小数部分从第一位开始循环，叫纯循环小数;如果小数部分不是从十分位开始循环，就叫混循环小数.计数单位、数位:整数和小数都是按照十进制计数法写出的数, 其中个、十、百、千……以及十分之一、百分之一…•…都是计数单位. 各个计数单位所占的位置，叫数位.互为倒数:乘积是一的两个数叫互为倒数.百分数:表示一个数是另一个数的百分之儿的数，叫百分数，也叫百分比或百分率.整除:整数a除以整数 b （b^O），除得的商正好是整数而没有余数，就说a能被b整除（也可以说b能整除a）.倍数、约数:如果整数a能被整数b整除，就说a叫b的倍数;b 叫a 的约数.公因数、公倍数:几个数公有的倍数叫做这几个数的公倍数.其中最小的一个叫这几个数的最小公倍数;几个数公有的因数叫这几个数的公因数，其中最大的一个叫这几个数的最大公因数.质数、合数:一个数，如果只有1和它本身两个因数，叫质数;一个数，如果除了1和它本身，还有别的因数，叫合数.1既不是质数，也不是合数,2是最小的质数，也是唯一的偶质数.互质数:公因数只有1的两个数，叫互质数.质因数:每个合数都可以写成几个质数相乘的形式，这几个质数都叫这个合数的质因数.把一个合数写成儿个质数相乘的形式，叫把这个合数分解质因数.奇数、偶数:不能被2整除的数叫奇数;能够被2整除的数叫偶数.0是偶数.方程、解方程:含有未知数的等式叫方程；求方程的解的过程叫解方程.方程的解:能使方程两边相等的未知数的值叫方程的解.比比值:两个数相除又叫两个数的比；比的前项除以比的后项所得的商叫比值.比例尺：图上距离和实际距离的比叫比例尺.比例:表示两个比相等的式子叫比例.正比例、反比例:两种相关联的量，一种量变化另一种量也随着变化如果这两种量中相对应的两个数的比值（或商）一定,就说这两种量是成正比例的量，它们的关系叫正比例关系.y+x=k （—定）；如果这两种量中相对应的两个数的积一定，就说这两种量成反比例，它们的关系叫反比例关系.xy=k （—定）最简比：比的前项和后项都是整数，而且互质的比，叫最简比.名数:计量的结果，要用数来表示，并且还要带上单位名称，通常把它们合起来叫名数.互相垂直:两条直线相交形成四个角，如果其中有一个角是直角, 就说两条直线互相垂直，其中的一条直线叫另一条直线的垂线，它们的交点叫垂足.互相平行：同一平面内不相交的两条直线叫互相平行，其中的一条直线叫另一条直线的平行线.轴对称图形:如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形叫轴对称图形,这条直线叫对称轴.弧：圆周上任意两点间的部分叫弧.由两条半径和一段孤所围成的图形叫扇形周长：围成平面图形所有线段的总和叫周长.物体的表面或平面图形的大小叫面积.表面积、体积(容积)：围成立体图形所有面积的总和叫表面积; 物体所占空间的大小叫体积;容器能容纳的最大体积叫它的容积.利率、税率:存款利息与本金的比值叫利率;应纳税额与各种收入的比率叫税率.二、公式长方形的周的二(长+宽)X2 C= (a+b) X2正方形的周长二边长X 4 C=4a圆的周长二圆周率X直径二圆周率X半径半2 O兀d=2兀r三角形面积二底X高小2 S=ah 4- 2 长方形面积二长X宽S=ab正方形面积二边长X边长S=a2平行四边形面积二底X高S 二ah梯形面积二(上底+卜底)X高4~2 S= (a+b) h4-2圆面积二圆周率X半径的平方S二兀r2税率二应纳税额周各种收入环形面积二外圆面积-内圆面积S=兀(R-r2)扇形面积二圆周率X半径平方X圆心角度数4-360 S=n兀K 4-360圆柱侧面积二底面周长X高S侧二ch 表面积二侧而积+底面积长方体表面积二（长X宽+长X高+宽X高）X2 S= （ab+ah+bh）X 2正方体表面积二棱长X棱长X6 S=6a2圆的直径二周长：圆周率d=c4-兀圆的半径二周长4■圆周率+ 2 r=c4-兀4-2 圆锥体体积二底面积X高3 v锥二sh 4-3氐方体体积二长X宽X高v=a.bh止方体体积二棱长X棱长X棱长3 v=aaa=a圆柱体体积二底而积X高v= sh 柱体体积二底面积X高v=sh利息二本金X时间X利率利息税二利息X 20%税后利息二利息X 80%出勤率二实到人数人应到人数X100% 合格率二合格产品人产品总数X100%出油率二油重：菜子重X100%成活率二成活棵数：植树总数x 100% mo室二烘干后重量：烘干前重量X100%三、进率1厘米二10毫米长度单位：1千米=1000米1米二10分米1分米二10厘米面积单位：1平方千米二100公顷=1000000平方米1公顷二100公亩=10000平方米1平方米二100平方分米1平方分米=100平方厘米体（容）积单位：1立方米=1000立方分米1立方分米=1000立方厘米1升=1000毫升1升二1立方分米1毫升二1立方厘米质量单位:1吨=1000千克1千克=1000克时间单位：1世纪二100年1年二12月二4季度1月二31天（1、3、5、7、8、10、12 各大月）1 月二30 天（4、6、9、11 各小月）1 月二29天（闰年2月）1月二28天（平年2月）1月二3旬（上旬、中旬、下旬）上旬二10天（1〜10日）中旬二10天（11〜20日）下旬二8、9、10、11天（21〜月末）1日=24时1时二60分1分二60秒1时二3600 秒四、定律、性质、法则加法交换律:两个数相加，交换加数的位置，和不变.a.+b=b+a 加法结合率:三个数相加,先把前两个数相加再加上第三个数，或者先把后两个数相加，再和第一个数相加，和不变.a+b + c=a+ （b + c）乘法交换律:两个数相乘，交换因数的位置,积不变ab=ba乘法结合律:三个数相乘,先把前两个数相乘再乘第三个数;或者先把后两个数相乘再和第一个数相乘，积不变.abc=a （be）乘法分配律:两个数的和的一个数相乘,可以用这个数分别去乘两个加数,再把乘得的积相加.（a+b）c=ac+bc减法的性质：一个数连续减去几个数，等于从这个数里减去这儿个数的和。

四年级下册数学背诵或默写知识点知识点一四则运算（背诵）得分：我要拿 100 分1、加法、减法、乘法和除法统称四则运算。

2、在没有括号的算式里，如果只有加、减法或者只有乘、除法，都要从左往右按顺序计算。

3、在没有括号的算式里，有乘、除法和加、减法、要先算乘除法，再算加减法。

4、算式有括号，要先算括号里面的，再算括号外面的；括号里面的算式计算顺序遵循以上的计算顺序。

知识点二0 的运算（默写）得分：我要拿 100 分1、“ 0”能做除数；不字母表示： a÷0 错误2、一个数加上 0还得原数；字母表示： a＋0= a3、一个数减去 0还得原数；字母表示： a－0= a4、被减数等于减数，差是 0；字母表示： a－ a = 04、一个数和 0 相乘，仍得 0；字母表示： a×0= 05、0 除以任何非0 的数，还得0；字母表示： 0÷a（a≠0）= 0知识点三运算定律（默写）得分：我要拿100 分1、加法交换律：a＋b ＝b ＋ a2、加法结合律：(a＋ b) ＋c ＝a＋(b ＋ c)3、乘法交换律：a×b ＝b×a4、乘法结合律：(a ×b) ×c ＝a×(b ×c)5、乘法分配律：(a＋ b) ×c ＝a×c ＋b×c拓展： (a－b) ×c ＝ a×c－ b×c 或或a ×(b＋ c)a ×(b －c)＝a×b＋ a×c＝ a×b －a×c6、连减： a—b — c＝ a— (b ＋c)7、连除：a÷b÷c ＝ a÷(b ×c)知识点四简便计算一（默写或自己举例子）得分：我要拿 100 分一、常见乘法计算：25×4＝100125×8＝ 100025×8=200125×4=500把 32 分成 4×8把 64 分成 8×8把 16 分成 4×4二、加法交换律简算例子：三、加法结合律简算例子：50+98+50488+40+60＝50+50+98＝488+ （ 40+60 ）＝100+98＝488+100＝198＝ 588四、乘法交换律简算例子：五、乘法结合律简算例子：25×56×499×125×8＝25×4×56＝99×（ 125×8）＝100×56＝99×1000＝5600＝ 99000六、含有加法交换律与结合律的简便计算：65+28+35+72＝（ 65+35 ） +（ 28+72 ）＝100+100＝200七、含有乘法交换律与结合律的简便计算：25×125×4×8＝（ 25×4）×（125×8）＝100×1000＝100000知识点四简便计算二（默写或自己举例子）我要拿 100得分：分乘法分配律简算例子：一、分解式二、合并式25×（40+4 ）135×12— 135×2＝ 25×40+25×4＝135×（12 —2 ）＝ 1000+100＝135×10＝ 1100＝1350三、特殊 1四、特殊 299×256+25645×102＝99×256+256× 1＝ 45×（100+2 ）＝256×（99+1 ）＝45×100+45×2＝256×100=4500+90＝25600=4590五、特殊 3六、特殊 499×2635 ×8+35 ×6—4 ×35＝（ 100 — 1）×26＝35 ×（ 8+6—4）＝100×26— 1×26＝ 35×10＝2600 —26＝350＝2574知识点四简便计算三（默写或自己举例子）我要拿 100得分：分一、连续减法简便运算例子：528 —65 —35528 —89 —128528 —（ 150+128 ）=528 —（ 65+35 ）=528 —128 —89=528 — 128 —150=528 — 100=400 —89=400 —150=428=311=250二、连续除法简便运算例子：3200÷25÷4=3200÷（25×4）=3200÷100=32三、其它便运算例子：256— 58+44250÷8×4=256+44 —58=250×4÷8=300 — 58=1000÷8=242=125知识点五三角形（第 1 条到第 13 条要背诵）得分：我要拿 100 分1、由三条段成的形（每相两条段的端点相）叫做三角形。

(完整版)小学数学总复习知识点整理(最全)总复习小学数学复习资料第一章数和数的运算一概念（一）整数1 .整数的意义自然数和0基本上整数。

2 .自然数我们在数物体的时候，用来表示物体个数的1，2，3……叫做自然数。

一具物体也没有，用0表示。

0也是自然数。

3.计数单位：一（个）、十、百、千、万、十万、百万、千万、亿……基本上计数单位。

每相邻两个计数单位之间的进率基本上10。

如此的计数法叫做十进制计数法。

4. 数位计数单位按照一定的顺序罗列起来，它们所占的位置叫做数位。

5.数的整除整数a除以整数b(b ≠0），除得的商是整数而没有余数，我们就讲a能被b 整除，或者讲b能整除a 。

假如数a能被数b（b ≠0）整除，a就叫做b的倍数，b就叫做a的约数（或a的因数）。

倍数和约数是相互依存的。

因为35能被7整除，因此35是7的倍数，7是35的约数。

一具数的约数的个数是有限的，其中最小的约数是1，最大的约数是它本身。

例如：10的约数有1、2、5、10，其中最小的约数是1，最大的约数是10。

一具数的倍数的个数是无限的，其中最小的倍数是它本身。

3的倍数有：3、6、9、12……其中最小的倍数是3 ，没有最大的倍数。

个位上是0、2、4、6、8的数，都能被2整除，例如：202、480、304，都能被2整除。

个位上是0或5的数，都能被5整除，例如：5、30、405都能被5整除。

一具数的各位上的数的和能被3整除，那个数就能被3整除，例如：12、108、204都能被3整除。

一具数各位数上的和能被9整除，那个数就能被9整除。

能被3整除的数别一定能被9整除，然而能被9整除的数一定能被3整除。

一具数的末两位数能被4（或25）整除，那个数就能被4（或25）整除。

例如：16、404、1256都能被4整除，50、325、500、1675都能被25整除。

一具数的末三位数能被8（或125）整除，那个数就能被8（或125）整除。

例如：1168、4600、5000、12344都能被8整除，1125、13375、5000都能被125整除。

四年级数学上册总复习资料 第一单元大数的认识第一部分重要知识点 一、 数位、计数单位和数位顺序表。

1. 个（一）、十、百、千、万……是计数单位；个位、十位、百位、千位、万 位是数位；数位和计数单位之间是一一对应的。

2. 数位顺序表中从个位开始，越往左数位越高，每四个数位组成一个数级（个 级：个位、十位、百位、千位；万级：万位、十万位、百万位、千万位；……） 注意：个位不是最低位。

3. 每相邻的两个数位之间的进率都是十，这种计数方法叫十进制计数法。

自然 数（1、2、3. 4、5、6……）时表示物体个数的数，一个也没有用0表示，0也 是自然数。

（体会自然数与物体个数的一一对应关系。

） 二、 亿以内数的读写。

1. 读出下面各数。

（四位一级，先画分级线。

）（按级读；先读万级再读个级；万级按照个级读，读完加“万”字；级末尾 的0不读；其它的一个或连续几个0只读一个。

）2467809010000001读作：读作：1000053602000读作：读作：2. 写出下面各数。

（万字后面画分级线。

）（按级写；先写万级再写个级；哪个数位上一个单位也没有，写“0”占位。

注意：万级完全写好后再去考虑个级。

读岀一个零，可能会写出多个0。

） 一千零四十万零五百 一百万零七 写作： 写作： 一千零四万零六百 二百零一万零三 写作：写作：三千零三万零三百零三一千零五十万四千零二十写作： 写作： 三、 亿以上数的读写。

（与亿以内数的读写方法类似）1. 读出下面各数。

1925080030 4330403330052. 写岀下面各数。

二亿零九 四十亿零四十万零四十四、数的组成。

1. 一个数由4个百万、7个十万和5个十组成，这个数是（）。

分析：百万位上是4,十万位上是7,十位上是5,其余数位上都是0。

2. 30900500 是由（）个（ ）、（）个（ ）和（）个（）2659000读作：260400读作：10000000005分析：根据题意，将三个非0数所表示的意义填入即可。