北师大版七年级上册《展开与折叠》
- 格式:ppt
- 大小:4.23 MB
- 文档页数:23
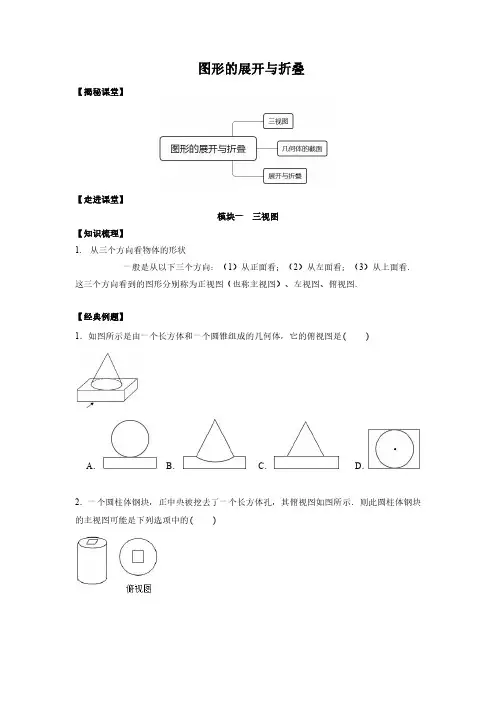
图形的展开与折叠【揭秘课堂】【走进课堂】模块一三视图【知识梳理】1.从三个方向看物体的形状一般是从以下三个方向:(1)从正面看;(2)从左面看;(3)从上面看.这三个方向看到的图形分别称为正视图(也称主视图)、左视图、俯视图.【经典例题】1.如图所示是由一个长方体和一个圆锥组成的几何体,它的俯视图是()A.B.C.D.2.一个圆柱体钢块,正中央被挖去了一个长方体孔,其俯视图如图所示.则此圆柱体钢块的主视图可能是下列选项中的()A.B.C.D.3.如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是()A.B.C.D.4.在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个办法:将从正面、左面、上面看这堆货物得到的平面图形画了出来.你能根据这三个图形帮他清点一下箱子的数量吗?5.一个几何体是由若干个棱长为3cm的小正方体搭成的,从左面、上面看到的几何体的形状图如图所示:(1)该几何体最少由个小立方体组成,最多由个小立方体组成.(2)将该几何体的形状固定好,①求该几何体体积的最大值;②若要给体积最小时的几何体表面涂上油漆,求所涂油漆的面积.模块二几何体的截面【知识梳理】1.圆柱体的横截面:圆,长方形,椭圆,特殊图形.2.正方体的横截面:三角形,四边形,五边形,六边形.【经典例题】1.用一个平面去截一个几何体,其截面形状是圆,则原几何体可能为()①圆柱②圆锥③球④正方体⑤长方体.A .①②B .①②③C .①②③④D .①②③④⑤2.如图,用平面去截圆锥,所得截面的形状是()A .B .C .D .3.用一个平面去截下列的几何体,可以得到三角形截面的有()A .4个B .3个C .2个D .1个4.用一个平面去截正方体1111ABCD A B C D (如图),所截得的截面不可能的是()A .正三角形B .正方形C .正五边形D .正六边形5.如图,一个正方体截去一个角后,剩下的几何体面的个数和棱的条数分别为()A.6,11B.7,11C.7,12D.6,12模块三展开与折叠【知识梳理】正方体的展开图(11种)小口诀:中间四个面,上下各一面;中间三个面,一二隔河见;中间两个面,楼梯天天见,中间没有面,三三连一线.一线不过四,田凹应弃之。


北师大版七年级上册初中数学《展开与折叠》教案一、教材分析:本节课是北师大版初中数学七年级上册第一章丰富的图形世界第2节《展开与折叠》,主要介绍了图形的展开与折叠的概念。
学生在这一节课中将学习如何将一个图形展开成平面图形,以及如何根据平面图形折叠成立体图形。
通过这一节的学习,学生可以培养对图形的观察力和空间想象力,提高他们的几何思维能力。
二、教学目标:1. 理解图形的展开与折叠的概念。
2. 能够将一个图形展开成平面图形。
3. 能够根据平面图形折叠成立体图形。
4. 培养学生的观察力和空间想象力。
5. 提高学生的几何思维能力。
三、教学重点和教学难点:教学重点:图形的展开与折叠的概念,展开与折叠的操作方法。
教学难点:根据平面图形折叠成立体图形的操作方法。
四、学情分析:学生已经学习了图形的基本知识,对于图形的名称和性质有一定的了解。
但是对于图形的展开与折叠的概念和操作方法可能还不太熟悉。
部分学生可能存在空间想象能力较弱的问题,需要通过具体的实例来帮助他们理解和掌握。
五、教学过程:第一环节:导入新知老师:同学们,回顾一下上节课我们学习的图形的基本知识,例如图形的名称和性质。
现在我有一个问题想问问你们,你们有没有想过如何将一个图形展开成平面图形?如何根据平面图形折叠成立体图形呢?请思考一下并且和你的同桌分享一下你的想法。
第二环节:引入展开与折叠的概念老师:好,现在请大家停止讨论,我来给大家介绍一下展开与折叠的概念。
请看这个立方体(出示一个立方体模型),我们知道立方体是一个有六个面的立体图形。
那么,如果我们将这个立方体展开成平面图形,你们觉得会是什么样子呢?(鼓励学生积极参与回答)学生:老师,我觉得展开后应该是六个正方形连在一起。
老师:很好,你的回答非常接近。
事实上,当我们将立方体展开时,会得到六个正方形,它们是立方体的六个面。
这个过程就是展开。
同样的,如果我们有这六个正方形,我们可以按照一定的方式折叠它们,重新组合成一个立方体,这个过程就是折叠。




教学设计展开与折叠第1课时正方体的展开与折叠教学目标1.让学生掌握正方体的展开图.2.让学生能根据正方体的展开图判断各面之间的关系.教学重难点重点:正方体的展开图.难点:引导学生根据正方体的展开图判断各面之间的关系.教学过程导入新课在生活中,我们会见到很多正方体形状的盒子,你知道这些正方体形状的盒子是怎样制作的吗?你能制作一个吗?探究新知正方体的展开与折叠阅读教材P8“做一做”和之前的内容,先完成书中所提出的问题,然后做下面的填空:正方体共有6个面,__12__条棱,将一个正方体的表面沿某些棱剪开时,面与面之间必须有__1__条棱相连,所以需剪开__7__条棱.探究:(学生动手操作,教师指导,共同探究规律,教师归纳总结)将小正方形纸盒沿某些棱任意剪开,你能得到哪些形状的平面图形?能否将得到的平面图形分类?归纳:将正方体沿不同的棱展开可得到不同的表面展开图,共有如下11种情形:可分为四类:(1)141型(共6种)四个一行中排列,两端各一个任意放.(2)231型(共3种) 二在三上露一端,一在三下任意放.(3)222型(1种) 两两三行排有序,恰似登天上云梯.(4)33型(1种) 三个三个排两行,中间一“日”放光芒.问题:要将一个正方体展开成一个平面图形,必须沿几条棱剪开?(学生分组进行讨论,得出结论)教师归纳:由于正方体有12条棱,6个面,将其表面展成一个平面图形,面与面之间相连的棱有5条(即未剪开的棱),因此需要剪开7条棱.例1下列的哪些图形能折叠成正方体?(学生自主解答,老师提问,进行总结)解:7、8、9、10这四个图形可以折叠成正方体.总结:展开图中含有“田”字形(如图3,4)、“凹”字形(如图5,6)和超过四个小正方形在同一行的(如图1,2)都不能折叠成正方体.拓展探究:例2 已知一不透明的正方体的六个面上分别写着1至6六个数字,如图是我们能看到的三种情况,那么5的对面数字是__4__.课堂练习1.下列图形中,是正方体表面展开图的是()A. B.C. D.2.国庆节的时候,小明准备了一个正方体礼盒,六个面分别写有“祝”“福”“祖”“国”“万”“岁”,其中“祝”的对面是“祖”,“万”的对面是“岁”,则它的平面展开图可能是()3.如图是一个正方体的平面展开图,那么3号面相对的面是________号面.4.如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值的是______.5.将下图中平面展开图折叠成正方体后,相对面上的两个数之和都为6,则x=____,y=____.参考答案1.D2.C3.64.65.5;3课堂小结布置作业完成教材习题1.3.板书设计第一章丰富的图形世界2 展开与折叠第1课时正方体的展开与折叠正方体的展开与折叠正方体的表面展开图共有11种情形,可分为四类:(1)141型(共6种).(2)231型(共3种).(3)222型(1种).(4)33型(1种).不能折叠成正方体的表面展开图:含有“田”字形、“凹”字形和超过四个小正方形在同一行的表面展开图.。




北师大版七年级数学上册展开与折叠教案一、教学目标:1. 知识与技能:(1)理解平面图形的折叠与展开,掌握其基本方法。
(2)能够将简单的几何体沿某个平面进行展开,并理解展开图形与原几何体的关系。
2. 过程与方法:(1)通过观察、操作、交流等活动,培养学生的空间想象能力和动手操作能力。
(2)学会用简单的语言描述展开与折叠的过程,提高学生的表达能力。
3. 情感态度与价值观:培养学生对数学的兴趣,激发学生探究问题的欲望,培养学生的团队协作精神。
二、教学重点与难点:重点:掌握平面图形的折叠与展开的方法,理解展开图形与原几何体的关系。
难点:如何将几何体沿某个平面进行展开,并理解展开图形与原几何体的联系。
三、教学准备:1. 教师准备一些简单的几何体模型,如长方体、正方体等。
2. 学生准备一张白纸、一把剪刀、一支笔。
四、教学过程:1. 导入新课:通过展示一些生活中的展开与折叠现象,如衣服、盒子等,引导学生思考:这些物体是如何展开与折叠的?展开后的图形与原物体有什么关系?2. 自主探究:(1)让学生尝试将一张白纸沿某个平面折叠,观察折痕所在的位置,思考折痕与纸张的关系。
(2)学生分组讨论,分享自己的折叠经验,探讨如何将几何体沿某个平面进行展开。
3. 教师讲解:(1)讲解平面图形的折叠与展开的基本方法。
(2)讲解如何将简单的几何体沿某个平面进行展开,并展示实例。
4. 动手实践:让学生动手操作,尝试将给定的几何体模型沿某个平面进行展开,并观察展开后的图形与原几何体的关系。
5. 巩固练习:设计一些有关展开与折叠的练习题,让学生独立完成,检查学生对知识的掌握程度。
五、课堂小结:通过本节课的学习,学生了解了平面图形的折叠与展开的基本方法,学会了如何将简单的几何体沿某个平面进行展开,并理解了展开图形与原几何体的关系。
在今后的学习中,我们将进一步拓展这一知识点,引导学生运用展开与折叠的知识解决实际问题。
六、教学拓展:1. 让学生思考:在实际生活中,还有哪些物体可以运用展开与折叠的知识进行制作?2. 引导学生尝试运用展开与折叠的知识解决实际问题,如制作一个纸盒、设计一个衣服的款式等。