正多边形和圆1
- 格式:pdf
- 大小:370.58 KB
- 文档页数:8


几何中的正多边形与圆的内切外切正多边形和圆是几何中常见的概念,它们之间存在着内切和外切的关系。
正多边形是一个有着相等边长和相等内角的多边形,而圆是一个由无数点组成的闭合曲线。
本文将探讨正多边形与圆的内切和外切关系,以及相关的性质和定理。
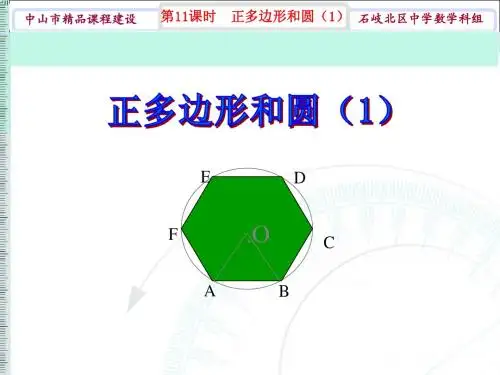
一、正多边形与圆的内切当一个正多边形的每条边都与一个圆相切,且这个圆同时与多边形的所有顶点都相切时,称这个圆为该正多边形的内切圆,多边形为内切圆的多边形。
内切圆的半径等于多边形各边边长的一半,而内切圆的圆心和多边形的重心重合。
以正五边形为例,假设其边长为a,内切圆的半径r,则有以下几何关系:- 五边形的中心到一条边的距离为r- 五边形的中心到两条相邻边的夹角为72度- 五边形的中心到五个顶点的距离等于r- 五边形的中心到相邻两个顶点和圆心连线的夹角为36度对于任意正多边形,以上的几何关系都成立。
内切圆是正多边形与圆相互联系的几何特征,它展现了正多边形的对称性和一致性。
二、正多边形与圆的外切当一个正多边形的每条边都与一个圆相切,且这个圆的圆心位于多边形各边的延长线上时,称这个圆为该正多边形的外切圆,多边形为外切圆的多边形。
外切圆的半径与内切圆的半径之间存在着特殊的关系。
以正六边形为例,假设其边长为a,外切圆的半径R,则有以下几何关系:- 六边形的中心到一条边的距离为R- 六边形的中心到两条相邻边的夹角为120度- 六边形的中心到六个顶点的距离等于R- 六边形的中心到相邻两个顶点和圆心连线的夹角为60度同样地,对于任意正多边形,以上的几何关系都成立。
外切圆也是正多边形的一个重要特征,它定义了多边形的圆心和对称性。
三、正多边形与圆内切外切的性质和定理正多边形与内切外切的圆之间有许多有趣的性质和定理,其中一些被广泛用于解决几何问题和证明定理。
1. 内切圆半径与正多边形边长的关系:对于正n边形(n>2),内切圆的半径r与多边形的边长a存在以下关系:r = (a/2) * cot(π/n)该关系可以用来计算内切圆的半径以及与多边形的边长的关系。







人教版九年级数学上册24.3.1《正多边形和圆(1)》教学设计一. 教材分析《正多边形和圆》是人教版九年级数学上册第24章第三节的第一课时内容,主要介绍了正多边形的定义、性质以及与圆的关系。
本节课的内容是学生对几何图形学习的进一步深化,对于培养学生的空间想象能力和抽象思维能力具有重要意义。
教材通过生活中的实例引入正多边形和圆的概念,让学生感受数学与生活的紧密联系,激发学生的学习兴趣。
二. 学情分析九年级的学生已经具备了一定的几何基础知识,对图形的认识有一定的深度。
但是,对于正多边形和圆的性质和关系,可能还比较陌生。
因此,在教学过程中,需要教师通过生动形象的实例和直观的图形,帮助学生理解和掌握正多边形和圆的概念和性质。
三. 教学目标1.了解正多边形的定义和性质,能够识别和判断正多边形。
2.理解圆的概念,掌握圆的性质。
3.掌握正多边形与圆的关系,能够运用正多边形和圆的知识解决实际问题。
四. 教学重难点1.重难点:正多边形的定义和性质,圆的概念和性质。
2.难点:正多边形与圆的关系的理解和运用。
五. 教学方法1.采用问题驱动的教学方法,通过提问引导学生思考和探索,激发学生的学习兴趣和积极性。
2.采用直观演示法,通过实物和图形的展示,帮助学生直观地理解和掌握正多边形和圆的概念和性质。
3.采用归纳总结法,通过总结和归纳,使学生对正多边形和圆的知识有一个系统的认识。
六. 教学准备1.准备相关的图形和图片,如正多边形和圆的实物图片,正多边形和圆的模型等。
2.准备相关的教学PPT,内容包括正多边形和圆的定义、性质和关系等。
七. 教学过程1.导入(5分钟)通过提问方式引导学生回顾已学过的几何图形,如三角形、四边形等,激发学生的学习兴趣。
然后,展示一些生活中的实例,如五角星、车轮等,引导学生思考这些图形的共同特征。
2.呈现(10分钟)教师展示正多边形和圆的实物图片和模型,引导学生观察和描述正多边形和圆的特征。
然后,教师通过PPT呈现正多边形和圆的定义和性质,让学生初步了解和掌握。