假分数化带分数全解

把假分数化成带分数教学要求 ①使学生理解带分数的意义，会读、会写带分数；能正确地把假分数化成带分数。

②培养学生总阅读数学材料的能力。

③渗透转化的数学思想。

教学重点 假分数化成带分数的方法。

教学过程一、创设情境1．判断下面各数哪些是真分数，哪些是假分数？71 22 1514 2524 18 209 511 38 412 613 95 515 2．观察以上假分数，根据分子能否被分母整除这一特征，假分数可以分成几类？分子是分母倍数的分数——整数板书：假分数分子不是分母倍数的分数3．分子是分母倍数的分数化成整数。

学生独立练习，集体订正。

二、揭示课题像这样分子不是分母倍数的假分数又可以改写成怎样的数呢？这节课我们就来学习“把假分数化成带分数”。

（板书课题）三、探索研究1、认识带分数的意义及读写方法。

（1）出示例2图③，向学生指出：这是我们昨天认识的假分数511。

从图上可以看到511是由510（就是2，教师把黑板上的圆片翻一面成2个整圆）和51合成的数，可以写成251。

251就是带分数。

（2）观察251，它是由哪两部分组成的？ 251 板书： 整数部分 分数部分（3）提问：什么是带分数？板书：由整数和真分数合成的数叫做带分数。

（4）认识带分数的读法。

①251读作：二又五分之一。

②练习。

读出下列各带分数。

132 574 3109 6207 2．学习把假分数化成带分数的方法。

（1）自学例4，把56和38这两个假分数化成带分数。

（2）组织学生讨论。

①把56和38这两个假分数化成带分数的方法是什么？根据分数单位的个数怎样想？根据分数与除法的关系怎样化？②根据分数与除法的关系改写的方法是什么？归纳：把假分数化成带分数，用分母除分子，不能整除的，商就是带分数的整数部分，余数是分数部分的分子，分母不变。

（3）练一练：把复习题第1题中分子不是分母倍数的假分数化成带分数。

（4）引导学生总结把假分数化成整数或者带分数的方法，并让学生阅读课本第99页最后一段话。

整数、假分数和带分数的互化答案典题探究（1）=9÷25=0.36；=11÷40=0.275；0.28==；0.035==．（2）=17÷6=2；=64；==；==．（3）=4；=3；=7．（4），，1，．演练方阵A档（巩固专练）1．解：（1）5÷6=，（2）7÷15=，（3）16÷9==1，（4）11÷16=，（5）19÷38==，（6）32÷16==2．2. 解：（1）16÷19=；（2）180=12；（3）27=；（4）104÷5==20．3．解：①0.9；②2；4. 2.25；8、26．5.解：把下列带分数化成假分数，假分数化成带分数．=；=45÷7=6；==；=17÷15=1；=35÷12=2．6．解：（1）=5；（2）=2；（3）=6；（4）7.解：（1）=1+；（2）1==；（3）=3；（4）=9+．故答案为：1，，7，21，10，9．8. 解：（1）；；；（2）=2；=3；=5．9．解：1======．故答案为：2，3，4，9，21，1000．10. 解：．故答案为：2、4、6．B档（提升精练）11．解：；；．12．解：分母是10的真分数分子＜10，假分数分子≥10，最小的带分数是1．所以分母是10的最大真分数，最小假分数，与最小带分数1相差一个分数单位．即这三个分数是、、1．13．解：9；14=1；18=2；18；14．解：5；1=；；7；；6；故答案为：；4、31；5；；6、13；21、4；53．15．解：由图中数轴可知，每一小格代表的数值为单位“1”的，那么：6格为==1，9格为=2，11格为，12格为，14格为，19格为=，20格为，见下图：16．解：=15÷4=3…3，所以=3；5==；=21÷7=3；2==．17．解：如：．18．解：6==；6==；6==．19．解：根据假分数与带分数的互化方法得：20．解：因为分母是1，所以这样的假分数都可以化为整数；故判断为：正确．C档（跨越导练）21．解：图一，图中有两个相同的长方形，每个长方形被平均分成8份，第一个长方形全部为阴影部分，第二个长方形中其中的三份为阴影部分，占这个长方形的，则所有阴影部分占4长方形的1+=1，即；图二，图中有三个相同的圆，每个圆被平均分成4份，第一个圆中其中的三份为阴影部分，占这个圆的，后两个圆全部为阴影部分，则全部阴影部分为2+=2，即．如图：故答案为：，1，，2．22．解：（1）20===4；（2）3=7=6=5．故答案为：320，26，4，7．23．解：（1）（45﹣9）÷3，=36÷3，（2）45÷12=3，故答案为：12，3．24．解：23﹣3=20，20=2×2×5，所以20的因数有1，2，4，5，10，20；又因为分母＞3，因此分母可以是4，5，10，20；相应的带分数有5，4，2，1，共4个；故答案为：4．25．解：=6，==2，==1，=13，==1．26．解：（1）；（2）；（3）；（4）；（5）；（6）；（7）；（8）．27．解：（1）=9；（2）；（3）；（4）=16；（5）=72÷24=3．28．24÷4==6，30÷19==，65÷7==，解：8÷13=，15÷8==，14÷3==，87÷87==1，86÷9==．故答案为：，6，，，，，1，．29．解：（1）2===；（2）3===；（3）1===；（4）8===．30．解：答案如图：。

把假分数化成带分数课题把假分数化成带分数第3课时年级学科五数备注教学⽬标使学⽣理解和掌握带分数的意义及特征,掌握把假分数化成带分数的⽅法,并能正确地把假分数化成带分数.重难点教学重点:理解和掌握带分数的意义及特征,能正确地把假分数化成带分数.教学难点:学会正确地把假分数化成带分数.课前准备课件教学过程⼀,复习引⼊,做好铺垫.1,下⾯的分数中哪些是真分数哪些是假分数3/4 8/5 7/7 11/18 36/12 51/17 19/14 50/502,把下⾯的假分数化成整数.6/6 25/5 45/15 67/67 65/133,下⾯的假分数哪些能化成整数哪些不能16/4 9/2 18/18 23/7 35/124,揭⽰课题.述:通过复习⼤家知道,当假分数的分⼦是分母的倍数时,能把假分数化成整数;但当假分数的分⼦不是分母的倍数时,不能把假分数化成整数.那么,这样的假分数⼜能⽤什么数来表⽰它们呢板书课题:把假分数化成带分数⼆,合作交流,探究新知1,教学带分数的概念.(1)分析:A,9/2可否看作是8/2和1/2合成的数 8/2化成整数是多少那么,9/2是否可以写成4B,4 中4是什么数 1/2是什么数C,23/7可否看作是21/7和2/7合成的数呢 21/7化成整数是多少那么,23/7是否可以写成3D,3 中3是什么数 2/7是什么数观察讨论:从上⾯的分析中,我们发现:假分数的分⼦不是分母的倍数的,可以⽤什么数来表⽰它们归纳:假分数的分⼦不是分母的倍数的,可以写成整数和真分数合成的数,通常叫做带分数.它是⼀部分假分数的另⼀种书写形式.2,介绍带分数各部分的名称和读法.板书: 4读作:四⼜⼆分之⼀整数部分分数部分3,教学把假分数化成带分数的⽅法.述:⽤上⾯实例中的⽅法化带分数⽐较⿇烦,下⾯向同学们介绍⼀种简便⽅法.教学(1) 把6/5,8/3化成带分数思考:能不能根据分数与除法的关系,通过计算来改写呢板书: 6/5=6÷5=1 8/3=8÷3=2※下⾯的假分数哪些可以化成带分数把它们化成带分数.7/3 8/2 15/5 9/4 13/13 11/6 30/11(2)总结假分数化成整数或者带分数的⽅法.提问:A,通过上例的学习谁能说说把假分数化成带分数的⽅法板述:把假分数化成带分数,⽤分母去除分⼦,得到的商作带分数的整数部分,余数作带分数分数部分的分⼦,分母不变.B,⽐较把假分数化成整数和把假分数化成带分数的⽅法什么共同点和不同点(共同点:都是⽤分母去除分⼦.不同点:商不同.⼀种⽆余数,可以写成整数;⼀种有余数,可以写成带分数.)三,巩固练习,提⾼能⼒四,全课总结,深化概念提问:A,什么是真分数什么是假分数B,把假分数化成整数和带分数的条件和⽅法是什么强调:带分数只是分⼦不是分母的倍数的假分数的另⼀种书写形式.作业布置练习册真假分数。

一赵敏强儿子的作业本上有一道题，经过解答，我发现这类题共有三种方法，但网上查找只能找出前两种，所以我写这篇文章把这个方法写出来，请大家批评指正。

题目是：一个假分数的分子是71，化成带分数后其整数部分、分子和分母是三个连续自然数。

求这个带分数。

方法一：列方程求解解：设带分数的整数部分是x ，则这个带分数的分子是（x+1）分母是（x+2），根据题意有x （x+2）+（x+1）=71。

解方程： x （x+2）+（x+1）=71x ^2+2 x+ x+1=71x ^2+3 x -70=0 ()270493-⨯-±-=x107-==⇒x x根据题意x=7所以这个带分数是798 方法二：列举法求解解：由于71是两位数，且化成带分数后整数部分和分母之差为2，所以分母最大为10，所以列举是分母从10开始逐渐变小，看看那个是答案。

分母若为10，则分数为8109，化为假分数则分子为89；8，化为假分数则分子为71；分母若为9，则分数为797，化为假分数则分子为55；分母若为8，则分数为688由此知道这个带分数是79方法三：开方法或直接测算法方法一不适于小学五年级的学生，方法二虽然可以，但没有这儿的第三种方法快速。

解：某个数和自己相乘（这个数的平方）的结果最接近71而且比71小？9*9=81 8*8=64 因此这个数是8，找出的这个数就是带分数的分子！8。

（分母比分子大1，整数部分比因此这个带分数是79分子小1）。

练习题：一个假分数的分子是55（这类分子的1000以内的数列是5、11、19、29、41、55、71、89、109、131、155、181、209、239、271、305、341、379、419、461、505、551、599、649、701、755、811、869、829、991），化成带分数后其整数部分、分子和分母是三个连续自然数。

求这个带分数。

把假分数化成带分数教案第一章：假分数与带分数的概念理解1.1 教学目标让学生理解假分数和带分数的含义。

让学生掌握假分数和带分数之间的转换方法。

1.2 教学内容假分数：分子大于或等于分母的分数。

带分数：整数部分加上真分数部分。

1.3 教学步骤引入假分数和带分数的概念。

通过示例，解释假分数和带分数之间的关系。

让学生进行小组讨论，探讨如何将假分数转换为带分数。

第二章：将假分数化成带分数的方法2.1 教学目标让学生掌握将假分数化成带分数的方法。

2.2 教学内容方法一：将假分数的分子减去分母的倍数，得到整数部分；剩余的分子作为真分数部分。

方法二：使用公式法，假分数化带分数的公式为：整数部分= 分子÷分母，余数作为真分数的分子，分母不变。

2.3 教学步骤介绍两种将假分数化成带分数的方法。

通过示例，讲解方法一的使用步骤。

通过示例，讲解方法二的使用步骤。

让学生进行练习，巩固方法。

第三章：带分数与假分数的转换练习3.1 教学目标让学生能够熟练地将假分数转换为带分数。

3.2 教学内容练习题：提供一些假分数，要求学生将其转换为带分数。

3.3 教学步骤给学生提供练习题。

学生在小组内进行讨论和解答。

教师进行讲解和指导，解答学生的疑问。

第四章：带分数与假分数的应用4.1 教学目标让学生理解带分数和假分数在实际问题中的应用。

4.2 教学内容示例：使用带分数和假分数解决实际问题，如烹饪、建筑等。

4.3 教学步骤提供一些实际问题，要求学生使用带分数和假分数进行解决。

学生进行小组讨论和解答。

教师进行讲解和指导，解答学生的疑问。

第五章：总结与评估5.1 教学目标让学生总结假分数化成带分数的过程和应用。

评估学生对假分数化成带分数的掌握程度。

5.2 教学内容学生总结假分数化成带分数的过程和应用。

教师评估学生的掌握程度。

5.3 教学步骤学生进行总结，分享自己的学习心得和经验。

教师提供评估问卷或测试，了解学生的掌握程度。

教师根据学生的表现给予反馈和建议。

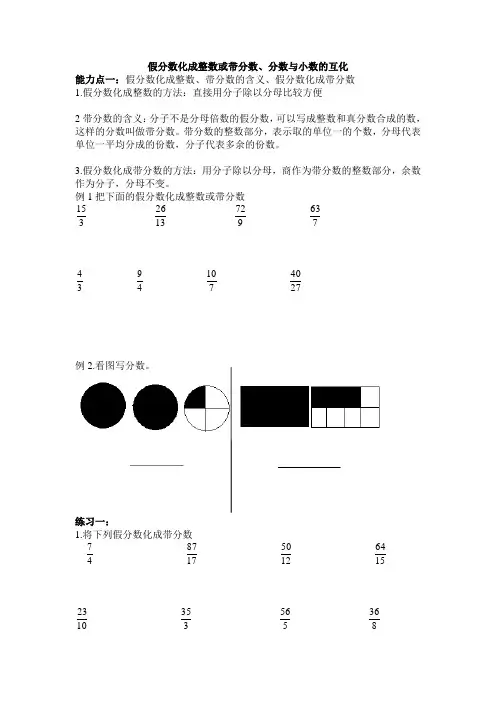
假分数化成整数或带分数、分数与小数的互化能力点一：假分数化成整数、带分数的含义、假分数化成带分数1.假分数化成整数的方法：直接用分子除以分母比较方便2带分数的含义：分子不是分母倍数的假分数，可以写成整数和真分数合成的数，这样的分数叫做带分数。

带分数的整数部分，表示取的单位一的个数，分母代表单位一平均分成的份数，分子代表多余的份数。

3.假分数化成带分数的方法：用分子除以分母，商作为带分数的整数部分，余数作为分子，分母不变。

例1把下面的假分数化成整数或带分数315 1326 972 76334 49 710 2740例2.看图写分数。

练习一：1.将下列假分数化成带分数47 1787 1250 15641023 335 556 836能力点二：分数化小数、分数与小数比较大小1.分数化小数：用分子除以分母。

2.分数与小数比较大小：统一化成小数，然后再比较大小。

例1、把分数化成小数（除不尽的保留三位小数）。

65 153 92 87 例2、比较下面各组数的大小。

32 0.66 0.41 72 0.91 2019 练习二：1.将0．875、86、53、109、8．25这几个数按从小到大的顺序排列。

2.把下面的分数化成小数。

（除不尽的，保留三位小数。

）119 78 916 1343.在（ ）里填 上“＞”、“＜”或“＝”。

59 （ ）57 47 （ ）35 4（ ）205 78 （ ）11124、王师傅5天做8个零件，张师傅8天做11个零件。

谁做得快些？5.因为7〈 9，所以74〈 94。

（ ） 6.一次跳远比赛中，小明第一次试跳跳了3.25米，第二试跳跳了325米，第三次试跳跳了338米。

小明三次试跳的最好成绩是多少米？7.李阿姨和王叔叔两人打字，李阿姨平均每秒打0.9个字，王叔叔1分钟打了50个字，平均每秒打65个字，谁打字打的快？8、3个同学走一条22千米的路，甲走了6小时，乙走了4．5小时，丙走了5小时，谁走得最快？谁走得最慢？9.小张、小王、小李三个工人做同样的零件，小张3小时做10个，小王4小时做13个，小李5小时做16个，谁的工作效率最高？为什么？10.甲、乙、丙三人同时合做一批零件，甲6分钟做4个，乙4分钟做3个，丙3分钟做2个。