余角补角对顶角()

余角、补角、对顶角（2）一、教学目标1、了解对顶角的定义2、3、能应用余角、补角、对顶角的性质进行简单推理说明二、教学重点、难点1、重点：对顶角的概念及其性质2、难点：运用性质推理说明三、教学过程1、复习余角、补角的定义及其性质余角：两角之和为90，则这两个角互余；其性质为同角的余角相等；补角：两角之和等于180，则这两个角互补；其性质为同角的补角相等。

2、新课引入：问题：直线AB和直线CD相交于点O，图中有哪些角？OBACD其中有互补的关系的角，那么∠AOD与∠BOC是什么关系呢？（1）定义：一个角的两边分别是另一个角的两边的反向延长线，则这两个角是对顶角。

如上图中的∠AOD与∠BOC，∠BOD与∠AOC是对顶角。

观察总结：两直线相交所成角，一种关系是互补，一种关系是对顶角（有公共边）。

例1 下图中，∠1与∠2是对顶角的有（）对例2 三条直线AB、CD、EF相交于点O，图中共有（）对对顶角。

EACFBDO（2）性质：对顶角相等OBDCA因为∠AOC+∠COB=∠BOD+∠COB=180,所以∠AOC=∠BOD（同角的补角相等）例3 如图，直线a和直线b相交，（1）已知∠1=40，则∠2=___，∠3=___，∠4=___；（2）已知∠2+∠4=280，则∠1=___，∠2=___，∠3=___，∠4=___；（3）已知∠1 ：∠2 =2 ：7，则∠3=___，∠4=___。

4231例4 如图，直线AB,CD 相交于点O ，∠DOE=90°，∠AOC=72°，求∠BOE 的度数。

BECODA解：∵直线AB 、CD 相交于点O ，∠AOC=72° ∴∠BOD=∠AOC=72°（对顶角相等） 又∵∠DOE=90°∴∠BOE=∠DOE-∠BOD=90°- 72°=18°例5 如图，直线AB 和直线CD 相交于点O ，∠DOE=∠BOD ，OF 平分∠AOE ，∠AOC=30，试求∠EOF 的度数。

6.3余角、补角、对顶角(1)教学目标：1、在具体情景了解余角、补角，概念2、知道等角的余角相等，等角的补角相等3、经历观察—操作—说理，交流等过程，进一步发展宽间的观念教学重难点：1、余角、补角，概念2、同角(等角)的余角相等，同角(等角)的补角相等教学过程：一、情景创设：用一副三角尺，在实际操作中，演示课本中的图通过直观、形象演示，引导学生观察，引入余角、补角概念1、探索活动活动1：通过直观、形象演示，引导学生观察，引入余角、补角概念如果两个角的和是直角，这两个的角叫做互为余角如果两个角的和是平角，这两个的角叫做互为补角( 1 )摆动两个三角板位置，∠α+∠β=90°∠α+∠β=180°不变（2）两个角的和是90 °，或者平角180°是一种特殊关系，它们分别叫做互为余角，互为补角。

（3）前面研究的角都是一个角，而互为余角、互为补角指的是两个角的关系。

（4）互补，互余是一种特殊的数量关系，思考:同一块三角板上有两个锐角互余吗？（5）如果∠α+∠β=90°那么∠α与∠β互余反过来，如果∠α与∠β互余，那么∠α+∠β=90°或∠α=90°—2∠β或∠β=90°—2∠α如果∠α+∠β=180°那么∠α与∠β互补反过来∠α与∠β互补，那么，∠α+∠β=180°或∠α=180°—2∠β或∠β=180°—2∠α活动2：填表(投影)可知：∠α的余角为90°—n°（∠α= n°）∠α的补角＝180°—n°做一做：书本上连线二、例题教学：探索余角补角的性质，让学生经历”观察-----猜想-----说理”的过程，例：如果∠1与∠2 互余，∠1与∠3互余，那么∠2与∠3 相等吗？为什么？解：∠2与∠3 相等因为∠1与∠2 互余，∠1与∠3互余所以∠2=90°—∠1 ，∠3=90°—∠1所以∠2=∠3引导学生交流得出结论，同角（或等角）的余角相等，同角（或等角）的补角相等。

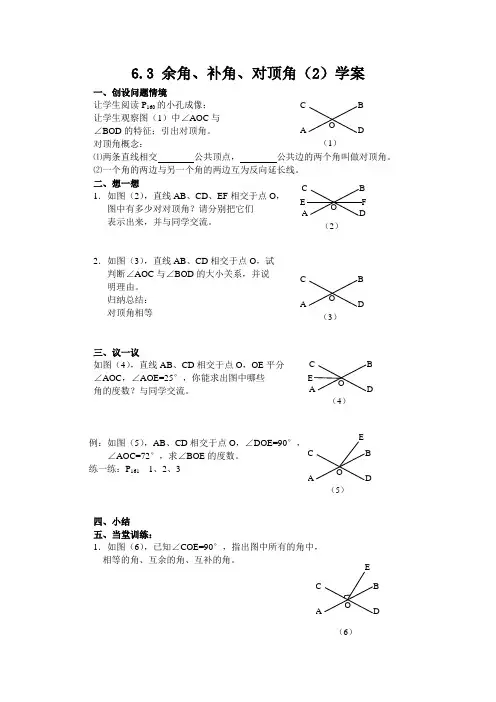
6.3 余角、补角、对顶角（2）学案一、创设问题情境让学生阅读P 160的小孔成像；让学生观察图（1）中∠AOC 与∠BOD 的特征；引出对顶角。

对顶角概念：⑴两条直线相交 公共顶点， 公共边的两个角叫做对顶角。

⑵一个角的两边与另一个角的两边互为反向延长线。

二、想一想 1．如图（2），直线AB 、CD 、EF 相交于点O ，图中有多少对对顶角？请分别把它们 表示出来，并与同学交流。

2．如图（3），直线AB 、CD 相交于点O ，试判断∠AOC 与∠BOD 的大小关系，并说 明理由。

归纳总结： 对顶角相等三、议一议如图（4），直线AB 、CD 相交于点O ，OE 平分∠AOC ，∠AOE=25°，你能求出图中哪些 角的度数？与同学交流。

例：如图（5），AB 、CD 相交于点O ，∠DOE=90°，∠AOC=72°，求∠BOE 的度数。

练一练：P 161 1、2、3四、小结五、当堂训练： 1．如图（6），已知∠COE=90°，指出图中所有的角中， 相等的角、互余的角、互补的角。

A CB OD （1） A C B O D（2） E FA CB O D（3） A C B O D （4） E A C B OD（5）EA C BO D（6）E2．如果∠1+∠2=90°，∠2+∠3=90°，则∠1与∠3的关系为 ， 其理由是 。

如果∠1+∠2=180°，∠2+∠3=180°， 则∠1与∠3的关系为 ， 其理由是 。

3．直线AB 、CD 相交于O ，且∠AOC+∠BOD=120°，求∠AOC 度数.4．如图（7），AB 、CD 、EF 相交于点O ，且AB ⊥CD ，OG 平分∠AOE ，∠FOD=24°，求∠BOE 和∠AOG5．如图（8），∠COE=90°，∠DOF=160°，OF 平分∠AOC ，求∠BOF 和∠AOE 的度数。

对顶角余角和补角的定义
顶角、余角和补角是在几何学和三角学中常见的概念。

顶角指的是两条直线相交时，形成的相对的两个角，这两个角的顶点是同一个点。

余角是指一个角的补角，即与该角相加为90度的角。

而补角则是两个角的和为90度的角。

从几何学的角度来看，顶角是指两条直线相交时形成的相对的两个角，它们共享一个公共顶点。

例如，在一个三角形中，顶角通常指的是三角形的顶点所对的角。

余角是指一个角的补角，也就是与该角相加为90度的角。

例如，如果一个角的度数是x度，那么它的余角就是90度减去x度。

补角是指两个角的和为90度的角。

例如，如果一个角的度数是x度，那么它的补角就是90度减去x度。

从三角学的角度来看，顶角、余角和补角也有特定的定义。

在三角函数中，余角是指角A的余角是90度减去角A的度数。

补角是指两个角的和为90度的角，例如，如果角A的度数是x度，那么角A的补角就是90度减去x度。

这些概念在解题和推导三角函数的过程中经常被用到。

总的来说，顶角、余角和补角是几何学和三角学中非常基础和
重要的概念，它们帮助我们理解角的关系，解决各种几何和三角学问题。

通过理解这些概念，我们能更好地应用它们解决实际问题，并且在数学推导和证明中起到重要的作用。

什么叫余角、补角？它们的性质是什么？难易度：★★★★关键词：角答案：（1）余角：如果两个角的和等于90°(直角），就说这两个角互为余角。

即其中一个角是另一个角的余角。

（2）补角：如果两个角的和等于180°（平角），就说这两个角互为补角。

即其中一个角是另一个角的补角。

(3）性质：等角的补角相等。

等角的余角相等。

（4）余角和补角计算的应用,常常与等式的性质、等量代换相关联。

注意：余角（补角)与这两个角的位置没有关系。

不论这两个角在哪儿，只要度数之和满足了定义,则它们就具备相应的关系。

【举一反三】典例：已知一个角的补角比这个角的余角的3倍大10°，求这个角的度数．思路引导：主要考查了余角和补角的概念以及运用．互为余角的两角的和为90°,互为补角的两角之和为180度．解此题的关键是能准确的从图中找出角之间的数量关系，从而计算出结果．利用题中“一个角的补角比这个角的余角的3倍大10°"作为相等关系列方程求解即可．设这个角是x，则(180°-x)—3（90°-x）=10°，解得x=50°．故答案为50°．标准答案:50°尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文稿在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。

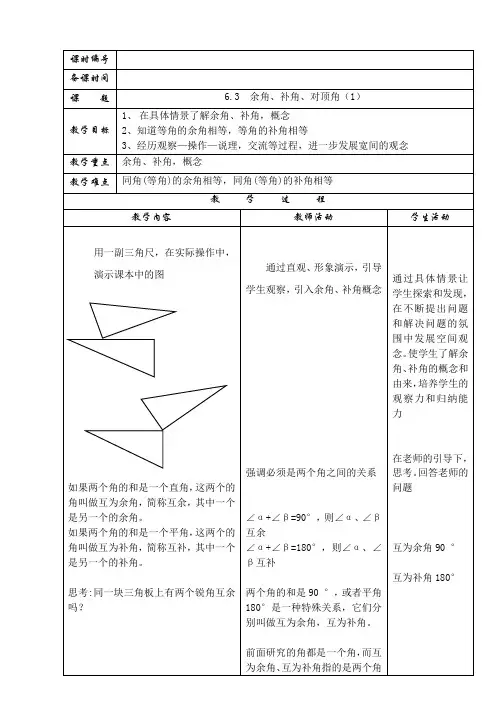
课题：6.3余角、补角、对顶角（1）课型：新授 主备： 备课组长： 教研组长：班级 姓名 学号【学习目标】1、 在具体情境中了解余角、补角的概念,知道“等角(同角)的余角相等、等角(同角) 的补角相等.”的性质2、会运用互为余角、互为补角的性质进行简单的计算，学习有条理的表述. 【重点难点】1、余角、补角的概念及性质2、余角、补角的性质的应用 【温故知新】1、三角板演示找出α与β之间的关系如果 互为余角，简称 ，其中一个叫做另一个角的 。

如果 互为补角，简称 ，其中一个叫做另一个角的 。

2、∠1、∠2互余，互补的符号语言的应用⑴ ∵1∠和2∠互余 反之：∵ ∴=∠+∠21______ ∴1∠和2∠互余 ⑵ ∵1∠和2∠互补 反之：∵=∠+∠21︒180 ∴=∠+∠21______ ∴ 尝试练习：1．填表：∠α的度数 50° n °(0<n<90)∠α的余角 45° ∠α的补角 120°同一锐角的补角与它的余角之间有怎样的数量关系？一批时间 二批时间 教师评价 家长签字α β αβ【变式训练】1、如果∠1与∠3 互余，∠2与∠3互余，那么∠1与∠2 有什么关系呢？为什么？2、如图，∠ A +∠B =90 °，∠ BCD +∠B =90 °，∠A 与∠BCD 有什么大小关系？3、如图,,90︒=∠=∠=∠BOD AOC EOC 图中 （1）与BOC ∠互补的角_________________ (2)相等的锐角有________________________ _____________________________(3)与BOC ∠互余的角有_____________________ (4)与AOD ∠互补的角有_________________________4、若一个角的余角比它的补角的31还小200，求这个角。

12 3【随堂检测】1．判断：⑴两个互补的角中必有一个是钝角 （ ） ⑵一个角的补角一定比这个角大 （ ） ⑶互补的两个角中，至少有一个角大于或等于直角 （ ） ⑷两个互余的角都是锐角 （ ） 2．一个角为50°17′，则它的余角为 ；补角为 。

余角和补角和对顶角余角：假如两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说个中一个角是另一个角的余角.∠A +∠C=90°,∠A= 90°-∠C ,∠C的余角=90°-∠C 即:∠A的余角=90°-∠A补角：假如两个角的和是一个平角,那么这两个角叫互为补角．个中一个角叫做另一个角的补角∠A +∠C=180°,∠A= 180°-∠C ,∠C的补角=180°-∠C 即:∠A的补角=180°-∠A对顶角：一个角的双方分离是另一个角的反向延伸线,这两个角是对顶角.两条直线订交后所得的只有一个公共极点且两个角的双方互为反向延伸线,如许的两个角叫做互为对顶角.两条直线订交,构成两对对顶角.对顶角相等.对顶角与对顶角相等.对顶角是对两个具有特别地位的角的名称;对顶角相等反应的是两个角间的大小关系.补角的性质：同角的补角相等.比方：∠A+∠B=180°,∠A+∠C=180°,则：∠C=∠B.等角的补角相等.比方：∠A+∠B=180°,∠D+∠C=180°,∠A=∠D则：∠C=∠B.余角的性质：同角的余角相等.比方：∠A+∠B=90°,∠A+∠C=90°,则：∠C=∠B.等角的余角相等.比方：∠A+∠B=90°,∠D+∠C=90°,∠A=∠D则：∠C=∠B.留意：①钝角没有余角;②互为余角.补角是两个角之间的关系.如∠A+∠B+∠C=90°,不克不及说∠A.∠B.∠C互余;同样：如∠A+∠B+∠C=180°,不克不及说∠A.∠B.∠C互为补角;③互为余角.补角只与角的度数相干,与角的地位无关.只要它们的度数之和等于90°或180°,就必定互为余角或补角.余角与补角概念熟悉提醒：（1）界说中的“互为”一词若何懂得？假如∠1与∠2互余,那么∠1的余角是∠2 ,同样∠2的余角是∠1 ;假如∠1与∠2互补,那么∠1的补角是∠2 , 同样∠2的补角是∠1.（2）互余.互补的两角是否必定有公共极点或公共边？两角互余或互补,只与角的度数有关,与地位无关.（3）∠1 + ∠2 + ∠3 = 90°（180°）,能说∠1 .∠2. ∠3 互余（互补）吗？不克不及,互余或互补是两个角之间的数目关系.已知∠A与∠B互余,∠B与∠C互补,若∠A=50°,则∠C的度数是[ D ] A．40°B．50°C．130°D．140°假如∠A的补角是它的余角的4倍,则∠A=______度．设∠A为x,则∠A的余角为90°-x,补角为180°-x,依据题意得,180°-x=4（90°-x）,解得x=60°．故答案为：60．已知∠ α=50°17',则∠α的余角和补角分离是[ B ]A．49°43',129°43'B．39°43',129°43'C ．39°83',129°83'D．129°43′,39°43′两个角的比是6：4,它们的差为36°,则这两个角的关系是（ ）A ．互余B ．相等C ．互补D ．以上都不合错误设一个角为6x,则另一个角为4x, 则有6x-4x=36°,∴x=18°,则这两个角分离为108°,72°, 而108°+72°=180°∴这两个角的关系为互补． 故选C ．假如∠A=35°18′,那么∠A 的余角等于______．假如∠A=35°18′,那么∠A 的余角等于90°-35°18′=54°42′． 故填54°42′．已知∠1和∠2互补,∠3和∠2互余,求证：∠3= =21（∠1-∠2）．证实：由题意得：∠2+∠3=90°,∠1+∠2=180°,∴2（∠2+∠3）=∠1+∠2, 故可得：∠3=21（∠1-∠2） 如图,∠1的邻补角是[ ]A.∠BOCB.∠BOC 和∠AOFC.∠AOFD.∠BOE 和∠AOF两个角互为补角,那么这两个角大小 [ D ]假如两个角互为补角,那么这两个角必定互为邻补角,证实此命题真——加原因 假如两个角互为补角,那么这两个角必定互为邻补角,这是假命题.假如两个角互为领补角,那么这两个角必定互为补角,这是真命题.譬如说,两直线平行,同旁内角互补,但互为同旁内角的两个角必定不互为领补角.假如两个角互补,那它们是邻补角”——————为什么说这个是假命题?两条平行线切出的同旁内角也互补,但是它们不是邻补角.所以说：“假如两个角互补,那它们是邻补角”是假命题!因为邻补角是相邻的两个角互补,那么这两个角是互为邻补角,而互补的两个角有不相邻的,比方四边形的两个对角互补,则这四点共圆假如一个角是36°,那么 [ D ]．它的余角是64° B．它的补角是64° C．它的余角是144° D．它的补角是144°下列说法中：①同位角相等;②两点之间,线段最短;③假如两个角互补,那么它们是邻补角;④两个锐角的和是锐角;⑤同角或等角的补角相等．准确的个数是（ ） A ．2个 B ．3个 C ．4个 D ．5个①同位角相等,说法错误;②两点之间,线段最短,说法准确;③假如两个角互补,那么它们是邻补角,说法错误;④两个锐角的和是锐角,说法错误;⑤同角或等角的补角相等,说法准确;说法准确的共有2个,故选：A．下列说法准确的是（）A．小于平角的角是锐角B．相等的角是对顶角C．邻补角的和等于180°D．同位角相A.小于平角的角有：锐角.直角.钝角,故本选项错误;B.对顶角相等,相等的角不必定是对顶角,故本选项错误;C.邻补角的和等于180°准确,故本选项准确;D.只有两直线平行,才有同位角相等,故本选项错误．故选C．下列说法准确的是（） A．相等的角是对顶角 B．对顶角相等 C．同位角相等 D．锐角大于它的余角A.相等的角是对顶角,说法错误;B.对顶角相等,说法准确;C.同位角相等,说法错误;D.锐角大于它的余角,说法错误;故选：B．下列说法中,准确的是（）A．对顶角相等B．内错角相等C．锐角相等D．同位角相等A.对顶角相等,说法准确;B.内错角相等,说法错误,只有两直线平行时,内错角才相等;C.锐角相等,说法错误,例如30°角和20°角;D.同位角相等,说法错误,只有两直线平行时,同位角才相等;故选：A．三条直线订交于一点可以构成几对对顶角？两条直线消失 2*（2-1）=2对对顶角三条直线消失 3*（3-1）=6对对顶角四条直线消失 4*（4-1）=12对对顶角依次类推,n条直线订交于一点有n*(n-1)对对顶角三条直线订交于一点,共可构成______对对顶角．如图,单个的角是对顶角的有3对,两个角的复合角是对顶角的有3对,所以,共有对顶角3+3=6对．故答案为：6．三条直线订交与一点,能构成几对对顶角？四条呢？五条呢？N条呢？我要办法和答案！三条直线订交与一点,6对;四条直线订交与一点,12对;五条直线订交与一点,20对;N条直线订交与一点,N(N-1)对;假如有n条直线订交于一点,有若干对对顶角？n的平方减去2条数个数2 2=2x13 6=3x24 12=4x35 20=5x4…………n n(n-1)三条直线订交于一点,对顶角最多有______对．把三条直线订交于一点,拆成三种两条直线交于一点的情形,因为两条直线订交于一点,形成两对对顶角,所以三条直线订交于一点,有3个两对对顶角,共6对对顶角两条直线订交,有一个交点.三条直线订交,最多有若干个交点？四条直线呢？你能发明什么纪律吗？这个其实就是组合问题.因为两条线构成一个交点,所以三条线时,从三条线中取两条线,有3*2/2=3种取法,所以有3个交点.四条线中取两条,有4*3/2=6种取法,所以有6个交点.n条线中取两条,有n(n-1)/2种取法,所以有n(n-1)/2个交点.邻补角是互补的角是真命题吗当然是,邻补角相加等于180度就是互补啊互补的角是邻补角是真命题照样假命题若是真命题,请举反例两个角有一条公共边,它们的另一条边互为反向延伸线,具有这种关系的两个角称为互为邻补角.可以随意画两个没有公共边的角,比方1个60度,另一个120度,显然它们是互补的,但是其实不是邻补角所以互补的角是邻补角这是一个假命题应当说邻补角是互补的角,这才是真命题既相邻又互补的两个角是邻补角吗两条平行线切出的同旁内角也互补,但是它们不是邻补角.所以说：“假如两个角互补,那它们是邻补角”是假命题！成互补关系的两个角互为邻补角是对照样错不合错误相邻的两个角互补称之为邻补角像两直线平行,同旁内角互补（这两个互补的角不相邻）.互补的两个角是邻补角用因为所以答因为两个角是邻补角所以两个角互补反过来不成立。

初中数学认识余角、补角、对顶角精讲精练【考点精讲】1. 互为余角与互为补角（1）概念：若，则称、互为余角；若则称、互为补角。

（2）记法的余角记作；的补角记作。

2. 余角（补角）的性质同角或等角的余（补）角相等。

3. 对顶角：如下图中，我们把叫做对顶角，也是对顶角。

OADBC4. 对顶角的性质：对顶角相等。

【典例精析】例题1 如图所示，O是直线AB上的一点，，平分，平分，则图中互为补角的对数有（）A. 6对B. 7对C. 8对D. 9对思路导航：是直线AB上的一点，，又，，平分，，，，。

答案：互补的角有：，，，，，共8对。

答案选C。

点评：本题涉及互补的角较多，根据题意计算有关角的度数，再根据互为补角的定义，按照一定的顺序来写，做到既不重复又不遗漏。

例题2 一个角的补角与它的余角的2倍的差是平角的，请你求出这个角的度数。

思路导航：可以直接设元（题中问什么就设什么，直接求出结果），也可以间接设元（先求出这个角，再求出它的余角），然后列方程求解。

答案：设这个角的度数为，则它的补角、余角分别为，（），根据题意得，解得，所以这个角的度数为60度。

点评：有关余角和补角的计算题目，常设未知数，根据题意列方程求解。

所设的未知数不同，所得到的方程也不同。

例题3 如图，直线AB、CD交于O点，且∠BOC=80°，OE平分∠BOC，OF为OE的反向延长线。

D（1）求∠2和∠3的度数；（2）OF平分∠AOD吗？为什么？思路导航：（1）根据邻补角的定义，即可求得∠2的度数，根据角平分线的定义和平角的定义即可求得∠3的度数；（2）根据OF分得∠AOD的两部分角的度数即可说明。

答案：（1）∵∠BOC+∠2=180°，∠BOC=80°，∴∠2=180°－80°=100°；∵OE是∠BOC的角平分线，∴∠1=40°。

∵∠1+∠2+∠3=180°，∴∠3=180°－∠1－∠2=180°－40°－100°=40°。

6.3余角、补角、对顶角（2）编写：徐雅萍审核：初一数学组时间：2023.12 班级姓名________学号_______一、自主研读初步学（一）认真阅读课本161-163页，并回答下列问题：知识点一：对顶角的概念写出图中的对顶角：；归纳：有顶点且角的两条边都互为线的两个角称为对顶角.注意：（1）对顶角形成的前提是两条直线相交，对顶角必须有公共的顶点.（2）对顶角是成对出现的，单独的一个角不能称为对顶角.例：下列图形中，表示1∠是对顶角的是()∠和2A．B．C．D．知识点二：对顶角的性质（1）如图，直线AC、BD相交于点O，问∠AOC与∠BOD有何大小关系？说明理由．关系：理由：总结：对顶角_____________________上述结论我们可用以下符号语言表述：∵∠AOC与∠BOD是对顶角∴∠AOC=∠BOD思考：对顶角一定相等，那相等的角一定是对顶角吗？如果是，说明理由；如果不是，画出反例.（2）例：如图，AB、CD相交于点O，∠BOE＝90°，∠1＝64°，求∠DOE的度数．分析：已知∠BOE的度数，要求∠DOE的度数，只要知道∠BOD的度数即可.解：∵∠1与∠2是对顶角∴（对顶角相等）12∵∠1=64°∴∠2= °．∵∠DOE=∠BOE-∠2，∠BOE＝90°．∴∠DOE=90°- 64°=26°．说明：要求一个角的度数，首先要观察图形，判断这个角与已知角有何关联，然后通过下列途径计算：①.先求出与它相等的角的度数，然后进行等量代换求得．②.将这个角转化为其他角的和差倍分的形式求得．练习：如图，AB，CD相交于点O，OB平分∠DOE，若∠AOC＝30°，求∠DOE的度数．1．下图中∠1与∠2是对顶角的是（）A B C D2．如图，AB与CD相交于点O，∠AOD＋∠BOC＝280°，则∠AOC的度数为( ) A．40°B．60°C．120°D．140°第2题第3题3. 如图，直线AB、CD、EF相交于点O，∠1＝50°，∠2＝67°，则∠COF＝°．4.若两个角是对顶角且互补，则这两个角都是________度．5.如图，已知直线AB、CD相交于点O，OE平分∠AOD，∠AOE=350，∠BOF=200,，求∠COF的度数.二、合作探究深化学（一）检查建构1.下列说法中正确的是（）A.有公共顶点的两个角是对顶角B.两条直线相交所成的角是对顶角C.对顶角一定相等D,两个相等的角一定是对顶角2.如图，直线AB、CD相交于点O，OA平分∠EOD，∠EOD=116°（1）写出图中的对顶角；（2）求∠BOC的度数.问题1 观察下列图形，找出对顶角（不含平角）(1) 如图①，图中共有对对顶角；（2）如图②，图中共有对对顶角；（3）如图③，图中共有对对顶角；（4）研究（1）～（3）小题中直线条数与对顶角的对数的关系。

第二章余角，补角，对顶角和平行的判定和性质一、定义：1、余角：如果两个角的和是90度，那么这两个角互为余角。

2、补角：如果两个角的和是180度，那么这两个角互为补角。

3、对顶角：如果两个角的两边互为反向延长线，那么这样的两个角叫对顶角二、性质定理：1、同角的余角或补角相等。

2、 对顶角相等。

三、解题方法：一般的，利用性质定理，结合三角形内角和定理，平角性质等，建立所求未知角的方程，即可解得所求角度。

四、概念：同位角，内错角，同旁内角五、两直线平行的判定定理：1.同位角相等，两直线平行2.内错角相等，两直线平行3.同旁内角互补，两直线平行4.如果两直线都平行于另一条直线，那么两直线也平行（推论）六、两直线平行的性质定理：1. 两直线平行，同位角相等2. 两直线平行，内错角相等3. 两直线平行，同旁内角互补例题1.已知∠α是它的余角的2倍，则∠α＝________.2.互为补角的两个角的度数之比为2∶7,则这两个角分别是________.3.如果一个角的余角和它的补角互补，那么这个角的度数为________4.如果两个角互为补角，以下说法不正确的是（）A．不可能都是锐角 B. 不可能都是钝角C. 不可能都是直角D. 可能都是直角5.2条直线相交 3条直线相交于一点 4条直线相交于一点n条直线相交于一点，对顶角有____对对顶角有____对对顶角有_____对对顶角有_______对(用含n的式子表示)6．如图所示，直线AB与CD相交于O点，A B⊥EO，则∠EOD与∠AOC的关系是（ ）A 对顶角B互补的角C互余的角D相等的角7．如图，直线a，b，c两两相交，∠1=2∠3，∠2=60度，求∠4.8．如图,∠A=50°,∠1＝∠2,则∠ACD等于___________9. 下列四个图形中,存在对顶角的是10. 一个角的余角比它的补角的还少12°，请求出这个角.11. 如图16,A、O、B在一条直线上,OC是射线,OE平分∠AOC, OF平分∠BOC.求∠EOF12. 如图，，求∠CAE的度数．课堂练习：1、若∠AOB=65015’，则它的余角是_________，它的补角是________．2、若∠α与∠β是对顶角，且∠α+∠β=1200 ，则∠α= ，∠β=3、如图：已知：，则4、一个角的补角等于这个角的余角的4倍，这个角是________．5．如图，CB⊥AB，∠CBA与∠CBD的度数比是5:1，则∠DBA＝________度，∠CBD 的补角是_________度.6．如图2，AC⊥BC，CD⊥AB，∠A的余角有______个，与∠A相等的角有_______个.7、 两条直线被第三条直线所截，则（ ）． A．同位角必相等 B．内错角必相等C．同旁内角必互补 D．同位角不一定相等8、如图，与是对顶角的为（ ）9、命题：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④同位角相等。

余角、补角、对顶角一、考点讲解：1．余角：如果两个角的和是直角，那么称这两个角互为余角．2．补角：如果两个角的和是平角，那．么称这两个角互为补角．3．对顶角：如果两个角有公共顶点，并且它们的两边互为反向延长线，这样的两个角叫做对顶角．4．互为余角的有关性质：①∠1＋∠2=90°，则∠1、∠2互余．反过来，若∠1，∠2互余．则∠1+∠2=90○．②同角或等角的余角相等，如果∠l十∠2=90○，∠1+∠3= 90○，则∠2= ∠3．5．互为补角的有关性质：①若∠A +∠B=180○则∠A、∠B互补，反过来，若∠A、∠B互补，则∠A+∠B＝180○．②同角或等角的补角相等．如果∠A ＋∠C=18 0○，∠A+∠B=18 0°，则∠B=∠C．6．对顶角的性质：对顶角相等．二、经典考题剖析：【考题1－1】已知：∠A= 30○，则∠A的补角是________度．解：150○点拨：此题考查了互为补角的性质．【考题1－2】如图l－2－1，直线AB，CD相交于点O，OE⊥AB于点O，OF 平分∠AOE，∠1＝15○30’，则下列结论中不正确的是（）A．∠2 =45○B．∠1=∠3C．∠AOD与∠1互为补角D．∠1的余角等于75○30′解：D 点拨：此题考查了互为余角，互为补角和对顶角之间的综合运用知识．三、针对性训练：1．_______的余角相等，_______的补角相等．2．∠1和∠2互余，∠2和∠3互补，∠1=63○，∠3=__3．下列说法中正确的是（ ）A ．两个互补的角中必有一个是钝角B ．一个角的补角一定比这个角大C ．互补的两个角中至少有一个角大于或等于直角D ．相等的角一定互余4．轮船航行到C 处测得小岛A 的方向为北偏东32○，那么从A 处观测到C 处的方向为（ ）A ．南偏西32○B ．东偏南32○C ．南偏西58○D ．东偏南58○5．若∠l=2∠2，且∠1+∠2=90○则∠1=___，∠2=___．6．一个角的余角比它的补角的九分之二多1°，求这个角的度数．7．∠1和∠2互余，∠2和∠3互补，∠3=153○，∠l=_8．如图 l －2－2，AB ⊥CD ，AC ⊥BC ，图中与∠CAB 互余的角有（ ）A ．0个B ．l 个C ．2个D ．3个9．如果一个角的补角是150○ ，那么这个角的余角是____________10．已知∠A 和∠B 互余，∠A 与∠C 互补，∠B 与∠C 的和等于周角的13 ，求∠A+∠B+∠C 的度数．11．如图如图1―2―3，已知∠AOC 与∠B 都是直角，∠BOC=59○．（1）求∠AOD 的度数；（2）求∠AOB 和∠DOC 的度数；（3）∠A OB 与∠DOC 有何大小关系；（4）若不知道∠BOC 的具体度数，其他条件不变，这种关系仍然成立吗？。