系统牛顿第二定律(质点系牛顿第二定律)Word版
- 格式:doc
- 大小:103.50 KB
- 文档页数:4

系统牛顿第二定律(质点系牛顿第二定律)主讲:黄冈中学教师郑成1、质量M=10kg的木楔ABC静止于粗糙水平地面上,如图,动摩擦因数μ=,在木楔的倾角α=30°的斜面上,有一质量m=的物块,由静止开始沿斜面下滑,当滑行至s=时,速度v=s,在这过程木楔没有动.求地面对木楔的摩擦力的大小、方向和地面对木楔的支持力.(g=10m/s2)解法一:(隔离法)先隔离物块m,根据运动学公式得:v2=2as=s2<gsinθ=5m/s2可见物块m受到沿斜面向上的滑动摩擦力,对物体m为对象对斜面M:假设地面对M静摩擦力向右:f地+N′sin30°-f′cos30°=0而N′=N=,f′=f=地=-Nsin30°+fcos30°=-说明地面对斜面M的静摩擦力f地=,负号表示方向水平向左.可求出地面对斜面M的支持力N地N地-f′sin30°-N′cos30°-Mg=0N地= fsin30°+Ncos30°+Mg=<(M+m)g=110N因m有沿斜面向下的加速度分量,故整体可看作失重状态方法二:当连接体各物体加速度不同时,常规方法可采用隔离法,也可采用对系统到牛顿第二定律方程.=m1a1x+m2a2x+…+m n a nx =m1a1y+m2a2y+…+m n a ny解法二:系统牛顿第二定律:把物块m和斜面M当作一个系统,则:x:f地=M×0 +macos30°=水平向左y:(M+m)g-N地=M×0+masin30°N地=(M+m)g-ma sin30°=例2:如图所示,一质量为M的楔形木块放在水平桌面上,它的顶角为90°,两底角为α和β;a、b为两个位于斜面上质量均为m的小木块.已知所有接触面都是光滑的,现发现a、b沿斜面下滑,而楔形木块静止不动,求楔形木块对水平桌面的压力和静摩擦力解法一:隔离法N a=mgcosαN b=mgcosβN地=mg+mgcosβsinα+mgcosαsinβ=Mg+mg(sin2α+cos2α)=Mg+mgf地=N b′cosα-N a′cosβ=mgcosβcosα-mgcosαcosβ=0N解法二:系统牛顿第二定律列方程:(M+2m)g-N地=M×0+mgsin2α+mgsin2βN地=(M+m)g向右为正方向:f地= M×0+mgsinαcosα-mgsinβcosβ=0。


系统牛顿第二定律(质点系牛顿第二定律)主讲:黄冈中学教师郑成1、质量M=10kg的木楔ABC静止于粗糙水平地面上,如图,动摩擦因数μ=0.02,在木楔的倾角α=30°的斜面上,有一质量m=1.0kg的物块,由静止开始沿斜面下滑,当滑行至s=1.4m时,速度v=1.4m/s,在这过程木楔没有动.求地面对木楔的摩擦力的大小、方向和地面对木楔的支持力.(g=10m/s2)解法一:(隔离法)先隔离物块m,根据运动学公式得:v2=2as=0.7m/s2<gsinθ=5m/s2可见物块m受到沿斜面向上的滑动摩擦力,对物体m为对象对斜面M:假设地面对M静摩擦力向右:f地+N′sin30°-f′cos30°=0而N′=N=,f′=f=4.3N f地=-Nsin30°+fcos30°=-0.61N说明地面对斜面M的静摩擦力f地=0.61N,负号表示方向水平向左.可求出地面对斜面M的支持力N地N地-f′sin30°-N′cos30°-Mg=0N地= fsin30°+Ncos30°+Mg=109.65N<(M+m)g=110N因m有沿斜面向下的加速度分量,故整体可看作失重状态方法二:当连接体各物体加速度不同时,常规方法可采用隔离法,也可采用对系统到牛顿第二定律方程.=m1a1x+m2a2x+…+m n a nx =m1a1y+m2a2y+…+m n a ny解法二:系统牛顿第二定律:把物块m和斜面M当作一个系统,则:x:f地=M×0 +macos30°=0.61N水平向左y:(M+m)g-N地=M×0+masin30°N地=(M+m)g-ma sin30°=109.56N例2:如图所示,一质量为M的楔形木块放在水平桌面上,它的顶角为90°,两底角为α和β;a、b为两个位于斜面上质量均为m的小木块.已知所有接触面都是光滑的,现发现a、b沿斜面下滑,而楔形木块静止不动,求楔形木块对水平桌面的压力和静摩擦力解法一:隔离法N a=mgcosαN b=mgcosβN地=mg+mgcosβsinα+mgcosαsinβ=Mg+mg(sin2α+cos2α)=Mg+mgf地=N b′cosα-N a′cosβ=mgcosβcosα-mgcosαcosβ=0N解法二:系统牛顿第二定律列方程:(M+2m)g-N地=M×0+mgsin2α+mgsin2βN地=(M+m)g向右为正方向:f地= M×0+mgsinαcosα-mgsinβcosβ=0【本文档内容可以自由复制内容或自由编辑修改内容期待你的好评和关注,我们将会做得更好】。

质点系牛顿第二定律例题
牛顿第二定律是物理学中最重要的定律之一,也是经典力学的主要原理。
它是由英国的力学家及数学家牛顿提出的。
根据牛顿第二定律,当一个质点或物体受到外力作用时,其受力大小与作用力大小成比例,而其受力方向与作用力方向完全相反。
这就是牛顿第二定律,它可以用数学表达式表示:
F= ma
其中,F表示外力,m表示质量,a表示受力的加速度方向。
二、牛顿第二定律例题
1、问题描述
一个质量为m的质点在x轴上受到外力F,请问该质点的加速度是多少?
2、解答
根据牛顿第二定律,加速度a与外力F成正比,a=F/m,所以该质点的加速度为F/m。
- 1 -。





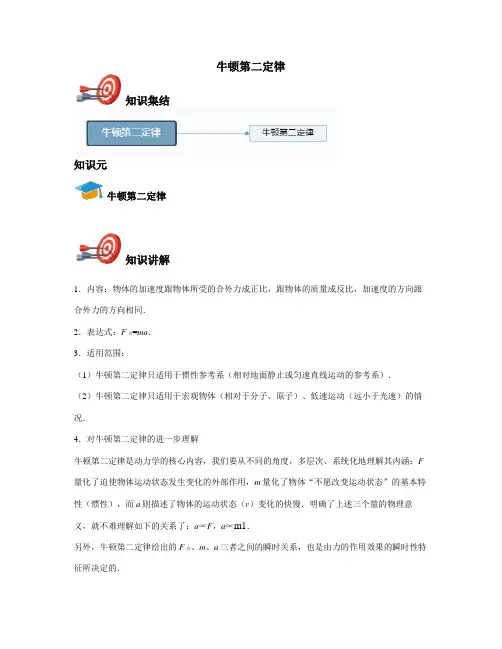
牛顿第二定律知识集结知识元牛顿第二定律知识讲解1.内容:物体的加速度跟物体所受的合外力成正比,跟物体的质量成反比,加速度的方向跟合外力的方向相同.2.表达式:F合=ma.3.适用范围:(1)牛顿第二定律只适用于惯性参考系(相对地面静止或匀速直线运动的参考系).(2)牛顿第二定律只适用于宏观物体(相对于分子、原子)、低速运动(远小于光速)的情况.4.对牛顿第二定律的进一步理解牛顿第二定律是动力学的核心内容,我们要从不同的角度,多层次、系统化地理解其内涵:F 量化了迫使物体运动状态发生变化的外部作用,m量化了物体“不愿改变运动状态”的基本特性(惯性),而a则描述了物体的运动状态(v)变化的快慢.明确了上述三个量的物理意义,就不难理解如下的关系了:a∝F,a∝m1.另外,牛顿第二定律给出的F合、m、a三者之间的瞬时关系,也是由力的作用效果的瞬时性特征所决定的.(1)矢量性:a与F合都是矢量,且方向总是相同.(2)瞬时性:a与F合同时产生、同时变化、同时消失,是瞬时对应的.(3)同体性:a与F合是对同一物体而言的两个物理量.(4)独立性:作用于物体上的每个力各自产生的加速度都遵循牛顿第二定律,而物体的合加速度则是每个力产生的加速度的矢量和,合加速度总是与合外力相对应.5.应用牛顿第二定律的解题步骤(1)通过审题灵活地选取研究对象,明确物理过程.(2)分析研究对象的受力情况和运动情况,必要时画好受力示意图和运动过程示意图,规定正方向.(3)根据牛顿第二定律和运动公式列方程求解.(列牛顿第二定律方程时可把力进行分解或合成处理,再列方程)(4)检查答案是否完整、合理,必要时需进行讨论.例题精讲牛顿第二定律例1.由F=ma可知()A.物体质量和加速度成反比B.因为有加速度才有力C.物体的加速度与物体受到的合外力方向一致D.物体的加速度与物体受到的合外力方向不一定相同例2.小明站在电梯里,当电梯以加速度5m/s2下降时,小明受到的支持力()A.小于重力,但不为零B.大于重力C.等于重力D.等于零例3.一轻质弹簧上端固定,下端挂一重物,平衡时弹簧伸长了5cm,再将重物向下拉2cm,然后放手,则在刚释放的瞬间重物的加速度大小是(弹簧始终在弹性限度内,g=10m/s2)()A.4m/s2B.6m/s2C.10m/s2D.14m/s2例4.一质量为m的人站在电梯中,电梯加速上升,加速度的大小为g,g为重力加速度.人对电梯底部的压力为()A.B.2mg C.mgD.当堂练习单选题练习1.如图所示将一小球从空中某一高度自由落下,当小球与正下方的轻弹簧接触时,小球将()A.立刻静止B.立刻开始做减速运动C.开始做匀速运动D.继续做加速运动练习2.如图所示的一种蹦床运动,图中水平虚线PQ是弹性蹦床的原始位置,A为运动员抵达的最高点,B为运动员刚抵达蹦床时刻时刻的位置,C为运动员的最低点,不考虑空气阻力,运动员从A下落到C的过程中速度最大的位置为()A.A点B.B点C.C点D.B、C之间练习3.如图所示,一根轻质弹簧竖直立在水平地面上,下端固定.一小球从高处自由落下,落到弹簧上端,将弹簧压缩至最低点.小球从开始压缩弹簧至最低点的过程中,小球的加速度和速度的变化情况是()A.加速度先变大后变小,速度先变大后变小B.加速度先变大后变小,速度先变小后变大C.加速度先变小后变大,速度先变大后变小D.加速度先变小后变大,速度先变小后变大练习4.“歼-20”是中国成都飞机工业(集团)有限责任公司为中国人民解放军研制的第四代双发重型隐形战斗机该机将担负中国未来对空、对海的主权维护任务.在某次起飞中,由静止开始加速,当加速度a不断减小至零时,飞机刚好起飞.关于起飞过程下列说法正确的是()A.飞机所受合力不变,速度增加越来越慢B.飞机所受合力减小,速度增加越来越快C.速度方向与加速度方向相同,速度增加越来越快D.速度方向与加速度方向相同,速度增加越来越慢小明站在电梯里,当电梯以加速度5m/s2下降时,小明受到的支持力()A.小于重力,但不为零B.大于重力C.等于重力D.等于零练习6.如图所示A、B两相同的木箱(质量不计)用细绳连接放在水平地面上,当两木箱内均装有质量为m的沙子时,用水平力F拉A木箱,使两木箱一起做匀加速直线运动,细绳恰好不被拉断。

系统的牛顿第二定律及应用一、系统的牛顿第二定律若将系统受到的每一个外力,系统内每一物体的加速度均沿正交坐标系的x轴与y轴分解,则系统的牛顿第二定律的数学表达式如下:F1x+F2x+…=m1a1x+m2a2x+…F1y+F2y+…=m1a1y+m2a2y+…与采用隔离法、分别对每一物体应用牛顿第二定律求解不同的是,应用系统的牛顿第二定律解题时将使得系统内物体间的相互作用力变成内力,因而可以减少不必求解的物理量的个数,导致所列方程数减少,从而达到简化求解的目的,并能给人以一种赏心悦目的感觉,现通过实例分析与求解,说明系统的牛顿第二定律的具体应用,并力图帮助大家领略到应用系统的牛顿第二定律求解的优势。
二、系统的牛顿第二定律的应用1、求系统所受到的外力例1 在图1中,A为电磁铁,C为胶木秤盘,A和C(包括支架)的总质量为M。
B为铁片,质量为m。
整个装置用轻绳悬挂于O点。
当电磁铁通电,铁片被吸引上升的过程,轻绳上的拉力F的大小为()A、F=MgB、Mg<F<(m+M)gC、F=(m+M)gD、F>(m+M)g分析与解以A、B、C系统为研究对象,它受到的外力为竖直向下的重力(m+M)g,绳对系统竖直向上的拉力F(电磁铁A与铁片B间的相互引力为内力)。
A、C的加速度为0,铁片上升时向上的加速度不为0。
若以竖直向上方向为正向,设某时刻铁片B向上的加速度为a,则由系统的牛顿第二定律得F-(m+M)g=ma∴F=(m+M)g+ma>(m+M)g因此,应选正确答案D。
例2 如图2所8示,一根长为l的轻杆,两端各固定一个质量均为m 的小球A和B。
若轻杆以它的中点O为轴在竖直平面内转动,求轻杆转到竖直位置时,杆对轴的作用力。
分析与解取小球A、B及杆为研究对象,它受到竖直向下的重力2mg,轴对它竖直向上的弹力N.A、B在最低点与最高点时向心加速度恰为反向。
若取竖直向上方向为正向,由系统的牛顿第二定律得:N-2mg=maA +maB∵aA =-aB∴N=2mg由牛顿第三定律知杆对轴的弹力大小为2mg,方向竖直向下。
牛顿第二定律的整体运用2013-04-08 15:19牛顿第二定律研究的对象可以是单个物体(质点),也可以是多个相互作用的物体组成的系统(质点系)。
设系统内各物体的质量分别为m1 、m2、……、mn ,系统所受到的合外力为F ,牛顿第二定律应用于整体时的表达式为:1.若系统内各物体的加速度a 相同,则有F =(m1 + m2 +…+ mn)a2.若系统内各物体的加速度不相同,设分别为a1 、a2、……、an ,则有F = m1a1 + m2a2 +…+ mnan (矢量和)若将各物体的加速度正交分解,则牛顿第二定律应用于整体的表达式为Fx = m1 a1x…+ mnanx + m2a2x +Fy = m1 a1y…+ mnany + m2a2y +在分析实际问题时要注意系统内各物体加速度的方向,与规定的正方向相同时加速度取正值,反之就取负值。
以下通过具体实例分析牛顿第二定律的整体运用。
例1 质量为m = 55 kg的人站在井下一质量为M = 15kg 的吊台上,利用如图1所示的装置用力拉绳,将吊台和自已以向上的加速度a = 0.2 m/s2 提升起来,不计绳质量和绳与定滑轮间的摩擦,g 取10 m/s2,求人对绳的拉力F 的大小。
解析对人与吊台整体受力如图1所示,由于吊台与人的加速度相同,由牛顿第二定律有代入相关数据解得 F = 350 N 。
点拨人与吊台间存在相互的作用力,但题目又不要求出此力。
我们若单独以人或吊台为研究对象,那就都要考虑这个作用力;若以人和吊台组成的整体为研究对象,这个作用力即为整体的内力,应用牛顿第二定律时就可以不予考虑。
例2 如图2所示,水平地面上有一倾角为θ质量为M斜面体,斜面体上有一质量为m 的物块以加速度a 沿斜面匀加速下滑,此过程中斜面体没有动,求地面对斜面体的支持力N 与摩擦力f 的大小。
解析将物块的加速度度a沿水平方向与竖直方向进行分解,对物块与斜面体整体在竖直方向上由牛顿第二定律有在水平方向上由牛顿第二定律有则,点拨本题中所要求的地面对斜面体的支持力N与摩擦力f分别在竖直方向上和水平方向上,由于斜面体没有加速度,而物块的加速度a是沿斜面方向的,故我们应将a沿水平方向与竖直方向进行分解。
系统中牛顿第二定律及其在整体法中的应用一、创新拓展 若系统由2个物体组成,两物体受到的外力分别为F1,F2,两物体的质量分别为m1,m2,对应的加速度分别为a1,a2,. 该系统受到的合外力为F,则对两个物体用牛顿第二定律有:F1=m 1 a 1 , F 2= m 2 a 2, 上式两边相加得:F 1+F 2=m 1 a 1+ m 2 a 2 即F= m 1 a 1+ m 2 a 2 这就是系统中的牛顿第二定律的数学表达式,其表述为:系统受到的合外力等于系统内各物体的质量与其加速度乘积的矢量和。
其正交分解的表达式为:F x =m 1 a 1x +m 2 a 2x ;F y =m 1 a 1y +m 2 a 2y . 若系统内有n 个物体,则系统中的牛顿第二第律的数学表达式为:F =m 1 a 1 +m 2 a 2 +…+m n a n 或正交分解式为F x =m 1 a 1x +m 2 a 2x +…+m n a nx ; F y =m 1 a 1y +m 2 a 2y +…+m n a ny二、应用范例整体法是物理中常用的一种思维方法。
它是将几个物体看作一个整体来作为研究对象即系统,这样就暂时回避了这些物体间的相互作用的内力,只考虑整体受到的外力,整体法列出的方程数目较少,解题变的简明快捷。
但运用整体法的条件是暂不求物体间的相互作用力,各个物体的加速度要相同,没有相对运动。
当各个物体的加速度不相同时,运用整体法求解就遇到了困难。
由于系统中的牛顿第二定律对系统中的物体无论有无相对运动,都可以求解,不受各个物体的加速度一定相同的限制。
对于由多个物体组成的系统,如果所求问题暂不涉及或不涉及系统内的作用力,系统中只有一个物体有加速度,而其它物体无加速度(静止或匀速),或者多个物体的加速度在同一直线上,不会出现繁琐的矢量运算时,可以运用系统中的牛顿第二定律求解。
故系统中的牛顿第二定律在原整体法的基础上使解题的范围扩大,给整体法赋予了新的生命力,对于解答多体动力学问题,简单方便,迅速准确,能起到出奇制胜的效果。
第一章 质点运动学和牛顿运动定律1.1平均速度 v =t △△r1.2 瞬时速度 v=lim△t →△t △r =dtdr1. 3速度v=dtds ==→→lim lim△t 0△t △t△r 1.6 平均加速度a =△t △v1.7瞬时加速度(加速度)a=lim△t →△t △v =dtdv1.8瞬时加速度a=dt dv =22dt rd1.11匀速直线运动质点坐标x=x 0+vt 1.12变速运动速度 v=v 0+at 1.13变速运动质点坐标x=x 0+v 0t+21at 2 1.14速度随坐标变化公式:v 2-v 02=2a(x-x 0) 1.15自由落体运动 1.16竖直上抛运动⎪⎩⎪⎨⎧===gy v at y gtv 22122 ⎪⎪⎩⎪⎪⎨⎧-=-=-=gyv v gt t v y gt v v 221202200 1.17 抛体运动速度分量⎩⎨⎧-==gt a v v av v yx sin cos 001.18 抛体运动距离分量⎪⎩⎪⎨⎧-•=•=20021sin cos gt t a v y t a v x 1.19射程 X=gav 2sin 21.20射高Y=gav 22sin 201.21飞行时间y=xtga —ggx 21.22轨迹方程y=xtga —av gx 2202cos 21.23向心加速度 a=Rv 21.24圆周运动加速度等于切向加速度与法向加速度矢量和a=a t +a n1.25 加速度数值 a=22n t a a +1.26 法向加速度和匀速圆周运动的向心加速度相同a n =Rv 21.27切向加速度只改变速度的大小a t =dtdv1.28 ωΦR dtd R dt ds v ===1.29角速度 dt φωd =1.30角加速度 22dt dtd d φωα== 1.31角加速度a 与线加速度a n 、a t 间的关系a n =222)(ωωR RR R v == a t =αωR dtd R dt dv ==牛顿第一定律:任何物体都保持静止或匀速直线运动状态,除非它受到作用力而被迫改变这种状态。
系统牛顿第二定律(质点系牛顿第二定律)主讲:黄冈中学教师郑成1、质量M=10kg的木楔ABC静止于粗糙水平地面上,如图,动摩擦因数μ=0、02,在木楔的倾角α=30°的斜面上,有一质量m=1、0kg的物块,由静止开始沿斜面下滑,当滑行至s=1、4m时,速度v=1、4m/s,在这过程木楔没有动.求地面对木楔的摩擦力的大小、方向与地面对木楔的支持力.(g=10m/s2)解法一:(隔离法)先隔离物块m,根据运动学公式得:v2=2as=0、7m/s2<gsinθ=5m/s2可见物块m受到沿斜面向上的滑动摩擦力,对物体m为对象对斜面M:假设地面对M静摩擦力向右:f地+N′sin30°-f′cos30°=0而N′=N=,f′=f=4、3N f地=-Nsin30°+fcos30°=-0、61N说明地面对斜面M的静摩擦力f地=0、61N,负号表示方向水平向左.可求出地面对斜面M的支持力N地N地-f′sin30°-N′cos30°-Mg=0N地= fsin30°+Ncos30°+Mg=109、65N<(M+m)g=110N因m有沿斜面向下的加速度分量,故整体可瞧作失重状态方法二:当连接体各物体加速度不同时,常规方法可采用隔离法,也可采用对系统到牛顿第二定律方程.=m1a1x+m2a2x+…+m n a nx =m1a1y+m2a2y+…+m n a ny解法二:系统牛顿第二定律:把物块m与斜面M当作一个系统,则:x:f地=M×0 +macos30°=0、61N水平向左y:(M+m)g-N地=M×0+masin30°N地=(M+m)g-ma sin30°=109、56N例2:如图所示,一质量为M的楔形木块放在水平桌面上,它的顶角为90°,两底角为α与β;a、b为两个位于斜面上质量均为m的小木块.已知所有接触面都就是光滑的,现发现a、b沿斜面下滑,而楔形木块静止不动,求楔形木块对水平桌面的压力与静摩擦力解法一:隔离法N a=mgcosαN b=mgcosβN地=mg+mgcosβsinα+mgcosαsinβ=Mg+mg(sin2α+cos2α)=Mg+mgf地=N b′cosα-N a′cosβ=mgcosβcosα-mgcosαcosβ=0N解法二:系统牛顿第二定律列方程:(M+2m)g-N地=M×0+mgsin2α+mgsin2βN地=(M+m)g向右为正方向:f地= M×0+mgsinαcosα-mgsinβcosβ=0。
系统牛顿第二定律(质点系牛顿第二定律)
主讲:黄冈中学教师郑成
1、质量M=10kg的木楔ABC静止于粗糙水平地面上,如图,动摩擦因数μ=0.02,在木楔的倾角α=30°的斜面上,有一质量m=1.0kg的物块,由静止开始沿斜面下滑,当滑行至s=1.4m时,速度v=1.4m/s,在这过程木楔没有动.求地面对木楔的摩擦力的大小、方向和地面对木楔的支持力.(g=10m/s2)
解法一:(隔离法)先隔离物块m,根据运动学公式得:
v2=2as=0.7m/s2<gsinθ=5m/s2
可见物块m受到沿斜面向上的滑动摩擦力,对物体m为对象
对斜面M:假设地面对M静摩擦力向右:
f地+N′sin30°-f′cos30°=0
而N′=N=,f′=f=4.3N f地=-Nsin30°+fcos30°=-0.61N
说明地面对斜面M的静摩擦力f地=0.61N,负号表示方向水平向左.
可求出地面对斜面M的支持力N地
N地-f′sin30°-N′cos30°-Mg=0
N地= fsin30°+Ncos30°+Mg=109.65N<(M+m)g=110N
因m有沿斜面向下的加速度分量,故整体可看作失重状态
方法二:当连接体各物体加速度不同时,常规方法可采用隔离法,也可采用对系统到牛顿第二定律方程.=m1a1x+m2a2x+…+m n a nx =m1a1y+m2a2y+…+m n a ny
解法二:系统牛顿第二定律:
把物块m和斜面M当作一个系统,则:
x:f地=M×0 +macos30°=0.61N水平向左y:(M+m)g-N地=M×0+masin30°N地=(M+m)g-ma sin30°=109.56N
例2:如图所示,一质量为M的楔形木块放在水平桌面上,它的顶角为90°,两底角为α和β;a、b为两个位于斜面上质量均为m的小木块.已知所有接触面都是光滑的,现发现a、b沿斜面下滑,而楔形木块静止不动,求楔形木块对水平桌面的压力和静摩擦力
解法一:隔离法
N a=mgcosαN b=mgcosβ
N地=mg+mgcosβsinα+mgcosαsinβ=Mg+mg(sin2α+cos2α)=Mg+mg
f地=N b′cosα-N a′cosβ=mgcosβcosα-mgcosαcosβ=0N
解法二:系统牛顿第二定律列方程:
(M+2m)g-N地=M×0+mgsin2α+mgsin2β
N地=(M+m)g
向右为正方向:f地= M×0+mgsinαcosα-mgsinβcosβ=0。