当前位置：文档之家 › 共轴球面光学系统

共轴球面光学系统

  • 格式：ppt
  • 大小：1.23 MB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

7.2-7.4共轴球面光学系统解析

7.2-7.4共轴球面光学系统解析

I ' U ' 同理，在像方可得 OE L 'sin U '/ cos 2
则
2
I Q
E
I ' U ' I ' U ' cos L sin U cos 2 2 L ' OE I U sin U ' sin U 'cos 2
A
U -L
φ O r
C L'
U'
7.2 单个折射球面的折射
近轴光的光路计算公式
近轴光线的光路计算则按实际光线的光路计算公式近似简化为
l r ， i r
n i' i ， n'
u#39; r (1 u'
当光线平行于光轴时
h sin I r
h i r
7.2 单个折射球面的折射
近轴光的光路计算公式
符号法则
注意：几何图形上各量一律标注其绝对值，因此，对图 中负量必须在该量的字母前加一负号。
7.2 单个折射球面的折射
单个折射球面的光路计算公式 光线的单个折射球面的光路计算，是指在给定单 个折射球面的结构参量n、n’和r，由已知入射光线 坐标L和U，计算折射后出射光线的坐标L’和U’。 L和 L’分别为物方、像方截距；U和U’分别为物方、 像方孔径角。 单考虑折射球面的折射原因是：大多数光学系统由 折、反射球面或平面组成的共轴球面光学系统；平面 可以看成曲率半径取于无穷大；反射是n’=-n时的特 例.
7.2 单个折射球面的折射
单个折射球面的光路计算公式
如图，在ΔAEC中，应用正弦定律 ，得
sin AEC sin(U ) L r r
又 sin I

第2章 共轴球面系统

第2章 共轴球面系统

β=
y′ l ′ r = y l r
l ′ r nl ′ = lr n ′l
因此横向放大率为: β
=
y′ nl′ = y n ′l
(1 )
2.2 单个折射球面的成像放大率 及拉赫不变量
2.
y′ nl ′ nu 讨论: 讨论:β = = = y n′l n′u ′
β > 1, 放大像 β < 1, 缩小像
(1)式表示物像位置的关系 物像位置的关系;(2)式称为阿贝 物像位置的关系 阿贝 不变量公式,它表示单个折射球面物方和像方的 不变量 Q值相等;(3)式表示近轴光线经球面折射后物 物 像方孔径角的关系. 像方孔径角 例题:有一折射球面,其参数为 r = 20mm, n = 1, n′ = 1.5163, 物距为 l = 60mm ,求像距的值.
2.1光线经单个折射球面的折射 2.1光线经单个折射球面的折射
2.近轴光线的光路计算公式 近轴光线的光路计算公式: 近轴光线的光路计算公式
Lr sinI = sinU r U′ =U + I I′ n ′ = sinI sinI n′ sinI′ ′ = r(1+ L ) ′ sinU
光线平行于光轴:光线的入射角用光线的入射高度 表示为: i = h / r
物点由A1移动到A2点,物方截距l2-l1,像方截距 l'2-l'1,则轴向放大率为: n′ α = β1 β 2 ——平均沿轴放大率
n
结论:只有当dl很小时,才能满足
dl ′ nl ′2 n′ 2 = 2 = β α= dl n′l n
5.角放大率 5.角放大率
2.2 单个折射球面的成像放大率 及拉赫不变量
2.2 单个折射球面的成像放 大率及拉赫不变量

共轴球面系统成像的原理

共轴球面系统成像的原理

共轴球面系统成像的原理
共轴球面系统（Spherical Coordinate Imaging，SCI）是一种用于成像的技术，其原理基于球面坐标系的数学模型，将空间中的点用三个参数（径向距离、角度和极角）来描述，即r（径向距离）、θ（角度）和φ（极角）。

共轴球面系统成像的原理如下：
1. 首先，将待成像区域划分为一系列小单元，每个小单元对应一个球面坐标系上的点。

2. 对于每个小单元，通过探测器阵列采集其反射或散射的光线，并将其转化为电信号。

3. 将每个小单元对应的球面坐标转化为直角坐标系中的坐标点，并将其输入到图像处理系统中。

4. 图像处理系统根据每个坐标点的位置和亮度信息，计算出其在图像中的像素值，并将其输出到显示器上，从而得到共轴球面系统的成像结果。

共轴球面系统成像的优点在于能够提供比传统成像技术更为全面和详细的图像信息，特别是在对复杂目标的成像方面具有优势。

此外，
共轴球面系统成像还具有高分辨率、高信噪比和低失真率等优点，因此在医学成像、工业检测、天文观测等领域得到了广泛应用。

第二章 共轴球面系统(1)

第二章 共轴球面系统(1)

符号规则的应用举例：
20º 20º
20º 20º
100
100
符号规则的应用举例：
光路图中所有几何量一律以绝对值标注，负号则
表示该几何量的方位。 应用一定形式的公式可进行各种光路的正确计算。 推导公式时，也要使用符号规则，以便使导出的 公式具有普遍性。
举例：
透镜的结构参数： r1 = 10
d=5
n1 = 1.0 n1’ = n2 = 1.5163 (K9)
r2 = -50
n2’ = 1.0
§ 2-3
近轴成像
当U很小时，U’ ，I与I’ 也相应很小，则这 些角度的正弦值可近似地用弧度值来代替， 并改用小写字母 u，u’ ，i，i’ 来表示。此时， 其他各量均用相应小写字母来表示。 此时，由于u角很小，光线很靠近光轴， 这样的光线称为近轴光线（或称傍轴光线）。 近轴光线所在的区域，称为近轴区（或称傍 轴区）(Paraxial region)。
〈讨论〉
③ 当一物点位于反射镜的球心时，此时 I= -I″= 0 ，即说明从球心发出的 光线被球面镜反射后，反射光线按原 路返回；也就是说，从C点发出的任 何光线经球面镜反射后，仍会聚于C点。
何谓理想光学系统？
此即是把近轴区成完善像的范围扩 大到整个光学系统的任意空间；亦即当 任意大范围的物体以任意宽的光束经光 学系统后均能成完善像的光学系统。
A
-u
C
A’ B’
- u’
O
-l’ -l
球面反射镜的成像特性
1、焦距公式：
f ′= f = r / 2 2、物像关系：
（2-18）
1 / l′+ 1 / l = 2 / r
β=-l’/l α= - β 2 γ= -1 / β

7.27.4共轴球面光学系统

7.27.4共轴球面光学系统

点的位置有关。这个量在像差中有重要用途。
h
（2） n ' u ' nu (n ' n )
孔径变化式
r
表示近轴光经球面折射前后的孔径角 u 和 u ' 的关系 。
2020/9/27
7.3 单个折射球面近轴区成像
（3） n' n n'n “距度”（距离倒数）变化式或物像公式 l' l r
该式表示折射球面成像时，物像位置 l 和l ' 之间的关系。已
2020/9/27
7.2 单个折射球面的折射
➢ 单个折射球面的光路计算公式
如图，在ΔAEC中，应用正弦定律 ，得
sinAECsin(U)
Lr
r
又 sinIsin A E C
sin I (L r) sin U r
2020/9/27
7.2 单个折射球面的折射
➢ 单个折射球面的光路计算公式
在光线的入射点处应用折射定律
②当β>0，y’和y同号，成正像；l '和l 同号，物像位于球面的同
侧，实物成虚像，虚物成实像。 ③当∣β∣>1，为放大像；∣β∣<1，为缩小像。
2020/9/27
7.3 单个折射球面近轴区成像
➢ 轴向放大率
当物体在给定位置有一微量位移dl，其像也在像点位置处有一
微量位移dl′，定义dl′与dl 的比值为轴向放大率，用 表示.
➢ 高斯公式和牛顿公式
将r
/(n'
n)
乘以物象公式
n' l'
ห้องสมุดไป่ตู้
n l
(n
r '
n)，得
f' f 1

第二章 球面与共轴球面系统

第二章 球面与共轴球面系统
3. 放大率公式1） Nhomakorabea轴放大率：

yk y1
1 2 k
n 1 l 1l 2 l k n k l1 l 2 l k

n1u 1 nkuk
意义：整个光学系统的放大率为各个折射面放大率的乘积。 2）轴向放大率： 3）角放大率： 4）三者关系：

lk lk rk
远轴光的过渡公式：
L 2 L 1 d 1 , L 3 L 2 d 2 ,......
U
2
L k L k 1 d k 1
U 1 , U
3
U 2 ,...... U
k
U k 1
n 2 n 1 , n 3 n 2 ,......, n k n k 1
第二章 球面与共轴球面系统
§ 2－1 光线光路计算与共轴光学系统
共轴球面系统— 光学系统一般由球面和平面组成， 各球面球心在一条直线（光轴）上。 物象关系的研究方法— 光线的光路计算。逐面计 算物象的大小、虚实、正倒、位置等特性。 子午面— 包含物面与光轴的截面。
一、 光线经过单个折射面的折射
n I E I′ φ U′ C n′ h -U
2. 转面公式
原则：前一折射面的象为后一面的物 ，前一面的象空间为后一面的物空间 n2 ＝ n1′， n3 ＝ n2′ …… nk ＝ nk-1′ u2 ＝ u1′， u3 ＝ u2′ …… uk ＝ uk-1′ y2 ＝ y1′， y3 ＝ y2′ …… yk ＝ yk-1′ l2 ＝ l1′- d1 ， l3 ＝ l2′- d2 …… lk ＝ lk-1′- dk-1 h2 ＝ h1 - d1u1′ ， h3 ＝ h2 – d2u2′ …… hk ＝ hk-1 – dk-1uk-1′ 各面近轴光线成像公式： n k n k nk nk

工程光学第2章 共轴球面光学系统

工程光学第2章 共轴球面光学系统
10
共轴球面光学系统
§2.4
共轴球面系统的成像
11
1. 过渡公式
共轴球面光学系统
, n3 n2 , , nk nk 1 n2 n1 , u3 u2 , , uk uk 1 u2 u1 , y3 y2 , , yk yk 1 y2 y1
a b 2
单个反射球面成像
1 1 2 l l r f f r 2
b 1
物点位于球心时
a 1
g 1 b
g 1
9
共轴球面光学系统
b l l
a b 2
g 1 b
J uy uy
球面镜的拉赫不变量
结论
a<0，物体沿光轴移动时，像总是以相反方向移动。 通过球心的光线沿原光路反射。 反射球面镜的焦距等于球面半径的1/2。
3、角放大率g
g
u l n n' l n 1 u l n' nl n' b
n
ag b
n
h
I
nuy nuy J
单折射球面光学系统 拉赫不变量
I
y
U
o

U
r
l'
y
-l
7
共轴球面光学系统
结论：
1.

b是有符号数，具体表现为
成像正倒：当b>0时，表明y’、y同号，成正像；否则，成倒像。 成像大小：当|b|＝1时，表明|y’|=|y|，像、物大小一致；|b|>1时， 表明|y’|>|y|，成放大的像；反之，成缩小的像。 成像虚实：当b>0时，表明l’、l同号，物像同侧，虚实相反；否 则，物像异侧，虚实相同。

球面和共轴球面系统培训课件

球面和共轴球面系统培训课件
物体位于有限 远处
三角形AEC中应用正弦定律有： sin I sin(U )
rL
r
由此推出入射角I公式：sin I L r sinU r
再由折射定律可以求得折射角I '的公式：sin I ' n sin I n'
由图可知：＝U I U ' I ', 所以有：U ' U I I '
在三角形A ' EC使用正弦定律得： sin I ' sinU '
L ' r
r
则像方截距为： L ' r r sin I ' sinU '
2.1.2 实际光线经过单个折射球面 旳光路计算公式
当物在无限远时， L = −∞，设一条光 线平行于光轴入射，入射高度为，则 有：
物体位于无限远 处
2.1.2 实际光线经过单个折射球面 旳光路计算公式
❖ 由上面提供旳公式，我们能够由已知旳L和U求出L’和 U’。
❖ 1）求高斯像面旳位置； ❖ 2）在平面上刻十字，问其共轭像在什么位
置；
❖ 3）当入射高度为h=10mm，问光线旳像方 截距是多少？和高斯像面相比相差多少？ 阐明什么问题？
2.3 共轴球面系统
单个折射球面不能作为一种基本成像元件 （反射镜例外，能够单面成像），基本成像元件 是至少两个球面或非球面所构成旳透镜。大部分 透镜都由球面构成，加工以便，成本降低。
❖ 课后习题： 2.2、2.3、2.4、2.5、2.6、2.7、2.8、
2.9 。
2、
n ' u '- nu n ' n h
r
该公式表达近轴光折射前后旳孔径角u和u’之间旳关系。

共轴球面光学系统特点

共轴球面光学系统特点

共轴球面光学系统特点
共轴球面光学系统是一种采用球面反射镜的光学系统，它由一个球面
反射镜和一个准直物镜组成，它可以聚焦起一束高度集中的光束来实现观
测或其他应用目的。

共轴球面光学系统能够提供高度集中的光束，使其能
够在极短的像差范围内获得高质量的图像，在科学、工业、医学、检测等
领域有着广泛的应用。

其主要特点有：
1、透射特性卓越：由于共轴球面光学系统采用的球面反射镜是镀铬
或钎焊的，具有良好的光学性能，其较高的反射率可以使光的各种波长的
透射率都达到较高的水平。

2、聚焦效果好：由于共轴球面光学系统采用的设计原理是根据透镜
来实现聚焦，因此可以较好的实现视野的高度放大，使其能够有效聚焦。

3、维护方便：共轴球面光学系统采用的是球面反射镜，它只需要定
期清洁即可，而且它没有润滑要求，所以维护非常方便。

4、耐用性强：共轴球面光学系统采用的是优质的、耐用的球面反射镜，可以保证长期使用的稳定性，耐用性也很强。

5、体积小：共轴球面光学系统采用的是非折射性镜片，所以体积小，可以更容易地应用于有空间限制的系统中。

第二章球面和共轴球面系统分析

第二章球面和共轴球面系统分析
要讨论成像规律，即像的虚实，成像的位置、正倒和大 小问题，必须计算出光线的走向，所以我们先讨论计算公式。 光线经过单个折射球面的情况如图所示。 包含光轴和物点的平面称为含轴面（纸面）或子午面。 计算的目的：光从何处来，经何处到哪里去（由此得出由物 点发出的光线经过系统后能否交到一点完善成像）？
首要问题：用什么量（怎样）来决定光线在空间中的位置？
对AEC应用正弦定理得 L r r Lr 即 sin I sin U 可求出I sin I sin （ U） r n 据折射定律 sin I ` sin I 可求出I ` n` 对AEC和A`EC应用外角定理 U I U ` I ` U ` U I I ` 可得到U ` sin I ' sin U ' sin I 在A ' EC中 ，利用正弦定律 L ' rr L ' r r sin U
从光轴起算，光轴转向光线（按锐角方向）， 顺时针为正，逆时针为负。
入射角、折射角 从光线起算，光线转向法线（按锐角方向）， 顺时针为正，逆时针为负。 ③ 光轴与法线的夹角（如） 从光轴起算，光轴转向法线（按锐角方向）， 顺时针为正，逆时针为负。
二、实际光线经过单个折射球面的光路计算
已知：折射球面曲率半径r，介质折射率n和n′，及物方坐标L和U。 求：像方L ′和 U ′。
共轴球面系统由许多单个球面构成，当计算出第一面后， 其折射光线就是第二面的入射光线。
U 2 U1; L2 L1 d1
再由相邻两折射球面间的关系，求出下一个球面的折 射光线。
第四节 球面反射镜成像
n n n n 成像公式： l l r

n n
1 1 2 l l r

球面与共轴球面系统

球面与共轴球面系统
y l r n l
y l r n l
说明：a) β取决于n、 n′、l′、l b) β> 0，l 、l′同号，物象同侧，虚实相反 β< 0，l 、l′异号，物象异侧，虚实相同 c) β> 0，成正象 β< 0，成倒象 d) β> 1，成放大象 β< 1，成缩小象
2. 轴向放大率：光轴上一对共轭点沿轴移动量之间的比值
§ 2－3 共轴球面系统
探讨方法：将光线的光路计算公式及放大率公式反复应用于各个 折射面，分别求出各面的u、 u′、l 、 l′、Q、Q ′、β、α、γ、 y、y′J、J′。 转面公式— 前后相邻面之间的基本量的转化关系。 主要内容：1、结构参量；
sin I L r sin U r
sin I n sin I n
U U I I
L r r sin I sin U
（点成象）
小结：
5、近轴光计算公式：
i lru r
i n i n
u u i i
l r r i u
6、四个常用的推导公式：
h lu lu
Q n(1 1) n(1 1 )
3、四线：截距：顶点到光线与光轴交点的距离（L、L′－物方截距、 象方截距）；r－球面曲率半径； h－入射高度；
4、界面：n 、n′－物象方空间折射率；OE－折射球面 。
三、 符号法则（线段和角度，便于统一计算）
1、线段：规定光线从左向右传播 a）沿轴线段 L、L′、r、d
以O为原点， 与光线传播方向相同，为“＋” 与光线传播方向相反，为“－”
逆时针为“－” 夹角的优先级：“光轴－光线－法线” 3、所有参量是含符号的量，但图示标为参量的大小。
四、 远轴光的计算公式（实际光线光路计算）（点成象）

第二章共轴球面系统

第二章共轴球面系统
dx' x' α= = dx x
讨论: ① α恒为正,当物点沿轴向移动时,像点沿轴同 向移动 ②一般α≠ β,即空间物体成像后要变形,如正方 体. ③只有在dl 很小时才适用
3. 角放大率
共轭光线与光轴夹角u ′和u 的比值,称为角放大率.
B' K B K'
H
A F
H'
F'
A'
对共轴理想光学系统性质第三点的解释: 一个共轴理想光学系统,如果已知两对共轭面的位置和放 大率,或者一对共轭面的位置和放大率,以及轴上两对共 轭点的位置,则其他一切物点的像点都可以根据这些已知 的共轭面和点确定
§2.8 理想光学系统的物像关系式
I I' B'
2.近轴光路计算公式 在近轴几何光学中,经常用到以下近似公式(一 级泰勒展开)
sin U ≈ U ≈ tan U
1 1 (sin θ = θ θ 3 + θ 5 ......) 3! 5!
U为物方孔径角,是个很小值(<<1rad),当 U<5°,近似代替误差大约为1%.
代入到(2-1)-(2-3),并用小写字母表示,得到以下公式:
dl ′ α = dl
(1)高斯公式求解:
f' f + =1 l' l
f ' dl ' fdl '2 2 = 0 l l
fl ' α = 2 f 'l
dl ′ nl ′2 n′ 2 = 2 = β α= dl n′l n
2
(2)牛顿公式求解:
xx' = ff '
xdx'+ x' dx = 0

包装印刷印刷光学之共轴球面光学系统培训课件

包装印刷印刷光学之共轴球面光学系统培训课件

像方孔径角 u i u i
像方截距
l r r i u
在近轴光路中，l´不随u角改变而改变。
高斯像
物点发出的一束细光束，经折射后交于 一点，成完善像，称为高斯像。
高斯像的位置由l´决定，通过高斯像点
垂直于光轴的相面，称为高斯相面。构 成物像关系的这对点成为共轭点。
近轴光学校对公式： h lu lu
天生我材必有用，千金散尽还复来。06:01:2406:01: 2406:0112/12/2020 6:01:24 AM
安全象只弓，不拉它就松，要想保安 全，常 把弓弦 绷。20.12.1206:01:2406:01Dec-2012-Dec-20
得道多助失道寡助，掌控人心方位上 。06:01:2406: 01:2406:01Sat urday, December 12, 2020
完善像
某一物点发出球面波，与之对应的是一束以该 物点为中心的同心光束，若经过光学系统之后 仍为球面波，那对应的光束仍为同心光束，称 该同心光束的中心为该物点经光学系统所成的 完善像。
物体可以看称有无数物点组成，那么物体上每 一个点经过光学系统所成的完善像点的集合就 是该物体经光学系统后所成的完善像。
安全在于心细，事故出在麻痹。20.12.1220.12.1206: 01:2406:01:24Decem ber 12, 2020
加强自身建设，增强个人的休养。2020年12月12日 上午6时 1分20.12.1220.12.12
扩展市场，开发未来，实现现在。2020年12月12日 星期六 上午6时 1分24秒06:01:2420.12.12
当β>0时，由于y’和y同号，成正像。此时l’和
l也同号，即物和像在球面的同一侧，若物为实 物，则像为虚像，物为虚物则像为实像。

共轴球面系统主平面和焦点位置的计算

共轴球面系统主平面和焦点位置的计算

共轴球面系统是一种通过两个球面透镜组合在一起形成的光学系统。

在共轴球面系统中，两个球面透镜的曲率半径和相对位置都对系统的成像性能产生重要影响。

本文将重点讨论共轴球面系统中主平面和焦点位置的计算方法。

一、共轴球面系统主平面的计算在共轴球面系统中，由于两个球面透镜的共轴排列，主平面的计算相对较为复杂。

在实际计算中，可以采用以下步骤进行推导和计算：1. 根据两个球面透镜的曲率半径R1和R2，以及两个球面透镜的相对位置d，首先计算出两个球面透镜之间的等效焦距Feq。

等效焦距Feq的计算公式为：Feq = (R1 * R2) / ((n - 1) * d)其中，n为介质的折射率。

2. 接下来，根据等效焦距Feq和两个球面透镜的位置，计算出主平面的位置H。

主平面的位置H的计算公式为：H = d * (Feq - (R1 + R2)) / Feq3. 根据主平面的位置H和两个球面透镜的位置，计算出主平面的曲率半径R。

主平面的曲率半径R的计算公式为：R = Feq * (1 + (H / d))通过以上步骤的计算，可以得到共轴球面系统中主平面的位置和曲率半径，为系统的设计和分析提供了重要的参数。

二、共轴球面系统焦点位置的计算在共轴球面系统中，焦点位置的计算也是系统设计和分析中的重要一环。

在实际计算中，可以采用以下步骤进行推导和计算：1. 根据两个球面透镜的曲率半径R1和R2，以及两个球面透镜的相对位置d，计算出系统的等效焦距。

系统的等效焦距F的计算公式为：F = (R1 * R2) / ((n - 1) * d)2. 根据等效焦距F和两个球面透镜的位置，计算出系统的合焦位置。

系统的合焦位置的计算公式为：S = F * (1 - (d / Feq))通过以上步骤的计算，可以得到共轴球面系统的焦点位置，为系统的成像性能和光学设计提供了重要的参数。

结论共轴球面系统的主平面和焦点位置的计算是系统设计和分析中的关键步骤。

工程光学第二章知识点

工程光学第二章知识点

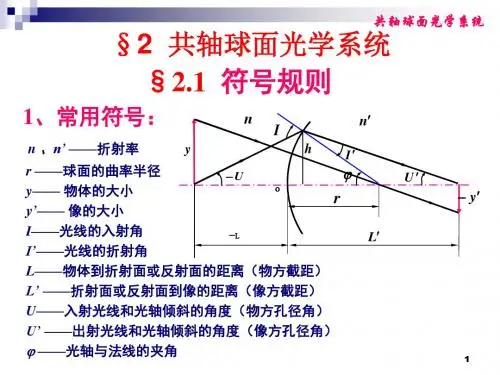
第二章共轴球面光学系统第一节符号规则●常见的光学系统有多个光学零件组成，每个光学零件往往由多个球面组成●这些球面的球心在一条直线上即为“共轴球面系统”●这条直线称为“光轴”●折射球面的结构参数：曲率半径r、物方折射率n、像方折射率n'●入射光线的参数：物方截距L、物方孔径角U●像方量在相应的物方量字母旁加“ ’ ”区分●光线的传播方向为自左向右●规定符号规则如下：●1）沿轴线段（如L、L’和r）●以顶点为原点，与光线方向相同为正，相反为负●2）垂轴线段（如h、y和y’）●以光轴为基准，光轴以上为正，以下为负●3）光线与光轴的夹角（如U、U’）●光轴转向光线；角量均以锐角计、顺时针为正、逆时针为负●4）光线与法线的夹角（如I、I’、I”）●光线转向法线●5）光轴与法线的夹角（如φ）●光轴转向法线●6）折射面间隔d●前一面顶点到后一面顶点，与光线方向相同为正，相反为负；在折射系统中，d恒为正●物方截距、像方截距、物方孔径角、像方孔径角等物理量是可以有正负的，但作为几何量AO、OA’、∠EAO、∠EA’O等应为正值；在负值物理量前加负号，以保证相应几何量为正●根据物像的位置判断物像的虚实●负（正）物距对应实（虚）物●正（负）像距对应实（虚）像第二节物体经过单个折射球面的成像1，单球面成像的光路计算已知折射球面的结构参数曲率半径r ，物方折射率n ，像方折射率n ’已知入射光线AE 的参数物方截距L ，物方孔径角U （轴上物点）求出射光线参数像方截距L ’，像方孔径角U ’（轴上像点）光路计算2在ΔAEC 中用正弦定律，有 sin sin()I U r L r -=-导出求入射角I 的公式sin sin L r I U r -=（2-1）由折射定律可以求得折射角I ’sin sin n I I n '=='（2-2）由角度关系，可以求得像方孔径角U ’U U I I ''=+-（2-3） 在ΔA ’EC 中应用正弦定律，得像方截距L ’ sin sin I L r r U ''=+' （2-4）式（2-1）至（2-4）就是子午面内实际光线的光路计算公式，利用这组公式可以由已知的L 和U 求L ’和U ’ sin sin L r I U r -= sin sin n I I n '=='U U I I ''=+-sin sin I L r r U ''=+'当物点A 位于轴上无限远处时，相应的L=∞，U=0，则式（2-1）须改变为sin hI r =（2-5）●若L 是定值，L ’是U 的函数，即从同一点发出的光线，孔径角不同，将在像方交在不同的点上 ● 同心光束经过单球面后不再是同心光束●这种误差被称为“球差” ●球差是各种像差中最常见的一种●如果把孔径角U 限制在很小的范围内，光线距光轴很近，称为“近轴光”，U 、U ’、I 和I ’都很小，式（2-1）~（2-4）中的正弦值用弧度来表示 ● 用小写字母u 、u ’、i 、i ’、l 和l ’表示近轴量● l r i u r n ii n u u i i i l r r u -='='''=+-''=+'（2-6）~（2-9） ● 当入射光线平行于光轴时，也以h 作为入射光线的参数，有●h i r =（2-10） ●近轴光线l ’与u 无关，即当物点位置确定后，其像点位置与孔径角u 无关，物点发出的同心光束经折射后在近轴区仍为同心光束 ●在近轴区成的是完善像，这个完善像通常称为“高斯像” ● 近轴区最常用的物像位置公式●n n n n l l r ''--='（2-14） ●已知物点位置l 求像点位置l ’时（或反过来）十分方便 ●1、轴上物点：轴上同一物点发出的近轴光线，经过球面折射以后聚交一点，即轴上物点近轴成像时是符合理想成像条件的。

共轴球面光学系统

共轴球面光学系统

作业－§7.4共轴球面光学系统
1 7-7
2 已知一透镜的结构参数如下(单位mm)：r1＝ 10，r2＝－25，d＝7，n1＝1.0，n1'＝n2＝ 1.5163，n2'＝1.0，在光轴上距透镜前顶点L1 ＝-140mm处有一点光源，求(1)U＝－10的光 路； (2)在近轴近似下，试求该光源的像点的 位置。
n1 n1' n2 n2'
nm nm'
y1
r1
-r2
A
o1 -y1' -y2 o2
rm
///
om
-ym'
d1
d2
dm
-l1
l1'
-l2
l2'
-lm lm'
－ 一、转面公式－公式 共轴球面光学系统
• 转面公式
(1) 光学系统参量 折射率： n2＝n1' ，n3＝n2' ，……，nm＝n' m－1 。 (2) 光线参数 孔径角： u2＝u1' ，u3＝u2' ，……，um＝u' m－1。 (3) 物像参量
U'=I+U-I'
Lm'【L'】 Li+1=Li'－di
+ －
UIIiii'
Ui'
U1'
U2'
Um'【U'】
2、近轴区光路计算列表－共轴球面光学系统
球面1(i=1) 球面2 (i=2) 球面i 球面k (i=m)
ni
ni’
ri
Di
－ × ÷
li－rurliiii ri
× ÷

第二章-共轴光学系统

第二章-共轴光学系统
物点参数为 (l1,u1, y1)
（1）对第一面做单个球面成像计算求得 (l1,u1, y1)
（2）用过渡公式由 (l1,u1, y1) 求得 (l2,u2, y2 ) （3）对第二面做单个球面成像计算求得 (l2 ,u2 , y2 )
……
（4）对第K面做单个球面成像计算求得(lk ,uk , yk )
I I '也U非' 常小。
sin x x x 为弧度值
用弧度值代替正弦值
u ~ sinU i ~ sin I l~L
u'~ sinU ' i ~ sin I l'~ L'
（2－1）～（2－4）式变为：
i (l r)u / r i n i / n u u i i l r r i/ u
处，如下图所示。
试求：像距、像高和垂轴放大率。
C
A
O
§2.4 共轴球面系统的成像
过渡公式luny2222l1uny111,,,undy3313,l3uny222l2d2 h2 h1 d1u1, h3 h2 d2u2
K个折（反）射面，系统参数为 r1, r2 , rk ; n1, n2 , nk1; d1, d2 dk1
dl
利用（2-14）式
n n n n l l r
对其求导
ndl l2
ndl l2
0
dl dl
nl2 nl 2
dl n (nl)2 n 2
dl n nl n
由上式可见：
n n
2
0
所以物和像同方向移动。
且一般： （除非 、1 n ） n
提问：立方体成像还是立方体吗？
③、角放大率
sin(180o I ) sin(U )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

C2
C1
C4
C3
光轴
2、光学系统的物
(1)物点 实物点：入射光线的会聚点;
虚物点：入射光线延长线的会聚点。 (2)物: 物点的集合。 实物：实物点的集合。 ——可以人为设置
虚物：虚物点的集合。——可由光学系统给出 (3)物平面：在光轴光学系统中，经过物点垂直光轴的平面称为物平 面。 (4)物空间：经光学系统成像以前的整个空间。 B A
在几何光学中，发光点被抽象为一个既无体积又无 大小的几何点，任何被成像的物体都是由无数个这样的 发光点所组成。
在几何光学中，光线被抽象为既无直径又无体积 的几何线。它的方向代表光线的传播方向即光能的传 播方向。 在各向同性介质中，光沿着波面的法线方向传播， 可以认为光波波面法线就是几何光学中的光线，与波 面对应的法线束称为光束。
A
B
这就是费马原理的数学表达式。
说明: 该处极值可以是极大值、极小值或常值.
任何一条实际的光路，其光程有一个共同的特 点，即它均满足极值条件。亦即，或者是所有光程 可能值中的极小值，或者是所有光程可能值中的极 大值，或者是某一稳定值。
5、马吕斯(Malus)定律－几何光学的基本定律
1’ A B C 1 2
2、光的独立传播定律 从不同光源发出的光线，以不同的方向通过介质 某点时，各光线彼此不影响，好像其它光线不存在 似的独立传播，这就是光的独立传播定律。
3、光的折射定律和反射定律 当光在传播中遇到两种不同介质的光滑界面时， 光线将发生折射和反射，其继续传播的规律遵循折射 定律和虑角量的符号规定。
平面波对应于平行光束；球面波对应于会聚或发 散光束；其光线既不相交于一点，又不平行所对应的 光束称为像散光束。如图所示。
几何光学中的传播规律和成像原理，是用光线的传 播途径加以表示的，光线的这种传播途径称为光路。
二、几何光学的基本定律 1、光的直线传播定律
在各向同性的均匀介质中，光线按直线传播， 这就是光的直线传播定律。--只有光在均匀介质中无 阻拦地传播时才成立。
3
光 学 系 统
Malus定律的解释图
A’ 2’ 3’ B’ C’
p1
p2
(1)内容
垂直于入射波面的入射光束，经过任意次的反射和折 射后，出射光束仍然垂直于出射波面，并且在入射波面和出 射波面间所有光路的光程相等。
(2)数学表示

A'
A
nds nds nds c
B C
B'
C'
三、物像的基本概念
理论都可以得到较满意的近似结果。
第一节
几何光学的基本定律
一、波面、光线和光束 光波是横波，在各向同性介质中，其电场的振动 方向与传播方向垂直，振动相位相同的各点在某时刻 所形成的曲面称为波面。 波面可以是平面、球面或其它曲面。 当发光体（光源）的大小和其辐射能的作用距离相 比可以忽略不计时，该发光体称为发光点或点光源。
四、费马原理
(1) 光程
指光在介质中经过的几何路径和介质折射率的 乘积，以字母L表示。 均匀介质中：L＝n×s
其中n为介质的折射率，s为光经过的几何路径。
光程
非均匀介质中
L n( s)ds
A
B
光程为光在介质中传播的时间和真空中光速的乘积.
L n(s)ds cds / v(s) cdt ct
应用光学
第五章 几何光学基础
在许多实际的光学工程应用中，由于光的频率 很高（10-14Hz），波长很短（10-7m），光的传输特 性可以利用波长趋于零的极限情况近似，这就是几 何光学处理光传输特性的基本思想。因此，可以认
为几何光学是波动光学在波长趋于零时的极限。
对于大多数光学工程技术问题，应用几何光学
1
2 A
B
3、光学系统的完善像
(1)像点 同心光束经光学系统后仍为同心光束，该同心光束的会 聚点。 实像点：出射光线的会聚点;
虚像点：出射光线反向延长线的会聚点。 (2)像: 像点的集合。 实像：实像点的集合。 ——可以用屏接收 虚像：虚像点的集合。——只可以观察
(3)像平面：经过像点垂直光轴的平面称为像平面。
如图，按照角度符号法
I
I
n
规的规定： 入射角和折射角均应以锐角 来量度，由光线沿锐角转向法线， 顺时针转成的角为正，反之为负。
I
n
反射和折射定律
折射定律
n sin I n sin I
如图，根据角度符 号法规的规定
I I
三、全反射现象 当光线由光密介质进入光疏介质时，当入射角大 于由两种介质折射率所决定的临界角时，光线将完全 被界面反射回来，这就是全反射。
A A tA
B
B
tB
(2) Fermat原理内容 费马原理指出：光线从A点到B点，是沿着光程 为极值的路径传播的。也就是说，光由A点到B点的 传播在几何方面存在着无数条可能的路径，每条路径 都对应着一个光程值，光由A点传播到B点的实际光 路包含在这些可能的路径之中。
数学表示：
L n( s)ds 0
使用光学仪器，离不开物像的基本概念，物体通 过光学系统(由基本的光学元件构成的系统)成像，所 成的像由人眼接收，这就是人们使用光学仪器的一般 过程。 光学系统由一系列的光学零件所组成。
常见的光学零件有：
透镜、棱镜、平行平板和反射镜等，其截面如图
所示。
1、共轴球面光学系统
(1) 球面光学系统：各光学元件表面均为球面或者平 面的光学系统。 (2) 共轴球面光学系统：球面光学系统中，各光学元 件表面的曲率中心在同一直线上的光学系统。 (3) 光轴：共轴球面光学系统中各光学元件表面的曲 率中心所在的直线。 (4) 子午面：共轴球面光学系统中，通过光轴的平面。
(4)像空间：经光学系统成像以后的整个空间。 B A B’2 1 A’1
B
A
2
A’2 B’1
4、光学系统成完善像的条件
从物点到像点的所有光路等光程
LAA' LAp1 Lp1 p 2 Lp 2 A'
p1 p2
A
A’
1
1
1
5、物点成完善像的界面方法
设置单一的反射或折射界面，一般可以对定点实现成完善像。 (1) 无限距离的物点反射成实像点 抛物面将无限距离的物点反射成有限距离的实(虚)像点 (2)有限距离的实物点反射成有限距离的实像点 椭球面将有限距离的实(虚)物点反射成有限距离的实(虚)像点 (3)有限距离的实物点反射成有限距离的虚像点 双曲面将有限距离的实(虚)物点反射成有限距离的虚(实)像点