半导体物理第七章作业答案

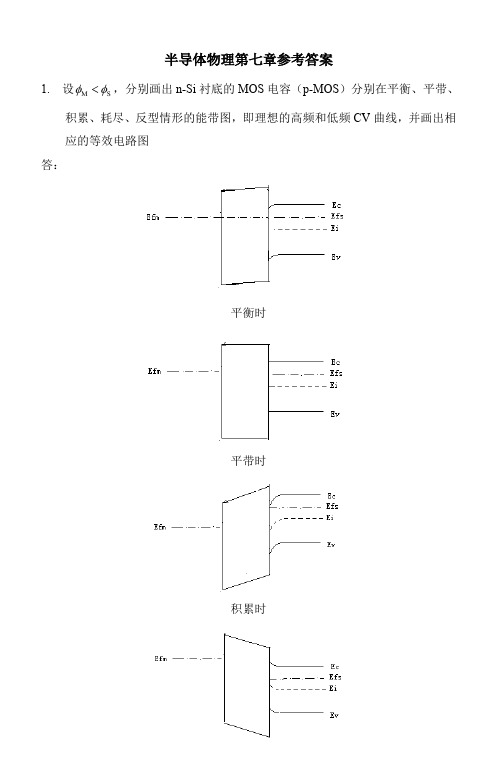
半导体物理第七章参考答案1. 设M S φφ<，分别画出n-Si 衬底的MOS 电容（p-MOS ）分别在平衡、平带、积累、耗尽、反型情形的能带图，即理想的高频和低频CV 曲线，并画出相应的等效电路图 答：平衡时平带时积累时耗尽时弱反时强反时理想的高频和低频CV曲线等效电路图2. 设氧化层厚度为1μm 的Si MOS 结构的p 型衬底的掺杂浓度分别为N ＝1015/cm 3和1016/cm 3，比较这两种结构的耗尽层电容和MOS 电容的极小值。

答：1) 耗尽层电容由耗尽层厚度决定，而耗尽层厚度与Si 表面势有关，根据耗尽层厚度、表面势，可求得耗尽层电容为：()d Sid sdd Q C d W εψ-==又由MOS 电容为氧化层电容与耗尽层电容串联而成：dox C C C 111+= 以及栅压方程：g fb s oxV V ψ-=消去表面势s ψ，可得：C =显然，相同氧化层厚度，即相同氧化层电容，相同栅压下，衬底掺杂浓度高的MOS 结构耗尽层电容大。

2) 由C =MOS 电容的极小值出现在强反型时，此时耗尽层厚度最大，表面势为2B φ：max d W ==min maxSid d C W ε==则：1minmin 11ox d C C C -⎛⎫=+ ⎪⎝⎭当N ＝1015/cm 3时，12min min 1126.7ox d C F m C C μ-⎛⎫=+= ⎪⎝⎭当N ＝1016/cm 3时，12min min 1131.3ox d C F m C C μ-⎛⎫=+= ⎪⎝⎭3. 从物理上说明F B i C C 随氧化层厚度及掺杂浓度的变化趋势，并计算315/10cm N =，nm t ox 10=的Si MOS 结构的FB i C C 值和德拜长度。

答：由公式：11ox D FB i Si ox t L C C εε=+=+有：11FB D i iSi C L C C ε==+ 其中oxi oxC t ε=。

半导体物理与器件上海电子信息职业技术学院智慧树知到答案2024年第一章测试1.半导体材料的导电性能介于金属材料和绝缘材料之间。

（）A:对 B:错答案:A2.电中性原子失去电子后带正电。

（）A:错 B:对答案:B3.半导体硫化银的电阻具有负的温度系数是因为？（）A:当硫化银受热时产生了更多的电子参与定向运动 B:当硫化银受热时产生了更少的电子参与定向运动答案:A4.常温下，半导体材料的电阻率在什么范围？（）A:＞1010Ω·cm B:10-3Ω·cm ~ 109Ω·cm C:＞109Ω·cm D:＜10-3Ω·cm答案:B5.是谁首先提出：将电、磁、光统归为电磁场现象的麦克斯韦方程组？（）A:奥斯特 B:安培 C:麦克斯韦 D:赫兹答案:C第二章测试1.中子是带正电的。

（）A:错 B:对答案:A2.中子是带负电的。

（）A:错 B:对答案:A3.核外的电子是分布在能量的轨道上的（）A:连续 B:不连续答案:B4.核外电子的能量是被量子化的，每份能量的大小由公式hυ确定，h是，υ表示。

（）A:普朗克常量，波的频率 B:波的频率，普朗克常量答案:A5.一个主量子数是不能精确确定电子的轨道的，每个轨道里面还可以再细分，即还有分壳层，它用表示的。

（）A:字母，例如s，p，d，… B:数字，例如1，2，3，…答案:A第三章测试1.N型半导体主要靠自由电子运动导电，也称为电子半导体。

（）A:对 B:错答案:A2.P型半导体主要靠空穴运动导电，也称为空穴半导体。

（）A:对 B:错答案:A3.PN结中载流子的运动是这样的：P型半导体中的多子空穴向N区扩散，留下不可移动的负离子；N型半导体的多子电子向P区扩散，留下不可移动的正离子。

（）A:错 B:对答案:B4.在硅或锗的晶体中掺入少量的5 价杂质元素，如磷、锑、砷等，可以构成。

（）A:P型半导体 B:N型半导体答案:B5.在硅或锗的晶体中掺入少量的3 价杂质元素，如硼、镓、铟等，可以构成。

半导体物理学第七版完整答案修订版IBMT standardization office【IBMT5AB-IBMT08-IBMT2C-ZZT18】第一章习题1．设晶格常数为a 的一维晶格，导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为：E C （K ）=0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ （1）禁带宽度;（2）导带底电子有效质量;（3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化解：（1）2. 晶格常数为0.25nm 的一维晶格，当外加102V/m ，107 V/m 的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：tkhqE f ∆∆== 得qE k t -∆=∆补充题1分别计算Si （100），（110），（111）面每平方厘米内的原子个数，即原子面密度（提示：先画出各晶面内原子的位置和分布图）Si 在（100），（110）和（111）面上的原子分布如图1所示：（a ）(100)晶面 （b ）(110)晶面（c ）(111)晶面补充题2一维晶体的电子能带可写为)2cos 81cos 87()22ka ka ma k E +-=（， 式中a 为 晶格常数，试求（1）布里渊区边界；（2）能带宽度；（3）电子在波矢k 状态时的速度；（4）能带底部电子的有效质量*n m ；（5）能带顶部空穴的有效质量*p m解：（1）由0)(=dk k dE 得 an k π= （n=0，?1，?2…）进一步分析an k π)12(+= ，E （k ）有极大值，ank π2=时，E （k ）有极小值所以布里渊区边界为an k π)12(+=(2)能带宽度为222)()mak E k E MINMAX =-（ (3）电子在波矢k 状态的速度)2sin 41(sin 1ka ka ma dk dE v -==（4）电子的有效质量能带底部 an k π2=所以m m n2*= (5)能带顶部 an k π)12(+=， 且**n p m m -=，所以能带顶部空穴的有效质量32*mm p =半导体物理第2章习题1. 实际半导体与理想半导体间的主要区别是什么答：（1）理想半导体：假设晶格原子严格按周期性排列并静止在格点位置上，实际半导体中原子不是静止的，而是在其平衡位置附近振动。

第 1 页第一章 半导体中的电子状态1. 设晶格常数为 a 的一维晶格，导带极小值附近能量 E c （k ）和价带极大值附近 能量 E v （k ）分别为：E c (k)=2 2h k + 3m 02h (k − m 0k1) 2和 E v (k)= 2 2h k － 6m 0322h k ； m 0m 0为电子惯性质量，k 1＝1/2a ；a ＝0.314nm 。

试求： ①禁带宽度；②导带底电子有效质量； ③价带顶电子有效质量；④价带顶电子跃迁到导带底时准动量的变化。

[解] ①禁带宽度 Eg22h k − k ＝0；可求出对应导带能量极小值 E min的 k 值：根据 dEc (k ) ＝2h k ＋2( dk 3m 0m 03 ，1 )k min＝ k 14由题中 E C式可得：E min＝E C(K)|k=k min=h k 2；m 401 由题中 E V式可看出，对应价带能量极大值 Emax 的 k 值为：k max＝0；2 2 2h 2并且 E min＝E V(k)|k=k max＝k ；∴Eg ＝E min－E max＝hk 1＝ h 21 6m 12m48m a 20 −27 20 0＝×−28× (6.62 ×10) −8 2 ×× −11＝0.64eV48 × 9.1 10(3.14 ×10 1.6 10②导带底电子有效质量 m n22 2 22d E C= 2h + 2h = 8h ；∴ m n＝ h2 / d E C =3 m 0dk 23m 0 m 0 3m 0dk 28 ③价带顶电子有效质量 m ’222d E V= −6h'=，∴ mh2/ d E V= − 1 mdk 2m 0ndk 2 6 0④准动量的改变量h△k ＝ h (k min-k max)=3 4h k1=3h 8a2. 晶格常数为 0.25nm 的一维晶格，当外加 102V/m ，107V/m 的电场时，试分别 计算电子自能带底运动到能带顶所需的时间。

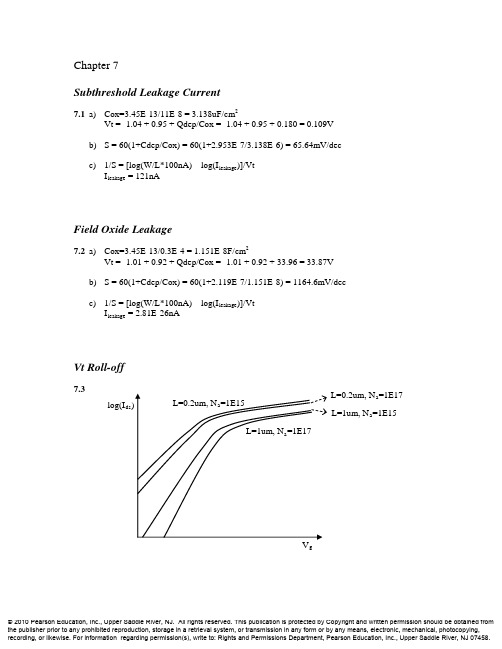
第一章习题1．设晶格常数为a 的一维晶格，导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为：E c =0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ （1）禁带宽度;（2） 导带底电子有效质量; （3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化 解：（1）2. 晶格常数为0.25nm 的一维晶格，当外加102V/m ，107 V/m 的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：tkh qE f ∆∆== 得qE k t -∆=∆η补充题1分别计算Si （100），（110），（111）面每平方厘米内的原子个数，即原子面密度（提示：先画出各晶面内原子的位置和分布图）Si 在（100），（110）和（111）面上的原子分布如图1所示： （a ）(100)晶面 （b ）(110)晶面（c ）(111)晶面补充题2一维晶体的电子能带可写为)2cos 81cos 87()22ka ka ma k E +-=η（， 式中a 为 晶格常数，试求（1）布里渊区边界； （2）能带宽度；（3）电子在波矢k 状态时的速度；（4）能带底部电子的有效质量*n m ；（5）能带顶部空穴的有效质量*p m解：（1）由0)(=dk k dE 得 an k π=（n=0，±1，±2…） 进一步分析an k π)12(+= ，E （k ）有极大值，ank π2=时，E （k ）有极小值所以布里渊区边界为an k π)12(+=(2)能带宽度为222)()ma k E k E MIN MAX η=-（ (3）电子在波矢k 状态的速度)2sin 41(sin 1ka ka ma dk dE v -==ηη （4）电子的有效质量 能带底部 an k π2=所以m m n2*= (5)能带顶部 an k π)12(+=， 且**n p m m -=，所以能带顶部空穴的有效质量32*mm p =半导体物理第2章习题1. 实际半导体与理想半导体间的主要区别是什么？答：（1）理想半导体：假设晶格原子严格按周期性排列并静止在格点位置上，实际半导体中原子不是静止的，而是在其平衡位置附近振动。

第七章金属和半导体的接触1. 基本概念1）什么是金属的功函数？答：金属费米能级的电子逸出到真空中所需要的能量，即()m F m E E W −=0。

其中E 0：真空中电子的静止能量，(E F )m ：金属的费米能。

随着原子序数的递增，金属的功函数呈周期性变化。

2）什么是半导体的电子亲和能？答：半导体导带底的电子逸出到真空中所需要的能量，即C 0E E −=χ。

其中E 0：真空中电子的静止能量，E C ：半导体导带底的能量。

3）以金属-n 型半导体接触为例，如果金属的功函数大于半导体的功函数，即W m >W s ，则半导体表面的空间电荷、电场和表面势垒具有什么特点？如果W m >W s ，又如何呢？答：金属-n 型半导体接触，如果W m >W s ，电子从半导体流向金属。

半导体表面形成正的空间电荷区，电场方向由体内指向表面，形成表面势垒。

在势垒区，空间电荷主要由电离施主形成，电子浓度比体内低很多，为高阻区域，称为阻挡层。

如果W m <W s ，电子从金属流向半导体，势垒区电子浓度比体内大很多，为高电导区，称为反阻挡层。

4）什么是表面态对势垒的钉扎？答：表面态密度存在时，即使不与金属接触，表面也会形成势垒。

高的表面态密度，可以屏蔽金属接触的影响，使半导体势垒高度几乎与金属的功函数无关，即势垒高度被高的表面态密度钉扎（pinned ）5）为什么金属-n 型半导体接触器件具有整流作用？答：外加电压V ，如果使金属的电势升高，由于n 型半导体高阻挡层为高阻区，外压V 将主要降落在阻挡层，则势垒下降，电阻下降。

反之，如果金属的电势下降，则势垒增高，势垒区电子减少（多子），电阻更高。

因此阻挡层具有类似于pn 结的整流作用。

6）以金属-n 型半导体接触为例，写出势垒宽度大于电子的平均自由程时，其扩散电流密度与电压的关系。

与pn 结的电流密度-电压关系比较，各自具有什么相同和不同的特点？答：金属-n 型半导体接触，扩散电流为⎟⎟⎠⎞⎜⎜⎝⎛−=1kT qV sD e J J ，()T k qVr D D sD D e V V qN J 02/102−⎭⎬⎫⎩⎨⎧−=εεσ 与pn 结的电流密度-电压关系比较，二者均具有单向性的特征；所不同的是，金属-n 型半导体接触的反向电流随外加电压增加呈1/2次方增加，而pn 结的反向电流不随电压变化。

固体物理与半导体物理智慧树知到课后章节答案2023年下浙江大学浙江大学第一章测试1.半导体电阻率的范围通常为（）Ω·cmA:B:＞10C:D:＞＞10答案:2.半导体的特性包括（）A:导通特性B:温度敏感性C:光敏感性D:杂质敏感性答案:温度敏感性;光敏感性;杂质敏感性3.随着温度升高，半导体的电阻率一定升高（）答案:错4.半导体材料的电阻率，跨越了非常大的范围，使得我们能够通过各种效应来对它们进行调制，比如，我们可以通过掺杂改变半导体的电阻率（）A:对 B:错答案:对5.摩尔定律，是指单位面积的集成电路上晶体管数目，或者说集成电路的集成度，每18个月要增加一倍。

（）A:错 B:对答案:对第二章测试1.半导体材料最常见的晶体结构不包括（）A:纤锌矿型结构B:闪锌矿型结构C:金刚石型结构D:密堆积结构答案:密堆积结构2.描述晶体结构的最小体积重复单元的是（）A:原胞B:晶胞D:基矢答案:原胞3.正四面体的对称操作有（）个A:24B:32C:16D:8答案:244.晶体结构的基本特点不包括（）A:周期性B:重复性C:各向异性D:单一性答案:各向异性;单一性5.各向异性不是晶体的基本特性之一。

（）A:对 B:错答案:错第三章测试1.每个布里渊区的体积均相等，都等于倒格子（）的体积。

A:单胞B:原胞C:晶胞D:晶体答案:原胞2.周期性边界条件决定了电子的波矢K在第（）布里渊区内可取值数量与晶体的初基元胞数N相等。

A:三B:二C:四D:一答案:一3.布里渊区的特点不包括 ( )A:各个布里渊区的形状都不相同B:各布里渊区经过适当的平移，都可移到第一布里渊区且与之重合C:每个布里渊区的体积都不相等D:晶体结构的布喇菲格子虽然相同，但其布里渊区形状却不会相同答案:每个布里渊区的体积都不相等;晶体结构的布喇菲格子虽然相同，但其布里渊区形状却不会相同4.对于一定的布喇菲晶格，基矢的选择是不唯一的，但是对应的倒格子空间是唯一的。