第一章 作业答案
- 格式:doc
- 大小:132.00 KB
- 文档页数:5

第一章课后作业一、单项选择题1.下列各项中,表述不正确的是()。
A.经济法是一个新兴的法律部门B.经济法是市场经济进入垄断阶段以后产生的C.经济法为中国法律体系中的一个独立的法律部门D.与经济有关的法都是经济法2.下列各项中,属于宏观调控法的是()。
A.反垄断法B.反不正当竞争法C.金融法D.消费者保护法3.下列法的形式中,属于国家根本大法的是()。
A.《中华人民共和国全国人民代表大会组织法》B.《中华人民共和国立法法》C.《中华人民共和国宪法》D.《中华人民共和国刑法》4.下列各项中,属于行政法规制定主体的是()。
A.全国人大及其常委会B.国务院C.省、自治区、直辖市以及较大的市的人大及其常委会D.国务院的各部、委、行、署以及具有行政管理职能的直属机构5.下列各项,关于经济法主体的表述正确的是()。
A.经济法主体只能是组织,不能是个人B.经济法主体只能是立法机关或执法机关,不能是各类企业或非营利性组织C.同一主体可以因其参加不同的法律关系,成为多个法律领域的主体D.外国人不可能成为我国经济法的主体6.关于经济法主体资格的取得,下列说法中,不正确的是()。
A.经济法主体资格取得的法律依据具有差异性B.经济法主体资格的取得具有多源性C.受控主体和受制主体主要由民商法确定其资格D.经济法规范不可以限定受控主体和受制主体的主体资格或资质条件等7.下列经济法主体的行为中,不属于宏观调控行为的是()。
A.金融调控行为B.财税调控行为C.金融市场规制行为D.计划调控行为8.从经济法主体行为效果角度出发,可以将经济法主体的行为分为()。
A.单方行为和双方行为B.抽象行为和具体行为C.积极行为和消极行为D.自为行为和代理行为9.下列各项中,关于经济法主体权利和义务的表述,不正确的是()。
A.经济法主体的职权可以放弃B.经济法主体的权利可以放弃C.职权和权力都要依法行使D.职责和义务都要依法履行10.下列各项中,不属于经济法主体权利义务的特殊性的是()。

《⼤学化学》课后习题答案⼤全第⼀章课后作业答案1-4.判断下列⼏种说法是否正确,并说明理由。
(1)原⼦是化学变化中最⼩的微粒,它由原⼦核和核外电⼦组成;正确原⼦是化学变化中的最⼩粒⼦。
原⼦是由居于原⼦中⼼的原⼦核和核外电⼦构成,原⼦核⼜由质⼦和中⼦两种粒⼦构成的。
构成原⼦的基本粒⼦是电⼦、质⼦、中⼦。
(2)相对原⼦质量就是⼀个原⼦的质量;错误相对原⼦质量是指以⼀个碳-12原⼦质量的1/12作为标准,任何⼀个原⼦的真实质量与⼀个碳-12原⼦质量的1/12的⽐值。
(3)4g H2和4g O2所含分⼦数⽬相等;错误4g H2含有2mol氧⽓分⼦。
氢⽓相对分⼦质量2,4g/(2g/mol)=2mol。
4g O2含有0.125mol氧⽓分⼦。
氧⽓相对分⼦质量32,4g/(32g/mol)=0.125mol。
所以分⼦数⽬不相等。
(4)0.5mol的铁和0.5mol的铜所含原⼦数相等;正确铁和铜都是由原⼦构成的⾦属,摩尔是物质的量的单位,物质的量相同,即摩尔数相同,就表⽰原⼦数相同。
(5)物质的量就是物质的质量;错误物质的量:表⽰物质所含微粒数(N)(如:分⼦,原⼦等)与阿伏加德罗常数(NA)之⽐,即n=N/NA。
物质的量是⼀个物理量,它表⽰含有⼀定数⽬粒⼦的集体,符号为n。
物质的量的单位为摩尔,简称摩,符号为mol。
物质的质量:质量不随物体的形状和空间位置⽽改变,是物质的基本属性之⼀,通常⽤m表⽰物质的量=物质的质量/物质的摩尔质量(6)化合物的性质是元素性质的加合。
错误化合物的性质是由组成该化合物的微观结构决定的,例如CO和CO2,组成元素相同,性质却不同。
1-5.硫酸铵(NH4)2SO4、碳酸氢铵NH4HCO3和尿素CO(NH2)2三种化肥的含氮量各是多少?哪种肥效最⾼?答:①硫酸铵(NH4)2SO4,含氮量为(14*2)/(14*2+1*8+32*1+16*4)≈0.212②碳酸氢铵NH4HCO3,含氮量为14/(14+1*5+12+16*3)≈0.177③尿素CO(NH2)2,含氮量为(14*2)/(12+16+14*2+1*4)≈0.467综上,0.177<0.212<0.467,这三种肥料中,尿素的含氮量最⾼,所以尿素的肥效最⾼。

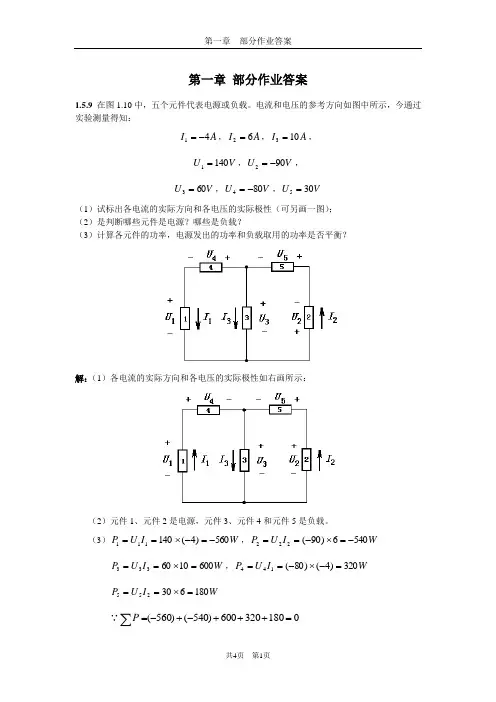
第一章 部分作业答案1.5.9 在图1.10中,五个元件代表电源或负载。
电流和电压的参考方向如图中所示,今通过实验测量得知:A I 41-=,A I 62=,A I 103=,V U 1401=,V U 902-=,V U 603=,V U 804-=,V U 305=(1)试标出各电流的实际方向和各电压的实际极性(可另画一图);(2)是判断哪些元件是电源?哪些是负载?(3)计算各元件的功率,电源发出的功率和负载取用的功率是否平衡?解:(1)各电流的实际方向和各电压的实际极性如右画所示:(2)元件1、元件2是电源,元件3、元件4和元件5是负载。
(3)W I U P 560)4(140111-=-⨯==,W I U P 5406)90(222-=⨯-==W I U P 6001060333=⨯==,W I U P 320)4()80(144=-⨯-==W I U P 180630255=⨯==∵0180320600)540()560(=+++-+-=∑P∴电源发出的功率和负载取用的功率平衡。
1.5.10 在图1.11中,已知mA I 31=,mA I 12=。
试确定电路元件3中的电流3I 和其两端电压3U ,并说明它是电源还是负载。
检验整个电路的功率是否平衡。
解:mA I I I 231123-=-=-=, V R I U U 60201802223=⨯-=-=元件3是电源mW I U P U 90330111=⨯==,mW I U P U 80180222-=⨯-=-= mW I U P 120)2(60333-=-⨯==,mW R I P R 9010321211=⨯== mW R I P R 2020122222=⨯==∵02090)120()80(90=++-+-+=∑P∴整个电路的功率平衡。
1.5.11 有一直流电源,其额定功率W P N 200=,额定电压V U N 50=,内阻Ω=5.0o R ,负载电阻R 可以调节,其电路如图1.5.1所示。

测量学作业第一次作业:第一章~第三章第一章作业1.测量学的基本任务是什么?答:确定地面点的点位。
2.测量工作中常采用哪几种基准面?各自定义和作用是什么?答:(1)大地水准面:由静止的海水面扩展延伸而形成的闭合曲面。
作用:测量外业工作的基准面。
(2)旋转椭球面:椭圆绕其短轴旋转而成的闭合曲面,其形状和大小可由长半径a,短半径b,以及扁率a ba-=α确定。
作用:精确确定地面点的点位的基准面。
(3)圆球面:计算精度要求不高时,近似代替椭球面进行计算的基准面。
作用:近似确定地面点的点位的基准面。
(4)水平面:小范围内(一般在R=10km),近似代替大地水准面进行计算的基准面。
作用:近似确定地面点的点位的基准面。
3.测量学里可以选用哪几种坐标系各自如何表示地面点的位置4.答: a) 地理坐标系:研究和测量整个地球的形状和大小,或进行大面积的测量工作时,可采用地理坐标系。
i.大地地理坐标系:用大地经度 L 和大地纬度B来表示。
ii.天文地理坐标系:用天文经度和天文纬度来表示。
b)平面直角坐标系:在R=10km的范围内,以水平面作为该区的基准面,直接将地面点沿铅垂线投影到水平面上。
c)高斯平面直角坐标系:以中央子午线的投影线为X轴,赤道的投影线为Y轴,两轴的交点为坐标原点O而建立起来的平面直角坐标系。
5.水准面是不是水平面在什么范围内可将水准面当作水平面处理为什么答:(1)水准面不是水平面。
水准面:由静止的海水面扩展延伸而形成的闭合曲面。
水平面:近似代替大地水准面进行计算的基准面。
(2)当测量的半径在10公里以内时,进行角度测量和距离测量时可用水平面代替水准面。
(3)原因:球面三角形化为平面三角形时每个角的球面角超影响为23/RP=''ε,P为平面三角形的面积,当三角形的边长为10km时,算得。
因此,在半径为10km的面积内进行普通测量时,水平面代替水准面所产生的水平角度误差可以忽略不计。
6.测定地面点位置的基本观测元素是什么?答:水平角、水平距离和高差(高程)是确定地面点空间位置的三个基本观测要素。

第一章法理学绪论1、法理学的研究对象是什么答:法理学的研究对象是法和全部法律现象的共同发展规律及其规律性,特别是社会主义法的基本问题,主要包括:一法律的起源、发展和消亡二法律的本质和作用三法律和其他社会现象的关系四法律的创制和实现五法律的价值2、法理学的基本范畴和基本问题答:法理学基本问题主要包括3个:法律是什么法律应该是什么如何认识法律前2个问题是法律的本体论问题,后1个问题则是法律的认识论问题.3、法理学在法学体系的地位答:法理学在法学体系中占有特殊地位,即是法学的一般理论、基础理论和方法论.1法学的一般理论.法理学以“一般法”即整体法律现象为研究对象.所谓“一般法”,首先指法的整个领域或者说整个法律现实,即包括宪法、行政法、民法、经济法、刑法、诉讼法、国际法等在内的整个法律领域,以及现行法从制定到实施的全部过程.其次指古今中外一切法.2法学的基础理论.法理学的对象是一般法,但它的内容不是一般法的全部,而仅仅是包含在一般法中的普遍问题和根本问题.法理学属于法学知识体系的最高层次,担负着探讨法的普遍原理或最高原理,为各个部门法学和法史学提供理论根据和思想指导的任务.3法学的方法论.除作为法的一般理论和法学基础理论之外,法理学还是法学的方法论.法理学通过研究法学的方法,建立起科学的方法论体系,为整个法学研究提供方法论4、法理学的学习方法有哪些答:马克思主义哲学方法论原则;一般的科学方法;具体的科学方法;法学特有的研究方法.第二章法学研究、法学教育与法律职业1、20世纪西方法学的理论发展答:20世纪以来,随着殖民地的独立,法律出现了社会化的趋势,一系列社会、劳动、教育、经济等社会立法大量出现.这时期的法学理论也异彩纷呈,原来的自然法学派、社会法学派、分析法学派等法学流派出现了新的面目,与此同时,一些新的法学流派又随着政治、经济、社会的发展而诞生,如行为主义法学、存在主义法学、经济分析法学等.西方法学的发展经历了一个长期的发展过程,法学的发展与当时的社会经济、政治、文化等方面有着密切的联系.2、中国法学的未来展望答:改革开放以来,中国法理学经过了比较曲折的发展,形成了比较有自己特色的一门法律基础学科,预计将来会以更加蓬勃发展的态势向前迈进.一树立学科形象.大力进行法律人才的培养,树立法律至上的观念,让法理学真正成为一门社会科学,并形成自己的学术传统.二增强法理学的社会实践属性法律是社会实践很强的一门学科.法理学固然有其深厚的理论特色,但是,他必须与社会生活相联系,其理论应该建立在具体的社会实践的基础之上.三法学流派的逐渐生成.四与其他学科之间日益密切法学与其他社会科学的联系随着社会生活的日益复杂化而逐步加强.五法理学学科的国际化.随着国际间经济、政治、文化交流方面的日益加强,我国法理学与外国法律理论法理学、法哲学方面的学者的交往也日益密切.3、谈谈当前中国法学教育的现状答:法学教育之存乎,则法治益兴,国家益盛.可见,法学教育关乎法治立与兴,国家安与盛.在法治建设不断开展和深入,法律信仰逐渐萌生的新时代背景下,法学教育成为了这整个过程的关键词之一.我国法学教育发展至今,毋庸置疑,已经在诸如办学规模,培养模式,教学方法和课程设置等方面取得了巨大的突破性发展.但也存在着与法律职业相脱节,国际竞争力不足,办学层次不合理以及就业前景不明朗等问题.通过改革和发展,中国法学教育最终走上持续稳定的健康之道,法治建设也将更好更快地得到发展.4、法律职业共同体的发展前景答:在当代中国,依法治国,建设法治国家,是中国社会和法律发展的必然,形成法律职业共同体正成为我国法治社会生活的内在要求,有着深刻而重要的现实意义.在我国法治进程中,法律职业共同体建立是员工必然趋势,是员工社会法治文明和法治化程度的重要标志,法律职业共同体的产生和成熟相应的是一个国家法治建设的深入和完善.法律职业共同体是以法官、检察官、律师、法学家为核心的法律职业人员所组成的特殊的社会群体,是一群精通法律专门知识和运用法律的人,是现代社会中法律秩序和社会正义的守护者.他们是具有统一的法律知识背景、模式化思维方式、共同法律语言的知识共同体;它以从事法律事务为本, 是有着共同的职业利益和范围,并努力维护职业共同利益的利益共同体;法律职业共同体是依法治国,建设法治国家,推进社会全面进步的精神力量、人力资源和制度保障.第三章历史的法1、原始社会的习惯与法有什么区别答:法和原始社会的习惯都是社会行为规范,起着调整社会关系的作用,所以在一定条件下原始社会的习惯能够转化为法.并且,它们都具有某种强制力,相互具有历史的联系,在形式上相似.然而,二者存在以下的区别:一、二者产生的方式不同原始习惯的产生和发展并不经由特殊的权力机关,而是人们在共同生产和生活过程中从必然的和无数偶然的相互联系和关系中,逐渐地、自然而然地自发形成,并世代相传和演变下来的;法律是由国家有意识地制定或认可的,是掌握国家政权的社会集团基于自己的根本利益和整体利益,并出于维护和发展这种利益的目的而有意识地对原始习惯加以选择、确认或自觉创制的.二、二者体现的意志不同原始社会习惯是在生产资料氏族公有制的经济基础上产生和存在的,原始习惯体现氏族全体成员的共同意志,反映的是人们之间利益的一致性和平等关系;而刚刚产生的法是在生产资料奴隶主占有制的经济基础上产生和存在的,要反映社会统治集团的意志,维护掌握政权的社会集团的根本利益.三、二者调整的内容不同原始人依习惯而行事,在一般情况下无所谓是行使权利还是履行义务.而法律对行为的调整是以权利和义务的分离为条件.如果没有权利与义务的区分,法律就不可能实现对各种行为的调整功能.四、二者的根本目的不同原始社会习惯调整社会关系的目的,在于维系氏族的血缘关系,维护原始人之间相互团结、平等互助的社会关系和社会秩序,维护共同利益;法调整社会关系的目的,在于确立和维护有利于社会统治集团的社会关系和社会秩序.由此可见,法律带有强烈的政治倾向;原始习惯具有平等性,而无政治色彩.五、二者适用的范围不同原始习惯限于在由血缘关系所结成的本氏族、部落范围内生效,适用于具有血缘亲属关系的同一氏族或部落的所有成员,与地域无关,遵循“属人主义”原则;法按地域划分其适用范围,即一般适用于一定地域中的所有居民,适用于国家权力管辖范围内的所有居民,而不分其属于何种血缘,即与血缘无关,遵循“属地主义”原则.六、二者实施的方式不同原始习惯和法律都有各自的实施方式和制裁手段.原始习惯是通过社会舆论、氏族首领的威信、传统力量、人们的自觉和内心驱使等因素保证实施.或者说,原始习惯虽然也具有一定的外在强制属性,但不是由什么特殊的权力机关来强迫人们遵守,因此,不具有国家强制性.而法律是由国家这一特殊的暴力机关保证实施,因而具有国家强制性.2、试述法产生的一般规律答:不同地区、不同民族、不同国家的法律产生过虽然有自己的特殊性但又具有一些共同的规律.1 伴随生产力发展进程渐变的规律.法律起源本身就取决于生产力发展的水平.2与国家同步产生的规律.法与国家是基于同一原因、同一条件、同一发展趋势而产生发展的.3与宗教、道德从融合到分化的规律.4法律的产生经历了由习惯法再到成文法的漫长过程.3、什么是法的历史类型法律继承的根据和理由有哪些答:法的历史类型是按照法所据以产生和赖以存在的经济基础的性质和体现的阶级意志的不同,对人类社会的法所作的分类.法的继承是不同历史类型的法律制度之间的延续和继受,一般表现为旧法对新法的影响和新法对旧法的承接和继受.法的继承的根据和理由主要表现为以下几方面:1社会生活条件的历史延续性决定了法的继承性.2法的相对立性决定了法的发展过程的延续性和继承性.3法作为人类文明成果决定了法的继承的必要性.4法的发展的历史事实验证了法的继承性.4、试论中国法制现代化的现实道路选择.答:首先,中国的法制化应当把尽快发展经济,提高效率作为其价值取向.在社会主义社会,由人民日益增长的物质文化需要同落后的社会生产之间的矛盾所决定,社会主义的根本任务是发展生产力.一方面,抓紧建立和完善社会主义市场经济法律体系,为市场主体创造公平的竞争环境,使市场主体在经济生活中拥有广泛的选择自由,保障市场主体的合法利益,促进经济效率的提高,另一方面,打击经济犯罪,维护经济秩序,为经济的发展和效率的提高创造良好的社会环境.其次,中国法制现代化的另一个价值取向乃是实现社会正义.正义所蕴含的公平、公正、公道、平等、自由、权利等价值内涵,成为政治社会中所有价值体系追求的最高目标.社会正义也就自然构成中国法制现代化的价值理想.在当代中国,社会正义具体表现为:消灭阶级,消除两极分化,实现社会的共同富裕.中国的法制现代化,将关注和解决社会公平或社会正义问题作为自己的根本的价值取向.一方面通过立法确认和保护社会主体在机会和手段选择过程中的平等权利;另一方面,通过制定一系列有关公民社会经济文化权利的法律法规和保护弱者群体的法律法规,强化法律的利益调控职能,促进社会利益需求与实现的平衡发展,解决收入分配不公的现象,在目前经济政治环境允许的情况下,最大限度地实现社会公正.当然,公平和公正的充分实现有赖于社会资源的极大丰富,在普遍贫穷的社会不会有真正意义上的公正与公平,充其量是自然经济基础上的平均主义.因此,经济的发展和物质的丰富是社会公正的基础.在发展经济成为核心任务的当代中国,公正会带来民心的归附和政治的稳定,但是发展会在更高的基础上实现社会的公正.“效率优先,兼顾公平”反映了初级阶段的社会主义价值观,因而也是中国法治现代化的价值选择.第四章静态的法1、什么是法的要素法的构成要素有哪些答:法的要素指法的基本成分,即构成法律的基本元素.法的要素由规则、原则和概念三个要素构成.1.法律概念是指在法律上对各种事实进行概括,抽象出它们的共同特征而形成的一种权威性的范畴.法律概念具有以下功能即表达功能、认识功能、改进法律、提高法律科学化程度的功能.2.法律规则是法律当中明确赋予一种事实状态与法律意义的一般性规定.法律规则有严密的逻辑结构法律规则的逻辑结构指的是一条完整的法律规则是由哪些要素或成分所组成的,这些要素或成分是以什么样的联系结为一个整体的. 有三种:两要素说:行为模式和法律后果.旧三要素说:假定、处理和制裁.新三要素说:条件预设、行为模式和法律后果.2、如何正确认识法的本质答:有三分法和二分法之说.三分法:1.法是统治阶级意志的体现;2.法的最终决定因素:物质生活条件; 3. 经济以外因素对法的影响.二分法:1.法是统治阶级意志的体现. 2.法的内容是由统治阶级的物质生活条件决定的.3、什么是法律规则法律规则的逻辑结构是怎样的答:法律规则是指经过国家制定或认可的人们行为或活动的命令、允许和禁止的一种规范.法律规则有严密的逻辑结构,这是它与习惯和道德规范相区别的重要特征之一.法律规则的逻辑结构,指的是一条完整的法律规则是由哪些要素或成分所组成,这些要素或成分是以何种逻辑联系结为一个整体的问题.一假定.假定是法律规则的必要成分之一,是法律规则中适用该规则的条件的规定.也把假定称为“条件”或“条件假设”.二处理.处理也是法律规则的必要成分之一,是法律规则行为模式的规定,即法律允许做什么、禁止做什么和必须做什么的规定.三法律后果.法律后果也是法律规则的必要成分之一,是法律规则中对遵守规则或违反规则的行为予以肯定或否定的规定.4、试述法律原则的功能及与法律规则的关系答:法律原则的功能表现在:①它为法律规则和概念提供基础或出发点,对法律的制定和理解法律规则具有指导意义.②它可以作为疑难案件的断案依据,当某一案件的特殊事实导致适用原有规则不公正时,法律原则可作为断案依据.③许多法律原则还可作为审判依据,其作用与法律规则无异.法律原则与法律规则两者之间极有联系又有区别:一两者之间的联系:一是法律原则和法律规则都是法律规范的范畴;二是法律原则和法律规则都需要法律概念进行能够表述;三是法律原则和法律规则都是法律体系中不可或缺的组成部分.法律规则可以反应处法律原则,法律原则可以弥补法律规则在适用过程中的不足和漏洞.法律原则为法律规则提供某种基础或根源的综合性、指导性的价值准则或规范,是法律诉讼、法律程序和法律裁决的确认规范.二两者之间的区别:1.来源的区别,法律规则在国家法上只能出自立法者,这在成文法国家中尤为突出;法律原则的来源较为广泛.2.内容的区别,法律规则是明确具体的;法律原则是笼统、模糊的.3.适用范围的区别,法律规则只适用于某一类行为,不具有普遍适用性;法律原则对人的行为及其条件有更大的覆盖性和抽象性.4.适用方式的区别,法律规则是以“全有全无的方式”应用于个案中;法律原则不是“全有全无的方式”应用于个案中,不同强度的原则甚至冲突的原则都可能存在于一部法律当中.5.适用条件的区别,法律规则与法律原则相比具有优先适用性.6.表现形式的区别,任何法律规则均由嘉定、行为模式和法律后果三部分组成;法律原则一般情况下无固定的表现构成形式.7.功能的区别,法律规则的基本功能在于对人们的行为提供确定的、可预测的导向;法律原则是法律规范的基础或在法律中较为稳定的袁立和准则,它不预先设定任何确定而具体的事实状态,也没有规定具体的权利、义务和责任.第五章动态的法1、如何培养守法的意识答:守法是指国家机关、社会组织和公民个人依照法的规定,行使权利和履行义务的活动.守法是法律实施的基本要求守法的构成要素:守法的主体、守法的范围和守法的内容.衡量一个国家是否实现了法治一个重要的标志就是公民的法律意识如何公民的法律意识是不是积极的、主动的自愿的守法.从理论上说公民法律意识中的知法、守法观念、法律信仰及法律信念是可以通过教育培养的.在我国必须通过普法教育在内的多种手段才能实现.一方面要对普法的方式方法进行反思另一方面从思想上对普法教育的长期性、艰巨性有正确的认识.普法教育的终极目标是使受教育者养成守法的品质并且特别要重视的是普法的重点对象是各级党政领导干部普法的内容上应该是让受教育者从心目中树立起正确的法制观念法制观念是守法的思想基础和精神条件是守法体系的核心.因此在普法过程中一方面要重视法律知识的普及另一方面更要重视法律观念和法制精神的教化和培养.2、当前行政执法领域存在的问题和主要对策答:当前我国行政执法领域存在的问题主要有:一是执法主体太多.行政执法机构设置不合理设置混乱;二是执法依据不统一.无法可依、有法难依的现象依然存在并且严重;三是执法范围不能按照法律规定.滥用职权、越权执法的现象;四是执法效率低;五是对行政执法的监督不力对策:一是加快行政执法体制改革.改革完善立法,使之更符合社会需要.二是培育行政执法人员的法治观念,使之遵循执法的原则.执法的原则合法性即依法行政的原则.合理性原则.效率原则.正当程序原则.三是完善行政执法监督机制.对行政执法的主体的执法活动进行有效的监督.3、试述司法权的属性答:司法权是指特定的国家机关通过开展依其法定职权和一定程序,由审判的形式将相关法律适用于具体案件的专门化活动而享有的权力.司法权的独立性是司法权区别于行政权、立法权的基本属性;中立性就是司法权核心性特点,是司法权法理存在的基础和灵魂;司法权的程序性是指司法权的运作是依据程序法律所规定的顺序、步骤、程式所开展的表现形态;司法权简而讲之,就是对法律的适用权,司法权的公正性自然是源于法律的平等、公平、公正的价值内涵,如果没有法律的公正价值,则司法权的公正性就难于体现;司法权的统一性是指一国之内司法权对相同性质的案件纠纷之处理是一致的,其法律评价是一样的.4、我国现行法律监督机制及其完善.答:法律监督是指一切国家机关、政治或社会组织和公民对法的全部运作过程的合法性所进行的监察、制控和督导.在我国当前法律监督的主体是国家机关、社会组织、人民群众和大众传媒.客体是法律监督中被监督人的行为和活动.法律监督的内容是法律监督客体的活动的合法性.我国法律监督机制的完善:第一法律监督应以国家权力结构中的充分分权和分权基础上的权力制约为基础. 第二法律监督应设立专门机构.第三监督权的实质化和监督操作的程序化.第四监督启动机制设置设计都应注意借助普通公民和组织对自己利益的关切,并力图使之成为监督的启动机制.第五对政党特别是执政党遵循宪法和法律情况的监督.第六章比较的法1、如何处理法与执政党政策的关系答:社会主义法与党的政策在本质上是一致的.首先它们都是工人阶级为领导的全国人民共同意志的体现.其次它们都决定并服务于社会主义经济基础,是社会主义上层建筑的重要组成部分再次它们都是在马克思主义、毛泽东思想指导下,从实际出发,遵循客观规律的要求和人民的意愿制定的,都是我国人民用来建设社会主义的有力武器.总之党的政策和社会主义法具有内在的本质的一致性,党的政策代表了法的基本精神,法是党的政策的具体化.两者的区别:两者制定的机构不同.党的政策是由党的组织制定的,社会主义法是由国家机关制定或认可的;两者表现的形式不同.党的政策通常以决议、决定、纲领、宣言、声明、通知、报告、纪要等党的文件的形式表现出来,法表现为宪法、法律、行政法规、地方性法规等特定的规范性法律文件的形式;两者实施的方式也不同.党的政策是党的主张和党的意志的表现,对党的组织和党员具有约束力,并以党的纪律制裁作为实施的保障;社会主义法是上升为国家意志的全体人民意志的体现,对国家主权所及范围内的人具有普遍的效力,并以国家强制力保证其实现.法与政策是辩证的关系.两者从总体上是统一的,但在实践中,它们的实际地位和效力可能会存在某种冲突和矛盾.2、试论法与道德冲突.答:道德主要表现为一种人情世理,法主要表现为国法.因此经常会发生冲突,主要表现在:1.法与理的区别 2.法与情的区别.法与道德的冲突的原因1.法律移植和改革造成法与社会原来的道德相冲突.2.社会发展道德随之发展,但法律滞后. 3.道德价值与法律价值的多元.4.法律的形式化要求有时会偏离实质内容.5.法的评价方式与道德的评价方式不同.3、科技进步对法的影响答:科学技术对法的影响一般体现在如下几个方面:1、科学技术对立法的影响1科技发展对一些传统法律领域提出了新的问题,使民法、刑法、国际法等传统法律部门面临着种种挑战,要求各个法律部门的发展不断深化.2随着科学技术的发展,出现了大量新的立法领域,科技法日趋成为一个独立的法律部门.3科技法的研究也随之广泛的开展起来,科技法学作为一个新的独立的学科也被广泛承认.2、科技进步对司法的影响司法过程中的三个主要环节:事实认定、法律适用和法律推理越来越深刻地受到了现代科学技术的影响.3、科技进步对法律思想的影响1对立法起着指导作用的法律意识常常受到科技发展的影响和启迪.2科技进步促进了人们法律观念的更新,出现了一些新的法律思想和法学理论.3科技进步对历史上已经形成的各个法系及对于法学流派的产生、分化和发展也产生了重要影响.4、试论法律全球化对中国法治建设的影响答:法律全球化就意味着整个世界生活在一个单一的法律制度之下的程度,即全世界都生活在单一的法律之下.说到底,法律全球化是其他众多领域全球化制度化的表现,没有其他领域制度化的发展,法律全球化就是无本之木;而没有法律的确认和保障,其他领域的全球化也只能是一句空话.。

物理初二第一章练习题答案1. 速度和加速度的关系根据物理学的基本概念,速度是物体运动的一个重要参量,而加速度则表示物体速度变化的快慢。
在初二的物理学习中,我们常常需要研究速度和加速度之间的关系。
以下是第一章练习题的答案:题目1:一个从静止开始的物体以恒定的加速度3 m/s²沿着一条直线运动,求它在5秒后的速度是多少?答案:根据物理学中的加速度公式v = u + at,其中v是末速度,u是初速度,a是加速度,t是时间。
给定初速度u=0,加速度a=3 m/s²,时间t=5秒。
代入公式计算可得v = 0 + 3 × 5 = 15 m/s。
题目2:一辆汽车在道路上以25 m/s的速度匀速行驶,经过10秒后它的位置是多少?答案:根据物理学中的位移公式s = ut,其中s是位移,u是速度,t 是时间。
给定速度u=25 m/s,时间t=10秒。
代入公式计算可得s = 25 ×10 = 250 m。
题目3:一个物体的速度从10 m/s增加到20 m/s,经过2秒的时间,求它的加速度是多少?答案:根据物理学中的加速度公式a = (v - u) / t,其中a是加速度,v是末速度,u是初速度,t是时间。
给定初速度u=10 m/s,末速度v=20 m/s,时间t=2秒。
代入公式计算可得a = (20 - 10) / 2 = 5 m/s²。
2. 动量守恒定律在物理学中,动量守恒定律是一个重要的原理,它指出在一个系统内,所有物体的总动量在没有外力作用的情况下保持不变。
以下是第一章练习题中涉及到动量守恒定律的答案:题目1:一辆质量为1000 kg的小轿车以20 m/s的速度向东行驶,和一辆质量为1500 kg的卡车以15 m/s的速度向东行驶发生碰撞,碰撞后两车结合在一起,求结合后的速度是多少?答案:根据动量守恒定律,碰撞前的总动量等于碰撞后的总动量。
小轿车的动量为mv1,卡车的动量为mv2,碰撞后的总动量为(m1 +m2)v。

第一章金属的晶体结构1、试用金属键的结合方式,解释金属具有良好的导电性、正的电阻温度系数、导热性、塑性和金属光泽等基本特性.答:(1)导电性:在外电场的作用下,自由电子沿电场方向作定向运动。
(2)正的电阻温度系数:随着温度升高,正离子振动的振幅要加大,对自由电子通过的阻碍作用也加大,即金属的电阻是随温度的升高而增加的。
(3)导热性:自由电子的运动和正离子的振动可以传递热能。
(4) 延展性:金属键没有饱和性和方向性,经变形不断裂。
(5)金属光泽:自由电子易吸收可见光能量,被激发到较高能量级,当跳回到原位时辐射所吸收能量,从而使金属不透明具有金属光泽。
2、填空:1)金属常见的晶格类型是面心立方、体心立方、密排六方。
2)金属具有良好的导电性、导热性、塑性和金属光泽主要是因为金属原子具有金属键的结合方式。
3)物质的原子间结合键主要包括金属键、离子键和共价键三种。
4)大部分陶瓷材料的结合键为共价键。
5)高分子材料的结合键是范德瓦尔键。
6)在立方晶系中,某晶面在x轴上的截距为2,在y轴上的截距为1/2;与z轴平行,则该晶面指数为(( 140 )).7)在立方晶格中,各点坐标为:A (1,0,1),B (0,1,1),C (1,1,1/2),D(1/2,1,1/2),那么AB晶向指数为(ī10),OC晶向指数为(221),OD晶向指数为(121)。
8)铜是(面心)结构的金属,它的最密排面是(111 )。
9) α-Fe、γ-Fe、Al、Cu、Ni、Cr、V、Mg、Zn中属于体心立方晶格的有(α-Fe 、 Cr、V ),属于面心立方晶格的有(γ-Fe、Al、Cu、Ni ),属于密排六方晶格的有( Mg、Zn )。
3、判断1)正的电阻温度系数就是指电阻随温度的升高而增大。
(√)2)金属具有美丽的金属光泽,而非金属则无此光泽,这是金属与非金属的根本区别。
(×)3) 晶体中原子偏离平衡位置,就会使晶体的能量升高,因此能增加晶体的强度。

第一章作业答案一、判断改错题1、薪酬是由于员工从事劳动而获得的报酬。
(X)改为:薪酬是由于员工从事劳动而获得的经济性报酬。
2、基本工资的数额随着劳动绩效的变动而变动。
(X)改为:可变薪酬的数额随着劳动绩效的变动而变动。
3、薪酬是企业合理配置劳动力、提高企业绩效的杠杆。
(√)4、政府可以通过财政政策、价格杠杆以及产业政策等对企业的薪酬水平进行间接调节。
(√)5、企业在初创期,往往采取稳定的基本薪酬和福利计划。
(X)改为:企业在成熟期,往往采取稳定的基本薪酬和福利计划。
二、单选题1.企业对于员工提供的超出正常努力水平的劳动报酬,称为( B )。
A.工资B.奖金C.津贴D.福利2. 衡量企业薪酬支付能力的指标是( A )。
A.经济效益B.企业文化C.薪酬政策D.管理水平3. 当企业追求( A )时,倾向于在短期内为员工提供水平较低的固定薪酬,同时实行长期可变薪酬计划。
A.成长战略B.稳定战略C.收缩战略D.精简战略4.“只有使每个劳动力的人力资本价值得到体现,社会总体劳动力资源才能得到有效的配置”,这一观点依据的理论是( C )。
A.效率工资理论B.边际生产力理论C.人力资本理论D.工资差别理论三、多选题1.薪酬包括(ACDE )。
A.工资B.学习机会C.奖金D.津贴E.福利2.奖金具有以下特征(BCDE)。
A.稳定性B.超常性C.货币性D.动态性E.多样性3. 对于企业而言,薪酬具有以下功能(ACDE)。
A.控制经营成本B.价值引导C.有效配置资源D.改善经营绩效E.支持企业变革4. 亚当∙斯密的工资差别理论认为:造成不同职业和雇员之间工资差别的原因主要是(BD)。
A.生活成本B.职业性质C.工资成本D.工资政策E.边际收入四、简答题1、简述薪酬的功能。
答:(1)对组织而言:控制经营成本;有效配置资源;改善经营成本;支持组织变革。
(2)对员工而言:补偿和保障;心理激励功能;价值引导功能。
(3)对社会而言:关系国民经济的正常运行;社会和经济发展水平的重要指标。

高等数学作业答案(高起专)第一章函数作业(练习一)参考答案一、填空题1.函数x x x f -+-=5)2ln(1)(的定义域是 。
解:对函数的第一项,要求02>-x 且0)2ln(≠-x ,即2>x 且3≠x ;对函数的第二项,要求05≥-x ,即5≤x 。
取公共部分,得函数定义域为]5,3()3,2( 。
2.函数392--=x x y 的定义域为 。
解:要使392--=x x y 有意义,必须满足092≥-x 且03>-x ,即⎩⎨⎧>≥33x x 成立,解不等式方程组,得出⎩⎨⎧>-≤≥333x x x 或,故得出函数的定义域为),3(]3,(+∞⋃--∞。
3.已知1)1(2+=-x e f x ,则)(x f 的定义域为 解. 令u e x =-1, 则()u x +=1ln , (),11ln )(2++=∴u u f 即(),11ln)(2++=∴x x f .故)(x f 的定义域为()+∞-,14.函数1142-+-=x x y 的定义域是 .解. ),2[]2,(∞+--∞ 。
5.若函数52)1(2-+=+x x x f ,则=)(x f .解. 62-x二、单项选择题1. 若函数)(x f y =的定义域是[0,1],则)(ln x f 的定义域是( ) .A . ),0(∞+B . ),1[∞+C . ]e ,1[D . ]1,0[ 解: C2. 函数x y πsin ln =的值域是)(.A . ]1,1[-B . ]1,0[C . )0,(-∞D . ]0,(-∞ 解: D3.设函数f x ()的定义域是全体实数,则函数)()(x f x f -⋅是( ). A.单调减函数; B.有界函数;C.偶函数;D.周期函数 解:A, B, D 三个选项都不一定满足。
设)()()(x f x f x F -⋅=,则对任意x 有)()()()()())(()()(x F x f x f x f x f x f x f x F =-⋅=⋅-=--⋅-=-即)(x F 是偶函数,故选项C 正确。

第一章练习与答案1.为什么说在决定生产和消费时,相对价格比绝对价格更重要?答案提示:当生产处于生产边界线上,资源则得到了充分利用,这时,要想增加某一产品的生产,必须降低另一产品的生产,也就是说,增加某一产品的生产是有机会机本(或社会成本)的。
生产可能性边界上任何一点都表示生产效率和充分就业得以实现,但究竟选择哪一点,则还要看两个商品的相对价格,即它们在市场上的交换比率。
相对价格等于机会成本时,生产点在生产可能性边界上的位置也就确定了。
所以,在决定生产和消费时,相对价格比绝对价格更重要。
2.仿效图1—6和图1—7,试推导出Y商品的国民供给曲线和国民需求曲线。
答案提示:3.在只有两种商品的情况下,当一个商品达到均衡时,另外一个商品是否也同时达到均衡?试解释原因。
答案提示:4.如果生产可能性边界是一条直线,试确定过剩供给(或需求)曲线。
答案提示:5.如果改用Y商品的过剩供给曲线(B国)和过剩需求曲线(A国)来确定国际均衡价格,那么所得出的结果与图1—13中的结果是否一致?答案提示:国际均衡价格将依旧处于贸易前两国相对价格的中间某点。
6.说明贸易条件变化如何影响国际贸易利益在两国间的分配。
答案提示:一国出口产品价格的相对上升意味着此国可以用较少的出口换得较多的进口产品,有利于此国贸易利益的获得,不过,出口价格上升将不利于出口数量的增加,有损于出口国的贸易利益;与此类似,出口商品价格的下降有利于出口商品数量的增加,但是这意味着此国用较多的出口换得较少的进口产品。
对于进口国来讲,贸易条件变化对国际贸易利益的影响是相反的。
7.如果国际贸易发生在一个大国和一个小国之间,那么贸易后,国际相对价格更接近于哪一个国家在封闭下的相对价格水平?答案提示:贸易后,国际相对价格将更接近于大国在封闭下的相对价格水平。
8.根据上一题的答案,你认为哪个国家在国际贸易中福利改善程度更为明显些?答案提示:小国。
9*.为什么说两个部门要素使用比例的不同会导致生产可能性边界曲线向外凸?答案提示:第二章答案1.根据下面两个表中的数据,确定(1)贸易前的相对价格;(2)比较优势型态。
1.写出下列单体形成聚合物的反应式。
说明属于何类聚合反应。
(1) CH2CHCl(2)CH2CHCOOH(3)OH(CH2)5COOH(4) CH2CH2CH2O(5) H2N(CH2)6NH2+HOOC(CH2)8COOH(6) OCN(CH2)6NCO+HO(CH2)4OH解:(1)nCH22CHCl CH2CHCln单体自由基聚合聚氯乙烯重复单元结构单元单体单元(2)nCH2CH2CHCOOH CH2CHCOOHn单体自由基聚合聚丙烯酸重复单元结构单元单体单元(3)nHO(CH2)5O(CH2)5CO+ nH2On单体缩聚反应聚己(内)酯O(CH2)5CO为重复单元和结构单元,无单体单元。
(4)nCH2CH2CH2O CH2CH2CH2O n单体开环聚合聚氧杂环丁烷CH2CH2CH2O为重复单元、结构单元、单体单元。
(5)nH2N(CH2)10NH2 + nHOOC(CH2)8COOH H NH(CH2)10NHCO(CH2)8CO OH+(2n-1)H2On缩聚反应聚癸二酰癸二胺H2N(CH2)10NH2和HOOC(CH2)8COOH为单体。
NH(CH2)10NHCO(CH2)8CO为重复单元,NH(CH2)10NH和CO(CH2)8CO分别为结构单元,无单体单元。
(6)nOCN(CH 2)6NCO+nHO(CH 2)4 O(CH 2)4OCONH(CH 2)6NHCOn聚氨酯②为聚加成反应,无单体单元。
O(CH 2)4OCONH(CH 2)6NHCO 为重复单元,H O(CH 2)4OH 和OCN(CH 2)6NCO 为单体。
2.简述高分子科学所包括的分支领域。
解:高分子化学、高分子物理、高分子工艺与工程学、功能高分子。
3.解释名词:结构单元、聚合度、高分子化合物。
结构单元:聚合物链中与单体相对应的最小结构单位。
聚合度:聚合物分子所含有的结构单元的数目。
高分子化合物:是一种或多种原子或原子团经无数次重复连接而成的分子所组成的化合物。
第一章作业答案1.7习题1 证(方法一)由2ln,贝U n=2m,又5ln,则512m,由51 5m,则5l(5m-2 •2m)=m ,设m=5k(k 为整数),则n = 10k.又由7ln,则有7110k,由717k,则有71(3 • 7k - 2 • 10k) = k ,设k = 7p(p 是整数), 则有n=70p,从而有70ln.(方法二)因为2ln,5ln,7ln,且[2 , 5, 7]=70 ,根据1.4定理7可得70ln.(方法三)因为2ln, 5ln , 7ln ,所以7OI35n , 70ll4n , 70 I lOn,从而有701(35- 14-2 ・ 10)n = n.4证:三个连续的整数可以写成,(a-1), a , (a+1),其中任意两个连续整数中必定有一个是偶数,所以2可以整除它们的乘积,即2l(a -l)a(a+l).又任意整数 a 可以写成 a = 3n+b(bEZ, lWbW3) 当 b = l 时,a—l=3n,所以3l(a-l), 当b=2 时,a + 1 = 3n+3 ,所以3l(a+l), 当b=3 时,a= 3n,所以31a .所以不论 b 是多少,均有3l(a-l)a(a+l),又(2, 3) = 1 ,故6l(a-l)a(a+l).6证(运用1.1定义2或1.1定理7)12证明形如3k-1形式的正整数必有同样形式的素因数.证(解析:任意整数可表示为3k-l或3k或3k+l ,其中为素因数形式只能为3k-1或3k+l的形式)假设形如3k-1的正整数只有3m+1 形式的素因数,那么3k-l = (3mi +l)(3m2+l)-(3m s +l)=3m+l其中nii GZ ,i=l,2,…,s .m是nii的整系数多项式,故m是一个整数,可推出3k - 1 = 3m + 1,这是矛盾的.14证明形如6k+5的素数有无穷多个.证:假设形如6k+5的素数只有有限个pi ,…,Ps ,令a = 6pi ---ps + 5因为n>pi , i=l,…,s,所以a一定是合数,(注:否则a是大于pi的素数),根据1. 1定理6 , a的大于5的最小正因数p 是素数,因此,P是P1,…,Ps中的某一个,即存在j, IWjWs,使得P=Pj ,根据1. 1定理3,我们有p|a-6pi •••ps =5,这与p>5是矛盾的,故存在有形如6k+5的素数有无穷多个.方法二反证法.假设形如6k+5的素数只有有限个,可设为pi , p2,…,Ps ,令 a = 6pi …p s + 5 ,贝U p】a ,i=l,…,s.所以有,a是异于Pi , p2,…,p s的形如6k+5的素因数.这与形于6k+5的素数只有pl ,p2,…,ps 有限个矛盾.故形如6k+5的素数有无限多个.17 答案:(111100*********)2 =(78F5)i6 ,(10111101001110)2 =(2F4E)1618 答案:(ABCDEFA)16 = (1010101111001101111011111010)2 (DEFACEDA) i6 = (11011110111110101100111011011010)2 (9A0AB)16=(10011010000010101011)229 答案:(2t - 1 ,2t + 1)=1 ; (2n ,2(n+1))=2.32 答案:(1613 ,3589) = 1 ,551X3589 - 1226X1613=1(2947 , 3772)= 1 , 951 X2947 - 743X3772 = 133 答案:(70 , 98 , 105) = 7整系数线性组合不唯一7= 24X70 - 16X98 - 105=105 +14X98 - 21X70=0X70 + 105 - 98—・・・34证明:不妨设mNn ,由带余数除法得m = qn + r OWr <n,则有a m-l = a qn+r-l + a r-a r = a r(a qn-l) + a r-l由于a qn-l = (a n-l)(a q(nl)+--- + l)由此及— 11 a.an— 1得(a m-l,a n-l) = (a n-l,a r-l)又(m , n) = (n , r).若r = 0,贝U (m , n) = n 结论成立.若r > o则继续对(a” — 1, a r - 1)作同样的讨论.由辗转相除法知,结论成立.51略62求9x + 24y -5z = 1000的一切整数解.解:(说明:这里只需要求出一组解即可)因为(9 , 24 ,5)=1 ,则1 = 24 - 2-9-5所以存在x 二-2000 , y 二1000 , z 二1000 使得9x + 24y -5z 二1000 或者1 = 6・9 -2・24 -5所以存在X= 6000 , y = -2000 , z = 1000 使得9x + 24y ~5z = 1000 可以有多解.。
[0068]《概率统计》网上作业题答案第一次作业 [论述题]作业1 参考答案:答案1第一章作业答案1:设A ,B ,C 为三个事件,用A ,B ,C 的运算关系表示下列各事件:(1) C B A (2) C B A (3) C B A (4) C B A (5) C B A (6) C B C A B A (7) C B A (8) CA BC AB2: 0.5 0.33:已知在10只产品中有2只次品,在其中取两次,每次任取一只,作不放回抽样。
求下列事件的概率:(1) 两只都是正品; (2) 两只都是次品;(3) 一只是正品,一只是次品; (4) 第二次取出的是次品。
解:(1)452821028=P P (2)45121022=P P(3)451622101218=P P P (4)459210221218=+P P P P4:在3题中若将不放回抽样改为有放回抽样,所求概率分别为多少? 解:(1)64.0101088=⨯⨯ (2)04.0101022=⨯⨯(3)32.010108228=⨯⨯+⨯ (4)2.010102228=⨯⨯+⨯5:在房间里有10个人,分别佩戴从1号到10号的纪念章,任选3人记录其纪念章的号码。
(1)求最小号码为5的概率。
(2)求最大号码为5的概率。
解:(1)12131025=C C (2)20131024=C C6:从5双不同的鞋子中任取4只,问这4只鞋子中至少有两只配成一双的概率是多少?解:21131410141618110=-P P P P P (用逆事件)7:在11张卡片上分别写上probability 这11个字母,从中任意连抽7张,求其排列结果为ability 的概率。
0000024.041111221711711==⨯⨯⨯⨯⨯⨯P P8:已知41)(=A P ,31)|(=AB P ,21)|(=B A P ,求)(B A P 。
解:)()()()(AB P B P A P B A P -+=而 )|()()(B A P AB P B P =,)|()()(A B P A P AB P =所以 31)|()()|()|()()()(=-+=A B P A P B A P A B P A P A P B A P9:某车间有三台设备生产同一型号的零件,每台设备的产量分别占车间总产量的25%,35%,40%。
第一章作业答案1-1 地面空气的主要成分是什么?矿井空气与地面空气有何区别?N2(78%) O2(20.96%) CO2(0.03%) Ar(1%) 其他稀有气体(0.01%)地面空气进入井下后,因发生物理和化学两种变化,使其成分种类增多,各种成分浓度改变1-2 氧气有哪些性质?造成矿井空气中氧浓度减少的主要原因有哪些?物理性质:氧是无色、无臭、无味、无毒和无害的气体,比重为1.105,是人和其他动物呼吸所必需的物质化学性质:氧是很活跃的元素,易使其他物质氧化,并能助燃主要原因:煤、岩、坑木等缓慢氧化耗氧,煤层自燃,人员呼吸,爆破。
1-3矿井空气中常见的有害气体有哪些?《规程》对矿井空气中有害气体的最高容许浓度有哪些具体规定?1-4CO的主要来源。
CO是无色、无臭、无味的有毒有害气体,比重为0.967,比空气轻,不易溶于水,当浓度在13~75%时可发生爆炸;CO比O2与血色素亲和力大250~300倍,它能够驱逐人体血液中的氧气使血液缺氧致命;井下爆炸工作、火区氧化、机械润滑油高温分解等都能产生CO。
1-5 什么是矿井气候?简述井下空气温度的变化规律。
矿井气候指井内的温度、湿度、风速等条件在金进风路线上:冬季,冷空气进入井下,冷气温与地温进行热交换,风流吸热,地温散热,因地温随深度增加且风流下行受压缩,故沿线气温逐渐升高;夏季,与冬季情况相反,沿线气温逐渐降低在采掘工作面内:由于物质氧化程度大,机电设备多,人员多以及爆破工作等,致使产生较大热量,对风流起着加热的作用,气温逐渐上升,而且常年变化不大。
1-8《规程》对矿井空气的质量有哪些具体规定?采掘工作面进风流中的氧气浓度不得低于20%;二氧化碳浓度不得超过0.5%;总回风流二氧化碳浓度不得超过0.75%。
当采掘工作面风流中二氧化碳浓度达到1.5%或采区,采掘工作面回风道中二氧化碳浓度超过1.5%时,必须停工处理。
1-9某矿一采煤工作面CO2的绝对涌出量为7.56m3/min,当供风量为850m3/min 时,该工作面回风流中CO2的浓度是多少?能否正常工作?取一分钟,工作面总风量为7.56 +850=862.56m3CO2总量为: 7.56+850×0.04%=7.90m3所以CO2的浓度为: 7.90÷862.56=0.92%>0.75%所以,不能进行正常工作。
1-5在历史上,对摄氏温标是这样规定的:假设测温属性X随温度t做线性变化,
即,并规定冰点为,汽化点为。
设和分别表示在冰点和汽化点时X的值,试求上式中的常数a和b。
解:
由题给条件可知
由(2)-(1)得
将(3)代入(1)式得
1-8当热电偶的一个触点保持在冰点,另一个触点保持任一摄氏温度t时,其热电动势由下式确定:
式中
题1-8题(1)题1-8图(2)
题1-9图(3)
(1)试计算当和时热电动势的值,并在此范围内作图。
(2)设用为测温属性,用下列线性方程来定义温标:
并规定冰点为,汽化点为,试求出a和b的值,并画出图。
(3)求出与和对应的值,并画出图
(4)试比较温标t和温标。
解:令
(1)
(2)在冰点时,汽化点,而,已知
解得:
(3)
当时
当时
当时
当时
(4)温标t和温标只有在汽化点和沸点具有相同的值,随线性变化,而t不随
线性变化,所以用作测温属性的温标比t温标优越,计算方便,但日常所用的温标是摄氏温标,t与虽非线性变化,却能直接反应熟知的温标,因此各有所长。
1-13一氧气瓶的容积是,其中氧气的压强是,规定瓶内氧气压强降到
时就得充气,以免混入其他气体而需洗瓶,今有一玻璃室,每天需用氧气,问一瓶氧气能用几天。
解:先作两点假设,(1)氧气可视为理想气体,(2)在使用氧气过程中温度不变。
则:
由可有
每天用掉的氧气质量为
瓶中剩余氧气的质量为
天
1-21 一打气筒,每打一次可将原来压强为,温度为,体积
的空气压缩到容器内。
设容器的容积为,问需要打几次气,才能使
容器内的空气温度为,压强为。
解:打气后压强为:,题上未说原来容器中的气体情况,可设原来容器中没有空气,设所需打气次数为,则
得:次
1-26按重量计,空气是由的氮,的氧,约的氩组成的(其余成分很少,可以忽略),计算空气的平均分子量及在标准状态下的密度。
解:设总质量为M的空气中,氧、氮、氩的质量分别为。
氧、氮、氩的分子
量分别为。
空气的摩尔数
则空气的平均摩尔质量为
即空气的平均分子量为28.9。
空气在标准状态下的密度。