当前位置：文档之家 › 第三章线性规划在工商管理中的应用(应用运筹学)).

第三章线性规划在工商管理中的应用(应用运筹学)).

  • 格式：ppt
  • 大小：1.58 MB
  • 文档页数：1

下载文档原格式

  / 1

合集下载

运筹学第三章习题答案详细

运筹学第三章习题答案详细

运筹学第三章习题答案详细运筹学是一门研究如何有效地做出决策的学科，它运用数学和逻辑的方法来解决实际问题。

在运筹学的学习中，习题是非常重要的一部分，通过解答习题可以加深对知识的理解和应用。

本文将详细解答运筹学第三章的习题，帮助读者更好地掌握该章节的内容。

第一题是关于线性规划的基本概念和性质的。

线性规划是运筹学中的重要分支，它的目标是在一组约束条件下，找到使目标函数最大或最小的变量值。

这个问题可以用一个线性规划模型来描述，其中包括决策变量、目标函数和约束条件。

在解答这个问题时，我们需要先确定决策变量、目标函数和约束条件，然后使用线性规划的方法求解最优解。

具体的计算过程可以通过线性规划的算法来完成。

第二题是关于线性规划的图解法的。

线性规划的图解法是一种直观的解法，它通过绘制变量的可行域和目标函数的等高线图来求解最优解。

在解答这个问题时，我们需要先将约束条件转化为直线或者曲线的形式，然后绘制出这些直线或曲线，并确定它们的交点。

最后，我们需要在可行域内找到使目标函数取得最大或最小值的点，这个点就是线性规划的最优解。

第三题是关于整数规划的应用的。

整数规划是线性规划的一种特殊形式，它要求决策变量取整数值。

在解答这个问题时，我们需要先确定整数规划的模型，包括决策变量、目标函数和约束条件。

然后，我们可以使用整数规划的算法来求解最优解。

在实际应用中，整数规划可以用来解决很多实际问题，比如生产计划、运输调度等。

第四题是关于线性规划的灵敏度分析的。

灵敏度分析是线性规划中的一种重要技术，它用来分析目标函数系数、约束条件右端常数和决策变量上下界的变化对最优解的影响。

在解答这个问题时，我们需要计算目标函数系数、约束条件右端常数和决策变量上下界的变化对最优解的影响程度，并进行相应的调整。

通过灵敏度分析，我们可以了解到线性规划模型对参数变化的敏感性，从而做出更加准确的决策。

第五题是关于线性规划的对偶问题的。

线性规划的对偶问题是线性规划的一个重要概念，它可以用来求解原始问题的最优解。

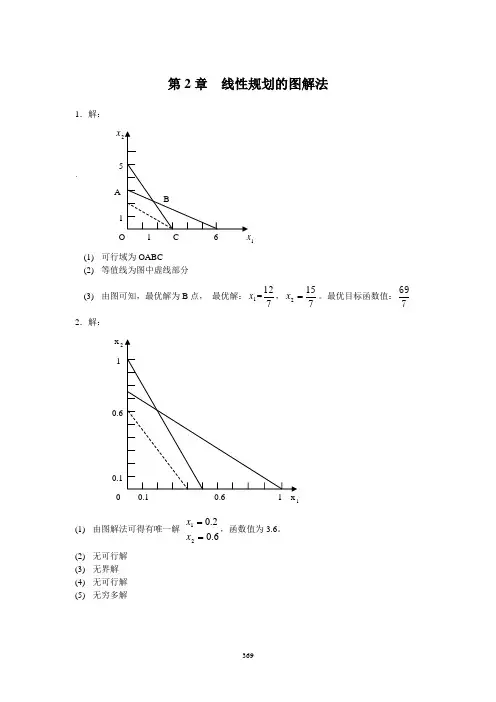
管理运筹学课后答案-----韩伯裳

管理运筹学课后答案-----韩伯裳

第2章 线性规划的图解法1．解：x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知，最优解为B 点， 最优解：1x =712，7152=x 。

最优目标函数值：7692．解： x 2 10 1(1) 由图解法可得有唯一解 6.02.021==x x ，函数值为3.6。

(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ，函数值为392。

3．解：(1). 标准形式：3212100023m ax s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式：21210064m in s s x x f +++=,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式：21''2'2'10022m in s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4．解：标准形式：212100510m ax s s x x z +++=,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量（0，0） 最优解为 1x =1，x 2=3/2.标准形式：32121000811m in s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量（0.0.13） 最优解为 x 1=1，x 2=5.6．解：(1) 最优解为 x 1=3，x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8，x 2=0. (6) 不变化。

线性规划在工商管理中的应用

线性规划在工商管理中的应用

线性规划的定义
01
线性规划是一种优化方法，用于解决线性约束条件下的优化问题
02
线性规划的目标是找到一组决策变量，使得目标函数达到最优值
03
线性规划的约束条件包括线性不等式约束和线性等式约束
04
线性规划的决策变量可以是连续的，也可以是离散的，但目标函数必须是线性的
线性规划的适用范围
01 线性规划适用于解决线性 目标函数和线性约束条件 的优化问题
线性规划在库存管理中的应用：通过优化库存 管理，降低库存成本，提高库存周转率
线性规划在供应链管理中的应用：通过优化供 应链管理，降低供应链成本，提高供应链效率
线性规划在销售预测中的应用：通过优化销售 预测，提高销售预测准确性，降低销售风险
运输与配送优化
D
线性规划在运输与配送优化中的实际应用案例
C 线性规划在运输与配送优化中的求解方法
粒子群优化算法： 模拟鸟群飞行，实 现全局优化
模拟退火算法：模 拟金属退火过程， 实现全局优化
启发式优化算法： 根据问题特点，实 现局部优化
跨学科的融合与创新
01
线性规划与其他 学科的融合：如 经济学、统计学、
计算机科学等
02
创新方法：如遗 传算法、模拟退 火算法、神经网
络等
03
应用领域：如供 应链管理、人力 资源管理、财务
某投资公司风险评估案例
背景：某投资公 司需要对其投资 项目进行风险评 估，以确定投资 策略
目标：通过线性 规划方法，评估 投资项目的风险 和收益
模型构建：建立 线性规划模型， 包括投资项目、 风险因素、收益 因素等变量
求解：通过求解 线性规划模型， 得到最优投资策 略
结果：根据求解 结果，确定投资 项目的风险和收 益，为投资决策 提供依据

运筹学例题-打印版

运筹学例题-打印版

运筹学例题-打印版⼀、绪论⼀个班级的学⽣共计选修A 、B 、C 、D 、E 、F 六门课程，其中⼀部分⼈同时选修D 、C 、A ，⼀部分⼈同时选修B 、C 、F ，⼀部分⼈同时选修B 、E ，还有⼀部分⼈同时选修A 、B ，期终考试要求每天考⼀门课，六天内考完，为了减轻学⽣负担，要求每⼈都不连续参加考试，试设计⼀个考试⽇程表。

⼆、图解法例1. 某⼯⼚在计划期内要安排Ⅰ、Ⅱ两种产品的⽣产，已知⽣产单位产品所需的设备台时及A 、B 两种原材料的消耗、资源的限制，如下表：⼯⼚应分别⽣产多少单位Ⅰ、Ⅱ产品才能使⼯⼚获利最多？ 3.1例2 某公司由于⽣产需要，共需要A ，B 两种原料⾄少350吨（A ，B 两种材料有⼀定替代性），其中A 原料⾄少购进125吨。

但由于A ，B 两种原料的规格不同，各⾃所需的加⼯时间也是不同的，加⼯每吨A 原料需要2个⼩时，加⼯每吨B 原料需要1⼩时，⽽公司总共有600个加⼯⼩时。

⼜知道每吨A 原料的价格为2万元，每吨B 原料的价格为3万元，试问在满⾜⽣产需要的前提下，在公司加⼯能⼒的范围内，如何购买A ，B 两种原料，使得购进成本最低？三、单纯形法例1. 某⼚⽣产甲⼄两种产品，各⾃的零部件分别在A 、B 车间⽣产，最后都需在C 车间装配，相关数据如表所⽰：问如何安排甲、⼄两产品的产量，使利润为最⼤。

例2. 某名牌饮料在国内有三个⽣产⼚，分布在城市A1、A2、A3,其⼀级承销商有4个，分布在城市B1、B2、B3、B4，已知各⼚的产量、各承销商的销售量及从A i 到B j 的每吨饮料运费为C ij ，为发挥集团优势，公司要统⼀筹划运销问题，求运费最⼩的调运⽅案。

四、线性规划在⼯商管理中的应⽤例1．某昼夜服务的公交线路每天各时间段内所需司机和乘务⼈员数如下：设司机和乘务⼈员分别在各时间段⼀开始时上班，并连续⼯作⼋⼩时，问该公交线路怎样安排司机和乘务⼈员，既能满⾜⼯作需要，⼜配备最少司机和乘务⼈员?例2．⼀家中型的百货商场，它对售货员的需求经过统计分析如下表所⽰。

第三章 线性规划在工商管理中的应用(应用运筹学))解析

第三章 线性规划在工商管理中的应用(应用运筹学))解析

Max z= 130TV + 60M + 50SS
广告费用约束: 30TV + 15M + 10SS ≤ 400
计划成本:
9TV + 3M + 4SS ≤ 100
电视广告数： TV ≤ 5
TV ≥ 0, M ≥ 0, SS ≥ 0.
B
C
D
E
F
G
H
3
TV Spots
Magazine Ads
SS Ads
用在杂志上刊登20次广告，在报纸增刊上刊登10 次广告。
模型准确性评价
P96
模型与实际情况并不是完全吻合，只是实际问题的抽象表 示.问题：
1. 如果解不是整数如何处理？
2. 成本与广告的数量是否成线性比例关系？
3.儿童电视广告没有投放是否合理？模型最优解
4. 不同广告媒体，受众群体不同， 如何保证儿童和家长看到食品广告；
≥14
x2＋x3＋x4＋x5＋x6
＋0.5 ( y2＋y3＋y4＋y5＋y6)
名售货人员。如果设xi ( i = 1,2,…,7)表示星期一至日开始休息的人数，
则模型？
假定每个售货人员每天工作8小时，商场除了聘用全时雇员外，还可以雇佣半天工作售货员， 半天工作售货员每天连续工作4小时，分成上、下午两班，工作时间不交叉，每周连续工 作5天，休息2天。设全天售货员和半天售货员的工资分别为10元∕小时和9元∕小时，并 且限制每周半天售货员的总工作量不应超过总工作量的四分之一，问百货商场如何安排聘
Number of TV Spots: TV ≤ 5
and
TV ≥ 0, M ≥ 0, SS ≥ 0.
二、市场营销调查问题

[讲解]运筹学应用例题

[讲解]运筹学应用例题

线性规划在工商管理中的应用一、人力资源分配的问题例1某昼夜服务的公交线路每天各时间段内所需司机和乘务人员人数如下表所示：设司机和乘务人员分别在各时间段开始时上班；并连续工作8小时，问该公交线路应怎样安排司机和乘务人员，既能满足工作需要，又使配备司机和乘务人员的人数最少？例2 一家中型的百货商场对售货员的需求经过统计分析如下表所示：为了保证售货员充分休息，要求售货员每周工作五天，休息两天，并要求休息的两天是连续的，问应该如何安排售货员的休息日期，既能满足工作需要，又使配备的售货员的人数最少？二、生产计划问题例3 某公司面临一个是外包协作还是自行生产的问题。

该公司有甲、乙、丙三种产品，这三种产品都要经过铸造、机械加工和装配三道工序。

甲、乙两种产品的铸件可以外包协作，亦可以自行生产，但产品丙必须由本厂铸造才能保证质量。

有关情况如下表所示，公司中可利用的总工时为：铸造8000小时，机械加工12000小时和装配10000小时。

为了获得最大利润，甲、乙、丙三种产品各应生产多少件？甲、乙两种产品的铸件有多少由本公司铸造？有多少为外包协作？三、套裁下料问题例4 某工厂要做100套钢架，每套钢架需要长度分别为2.9米、2.1米、和1.5米的圆钢各一根。

已知原料每根长7.4米，问应如何下料，可使所用原料最省？四、配料问题例5某工厂要用三种原料1、2、3混合调配出三种不同规格的产品甲、乙、丙，产品的规格要求、产品的单价、每天能供应的原材料数量及原材料单价如下表所示：问该厂应如何安排生产，才能使利润最大？五、投资问题例6某部门现有资金200万元，今后五年内考虑给以下的项目投资：项目A：从第一年到第五年每年年初都可以投资，当年末能收回本利110%；项目B：从第一年到第四年每年年初都可以投资，次年末能收回本利125%，但规定每年最大投资额不能超过30万元；项目C：第三年初需要投资，到第五年末能收回本利140%，但规定每年最大投资额不能超过80万元；项目D：第二年初需要投资，到第五年末能收回本利155%，但规定每年最大投资额不能超过100万元。

管理运筹学期末复习资料【韩伯棠】

运筹学（Operational Research）复习资料第一章绪论一、名词解释1.运筹学：运筹学是应用分析、试验、量化的方法，对经济管理系统中的人力、物力、财力等资源进行统筹安排，为决策者提供有依据的最优方案，以实现最有效的管理。

二、选择题1.运筹学的主要分支包括（ABDE ）A图论B线性规划C非线性规划D整数规划E目标规划2. 最早运用运筹学理论的是（ A ）A . 二次世界大战期间，英国军事部门将运筹学运用到军事战略部署B . 美国最早将运筹学运用到农业和人口规划问题上C . 二次世界大战期间，英国政府将运筹学运用到政府制定计划D . 50年代，运筹学运用到研究人口，能源，粮食，第三世界经济发展等问题上第二章线性规划的图解法一、选择题/填空题1.线性规划标准式的特点：（1）目标函数最大化（2）约束条件为等式（3 决策变量为非负（4 ) 右端常数项为非负2. 在一定范围内，约束条件右边常数项增加一个单位：（1）如果对偶价格大于0，则其最优目标函数值得到改进，即求最大值时，最优目标函数值变得更大，求最小值时最优目标函数值变得更小。

（2）如果对偶价格小于0，则其最优目标函数值变坏，即求最大值时，最优目标函数值变小了；求最小值时，最优目标函数值变大了。

（3）如果对偶价格等于0，则其最优目标函数值不变。

3.LP模型（线性规划模型）三要素：（1）决策变量（2）约束条件（3）目标函数4. 数学模型中，“s·t”表示约束条件。

5. 将线性规划模型化成标准形式时，“≤”的约束条件要在不等式左端加上松弛变量。

6. 将线性规划模型化成标准形式时，“≥”的约束条件要在不等式左端减去剩余变量。

7．下列图形中阴影部分构成的集合是凸集的是A【解析】：如何判断是凸集？凸集：两点之间连线在图内凹集：两点之间连线在图外8. 线性规划问题有可行解且凸多边形无界，这时CA没有无界解 B 没有可行解 C 有无界解 D 有有限最优解9. 对于线性规划问题，下列说法正确的是（ D ）A. 线性规划问题可能没有可行解B. 在图解法上，线性规划问题的可行解区域都是“凸”区域C. 线性规划问题如有最优解，则最优解可在可行解区域顶点上到达D. 上述说法都正确第三章线性规划问题的计算机求解一、名词解释1.相差值：相应的决策变量的目标系数需要改进的数量，使得决策变量为正值。

《管理运筹学》第三版(韩伯棠 )课后习题答案 高等教育出版社

x1＝8，x2＝0，x3＝1，x4＝1，x5＝0，x6＝4，x7＝0，x8＝6，x9＝0， x10＝0，x11＝0 最优值为 320。
a、 在满足对职工需求的条件下，在 10 时安排 8 个临时工，12 时新安排 1 个临时工，13 时新安排 1 个临时工，15 时新安排 4 个临时工，17 时新 安排 6 个临时工可使临时工的总成本最小。
50xa + 100xb ≤ 1200000 5xa + 4xb ≥ 60000 100xb ≥ 300000 xa , xb ≥ 0 基金 a,b 分别为 4000，10000。 回报率：60000
b 模型变为： max z = 5xa + 4xb
50xa + 100xb ≤ 1200000 100xb ≥ 300000 xa , xb ≥ 0
xi ≥ 0, yi ≥ 0 i=1,2,…,11
稍微变形后，用管理运筹学软件求解可得：总成本最小为 264 元。 安排如下：y1=8（ 即在此时间段安排 8 个 3 小时的班），y3=1，y5=1，y7=4，x8=6 这样能比第一问节省：320-264=56 元。
x2＋x3＋x4＋x5＋1 ≥ 3 x3＋x4＋x5＋x6＋2 ≥ 3 x4＋x5＋x6＋x7＋1 ≥ 6 x5＋x6＋x7＋x8＋2 ≥ 12 x6＋x7＋x8＋x9＋2 ≥ 12 x7＋x8＋x9＋x10＋1 ≥ 7 x8＋x9＋x10＋x11＋1 ≥ 7 x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11≥ 0 用管理运筹学软件我们可以求得此问题的解为：
b、 这时付给临时工的工资总额为 80 元，一共需要安排 20 个临时工的班 次。
约束 -------
1 2 3 4 5 6 7 8 9 10 11

线性问题在管理中的应用

DEA应用中的“窗口”技术——空军基地的效率评价（美国） 窗口技术有许多优点，主要为：
1) 适用于决策单元个数 n 较小的情况。 2) 可以获得各个决策单元关于效率的稳定性。以及变化趋势、
但在每项评价时，只使用相邻的 3 个季度，即 n = 21 ， 接近 2ms = 2×3×4 = 24 ，将它们构成一个“窗口”。评价 结束后，将“窗口”向下一季度递推，进行第二轮 DEA 评价。 如此进行，共作三轮，获得了良好的结果。
线性规划 Linear Programming（LP）
DEA分析应用举例
DEA分析应用举例
解： 若先确定分理处1的运行是否DEA有效。建立线性规划 模型
min E
18001 +10002 + 8003 + 9004 ≥1800
2001 + 3502 + 4503 + 4204 ≥ 200
16001 +10002 +13003 +15004 ≥1600
S.t.
151 + 202 + 213 + 204 ≤ 15E
线组成的生产前沿面上，先构造一个由 n 个决策单元组成（ 线性组合成）的假想决策单元。如果该假想单元的各项产出均 不低于 j0 决策单元的各项产出，它的各项投入均低于 j0 决策 单元的各项的各项投入。 即有：
线性规划 Linear Programming（LP）
数据包络分析DEA问题线性规划数学模型
aij ——第 j 决策单元的第 i 项投入 brj ——第 j 决策单元的第 r 项产出
评价（衡量）第 j0 决策单元是否DEA有效
线性规划 Linear Programming（LP）

线性规划在工商管理中的应用

线性规划在工商管理中的应用摘要线性规划是运筹学的一个重要分支，它被广泛应用于工业、农业、商业等领域，来解决实际中的问题。

本文通过介绍线性规划及其在工商管理中应用的实例，来说明它在工商管理中的重要作用。

关键词运筹学；线性规划；方法；应用1.线性规划在工商管理中运用的广泛性工商管理[1]是研究工商企业经济管理基本理论和一般方法的学科，它通过运用现代管理的方法和手段来进行有效的企业管理和经营决策，保证企业的生存和发展。

在当今社会，随着市场竞争的日益加剧，如何统筹安排，合理利用有限的人力、物力、财力等资源，使总的经济效益最好，已经成为企业经营管理过程中实现利益最优必须解决的问题。

例如：人力资源分配：用最少的劳动力来满足工作的需要?产品生产计划：合理利用人力、物力、财力等，使获利最大?套裁下料：如何在保证生产的条件下，下料最少?配料问题：在原料供应量的限制下如何获取最大利润?投资问题：从投资项目中选取方案，使投资回报最大?运输问题：如何制定调运方案，使总运费最小?这样的问题常常可以化成或近似地化成“线性规划”（Linear Programming, 简记为LP）问题。

线性规划所研究的是：在一定条件下，合理安排人力物力等资源，使经济效果达到最好。

一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题[2]。

利用线性规划我们可以解决很多问题，例如上述人力资源分配、计划安排、套裁下料等诸多方面的问题，在本文的后面我们将用线性规划方法对企业在生产中的具体问题进行探讨。

2.线性规划的模型线性规划[2]是运筹学的一个重要分支。

自1947年丹捷格（G. B. Dantzig ）提出了一般线性规划问题求解的方法——单纯形法之后，线性规划在理论上趋向成熟，在实用中日益广泛与深入。

特别是在电子计算机能处理成千上万个约束条件和决策的线性规划问题之后，线性规划的适用领域更为广泛了，它已是现代科学管理的重要手段之一了。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
B 3 4 5 6 7 8 9 10 11 12 13 14 15 Exposures per Ad (thousands) C TV Spots 1,300 D Magazine Ads 600 E SS Ads 500 F G H
Ad Budget Planning Budget
300 90
Cost per Ad ($thousands) 150 100 30 40
求解得： TV =0 ；M = 20； SS =10；Z* =17000000。即电视广告不采 用在杂志上刊登20次广告，在报纸增刊上刊登10 次广告。
模型准确性评价
P96
模型与实际情况并不是完全吻合，只是实际问题的抽象表 示.问题： 1. 如果解不是整数如何处理？ 2. 成本与广告的数量是否成线性比例关系？ 3.儿童电视广告没有投放是否合理？模型最优解 4. 不同广告媒体，受众群体不同， 如何保证儿童和家长看到食品广告； 5.是否考虑杂志和报纸的优惠券问题； 6.受众量最大化与利润最大化是否一致。
Super Grain Corp. Advertising-Mix Problem

Goal: Design the promotional campaign for Crunchy Start. The three most effective advertising media for this product are

The limited resources in the problem are

The objective will be measured in terms of the expected number of exposures. Question: At what level should they advertise Crunchy Start in each of the three media?

Cost and Exposure Data
Costs Cost Category
Each TV Commercial $300,000
90,000 1,300,000
Each Magazine Ad $150,000
30,000 600,000
Each Sunday Ad $100,000
40,000 500,000
Budget Spent 4,000 1,000
<= <=
Budget Av ailable 4,000 1,000 Total Exposures (thousands) 17,000
Number of Ads Max TV Spots
TV Spots 0 <= 5
Magazine Ads 20
SS Ads 10
模型准确性评价
目标群
P96
增加目标客户约束后的模型与解
到达各目标客户群的数量（百万）
电视广告
1.2 0.5
杂广告
0.1 0.2
报纸增刊广告
0 0.2
最低要求数
5 5
儿童 儿童家长
1.2TV + 0.1M ≥5 0.5TV + 0.2M + 0.2SS ≥5 增加约束后,求解得： TV =3 ；M = 14； SS =7.75； Z* =16175000。比17000000少，更好实现活动的目标。 还可增加增加优惠卷资金约束等
30
9
15
3
10
4
预期广告受众（万人）
130
60
50
儿童电视节目广告只有5个可用时段可供选择，其他广告数量 无限制，超级食品公司为了使食品广告的预期受众数量最大， 应如何选择广告媒体？

数学模型与求解：
设 TV = 儿童电视广告投放数；M = 食品杂志广告投放数； SS = 星期天报纸增刊广告的投放数 Max z= 130TV + 60M + 50SS 广告费用约束: 30TV + 15M + 10SS ≤ 400 计划成本: 9TV + 3M + 4SS ≤ 100 电视广告数： TV ≤ 5 TV ≥ 0, M ≥ 0, SS ≥ 0.

Television commercials on Saturday morning programs for children. Advertisements in food and family-oriented magazines. Advertisements in Sunday supplements of major newspapers. Advertising budget ($4 million). Planning budget ($1 million). TV commercial spots available (5).
Ad Budget
Planning budget Expected number of exposures
Algebraic Formulation
Let TV = Number of commercials for separate spots on television M = Number of advertisements in magazines. SS = Number of advertisements in Sunday supplements. Maximize Exposure = 1,300TV + 600M + 500SS subject to Ad Spending: 300TV + 150M + 100SS ≤ 4,000 ($thousand) Planning Cost: 90TV + 30M + 30SS ≤ 1,000 ($thousand) Number of TV Spots: TV ≤ 5 and TV ≥ 0, M ≥ 0, SS ≥ 0.
1、星期六上午儿童节目的电视广告；
2、食品与家庭导向的杂志上的广告； 3、主要报纸星期天增刊上的广告；
三种广告的计划成本（包括设计和管理费用）、广告媒体每次投放成本和 广告的期望受众数量见下表：
第一节市场营销中的应用
成本 成本分类 儿童电视广告 食品元）
设计与服务 成本（万元）
第三章 建模与应用 线性规划在工商管理中的应用






§1 §2 §3 §4 §5 §6
市场营销中的应用
人力资源分配的问题 生产计划的问题 套裁下料问题 配料问题 投资问题
第一节市场营销中的应用
一、超级食品公司的广告媒体选择问题

P93
超级食品公司某种新食品(crunchy start)全国性促销活动，该产品成功 与否关系到公司的前途。营销部副总裁克莱略负责此事，上次产品促销 由于考虑的因数不全而导致失败，公司总裁斯隆对此事非常重视。雇佣 广告公司G&J公司来帮助设计某种食品(crunchy start)的全国性促销活 动。超级食品公司计划用于支付给G&J公司的设计服务费用不超过100 万元，并预留了另外的400万元作为媒体的广告费用。 G&J公司确定了 这一产品最有效的三种广告媒体，三种广告分别为：