专题一：正方形中的十字架模型

十字架模型【模型讲解】1◎结论1：正方形内部，AE⊥BF，则AE=BF,△ABE≌△BCF .相等未必垂直过点H作HP⊥CD与P，作I关于HP对称点Q,虽然HI=JK，但HQ≠JK方法总结：正方形内两条互相垂直的直线与各边的交点所得的线段，那么这两条线段相等。

证明方法往往通过证明三角形全等，如果没有，则按照上图构造两个全等三角形，结合平行四边形的性质节课得出结论1(2023春·八年级课时练习)如图，将边长为3的正方形ABCD纸片沿EF折叠，点C落在AB边上的点G处，点D 与点H重合，CG与EF交于点P，取GH的中点Q，连接PQ，则△GPQ的周长最小值是()A.32+22 B.3+352C.32+23 D.92【答案】B【分析】连接BP，取CD的中点M，连接PM，根据折叠的性质，PM=PQ，GH=DC，PC=PG，要求△GPQ的周长的最小值，只需求PM+PB的最小值，当M、P、B三点共线时，PM+BP=BM最小，在Rt△BCM中，勾股定理求出BM，即可求解．【详解】解：连接BP，取CD的中点M，连接PM，由折叠可知，PM=PQ，GH=DC，PC=PG，在Rt△BCG中，P是CG的中点，∴BP=PG=12GC，∵Q是GH的中点，∴QG=12GH，∴△GPQ的周长=PQ+QG+PG=PM+12GH+PB=PM+PB+12CD，∵CD=3，∴△GPQ的周长=PM+PB+32，当M、P、B三点共线时，PM+BP=BM最小，在Rt△BCM中，BM=35 2，∴△GPQ的周长的最小值为3+352.故选B．【点评】本题考查图形的翻折变换，熟练掌握正方形的性质、直角三角形的性质，正确添加辅助线是解题的关键．2(2021·黑龙江牡丹江·统考中考真题)如图，正方形ABCD的边长为3，E为BC边上一点，BE=1.将正方形沿GF折叠，使点A恰好与点E重合，连接AF，EF，GE，则四边形AGEF的面积为()A.210B.25C.6D.5【答案】D【分析】作FH⊥AB于H，交AE于P，设AG=GE=x，在Rt△BGE中求出x，在Rt△ABE中求出AE，再证明△ABE≌△FHG，得到FG=AE，然后根据S四边形AGEF=S△AGF+S△EGF求解即可【详解】解：作FH⊥AB于H，交AE于P，则四边形ADFH是矩形，由折叠的性质可知，AG=GE，AE⊥GF，AO=EO．设AG=GE=x，则BG=3-x，在Rt△BGE中，∵BE2+BG2=GE2，∴12+(3-x)2=x2，∴x=53．在Rt △ABE 中，∵AB 2+BE 2=AE 2，∴32+12=AE 2，∴AE =10．∵∠HAP +∠APH =90°，∠OFP +∠OPF =90°，∠APH =∠OPF ，∴∠HAP =∠OFP ，∵四边形ADFH 是矩形，∴AB =AD =HF ．在△ABE 和△FHG 中，∠HAP =∠OFP∠ABE =∠GHF AB =HF，∴△ABE ≌△FHG ，∴FG =AE =10，∴S 四边形AGEF =S △AGF +S △EGF=12GF ⋅OA +12GF ⋅OE =12GF ⋅OA +OE =12GF ⋅AE =12×10×10=5．故选D ．【点睛】本题考查了折叠的性质，正方形的性质，矩形的判定与性质，三角形的面积，以及勾股定理等知识，熟练掌握折叠的性质是解答本题的关键．3(2023春·八年级课时练习)如图，将边长为6cm 的正方形纸片ABCD 折叠，使点D 落在AB 边中点E 处，点C 落在点Q 处，折痕为FH ，则线段AF 的长为()A.32B.3C.94D.154【答案】C【分析】设EF =FD =x ，在RT △AEF 中利用勾股定理即可解决问题．【详解】解：∵将边长为6cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，∴EF=DE，AB=AD=6cm，∠A=90°∵点E是AB的中点，∴AE=BE=3cm，在Rt△AEF中，EF2=AF2+AE2，∴(6-AF)2=AF2+9∴AF=94故选C．【点睛】本题考查翻折变换、正方形的性质、勾股定理等知识，解题的关键是设未知数利用勾股定理列出方程解决问题，属于中考常考题型．4(2023春·全国·八年级专题练习)如图，将一边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E，使DE=5，折痕为PQ，则PQ的长为()A.12B.13C.14D.15【答案】B【详解】过点P作PM⊥BC于点M，由折叠得到PQ⊥AE，∴∠DAE+∠APQ=90°，又∠DAE+∠AED=90°，∴∠AED=∠APQ，∵AD∥BC，∴∠APQ=∠PQM，则∠PQM=∠APQ=∠AED，∠D=∠PMQ，PM=AD∴△PQM≌△ADE∴PQ=AE=52+122=13.【点睛】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．5(2023春·八年级课时练习)如图，现有一张边长为8的正方形纸片ABCD，点E为正方形CD边上的一点(不与点A，点D重合)将正方形纸片折叠，使点A落在CD边上的G处，点B落在H处，HG交BC于P，折痕为EF，连接AP，AG.则ΔPGC的周长是．【答案】16.【分析】解过点A作AM⊥GH于M，由正方形纸片折叠的性质得出∠EGH=∠EAB=∠ADC=90°，AE=EG，则EG⊥GH，∠EAG=∠EGA，由垂直于同一条直线的两直线平行得出AM∥EG，得出∠EGA=∠GAM，则∠EAG=∠GAM，得出AG平分∠DAM，则DG=GM，由AAS证得△ADG≌△AMG得出AD=AM=AB，由HL证得Rt△ABP≌Rt△AMP得出BP=MP，则△PGC的周长=CG+PG+PC=CG+MG+PM+PC= CG+DG+BP+PC=CD+CB=16．【详解】解：过点A作AM⊥GH于M，如图所示：∵将正方形纸片折叠，使点A落在CD边上的G处，∴∠EGH=∠EAB=∠ADC=90°，AE=EG，∴EG⊥GH，∠EAG=∠EGA，∴AM∥EG，∴∠EGA=∠GAM，∴∠EAG=∠GAM，∴AG平分∠DAM，∴DG=GM，在△ADG和△AMG中∠DAG=∠GAM∠ADG=∠AMG=90°DG=GM，∴△ADG≌△AMG(AAS)，∴AD=AM=AB，在Rt△ABP和Rt△AMP中AB=AM AP=AP ，∴Rt△ABP≌Rt△AMP(HL)，∴BP=MP，∴△PGC的周长=CG+PG+PC=CG+MG+PM+PC=CG+DG+BP+PC=CD+CB=8+8=16，故答案为16．【点睛】本题考查了折叠的性质、正方形的性质、角平分线的判定与性质、全等三角形的判定与性质等知识，熟练掌握折叠的性质，通过作辅助线构造全等三角形是解题的关键．6(2023春·全国·八年级专题练习)如图，在正方形ABCD中，点E是BC上一点，BF⊥AE交DC于点F，若AB= 5，BE=2，则AF=．【答案】34.【分析】根据正方形的性质得到AB =BC ，∠ABE =∠BCF =90°，推出∠BAE =∠EBH ，根据全等三角形的性质得到CF =BE =2，求得DF =5-2=3，根据勾股定理即可得到结论．【详解】∵四边形ABCD 是正方形，∴AB =BC ，∠ABE =∠BCF =90°，∴∠BAE +∠AEB =90°，∵BH ⊥AE ，∴∠BHE =90°，∴∠AEB +∠EBH =90°，∴∠BAE =∠EBH ，在△ABE 和△BCF 中，∠BAE =∠CBF AB =BC ∠ABE =∠BCF，∴△ABE ≌△BCF (ASA )，∴CF =BE =2，∴DF =5-2=3，∵四边形ABCD 是正方形，∴AB =AD =5，∠ADF =90°，由勾股定理得：AF =AD 2+DF 2=52+32=34．故答案为34．【点睛】此题考查了正方形的性质、全等三角形的判定与性质、勾股定理，本题证明△ABE ≌△BCF 是解本题的关键．7(2023春·全国·八年级专题练习)正方形ABCD 中，点E 、F 在BC 、CD 上，且BE =CF ，AE 与BF 交于点G ．(1)如图1，求证AE ⊥BF ；(2)如图2，在GF 上截取GM =GB ，∠MAD 的平分线交CD 于点H ，交BF 于点N ，连接CN ，求证：AN+CN =2BN ；【答案】(1)见解析；(2)见解析；【分析】(1)根据正方形的性质得AB =BC ，∠ABC =∠BCD =90°，用SAS 证明△ABE ≌△BCF ，得∠BAE =∠CBF ，根据三角形内角和定理和等量代换即可得；(2)过点B 作BH ⊥BN ，交AN 于点H ，根据正方形的性质和平行线的性质，用SAS 证明△AGB ≌△AGM ，得∠BAG =∠MAG ，根据角平分线性质得∠BHA =∠GAN =45°，则△HBN 是等腰直角三角形，用SAS 证明△ABH ≌△CBN ，得AH =CN ，在Rt △HBN 中，根据勾股定理即可得；【详解】解：(1)∵四边形ABCD是正方形，∴AB=BC，∠ABC=∠BCD=90°，在△ABE和△BCF中，AB=BC∠ABE=∠BCF BE=CF∴△ABE≌△BCF(SAS)，∴∠BAE=∠CBF，∵∠AEB+∠BAE=180°-∠ABC=180°-90°=90°，∴∠AEB+∠CBF=90°，∴∠EGB=180°-(∠AEB+∠CBF)=180°-90°=90°，∴AE⊥BF；(2)如图所示，过点B作BH⊥BN，交AN于点H，∵四边形ABCD是正方形，∴AB=AC，∠ABC=∠HBN=90°，∵∠HBN=∠HBA+∠ABN=90°，∠ABC=∠CBN+∠ABN=90°，∴∠HBA=∠CBN，由(1)得，AE⊥BF，∴∠AGB=∠AGM=90°，∴∠HBG=∠AGM=90°,∴HB⎳AE，∴∠BHA=∠EAN，在△AGB和△AGM中，AG=AG∠AGB=∠AGM GB=GM∴△AGB≌△AGM(SAS)，∴∠BAG=∠MAG，∵AN平分∠DAM，∴∠DAN=∠MAN，∴∠BAG+∠MAG+∠MAN+∠DAN=90°，2∠MAG+2∠MAN=90°，∠MAG+∠MAN=45°，∠GAN=45°，∴∠BHA=∠GAN=45°，∴∠BNH=180°-∠HBN-∠BHA=180°-90°-45°=45°，∴△HBN是等腰直角三角形，∴BH=BN，在△ABH和△CBN中，BH=BN∠HBA=∠CBN AB=CB∴△ABH≌△CBN(SAS)，∴AH=CN，在Rt△HBN中，根据勾股定理HN=BH2+BN2=2BN，∴AN+CN=AN+AH=HN=2BN；【点睛】本题考查了正方形的性质，全等三角形的判定与性质，三角形内角和定理，角平分线，等腰直角三角形的判定与性质，勾股定理和锐角三角函数，解题的关键是掌握并灵活运用这些知识点．8(2023春·全国·八年级专题练习)如图1，在正方形ABCD中，E为BC上一点，连接AE，过点B作BG⊥AE于点H，交CD于点G．(1)求证：AE=BG；(2)如图2，连接AG、GE，点M、N、P、Q分别是AB、AG、GE、EB的中点，试判断四边形MNPQ的形状，并说明理由；(3)如图3，点F、R分别在正方形ABCD的边AB、CD上，把正方形沿直线FR翻折，使得BC的对应边B'C'恰好经过点A，过点A作AO⊥FR于点O，若AB'=1，正方形的边长为3，求线段OF的长．【答案】(1)见解析；(2)四边形MNPQ为正方形，理由见解析；(3)10 6【分析】(1)由四边形ABCD为正方形，可得∠ABC=∠BCD=90°，推得∠ABG+∠CBG=90°，由BG⊥AE，可得∠BAE+∠ABG=90°，可证△ABE≅△BCG ASA即可；(2)M、N为AB、AG中点，可得MN为△ABG的中位线，可证MN⎳BG，MN=12BG，由点M、N、P、Q分别是AB、AG、GE、EB的中点，可得PQ是△BEG的中位线，MQ为△ABE的中位线，NP为△AEG的中位线，可证PQ⎳BG，PQ=12BG，MQ⎳AE，MQ=12AE，NP⎳AE，NP=12AE，可证四边形MNPQ为平行四边形．再证四边形MNPQ为菱形，最后证MN⊥MQ即可；(3)延长AO交BC于点S，由对称性可得BF=B'F，AB'=BS=1，AO=SO，由勾股定理可求AS=10，可得AO=12AS=102，设AF=x，在Rt△AB'F中，12+(3-x)2=x2，解得x=53，在Rt△AOF中，可求OF=106．【详解】(1)证明：∵四边形ABCD为正方形，∴∠ABC=∠BCD=90°，∴∠ABG+∠CBG=90°，∵BG⊥AE，∴∠AHB=90°，∴∠BAE+∠ABG=90°，∴∠BAE=∠CBG，在△ABE与△BCG中，∠BAE=∠CBG AB=BC∠ABC=∠BCD，∴△ABE≅△BCG ASA，∴AE=BG．(2)解：四边形MNPQ为正方形，理由如下：∵M、N为AB、AG中点，∴MN为△ABG的中位线，∴MN⎳BG，MN=12BG，∵点M、N、P、Q分别是AB、AG、GE、EB的中点，∴PQ是△BEG的中位线，MQ为△ABE的中位线，NP为△AEG的中位线，，∴PQ⎳BG，PQ=12BG，MQ⎳AE，MQ=12AE，NP⎳AE，NP=12AE，∴MN=PQ，MQ=NP，∴四边形MNPQ为平行四边形．∵AE=BG，∴MN=MQ，∴四边形MNPQ为菱形，∵BG⊥AE，MQ⎳AE，∴MQ⊥BG，∵MN⎳BG，∴MN⊥MQ，∴四边形MNPQ为正方形．(3)解：延长AO交BC于点S，由对称性可知BF=B'F，AB'=BS=1，AO=SO，在Rt△ABS中，AS=AB2+BS2=10，∴AO=12AS=102，设AF=x，则BF=B'F=3-x，在Rt△AB'F中，12+(3-x)2=x2，x=53，∴AF=53，在Rt△AOF中，OF=AF2-AO2=53 2-102 2=106．【点睛】本题考查正方形性质与判定，等角的余角性质三角形全等判定与性质，三角形中位线判定与性质，勾股定理，根据勾股定理建构方程，解拓展一元一次方程等知识，掌握以上知识是解题关键．。

重难点专项突破：正方形中的十字架模型【知识梳理】【考点剖析】一．解答题（共10小题）1．（2022•越秀区校级一模）如图，正方形ABCD中，点P，Q分别为CD，AD边上的点，且DQ＝CP，连接BQ，AP．求证：BQ⊥AP．【分析】根据题意证明△ABQ≌△DAP即可．【解答】解：在正方形ABCD中，AB＝AD＝CD，∠BAD＝∠ADC＝90°，∵DQ＝CP，∴AD﹣DQ＝CD﹣CP，∴AQ＝DP，∴△ABQ≌△DAP（SAS），∴∠DAP＝∠ABQ，∵∠DAP+∠BAP＝90°，∴∠ABQ+BAP＝90°，∴BQ⊥AP．【点评】本题考查正方形的性质，熟练掌握正方形中的“十字架”模型是解题关键．2．（2022•湘潭县校级模拟）如图，有两个动点E，F分别从正方形ABCD的两个顶点B，C同时出发，以相同速度分别沿边BC和CD移动，问：在E，F移动过程中，AE与BF的位置和大小有什么关系吗？并给予证明．【考点】正方形的性质；全等三角形的判定与性质．版权所有【分析】由题中已知的四边形ABCD为正方形，根据正方形的性质，可得一对直角边和一对直角的对应相等，又根据两个动点E，F以相同速度分别沿边BC和CD移动，得到CF＝BC，利用“SAS”证得△ABE≌△BCF，由全等三角形的对应角和对应边分别相等可得，AE＝BF，∠EAB＝∠FBC，利用转化的方法可得∠AOB＝90°，从而得到AE与BF的关系为相互垂直且相等；【解答】解：AE与BF的位置关系是：垂直；大小关系是：相等．证明：∵四边形ABCD为正方形，∴AB＝BC，∠ABC＝∠BCD＝90°，又动点E，F分别从正方形ABCD的两个顶点B，C同时出发，以相同速度分别沿边BC和CD移动，∴BE＝CF，在△ABE和△BCF中，，∴△ABE≌△BCF（SAS），∴∠EAB＝∠FBC，AE＝BF，∵∠CBF+∠ABO＝90°，∴∠EAB+∠ABO＝90°，在△ABO中，∠AOB＝180°﹣（∠EAB+∠ABO）＝90°，∴AE⊥BF．【点评】此题考查了全等三角形的判定与性质，以及正方形的性质，要求学生会从动态变化中找出相等的量，确定相等关系，构造全等三角形，利用转化的思想，从而达到解题的目的．解本题的关键是根据已知条件得出三角形ABE与三角形BCF全等．3．（2023•运城二模）综合与实践：问题情境：在数学活动课上，老师出了这样一道题：在矩形ABCD中，AB＝6，BC＝10，将矩形ABCD绕着点C顺时针旋转α到矩形CEFG的位置，点D 恰好在边CG上．问题解决：（1）如图1，连接AC，CF，AF，AF与CG交于点H．①α的值为，AF＝；②求GH的长．（2）如图2，若将四边形ABCP沿渞直线CP折叠，得到四边形A′PCB′，使得点B的对应点B′恰好在EF上，点A的对应点为A′，点G在A′P上，求AP的长．【考点】解直角三角形的应用；翻折变换（折叠问题）．版权所有【分析】（1）①根据矩形的每一个角都是直角，以及点D恰好在边CG上和得出旋转角α的度数；②先由旋转的性质可得出：AC＝ACF＝90°，然后在Rt△ABC中由勾股定理求出AC的长，进而即可求出AF的长；（2）连接B′G，先求出CB’的长，进而可求出FB'，再利用勾股定理可求出B′G，A′G，然后设AP＝y，则A′P＝y，GP＝x﹣2，DP＝10﹣x，GD＝4，最后在Rt△GDP中由勾股定理列出关于x的方程即可得出答案．【解答】解：（1）①∵四边形ABCD为矩形，AB＝6，BC＝10，∠BCD＝∠B＝∠ADC＝90°，∴AD＝BC＝10，CD＝AB＝6，当矩形ABCD绕着点C顺时针旋转α到矩形CEFG的位置，点D恰好在边CG上时，旋转角α＝∠BCD＝90°，由旋转的性质可知：点A与点F为旋转前、后的对应点，∴AC＝CF，∠ACF＝90°，在Rt△ABC中，AB＝6，BC＝10，由勾股定理得：，∴，在Rt△ACF中，，由勾股定理得：．②由旋转的性质可知：CG＝BC＝10，∠G＝∠B＝90°，FG＝AB＝6，∴GD＝CG﹣CD＝10﹣6＝4，设GH＝x，则HD＝GD﹣GH＝4﹣x，∵∠G＝∠ADC＝90°，∴GF∥AD，∴△GHF∽△DHA，∴FG：AD＝GH：HD，∴FG•HD＝AD•GH，∵FG＝6，HD＝4﹣x，AD＝10，GH＝x，∴6•（4﹣x）＝10x，解得：x＝1.5，∴GH＝1.5．故答案为：①90°，；②1.5．（2）连接B′G．由旋转的性质可知：CE＝CD＝6，EF＝AD＝10，由翻折的性质可知：CB'＝CB＝10，A'B'＝AB＝6，AP＝A'P，在Rt△CEB'中，CE＝6，CB'＝10，由勾股定理得：．∴FB'＝EF﹣EB'＝2，在Rt△GFB'中，FB'＝2，FG＝6，由勾股定理得：，在Rt△A′GB′中，A'B'＝6，，由勾股定理得：．设AP＝y，则A′P＝y，∴GP＝A′P﹣A′G＝x﹣2，DP＝AD﹣AP＝10﹣x，GD＝CG﹣CD＝10﹣6＝4．在Rt△GDP中，由勾股定理得：DP2+DG2＝PG2，∴（10﹣y）2+42＝（y﹣2）2，解得：y＝7，∴AP＝7．【点评】此题主要考查了图形的旋转变换及性质，图形的翻折变换及性质，矩形的性质，相似三角形的判定及性质，勾股定理的应用等，解答此题的关键是准确识图，熟练掌握图形的旋转、翻折变换，难点是设置适当的未知数，灵活利用勾股定理进行计算．4．（2023•遵义模拟）【问题探究】如图1，在正方形ABCD中，点E、F分别在边DC、BC上，且AE⊥DF，求证：AE＝DF．【知识迁移】如图2，在矩形ABCD中，AB＝3，BC＝4，点E在边AD上，点M、N分别在边AB、CD 上，且BE⊥MN，求的值．【拓展应用】如图3，在平行四边形ABCD中，AB＝m，BC＝n，点E、F分别在边AD、BC上，点M、N分别在边AB、CD上，当∠EFC与∠MNC的度数之间满足什么数量关系时，有试写出其数量关系，并说明理由．【考点】相似形综合题．版权所有【分析】【问题探究】利用ASA证明△ADE≌△DCF，得AE＝DF；【知识迁移】过点N作NO⊥AB于点O，利用△ABE∽△ONM，得，即可得出答案；【拓展应用】作AG∥EF，交BC于G，NH∥BC，交AB于H，说明△ABG∽△NHM，得，且四边形AEFG、HNCB是平行四边形，进而解决问题．【解答】【问题探究】证明：∵四边形ABCD是正方形，∴AD＝DC，∠ADC＝∠BCD＝90°，∠AED+∠DAE＝90°，∵AE⊥DF，∴∠AED+∠CDF＝90°，∴∠DAE＝∠CDF，在△ADE与△DCF中，，∴△ADE≌△DCF（ASA），∴AE＝DF；【知识迁移】解：如图，过点N作NO⊥AB于点O，∴∠BMN+∠MNO＝90°，∵BE⊥MN，∴∠BMN+∠MBE＝90°，∴∠MNO＝∠MBE，∠BMN＝∠AEB，在△ABE与△MNO中，∠MNO＝∠MBE，∠BMN＝∠AEB，∴△ABE∽△ONM，∴，∵ON＝BC，∴；【拓展应用】解：当∠EFC＝∠MNC时，，作AG∥EF，交BC于G，NH∥BC，交AB于H，则∠EFC＝∠AGC，∠MNC+∠BMN＝180°，∠MHN＝∠ABC，∵∠AGB+∠AGC＝180°，∴∠AGB＝∠NMH，∴△ABG∽△NHM，∴，∵HN∥BC，AB∥CD，AG∥EF，AD∥BC，∵四边形AEFG、HNCB是平行四边形，∴AG＝EF，MN＝BC，∴当∠EFC＝∠MNC时，．【点评】本题是相似形综合题，主要考查了正方形的性质，平行四边形的判定与性质，相似三角形的判定与性质，熟练掌握正方形中的十字架模型是解题的关键．5．（2023•湘潭县三模）已知点E、F分别是四边形ABCD边AB、AD上的点，且DE与CF相交于点G．（1）如图①，若AB∥CD，AB＝CD，∠A＝90°，且AD•DF＝AE•DC，求证：∠CGE＝90°；（2）如图②，若AB∥CD，AB＝CD，且∠A＝∠EGC时，求证：DE•CD＝CF•DA；（3）如图③，若BA＝BC＝3，DA＝DC＝4，设DE⊥CF，当∠BAD＝90°时，直接写出的值．【考点】相似形综合题．版权所有【分析】（1）根据矩形的判定知四边形ABCD是矩形，利用两边成比例且夹角相等的两个三角形相似，可知△ADE∽△DCF，则∠ADE＝∠DCF，从而证明结论成立；（2）首先可知△GDF∽△ADE，得，再通过△DCF∽△GCD，得，进而解决问题；（3）作CN⊥AD于点N，CM⊥AB交AB的延长线于点M，连接BD，设CN＝x，可知四边形AMCN是矩形，利用SSS证明△ABD≌△CBD，得∠BCD＝∠BAD＝90°，根据△BCN∽△DCN，得，则CM＝x，在Rt△BCM中，利用勾股定理列方程，再利用（1）中基本模型解决问题．【解答】（1）证明：∵AB∥CD，AB＝CD，∴四边形ABCD是平行四边形，∵∠A＝90°，∴四边形ABCD是矩形，∴∠A＝∠FDC＝90°，∵AD•DF＝AE•DC，∴，∴△ADE∽△DCF，∴∠ADE＝∠DCF，∴∠ADE+∠DFC＝∠DCF+∠DFC＝∴∠DGF＝90°，∴∠CGE＝∠DGF＝90°；（2）证明：∵∠DGF＝∠EGC，∠A＝∠EGC，∴∠DGF＝∠A，∴∠GDF＝∠ADE，∴△GDF∽△ADE，∴，∴，∵AB∥CD，∴∠AED＝∠CDG，∵∠AED＝∠CFD，∴∠CFD＝∠CDG，∵∠DCF＝∠GCD，∴△DCF∽△GCD，∴，∴，∴DE•CD＝CF•DA；（3）解：如图，作CN⊥AD于点N，CM⊥AB交AB的延长线于点M，连接BD，设CN＝x，∵∠BAD＝∠AMC＝∠ANC＝90°，∴四边形AMCN是矩形，∴CM＝AN，AM＝CN＝x，∠MCN＝90°，∵BA＝BC＝3，DA＝DC＝4，BD＝BD，∴△ABD≌△CBD（SSS），∴∠BCD＝∠BAD＝90°，∴∠BCM＝∠DCN＝90°﹣∠BCN，∴∠M＝∠CND＝90°，∴△BCN∽△DCN，∴，∴CM＝x，在Rt△BCM中，由勾股定理得，∴（x﹣3），解得x＝或x＝0（不合题意舍去），∴CN＝，∵DE⊥CF，∴∠DGF＝90°，∴∠CFN+∠ADE＝90°，∵∠DEA+∠ADE＝90°，∴∠DEA＝∠CFN，∴∠A＝∠CNF＝90°，∴△ADE∽△NCF，∴．【点评】本题是相似形综合题，主要考查了矩形的判定与性质，平行四边形的性质，全等三角形的判定与性质，相似三角形的判定与性质等知识，构造模型、应用模型解决问题是解题的关键．6．（2022•天桥区一模）（1）如图1，在正方形ABCD中，点E，F分别是AB，AD上的两点，连接DE，CF，DE⊥CF，则的值为；（2）如图2，在矩形ABCD中，AD＝5，CD＝3，点E是AD上的一点，连接CE，BD，且CE⊥BD，则的值为；（3）如图3，在四边形ABCD中，∠A＝∠B＝90°，点E为AB上一点，连接DE，过点C作DE的垂线交ED的延长线于点G，交AD的延长线于点F，求证：；（4）如图4，在Rt△ABD中，∠BAD＝90°，AB＝3，AD＝9，将△ABD沿BD翻折，点A落在点C处得△CBD，点E，F分别在边AB，AD上，连接DE，CF，DE⊥CF．请问．是定值吗？若是，直接写出这个定值，若不是，请说明理由．【考点】相似形综合题．版权所有【分析】（1）根据正方形的性质，利用ASA证明△ADE≌△DCF，得DE＝CF，从而得出答案；（2）首先根据同角的余角相等知∠ADB＝∠DCE，则△ADB∽△DCE，得；（3）过点作CH⊥AD，交AD延长线于H，利用两个角相等可证明△ADE∽△HCF，得；（4）连接AC交BD于H，CF与DE交于G，CF与DB交于P，首先可证明△ACF∽△BDE，得，再利用勾股定理求出BD，面积法求出AC的长，从而得出答案．【解答】（1）解：∵四边形ABCD是正方形，∴AD＝DC，∠A＝∠FDC＝90°，∵DE⊥CF，∴∠ADE+∠DFC＝90°，∠DFC+∠DCF＝90°，∴∠ADE＝∠DCF，在△ADE与△DCF中，，∴△ADE≌△DCF（ASA），∴DE＝CF，∴，故答案为：1；（2）解：∵四边形ABCD为矩形，∴∠A＝∠EDC＝90°，∵CE⊥BD，∴∠ADB+∠CED＝90°，∠CED+∠DCE＝90°，∴∠ADB＝∠DCE，∴△ADB∽△DCE，∴，故答案为：；（3）证明：如图，过点作CH⊥AD，交AD延长线于H，∵∠H＝∠A＝∠B＝90°，∴四边形ABCH为矩形，∴CH＝AB，∵CG⊥EG，∴∠G＝90°＝∠A＝∠H，∵∠ADE＝∠GDF，∵∠GFD＝∠HFC，∴∠ADE＝∠HCF，∴△ADE∽△HCF，∴；（4）解：是定值，理由如下：连接AC交BD于H，CF与DE交于G，CF与DB交于P，∵将△ABD沿BD翻折，点A落在点C处得△CBD，∴AC⊥BD，∴∠BAH+∠CAF＝90°，∠BAH+∠EBD＝90°，∠CHP＝90°，∴∠CAF＝∠DBE，∵CF⊥DE，∴∠PGD＝90°＝∠CHP，∵∠HPC＝∠GPD，∴∠ACF＝∠BDE，∴△ACF∽△BDE，∴，∵AB＝3，AD＝9，由勾股定理得BD＝＝3，∴，∴AH＝，∴AC＝2AH＝，∴．【点评】本题是相似形综合题，主要考查了正方形和矩形的性质，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理等知识，熟练掌握相似三角形的判定与性质是解题的关键．7．（2022春•潮阳区期末）（1）如图1，在正方形ABCD中，AE、DF相交于点O且AE⊥DF则AE和DF 的数量关系为．（2）如图2，在正方形ABCD中，E、F、G分别是边AD、BC、CD上的点，BG⊥EF，垂足为H．求证：EF＝BG．（3）如图3，在正方形ABCD中，E、F、M分别是边AD、BC、AB上的点，AE＝2，BF＝5，BM＝1，将正方形沿EF折叠，点M的对应点恰好与CD边上的点N重合，求CN的长度．【考点】四边形综合题．版权所有【分析】（1）证明∠BAE＝∠ADF，则△ABE≌△DAF（AAS），即可求解；（2）证明△BCG≌EMF△（ASA），即可求解；（3）证明知△EHF≌△MGN（ASA），则NG＝HF，而AE＝2，BF＝5，故NG＝HF＝5﹣2＝3，进而求解．【解答】解：（1）∵∠DAO+∠BAE＝90°，∠DAO+∠ADF＝90°，∴∠BAE＝∠ADF，在△ABE和△DAF中，，∴△ABE≌△DAF（ASA），∴AE＝DF，故答案为AE＝DF；（2）如图1，故点E作EM⊥BC于点M，则四边形ABME为矩形，则AB＝EM，在正方形ABCD中，AB＝BC，∴EM＝BC，∵EM⊥BC，∴∠MEF+∠EFM＝90°，∵BC⊥EM，∴∠CBG+∠EFM＝90°，∴∠CBG＝∠MEF，在△BCG和△EMF中，，∴△BCG≌△EMF（ASA），∴BG＝EF；（3）如图2，连接MN，∵M、N关于EF对称，∴MN⊥EF，过点E作EH⊥BC于点H，过点M作MG⊥CD于点G，则EH⊥MG，由（2）同理可得：△EHF≌△MGN（ASA），∴NG＝HF，∵AE＝2，BF＝5，∴NG＝HF＝5﹣2＝3，又∵GC＝MB＝1，∴NC＝NG+CG＝3+1＝4．【点评】本题为四边形综合题，主要考查的是三角形全等和正方形的性质，有一定的综合性，难度适中．8．（2023春•青秀区校级期中）在正方形ABCD中：（1）已知：如图①，点E、F分别在BC、CD上，且AE⊥BF，垂足为M，求证：AE＝BF．（2）如图②，如果点E、F、G分别在BC、CD、DA上，且GE⊥BF，垂足M，那么GE、BF相等吗？证明你的结论．（3）如图③，如果点E、F、G、H分别在BC、CD、DA、AB上，且GE⊥HF，垂足M，那么GE、HF 相等吗？证明你的结论．【考点】正方形的性质；全等三角形的判定与性质．版权所有【分析】（1）根据正方形的性质，得到∠ABE＝∠BCF＝90°，AB＝BC，进而得到∠BAE＝∠CBF，则△ABE≌△BCF，进一步根据全等三角形的性质进行证明；（2）过点A作AN∥GE，可证四边形ANEG是平行四边形，根据平行四边形的对边相等可得AN＝GE，由（1）的结论可知AN＝BF，所以GE＝BF；（3）分别过点A、B作AP∥GE，BQ∥HF，可证四边形APEG、四边形BQFH为平行四边形，根据平行四边形的对边相等可得AP＝GE，BQ＝HF，由（1）的结论可知AP＝BQ，所以GE＝HF．【解答】（1）证明：∵四边形ABCD是正方形，AE⊥BF，∴∠BAE+∠ABM＝90°，∠CBF+∠ABM＝90°，∴∠BAE＝∠CBF，∵在△ABE和△BCF中，，∴△ABE≌△BCF（AAS），∴AE＝BF；（2）GE＝BF．证明：如图②，过点A作AN∥GE，∵AD∥BC，∴四边形ANEG是平行四边形，∴AN＝GE，∵GE⊥BF，∴AN⊥BF，由（1）可得△ABN≌△BCF，∴AN＝BF，∴GE＝BF；（3）GE＝HF．证明：如图③，分别过点A、B作AP∥GE，BQ∥HF，∵AD∥BC，AB∥DC，∴四边形APEG、四边形BQFH为平行四边形，∴AP＝GE，BQ＝HF，∵GE⊥HF，∴AP⊥BQ，由（1）可得△ABP≌△BCQ，∴AP＝BQ，∴GE＝HF．【点评】本题主要考查了正方形的性质和全等三角形的判定，熟练掌握正方形性质确定三角形全等的条件是解题的关键，（2）（3）两题通过作辅助线构造成（1）的形式是得解的关键．9．（2020秋•漳州期中）（1）如图1，在正方形ABCD中，AE，DF相交于点O且AE⊥DF．则AE和DF的数量关系为．（2）如图2，在正方形ABCD中，E，F，G分别是边AD，BC，CD上的点，BG⊥EF，垂足为H．求证：EF＝BG．（3）如图3，在正方形ABCD中，E，F，M分别是边AD，BC，AB上的点，AE＝2，BF＝4，BM＝1，将正方形沿EF折叠，点M的对应点与CD边上的点N重合，求CN的长度．【考点】四边形综合题．版权所有【分析】（1）证明∠BAE＝∠ADF，则△ABE≌△DAF（ASA），即可求解；（2）由正方形的性质得出∠CBG＝∠MEF，证明△BCG≌△EMF（ASA），即可求解；（3）证明△EHF≌△MGN（ASA），则NG＝HF，而AE＝2，BF＝4，故NG＝HF＝4﹣2＝2，进而求解．【解答】解：（1）依题意得：∠DAO+∠BAE＝90°，∠DAO+∠ADF＝90°，∴∠BAE＝∠ADF，在△ABE和△DAF中，，∴△ABE≌△DAF（ASA），∴AE＝DF，故答案为：AE＝DF；（2）如图1，过点E作EM⊥BC于点M，则AB＝EM，∵AB＝BC，∴EM＝BC，∵EM⊥BC，∴∠MEF+∠EFM＝90°，∵BC⊥EM，∴∠CBG+∠EFM＝90°，∴∠CBG＝∠MEF，在△BCG和△EMF中，，∴△BCG≌△EMF（ASA），∴EF＝BG；（3）如图2，连接MN，∵MN⊥EF，过点E作EH⊥BC于点H，过点M作MG⊥CD于点G，由（2）同理可得：△EHF≌△MGN（ASA），∴NG＝HF，∵AE＝2，BF＝4，∴NG＝HF＝4﹣2＝2，∴NC＝NG+CG＝2+1＝3．∴CN的长度为3．【点评】本题为四边形综合题，考查了直角三角形的性质，全等三角形的判定与性质，正方形的性质，轴对称的性质，熟练掌握正方形的性质是解题的关键．【过关检测】一．解答题（共13小题）1．如图，正方形ABCD中，E、F分别是AB、BC边上的点，且AE＝BF，求证：AF⊥DE．【考点】正方形的性质；全等三角形的判定与性质．版权所有【分析】由题意先证明△ADE≌△BAF，得出∠EDA＝∠FAB，再根据∠ADE+∠AED＝90°，推得∠FAE+∠AED ＝90°，从而证出AF⊥DE．【解答】证明：∵四边形ABCD为正方形，∴DA＝AB，∠DAE＝∠ABF＝90°，又∵AE＝BF，∴△DAE≌△ABF，∴∠ADE＝∠BAF，（4分）∵∠ADE+∠AED＝90°，∴∠FAE+∠AED＝90°，∴∠AGE＝90°，∴AF⊥DE．（3分）【点评】本题考查了正方形的性质以及全等三角形．2．如图，在正方形ABCD中，E，F分别是边AD，DC上的点，且AF⊥BE．求证：AF＝BE．【考点】全等三角形的判定与性质；正方形的性质．版权所有【分析】根据正方形的性质可得AB＝AD，∠BAE＝∠D＝90°，再根据同角的余角相等求出∠ABE＝∠DAF，然后利用“角边角”证明△ABE和△DAF全等，再根据全等三角形的证明即可．【解答】解：∵四边形ABCD是正方形，∴AB＝AD，∠D＝∠BAE＝90°，∵BE⊥AF，∴∠ABE+∠BAF＝90°，∠DAF+∠＝90°∴∠ABE＝∠DAF，在△ABE和△DAF中，，∴△ABE≌△DAF（ASA），∴BE＝AF．【点评】本题考查了正方形的性质，全等三角形的判定与性质，主要利用了正方形的四条边都相等，每一个角都是直角的性质，同角的余角相等的性质，利用三角形全等证明相等的边是常用的方法之一，要熟练掌握并灵活运用．3．如图，在正方形ABCD中，点E、F分别在BC、CD上，BE＝CF，连接AE、BF相交于点G．现给出了四个结论：①AE＝BF；②∠BAE＝∠CBF；③BF⊥AE；④AG＝FG．请在这些结论中，选择一个你认为正确的结论，并加以证明．结论：BF⊥AE．【考点】正方形的性质；全等三角形的判定与性质．版权所有【分析】根据正方形的性质证明三角形的全等，选择一个正确的答案进行证明即可．【解答】解：正确结论：①②③；证明：在正方形ABCD中，AB＝BC，∠ABE＝∠C＝90，又∵BE＝CF，∴△ABE≌△BCF（SAS），∴AE＝BF∠BAE＝∠CBF，∴∠FBC+∠BEG＝∠BAE+∠BEG＝90°，∴∠BGE＝90°，∴BF⊥AE．故答案为：BF⊥AE．【点评】本题的考点是：正方形的性质、证明线段的相等、线段垂直和三角形全等．4．已知：正方形ABCD．（1）如图①，E，F分别是边CD，AD上的一点，且AE⊥BF，求证：AE＝BF．（2）M，N，E，F分别在边AB，CD，AD，BC上，且MN＝EF，那么MN⊥EF？请画图表示，并作简要说明：（3）将正方形ABCD折叠，使得点A落在边CD上的E点，折痕为MN，若已知该正方形边长为12，MN的长为13，求CE的长．【考点】四边形综合题．版权所有【分析】（1）由正方形的性质得出AB＝AD，∠BAF＝∠ADE＝90°，证出∠ABF＝∠DAE，由ASA证明△BAF ≌△ADE，得出对应边相等即可；（2）过点E作EG⊥BC于点G，过点M作MP⊥CD于点P，设EF与MN相交于点O，MP与EF相交于点Q，由正方形的性质可得EG＝MP，先利用“HL”证明Rt△EFG≌Rt△MNP，由全等三角形对应角相等可得∠MNP＝∠EFG，再由角的关系推出∠EQM＝∠MNP，由∠MNP+∠NMP＝90°得出∠NMP+∠EQM＝90°，得出∠MOQ＝90°，由垂直的定义得出MN⊥EF，当E向D移动，F向B移动，同样使MN＝EF，此时就不垂直；（3）连接AE时，则线段MN垂直平分AE，过点B作BF∥MN，则BF＝MN，且AE⊥BF，由（1）知AE＝BF＝MN＝13，由勾股定理求出DE，即可得出CE的长．【解答】（1）证明：∵四边形ABCD为正方形，∴AB＝AD，∠BAF＝∠ADE＝90°，∵AE⊥BF，∴∠BAE+∠ABF＝90°，∵∠BAE+∠DAE＝90°，∴∠ABF＝∠DAE，在△BAF和△ADE中，，∴△BAF≌△ADE（ASA），∴AE＝BF；（2）解：MN与EF不一定垂直；如图1所示，当MN＝EF时，MN⊥EF，如图2所示，当MN＝EF时，MN与EF就不垂直了；理由如下：过点E作EG⊥BC于点G，过点M作MP⊥CD于点P，设EF与MN相交于点O，MP与EF相交于点Q，∵四边形ABCD是正方形，∴EG＝MP，在Rt△EFG和Rt△MNP中，，∴Rt△EFG≌Rt△MNP（HL），∴∠MNP＝∠EFG，∵MP⊥CD，∠C＝90°，∴MP∥BC，∴∠EQM＝∠EFG＝∠MNP，又∵∠MNP+∠NMP＝90°，∴∠EQM+∠NMP＝90°，在△MOQ中，∠MOQ＝180°﹣（∠EQM+∠NMP）＝180°﹣90°＝90°，∴MN⊥EF，当E向D移动，F向B移动，同样使MN＝EF，此时就不垂直，故此，MN与EF不一定垂直；（3）解：如图3所示，连接AE，则线段MN垂直平分AE，过点B作BF∥MN，则四边形MNBF是平行四边形，∴BF＝MN，且AE⊥BF，由（1）知AE＝BF＝MN＝13，由勾股定理得：DE＝＝＝5，∴CE＝CD﹣DE＝12﹣5＝7．【点评】本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质、勾股定理、平行四边形的判定与性质等知识；本题难度较大，综合性强．5．探究一：如图1，已知正方形ABCD，E、F分别是BC、AB上的两点，且AE⊥DF．小明经探究，发现AE＝DF．请你帮他写出证明过程．探究二：如图2，在矩形ABCD中，AB＝3，BC＝4，E、G分别在边BC、AD上，F、H分别在边AB、CD上，且GE⊥FH．小明发现，GE与FH并不相等，请你帮他求出的值．探究三：小明思考这样一个问题：如图3，在正方形ABCD中，若E、G分别在边BC、AD上，F、H分别在边AB、CD上，且GE＝FH，试问：GE⊥FH是否成立？若一定成立，请给予证明；若不一定成立，请画图并作出说明．【考点】四边形综合题．版权所有【分析】探究一、求出∠ADF＝∠BAE，∠DAF＝∠ABE＝90°，求出△ADF≌△DAE即可；探究二、作GM⊥BC于M，FN⊥CD于N，证出△GME∽△FNH即可；探究三、画出图形，即可得出答案．【解答】探究一证明：∵四边形ABCD是正方形，∴∠DAF＝∠ABE＝90°，AD＝AB，∴∠DAE+∠BAE＝90°，∵AE⊥DF，∴∠DAE+∠ADF＝90°，∴∠ADF＝∠BAE，在△ADF和△BAE中，，∴△ADF≌△DAE（ASA），∴AE＝DF；探究二、解：作GM⊥BC于M，FN⊥CD于N，如图2，则GM＝AB＝3，FN＝AD＝4，∠GME＝∠FNH＝∠GOF＝90°，∴∠EGM+∠GQO＝90°，∠HFN+∠FQR＝90°，∵∠FQR＝∠GQO，∴∠HFN＝∠EGM，∵∠GME＝∠FNH，∴△GME∽△FNH，∴＝，又∵AB＝GM＝3，FN＝BC＝4，∴＝；探究三、解：不一定成立，如图3，当在GE时，GE和FH垂直，当在G′E′时，G′E′和FH就不垂直．【点评】本题考查了矩形性质，全等三角形的性质和判定，相似三角形的性质和判定的应用，主要考查学生的推理能力．6．问题背景某课外学习小组在一次学习研讨中，得到如下命题：①如图1，在正三角形ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON＝60°，则BM＝CN．②如图2，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON＝90°，则BM＝CN．然后运用类比的思想提出了如下的命题：③如图3，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON＝108°，则BM＝CN．任务要求（1）请你对命题③进行证明；（2）请你继续完成下面的探索：如图4，在五边形ABCDE中，M、N分别是DE、AE上的点，BM与CN 相交于点O，当∠BON＝108°时，请问结论BM＝CN是否还成立？若成立，请给予证明；若不成立，请说明理由．【考点】四边形综合题．版权所有【分析】（1）根据正五边形性质得出∠D＝∠BCM＝108°，BC＝CD，求出∠CBM＝∠DCN，根据ASA推出△BCM≌△CDN即可；（2）连接CE，BD，根据正五边形性质得出∠AED＝∠EDC＝∠BCD＝108°，ED＝DC＝BC，求出N、E、M、O四点共圆，求出∠ENC＝∠BMD，证△BCD≌△CDE，推出BD＝CE，∠DEC＝∠BDC，求出∠NEC＝∠MDB，根据AAS证△ECN≌△DBM，即可得出答案．【解答】（1）证明：∵五边形ABCDE是正五边形，∴∠D＝∠BCM＝＝108°，BC＝CD，∵∠BON＝108°，∴∠BON＝∠CBM+∠BCN＝108°，∠BCD＝∠BCN+∠DCN＝108°，∴∠CBM＝∠DCN，在△BCM和△CDN中，，∴△BCM≌△CDN（ASA），∴BM＝CN．（2）BM＝CN还成立，理由是：连接CE，BD，∵五边形ABCDE是正五边形，∴∠AED＝∠EDC＝∠BCD＝108°，ED＝DC＝BC，∵∠BON＝108°，∴∠NOM+∠AED＝180°，∴N、E、M、O四点共圆，∴∠ENC+∠EMB＝180°，∵∠EMB+∠DMB＝180°，∴∠ENC＝∠BMD，在△BCD和△CDE中，，∴△BCD≌△CDE（SAS），∴BD＝CE，∠DEC＝∠BDC，∵∠EDC＝∠AED＝108°，∴∠AED﹣∠DEC＝∠CDE﹣∠CDB，即∠NEC＝∠MDB，在△ECN和△DBM中，，∴△ECN≌△DBM（AAS），∴BM＝CN，即BM＝CN还成立．【点评】本题考查了四点共圆，圆内接四边形的性质，全等三角形的性质和判定，正多边形的性质的应用，主要考查学生的推理能力．7．（1）如图1，正方形ABCD中，E、F分别是BC、CD边上的点，且满足BE＝CF，连接AE、BF交于点H..请直接写出线段AE与BF的数量关系和位置关系；（2）如图2，正方形ABCD中，E、F分别是BC、CD边上的点，连接BF，过点E作EG⊥BF于点H，交AD于点G，试判断线段BF与GE的数量关系，并证明你的结论；（3）如图3，在（2）的条件下，连接GF、HD．求证：①FG+BE≥BF；②∠HGF＝∠HDF．【考点】四边形综合题．版权所有【分析】（1）证△ABE≌△BCF，推出AE＝BF，∠BAE＝∠CBF，求出∠CBF+∠AEB＝90°，求出∠BHE＝90°即可；（2）过点A作AM∥GE交BC于M，证△ABM≌△BCF，推出AM＝BF，根据AM∥GE且AD∥BC推出AM ＝GE即可；（3）①过点B作BN∥FG，且使BN＝FG，连接NG、NE，根据四边形NBFG是平行四边形的性质求出BF＝NG，BF∥NG，求出△NGE为等腰直角三角形，由勾股定理得NE＝NG，即NE＝BF，即可求出答案；②证G、H、F、D四点共圆，根据圆周角定理得出∠HGF＝∠HDF即可．【解答】（1）解：AE＝BF且AE⊥BF，理由是：∵四边形ABCD是正方形，∴∠ABE＝∠C＝90°，AB＝BC，∵在△ABE和△BCF中，∴△ABE≌△BCF（SAS），∴AE＝BF，∠BAE＝∠CBF，∵∠ABE＝90°，∴∠BAE+∠AEB＝90°，∴∠CBF+∠AEB＝90°，∴∠BHE＝180°﹣90°＝90°，∴AE⊥BF．（2）BF＝GE，证明：过点A作AM∥GE交BC于M，∵EG⊥BF，∴AM⊥BF，∴∠BAM+∠ABF＝90°，∵正方形ABCD，∴AB＝BC，AD∥BC，∠ABC＝∠BCD＝90°，∴∠CBF+∠ABF＝90°，∴∠BAM＝∠CBF，∵在△ABM和△BCF中，∴△ABM≌△BCF（ASA），∴AM＝BF，∵AM∥GE且AD∥BC，∴AM＝GE，∴BF＝GE；（3）证明：①：过点B作BN∥FG，且使BN＝FG，连接NG、NE，∴四边形NBFG是平行四边形，∴BF＝NG，BF∥NG，由（2）可知，BF⊥GE，且BF＝GE，∴NG⊥EG且NG＝EG，∴△NGE为等腰直角三角形，由勾股定理得NE＝NG，∴NE＝BF，当点F与点D不重合，点E与点C不重合时，N、B、E三点不共线，此时，在△BEN中，NB+BE＞NE，即FG+BE＞BF，当点F与点D重合，点E与点C重合时，N、B、E三点共线，此时，NB+BE＝NE，即FG+BE＝BF；②证明：∵正方形ABCD∴∠ADC＝90°以GF为直径作⊙P，则点D在⊙P上∵∠GHF＝90°∴点H也在⊙P上∴∠HGF＝∠HDF．【点评】本题考查了圆周角定理，正方形性质，勾股定理，等腰直角三角形的性质和判定，全等三角形的性质和判定的应用，主要考查学生综合运用性质进行推理和计算的能力．8．（1）如图1，在正方形ABCD中，点E，F分别在边BC，CD上，AE，BF交于点O，∠AOF＝90°．求证：BE＝CF．（2）如图2，在正方形ABCD中，点E，H，F，G分别在边AB，BC，CD，DA上，EF，GH交于点O，∠FOH＝90°，EF＝4．求GH的长．【考点】正方形的性质；全等三角形的判定与性质．版权所有【分析】（1）根据∠AOF＝90°，利用同角的余角相等得出∠EAB＝∠FBC，再根据ASA即可证出△FBC≌△EAB；（2）过A作AM∥GH，交BC于M，过B作BN∥EF，交CD于N，AMBN交于点O′，利用平行四边形的判定，可知四边形AMHG和四边形BNFE是▱，那么AM＝GH，BN＝EF，由于∠EOH＝90°，结合平行线的性质，可知∠AO′N＝90°，那么此题就转化成（1），求△BCN≌△ABM即可；【解答】（1）证明：∵正方形ABCD中，∴AB＝BC，∠ABE＝∠BCF＝90°，∵∠AOF＝90°，∠AOB＝90°，∴∠BAE+∠OBA＝90°，又∵∠FBC+∠OBA＝90°，∴∠BAE＝∠CBF（同角的余角相等），∴△ABE≌△BCF（ASA）．∴BE＝CF；（2）解：如图，过点A作AM∥GH交BC于M，过点B作BN∥EF交CD于N，AM与BN交于点O′，则四边形AMHG和四边形BNFE均为平行四边形，∴EF＝BN，GH＝AM，∵∠FOH＝90°，AM∥GH，EF∥BN，∴∠NO′A＝90°，故由（1）得，△ABM≌△BCN＝BN，∴GH＝EF＝4；【点评】本题利用了正方形的性质、平行四边形的判定、平行线的性质、全等三角形的判定和性质等知识，关键是作辅助线，构造全等三角形．9．如图1，正方形ABCD中，E、F分别是CD、AD上的点，且满足AF＝DE，连接BF、AE，交点为O，（1）请判断AE与BF的关系，并证明你的结论．（2）如图2，连接BE、EF，若G、H、P、Q分别是AB、BE、EF、F A的中点，试说明四边形GHPQ是正方形．【考点】正方形的性质；正方形的判定；全等三角形的判定与性质．版权所有【分析】（1）根据条件证明△ABF≌△DAE，利用全等的性质证明AE＝BF，AE⊥BF；（2）由（1）的结论可知，四边形ABEF的对角线互相垂直且相等，根据三角形中位线的性质可证明四边形GHPQ是正方形．【解答】解：（1）AE＝BF，AE⊥BF．证明：在△ABF和△DAE中，∵，∴△ABF≌△DAE（SAS），∴BF＝AE，∠BFA＝∠AED，又∠EAD+∠AED＝90°，∴∠BFA+∠AED＝90°，∴AE⊥BF；（2）理由：由（1）可知四边形ABEF的对角线互相垂直且相等，∵GQ为△ABF的中位线，∴GQ＝BF，GQ∥BF，同理可证PH＝BF，PH∥BF，即PH＝GQ，PH∥GQ，四边形PQGH为平行四边形，易证PQ＝AE＝BF＝PH，∴▱PQGH菱形，∵AE⊥BF，∴PQ⊥PH，菱形PQGH为正方形．【点评】本题考查了正方形的性质，与判定，全等三角形的判定与性质．关键是利用正方形的性质证明三角形全等，利用性质证明AE与BF的相等与垂直关系．10．在正方形ABCD中：（1）如图①，点E、F分别在BC、CD上，且AE⊥BF，垂足为M．求证：AE＝BF．（2）如图②，如果点E、F、G、H分别在BC、CD、DA、AB上，且GE⊥HF，垂足M．那么GE、HF 相等吗？证明你的结论．（3）如图③，在等边三角形ABC中，点E、F分别在BC、CA上，且BE＝CF，你能猜想∠AMF的度数吗？证明你的结论．【考点】正方形的性质；全等三角形的判定与性质；等边三角形的性质．版权所有【分析】有三角形的直接证明三角形全等，没三角形的构造直角三角形，利用正方形的性质证明三角形全等；对于第4问也是证明三角形全等，再用角等量代换求解．【解答】（1）证明：∵AE⊥BF，∴∠BAE+∠ABM＝90°，∠CBF+∠ABM＝90°，∴∠BAE＝∠CBF，在△BAE和△CBF中，△BAE≌△CBF（AAS），∴AE＝BF；（2）结论：HF＝GE分别过G、H作GT⊥BC、HN⊥CD，∴GT⊥HN，∴∠FHN+∠HPO＝90°，∠EGT+∠GPM＝90°，∠GPM＝∠HPO，∴∠FHN＝∠EGT，∵HN＝GT，∠GTE＝∠NHF＝90°，在△GTE与△HNF中，，∴△GTE≌△HNF，∴GE＝HF；（3）结论：∠AMF＝60°．在△ABE和△BCF中，∴△ABE≌△BCF（SAS），∴∠BAE＝∠CBF，∴∠ABE＝∠BME＝60°，∴∠AMF＝∠BME＝60°．【点评】本题考查正方形的性质，全等三角形的判定和性质以及作辅助线的能力和适时等量代换的能力．11．如图，有两个动点E，F分别从正方形ABCD的两个顶点B，C同时出发，以相同速度分别沿边BC和CD移动，问：（1）在E，F移动过程中，AE与BF的位置和大小有何关系？并给予证明；（2）若AE和BF相交点O，图中有多少对相似三角形？请把它们写出来．【考点】相似三角形的判定；全等三角形的判定与性质；正方形的性质．版权所有【分析】（1）两个动点E，F以相同速度分别沿边BC和CD移动，所以CF＝BE，△ABE≌△BCF（SAS）可得，AE＝BF，∠AOB＝90°，AE与BF的关系式相互垂直且相等；（2）由（1）中的相等关系可知相似三角形有△ABO∽△BEO△ABO∽△AEB△BEO∽△BFO△ABE∽△BCF△ABO∽△BFC．【解答】解：（1）在正方形ABCD中，AB＝BC，∠ABC＝∠BCD＝90°，∵BE＝CF，∴△ABE≌△BCF（SAS）．∴∠EAB＝∠FBC，AE＝BF．∵∠CBF+∠ABO＝90°，∴∠EAB+∠ABO＝90°．在△ABO中，∠AOB＝180°﹣（∠EAB+∠ABO）＝90°，∴AE⊥BF．（2）有6对相似三角形，△ABO∽△BEO；△ABO∽△AEB；△BEO∽△BFC；△ABE∽△BCF；△ABO∽△BFC；△BOE∽△ABE【点评】考查了相似三角形和全等三角形的判定，会从动态变化中找出相等的量，确定相等关系，利用相似三角形判定定理进行判定．12．问题背景：某课外学习小组在一次学习研讨中，得到了如下两个命题：①如图a，在正三角形ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON＝60°，则BM＝CN；②如图b，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON＝90°，则BM＝CN；然后运用类比的思想提出了如下命题：③如图c，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON＝108°，则BM＝CN；任务要求：（1）请你从①，②，③三个命题中选择一个进行证明；（说明选①做对的得4分，选②做对的得3分，选③做对的得5分）（2）请你继续完成下面的探索：ⅰ、如图d，在正n（n≥3）边形ABCDEF…中，M、N分别是CD、DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM＝CN成立？（不要求证明）ⅱ、如图e，在正五边形ABCDE中，M、N分别是DE、AE上的点，BM与CN相交于点O，若∠BON＝108°时，试问结论BM＝CN是否还成立？若成立，请给予证明；若不成立．请说明理由．【考点】四边形综合题．版权所有【分析】（1）正三角形ABC BM＝CN，由于∠BON＝∠MBC+∠BCO＝60°，而∠ACB＝∠ACN+∠OCB＝60°，因此∠ACN＝∠MBC，又知道∠A＝∠BCM＝60°，AC＝BC，因此△ACN≌△CBM，可得出BM＝CN；正方形和正五边形的证明过程与正三角形的一样，都是通过全等三角形来得出线段的相等，证三角形的过程中都是根据∠BON和多边形的内角相等得出一组两三角形中的一组对应角相等，然后根据正多边形的内角和边相等，得出BCM和CND全等，进而得出BM＝CN；（2）①由（1）的证明过程可知道∠MON的度数应该是正多边形的内角的度数，当∠BON＝时，结论BM＝CN成立，②可参照（1）先得出三角形BCD和CDE全等，然后通过证三角形CEN和BDM全等来得出结论，在证三角形CEN和BDM全等的过程中也是通过∠BON与正五边形的内角相等得出一组对应角相等，然后根据正五边形的内角减去第一对全等三角形中得出的相等角来得出另一组对应角相等，可通过△BCD≌△CDE得出CE ＝BD，那么可得出三角形CEN和BDM全等，由此可得证．【解答】解：（1）选命题①。

专题02正方形中十字架模型十字架模型分别连接正方形的两组对边上任意两点，得到的两条线段（如：图1中的线段AF 与BE，图2中的线段EF与MN，图3中的线段BE与AF）满足：若垂直，则相等。

【典例1】问题情境：苏科版八年级下册数学教材第94页第19题第（1）题是这样一个问题：如图1，在正方形ABCD中，点E、F分别在边BC、CD上，且AE⊥BF，垂足为M．那么AE与BF相等吗？（1）直接判断：AE BF（填“＝”或“≠”）；在“问题情境”的基础上，继续探索：问题探究：（2）如图2，在正方形ABCD中，点E、F、G分别在边BC、CD和DA上，且GE⊥B F，垂足为M．那么GE与BF相等吗？证明你的结论；问题拓展：（3）如图3，点E在边CD上，且MN⊥AE，垂足为H，当H在正方形ABCD的对角线BD上时，连接AN，将△AHN沿着AN翻折，点H落在点H′处．①四边形AHNH′是正方形吗？请说明理由；②若AB＝6，点P在BD上，BD＝3BP，直接写出PH′+AN的最小值为．【变式1-1】如图，在正方形ABCD中，点E、F分别在边CD，AD上，BE与CF交于点G，若BC＝4，DE＝AF＝1，则CG的长是（）A．2B．C．D．【变式1-2】如图，点E、F、G分别是正方形ABCD的边AD、BC、AB上的点，连接DG，EF，GF．且EF＝DG，DE＝2AG，∠ADG的度数为α，则∠EFG的度数为（）A．αB．2αC．45°﹣αD．45°+α【变式1-3】如图，E、F分别是正方形ABCD的边CD，AD上的点，且CE＝DF，AE，BF＝S四边形DEOF中，相交于点O，下列结论①AE＝BF；②AE⊥BF；③AO＝OE；④S△AOB 正确结论的个数为（）A．4个B．3个C．2个D．1个1．在矩形纸片ABCD中，AB＝5，BC＝8，可以裁出一个最大正方形的边长是（）A．4B．5C．6D．82．如图所示，E、F、G、H分别为正方形ABCD的边AB，BC，CD，DA上的点，且AE＝BF＝CG＝DH＝AB，则图中阴影部分的面积与正方形ABCD的面积之比为（）A．B．C．D．3．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，那么CH的长是（）A．2.5B．2C．D．4．如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE＝DF，AE与BF相交于O；下列结论：＝S四边形DEOF．（1）AE＝BF；（2）AE⊥BF；（3）AD＝OE；（4）S△AOB其中正确的有（）A．4个B．3个C．2个D．1个5．如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE＝DF，AE、BF相交于点O，下列结论：①AE＝BF，②BO＝OE，③AE⊥BF，④∠ABO＝∠FAO，⑤S四边形DE OF＝S△AOB中，正确的有（）A．1个B．2个C．3个D．4个6．如图，正方形ABCD，点E，F在对角线AC上，连接BE、DF，满足BE∥DF，过点E 作EG⊥DF，垂足为G，若DG＝4，EG＝3，则AD＝．7．已知正方形ABCD的边长为4，CE＝DF＝3，DE和AF相交于点G，连接BG，点H是线段AE的中点，连接HG，若∠HGB＝∠DAF，则GB＝．8．如图，正方形ABCD的对角线AC、BD相交于点O，M是AD上的一点，连接OM，过点O作ON⊥OM，交CD于点N，若四边形MOND的面积是3，则AB的长为．9．如图，在正方形ABCD中，点E，F分别是BC，CD上的点，AE与BF相交于点G，连接AC交BF于点H．若CE＝DF，BG＝GH，AB＝2，则△CFH的面积为．10．如图，四边形ABCD是正方形，点E、N分别在DC、BC上，点F在CB的延长线上．△ADE≌△DCN，将△ADE顺时针旋转n度后，恰好与△ABF重合．（1）请写出n的值；（2）连结EF，试求出∠AFE的度数；（3）猜想线段AE和DN的数量关系和位置关系，并说明理由．11．【探索发现】（1）如图1，正方形ABCD的对角线相交于点O，点O又是正方形A1B1C1 O的一个顶点，而且这两个正方形的边长相等，我们知道，无论正方形A1B1C1O绕点O 怎么转动，总有△AEO≌△BFO，连接EF，求证：AE2+CF2＝EF2；【类比迁移】（2）如图2，矩形ABCD的中心O是矩形A1B1C1O的一个顶点，A1O与边AB相交于点E，CO与边CB相交于点F，连接EF，矩形A1B1C1O可绕着点O旋转，判断（1）中的结论是否成立，若成立，请证明，若不成立，请说明理由；【迁移拓展】（3）如图3，在Rt△ACB中，∠C＝90°，AC＝3cm，BC＝4cm，直角∠E DF的顶点D在边AB的中点处，它的两条边DE和DF分别与直线AC，BC相交于点E，F，∠EDF可绕着点D旋转，当BF＝1cm时，直接写出线段EF的长度．12．如图，已知四边形ABCD是正方形，点F是DC边上的动点（不与端点重合），点E在线段AF上，AD＝m2+1，AE＝2m，DE＝m2﹣1，M为线段BF的中点，点N在线段AF上（不与点F重合），且MN＝BF．（1）求证：BN⊥AF；（2）随着点F的运动，试猜想AB﹣AN的值是否是发生变化，若不变，请求出定值，若变化，请说明理由．13．（1）如图1，在正方形ABCD中，AE、DF相交于点O且AE⊥DF则AE和DF的数量关系为．（2）如图2，在正方形ABCD中，E、F、G分别是边AD、BC、CD上的点，BG⊥EF，垂足为H．求证：EF＝BG．（3）如图3，在正方形ABCD中，E、F、M分别是边AD、BC、AB上的点，AE＝2，B F＝5，BM＝1，将正方形沿EF折叠，点M的对应点恰好与CD边上的点N重合，求C N的长度．14．（1）如图①，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，过A 点作AG⊥EB，垂足为G，求证：OE＝FO；（2）如图②，若点E在AC的延长线上，AG⊥EB，交EB的延长线于G．AG的延长线交DB的延长线于F，其他条件不变，则结论“OE＝OF”还成立吗？若成立，请给予证明，若不成立，请说明理由．15．综合与实践：如图，在正方形ABCD中，点E是边AB上的一个动点（点E与点A，B不重合），连接CE，过点B作BF⊥CE于点G，交AD于点F．（1）如图1，求证：△ABF≌△BCE；（2）如图2，当点E运动到AB中点时，连接DG，求证：DC＝DG；（3）如图3，若AB＝4，连接AG，当点E在边AB上运动的过程中．AG是否存在最小值，若存在，请直接写出AG最小值，及此时AE的值；若不存在，请说明理由．16．如图1，P为正方形ABCD的边BC上一动点（P与B、C不重合），点Q在CD边上，且BP＝CQ，连接AP、BQ交于点E．（1）求证：AP⊥BQ；（2）当P运动到BC中点处时（如图2），连接DE，请你判断线段DE与AD之间的关系，并说明理由；（3）如图3，在（2）的条件下，过A点作AM⊥DE于点H，交BQ、CD于点N、M，若AB＝2，求QM的长度．17．如图，在正方形ABCD中，E是边AB上的点，连接CE，过点D作DF⊥CE，分别交BC，CE于点F、G．（1）求证：CE＝DF；（2）若AB＝3，图中阴影部分的面积和与正方形ABCD的面积之比为2：3，则△DCG 的面积为，CG+DG的长为．18．如图1，已知正方形ABCD和正方形AEFG有公共顶点A，连接BE，DG．（1）请判断BE与DG的数量关系与位置关系，并证明你的结论．（2）如图2，已知AB＝4，，当点F在边AD上时，求BE的长．19．如图1，在正方形ABCD中，，点E在边BC上，连接AE，且∠BAE＝30°，点F是AE的中点．（1）求AE的长；（2）过点F作直线GH，分别交AB，CD于点G，H，且GH＝AE，求AG的长；（3）如图2，过点F作AE的垂线，分别交AB，BD，CD于点M，O，N，连接OE，求∠AEO的度数．20．如图，Rt△ABC两条外角平分线交于点D，∠B＝90°，过点D作DE⊥BA于点E，D F⊥BC于点F．（1）求证：四边形BFDE是正方形；（2）若BF＝6，点C为BF的中点，直接写出AE的长．21．在正方形ABCD中，P是边BC上一动点（不与点B、C重合），E是AP的中点，过点E作MN⊥AP，分别交AB、CD于点M，N．（1）判定线段MN与AP的数量关系，并证明；（2）连接BD交MN于点F．①根据题意补全图形；②用等式表示线段ME，EF，FN之间的数量关系，直接写出结论EF＝EM+FN．22．如图1，正方形ABCD中，点P为线段BC上一个动点，若线段MN垂直AP于点E，交线段AB于M，CD于N，证明：AP＝MN；如图2，正方形ABCD中，点P为线段BC上一动点，若线段MN垂直平分线段AP，分别交AB、AP、BD、DC于点M、E、F、N．（1）求证：EF＝ME+FN；（2）若正方形ABCD的边长为2，则线段EF的最小值＝，最大值＝．。

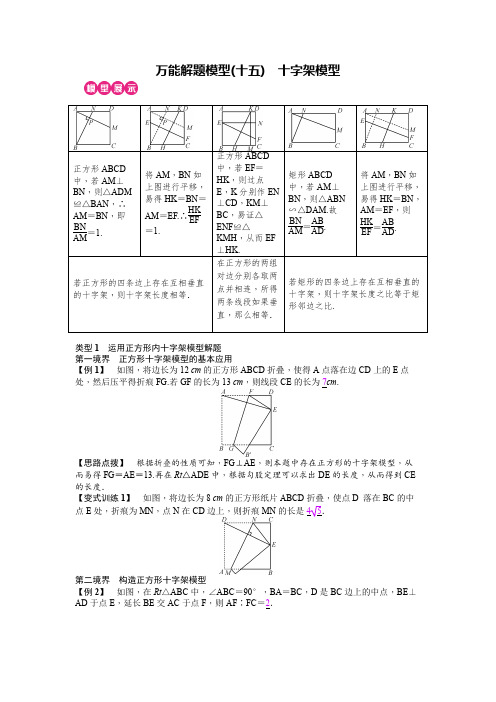
万能解题模型(十五) 十字架模型正方形ABCD 类型1 运用正方形内十字架模型解题 第一境界 正方形十字架模型的基本应用【例1】 如图，将边长为12 cm 的正方形ABCD 折叠，使得A 点落在边CD 上的E 点处，然后压平得折痕FG.若GF 的长为13 cm ，则线段CE 的长为7cm .【思路点拨】 根据折叠的性质可知，FG ⊥AE ，则本题中存在正方形的十字架模型，从而易得FG ＝AE ＝13.再在Rt △ADE 中，根据勾股定理可以求出DE 的长度，从而得到CE 的长度．【变式训练1】 如图，将边长为8 cm 的正方形纸片ABCD 折叠，使点D 落在BC 的中点E 处，折痕为MN ，点N 在CD 边上，则折痕MN 的长是第二境界 构造正方形十字架模型【例2】 如图，在Rt △ABC 中，∠ABC ＝90°，BA ＝BC ，D 是BC 边上的中点，BE ⊥AD 于点E ，延长BE 交AC 于点F ，则AF ∶FC ＝2．【思路点拨】 图中有一个垂直的十字架，可以考虑将十字架放在一个正方形或矩形中，运用模型解题．如图，过点C 作CG ∥AB ，过点A 作AG ∥BC ，两条直线交于点G ，则可得四边形ABCG 是正方形，延长BF 交CG 于点H.根据“正方形内十字架模型”可以得到△ABD ≌△BCH ，则CH ＝BD.在根据△AFB ∽△CFH ，由相似的性质可以求出AF ∶FC 的值．类型2 运用矩形内十字架模型解题 第一境界 矩形十字架模型的基本应用【例3】 如图所示，在矩形ABCD 中，EF ⊥GH ，AM ⊥BN.EF 分别交AB ，CD 于点E ，F ，点M ，N 分别在BC ，CD 上．若EF GH ＝79，则BN AM ＝79．【思路点拨】 分析出图中的十字架模型，然后根据矩形内十字架模型可以求出． 【变式训练2】 (九上北师大教材P 19第4题改编)如图，在矩形纸片ABCD 中，AB ＝6，BC ＝8，将纸片折叠，使点C 与点A 重合，折痕为EF ，则EF 的长为152．提示：∵EF ⊥AC ，∴EF AC ＝ABBC，即EF 10＝68.∴EF ＝152. 第二境界 构造矩形十字架模型【例4】 如图，在▱ABCD 中，AB ＝2，BC ＝2，且∠B ＝45°，将▱ABCD 对折，使点B 和点D 重合，则折痕MN 3【思路点拨】 图中有垂直的十字架，补全图形将十字架放在矩形中，过点B 作BE ⊥AD于点E ，过点D 作DF ⊥BC 于点F ，则由矩形十字架型可得MN BD ＝BEDE.【变式训练3】 如图，在四边形ABCD 中，∠ABC ＝90°，AB ＝AD ＝10，BC ＝CD ＝5，AM ⊥DN ，点M ，N 分别在BC ，AB 边上，求DNAM的值．解：连接AC ，易证△ADC ≌△ABC(SSS )，∴∠ADC ＝∠ABC ＝90°. 过点D 作EF ∥AB ，过点A 作AF ⊥EF 于点F ，延长BC 交EF 于点E. 易证△DEC ∽△AFD ，且相似比为1∶2. 设CE ＝x ，则DF ＝2x ，∴DE ＝10－2x. ∴AF ＝20－4x ＝BE ＝5＋x. ∴x ＝3.∴BE ＝8.根据“矩形内十字架模型”可得DN AM ＝BE AB ＝45.启示：一般情况下，当矩形、正方形、直角三角形等图形内出现“垂直”情况时，可考虑十字架结构模型，通过相似(或全等)求线段的长．1．如图，已知正方形ABCD 的边长为5，点E ，F 分别在AD ，DC 上，AE ＝DF ＝2，BE 与AF 相交于点G ，点H 为BF 的中点，连接GH ，则GH 的长为(B )A ．25B .342C ．42D .8532．如图，已知直线y ＝－12x ＋2分别与x 轴、y 轴交于B ，A 两点，将△AOB 沿着AB 翻折，使点O 落在点D 上．若反比例函数y ＝kx的图象经过点D ，则k 的值为(D )A ．4B .12125C ．5D .128253．(2019·张家界)如图，正方形ABCD 的边长为1，点E ，F 分别为BC ，CD 边的中点，连接AE ，BF 交于点P ，连接PD ，则tan ∠APD ＝2．4．(2017·安徽)已知正方形ABCD ，点M 为边AB 的中点．(1)如图1，点G 为线段CM 上的一点，且∠AGB ＝90°，延长AG ，BG 分别与边BC ，CD 交于点E ，F.求证： ①BE ＝CF ； ②BE 2＝BC·CE.(2)如图2，在边BC 上取一点E ，满足BE 2＝BC·CE ，连接AE 交CM 于点G ，连接BG 并延长交CD 于点F ，求tan ∠CBF 的值．解：(1)①∵四边形ABCD 是正方形， ∴AB ＝BC ，∠ABC ＝∠BCF ＝90°. ∴∠ABG ＋∠CBF ＝90°.∵∠AGB ＝90°，∴∠ABG ＋∠BAG ＝90°. ∴∠BAG ＝∠CBF.∴△ABE ≌△BCF(ASA )． ∴BE ＝CF.②∵∠AGB ＝90°，点M 为AB 的中点， ∴MG ＝MA ＝MB.∴∠GAM ＝∠AGM. 又∵∠CGE ＝∠AGM ，∠GAM ＝∠CBG ， ∴∠CGE ＝∠CBG.又∵∠ECG ＝∠GCB ，∴△CGE ∽△CBG. ∴CE CG ＝CGBC，即CG 2＝BC·CE. 由∠CFG ＝∠GBM ＝∠BGM ＝∠CGF 得CF ＝CG ， 由①知BE ＝CF ， ∴BE ＝CG. ∴BE 2＝BC·CE.(2)延长AE ，DC 交于点N ， ∵四边形ABCD 是正方形， ∴AB ∥CD.∴∠N ＝∠EAB. 又∵∠CEN ＝∠BEA ， ∴△CEN ∽△BEA. ∴CE BE ＝CNBA，即BE·CN ＝AB·CE. ∵AB ＝BC ，BE 2＝BC·CE ，∴CN ＝BE.∵AB ∥DN ，∴CN AM ＝CG GM ＝CFBM.∵AM ＝MB ， ∴FC ＝CN ＝BE.设正方形的边长为1，BE ＝x ，由BE 2＝BC·CE 可得x 2＝1×(1－x)，解得x 1＝5－12，x 2＝－5－12(舍去)．∴BEBC ＝5－12.FC BC＝BEBC＝5－12.则tan∠CBF＝。

初中数学：正⽅形中⼗字架模型01弦图的应⽤在勾股定理的证明中，我们学习过赵爽弦图，如下，有△AED≌△BFA≌△CGB≌DHC．稍作变形，若DE⊥AF，则可得：△DAE≌△ABF．（证明思路类似三垂直模型）⼀般地，在正⽅形ABCD中，若MN⊥PQ，则必有MN=PQ．法⼀：分别将PQ、MN平移⾄AF、DE位置（作平⾏线）证明AF=DE即可．法⼆：过点P作PE⊥BC，过点N作NF⊥AB交AB于点F，易证△PEQ≌△NFM．反之，若已知PQ=MN，但不⼀定存在PQ⊥MN．如下：EF=PQ=MN，但EF不与MN垂直．由位置关系可推数量关系，但由数量关系未必可推位置关系．除此之外，还有⼀些常⽤的性质和结论：1、弦图与对称考虑对称点连线被对称轴垂直且平分．将正⽅形ABCD沿MN折叠，则AA'MN且AA'⊥MN．2、弦图与辅助圆如图，垂⾜H轨迹是个圆弧（定边对直⾓）．以AD中点M为圆⼼，MA为半径的圆，两端分别的点A及对⾓线交点O．3、弦图与四点共圆如图，C、D、H、F四点共圆．∵∠DCF=∠DHF=90°，∴C、D、H、F四点共圆．连接DF，取DF中点N，以点N为圆⼼，DN为半径作圆．特别地，若E、F分别是AB、BC中点，连接CH，则CH=CD．证明：∵∠CHD=∠CFD=∠AED=∠CDE，∴CH=CD．4、矩形中的弦图构造在矩形ABCD中，E、F分别是AB、BC上的点，且AF⊥DE，则AF/DE=AB/AD．证明：易证△ABF∽△DAE，∴AF/DE=AB/AD．02真题练习2018 青岛中考2018 聊城中考2018 上海中考2018 长春中考2019 ⼴西中考2018 杭州中考2019 襄阳中考⽂章选⾃：有⼀点数学、作者：刘岳； .更多优质资源可关注公众号后查看历史消息，妙解之慧由陕西西安孙冰钰⽼师创建专注分享初，⾼中数学优质资源，旨在服务于全国师⽣，让更多朋友受益。

平台所选⽂章贵在分享，公益传播，尊重原创⽂章，公众号前会注明作者姓名，来源，如不当，请⽂末添加微信联系处理，如有侵权，请联系删除如转载，请注明来源于公众号：妙解之慧（ID:WanZhuanShuXue1）及作者信息。

专题10.“十字架模型”一．知识点:1.正方形内部，BF⊥CE，则BF＝CE（无论怎么变，只要垂直，十字架就会相等）2.如图：在矩形ABCD中，点F是AD上一点，DE ⊥CF ，则有二．典型例题1.如图1，在正方形ABCD中，点E是AB边上的一个动点（点E与点A，B不重合），连接CE，过点B作BF⊥CE于点G，交AD于点F．（1）求证：△ABF≌△BCE；（2）如图2，当点E运动到AB中点时，连接DG，求证：DC＝DG；（3）如图3，在（2）的条件下，过点C作CM ⊥DG于点H，分别交AD，BF于点M，N，求的值．2.已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．（1）如图①，若四边形ABCD是矩形，且DE⊥CF，求证：△ADE∽△DCF；（2）如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC 满足什么关系时，成立？并证明你的结论；（3）如图③，若BA＝BC＝6，DA＝DC＝8，∠BAD ＝90°，DE⊥CF ，请直接写出的值．三．变式练习1.如图，在正方形ABCD中，E、F、G、H分别为边AB、BC、CD、DA上的点，EG⊥FH，连接EF、FG、GH、HE，若EG＝8，求,四边形EFGH的面积．2.如图2，正方形ABCD边长为12，将正方形沿MN 折叠，使点A落在DC边上的点E处，且DE＝5，求折痕MN的长．3.．如图，在Rt△ABC中，∠ABC＝90°，BA＝BC，点D为BC边的中点，BE⊥AD于点E，交AC 于点F ，求的值．4.（1）证明推断：如图（1），在正方形ABCD中，点E，Q分别在边BC，AB上，DQ⊥AE于点O，点G，F分别在边CD，AB上，GF⊥AE．①求证：DQ＝AE；②推断：的值为；（2）类比探究：如图（2），在矩形ABCD中，＝k（k为常数）．将矩形ABCD沿GF折叠，使点A落在BC边上的点E处，得到四边形FEPG，EP交CD于点H，连接AE交GF于点O．试探究GF与AE之间的数量关系，并说明理由；（3）拓展应用：在（2）的条件下，连接CP，当k＝时，若tan∠CGP＝，GF＝2，求CP 的长．5．如图，在正方形ABCD中，E是边CD上一点（点E不与点C、D重合），连接BE，取BE的中点M，连接CM．过点C作CG⊥BE交AD于点G，连接EG、MG．若CM＝3，则四边形GMCE的面积为．6.如图，正方形ABCD中，AB＝1，连接AC，∠ACD 的平分线交AD于点E，在AB上截取AF＝DE，连接DF，分别交CE，AC于点G，H，点P是线段GC上的动点，PQ⊥AC于点Q，连接PH，以下结论：①CE⊥DF；②DE+DC＝AC；③EA＝AH；④PH+PQ的最小值是，其中正确的结论有（）个．A．1 B．2 C．3 D．4。

专题05正方形的几何模型（十字架模型）1．A【分析】过点P 作PM ⊥BC 于点M ，由折叠得到PQ ⊥AE ，从而得到∠AED =∠APQ ，可得△PQM ≌△ADE ，从而得到PQ =AE ，再由勾股定理，即可求解．解：过点P 作PM ⊥BC 于点M ，由折叠得到PQ ⊥AE ，∴∠DAE +∠APQ =90°，在正方形ABCD 中，AD ∥BC ，∠D =90°，CD ⊥BC ，∴∠DAE +∠AED =90°，∴∠AED =∠APQ ，∴∠APQ =∠PQM ，∴∠PQM =∠APQ =∠AED ，∵PM ⊥BC ，∴PM =AD ，∵∠D =∠PMQ =90°，∴△PQM ≌△ADE ，∴PQ =AE ，在Rt ADE △中，5DE =，AD =12，由勾股定理得：13AE =，∴PQ =13．故选：A ．【点拨】本题主要考查了正方形的性质，全等三角形的判定和性质，勾股定理，得到△PQM ≌△ADE 是解题的关键．2．D【分析】作FH ⊥AB 于H ，交AE 于P ，设AG =GE =x ，在Rt △BGE 中求出x ，在Rt △ABE 中求出AE ，再证明△ABE ≌△FHG ，得到FG =AE ，然后根据S 四边形AGEF =S △AGF +S △EGF 求解即可解：作FH ⊥AB 于H ，交AE 于P ，则四边形ADFH 是矩形，由折叠的性质可知，AG =GE ，AE ⊥GF ，AO =EO ．设AG =GE =x ，则BG =3-x ，在Rt △BGE 中，∵BE 2+BG 2=GE 2，∴12+(3-x )2=x 2，∴x =53．在Rt △ABE 中，∵AB 2+BE 2=AE 2，∴32+12=AE 2，∴AE．∵∠HAP +∠APH =90°，∠OFP +∠OPF =90°，∠APH =∠OPF ，∴∠HAP =∠OFP ，∵四边形ADFH 是矩形，∴AB =AD =HF ．在△ABE 和△FHG 中，HAP OFP ABE GHF AB HF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△FHG ，∴FG =AE，∴S 四边形AGEF =S △AGF +S △EGF =1122GF OA GF OE ⋅+⋅=()12GF OA OE ⋅+=12GF AE ⋅=12=5．故选D．【点拨】本题考查了折叠的性质，正方形的性质，矩形的判定与性质，三角形的面积，以及勾股定理等知识，熟练掌握折叠的性质是解答本题的关键．3．C【分析】设EF=FD=x ，在RT △AEF 中利用勾股定理即可解决问题．解：∵将边长为6cm 的正方形纸片ABCD 折叠，使点D 落在AB 边中点E 处，∴EF ＝DE ，AB ＝AD ＝6cm ，∠A ＝90°∵点E 是AB 的中点，∴AE ＝BE ＝3cm ，在Rt △AEF 中，EF 2＝AF 2+AE 2，∴（6﹣AF ）2＝AF 2+9∴AF ＝94故选C ．【点拨】本题考查翻折变换、正方形的性质、勾股定理等知识，解题的关键是设未知数利用勾股定理列出方程解决问题，属于中考常考题型．4．B解：过点P 作PM ⊥BC 于点M ，由折叠得到PQ ⊥AE ，∴∠DAE+∠APQ=90°，又∠DAE+∠AED=90°，∴∠AED=∠APQ ，∵AD ∥BC ，∴∠APQ=∠PQM ，则∠PQM=∠APQ=∠AED ，∠D=∠PMQ ，PM=AD∴△PQM ≌△ADE∴13=.【点拨】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．5．D【分析】由已知可求QF =QB ，在Rt △BPQ 中，由勾股定理求得QB ，可求出S △BQF =25，再证明△ABE ≌△BCF （SAS ），△BGE ∽△BCF ，由此得BF ，GE ，BG ，过点G 作GN ⊥AB 交AB 于N ，可证明△ANG ∽△ABE ，再由GA =AE -GE ，可求得GN ，根据S △QGF =S △BQF -S △BQG 即可求解．解：将BCF △沿BF 翻折得到BPF △，∴PF =FC ，∠PFB =∠CFB ，四边形ABCD 是正方形∴∠FPB =90°，CD ∥AB ，,90AB BC ABE BCF =∠=∠=︒∴∠CFB =∠ABF ，∴∠ABF =∠PFB ，∴QF =QB ，∵PF =FC =12CD 12AB ==PB =AB ，在Rt △BPQ 中，222QB BP PQ =+，∴222(QB QB =-+，∴QB∴S △BQF =1252，∵AB =BC ，BE =CF ，∠ABE =∠BCF =90°，∴△ABE ≌△BCF （SAS ），∴∠AEB =∠BFC ，又∵∠EBG =∠CBF ，∴△BGE ∽△BCF ，GEBGBECF BC BF ∴==，∵CF ，BC∴BF∴GE BG ，过点G 作GN ⊥AB 交AB 于N ，∵∠GAN =∠EAB ，∠ANG =∠ABE =90°，∴△ANG ∽△ABE ，∴GN GABE EA=∵GA =AE -GE =∴GN∴S △BQG =12×QB ×GN =12，∴S故选：D．【点拨】本题考查折叠的性质，熟练掌握三角形全等的判定和性质、三角形相似的判定和性质是解题的关键．6．B【分析】连接BP，取CD的中点M，连接PM，根据折叠的性质，PM＝PQ，GH＝DC，PC＝PG，要求△GPQ 的周长的最小值，只需求PM+PB的最小值，当M、P、B三点共线时，PM+BP＝BM最小，在Rt△BCM中，勾股定理求出BM，即可求解．解：连接BP，取CD的中点M，连接PM，由折叠可知，PM＝PQ，GH＝DC，PC＝PG，在Rt△BCG中，P是CG的中点，∴BP＝PG＝12 GC，∵Q是GH的中点，∴QG＝12 GH，∴△GPQ的周长＝PQ+QG+PG＝PM+12GH+PB＝PM+PB+12CD，∵CD＝3，∴△GPQ的周长＝PM+PB+3 2，当M、P、B三点共线时，PM+BP＝BM最小，在Rt△BCM中，BM，∴△GPQ故选B．【点评】本题考查图形的翻折变换，熟练掌握正方形的性质、直角三角形的性质，正确添加辅助线是解题的关键．7．13【分析】先过点P作PM⊥BC于点M，利用三角形全等的判定得到△PQM≌△AED，从而求出PQ=AE．解：过点P作PM⊥BC于点M，由折叠得到PQ ⊥AE ，∴∠DAE+∠APQ=90°，又∠DAE+∠AED=90°，∴∠AED=∠APQ ，∵AD ∥BC ，∴∠APQ=∠PQM ，则∠PQM=∠APQ=∠AED ，∠D=∠PMQ ，PM=AD∴△PQM ≌△AED∴22512+=13．故答案是：13．【点拨】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．834【分析】根据正方形的性质得到AB ＝BC ，∠ABE ＝∠BCF ＝90°，推出∠BAE ＝∠EBH ，根据全等三角形的性质得到CF ＝BE ＝2，求得DF ＝5﹣2＝3，根据勾股定理即可得到结论．解：∵四边形ABCD 是正方形，∴AB ＝BC ，∠ABE ＝∠BCF ＝90°，∴∠BAE +∠AEB ＝90°，∵BH ⊥AE ，∴∠BHE ＝90°，∴∠AEB +∠EBH ＝90°，∴∠BAE ＝∠EBH ，在△ABE 和△BCF 中，BAE CBF AB BC ABE BCF ∠∠⎧⎪⎨⎪∠∠⎩＝＝，＝∴△ABE ≌△BCF （ASA ），∴CF ＝BE ＝2，∴DF ＝5﹣2＝3，∵四边形ABCD 是正方形，∴AB ＝AD ＝5，∠ADF ＝90°，由勾股定理得：AF【点拨】此题考查了正方形的性质、全等三角形的判定与性质、勾股定理，本题证明△ABE ≌△BCF 是解本题的关键．9．3【分析】过点M 作MH ⊥CD 于点H ．连接DE ，结合题意可知MN 垂直平分DE ，先通过证明△MHN ≅△DCE得出DE ＝MN ＝CE 的长，最后在Rt △ENC 中利用勾股定理求出DN ，最后进一步求出CN 即可.解：如图所示，过点M 作MH ⊥CD 于点H ．连接DE ．根据题意可知MN 垂直平分DE ，易证得：∠EDC ＝∠NMH ，MH ＝AD ，∵四边形ABCD 是正方形，∴MH ＝AD ＝CD ，∵∠MHN ＝∠C ＝90°，∴△MHN ≅△DCE （ASA ），∴DE ＝MN ＝在Rt △DEC 中，4CE =，设DN ＝EN ＝x ，则CN ＝8x -，在Rt △ENC 中，222NE NC EC =+，∴()22284x x =-+，解得：5x =，∴CN ＝83x -=，故答案为：3．【点拨】本题主要考查了正方形性质和全等三角形性质与判定及勾股定理的综合运用，熟练掌握相关方法是解题关键.10．16.【分析】解过点A 作AM ⊥GH 于M ，由正方形纸片折叠的性质得出∠EGH=∠EAB=∠ADC=90°，AE=EG ，则EG ⊥GH ，∠EAG=∠EGA ，由垂直于同一条直线的两直线平行得出AM ∥EG ，得出∠EGA=∠GAM ，则∠EAG=∠GAM ，得出AG 平分∠DAM ，则DG=GM ，由AAS 证得△ADG ≌△AMG 得出AD=AM=AB ，由HL 证得Rt △ABP ≌Rt △AMP 得出BP=MP ，则△PGC 的周长=CG+PG+PC=CG+MG+PM+PC=CG+DG+BP+PC=CD+CB=16．解：过点A 作AM ⊥GH 于M，如图所示：∵将正方形纸片折叠，使点A 落在CD 边上的G 处，∴∠EGH=∠EAB=∠ADC=90°，AE=EG ，∴EG ⊥GH ，∠EAG=∠EGA ，∴AM ∥EG ，∴∠EGA=∠GAM ，∴∠EAG=∠GAM ，∴AG 平分∠DAM ，∴DG=GM ，在△ADG 和△AMG 中90DAG GAM ADG AMG DG GM ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩，∴△ADG ≌△AMG （AAS ），∴AD=AM=AB ，在Rt △ABP 和Rt △AMP 中AB AM AP AP =⎧⎨=⎩，∴Rt △ABP ≌Rt △AMP （HL ），∴BP=MP ，∴△PGC 的周长=CG+PG+PC=CG+MG+PM+PC=CG+DG+BP+PC=CD+CB=8+8=16，故答案为16．【点拨】本题考查了折叠的性质、正方形的性质、角平分线的判定与性质、全等三角形的判定与性质等知识，熟练掌握折叠的性质，通过作辅助线构造全等三角形是解题的关键．11．（1）见分析；（2）见分析；【分析】（1）根据正方形的性质得AB =BC ，90ABC BCD ∠=∠=︒，用SAS 证明ABE BCF △△≌，得BAE CBF ∠=∠，根据三角形内角和定理和等量代换即可得；（2）过点B 作BH BN ⊥，交AN 于点H ，根据正方形的性质和平行线的性质，用SAS 证明AGB AGM ≌，得BAG MAG ∠=∠，根据角平分线性质得45BHA GAN ∠=∠=︒，则HBN 是等腰直角三角形，用SAS 证明ABH CBN ≌，得AH =CN ，在Rt HBN 中，根据勾股定理即可得；解：（1）∵四边形ABCD 是正方形，∴AB =BC ，90ABC BCD ∠=∠=︒，在ABE 和BCF △中，AB BC ABE BCF BE CF =⎧⎪∠=∠⎨⎪=⎩∴ABE BCF △△≌（SAS ），∴BAE CBF ∠=∠，∵1801809090AEB BAE ABC ∠+∠=︒-∠=︒-︒=︒，∴90AEB CBF ∠+∠=︒，∴180()1809090EGB AEB CBF ∠=︒-∠+∠=︒-︒=︒，∴AE BF ⊥；（2）如图所示，过点B 作BH BN ⊥，交AN 于点H，∵四边形ABCD 是正方形，∴AB =AC ，90ABC HBN ∠=∠=︒，∵90HBN HBA ABN ∠=∠+∠=︒，90ABC CBN ABN ∠=∠+∠=︒，∴HBA CBN ∠=∠，由（1）得，AE BF ⊥，∴90AGB AGM ∠=∠=︒，∴90HBG AGM ∠=∠=︒,∴//HB AE ，∴BHA EAN ∠=∠，在AGB 和AGM 中，AG AG AGB AGM GB GM =⎧⎪∠=∠⎨⎪=⎩∴AGB AGM ≌（SAS ），∴BAG MAG ∠=∠，∵AN 平分DAM ∠，∴DAN MAN ∠=∠，∴90BAG MAG MAN DAN ∠+∠+∠+∠=︒，2290MAG MAN ∠+∠=︒，45MAG MAN ∠+∠=︒，45GAN ∠=︒，∴45BHA GAN ∠=∠=︒，∴180180904545BNH HBN BHA ∠=︒-∠-∠=︒-︒-︒=︒，∴HBN 是等腰直角三角形，∴BH =BN ，在ABH 和CBN △中，BH BN HBA CBN AB CB =⎧⎪∠=∠⎨⎪=⎩∴ABH CBN ≌（SAS ），∴AH =CN ，在Rt HBN中，根据勾股定理HN ==，∴AN CN AN AH HN +=+==；【点拨】本题考查了正方形的性质，全等三角形的判定与性质，三角形内角和定理，角平分线，等腰直角三角形的判定与性质，勾股定理和锐角三角函数，解题的关键是掌握并灵活运用这些知识点．12．（1）见分析；（2）四边形MNPQ 为正方形，理由见分析；（3）106【分析】（1）由四边形ABCD 为正方形，可得90ABC BCD ∠=∠=︒，推得90ABG CBG ∠+∠=︒，由BG AE ⊥，可得90BAE ABG ∠+∠=︒，可证()ABE BCG ASA ≅△△即可；（2）M 、N 为AB 、AG 中点，可得MN 为ABG 的中位线，可证//MN BG ，12MN BG =，由点M 、N 、P 、Q 分别是AB 、AG 、GE 、EB 的中点，可得PQ 是BEG 的中位线，MQ 为ABE 的中位线，NP 为AEG △的中位线，可证//PQ BG ，12PQ BG =，//MQ AE ，12MQ AE =，//NP AE ，12NP AE =，可证四边形MNPQ 为平行四边形．再证四边形MNPQ 为菱形，最后证MN MQ ⊥即可；（3）延长AO 交BC 于点S ，由对称性可得'BF B F =，'1AB BS ==，AO SO =，由勾股定理可求AS ，可得12AO AS ==设AF x =，在'Rt AB F △中，2221(3)x x +-=，解得53x =，在Rt AOF 中，可求OF =解：（1）证明：∵四边形ABCD 为正方形，∴90ABC BCD ∠=∠=︒，∴90ABG CBG ∠+∠=︒，∵BG AE ⊥，∴∠AHB =90°，∴90BAE ABG ∠+∠=︒，∴BAE CBG ∠=∠，在ABE 与BCG 中，BAE CBG AB BC ABC BCD ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ABE BCG ASA ≅△△，∴AE BG =．（2）解：四边形MNPQ 为正方形，理由如下：∵M 、N 为AB 、AG 中点，∴MN 为ABG 的中位线，∴//MN BG ，12MN BG =，∵点M 、N 、P 、Q 分别是AB 、AG 、GE 、EB 的中点，∴PQ 是BEG 的中位线，MQ 为ABE 的中位线，NP 为AEG △的中位线，，∴//PQ BG ，12PQ BG =，//MQ AE ，12MQ AE =，//NP AE ，12NP AE =，∴MN PQ =，MQ NP =，∴四边形MNPQ 为平行四边形．∵AE BG =，∴MN MQ =，∴四边形MNPQ 为菱形，∵BG AE ⊥，//MQ AE ，∴MQ BG ⊥，∵//MN BG ，∴MN MQ ⊥，∴四边形MNPQ 为正方形．（3）解：延长AO 交BC 于点S ，由对称性可知'BF B F =，'1AB BS ==，AO SO =，在Rt ABS 中，AS =∴122AO AS ==，设AF x =，则'3BF B F x ==-，在'Rt AB F △中，2221(3)x x +-=，53x =，∴53AF =，在Rt AOF 中，6OF ===．【点拨】本题考查正方形性质与判定，等角的余角性质三角形全等判定与性质，三角形中位线判定与性质，勾股定理，根据勾股定理建构方程，解拓展一元一次方程等知识，掌握以上知识是解题关键．13．（1）178；（2）8-3）①见分析；②164410xy x y ---=，理由见分析【分析】（1）根据EF 是线段BG 的垂直平分线，BE =EG ，设EG =EB =x ，则AE =AB -BE =4-x ，再由勾股定理求解即可；（2）过点F 作FH ⊥AB 于H ，连接FB ，FG ，由BE =8-2DF ，CF =CD -DF =4-DF ，得到BE =2CF ，先证明四边形BCFH 是矩形，得到CF =HB ，则BH =EH =FC ，设AG =x ，BE =y ，则AE =4-y ，GD =4-x ，CF =12y ，142DF y =-由222AE AG EG +=，222GD DF GF +=，222BC FC BF +=，可以得到()2224y x y -+=①，()22221144422x y y ⎛⎫⎛⎫-+-=+ ⎪ ⎪⎝⎭⎝⎭②，联立①②求解即可得到答案；（3）①先证明∠EBG =∠EGB ，然后根据ABG +∠AGB =90°，∠EGB +∠BGM =90°，即可得到∠AGB =∠BGM ；②连接BM ，过点B 作BH ⊥GM ，由角平分线的性质得到BH =AB =4，由=44=16ABG MBG BCM CDM ABCD S S S S S +++=⨯△△△△正方形，可以得到()()122244=162x GM y x y +++--，由勾股定理可以得到222DM GD GM +=即()()2224444xy x y ⎛⎫-+-=- ⎪⎝⎭，最后解方程即可得到答案．解：（1）∵EF 是线段BG 的垂直平分线，∴BE =EG ，∵四边形ABCD 是正方形，且边长为4，∴AB =4，∠A =90°，设EG =EB =x ，则AE =AB -BE =4-x ，∵222AE AG EG +=，∴()22241x x -+=，解得178=x ，∴178EG =；（2）如图所示，过点F 作FH ⊥AB 于H ，连接FB ，FG∵EF 是线段BG 的垂直平分线，∴BF =FG ，∵BE =8-2DF ，CF =CD -DF =4-DF ，∴BE =2CF ，∵四边形ABCD 是正方形，FH ⊥AB ，∴∠HBC =∠C =∠BHF =90°，∴四边形BCFH 是矩形，∴CF =HB ，∴BH =EH =FC ，设AG =x ，BE =y ，则AE =4-y ，GD =4-x ，CF =12y ，142DF y =-∵222AE AG EG +=，222GD DF GF +=，222BC FC BF +=，∴()2224y x y -+=①，()22221144422x y y ⎛⎫⎛⎫-+-=+ ⎪ ⎪⎝⎭⎝⎭②，联立①②解得8x =-8x =+，∴当8AG =-BE =8-2DF ，故答案为：8-（3）①∵EF 是线段BG 的垂直平分线，∴EG =BE ，∴∠EBG =∠EGB ，∵四边形ABCD 是正方形，EG ⊥GM ，∴∠A =∠EGM =90°，∴∠ABG +∠AGB =90°，∠EGB +∠BGM =90°，∴∠AGB =∠BGM ，∴BG 平分∠AGM ；②如图，连接BM ，过点B 作BH ⊥GM ，由（3）①得BG 平分∠AGM ，∴BH =AB =4，∵AG =x ，CM =y ，∴DG =4-x ，DM =4-y ，∵=44=16ABGMBG BCM CDM ABCD S S S S S +++=⨯△△△△正方形，∴1111=162222AG AB GM BH CM BC DM GD +++g g g g ，∴()()122244=162x GM y x y +++--，∴44xy GM =-，∵222DM GD GM +=，∴()()2224444xy x y ⎛⎫-+-=- ⎪⎝⎭∴222216816816216x y x x y y xy -++-+=-+∴()()22281616x y x y x y +-++=，∴()222416x y x y +-=，∴44xy x y +-=±，当44xy x y +-=时，则4416x y xy +-=，∴16444x y x-==-（不符合题意），∴4416x y xy+-=-∴164410xy x y---=．【点拨】本题主要考查了正方形的性质，勾股定理，角平分线的性质，线段垂直平分线的性质，等腰三角形的性质与判定，三角形的面积等等，解题的关键在于能够熟练掌握相关知识进行求解．。

十字模型专题知识解读【专题说明】“十字架模型”是数学平面几何中比较重要的一个模型。

常见的类型有正方形中的十字架和矩形中的十字架。

围绕着这两种模型的条件之下，可以推导出一些比较实用的结论。

这些结论对我们分析一些几何问题会比较大的帮助。

【方法技巧】类型一：【十字架模型】--正方形第一种情况：过顶点在正方形ABCD中，AE⊥BF，可得AE=BF，借助于同角的余角相等，证明△BAF≌△ADE（ASA）所以AE=BF第二种情况：不过顶点在正方形ABCD中，E，F，G，H分别为AB，BC，CD，DA边上的点，其中：EG⊥FH，可得EG=FH也可以如下证明在正方形ABCD中，E，F，G，H分别AB、BC、CD、DA边上的点，其中：EG⊥FH，可得EG=FH类型二：【十字架模型】--矩形在矩形ABCD中，AB=a，AD=b，其中：AE⊥BF，探究AE与BF的关系；可证：△ADE ∽△BAF 所以BF AE AB AD BF AE ⋅=⋅==ab a b在矩形ABCD 中，AB=a ，AD=b ，E ，F ，G ，H 分别为AB ，BC ，CD ，DA 边上的点，其中：EG ⊥FH ，探究EG 与FH 的关系【解答】可证：△ADN ∽△BAM∴∴但是只有垂直的条件，点的位置发生变化，那么可以证明出相似三角形，但是线段之间的关系不在成立 在矩形ABCD 中，AB=a ，AD=b ，其中EG ⊥FH ，探究EG 与FH 的关系可证△EOH∽△GOF【典例分析】【典例1-1】基本模型如图，在正方形ABCD中，点E、F分别在AD，DC边上，且AF⊥BE．结论：①△ABE≌△DAF；②AF＝BE；请证明【基本模型】中的结论．求证：①△ABE≌△DAF；②AF＝BE．自主探究：若将已知条件AF⊥BE改为AF＝BE，是否可以得到AF⊥BE？进而是否可以探究AF与BE交点的轨迹？【解答】基本模型：证明：①∵四边形ABCD为正方形，∴∠BAE＝∠D＝90°，AB＝AD，∴∠ABE+∠BEA＝90°，∵AF⊥BE，∴∠DAF+∠BEA＝90°，∴∠ABE＝∠DAF，在△ABE和△DAF中，，∴△ABE≌△DAF（ASA），②∵△ABE≌△DAF（ASA），∴AF＝BE；自主探究：解：∵四边形ABCD为正方形，∴∠BAE＝∠D＝90°，AB＝AD，在Rt△ABE和Rt△DAF中，，∴Rt△ABE≌Rt△DAF（HL），∴∠ABE＝∠DAF，∵∠ABE+∠BEA＝90°，∴∠DAF+∠BEA＝90°，∴∠AGE＝90°，则BE⊥AF．如图，设AF、BE交于点H，AC、BD交于点O，∵BE⊥AF，∴∠AHB＝90°，点H在以AB为直径的圆上，∵点E、F分别在AD，DC边上，∴AF与BE交点的轨迹为．【典例1-2】模型演变①如图①，在正方形ABCD中，点E，F，G分别在DC，AD，BC边上，且AE⊥GF．结论：AE＝GF模型演变②如图②，在正方形ABCD中，点E，F，G，H分别在AB，DC，BC，AD边上，且EF⊥GH．结论：EF＝GH请证明【模型演变②】的结论，求证：EF＝GH．自主探究：在【模型演变①】和【模型演变②】中，若将已知条件中两线段垂直与结论中两线段相等互换，判断结论是否还成立？请选择其中一个图形进行证明．【解答】证明：过点E作EM⊥DC于点M，过点H作HN⊥BC于点N，∵四边形ABCD是正方形，∴EM＝AD＝DC＝HN，∵EM⊥HN，EF⊥HG，∴∠MEF＝∠NHG，在△MEF与△NHG中，，∴△MEF≌△NHG（ASA），∴EF＝GH；自主探究：解：不成立，证明：选择[模型演变①]，设AE与FG相交于点O，过点O作DC的平行线l，将FG沿直线l对称得到F'G'，则FG＝F'G'，由（1）可得：AE⊥FG，∴F'G'与AE不垂直，∴若条件与结论互换，结论不成立．【典例2-1】模型演变③如图，在矩形ABCD中，点E在AD边上，且CE⊥BD．结论：△DCE∽△ADB请证明【模型演变③】的结论．求证：△DCE∽△ADB．【解答】证明：∵四边形ABCD是矩形，∴∠A＝∠ADC＝90°，∴∠ADB+∠CDO＝90°，∵CE⊥BD，∴∠DOC＝90°，∴∠DCE+∠CDO＝90°，∴∠ADB＝∠DCE，∵∠A＝∠EDC＝90°，∴△DCE∽△ADB．【典例2-2】模型演变④如图，在矩形ABCD中，点E，F，G，H分别在AD，BC，AB，DC边上，且EF⊥GH．结论：＝请证明【模型演变④】的结论．求证：＝．【解答】证明：如图，过点G作GM⊥CD于M，过点E作EN⊥BC于点N，∴∠GMH＝∠ENF＝90°，∵四边形ABCD是矩形，∴∠B＝∠C＝90°，∵EF⊥GH，∴∠BGH+∠BFE＝180°，∠BGH+∠GHM＝90°，∴∠BFE＝∠GHM，∴△EFN∽△GHM，∴＝＝．【变式1-1】如图，正方形ABCD的边长为4，E，F分别是BC，CD上的点，连接AE，BF 交于点O．若BE＝3，DF＝1，则OB的长为．【解答】解：∵正方形ABCD的边长为4，∴∠ABC＝90°＝∠BCD，AB＝BC＝CD＝4，∵BE＝3，DF＝1，∴BE＝CF＝3，∴△ABE≌△BCF（SAS），∴∠AEB＝∠BFC，∵∠BFC+∠FBC＝90°，∴∠AEB+∠FBC＝90°，∴∠BOE＝90°，∴BO⊥AE，∴2S△ABE＝AB•BE＝AE•OB，∵AB＝4，BE＝3，∴AE＝＝5，∴OB＝＝，故答案为：．【变式1-2】如图，在矩形ABCD中，点E是边AB上一点，将△BCE沿CE折叠，使点B 落在AD边上的点F处，连接BF交CE于点G．已知AD＝5，AB＝3，则折痕CE的长为．【解答】解：由翻折的性质可知，BE＝EF，BC＝FC＝AD＝5，在Rt△CDF中，CF＝5，CD＝AB＝3，∴DF＝＝4，∴AF＝AD﹣DF＝5﹣4＝1，设BE＝x，则EF＝x，AE＝3﹣x，在Rt△AEF中，由勾股定理得，AF2+AE2＝EF2，即1+（3﹣x）2＝x2，解得x＝，即BE＝，在Rt△BCE中，由勾股定理得，CE＝＝＝，故答案为：．【变式1-3】如图，在面积为16的正方形ABCD中，E是BA延长线上一点，F是CB上一点，CF＝AE，连接EF，过点D作DG⊥EF于点H，若S△BEF＝6，则CF＝，DG ＝．【解答】解：∵正方形ABCD的面积为16，∴正方形ABCD的边长为4，设CF＝x，则BF＝4﹣x，BE＝4+x，∵S△BEF＝6，∴（4﹣x）（4+x）＝6，∴x＝±2（负值舍去），∴CF＝2＝AE，∴BF＝BC﹣CF＝4﹣2＝2，BE＝AB+AE＝4+2＝6，∴EF＝＝＝2，∵DG⊥EF，∴∠AGD＝90°﹣∠E＝∠BFE，又∠B＝90°＝∠DAG，∴△EBF∽△DAG，∴＝，即＝，解得DG＝，故答案为：2．【变式1-4】如图，在四边形ABCD中，∠ABC＝90°，AB＝AD＝10，BC＝CD＝5，点M，N分别在边BC，AB上，且AM⊥DN，的值．【解答】解：过点D作AB的平行线，交过点A作BC的平行线于G，交BC的延长线于H，过点D作DP⊥AB于P，则四边形ABHG是矩形，∵AB＝AD，CB＝CD，∴∠ADC＝∠ABC＝90°，∴∠ADG+∠CDH＝90°，∵∠ADG+∠DAG＝90°，∴∠DAG＝∠HDC，又∵∠G＝∠H，∴△ADG∽△DCH，∴，∴设CH＝x，则DG＝2x，∴DH＝10﹣2x，AG＝5+x，∴5+x＝2（10﹣2x），解得x＝3，∴BH＝8，∵∠NDP＝∠BAM，∠DPN＝∠ABM，∴△ABM∽△DPN，∴．【变式1-5】如图①，在矩形ABCD中，AB＝6，BC＝8．点E，F分别在边AD，BC上，将该矩形沿直线EF折叠，使点B的对应点B'落在CD边上，点A的对应点为A'，连接BB'．（1）如图②，当点B'与点D重合时，连接BE，试判断四边形BEB'F的形状，并证明；（2）求折痕EF的最大值；（3）如图③，过点E作EM⊥BC于点M，当四边形EMCD为正方形时，求CF的长．【解答】解：（1）四边形BEB'F是菱形，理由如下：由折叠的性质得：∠BFE＝∠B′FE，EF垂直平分BB′，∴BE＝B′E，BF＝B′F，∵四边形ABCD是矩形，∴AD∥BC，∴∠B′EF＝∠BFE，∴∠B′EF＝∠B′FE，∴B′E＝B′F，∴BE＝B′E＝B′F＝BF，∴四边形BEB′F是菱形；（2）过点E作EG⊥BC于G，设EF与BB′交于点O，如图①所示：则∠EGF＝90°，四边形ABGE为矩形，∴∠GEF+∠EFG＝90°，EG＝AB＝6，由折叠的性质得：EF⊥BB′，∴∠BOF＝90°，∴∠EFG+∠B′BF＝90°，∴∠GEF＝∠B′BF，∵四边形ABCD为矩形，∴CD＝AB＝6，∠C＝90°，∴∠C＝∠EGF，∴△EGF∽△BCB′，∴＝＝＝，∴EF＝BB′，∴当BB′取最大值，EF取得最大值，此时，点B′与点D重合，连接BD，在Rt△BCD中，BD＝＝＝10，∴EF最大＝BD＝×10＝；（3）连接BE、B′E，如图③所示：由折叠的性质得：EF垂直平分BB′，∴BF＝B′F，BE＝B′E，∵四边形EMCD是正方形，∴EM＝MC＝CD＝ED＝6，∴AE＝BM＝8﹣6＝2，在Rt△EMB和Rt△EDB′中，，∴Rt△EMB≌Rt△EDB′（HL），∴DB′＝BM＝2，∴CB′＝CD﹣DB′＝6﹣2＝4，设CF＝x，则BF＝B′F＝8﹣x，在Rt△CB′F中，由勾股定理得：CF2+CB′2＝B′F2，即x2+42＝（8﹣x）2，解得：x＝3，∴CF的长为3．【变式1-6】【教材背景】课本上有这样一道题目；如图①，在正方形ABCD中，E是边AB的中点，F是边BC的中点，连接CE，DF．发现其中CE＝DF．【拓展延伸】如图②，在正方形ABCD中，O为对角线BD上一点，连接AO并延长，交DC于点E，过点B作BF⊥AE于点G，交AD于点F，连接FE，BE．【问题解决】（1）若DO＝DE，求证：△ABG≌△OBG；（2）若BF＝6，求四边形AFEB的面积；（3）如图③，连接CG，若CG＝BC，求证：E是边DC的中点．【解答】【教材背景】证明：如图1中，∵ABCD是正方形，∴AB＝BC＝CD，∠EBC＝∠FCD＝90°，又∵E、F分别是AB、BC的中点，∴BE＝CF，在△CEB和△DFC中，，∴△CEB≌△DFC，∴CE＝DF；【问题解决】（1）证明：如图②中，∵四边形ABCD是正方形，∴AB∥CD，∴∠BAO＝∠AED，∵DO＝DE，∴∠DOE＝∠DEO，∵∠AOB＝∠DOE，∴∠BAO＝∠AOB，∴BA＝BO，∵BF⊥AE，∴AG＝OG，在△BAG和△BOG中，，∴△ABG≌△OBG（SSS）；（2）解：如图②中，过点E作EH⊥AB于点H．∵AE⊥BF，∴∠AGB＝90°，∵∠ABF+∠BAG＝90°，∠DAE+∠BAG＝90°，∴∠ABF＝∠DAE，∵BA＝AD，∠BAF＝∠ADE＝90°，∴△BAF≌△ADE（ASA），∴BF＝AE＝6，∵AE⊥BF，∴S四边形AFEB＝•AE•BF＝×6×6＝18；（3）证明：过点C作CT⊥BG交AB于点T，连接GT．∵CG＝CB，BT⊥BG，∴CT垂直平分线段BG，∴TB＝TG，∴∠TBG＝∠TGB，∵∠TBG+∠BAG＝90°，∠AGT+∠TGB＝90°，∴∠TAG＝∠TGA，∴TA＝TG，∴AT＝TB，∵AE⊥BF，CT⊥BF，∴AE∥CT，∵AT∥CE，∴四边形ATCE是平行四边形，∴AT＝CE，∵AB＝CD＝2AT，∴CD＝2CE，∴DE＝EC．【变式1-7】（滕州市校级模拟）已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．（1）如图①，若四边形ABCD是矩形，且DE⊥CF，求证：＝；（2）如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，使得＝成立？并证明你的结论；（3）如图③，若BA＝BC＝2，DA＝DC＝，∠BAD＝90°，DE⊥CF，试求的值．【解答】（1）证明：∵四边形ABCD是矩形，∴∠A＝∠FDC＝90°，∵CF⊥DE，∴∠DGF＝90°，∴∠ADE+∠CFD＝90°，∠ADE+∠AED＝90°，∴∠CFD＝∠AED，∵∠A＝∠CDF，∴△AED∽△DFC，∴＝；（2）当∠B+∠EGC＝180°时，＝成立．当∠B+∠EGC＝180°时：∵四边形ABCD是平行四边形，∴∠B＝∠ADC，AD∥BC，∴∠B+∠A＝180°，∵∠B+∠EGC＝180°，∴∠A＝∠EGC＝∠FGD，∵∠FDG＝∠EDA，∴△DFG∽△DEA，∴＝，∵∠B＝∠ADC，∠B+∠EGC＝180°，∠EGC+∠DGC＝180°，∴∠CGD＝∠CDF，∵∠GCD＝∠DCF，∴△CGD∽△CDF，∴＝，∴＝，∴＝，即当∠B+∠EGC＝180°时，＝成立．（3）解：过C作CN⊥AD于N，CM⊥AB交AB延长线于M，连接BD，设CN＝x，∵∠BAD＝90°，即AB⊥AD，∴∠A＝∠M＝∠CNA＝90°，∴四边形AMCN是矩形，∴AM＝CN，AN＝CM，∵在△BAD和△BCD中，∴△BAD≌△BCD（SSS），∴∠BCD＝∠A＝90°，∴∠ABC+∠ADC＝180°，∵∠ABC+∠CBM＝180°，∴∠MBC＝∠ADC，∵∠CND＝∠M＝90°，∴△BCM∽△DCN，∴＝，∴＝，∴CM＝x，在Rt△CMB中，CM＝x，BM＝AM﹣AB＝x﹣2，由勾股定理得：BM2+CM2＝BC2，∴（x﹣2）2+（x）2＝22，x＝0（舍去），x＝，CN＝，∵∠A＝∠FGD＝90°，∴∠AED+∠AFG＝180°，∵∠AFG+∠NFC＝180°，∴∠AED＝∠CFN，∵∠A＝∠CNF＝90°，∴△AED∽△NFC，∴＝＝＝．。

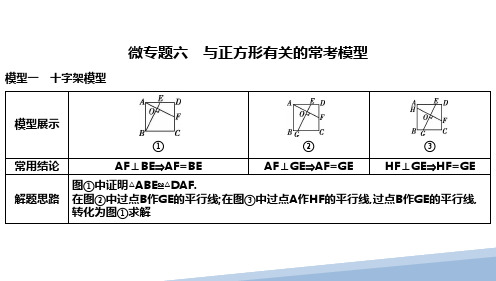
正方形中的常用模型专项探究模型一 正方形的“十字架”模型【知识点睛】【典题练习】1．（2023•余杭区校级模拟）如图，在正方形ABCD 中，点E 、F 分别在边CD ，AD 上，BE 与CF 交于点G ，若BC ＝4，DE ＝AF ＝1，则CG 的长是（ ）A ．2B ．C ．D ．【分析】先证明△CDF ≌△BCE ，得到∠BGC ＝90°，利用面积法即可求出CG ＝． 【解答】解：∵四边形ABCD 为正方形，BC ＝4，∴∠CDF ＝∠BCE ＝90°，AD ＝DC ＝BC ＝4，又∵DE ＝AF ＝1，∴CE ＝DF ＝3，在△CDF 和△BCE 中，，∴△CDF ≌△BCE （SAS ），∴∠DCF ＝∠CBE ，∵∠DCF +∠BCF ＝90°，∴∠CBE +∠BCF ＝90°，A B CD H GEF∴∠BGC＝90°，在Rt△BCE中，BC＝4，CE＝3，∴BE＝＝5，∴BE•CG＝BC•CE，∴CG＝＝＝．故选：D．2．（2023秋•沙坪坝区校级期末）如图，在正方形ABCD中，点E，F分别在AD，AB上，满足DE＝AF，连接CE，DF，点P，Q分别是DF，CE的中点，连接PQ．若∠ADF＝α．则∠PQE可以用α表示为（）A．αB．45°﹣αC．D．3α﹣45°【分析】连接DQ，根据正方形的性质先证明△ADF≌△DCE，得出∠DCE＝α，DF＝CE，进而得出DQ ＝PD，∠PDQ＝90°﹣2α，根据三角形的内角和表示出∠PQD即可求解．【解答】解：连接DQ∵四边形ABCD是正方形，∴AD＝CD，∠A＝∠CDE＝90°，∵AF＝DE，∴△ADF≌△DCE（SAS），∴DF＝CE，∠ADF＝∠DCE＝α，∵点P，Q分别是DF，CE的中点，∴PD＝DF＝DQ＝CE，∴∠DPQ＝∠DQP，∠CDQ＝α，∴∠PDQ＝90°﹣2α，∠DQE＝2α，∴∠PQD＝＝45°+α，∴∠PQE＝45°+α﹣2α＝45°﹣α，故选：B．3．（2023•鄞州区模拟）如图，在正方形ABCD中，E为AB边上一点，BF⊥CE于点G，若已知下列三角形面积，则可求阴影部分面积和的是（）A．S△BAF B．S△BCF C．S△BCG D．S△FCG【分析】根据正方形的性质得到AB＝BC，∠ABC＝∠A＝90°，求得∠ABF＝∠BCE，根据全等三角形的性质得到S△ABF＝S△BCE，根据三角形的面积的和差即可得到结论．【解答】解：∵四边形ABCD∴AB＝BC，∠ABC＝∠A＝90°，∵BF⊥CE，∴∠BGC＝90°，∴∠ABF+∠CBG＝∠CBG+∠BCG＝90°，∴∠ABF＝∠BCE，在△ABF与△BCE中，，∴△ABF≌△BCE（ASA），∴S△ABF＝S△BCE，∵S△BCF＝S正方形ABCD，∴S△ABF+S△DCF＝S△BCE+S△DCF＝S正方形ABCD，∴阴影部分面积和＝S△BCE+S△DCF﹣S△BCG＝S△BCF﹣S△BCG＝S△FCG，故选：D．4．（2023•双峰县三模）如图，在边长为4的正方形ABCD中，点E，F分别是边BC，AB的中点，连接AE，DF交于点O，将△ABE沿AE翻折，得到△AGE，延长EG交AD的延长线于点H，连接CG．有以下结论：①AE⊥DF；②AH＝EH；③CG∥AE；④S四边形BEOF：S△AOF＝4．其中正确的有（）A．1个B．2个C．3个D．4个【分析】①根据正方形的性质可得AD＝AB＝BC，∠DAB＝∠B＝90°，从而可证△DAF≌△ABE，进而可得∠BAE＝∠ADF，然后可得∠BAE+∠AFD＝90°，即可解答；②根据正方形的性质可得AD∥BC，从而可得∠DAC＝∠AEB，再利用折叠可得∠AEB＝∠AEG，进而可得∠DAE＝∠AEG，即可解答；③由折叠得：∠AEB＝∠AEG＝（180°﹣∠GEC），GE＝GC，从而可得∠EGC＝∠ECG＝（180°﹣∠GEC），进而可得∠AEB＝∠GCE，即可解答；④在Rt△ABE中，利用勾股定理求出AE，然后证明△AOF∽△ABE，利用相似三角形的性质，进行计算即可解答．【解答】解：∵四边形ABCD是正方形，∴AD＝AB＝BC，∠DAB＝∠B＝90°，∴∠ADF+∠AFD＝90°，∵点E，F分别是边BC，AB的中点，∴AF＝AB，BE＝EC＝BC，∴AF＝BE，∴△DAF≌△ABE（SAS），∴∠BAE＝∠ADF，∴∠BAE+∠AFD＝90°，∴∠AOF＝180°﹣（∠BAE+∠AFD）＝90°，∴AE⊥DF，故①正确；∵四边形ABCD是正方形，∴AD∥BC，∴∠DAE＝∠AEB，由折叠得：∠AEB＝∠AEG，∴∠DAE＝∠AEG，∴AH＝EH，故②正确；由折叠得：∠AEB＝∠AEG＝（180°﹣∠GEC），GE＝BE，∴GE＝EC，∴∠EGC＝∠ECG＝（180°﹣∠GEC），∴∠AEB＝∠GCE，∴AE∥CG，故③正确；∵∠B＝90°，AB＝4，BE＝2，∴AE＝＝＝2，∵∠B＝∠AOF＝90°，∠F AO＝∠BAE，∴△AOF∽△ABE，∴＝（）2＝（）2＝，∴S四边形BEOF：S△AOF＝4，故④正确；所以，以上结论，正确的有4个，故选：D．5．（2023秋•惠山区期末）如图，在正方形ABCD中，AD＝4，点E、F分别为AB、BC上的动点，且AE ＝BF，AF与DE交于点O，点P为EF的中点．（1）若AE＝1，则EF的长＝；（2）在整个运动过程中，OP长的最小值为．【分析】（1）先根据正方形的性质得到△DAE≌△ABF，得出∠ADE＝∠BAF，AE＝BF，根据勾股定理求出EF即可；（2）然后得到∠EOF＝∠AOD＝90°，即得到OP＝EF，设AE＝BF＝x，则BE＝4﹣x，根据勾股定理得出EF＝＝＝，然后求出结果即可．【解答】解：（1）∵ABCD∴AD＝AB＝4，∠DAB＝∠ABF＝90°，又∵AE＝BF，∴△DAE≌△ABF（SAS），∴∠ADE＝∠BAF，AE＝BF，∵AE＝1，∴BF＝1，BE＝3，∴EF＝＝；故答案为：；（2）∵∠ADE＝∠BAF，∴∠ADE+∠DAF＝∠BAF+∠DAF＝90°，∴∠EOF＝∠AOD＝90°，又∵点P为EF的中点，∴OP＝EF，设AE＝BF＝x，则BE＝4﹣x，∴EF＝＝＝，∴当x＝2时，EF最小为2，即OP最小为；故答案为：．6．（2023•越秀区校级自主招生）如图，在正方形ABCD中，点E，F分别是BC，CD上的点，AE与BF相交于点G，连接AC交BF于点H．若CE＝DF，BG＝GH，AB＝2，则△CFH的面积为．【分析】过点H作HM⊥CD，垂足为M，利用正方形的性质可得AB＝BC＝CD＝2，AB∥CD，∠ABC ＝∠BCD＝90°，∠ACD＝45°，从而利用等腰直角三角形的性质可得AC＝2，再根据等式的性质可得BE＝CF，从而可证△ABE≌△BCF，进而可得∠1＝∠2，然后利用等量代换可得∠1+∠3＝90°，从而可得∠AGB90°，进而可得是BH的垂直平分线，再利用线段垂直平分线的性质可得AB＝AH＝2，从而可得∠3＝∠AHB，CH＝2﹣2，最后利用平行线的性质可得∠3＝∠CFH，从而可得∠CFH＝∠CHF，进而可得CH＝CF＝2﹣2，再在Rt△HMC中，利用等腰直角三角形的性质可求出HM的长，从而利用三角形的面积公式进行计算，即可解答．【解答】解：如图：过点H作HM⊥CD，垂足为M，∵四边形ABCD是正方形，∴AB＝BC＝CD＝2，AB∥CD，∠ABC＝∠BCD＝90°，∠ACD＝45°，∴AC＝AB＝2，∵CE＝DF，∴BC﹣CE＝CD﹣DF，∴BE＝CF，∴△ABE≌△BCF（SAS），∴∠1＝∠2，∵∠ABC＝∠2+∠3＝90°，∴∠1+∠3＝90°，∴∠AGB＝180°﹣（∠1+∠3）＝90°，∵BG＝GH，∴AG是BH的垂直平分线，∴AB＝AH＝2，∴∠3＝∠AHB，CH＝AC﹣AH＝2﹣2，∵AB∥CD，∴∠3＝∠CFH，∵∠AHB＝∠CHF，∴∠CFH＝∠CHF，∴CH＝CF＝2﹣2，在Rt△HMC中，HM＝＝＝2﹣，∴△CFH的面积＝CF•HM＝×（2﹣2）×（2﹣）＝3﹣4，故答案为：3﹣4．7．（2023•拱墅区二模）如图，在正方形ABCD中，E、F分别为边AB、BC上的两点，且BE＝CF，连结AF、DE交于点G．（1）试判断AF与DE的数量关系与位置关系，并说明理由．（2）若AB＝2，点E是AB的中点．①求线段AG的长；②连结BG，求证：BG平分∠EGF．【分析】（1）利用SAS证明△ABF≌△DAE即可得出结论；（2）①在△ADE中利用面积法即可得出AG的长；②连接BG，过点B作BH⊥AF，证明△AEG∽△ABH，得出GH＝AG＝，证明△BMG为等腰直角三角形，即可推出结论．【解答】解：（1）DE＝AF，DE⊥AF，在正方形ABCD中，AB＝BC，又∵BE＝CF，∴AB﹣BE＝BC﹣CF，∴AE＝BF．∵AD＝AB，∠DAE＝∠ABF＝90°，∴△ABF≌△DAE（SAS），∴∠ADE＝∠BAF，DE＝AF．∴∠DAG+∠ADE＝∠DAG+∠＝∠DAE＝90°．∴DE⊥AF；（2）①∵AB＝2，点E是AB的中点，∴AE＝AB＝1．∵∠DAE＝90°，∴DE＝．∴AG＝＝；②证明：连接BG，过点B作BH⊥AF于H．∵DE⊥AF，∴EG∥BH．∴△AEG∽△ABH．∴＝＝，即GH＝AG＝，∵BH＝＝，∴BH＝GH，∴△BGH为等腰直角三角形．∴∠BGH＝45°，∴∠BGE＝90°﹣45°＝45°．∴∠BGH＝∠BGE．即BG平分∠EGF．8．（2023春•淮安期末）问题情境：苏科版八年级下册数学教材第94页第19题第（1）题是这样一个问题：如图1，在正方形ABCD中，点E、F分别在边BC、CD上，且AE⊥BF，垂足为M．那么AE与BF相等吗？（1）直接判断：AE BF（填“＝”或“≠”）；问题探究：（2）如图2，在正方形ABCD中，点E、F、G分别在边BC、CD和DA上，且GE⊥BF，垂足为M．那么GE与BF相等吗？证明你的结论；问题拓展：（3）如图3，点E在边CD上，且MN⊥AE，垂足为H，当H在正方形ABCD的对角线BD上时，连接AN，将△AHN沿着AN翻折，点H落在点H′处．①四边形AHNH′是正方形吗？请说明理由；②若AB＝6，点P在BD上，BD＝3BP，直接写出PH′+AN的最小值为．【分析】（1）证明△ABE≌△BCF即可得出结论；（2）过点A作AN∥GE，证明△ABN≌△BCF（AAS），由此可得AN＝GE＝BF；（3）①如图3，连接CH，证明△ABH≌△CBH（SAS），所以∠BAH＝∠BCH，AH＝CH；由折叠可知，AH＝AH′，NH＝NH′，由四边形内角和和平角的定义可得∠HNC＝∠NCH，所以NH＝CH，则NH＝CH＝AH＝AH′＝NH′，所以四边形AHNH′是菱形，再由“有一个角是直角的菱形是正方形”可得结论；②作H′Q⊥BC交CB的延长线于点Q，作HF⊥BC于点M，可证明△H′QN≌△NFH′（AAS），由此可得H′Q＝NF；易证△BHF是等腰直角三角形，所以HF＝BF＝NF+BN，则NF＝QB＝QH′，可得∠H′BQ＝∠ABH′＝45°，则∠H′BD＝90°；作P关于BH′的对称点P′，则PH′＝P′H′，可得PH′+AN＝PH′+AH′＝P′H′+AH′≥AP′，求出AP′的值即可得出结论．【解答】解：（1）∵AE⊥BF，∴∠EMB＝90°，∴∠FBC+∠BEM＝90°，∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝∠C＝90°，∴∠FBC+∠BFC＝90°，∴∠BEM＝∠BFC，在△ABE和△BCF中，，∴△ABE≌△BCF（AAS），∴AE＝BF．故答案为：＝；（2）GE＝BF，理由如下：如图2，过点A作AN∥GE，交BF于点H，交BC于点N，∴∠EMB＝∠NHB＝90°，∴∠FBC+∠BNH＝90°，∵四边形ABCD是正方形，∴AD∥BC，AB＝BC，∠BAD＝∠ABC＝∠C＝90°，∵AD∥BC，AN∥GE，∴四边形ANEG是平行四边形，∴AN＝EG，∵∠C＝90°，∴∠FBC+∠BFC＝90°，∴∠BNH＝∠BFC，∴△ABN≌△BCF（AAS），∴AN＝BF，∵AN＝EG，∴GE＝BF．（3）①如图3，连接CH，由（2）的结论可知，AE＝MN，∵四边形ABCD是正方形，BD是正方形的对角线，∴∠ABD＝∠CBD＝45°，AB＝BC，∵BH＝BH，∴△ABH≌△CBH（SAS），∴∠BAH＝∠BCH，AH＝CH，由折叠可知，AH＝AH′，NH＝NH′，∵∠ABN+∠AHN＝180°，∴∠BAH+∠BNH＝180°，∵∠BNH+∠HNC＝180°，∴∠BAH＝∠HNC，∴∠HNC＝∠NCH，∴NH＝CH，∴NH＝CH＝AH＝AH′＝NH′，∴四边形AHNH′是菱形，∵∠AHN＝90°，∴菱形AHNH′是正方形；②如图4，作H′Q⊥BC交CB的延长线于点Q，作HF⊥BC于点M，∴∠H′QN＝∠HFB＝90°，由上知四边形AHNH′是正方形，∴H′N＝HN，∠H′NH＝90°，AH′＝AN，∴∠H′NQ+∠HNF＝∠HNF+∠NHF＝90°，∴∠H′NQ＝∠NHF，∴△H′QN≌△NFH′（AAS），∴H′Q＝NF，QN＝HF；∵∠HBF＝45°，∠HFB＝90°，∴△BHF是等腰直角三角形，∴HF＝BF＝NF+BN，∵QN＝QB+BN，∴NF＝QB＝QH′，∴∠H′BQ＝∠ABH′＝45°，∴∠H′BD＝90°；如图4，作P关于BH′的对称点P′，则PH′＝P′H′，过点P′作PK⊥AB交AB延长线于点K，则△PBK是等腰直角三角形，∴PH′+AN＝PH′+AH′＝P′H′+AH′≥AP′，即当A，H′，P′三点共线时，PH′+AN 最小，最小值为AP′的长．∵AB＝6，∴BD＝6，∵BD＝3BP，∴BP＝BP′＝2，∴PK＝BK＝2，∴AK＝8，∴AP′＝＝2，即PH′+AN的最小值为2．故答案为：2．模型二 K型全等模型（即：正方形中的“三垂定理”模型）【知识点睛】如图，已知正方形ABCD，过点B、D两点分别向过点C的直线作垂线，垂足分别为E、F，则有△BCE≌△CDF【典题练习】1．（2023秋•建邺区期末）如图，在平面直角坐标系中，正方形ABCD的边长为2，∠DAO＝60°，则点C 的坐标为．【分析】过点C作CE⊥x轴，CF⊥y轴，证明△AOD≌△DFC即可求出CE，CF，进而得到点C的坐标．【解答】解：过点C作CE⊥x轴，CF⊥y轴，如图：∵正方形ABCD的边长为2，∠DAO＝60°，∴∠ADO＝30°，∴AO＝1，DO＝，∵四边形ABCD是正方形，∴AD＝CD，∠ADC＝90°，∴∠ADO＝∠DCF，∴△AOD≌△DFC（AAS），∴AO＝DF＝1，DO＝CF＝，∴CE＝1+，∴点C的坐标为：（，1+）．故答案为：（，1+）．2．（2024•渝中区校级开学）如图，点A在线段BG上，四边形ABCD和四边形DEFG都是正方形，面积分别是10和18，则△CDE的面积为．【分析】过点E作EH⊥CD，交CD的延长线于H，由题意可证△ADG≌△DEH，即可得EH＝AG＝3．则可求△CDE的面积．【解答】解：如图：过点E作EH⊥CD，交CD的延长线于H．∵四边形ABCD和四边形DEFG都是正方形，面积分别是10和18，∴AD⊥CD，DG＝DE＝＝3，∠BAD＝90°，AD＝CD＝，在Rt△ADG中，AG＝＝2，∵∠ADG+∠GDH＝90°，∠DGH+∠EDH＝90°，∴∠EDH＝∠ADG，且∠DAG＝∠H＝90°，DE＝DG，∴△ADG≌△DEH，∴EH＝AG＝2，∴S△CDE＝×CD×EH＝＝2，故答案为：2．3．（2023秋•白银期末）一组正方形按如图所示的方式放置，其中顶点B1在y轴上，顶点C1，E1，E2，C2，E3，E4，C3，…在x轴上，已知正方形A1B1C1D1的边长为1，∠B1C1O＝60°，B1C1∥B2C2∥B3C3，…，则正方形A2024B2021C2024D2024的边长是．【分析】利用正方形的性质，结合含30度的直角三角形的性质以及勾股定理得出正方形的边长，进而得出变化规律即可得出答案．【解答】解：∵∠B1C1O＝60°，∠B1C1D1＝90°，∴∠D1C1E1＝30°，∴D1E1＝C1D1＝，∴B2E2＝，∵B1C1∥B2C2，∴∠B1C1O＝∠B2C2E2＝60°，∴B2C2＝×2＝，∴正方形A2B2C2D2的边长为，同理可求正方形A3B3C3D3的边长为（）2＝，∴正方形A n B n∁n D n的边长为（）n﹣1，∴正方形A2024B2021C2024D2024的边长为（）2023，故答案为：（）2023．4．（2023春•句容市期末）如图，平面内直线l1∥l2∥l3∥l4，且相邻两条平行线间隔均为1，正方形ABCD 四个顶点分别在四条平行线上，则正方形的面积为．【分析】过C点作直线EF与平行线垂直，与l1交于点E，与l4交于点F．易证△CDE≌△CBF，得CF ＝1，BF＝2．根据勾股定理可求BC2得正方形的面积．【解答】解：过C点作EF⊥l2，交l1于E点，交l4于F点．∵l1∥l2∥l3∥l4，EF⊥l2，∴EF⊥l1，EF⊥l4，即∠CED＝∠BFC＝90°．∵ABCD为正方形，∴∠BCD＝90°．∴∠DCE+∠BCF＝90°．又∵∠DCE+∠CDE＝90°，∴∠CDE＝∠BCF．在△CDE和△BCF中，∴△CDE≌△BCF（AAS），∴BF＝CE＝2．∵CF＝1，∴BC2＝12+22＝5，即正方形ABCD的面积为5．故答案为：5．5．（2022•大庆三模）如图，已知四边形ABCD为正方形AB＝2，点E为对角线AC上一点，连接DE，过点E作EF⊥DE，交BC延长线于点F，以DE、EF为邻边作矩形DEFG，连接CG．在下列结论中：①矩形DEFG是正方形；②2CE+CG＝AD；③CG平分∠DCF；④CE＝CF．其中正确的结论有（）A．①③B．②④C．①②③D．①②③④【分析】过E作EM⊥BC于M点，过E作EN⊥CD于N点，如图所示：根据正方形的性质得到∠BCD ＝90°，∠ECN＝45°，推出四边形EMCN为正方形，由矩形的性质得到EM＝EN，∠DEN+∠NEF＝∠MEF+∠NEF＝90°，根据全等三角形的性质得到ED＝EF，推出矩形DEFG为正方形；故①正确；根据正方形的性质得到AD＝DC，∠ADE+∠EDC＝90°推出△ADE≌△CDG（SAS），得到AE＝CG，求得AC＝AE+CE＝CE+CG＝AD，故②错误；当DE⊥AC时，点C与点F重合，得到CE不一定等于CF，故④错误．【解答】解：过E作EM⊥BC于M点，过E作EN⊥CD于N点，如图所示：∵四边形ABCD是正方形，∴∠BCD＝90°，∠ECN＝45°，∴∠EMC＝∠ENC＝∠BCD＝90°，∴NE＝NC，∴四边形EMCN为正方形，∵四边形DEFG是矩形，∴EM＝EN，∠DEN+∠NEF＝∠MEF+∠NEF＝90°，∴∠DEN＝∠MEF，又∠DNE＝∠FME＝90°，在△DEN和△FEM中，，∴△DEN≌△FEM（ASA），∴ED＝EF，∴矩形DEFG为正方形；故①正确；∴DE＝DG，∠EDC+∠CDG＝90°，∵四边形ABCD是正方形，∵AD＝DC，∠ADE+∠EDC＝90°，∴∠ADE＝∠CDG，在△ADE和△CDG中，，∴△ADE≌△CDG（SAS），∴AE＝CG，∠DAE＝∠DCG＝45°，∵∠DCF＝90°，∴CG平分∠DCF，故③正确；∴AC＝AE+CE＝CE+CG＝AD，故②错误；当DE⊥AC时，点C与点F重合，∴CE不一定等于CF，故④错误，故选：A．6．（2023秋•福田区校级期末）如图，分别以△ABC的三边AB，BC，AC为边向外侧作正方形AFGB，正方形BHLC，正方形ACDE，连接EF，GH，DL，再过A作AK⊥BC于K，延长KA交EF于点M．①S+S正方形ACDE＝S正方形BHLG；②EM＝MF；③2AM＝BC；④当AB＝3，BC＝5，∠BAC＝90°时，正方形AFGBS阴影部分＝20）个．A．1B．2C．3D．4【分析】①运用正方形性质和勾股定理即可判断结论①不正确；②过点E作ER⊥AK于R，过点F作FT⊥AK于T，可证得△AER≌△CAK（AAS），△EMR≌△FMT（AAS），即可判断结论②正确；③过点E作EJ∥AF交AM的延长线于J，可证得△MEJ≌△MF A（AAS），△AEJ≌△CAB（SAS），即可判断结论③正确；④分别过点A、G、D作AP⊥BH于P，AK⊥BC于K，AN⊥CL于N，GQ⊥BH于Q，DM⊥CL于M，运用全等三角形的判定和性质可证得GQ＝BP＝AK，DM＝CN＝AK，再运用面积法可得AK＝＝＝，再利用S阴影部分＝S△AEF+S△BGH+S△CDL，即可判断结论④错误．【解答】解：①由正方形的性质可得：S正方形AFGB+S正方形ACDE＝AB2+AC2，S正方形BHLC＝BC2，∵∠BAC不一定是直角，∴AB2+AC2＝BC2不一定成立，故结论①不正确；②如图，过点E作ER⊥AK于R，过点F作FT⊥AK于T，则∠ERA＝∠ATF＝90°，∴∠EAR+∠AER＝90°，∵四边形ACDE是正方形，∴AC＝AE，∠CAE＝90°，∴∠EAR+∠CAK＝90°，∴∠AER＝∠CAK，在△AER和△CAK中，，∴△AER≌△CAK（AAS），∴ER＝AK，同理可得：FT＝AK，∴ER＝FT，在△EMR和△FMT中，，∴△EMR≌△FMT（AAS），∴EM＝MF，故结论②正确；③如图，过点E作EJ∥AF交AM的延长线于J，则∠AEJ+∠EAF＝180°，∠MEJ＝∠MF A，在△MEJ和△MF A中，，∴△MEJ≌△MF A（AAS），∴EJ＝AF＝AB，MJ＝MA，∴AJ＝2AM，∵∠BAF＝∠CAE＝90°，∴∠BAC+∠EAF＝180°，∴∠AEJ＝∠BAC，在△AEJ和△CAB中，，∴△AEJ≌△CAB（SAS），∴AJ＝BC，∴2AM＝BC，故结论③正确；④∵AB＝3，BC＝5，∠BAC＝90°，∴AC＝＝＝4，如图，分别过点A、G、D作AP⊥BH于P，AK⊥BC于K，AN⊥CL于N，GQ⊥BH于Q，DM⊥CL于M，同理可得GQ＝BP＝AK，DM＝CN＝AK，∵BC•AK＝AB•AC，∴AK＝＝＝，∴S阴影部分＝S△AEF+S△BGH+S△CDL＝×3×4+×5×+×5×＝18，故结论④错误；故选：B．7．（2024•立山区模拟）如图，四边形ABCD是边长为4的正方形，点E在边CD所在直线上，连接AE，以AE为边，作正方形AEFG（点A，E，F，G按顺时针排列）．当正方形AEFG中的某一顶点落在直线BD上时（不与点D重合），则正方形AEFG的面积为．【分析】分两种情况：当点F在直线BD上时，过点F作FM⊥CD，交CD的延长线于M，可得△DFM 是等腰直角三角形，得出DM＝FM，再证得△AED≌△EFM（AAS），利用勾股定理可得：AE＝AD2+DE2＝42+22＝20，正方形的面积为20；当点G在直线上BD时，过点G作GM⊥AD，交AD的延长线于M，同理可求得答案．【解答】解：当点F在直线BD上时，过点F作FM⊥CD，交CD的延长线于M，B，则∠M＝90°，∵四边形ABCD是正方形，∴∠BDC＝45°，∠ADE＝90°，∴∠FDM＝∠BDC＝45°，∠AED+∠EAD＝90°，∴△DFM是等腰直角三角形，∴DM＝FM，∵四边形AEFG是正方形，∴EF＝AE，∠AEF＝90°，∴∠AED+FEM＝90°，∴∠EAD＝∠FEM，在△AED和△EFM中，，∴△AED≌△EFM（AAS），∴DE＝FM，AD＝EM，∴DE＝DM＝FM，∵DE+DM＝EM，∵2DE＝AD＝4，∴DE＝2，在Rt△ADE中，AE＝AD2+DE2＝42+22＝20，∴正方形的面积为20．当点G在直线上BD时，过点G作GM⊥AD，交AD的延长线于M，如图，同理可得：△AED≌△GAM（AAS），∴GM ＝AD ＝4，AM ＝DE ，∵∠ADB ＝MDG ＝45°，∠M ＝90°，∴△DGM是等腰直角三角形，∴DM ＝GM ，∴DM ＝AD ＝4，∴AM ＝8， 在Rt △AGM 中，AG 2＝AM 2+GM 2＝82+42＝802，∴正方形的面积为80．综上，正方形AEFG 的面积为20或80．故答案为：20或80．模型二 K 型全等模型（即：正方形中的“三垂定理”模型）【知识点睛】条件：①正方形ABCD ，②∠EAF=45° 结论： ①EF=BE+DF ；(△CEF 的周长=正方形ABCD 周长的一半） ②EA 平分∠BEF ③FA 平分∠DAE条件：①正方形ABCD ；②∠EAF=45° 结论：EF=DF-BE☆：当∠EAF 旋转到正方形ABCD 外部时，则有：【典题练习】1．（2023•新乡一模）如图，在正方形ABCD中，点M，N为边BC和CD上的动点（不含端点），若AB＝，∠MAN＝45°，则△MNC的周长是（）A．B．2C．2D．3【分析】将△ABM绕点A顺时针旋转90°得△ADE，根据正方形的性质、折叠的性质证明Rt△ABM≌Rt △ADE（HL），△EAN≌△MAN（SAS），根据全等三角形的性质推出△MNC的周长＝DC+BC，据此求解即可．【解答】解：如图，将△ABM绕点A顺时针旋转90°得△ADE，则∠EAN＝∠EAM﹣∠MAN＝90°﹣45°＝45°＝∠MAN，AE＝AM，∵四边形ABCD是正方形，∴AB＝AD，∠ADC＝90°，∴∠ADE＝90°，在Rt△ABM和Rt△ADE中，，∴Rt△ABM≌Rt△ADE（HL），∴BM＝DE，在△EAN和△MAN中，，∴△EAN≌△MAN（SAS），∴MN＝EN＝DE+DN＝BM+DN，∴△MNC的周长为：MC+NC+MN＝（MC+BM）+（NC+DN）＝DC+BC，∵DC＝BC＝，∴△MNC的周长为2，故选：C．2．（2023秋•武城县期末）如图，点E、F分别在正方形ABCD的边BC、CD上，∠EAF＝45°，已知AD ＝6（正方形的四条边都相等，四个内角都是直角），DF＝2，则S△AEF＝（）A．6B．12C．15D．30【分析】过点A作AH⊥AE，交CD的延长线于点H，由“ASA”可证△ADH≌△ABE，可得BE＝HD，AH＝AE，由“SAS”可证△AFH≌△AFE，可得EF＝HF，利用勾股定理可求BE的长，即可求解．【解答】解：如图，过点A作AH⊥AE，交CD的延长线于点H，∵四边形ABCD是正方形，∴AB＝AD＝CD＝BC＝6，∠BAD＝∠ADC＝90°，∵AH⊥AE，∴∠HAE＝∠BAD＝90°，∴∠HAD＝∠BAE，在△ADH和△ABE中，，∴△ADH≌△ABE（ASA），∴BE＝HD，AH＝AE，∵∠EAF＝45°，∴∠HAF＝∠EAF＝45°，在△AFH和△AFE中，，∴△AFH≌△AFE（SAS），∴EF＝HF，∵DF＝2，∴CF＝4，∵EF2＝CE2+CF2，∴（2+BE）2＝16+（6﹣BE）2，∴BE＝3，∴HF＝HD+DF＝5，∵△AFH≌△AFE，∴S△AEF＝S△AFH＝×HF×AD＝×5×6＝15，故选：C．3．（2023•增城区二模）在正方形ABCD中，点E、F分别在边BC、CD上，且∠EAF＝45°，连接EF．（1）如图1，若BE＝2，DF＝EF的长度；（2）如图2，连接BD，BD与AF、AE分别相交于点M、N，若正方形ABCD的边长为6，BE＝2，求DF的长；（3）判断线段BN、MN、DM三者之间的数量关系并证明你的结论．【分析】（1）延长CB至点G，使BG＝DF，连接AG，先根据SAS证明△ABG≌△ADF，得到∠BAG＝∠DAF，BG＝DF，AG＝AF，于是可通过SAS证明△AEG≌△AEF，得到EG＝EF，则EF＝EG＝BG+BE ＝DF+BE；（2）设DF＝x，则CF＝6﹣x，由（1）可得EF＝DF+BE＝2+x，于是在Rt△CEF中，根据勾股定理列出方程，求解即可；（3）延长CB至点G，使BG＝DF，连接AG，在AG上截取AH＝AM，连接HN，BH，易通过SAS证明△ABH≌△ADM，得到BH＝DM，∠ABH＝∠ADM＝45°，进而得出∠HBN＝90°，再通过SAS证明△AHN≌△AMN，得到NH＝MN，在Rt△BHN中，根据勾股定理得BN2+BH2＝NH2，再等量代换即可得到结论．【解答】解：（1）如图，延长CB至点G，使BG＝DF，连接AG，∵四边形ABCD为正方形，∴DAB＝∠ABC＝∠BCD＝∠ADC＝90°，AB＝AD，∴∠ABG＝90°，在△ABG和△ADF中，，∴△ABG≌△ADF（SAS），∴∠BAG＝∠DAF，BG＝DF，＝AF，∵∠EAF＝45°，∴∠DAF+∠BAE＝∠BAG+∠BAE＝∠EAG＝45°，∴∠EAF＝∠EAG，在△AEG和△AEF中，，∴△AEG≌△AEF（SAS），∴EG＝EF，∵BE＝2，DF＝3，∴EF＝EG＝BG+BE＝DF+BE＝5；（2）∵四边形ABCD是边长为6的正方形，∴BC＝CD＝6，设DF＝x，则CF＝CD﹣DF＝6﹣x，由（1）知，EF＝DF+BE，∵BE＝2，∴CE＝BC﹣BE＝4，EF＝2+x，在Rt△CEF中，CE2+CF2＝EF2，∴42+（6﹣x）2＝（2+x）2，解得：x＝3，∴DF＝3；（3）BN2+DM2＝MN2，证明如下：如图，延长CB至点G，使BG＝DF，连接AG，在AG上截取AH＝AM，连接HN，BH，由（1）知，∠BAG＝∠DAF，∠EAG＝∠EAF＝45°，∵四边形ABCD为矩形，∴AB＝AD，∠ADB＝∠ABD＝45°，在△ABH和△ADM中，，∴△ABH≌△ADM（SAS），∴BH＝DM，∠ABH＝∠ADM＝45°，∴∠HBN＝∠ABH+∠ABN＝90°，在△AHN和△AMN中，，∴△AHN≌△AMN（SAS），∴NH＝MN，在Rt△BHN中，BN2+BH2＝NH2，∴BN2+DM2＝MN2．。

专题1.7 正方形十字模型【例题精讲】【例1】如图，在正方形ABCD中，点E，F分别在边BC，CD上，AE，BF交于点O，90AOFÐ=°．求证：BE CF=．【解答】证明：Q四边形ABCD是正方形，AB BC\=，90ABE BCFÐ=Ð=°，90AOFÐ=°Q，90AOBÐ=°，90BAE OBA\Ð+Ð=°，又90FBC OBAÐ+Ð=°Q，BAE CBF\Ð=Ð（同角的余角相等），在ABED和BCFD中\BCF ABE AB BCBAE FBCÐ=Ðìï=íïÐ=Ðî，() ABE BCF ASA\D@D．BE CF\=．【题组训练】1．如图，点E ，F 分别是正方形ABCD 的边BC ，CD 的中点，AF 与DE 交于点G ，连接BG ．（1）写出线段AF 与DE 的数量关系和位置关系，并证明；（2）求证：BGE DAF Ð=Ð．【解答】证明：（1）AF DE =且AF DE ^．理由如下：Q 四边形ABCD 是正方形，E ，F 均为中点，AD BC DC \==，EC DF =，在ADF D 和DCE D 中，AD DC ADF DCE DF CE =ìïÐ=Ðíï=î，()ADF DCE SAS \D @D ，AF DE \=，AFD DEC Ð=Ð，90DEC CDE Ð+Ð=°Q ，90AFD CDE DGF \Ð+Ð=°=Ð，AF DE \^；（2）延长DE 交AB 的延长线于H ，1122BE BC AD ==Q ，//BE AD ，BH AB \=，AF DE ^Q ，90AGH \Ð=°，GB HB \=，H BGH \Ð=Ð，H ADG DAG ADG Ð+Ð=Ð+ÐQ ，H DAG \Ð=Ð，BGE DAF\Ð=Ð．2．如图，在正方形ABCD中，点E是BC的中点，连接DE，过点A作AG ED^交DE于点F，交CD于点G．（1）证明：ADG DCED@D；（2）连接BF，求证：AB FB=．【解答】证明：（1）Q四边形ABCD是正方形，=，\Ð=Ð=°，AD DC90ADG C又AG DE^Q，DAG ADF CDE ADF\Ð+Ð=°=Ð+Ð，90\Ð=Ð，DAG CDE\D@D；ADG DCE ASA()（2）如图所示，延长DE交AB的延长线于H，Q是BC的中点，E\=，BE CE又90Q，DEC HEBÐ=Ð，Ð=Ð=°C HBE\D@D，DCE HBE ASA()\==，BH DC AB即B是AH的中点，又90AFH Ð=°Q ，Rt AFH \D 中，12BF AH AB ==．3．如图，正方形ABCD 中，E ，F 分别为BC ，CD 上的点，且AE BF ^，垂足为G ．（1）求证：AE BF =．（2）若BE =，2AG =，求正方形的边长．【解答】（1）证明：Q 四边形ABCD 是正方形，AB BC \=，90ABC C Ð=Ð=°，90BAE AEB \Ð+Ð=°，AE BF ^Q ，垂足为G ，90CBF AEB \Ð+Ð=°，BAE CBF \Ð=Ð，在ABE D 与BCF D 中，90BAE CBF AB BC ABE C Ð=Ðìï=íïÐ=Ð=°î，()ABE BCF ASA \D @D ，AE BF \=；（2）解：Q 四边形ABCD 为正方形，90ABC \Ð=°，AE BF ^Q ，90BGE ABE \Ð=Ð=°，BEG AEB Ð=ÐQ ，BGE ABE \D D ∽，\BE EG AE BE=，即：2BE EG AE =g ，设EG x =，则2AE AG EG x =+=+，2(2)x x \=+g ，解得：11x =，23x =-（不合题意舍去），3AE \=，AB \===4．如图，正方形ABCD 中，点E ，F 分别在边AD ，AB 上，且AE BF =，连接CE ，DF 相交于点M ．（1）当40ADF Ð=°时，DCE Ð=　40　°；（2）判断CE 与DF 的关系，并证明．【解答】解：（1）Q 四边形ABCD 是正方形，CD AD AB \==，90CDE DAF Ð=Ð=°，又AE BF =Q ，DE AF \=，在CDE D 和DAF D 中，CD DA CDE DAE DE AF =ìïÐ=Ðíï=î，()CDE DAF SAS \D @D，DCE ADF\Ð=Ð，Q，Ð=°ADF40\Ð=°，40DCE故答案为：40；（2）CE，DF的位置关系互相垂直，证明：由（1）知DCE ADFÐ=Ð，Q，Ð+Ð=Ð=°ADF MDC CDE90\Ð+Ð=°，90DCE MDC\Ð=°，DMC90\^，CE DF即CE，DF的位置关系互相垂直．5．如图，在正方形ABCD中，点P在AD上，且不与A、D重合，BP的垂直平分线分别交CD、AB于E、F两点，垂足为Q，过E作EH AB^于H．（1）求证：HF AP=；（2）若正方形ABCD的边长为12，4AP=，求线段EQ的长．【解答】（1）证明：Q四边形ABCD是正方形，Ð=Ð=Ð=°C A ABC\=，90AB BC^，Q，EH ABEQ BP^90EQN BHM \Ð=Ð=°，\四边形BCEH 是矩形，BC EH \=，AB EH \=，EMQ BMH Ð=ÐQ ，EMQ BMH \D D ∽，QEM HBM \Ð=Ð．在Rt APB D 与Rt HFE D 中，PAB FHE AB EH Ð=Ðìí=î，APB HFE \D @D ，HF AP \=；（2）解：由勾股定理得，BP ===EF Q 是BP 的垂直平分线，12BQ BP \==，4tan tan 12QF BQ FBQ BQ ABP \=×Ð=×Ð==由（1）知，APB HFE D @D ，EF BP \==，EQ EF QF \=-=．6．如图1，在正方形ABCD 中，E 、F 分别是边AD 、DC 上的点，且AF BE ^．（1）求证：AF BE =；（2）如图2，在正方形ABCD 中，M 、N 、P 、Q 分别是边AB 、BC 、CD 、DA 上的点，且MP NQ ^．MP 与NQ 是否相等？并说明理由．【解答】（1）证明：在正方形ABCD 中，AB AD =，90BAE D Ð=Ð=°，90DAF BAF \Ð+Ð=°，AF BE ^Q ，90ABE BAF \Ð+Ð=°，ABE DAF \Ð=Ð，Q 在ABE D 和DAF D 中，ABE DAF AB ADBAE D Ð=Ðìï=íïÐ=Ðî，()ABE DAF ASA \D @D ，AF BE \=；（2）解：MP 与NQ 相等．理由如下：如图，过点A 作//AF MP 交CD 于F ，过点B 作//BE NQ 交AD 于E ，//AB CD Q ，//AD BC ，\四边形AMPF 与四边形BNQE 是平行四边形，AF PM \=，BE NQ =，Q 在正方形ABCD 中，AB AD =，90BAE D Ð=Ð=°，90DAF BAF \Ð+Ð=°，AF BE ^Q，90ABE BAF \Ð+Ð=°，ABE DAF \Ð=Ð，Q 在ABE D 和DAF D 中，ABE DAF AB ADBAE D Ð=Ðìï=íïÐ=Ðî，()ABE DAF ASA \D @D ，AF BE \=；MP NQ \=．9．如图，在正方形ABCD 中，AF BE =，AE 与DF 相交于点O ．（1）求证：DAF ABE D @D ；（2）求AOD Ð的度数．【解答】（1）证明：Q 四边形ABCD 是正方形，90DAB ABC \Ð=Ð=°，AD AB =，在DAF D 和ABE D 中，90AD AB DAF ABE AF BE =ìïÐ=Ð=°íï=î，()DAF ABE SAS \D @D，（2）由（1）知，DAF ABE D @D ，ADF BAE \Ð=Ð，90ADF DAO BAE DAO DAB Ð+Ð=Ð+Ð=Ð=°Q ，180()90AOD ADF DAO \Ð=°-Ð+Ð=°．10．已知正方形ABCD ，E 、F 分别在DC 、BC 上，DE CF =，AE 、DF 相交于点G ．（1）求证：AE DF ^；（2）当E 是DC 中点时，求证：AB BG =．【解答】证明：（1）Q 四边形ABCD 是正方形，AD DC \=，90ADC C Ð=Ð=°，在ADE D 和DCF D 中，AD DC ADC C DE CF =ìïÐ=Ðíï=î，()ADE DCF SAS \D @D ，DAE CDF \Ð=Ð，90CDF ADF Ð+Ð=°Q ，90DAE ADF \Ð+Ð=°，90AGD \Ð=°，AE DF \^；（2）方法一：如图，过点B 作BH AG ^于点H，AE DF ^Q ，90ADG DAG BAH DAG \Ð+Ð=Ð+Ð=°，ADG BAH \Ð=Ð，在ADG D 和BAH D 中，90ADG BAH AGD BHA AD BA Ð=ÐìïÐ=Ð=°íï=î，()ADG BAH AAS \D @D ，DG AH \=，E Q 是DC 中点，DE EC \=，设DE a =，则2AD a =，AE \=，1122ADE S AE DG AD DE D =×=×Q ，\2a a ××，DG \=，AH DG \==，在Rt DEG D 中，DE a =，DG=，EG \==，HG AE AH GE \=--=-=，AH GH \=，BH AG ^Q ，AB BG \=．方法二：如图，延长DF ，与AB 交于点M ，E Q 是DC 中点，DE CE \=，在正方形ABCD 中，90ABC C Ð=Ð=°，AB DC BC ==，//AB DC ，M FDC \Ð=Ð，DE CF \=，BF CF \=，在BFM D 和CDF D 中，M FDC BFM CFD BF CF Ð=ÐìïÐ=Ðíï=î，()BFM CDF AAS \D @D ，BM CD \=，AB CD =Q ，AB BM \=，AE DF ^Q ，12BG AM AB \==，即AB BG =．11．已知正方形ABCD ，E 、F 分别为边BC 、CD 上的点，DE AF =．（1）求证：ADF DCE D @D ；（2）求证：AF DE ^．【解答】证明：（1）Q 四边形ABCD 为正方形，AD DC \=，90ADC C Ð=Ð=°，在Rt ADF D 与Rt DCE D 中，AD DC AF DE=ìí=îRt ADF Rt DCE(HL)\D @D ；（2）设AF 与DE 交于G ，Rt ADF Rt DCE(HL)D @D Q ，DAF CDE \Ð=Ð，90DGF DAF ADE ADC \Ð=Ð+Ð=Ð=°，AF DE \^．12．综合与实践：如图，在正方形ABCD 中，点E 是边AB 上的一个动点（点E 与点A ，B 不重合），连接CE ，过点B 作BF CE ^于点G ，交AD 于点F ．（1）如图1，求证：ABF BCE D @D ；（2）如图2，当点E 运动到AB 中点时，连接DG ，求证：DC DG =；（3）如图3，若4AB =，连接AG ，当点E 在边AB 上运动的过程中．AG 是否存在最小值，若存在，请直接写出AG 最小值，及此时AE 的值；若不存在，请说明理由．【解答】（1）证明：Q 四边形ABCD 是正方形，AB BC \=，90BAD CBA Ð=Ð=°，90CEB BCE \Ð+Ð=°，BF CE ^Q ，90ABF CEB \Ð+Ð=°，ABF BCE \Ð=Ð，在ABF D 和BCE D 中，90FAB EBC AB BCABF BCE Ð=Ð=°ìï=íïÐ=Ðî，()ABF BCE ASA \D @D ，（2）证明：如图2，延长CD ，BF 交于点H ，Q 点E 是AB 的中点，12BE AB \=，Q 四边形ABCD 是正方形，//CD AB \，AD AB BC ==，90BAD CBA Ð=Ð=°，90CEB BCE \Ð+Ð=°，BF CE ^Q，90ABF CEB \Ð+Ð=°，ABF BCE \Ð=Ð，又AB BC =Q ，90FAB EBC Ð=Ð=°，()ABF BCE ASA \D @D ，BE AF \=，1122BE AF AB AD \===，AF DF \=，//AB CD Q ，ABF H \Ð=Ð，在ABF D 和DHF D 中，ABF H DFH AFB AF DF Ð=ÐìïÐ=Ðíï=î，()ABF DHF AAS \D @D AB DH \=，DH CD \=，又BF CE ^Q ，90BGH \Ð=°，DC DH DG \==．（3）解：AG 存在最小值．如图3，以BC 为直径作O e ，连接AO ，OG ，BF CE ^Q ，90BGC \Ð=°，\点G 在以BC 为直径的O e上，在AGO D 中，AG AO GO -…，\当点G 在AO 上时，AG 有最小值，此时：如图4，4BC AB ==Q ，点O 是BC 中点，2BO CO \==，AO ===Q2AG \=-，OG OB =Q ，OBG OGB \Ð=Ð，//AD BC Q ，AFG OBG \Ð=Ð，AFG OBG OGB AGF \Ð=Ð=Ð=Ð，2AG AF \==-，由（2）可得2AF BE ==，42)6AE AB BE \=-=--=-．13．如图1，P 为正方形ABCD 的边BC 上一动点(P 与B 、C 不重合），点Q 在CD 边上，且BP CQ =，连接AP 、BQ 交于点E ．（1）求证：AP BQ ^；（2）当P 运动到BC 中点处时（如图2)，连接DE ，请你判断线段DE 与AD 之间的关系，并说明理由；（3）如图3，在（2）的条件下，过A 点作AM DE ^于点H ，交BQ 、CD 于点N 、M ，若2AB =，求QM 的长度．【解答】解：（1）在正方形ABCD 中有：AB BC =，90ABP BCQ Ð=Ð=°，BP CQ =Q ，()ABP BCQ SAS \D @D ，PAB QBC \Ð=Ð，90QBC ABQ Ð+Ð=°Q ，90PAB ABQ \Ð+Ð=°，90AEB \Ð=°，AP BQ \^；（2）AD DE =，理由如下：如图，延长BQ 、AD 交于一点F ，当点P 为BC 中点时，Q 为CD 中点，即CQ DQ =，FQD BQC Ð=ÐQ ，FDQ C Ð=Ð，()FDQ BCQ ASA \D @D ，FD BC \=，FD AD \=，由（1）得：90FEA Ð=°，12DE FA AD \==；（3）由（1）得：AP BQ ^，90ANE NAE \Ð+Ð=°，90NAE AEH Ð+Ð=°Q ，ANE AEH \Ð=Ð，设ANE AEH a Ð=Ð=，DE DA =Q ，DAE AEH a \Ð=Ð=，//AD BC Q ，APB DAE a \Ð=Ð=，PAB QBC D @D Q ，CQB APB a \Ð=Ð=，QNM ANE a Ð=Ð=Q ，CQB QNM \Ð=Ð，QM MN \=，//CD AB Q ，ABQ CQB a \Ð=Ð=，ABQ ANE \Ð=Ð，2AN AB \==，设QM MN x ==，则1DM DQ QM x =+=+，2AM AN MN x =+=+，222AD DM AM +=Q ，2222(1)(2)x x \++=+，解得：12x =，12QM \=．14．（1）如图1，在正方形ABCD 中，AE 、DF 相交于点O 且AE DF ^则AE 和DF 的数量关系为 AE DF =　．（2）如图2，在正方形ABCD 中，E 、F 、G 分别是边AD 、BC 、CD 上的点，BG EF ^，垂足为H ．求证：EF BG =．（3）如图3，在正方形ABCD 中，E 、F 、M 分别是边AD 、BC 、AB 上的点，2AE =，5BF =，1BM =，将正方形沿EF 折叠，点M 的对应点恰好与CD 边上的点N 重合，求CN 的长度．【解答】解：（1）90DAO BAE Ð+Ð=°Q ，90DAO ADF Ð+Ð=°，BAE ADF \Ð=Ð，在ABE D 和DAF D 中，BAE ADF AD AB ABE DAF Ð=Ðìï=íïÐ=Ðî，()ABE DAF ASA \D @D ，AE DF \=，故答案为AE DF =；（2）如图1，故点E 作EM BC ^于点M ，则四边形ABME为矩形，则AB EM =，在正方形ABCD 中，AB BC =，EM BC \=，EM BC ^Q ，90MEF EFM \Ð+Ð=°，BC EM ^Q ，90CBG EFM \Ð+Ð=°，CBG MEF \Ð=Ð，在BCG D 和EMF D 中，90CBG MEF BC EMC EMF Ð=Ðìï=íïÐ=Ð=°î，()BCG EMF ASA \D @D ，BG EF \=；（3）如图2，连接MN ，M Q 、N 关于EF 对称，MN EF \^，过点E 作EH BC ^于点H，过点M作MG CD^，^于点G，则EH MG由（2）同理可得：()D@D，EHF MGN ASANG HF\=，AE=Q，52BF=，\==-=，523NG HF又1GC MBQ，==\=+=+=．314NC NG CG。

专题03 十字架模型【模型解读】十字架模型，多出现在正方形或者矩形等特殊图形中，由垂直，我们可以得到全等或相似，从而得到线段之间的数量关系！下面我对十字架模型进行简单的梳理和总结！【模型一】正方形内的十字架结构1、在正方形ABCD中，BN⊥AM，则常见的结论有哪些？2、在正方形ABCD中，E、F、G、H分别为AB、CD、BC、AD边上的点，若EF⊥GH，上述结论是否仍然成立？【思考】从相等是否可推导出垂直？3、在正方形ABCD中，E、F、G、H分别为AB、CD、BC、AD边上的点，若EF＝GH，则EF与GH是否垂直，若不是，请画出反例．如图，垂直只是相等时的一种情况，另一种，只需使得AH’＝DH，BG’＝CG’即可作出HG＝H’G’【模型二】十字结构在矩形中【思考】既然正方形内可出现垂直，那么矩形内出现垂直会有什么结论呢？1、如图，在矩形ABCD中，AB＝m，AD＝n，在AD上有一点E，若CE⊥BD，则CE和BD之间有什么数量关系？2、如图1，一般情况，在矩形ABCD中，E、F、G、H分别为AD、BC、AB、CD边上的点，当EF⊥GH 时，有的结论，证明方法如图2，证明△FME∽GNH即可看到上面加粗的字了吗？这个点的所在边为什么要确定？因为，仅仅使得EF⊥GH，会出现下图情况，此时仍有相似，但EF ABGH AD=不再成立【模型三】十字结构在直角三角形中和其他四边形中我们知道直角三角形是可以看成是连接矩形对角线后分成的图形，所以矩形的结论可沿用至直角三角形内，例题1．在Rt △ACB 中，AC ＝4，BC ＝3，点D 为AC 上一点，连接BD ，E 为AB 上一点，CE ⊥BD ，当AD ＝CD 时，求AE 的长；同样的，一般四边形也可以补成矩形例题2.如图，把边长为AB ＝、BC ＝4且∠B ＝45°的平行四边形ABCD 对折，使点B 和D 重合，求折痕MN 的长．【巩固练习】简析：，设由得解得235820,,433AG CG AG CG ====20,3CE x EG x ==-,AG EG BC CE =82033,3x x -=6017x =1．如图，正方形ABCD 中，点E 、F 分别在边CD ，AD 上，BE CF ^于点G ．若4BC =，1AF =，则CE 的长为( )A ．3B ．125C ．195D ．165【解答】解：正方形ABCD 中，4BC =Q ，4BC CD AD \===，90BCE CDF Ð=Ð=°，BE CF ^Q 于点G ．90CBG BCG BCG DCF \Ð+Ð=Ð+Ð=°，CBE DCF \Ð=Ð，在BCE D 和CDF D 中，BCE CDF BC CDCBE DCF Ð=Ðìï=íïÐ=Ðî，()BCE CDF ASA \D @D ，CE DF \=，413DF AD AF =-=-=Q ，3CE \=．故选：A ．2．如图，点O 是正方形ABCD 的中心，E 、F 、G 、H 分别是边AB 、CD 、BC 、AD 上的点，且EF GH ^，EF 、GH 相交于点O ，下列结论：①AE BG =；②BEO CGO Ð=Ð；③OE OH =；④4ABCD AEOH S S ¹正方形四边形中正确的有( )A ．1个B ．2个C ．3个D ．4个【解答】解：连接OA 、OB 、OC 、OD ，如图所示：Q 点O 是正方形ABCD 的中心，90AOB \Ð=°，45OAE OBG Ð=Ð=°，OA OB OC OD ===，EF GH ^Q ，90EOG \Ð=°，AOE BOG \Ð=Ð，在AOE D 和BOG D 中，OAE OBG OA OBAOE BOG Ð=Ðìï=íïÐ=Ðî，()AOE BOG ASA \D @D ，AE BG \=，①正确；同理：OBE OCG D @D ，BEO CGO \Ð=Ð，②正确；同理：AOH BOE D @D ，OE OH \=，③正确；\四边形AEOH 的面积=四边形BGOE 的面积14=正方形ABCD 的面积，\正方形ABCD 的面积4=四边形AEOH 的面积，\④不正确；正确的有3个．故选：C ．3．如图，在边长为4的正方形ABCD 中，点E 、F 分别是边BC 、CD 上的动点．且BE CF =，连接BF 、DE ，则BF DE +的最小值为( )A．B．C．D．【解答】解：连接AE，如图1，Q四边形ABCD是正方形，AB BCABE BCFÐ=Ð=°．\=，90又BE CF=，\D@D．()ABE BCF SAS\=．AE BF+最小值等于AE DE+最小值．所以BF DE作点A关于BC的对称点H点，如图2，连接BH，则A、B、H三点共线，连接DH，DH与BC的交点即为所求的E点．根据对称性可知AE HE=，+=．所以AE DE DH在Rt ADHD中，DH==BF DE\+最小值为．故选：C．4．如图，正方形纸片ABCD的边长为12，E是边CD上一点，连接AE、折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，点F在AD上，若5DE=，则GE的长为　4913　．【解答】解：Q四边形ABCD为正方形，12AB AD\==，90BAD DÐ=Ð=°，由折叠及轴对称的性质可知，ABF GBFD@D，BF垂直平分AG，BF AE\^，AH GH=，90BAH ABH\Ð+Ð=°，又90FAH BAHÐ+Ð=°Q，ABH FAH\Ð=Ð，()ABF DAE ASA\D@D，5AF DE\==，在Rt ABFD中，13BF==，1122ABF S AB AF BF AH D =×=×，12513AH \´=，6013AH \=，120213AG AH \==，13AE BF ==Q ，12049131313GE AE AG \=-=-=，故答案为：4913．5．（1）如图①把边长为6AB =、8BC =的矩形ABCD 对折，使点B 和D 重合，求折痕MN 的长；（2）如图②把边长为AB =4BC =且45B Ð=°的平行四边形ABCD 对折，使点B 和D 重合，求折痕MN 的长．【解答】解：（1）如图1，过点M 作ME BC ^，垂足为E ，连接BD ，在Rt ABD D 中，6AB =，8BC =．10BD \=，由折叠得，MN BD ^，90ADB NMD \Ð+Ð=°，90NME NMD Ð+Ð=°Q ，ADB NME \Ð=Ð，90MEN A Ð=Ð=°QMNE DBA\D D∽，\MN ME DB AD=，\6 108 MN=，7.5 MN\=（2）如图2，过点B作BE AD^的延长线于E，过F作MF BC^，连接BD，2MF BE\==，6DE\=．BD\==同（1）的方法，得出，MNF DBED D∽，\MN MF DB DE=\\6．问题背景：某课外学习小组在一次学习研讨中，得到了如下两个命题：Ⅰ．如图①，在正三角形ABCD中，M、N分别是AC、AB上的点，BM与CN相交于点O，若60BONÐ=°，则BM CN=．Ⅱ．如图②，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若90BONÐ=°，则BM CN=．任务要求：（1）请你从Ⅰ、Ⅱ两个命题中选择一个进行证明．（2）如图，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若108BONÐ=°，请问结论BM CN=是否还成立？若成立，请给予证明；若不成立，请说明理由．【解答】解：（1）选命题Ⅰ．证明：在图1中，ABCDQ是正三角形，BCM CANÐ=Ð=°．\=，60BC CAÐ=°Q，BON60\Ð+Ð=°．CBM BCN60Q，Ð+Ð=°BCN ACN60\Ð=Ð．CBM ACN\D@D．()BCM CAN ASA\=．BM CN选命题Ⅱ．证明：在图2中Q四边形ABCD是正方形，Ð=Ð=°．BCM CDN\=，90BC CDQ，Ð=°BON90\Ð+Ð=°．CBM BCN90Ð+Ð=°Q，BCN DCN90\Ð=Ð．CBM DCN\D@D．()BCM CDN ASA\=．BM CN（2）BM CN=成立．证明：在图3中，Q五边形ABCDE是正五边形，Ð=Ð=°．BCM CDN\=，108BC CDQ，Ð=°BON108CBM BCN\Ð+Ð=°．108Q，Ð+Ð=°BCN DCN108CBM DCN \Ð=Ð．()BCM CDN ASA \D @D ．BM CN \=．7．在四边形ABCD 中，对角线AC 、BD 相交于点O ，过点O 的直线分别交边AB 、CD 、AD 、BC 于点E 、F 、G 、H【感知】如图①，若四边形ABCD 是正方形，且EF GH ^，易知BOE AOG S S D D =，又因为14AOB ABCD S S D =四边形，所以14ABCD AEOG S S =正方形四边形（不要求证明）；【拓展】如图②，若四边形ABCD 是矩形，且14ABCD AEOG S S =矩形四边形，若AB a =，AD b =，BE m =，求AG 的长（用含a 、b 、m 的代数式表示）；【探究】如图③，若四边形ABCD 是平行四边形，且14ABCD AEOG S S =Y 四边形，若3AB =，5AD =，1BE =，则AG =　53　．【解答】解：【拓展】如图②，过O 作OM AB ^于M ，ON AD ^于N ，（1分）14AOB ABCD S S D =Q 矩形，（2分）14ABCD AEOG S S =矩形四边形，AOB AEOG S S D \=四边形，（3分）11112224BOE S BE OM m b mb D ===Q g g ，（4分）11112224AOG S AG ON AG a AG a D ===g g g ，（5分）\1144mb AG a =g ，（6分）bm AG a \=；（7分）【探究】如图③，过O 作QM AB ^，PN AD ^，则2MQ OM =，2PN ON =，S ABCD AB MQ AD PN =×=×Q Y ，3252OM ON \´=´，\53OM ON =，14AOB ABCD S S D =Y Q ，14ABCD AEOG S S =Y 四边形，AOB AEOG S S D \=四边形，11122BOE S BE OM OM D ==´´Q g ，12AOG S AG ON D =g ，\11122OM AG ON ´´=g ，OM AG ON =g ，53OM AG ON ==，53AG \=；（9分）故答案为：53．8．已知四边形ABCD 中，E 、F 分别是AB 、AD 边上的点，DE 与CF 交于点G ．（1）如图①，若四边形ABCD是矩形，且DE CF^，求证：ADE DCFD D∽；（2）如图②，若四边形ABCD是平行四边形，试探究：当BÐ与EGCÐ满足什么关系时，DE ADCF CD=成立？并证明你的结论；（3）如图③，若6BA BC==，8DA DC==，90BADÐ=°，DE CF^，请直接写出DECF的值．【解答】（1）证明：Q四边形ABCD是矩形，90A ADC\Ð=Ð=°，90ADE CDG\Ð+Ð=°，又DE CF^Q，90CDG DCFÐ+Ð=°，ADE DCF\Ð=Ð，ADE DCF\D D∽．（2）解：当180B EGCÐ+Ð=°时，DE ADCF CD=成立，理由如下：在AD的延长线上取点M，使CM CF=，如图1所示：则CMF CFMÐ=Ð．Q四边形ABCD是平行四边形，//AB CD\，//AD BC，A CDM\Ð=Ð，FCB CFMÐ=Ð，180B EGCÐ+Ð=°Q，360()180BEG FCB B EGC\Ð+Ð=°-Ð+Ð=°，又180BEG AEDÐ+Ð=°Q，AED FCB\Ð=Ð，CMF AED\Ð=Ð．ADE DCM\D D∽，\DE AD CM CD=，\DE AD CF CD=；（3）解：2524DECF=；理由如下：连接AC、BD，交于点M，作CN AD^于N，如图2所示：90BADÐ=°Q，6AB=，8AD=，10BD\===，在ABDD和CBDD中，AB CBDA DCBD BD=ìï=íï=î，()ABD CBD SSS\D@D，ABD CBD\Ð=Ð，AB CB=Q，BD AC\^，AM CM=，90AMD BAD\Ð=°=Ð，又ADB MDAÐ=ÐQ，ABD MAD\D D∽，::AD DM BD AD\=，2AD BD DM\=g，即2810DM=，6.4DM\=，4.8 AM\===，29.6AC AM\==，ACDDQ的面积1122AD CN AC DM==g g，89.6 6.4CN\´=´，解得：7.68CN=，DE CF^Q，FCN EDA\Ð=Ð，CN AD^Q，CNF DAE\Ð=Ð，ADE NCF\D D∽，\8257.6824DE AD CF CN ===．9．（1）证明推断：如图（1），在正方形ABCD 中，点E 、Q 分别在边BC 、AB 上，DQ AE ^于点O ，点G 、F 分别在边CD 、AB 上，GF AE ^．①填空：DQ =　AE （填“>”“ <”或“=” )；②推断GF AE 的值为 ；（2）类比探究：如图（2），在矩形ABCD 中，(BC k k AB=为常数）．将矩形ABCD 沿GF 折叠，使点A 落在BC 边上的点E 处，得到四边形FEPG ，EP 交CD 于点H ，连接AE 交GF 于点O ．试探究GF 与AE 之间的数量关系，并说明理由；（3）拓展应用：在（2）的条件下，连接CP ，当23k =时，若34BE BF =，GF =，求CP 的长．【解答】（1）①解：Q 四边形ABCD 是正方形，AB DA \=，90ABE DAQ Ð=°=Ð．90QAO OAD \Ð+Ð=°．AE DQ ^Q ，90ADO OAD \Ð+Ð=°．QAO ADO \Ð=Ð．()ABE DAQ ASA \D @D ，AE DQ \=．故答案是：=；②解：DQ AE ^Q ，FG AE ^，//DQ FG \，//FQ DG Q ，\四边形DQFG 是平行四边形，FG DQ \=，AE DQ =Q ，FG AE \=，\1GF AE=．故答案为：1．（2）解：结论：FG k AE=．理由：如图2中，作GM AB ^于M ．AE GF ^Q ，90AOF GMF ABE \Ð=Ð=Ð=°，90BAE AFO \Ð+Ð=°，90AFO FGM Ð+Ð=°，BAE FGM \Ð=Ð，ABE GMF \D D ∽，\GF GM AE AB=，90AMG D DAM Ð=Ð=Ð=°Q ，\四边形AMGD 是矩形，GM AD \=，\GF AD BC k AE AB AB===．（3）解：如图2中，作PN BC ^交BC 的延长线于N ．由34BE BF =，可以假设3BE k =，4BF k =，5EF AF k ==，Q23FG AE =，FG =，AE \=222(3)(9)k k \+=，1k \=或1-（舍弃），3BE \=，9AB =，:2:3BC AB =Q ，6BC \=，3BE CE \==，6AD PE BC ===，90EBF FEP PME Ð=Ð=Ð=°Q ，90FEB PEN \Ð+Ð=°，90PEN EPN Ð+Ð=°，FEB EPN \Ð=Ð，FBE ENP \D D ∽，\EF BF BE PE EM PM==，\5436EM PM==，245EN\=，185PN=，249355CM EN EC\=-=-=，PC\==．。

探究正方形中的“十字架模型”一、考题研究在特殊的四边形问题中翻折的问题是比较常见的，不论是期中、期末和中考中都比较常见，能否采用合适的方法求出线段长，或者是利用面积之间关系求线段之间关系，这就是我们今天重点学习的一个模型“十字架模型”二、知识回顾1、全等三角形的性质与判定2、相似三角形的性质与判定3、矩形和正方形的性质与判定4、图形的变换--轴对称三、十字架模型【十字架模型】--正方形第一种情况：过顶点在正方形ABCD中，AE⊥BF，可得AE=BF，借助于同角的余角相等，证明△BAF≌△ADE（ASA）所以AE=BF第二种情况：不过顶点在正方形ABCD中，E，F，G，H分别为AB，BC，CD，DA边上的点，其中：EG⊥FH，可得EG=FH也可以如下证明在正方形ABCD中，E，F，G，H分别AB、BC、CD、DA边上的点，其中：EG⊥FH，可得EG=FH【导入】如图，将边长为4的正方形纸片ABCD折叠，使得点A落在边CD的中点E处，折痕为FG，点F、G分别在边AD、BC上，则折痕FG的长度为______．【分析】过点G作GH AD∠=∠，⊥，然后求出GFH D⊥于H，根据翻折变换的性质可得GF AE再利用“角角边”证明ADE∆和GHF=，再利用勾股定∆全等，根据全等三角形对应边相等可得GF AE理列式求出AE，从而得解．【解答】法一：解：如图，过点G作GH AD=，⊥于H，则四边形ABGH中，HG AB 由翻折变换的性质得GF AE⊥，AED DAE∠+∠=︒，AFG DAE90∠+∠=︒，90∴∠=∠，AFG AED四边形ABCD是正方形，∴=，AD ABHG AD ∴=，在ADE ∆和GHF ∆中， GHF D AFG AED GH AD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()ADE GHF AAS ∴∆≅∆， GF AE ∴=，点E 是CD 的中点， 122DE CD ∴==，在Rt ADE ∆中，由勾股定理得，AE GF ∴的长为故答案为：【点评】本题考查翻折变换的问题，折叠问题其实质是轴对称，对应线段相等，对应角相等，找到相应的直角三角形利用勾股定理求解是解决本题的关键．法二：分析：连接AE ，求解FG 相当于求AE 。