上海交大设宴“拉拢”家长 为高招生源战埋伏笔(整理精校版)

上海交通大学附属中学2023-2024学年高一下学期期末考试语文试卷（满分150分，150分钟完成。

答案请写在答题纸上。

）一、积累运用（10分）1. 按要求填空。

（1）浴乎沂，______，咏而归。

（《子路、曾皙、冉有、公西华侍坐》）（2）《阿房宫赋》中，作者指出秦王朝如果爱惜六国百姓，就能世代为君、安享天下的句子是“______，______”。

（3）苏洵在《六国论》中借助“______，______”，敏锐地指出了对抗秦国的办法，此举会让对方寝食难安。

2. 按要求选择。

（1）有评论家指出：《红楼梦》的含蓄风格，反映在书中可以说是无所不在的。

以下不能表现其含蓄风格的一项是（）A. 满纸荒唐言，一把辛酸泪。

都云作者痴，谁解其中味！B. 《红楼梦》原来的书名为《石头记》。

C. 贾宝玉、甄士隐、四春姐妹等人名皆有隐喻。

D. 湘云喝醉酒后，沉酣于芍药花丛中。

（2）下列说法正确的一项是（）A. 曹禺认为：写戏主要是要发现社会矛盾，反映社会问题。

B. 《谏太宗十思疏》《答司马谏议书》都是优秀的论辩文，前者峻切坚定，后者循循善劝。

C. 《阿房宫赋》《六国论》均为借古鉴今、针砭时弊的名篇。

D. 只有多采用铺陈、夸张的写作手法，才能达到理足气盛的表达效果。

二、阅读（70分）（一）（15分）阅读下文，完成小题。

①我写了许多信，还没有郑重其事地谈到人生问题，这是一则因为这个问题实在谈滥了，一则也因为我看这个问题并不如一般人看得那样重要。

在这最后一封信里我之所以提出这个滥题来讨论，并不是要说出什么一番大道理，不过把我自己平时几种对于人生的态度随便拿来做一次谈料。

②我有两种看待人生的方法。

在第一种方法里，我把我自己摆在前台，和世界一切人和物在一块玩把戏：在第二种方法里，我把我自己摆在后台，袖手看旁人在那儿装腔作势。

③站在前台时，我把我自己看得和旁人一样，不但和旁人一样，并且和鸟兽虫鱼诸物也都一样。

人类比其他物类痛苦，就因为人类把自己看得比其他物类重要。

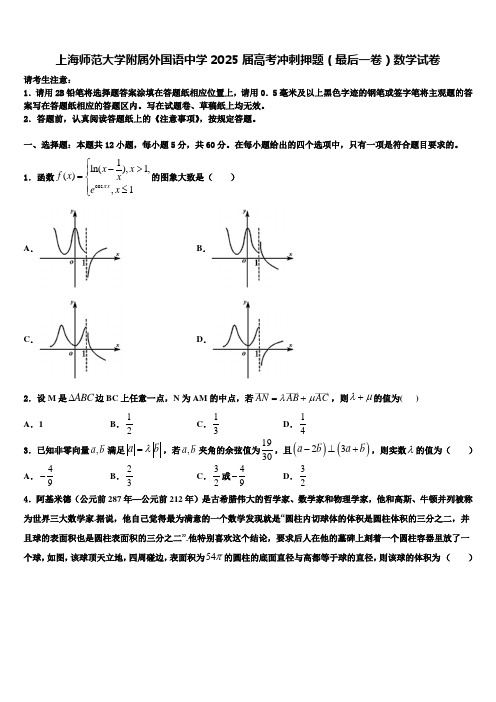
上海师范大学附属外国语中学2025届高考冲刺押题（最后一卷）数学试卷请考生注意：1．请用2B 铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。

写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．函数cos 1ln(),1,(),1x x x f x x ex π⎧->⎪=⎨⎪≤⎩的图象大致是（ ） A ． B ．C ．D ． 2．设M 是ABC ∆边BC 上任意一点，N 为AM 的中点，若AN AB AC λμ=+，则λμ+的值为( ) A ． 1 B ．12 C ．13 D ．143．已知非零向量,a b 满足a b λ=，若,a b 夹角的余弦值为1930，且()()23a b a b -⊥+，则实数λ的值为（ ） A ．49- B ．23 C ．32或49- D ．32 4．阿基米德（公元前287年—公元前212年）是古希腊伟大的哲学家、数学家和物理学家，他和高斯、牛顿并列被称为世界三大数学家.据说，他自己觉得最为满意的一个数学发现就是“圆柱内切球体的体积是圆柱体积的三分之二，并且球的表面积也是圆柱表面积的三分之二”.他特别喜欢这个结论，要求后人在他的墓碑上刻着一个圆柱容器里放了一个球，如图，该球顶天立地，四周碰边，表面积为54π的圆柱的底面直径与高都等于球的直径，则该球的体积为 （ ）A ．4πB ．16πC ．36πD ．643π 5．已知双曲线)，其右焦点F 的坐标为，点是第一象限内双曲线渐近线上的一点，为坐标原点，满足，线段交双曲线于点.若为的中点，则双曲线的离心率为（ ） A ． B ．2 C ． D ．6．点O 在ABC ∆所在的平面内，OA OB OC ==，2AB =，1AC =，AO AB AC λμ=+(),R λμ∈，且()420λμμ-=≠，则BC =（ ）A ．73B ．72C ．7D ．77．复数21i z i+=-，i 是虚数单位，则下列结论正确的是 A ．5z =B ．z 的共轭复数为31+22iC ．z 的实部与虚部之和为1D ．z 在复平面内的对应点位于第一象限8．从5名学生中选出4名分别参加数学，物理，化学，生物四科竞赛，其中甲不能参加生物竞赛，则不同的参赛方案种数为A ．48B ．72C ．90D ．969．某中学2019年的高考考生人数是2016年高考考生人数的1.2倍，为了更好地对比该校考生的升学情况，统计了该校2016年和2019年的高考情况，得到如图柱状图：则下列结论正确的是（ ）.A ．与2016年相比，2019年不上线的人数有所增加B ．与2016年相比，2019年一本达线人数减少C ．与2016年相比，2019年二本达线人数增加了0.3倍D ．2016年与2019年艺体达线人数相同10．历史上有不少数学家都对圆周率作过研究，第一个用科学方法寻求圆周率数值的人是阿基米德，他用圆内接和外切正多边形的周长确定圆周长的上下界，开创了圆周率计算的几何方法，而中国数学家刘徽只用圆内接正多边形就求得π的近似值，他的方法被后人称为割圆术．近代无穷乘积式、无穷连分数、无穷级数等各种π值的表达式纷纷出现，使得π值的计算精度也迅速增加．华理斯在1655年求出一个公式：π2244662133557⨯⨯⨯⨯⨯⨯=⨯⨯⨯⨯⨯⨯，根据该公式绘制出了估计圆周率π的近似值的程序框图，如下图所示，执行该程序框图，已知输出的 2.8T >，若判断框内填入的条件为?k m ≥，则正整数m 的最小值是A ．2B ．3C ．4D ．5 11．已知()5x a +展开式的二项式系数和与展开式中常数项相等，则2x 项系数为（ ）A ．10B ．32C ．40D ．8012．某校团委对“学生性别与中学生追星是否有关”作了一次调查，利用22⨯列联表，由计算得27.218K ≈,参照下表: 20()P K k ≥ 0.01 0.05 0.025 0.010 0.005 0.001 0k2.7063.841 5.024 6.635 7.879 10.828得到正确结论是( ) A ．有99%以上的把握认为“学生性别与中学生追星无关”B ．有99%以上的把握认为“学生性别与中学生追星有关”C ．在犯错误的概率不超过0.5%的前提下，认为“学生性别与中学生追星无关”D ．在犯错误的概率不超过0.5%的前提下，认为“学生性别与中学生追星有关”二、填空题：本题共4小题，每小题5分，共20分。

上海市比乐中学2024届高考临考冲刺语文试卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．1、下列各句中，没有语病的一句是A．真佛山不但担负着弘扬中华民族的孝德文化重任，而且传承着巴蜀人民敬老爱老助老的道德文明。

B．日前，有关部门初步完成了高铁达州站设计方案的研究工作，并报请铁路枢纽工程指挥部审查通过。

C．美国枪支袭击事件备受关注，事发后，各大网络关于这一事件报道的新闻点击量超过了万次以上。

D．经过改革开放多年来的我国经济建设的实践，证实了“绿水青山就是金山银山”这一理念的正确性。

2、补写出下列句子的空缺部分。

(1)《出师表》中，诸葛亮认为，蜀国处在危急存亡之时，文臣武将仍尽心竭力的原因是“________，________”。

(2)苏轼《赤壁赋》中，“客”认为“________，________”的心感难以实现，只好将无奈化为秋风中飘散的箫声。

(3)李白在《蜀道难》中写到，因“ ________，________”的险要地势，以致泰蜀两地自古以来相互隔绝。

3、阅读下面的文字，完成下列小题汉字是表意文字，但对其中的“意”，但相当多的人对“表意文字”理解得比较简单。

以为每个字的意义均可以从其楷书字形中找到解释。

( ) 。

东汉许慎在《说文解宇》中，将古文字的构成规则归纳为“象形、指事、会意、形声、转注、假借”，称之为“六书”，而“六书”之首即为“象形”。

殊不知经历了几千年的变化，很多现代字形与造字之初，不同汉字中相同的构件，其来源可能完全不同。

押题！2020年高考名校联考热点金题汇编广州二模：公筷行动围桌共食是中国的传统饮食习惯。

家人共餐或亲友聚会，许多人习惯用相互夹菜来表达情感。

但2020年春天，广东、北京等多地卫生部门发出倡议，推广使用公筷公勺，分餐进食。

为此，小武爸爸决定开始在家里实行分餐制，家人就餐，必须用公勺公筷从公盘里取食物。

但爷爷奶奶对此颇有微词，认为家人、亲友之间，分餐而食不仅生分，也让人有被嫌弃的感觉。

请你以小武的身份选择某一类长辈，就“公共生活与卫生安全”的问题，谈谈你的思考和认识。

要求：自拟标题，自选角度，确定立意；不要套作，不得抄袭；不得泄露个人信息；不少于800字。

德阳“三诊”：奔涌后浪奔涌吧，后浪，我们在同一条奔涌的河流！”五四青年节，某网站推出视频《后浪》演讲，引起各主流媒体的广泛演讲词里有：“你们拥有了我们曾经梦寐以求的权利——选择的权利。

”“君子美美与共，和而不同，更年轻的身体，容得下更多的文化审美和价值观。

”“我们这一代人的想象力，不足以想象你们的未来！”“一个国家最好看的风景，就是这个国家的年轻人。

因为你们，是心里有火，眼里有光！”作为“后浪”的你，有怎样的认识和思考？请结合演讲词，写一篇文章。

自定立意，明确文体，自拟标题，不要套作，不得抄袭，不少于800字。

武汉五月质量检测:健康生活阅读下面的材料，根据要求写作。

(60分）“每个人都是自己健康的第一责任人”。

世界卫生组织发现，影响健康的因素中，生物学因素占15%、环境影响占17%、行为和生活方式占60%、医疗服务仅占8%。

由此可见，获得健康最简单也是最有效的方法，个人健康管理最日常也是最重要的策略，就是培养健康生活方式，把健康融入生活的方方面面。

上面的材料引发你怎样的认识和思考？请你以宣传委员小李的身份为“倡导健康生活方式”的主题班会写一篇“倡议书”。

要求：综合材料内容及含意，选好角度，确定立意，明确文体，自拟标题；不要套作，不得抄袭，不少于800字。

上海市高中名校2025届高三压轴卷语文试卷请考生注意：1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。

写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

1、阅读下面的新闻，完成后面的题目。

12月7日16时52分，我国在太原卫星发射中心用快舟一号甲运载火箭，采用一箭六星的方式，成功将和德二号A/B卫星、天仪16/17卫星、天启四号A/B卫星发射升空。

卫星顺利进入预定轨道，任务获得圆满成功。

记者注意到，受火箭发射影响，昨天傍晚，北京上空出现“奇观”，“龙状云”刷爆朋友圈，其是如何形成的呢？北京市气象局在官方微博对此作出了解释，火箭升空时的尾迹被太阳余晖照亮，就形成了这样的航迹云。

因为火箭尾流中含有大量的三氧化二铝粒子，这些粒径比较小的粒子被喷口喷出后在高层大气中所受的阻力比较小，因此能够持续好几公里。

由于平流层和中间层之间的循环气流，造成火箭流场远端与空气混合具有强烈的不稳定性，因而将尾迹吹成了螺旋状。

我们人眼所见的火箭尾迹主要来自于尾流中含铝的固体推进剂燃烧生成的三氧化二铝粒子散射太阳光所致。

（2019年12月8日《北京青年报》）（1）给这则新闻拟一个标题，不超过15个字。

（2）根据材料，说明“龙”状云形成的几个关键要素。

2、下列各句中，没有语病的一项是（）A．我市将举办第12届中学生运动会，我校参加这届运动会的20名男运动员和16名女运动员，均是由班级和年级层层选拔出来的优秀选手组成。

B．中国正在经历一场从“吃饱”向“吃健康”的转变，在这一历史进程中，能否保证公众的食品安全取决于政府的执政水平，事关老百姓的切身利益。

C．会议围绕充分发挥学生信息员的作用、加强教学质量监控、促进教风和学风建设，健全了学生信息源组织机构，布置了今年评教评学的主要工作。

D．最近几年，我省科协走协商、协调、协作之路，团结、动员、发挥科技工作者的独特作用，开展了一系列活动，有效提高了人民的科学素养。

2024年中考第一次模拟考试（南京卷）语文（考试时间：120分钟试卷满分：120分）注意事项：1．本试卷6页，共120分。

考试时间为120分钟。

考生答题全部答在答题卡上，答在本试卷上无效。

2．请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、考试证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上。

3．答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑。

如需改动，请用橡皮擦干净后，再选涂其他答案。

答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡的指定位置，在其他位置答题一律无效。

4．测试范围：上册全册。

5．考试结束后，将本试卷和答题卡一并交回。

一、积累与运用（共23分）学校开展“传承中华优秀传统文化”活动，请你阅读下面文字，完成下面小题。

（16分）（1）中华优秀传统文化（甲），历经沧桑仍绵延不绝。

历史文化的xūn（）陶，既在思接千载的古诗文中，也在可感、可知、可参与的日常生活中。

（2）古诗文是文化的薪火。

读古诗文就是读百种生活、千样人生，在这些作品里，你可赏自然之趣，“树绕村庄，①”；你可寄思乡之情，“②，燕然未勒归无计”；你可悟人生之理，“③，病树前头万木春”；你可知情感之真，“春蚕到死丝方尽，④”；你可抒报国之志，“了却君王天下事，⑤”。

此外，读“⑥，⑦”（《出师表》），你应慕诸葛亮淡泊名利的志趣；读“⑧？留取丹青照汗青”（《过零丁洋》）你定知文天祥坚贞不屈的气节。

（3）日常生活是文化的载体。

当博物馆“打卡”成为休闲娱乐的方式，当扬州剪纸受到顾客青睐，“活起来”的不仅是文化遗产，更有民族的优良传统“活起来”。

（乙），这是传承中华优秀传统文化瑰．（）宝的必经之路。

1．根据拼音写汉字，给加点字注音。

（2分）xūn陶（）瑰．（）宝2．填入横线甲处的成语最恰当的一项是（）（2分）A．巧妙绝伦B．富丽堂皇C．博大精深D．川流不息3．修改文中画横线的病句。

（写出修改意见即可）（2分）4．根据语境，在第（2）段画横线处，填写相应的古诗文名句。

2023-2024学年河南省青桐鸣大联考高三（上）期中数学试卷一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集U＝R，集合A＝{x|2x≤2}，B={x|x2≥14}，则（∁U A）∩B＝（）A．(−∞，−12]B．(−12，1]C．(12，1]D．（1，+∞）2．已知i为虚数单位，则复数z=21+i−21−i=（）A．﹣2B．2C．﹣2i D．2i3．为了得到函数y＝sin（4x+2）的图象，可以将函数y＝sin（4x﹣6）的图象（）A．向右平移8个单位长度B．向左平移8个单位长度C．向右平移2个单位长度D．向左平移2个单位长度4．在一个空旷的房间中大声讲话会产生回音，这种现象叫做“混响”．用声强的大小来度量声音的强弱，假设讲话瞬间发出声音的声强为W0，则经过t秒后这段声音的声强变为W(t)=W0e−tτ（τ为常数）．把混响时间（T R）定义为声音的声强衰减到讲话之初的10﹣6倍所需时间，则T R约为（）（参考数据ln2≈0.7，ln5≈1.6）A．4.2τB．9.6τC．13.8τD．23τ5．下列函数中，满足f（xy）＝f（x）+f（y）﹣1的为（）A．f（x）＝lg（1+x）B．f（x）＝1+lgxC．f（x）＝21+x D．f（x）＝1+2x6．若cos2θ=35，则tan2θ−1tan2θ=（）A．−154B．−1316C．1316D．1547．已知函数f（x）的定义域为R，设p：y＝|f（x）|的图象关于y轴对称；q：f（x）是奇函数或偶函数，则p是q的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件8．记S n为数列{a n}的前n项和，若a1＝2，a2＝﹣3，a n+2=a n+12−13a n，n∈N*，则∑2024k=1S k=（）A．﹣2024B．﹣1012C．﹣506D．0二、选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 9．已知函数f(x)=√3sin x 4+cos x4，则（ ）A ．f （x ）的最小正周期为8πB ．f （x ）的最大值为√3+1C ．f （x ）在区间（﹣π，π）上单调递增D ．y ＝f （x ）的图象关于点(4π3，0)中心对称 10．下列函数中，满足f （x ）≥f （1）的为（ ） A ．f （x ）＝x 2﹣2x +2 B ．f （x ）＝e x ﹣2+e ﹣xC ．f(x)=x +1xD ．f(x)=x 2+4x 2+111．已知数列{a n }各项均为正数，S n 为数列{a n }的前n 项和，且{S na n}是公差为d （d ∈R ）的等差数列，n ∈N *，下列命题正确的是（ ） A ．若{a n }为等比数列，则d ＝1 B ．若d =12，则{a n }为等差数列C ．若d ＞1，则{a n }为递减数列D ．若d ＞1，则{na n }为递增数列12．设函数f （x ）＝2x ﹣ax ﹣b （a ，b ∈R ），下列命题正确的是（ ） A ．若f （x ）存在负零点，则b ＞1B ．若a ＜0，则f （x ）有且只有一个零点C ．若f （x ）有且只有两个正零点，则b ＜1D ．若a （b ﹣1）＜0且f （x ）存在零点，则f （x ）的零点都是正的 三、填空题：本大题共4小题，每小题5分，共20分． 13．函数f （x ）＝x 4e x﹣1在点（1，f （1））处的切线方程为 ．14．若向量a →，b →满足|a →+3b →|=10，|a →−3b →|=4，则a →•b →= ．15．若函数f （x ）＝sin x +alnx 的图象在区间(π2，π)上单调递增，则实数a 的最小值为 ．16．已知函数f(x)=2√33sin(ωx −π6)(ω＞0)，曲线y ＝f （x ）与x 轴的两个相邻交点为P ，Q ，曲线y ＝f （x ）与直线y ＝1的一个交点为M ，若tan ∠PMQ =−√2，则实数ω＝ ． 四、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17．（10分）已知在平面直角坐标系中，点A （1，2），B （4，6），C （0，3）． （1）若t ＞0，且（AB →+t AC →）⊥（AB →−t AC →），求t 的值；（2）记AB →在AC →方向上的投影向量为u →，求u →的坐标． 18．（12分）在△ABC 中，已知3tan A +3tan B +2tan C ＝0． （1）求tan A tan B ；（2）若△ABC 的面积为√3，tanA +tanB =2√33，求AB 的长度． 19．（12分）已知函数f(x)=13x 3+(a −1)x 2−4ax +1，a ∈R ．（1）若曲线y ＝f （x ）关于点（0，1）对称，求a 的值； （2）若f （x ）在区间[0，1]上的最小值为1，求a 的取值范围．20．（12分）已知函数f （x ）＝（cos2x +1）（cos x +a ），a ∈（﹣1，1），g(x)=f(x)−f(0)cosx−1．（1）求g （x ）的值域；（2）记g （x ）的值域为D ，试问是否存在a ，使得集合D ∩Z 有且只有2个元素？若存在，求a 的取值范围；若不存在，请说明理由． 参考公式：a 3﹣b 3＝（a ﹣b ）（a 2+ab +b 2）．21．（12分）记S n 为数列{a n }的前n 项和，已知等比数列{b n }满足b n ＝a 3n ﹣2，n ∈N *，b 1+b 3＝5，b 2+b 4=52．（1）求数列{b n }的通项公式；（2）若对任意n ∈N *，a 3n ﹣2，a 3n ﹣1，a 3n ，a 3n +1成等差数列． ①求S 1和S 4的值； ②求S 3n ﹣2．22．（12分）已知函数f （x ）＝xln （1+ax ）﹣x 2（a ＞0）． （1）若a ＝1，求f （x ）的单调区间；（2）若x ＝0是f （x ）的极小值点，求实数a 的取值范围．2023-2024学年河南省青桐鸣大联考高三（上）期中数学试卷参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集U＝R，集合A＝{x|2x≤2}，B={x|x2≥14}，则（∁U A）∩B＝（）A．(−∞，−12]B．(−12，1]C．(12，1]D．（1，+∞）解：由题意，得A＝{x|x≤1}，B={x|x≤−12或x≥12}，所以∁U A＝{x|x＞1}，所以（∁U A）∩B＝（1，+∞）．故选：D．2．已知i为虚数单位，则复数z=21+i−21−i=（）A．﹣2B．2C．﹣2i D．2i解：21+i−21−i=2(1−i)(1+i)(1−i)−2(1+i)(1−i)(1+i)=(1−i)−(1+i)=−2i．故选：C．3．为了得到函数y＝sin（4x+2）的图象，可以将函数y＝sin（4x﹣6）的图象（）A．向右平移8个单位长度B．向左平移8个单位长度C．向右平移2个单位长度D．向左平移2个单位长度解：设g（x）＝sin（4x﹣6）．把函数y＝g（x）的图象平移a（向左a为正数，向右a为负数）个单位长度后，得到y＝g（x+a）＝sin（4x+4a﹣6）的图象．令f（x）＝sin（4x+2），易知f（x）＝sin（4x+2）的周期T=π2，为了得到函数y＝f（x）的图象，只需令4a﹣6＝2+kT，（k∈Z），得a=2+kT4=2+kπ8，k∈Z，根据选项可知，a＝2，即把函数y＝sin（4x﹣6）的图象向左平移2个单位长度即可得到y＝sin（4x+2）的图象．故选：D．4．在一个空旷的房间中大声讲话会产生回音，这种现象叫做“混响”．用声强的大小来度量声音的强弱，假设讲话瞬间发出声音的声强为W0，则经过t秒后这段声音的声强变为W(t)=W0e−tτ（τ为常数）．把混响时间（T R）定义为声音的声强衰减到讲话之初的10﹣6倍所需时间，则T R约为（）（参考数据ln2≈0.7，ln5≈1.6）A．4.2τB．9.6τC．13.8τD．23τ解：由题意，W(T R)=10−6W0，即e−T Rτ=10−6，所以T R=τ⋅ln106=τ×6×(ln2+ln5)≈13.8τ．故选：C．5．下列函数中，满足f（xy）＝f（x）+f（y）﹣1的为（）A．f（x）＝lg（1+x）B．f（x）＝1+lgxC．f（x）＝21+x D．f（x）＝1+2x解：（方法1）令g（x）＝f（x）﹣1，则g（xy）＝f（xy）﹣1，g（x）+g（y）＝f（x）+f（y）﹣2，由于f（xy）＝f（x）+f（y）﹣1，即f（xy）﹣1＝f（x）+f（y）﹣2，所以g（xy）＝g（x）+g（y），而满足g（xy）＝g（x）+g（y）的函数有对数函数g（x）＝log a x（a＞0，a≠1），所以f（x）＝g（x）+1＝1+log a x，只有B选项符合题意，其它选项均不符合．（方法2）令x＝y＝1，则f（1）＝f（1）+f（1）﹣1，得f（1）＝1．在四个选项中，只有B选项满足f（1）＝1，其它选项均不符合．故选：B．6．若cos2θ=35，则tan2θ−1tan2θ=（）A．−154B．−1316C．1316D．154解：方法1：因为cos2θ=2cos2θ−1=1−2sin2θ=3 5，所以cos2θ=45，sin2θ=15，故tan2θ=1 4，所以tan2θ−1tan2θ=14−4=−154．方法2：因为cos2θ=3 5，所以tan2θ−1 tan2θ=sin 2θcos 2θ−cos 2θsin 2θ=sin 4θ−cos 4θsin 2θcos 2θ=(sin 2θ+cos 2θ)(sin 2θ−cos 2θ)14sin 22θ =−4cos2θ1−cos 22θ=−4×351−925=−154． 故选：A ．7．已知函数f （x ）的定义域为R ，设p ：y ＝|f （x ）|的图象关于y 轴对称；q ：f （x ）是奇函数或偶函数，则p 是q 的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解：令g （x ）＝|f （x ）|，若f （x ）是奇函数或偶函数，则g （﹣x ）＝|f （﹣x ）|＝|f （x ）|＝g （x ）， 所以g （x ）是偶函数，所以y ＝|f （x ）|的图象关于y 轴对称，所以必要性成立； 反之，若f(x)={1，x ＜1，−1，x ≥1，则|f （x ）|＝1，所以y ＝|f （x ）|的图象关于y 轴对称，但是f （x ）图象不关于原点对称也不关于y 轴对称，故是非奇非偶函数，所以充分性不成立； 故p 是q 的必要不充分条件． 故选：B ．8．记S n 为数列{a n }的前n 项和，若a 1＝2，a 2＝﹣3，a n+2=a n+12−13a n，n ∈N *，则∑ 2024k=1S k =（ ） A ．﹣2024B ．﹣1012C ．﹣506D ．0解：依题意，由a n+2=a n+12−13a n，及a 1＝2，a 2＝﹣3，可得a 3=a 22−13a 1=−2，a 4=a 32−13a 2=3，a 5=a 42−13a 3=2，a 6=a 52−13a 4=−3，…∴数列{a n}是以4为最小正周期的周期数列，∴S1＝a1＝2，S2＝S1+a2＝2﹣3＝﹣1，S3＝S2+a3＝﹣1﹣2＝﹣3，S4＝S3+a4＝﹣3+3＝0，S5＝S4+a5＝0+2＝2，S6＝S5+a6＝2﹣3＝﹣1，…∴数列{S n}也是以4为最小正周期的周期数列，∵2024÷4＝506，∴∑2024k=1S k=506×(S1+S2+S3+S4)=506×(−2)=−1012．故选：B．二、选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．已知函数f(x)=√3sin x4+cosx4，则（）A．f（x）的最小正周期为8πB．f（x）的最大值为√3+1C．f（x）在区间（﹣π，π）上单调递增D．y＝f（x）的图象关于点(4π3，0)中心对称解：f(x)=√3sin x4+cosx4=2sin(x4+π6)，故f（x）的最小正周期T=2π14=8π，故A选项正确；f（x）的最大值是2，B选项错误；令x4+π6∈(−π2，π2)，可得x∈(−8π3，4π3)为f（x）的一个单调递增区间，而(−π，π)⊆(−8π3，4π3)，所以f（x）在区间（﹣π，π）上单调递增，C选项正确；因为f(4π3)=2sin(π3+π6)=2≠0，所以f（x）的图象不关于点(4π3，0)中心对称，D选项错误．故选：AC．10．下列函数中，满足f（x）≥f（1）的为（）A．f（x）＝x2﹣2x+2B．f（x）＝e x﹣2+e﹣xC．f(x)=x+1xD．f(x)=x2+4x2+1解：对于A选项：f（x）＝（x﹣1）2+1，在x＝1处取最小值，正确；对于B选项：f(x)≥2√e x−2⋅e−x=2e−1，等号成立的条件是e x﹣2＝e﹣x，即x＝1，故f（x）≥f（1），正确；对于C选项：f（﹣1）＝﹣2，f（1）＝2，所以f（﹣1）＜f（1），不满足题意，错误；对于D选项：f(x)=x2+1+4x2+1−1≥2√(x2+1)⋅4x2+1−1=3，等号成立的条件是x2+1=4x2+1，x2+1＝2，即x＝±1，因此f（x）≥f（1）成立，正确．故选：ABD．11．已知数列{a n}各项均为正数，S n为数列{a n}的前n项和，且{S na n}是公差为d（d∈R）的等差数列，n∈N*，下列命题正确的是（）A．若{a n}为等比数列，则d＝1B．若d=12，则{a n}为等差数列C．若d＞1，则{a n}为递减数列D．若d＞1，则{na n}为递增数列解：因为S1a1=1，且数列{S na n}是公差为d的等差数列，所以S na n=1+(n−1)d，①所以S n＝[1+（n﹣1）d]a n，则S n+1＝（1+nd）a n+1，所以a n+1＝S n+1﹣S n＝（1+nd）a n+1﹣[1+（n﹣1）d]a n，整理得nda n+1＝[1+（n﹣1）d]a n．②对于A选项，若{a n}为等比数列，记a n=a1q n−1．当q＝1时，a n＝a1，S n＝na1，所以S na n=n，由①可得d＝1．当q≠1时，取n＝2可得S2a2=q−1+1=1+d，故d＝q﹣1；取n＝3可得S3a3=q−2+q−1+1=d2+d+1，再由①可得S3a3=1+2d，所以d2+d+1＝1+2d，即d2﹣d＝0，所以d＝0或d＝1．但是如果d＝0，则S2a2=1+d=1，从而a1＝0，这与{a n}各项为正数矛盾，因此，必有d＝1，故A选项正确；对于B选项，若d=12，由②得，n2a n+1=n+12a n，即a n+1n+1=a nn，因此a nn=⋯=a11，即a n＝na1，所以{a n}是以a1为公差的等差数列，故B选项正确；对于C选项，若d＞1，因为{a n}各项为正数，所以由②可得，a n+1a n=1+(n−1)dnd=1d+(n−1)n＜1+(n−1)n=1，所以{a n}是递减数列，故C选项正确；对于D选项，若d＞1，因为{a n}各项为正数，所以由②可得(n+1)a n+1na n=(n+1)[1+(n−1)d]n2d=n+1d+n2−1n2．令n＝1，可得：2×a21×a1=2d．所以当d∈[2，+∞）时，2×a21×a1≤1，此时{na n}不是递增数列，故D选项错误．故选：ABC．12．设函数f（x）＝2x﹣ax﹣b（a，b∈R），下列命题正确的是（）A．若f（x）存在负零点，则b＞1B．若a＜0，则f（x）有且只有一个零点C．若f（x）有且只有两个正零点，则b＜1D．若a（b﹣1）＜0且f（x）存在零点，则f（x）的零点都是正的解：f（x）的零点等价于曲线y＝2x与直线y＝ax+b的交点，其中a是直线的斜率，对于A，D选项，取曲线y＝2x上位于第二象限的点P，Q，并固定点P（如图所示）：则当Q与y轴的距离充分大的时候，直线PQ的斜率a可以无限趋近于0，并且直线PQ与y轴的交点位于（0，1）的下方，于是当a＞0且0＜b＜1时，满足a（b﹣1）＜0，此时曲线y＝2x与直线y＝ax+b的交点的横坐标是负数，即f（x）的零点都是负的，故D选项错误；而此时f （x ）存在负零点，但不满足b ＞1，故A 选项错误； 对于B 选项，若a ＜0，则f （x ）在R 上单调递增， 取x 1＝log2（|b |+1），则x 1≥0，所以f （x 1）≥|b |+1﹣b ＞0， 再取x 2=1+|b|a，则x 2＜0， 所以f （x 2）＜﹣ax 2﹣b +1＝﹣|b |﹣b ≤0，所以f （x ）有且只有一个零点，并且这个零点位于区间（x 2，x 1）中，B 选项正确； 对于C 选项，若f （x ）有且只有两个正零点， 因为f ′（x ）＝2x ln 2﹣a ，而函数f ′（x ）单调递增， 所以f （x ）至多只有一个极值点x 0，且2x 0ln 2﹣a ＝0， 则这个极值点必为正，且f （x 0）＜0，并且f （x ）在（0，x 0）上单调递减，在（x 0，+∞）上单调递增， 故必有f （0）＞0，即1﹣b ＞0，解得b ＜1，故C 选项正确． 故选：BC ．三、填空题：本大题共4小题，每小题5分，共20分． 13．函数f （x ）＝x 4e x﹣1在点（1，f （1））处的切线方程为 y ＝5x ﹣4 ．解：因为f （x ）＝x 4e x ﹣1，所以f （1）＝1，f ′（x ）＝（x 4+4x 3）e x ﹣1，则f ′（1）＝5， 故函数f （x ）＝x 4e x﹣1在点（1，f （1））处的切线方程为y ﹣1＝5（x ﹣1），即y ＝5x ﹣4．故答案为：y ＝5x ﹣4．14．若向量a →，b →满足|a →+3b →|=10，|a →−3b →|=4，则a →•b →= 7 ． 解：由|a →+3b →|=10，|a →−3b →|=4，可得|a →+3b →|2=|a →|2+6a →⋅b →+9|b →|2=100，① |a →−3b →|2=|a →|2−6a →⋅b →+9|b →|2=16，② 联立①②，可得12a →⋅b →=84， 所以a →⋅b →=7． 故答案为：7．15．若函数f （x ）＝sin x +alnx 的图象在区间(π2，π)上单调递增，则实数a 的最小值为 π ．解：因为f （x ）＝sin x +alnx ，所以f ′(x)=cosx +a x =xcosx+a x．由f（x）的图象在区间(π2，π)上单调递增，可知不等式f′（x）≥0，即x cos x+a≥0在区间(π2，π)上恒成立．令g（x）＝x cos x+a，则g′（x）＝cos x﹣x sin x，当x∈(π2，π)时，g′（x）＜0，所以g（x）在(π2，π)上单调递减，故要使f′（x）≥0在x∈(π2，π)上恒成立，只需g（π）≥0．由g（π）＝﹣π+a≥0，解得a≥π，故实数a的取值范围为[π，+∞），则a的最小值为π．故答案为：π．16．已知函数f(x)=2√33sin(ωx−π6)(ω＞0)，曲线y＝f（x）与x轴的两个相邻交点为P，Q，曲线y＝f（x）与直线y＝1的一个交点为M，若tan∠PMQ=−√2，则实数ω＝√2π6．解：令f（x）＝0，得ωx−π6=kπ，k∈Z，解得x=π6ω+kπω，k∈Z；所以f（x）的零点为x=π6ω+kπω，k∈Z．设P（x P，0），Q（x Q，0），并且x Q−x P=πω＞0．因为∠PMQ是钝角，所以M（x M，1）满足x M∈（x P，x Q）（否则，∠PMQ是锐角）．不妨取x P=π6ω，x Q=7π6ω，令f（x M）＝1，则sin(ωx M−π6)=√32，由x∈（x P，x Q），可得x M=π2ω或x M=5π6ω．根据对称性，不妨取x M=π2ω．在△PMQ中，∠MPQ+∠MQP＝π﹣∠PMQ，所以tan(∠MPQ+∠MQP)=−tan∠PMQ=√2．因为tan∠MPQ=1x M−x P=3ωπ，tan∠MQP=1x Q−x M=3ω2π，所以tan(∠MPQ+∠MQP)=tan∠MPQ+tan∠MQP1−tan∠MPQ⋅tan∠MQP=3ωπ+3ω2π1−3ωπ⋅3ω2π=9ω2π1−9ω22π2=√2，即9√2ω22π2+9ω2π−√2=0．所以根据二次函数求根公式可得ωπ=−9±(9)−4×9√2×(−√2)2×9√22=−92±1529√2．而ω＞0，所以ω=−92+15292=√2π6．故答案为：√2π6． 四、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17．（10分）已知在平面直角坐标系中，点A （1，2），B （4，6），C （0，3）． （1）若t ＞0，且（AB →+t AC →）⊥（AB →−t AC →），求t 的值； （2）记AB →在AC →方向上的投影向量为u →，求u →的坐标． 解：（1）由题意，得AB →=(3，4)，AC →=(−1，1)， 所以AB →+tAC →=(3−t ，4+t)， AB →−tAC →=(3+t ，4−t)， 因为(AB →+tAC →)⊥(AB →−tAC →)， 所以(AB →+tAC →)⋅(AB →−tAC →)=0， 即（3﹣t ）（3+t ）+（4+t ）（4﹣t ）＝0， 即9﹣t 2+16﹣t 2＝0，又t ＞0，故t =5√22； （2）AB →⋅AC →=3×(−1)+4×1=1，|AC →|=√2， 由投影向量的定义得，u →=λAC→|AC →|其中，λ=|AB →|⋅cos(AB →，AC →)=AB →⋅AC→|AC →|=1√2，所以u →=AC →√2⋅1|AC →|=12AC →=(−12，12)．18．（12分）在△ABC 中，已知3tan A +3tan B +2tan C ＝0． （1）求tan A tan B ；（2）若△ABC 的面积为√3，tanA +tanB =2√33，求AB 的长度． 解：（1）由于A +B +C ＝π，所以tanC =tan(π−A −B)=−tan(A +B)=−tanA+tanB1−tanAtanB．由3tan A +3tan B +2tan C ＝0，得(tanA +tanB)⋅(3−21−tanAtanB )=0．因为C ∈（0，π）， 所以tanA +tanB =sinA cosA +sinB cosB =sinAcosB+cosAsinB cosAcosB =sin(A+B)cosAcosB =sinCcosAcosB≠0．故3−21−tanAtanB=0，解得tanAtanB=1 3．（2）（方法1）因为tanA+tanB=2√3 3，所以tanC=−32(tanA+tanB)=−√3．而C∈（0，π），故C=2π3．所以cosC=−cos(A+B)=sinAsinB−cosAcosB=−12，①由（1）知，sinAsinB=13 cosAcosB．②由①②可得sinAsinB=14，cosAcosB=34．由于△ABC面积为√3，所以12absinC=√3．又asinA=bsinB=csinC，因此12⋅csinAsinC⋅csinBsinCsinC=√3，即c2sinAsinB=2√3sinC，又sinAsinB=14，sinC=sin2π3=√32，解得c=2√3，即AB的长度为2√3．（方法2）因为tanA+tanB=2√3 3，所以tanC=−32(tanA+tanB)=−√3．而C∈（0，π），故C=2π3．由S△ABC=12absinC=12ab×√32=√3，得ab＝4，因为tanA+tanB=2√33，tanAtanB=13，得tanA=tanB=√33，故A=B=π6，a＝b＝2，由正弦定理得，a sinA=csinC ，即22=√32， 解得c =2√3，即AB 的长度为2√3．19．（12分）已知函数f(x)=13x 3+(a −1)x 2−4ax +1，a ∈R ．（1）若曲线y ＝f （x ）关于点（0，1）对称，求a 的值； （2）若f （x ）在区间[0，1]上的最小值为1，求a 的取值范围． 解：（1）设g(x)=f(x)−1=13x 3+(a −1)x 2−4ax ．由题意知，g （x ）是奇函数，所以﹣g （x ）＝g （﹣x ），即对任意x ∈R ，有−[13x 3+(a −1)x 2−4ax]=−13x 3+(a −1)x 2+4ax ，化简得（1﹣a ）x 2＝（a ﹣1）x 2， 所以a ﹣1＝0，即a ＝1．（2）方法1：由题意知f(x)=13x 3+(a −1)x 2−4ax +1≥1，即13x 3+(a −1)x 2−4ax ≥0，又x ∈[0，1]，x ＝0时，13x 3+(a −1)x 2−4ax =0，所以f （x ）≥1等价于13x 2+(a −1)x −4a ≥0，令m(x)=13x 2+(a −1)x −4a ，分情况讨论，①{3(1−a)2＞1m(1)=13+a −1−4a ≥0，即{a ＜13a ≤−29，故a ≤−29； ②{0≤3(1−a)2≤1m[3(1−a)2]=3(1−a)24−3(1−a)22−4a ≥0，即{13≤a ≤1−3≤a ≤−13，无解； ③{3(1−a)2＜0m(0)=−4a ≥0，即{a ＞1a ≤0，无解． 综上所述，a 的取值范围是(−∞，−29]．方法2：因为f （x ）在[0，1]上的最小值为1， 故f(1)=13+(a −1)−4a +1≥1，解得a ≤−29． f ′（x ）＝x 2+2（a ﹣1）x ﹣4a ＝（x ﹣2）（x +2a ） 当x ∈[0，1]时，x ﹣2＜0．若−12＜a≤−29，则−2a∈[49，1)．当x∈（0，﹣2a）时，f′（x）＞0；当x∈（﹣2a，1）时，f′（x）＜0，所以f（x）在（0，﹣2a）上单调递增，在（﹣2a，1）上单调递减．而f（0）＝1，f（1）≥1，因此f（x）在[0，1]上的最小值为1，满足题意．若a≤−12，则﹣2a≥1，当x∈[0，1]时，f′（x）≥0，所以f（x）在（0，1）上单调递增，故f（x）在[0，1]上的最小值为f（0）＝1，满足题意．综上所述，a的取值范围为(−∞，−29 ]．20．（12分）已知函数f（x）＝（cos2x+1）（cos x+a），a∈（﹣1，1），g(x)=f(x)−f(0) cosx−1．（1）求g（x）的值域；（2）记g（x）的值域为D，试问是否存在a，使得集合D∩Z有且只有2个元素？若存在，求a的取值范围；若不存在，请说明理由．参考公式：a3﹣b3＝（a﹣b）（a2+ab+b2）．解：（1）g（x）的定义域为{x|cos x≠1}＝{x|x≠2kπ，k∈Z}，因为f（x）＝2cos2x（cos x+a）＝2cos3x+2a cos2x，所以当cos x≠1时，g(x)=f(x)−f(0)cosx−1=2(cos3x−1)cosx−1+2a(cos2x−1)cosx−1=2(cosx−1)(cos2x+cosx+1)cosx−1+2a(cosx−1)(cosx+1)cosx−1＝2（cos2x+cos x+1）+2a（cos x+1），设函数u(t)=2(t2+t+1)+2a(t+1)=2(t+a+12)2+2(a+1)−(a+1)22，则u（t）是二次函数，t∈[﹣1，1）时恰好满足g（x）＝u（cos x）＝u（t），g（x）的值域与u（t）在[﹣1，1）上的值域相同，故可讨论u（t）在[﹣1，1）上的值域，因为a∈（﹣1，1），故−a+12∈(−1，0)，则u（t）在[﹣1，1）上的最小值为u(−a+12)=−12a2+a+32，又u（1）＝4a+6，则u(t)∈[−12a2+a+32，4a+6)，即g（x）的值域为[−12a2+a+32，4a+6）．（2）存在，证明如下：因为D∩Z有且只有2个元素，而u（﹣1）＝2，所以D是区间（0，4）的子集，由（1）知，u（t）在[−1，−a+12)上单调递减，在[−a+12，1)上单调递增，且u(t)∈[−12a2+a+32，4a+6)，故u（1）＝4a+6∈（2，4]，则a∈(−1，−12 ]，D∩Z有且只有2个元素可分成下面2种情况：①若D∩Z＝{1，2}，此时u（1）＝4a+6∈（2，3]，且u(−a+12)=−12a2+a+32=−12(a−1)2+2∈(0，1]，解得a∈(−1，−34 ]；②若D∩Z＝{2，3}，u（1）＝4a+6∈（3，4]，且u(−a+12)=−12a2+a+32=−12(a−1)2+2∈(1，2]，无解．综上，a的取值范围是(−1，−34 ]．21．（12分）记S n为数列{a n}的前n项和，已知等比数列{b n}满足b n＝a3n﹣2，n∈N*，b1+b3＝5，b2+b4=5 2．（1）求数列{b n}的通项公式；（2）若对任意n∈N*，a3n﹣2，a3n﹣1，a3n，a3n+1成等差数列．①求S1和S4的值；②求S3n﹣2．解：（1）设{b n}的公比为q，则b2+b4＝（b1+b3）q，代入b1+b3＝5，b2+b4=52，可得q=12．又由b1+b3=b1(1+q2)=5，得b1＝4．则{b n}的通项公式为b n=4(12)n−1=23−n．（2）①因为对任意n∈N*，a3n﹣2，a3n﹣1，a3n，a3n+1成等差数列，所以a3n﹣1+a3n＝a3n﹣2+a3n+1．S1＝a1＝b1＝4；S4＝a1+a2+a3+a4＝2a1+2a4＝2（b1+b2）＝12．②当n≥3时，S3n﹣2＝a1+（a2+a3+a4）+（a5+a6+a7）+…+（a3n﹣4+a3n﹣3+a3n﹣2）＝a1+（a1+a4+a4）+（a4+a7+a7）+…+（a3n﹣5+a3n﹣2+a3n﹣2）＝2a1+3a4+3a7+…+3a3n﹣5+2a3n﹣2＝2b1+3b2+3b3+…+3b n﹣1+2b n=3×4[1−(12)n]1−12−b1−b n=24−24(12)n−4−23−n＝20﹣25﹣n．当n＝1，2时上式也成立，因此，对任意正整数n，S3n−2=20−25−n．22．（12分）已知函数f（x）＝xln（1+ax）﹣x2（a＞0）．（1）若a＝1，求f（x）的单调区间；（2）若x＝0是f（x）的极小值点，求实数a的取值范围．解：（1）若a＝1，则f（x）＝xln（1+x）﹣x2，f（x）的定义域是（﹣1，+∞）．f′(x)=ln(1+x)+x1+x−2x．令g（x）＝f′（x），则g′(x)=11+x+1(1+x)2−2=−x(2x+3)(1+x)2．当x∈（﹣1，0）时，g′（x）＞0；当x∈（0，+∞）时，g′（x）＜0，所以g（x）在（﹣1，0）上单调递增，在（0，+∞）上单调递减．因为g（0）＝0，所以当x∈（﹣1，+∞）时，f′（x）＝g（x）≤g（0）＝0恒成立，当且仅当x＝0时等号成立．所以f（x）的单调递减区间为（﹣1，+∞），无单调递增区间．（2）f（x）的定义域为(−1a，+∞)，f′(x)=ln(1+ax)+ax1+ax−2x．由（1）得，当x＞0时，xln（1+x）﹣x2＜0，即ln（1+x）＜x；当x＜0时，xln（1+x）﹣x2＞0，即ln（1+x）＜x．所以当x≠0时，ln（1+x）＜x．因此，当x≠0时，f′(x)=ln(1+ax)+ax1+ax−2x＜ax+ax1+ax−2x=x(a−2+a1+ax)．①（ⅰ）若0＜a≤1，则当x＞0时，由①可得f′（x）＜x（2a﹣2）≤0．所以f（x）在（0，+∞）上单调递减，故x＝0不可能为f（x）的极小值点．（ⅱ）若a＞1，当−1a＜x＜0时，0＜1+ax＜1，所以a−2+a1+ax＞2a−2＞0，则由①可得f′（x）＜x（2a﹣2）＜0；当0＜x＜a−12a时，1＜1+ax＜a+12，设m(x)=f′(x)=ln(1+ax)+ax1+ax−2x，则m′(x)=a1+ax+a(1+ax)2−2＞2aa+1+4a(a+1)2−2=2(a−1)(a+1)2＞0，所以m（x）在区间(0，a−12a)上单调递增，从而f′（x）＝m（x）＞m（0）＝0．故f（x）在(−1a，0)上单调递减，在(0，a−12a)上单调递增，所以x＝0为f（x）的极小值点．综上所述，a的取值范围为（1，+∞）．。

2025届甘肃省白银市第八中学高三六校第一次联考语文试卷考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

1、阅读下面的文字，完成下面小题。

霍乱之乱（节选）池莉霍乱发生的那一天没有一点预兆。

天气非常闷热，闪电在遥远的云层里跳动，有大雨将至的迹象。

那天是我和秦静在防疫站值夜班。

流行病科室里的人都走了，只有科室主任闻达在伏案写他永远也写不完的流行病学调查报告。

他对各种流行病怀有着巨大的兴趣和热情。

写报告使他每天都要推迟一小时下班。

他的妻子认定他这么做是为了逃避做晚饭，有一次吵到单位来了，闻达闻讯仓皇地向楼顶逃窜。

他的妻子在顶楼逮住了他，将他的一只皮鞋扔了下去。

第二次闻达又逃到了顶楼，他的妻子又将他的一只皮鞋扔了下去，凑巧的是，这两只皮鞋正好都被扔在了飞驰的大卡车上。

从此闻达只好穿一双两只不同的皮鞋，但他还是照样在下班之后写他的报告。

闻达头发凌乱的脑袋在满满一桌的书本、卡片和资料堆中微微摇晃，嘴唇嚅动，口中念念有词。

从油漆斑驳的办公桌底探出老远的，是他瘦骨伶仃的长腿和那双穿着不配套皮鞋的大脚。

这哪里像马来西亚的归国华侨，新中国第一代科班出身的流行病学专家？闪电穿过了云层，接近了我们抬头可见的天空，暴风雨就要来了。

闻达骑上他那破旧的自行车，摇晃不定地回家去了。

秦静幽幽地叹了一口气，我说：“难怪人家说：远看是个要饭的，近看是个烧炭的，一问才知道是防疫站的。

”闪电如游蛇窜行在楼房的玻璃窗之间，雷声冷不丁在耳边爆响，密集的大雨从远处忽隆隆黑压压地横扫了过来。

大马路上的汽车都大开车灯，纷纷地揿喇叭。

晚上八点多，电话铃声骤然响起，是第十九医院肠道门诊的洪大夫打来的，她战战兢兢地说：“我们发现一例霍乱。

九江市稳派联考2024-2025学年高三上学期开学摸底考试语文试卷试卷共8页，23小题，满分150分。

考试用时150分钟。

注意事项：1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考生必须保持答题卡的整洁。

考试结束后，请将答题卡交回。

一、现代文阅读（35分）（一）现代文阅读［（本题共5小题，19分）阅读下面的文字，完成1～5题。

材料一：北京中轴线创始于元代，形成、完善于明清乃至近现代，历经700余年，全长约7.8千米，是“世界上现存最长、保存最为完整”的古代城市轴线。

中华文明具有源远流长的历史连续性，这条纵贯南北、穿越古今的城市中轴线，与我国延续数千年的古都发展史一脉相承。

东周时期《周礼·考工记》提出“以中为尊”的城市规划理念。

在青铜文明极盛期，这一筑城理念成为王朝统治阶级的共识，但在连年征战的背景下难以实现。

曹操营造的邺城，出现中国最早的城市中轴线，沿线建筑已经具有礼仪性与等级性。

东晋建康城中轴线进一步升华，以西南牛首山两个山峰为“天阙”，将城市中轴与自然相融，相映成趣。

北魏平城用将近一个世纪的时间打造都城，形成以朝堂宫区、中阳门为轴线的中轴线规制。

唐朝人对都城中轴线的礼制作用已经形成清晰的认知，但面对地理环境约束时，并不强求中轴对称。

其理念播散影响至朝鲜半岛和日本的城市营建，到了北宋东京，御街同时具有中轴线和宫廷广场性质，宽达300米。

元大都作为一座全新规划的都城，拥有笔直的城市中轴线和规整的结构布局，严格遵循了《周礼·考工记》对于理想都城的设计要求，奠定了今日北京城市的基本格局。

时光流转，北京中轴线被推荐为我国2024年世界文化遗产申报项目。

它见证了中华人民共和国成立以来重大的历史进程，也寄托了中华民族伟大复兴的梦想。

本月聚焦:高校争抢生源作者：来源：《广东教育·综合》2011年第08期编者按：近日，有关高校生源大战的争论愈演愈烈，由“暗战”转为“明战”——先是7月1日复旦大学招生办发表了措辞严厉的《关于部分省市考生受骗修改志愿的严正声明》，指责同城一工科院校抢生源；2日上海交通大学招生办通过其官方微博回应称，“本校招生老师无人冒充其他院校老师通知考生取消其与他校所签协议”；其后，复旦大学湖北招生组组长、历史系教授冯玮又在其微博上披露“招生内幕”，指出清华、北大为抢生源也连出怪招、损招：如给对手招办打电话，让考生打不进。

10日晚上，两所高校的上海招生组组长纷纷回应说，从未为招生而出过“怪招”。

事实上，复旦、上海交大因争抢生源而起的这一场冲突，暴露的只是国内知名高校生源大战的冰山一角。

名校间的招生竞争在近几年里已愈演愈烈，渐呈白热化趋势，“挖墙角”、相互贬低宣传等手段，早已屡见不鲜。

教育专家纷纷呼吁，高校要抢生源，应该光明正大，用自己的教育质量、教育服务来抢。

招生难，抢生源也是一种竞争意识招生难，高校有压力教育部在今年高考前公布的数据显示，今年全国普通高校招生报名总数约为933万。

这是自2008年以来第三年出现报名人数的较大幅度下降。

伴随着生源的逐渐减少，很多原来坐等考生上门的高校开始逐渐有了压力，于是一出出的国内高校生源抢夺大战也在各处上演。

一方面，由于北大清华已经圈走了一些高考状元，另一方面，由于香港、澳门等知名院校的介入，加剧了国内高校争夺优秀考生资源的竞争。

广东省从2010年开始实施平行志愿投档录取模式，考生不需再因志愿填报不合理导致“高分低录”而头疼，但对于各大高校来说，捡漏机会少了，招收尖子生的压力也更大了。

而招生已成一些高校的“面子工程”，比拼状元数，比拼分数线——生源被看成衡量高校实力的重要标准，学校下任务、定指标、许重奖，承受巨大压力的招生工作出现无序竞争，也就在所难免。

抢生源，体现竞争意识高校乃至名校之间大打生源争夺战，从理想角度看，并不是什么坏事，既是对优秀考生的重视与认可，也是对学校未来发展竞争力的一种重视。