3.2 代数式(第2课时)

3.2 代数式第2课时教学目标：能正确分析词语所描述的数量关系及运算顺序，并会列出代数式表示复杂的数量关系．重点能根据题意正确列出代数式，解决实际问题．难点用代数式正确表示数量和实际问题的数量关系．教学过程设计：复习回顾用字母表示数，可以把一些数量关系更简明地表示出来，把具体的数换成抽象的字母，是所得式子反应的规律具有普遍意义，从而为叙述和研究问题带来方便。

前面出现的91n，2k-1等，像这样用加减乘除乘方等符号把数或表示数的字母连接而成的式子，叫做代数式。

单个的数或字母也是代数式。

在代数式中乘号的书写方式：“.”或不写。

代数式的书写要求：（1）在代数式中出现的乘号，通常简写成“•”或者省略不写；（2）数字与字母相乘时，数字要写在字母的前面；（3）在代数式中出现的除法运算，一般按照分数的写法来写．带分数要写成假分数的形式．活动1：填空，观察所填式子的特点（1）边长为x的正方形的周长是__________；（2）一辆汽车的速度是v千米/小时，行驶t小时所走的路程是_______千米；（3）若正方体的的边长是a，则它的表面积是_______,体积是________；（4）设n是一个数，则它的相反数是________．【答案】（1）4x（2）vt（3）6a2a3（4）－n学生活动设计：学生自己解决上述问题，然后观察所填式子，归纳其特点，进而初步理解单项式的概念．所填式子是4x、vt、6a2.a3.－n，特点是都是数字或字母的乘积．教师活动设计：引导学生在观察的基础上归纳kx式的代数式的特征：活动2：解决下列问题．（1）小明房间的窗户如图（1）所示，其中上方的装饰物由两个四分之一圆和一个半圆组成（它们的半径相同）．图（1）装饰物所占的面积是______．（2）某校学生总数为x ，其中男生人数占总数的53，男生人数为__________；（3）一个长方体的底面是边长为a 的正方形，高是h ，体积是________．学生活动设计：学生独立思考，分析第（1）个问题中装饰物是由两个四分之一圆和一个半圆组成，它们的半径相同，由图中的已知条件可知半径为4b ，所以装饰物所占的面积恰好是半径为4b的一个圆的面积即216b ；（2）中男生人数为53x ；（3）中这个长方体的体积是a2h ．教师活动设计：引导学生在解决问题并进行交流，在交流中纠正一些不正确的想法．应用提高、拓展创新1.列出代数式：（1）每包书有12册，n 包书有___________册；（2）底边长为a ，高为h 的三角形的面积是_________；（3）一个长方体的长、宽都是a ，高是h ，它的体积是________；（4）一台电视机原价是a 元，现按原价的9折出售，那么这台电视机现在的售价为______元；（5）一个长方形的长是0.9，宽是a ，这个长方形的面积是_________．解：（1）12n ；（2）ah12；（3）a h 2；（4）0.9a ；（5）0.9a．2．产量由m千克增长10%就达到千克，a千克大米售价8元，1千克大米售价元．解：产量由m千克增长10%就达到（1+10%）m=1.1m千克，a千克大米售价8元，1千克大米售价元．故答案为：1.1m，．例题讲解例1.小明t小时走了s千米的路，则他走这段路的平均速度是___________千米/时．【答案】s t【解析】解：小明走这段路的平均速度是st千米/时．例2.因季节变化，商店将进价为a元的某种服装按80%标价．用语言叙述（1﹣80%）a 表示的意义是___________．【答案】每件服装亏损的价值【解析】解：（1﹣80%）a表示的意义是每件服装亏损的价值．归纳小结、布置作业小结：会根据实际情况列出kx形式的代数式．作业：教材习题．。

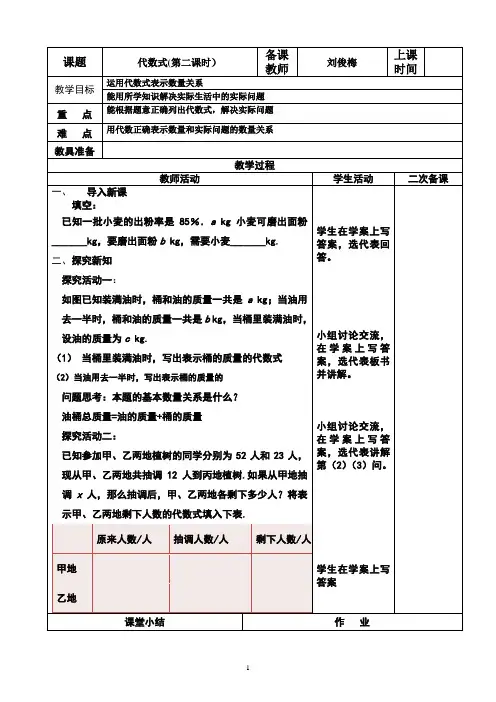
一、创设情境现在，我们请四位同学来做一个传数游戏．游戏规则：第一位同学任意报一个数给第二位同学，第二位同学把这个数加上1传给第三位同学，第三位同学再把听到的数平方后传给第四位同学，第四位同学把听到的数减去1报出答案．活动过程：四位同学站到台前，面向全体学生，再请一位同学担任裁判，面向这四位同学．教师站到黑板前，当听到第一位同学报出数字时马上在黑板上写出答案，然后判断和第四位同学报出的数是否一致（可试3～4个数）．师：为什么老师会很快地写出答案呢（根据学生的回答，教师启发学生归纳出计算的代数式：(x＋1)2－1）？二、探究归纳１．引导学生得出游戏过程实际是一个计算程序（如下图）：当第一个同学报出一个数时，老师就是在用这个具体的数代替了代数式(x＋1)2－1中的字母x，把答案很快地算了出来．掌握了这个规律，我们每位同学只要知道第一位同学报出的数都可以很快的得出游戏的结果．2．代数式的值的概念像这样，用数值代替代数式里的字母，按照代数式中的运算关系计算得出的结果称为代数式的值（value of algebraic expression）．通过上面的游戏，我们知道，同一个代数式，由于字母的取值不同，代数式的值会有变化．三、实践应用例1当a＝2，b＝－1，c ＝－3时，求下列各代数式的值：（1）b2－4ac;（2）a2＋b2＋c2＋2ab＋2bc＋2ac;（3）(a＋b＋c)2．解（1）当a＝2，b ＝－1，c＝－3时，b2－4ac＝(－1)2－4×2×(－3)＝1＋24＝25．（2）当a＝2，b＝－1，c＝－3时，a2＋b2＋c2＋2ab＋2bc＋2ac＝22＋(－1)2＋(－3)2＋2×2×(－1)＋2×(－1)×(－3)＋2×2×(－3)＝4＋1＋9－4＋6－12＝4．（3）当a ＝2，b ＝－1，c ＝－3时， (a ＋b ＋c )2 ＝(2－1－3)2 ＝ 4．注：1．比较（2）、( 3 ) 两题的运算结果，你有什么想法？2．换a ＝3 , b ＝ －2 , c ＝4再试一试，检验你的猜想是否正确． 3．对于这一猜想，我们通过学习，将来有能力证实它的正确性． 方法总结：（1）代入时要“对号入座”，避免代错字母；（2）代入后要恢复省略的乘号；（3）分数的立方、平方运算，要用括号括起来.例2 如图所示，某水渠的横断面为梯形，如果水渠的上口宽为a m ，水渠的下口宽和深都为b m.（1）请你用代数式表示水渠的横断面面积； （2）计算当a ＝3，b ＝1时，水渠的横断面面积.解析：（1）根据梯形面积＝12（上底＋下底）×高，即可用含有a 、b 的代数式表示水渠横断面面积；（2）把a ＝3、b ＝1带入到（1）中求出的代数式中，其结果即为水渠的横断面面积.解：（1）∵梯形面积＝12（上底＋下底）×高，∴水渠的横断面面积为：12（a ＋b ）b （m 2）；（2）当a ＝3，b ＝1时水渠的横断面面积为12（3＋1）×1＝2（m 2）.方法总结：解答本题时需搞清下列几个问题：（1）题目中给出的是什么图形？（2）这种图形的面积公式是什么？（3）根据公式求图形的面积需要知道哪几个量？（4）这些量是否已知或能求出？搞清楚了这些问题，求解就水到渠成.例3 当x ＝－3时，多项式mx 3＋nx －81的值是10，当x ＝3时，求该代数式的值． 解当x ＝－3时，多项式mx 3＋nx －81＝－27m －3n －81, 此时－27m －3n －81＝10, 所以27m ＋3n ＝－91．则当x ＝3，mx 3＋nx －81＝( 27m ＋3n )－81＝－91－81＝－172．注：本题采用了一种重要的数学思想——“整体思想”．即是考虑问题时不是着眼于他的局部特征，而是把注意力和着眼点放在问题的整体结构上，把一些彼此独立，但实质上又相互紧密联系着的量作为整体来处理的思想方法． 练习1．按下图所示的程序计算，若开始输入的n 值为2，则最后输入的结果是____________．2．根据下列各组x ，y 的值，分别求出代数式 x 2＋2xy+2y 2 与 x 2－2xy +y 2 的值.四、板书设计。