专题：一次函数与面积

面积与一次函数将一次函数与面积综合在一起进行考查，是目前比较热点的一类题型，充分体现了数形结合思想的具体应用，现举例加以说明．一、由一次函数图象求面积例1 已知直线y=kx+b过点A（－1，5），且平行于直线y=－x+2．（1）求直线y=kx+b的关系式；（2）若B（m，－5）在这条直线上，O二、由面积关系求一次函数关系式 例2 如图2，直线PA 是一次函数y=x+n(n ＞0)＞n) 的图象．（1）用m 、n 表示A 、B 、P 的坐标；（2）设PA 交y 轴于点Q ，若AB=2，四边形 PQOB 的面积为65，求P 点坐标和直线PA 、PB 分析：（1）分别令y=0，代入两个一次函数，可求出A 、B 两点的坐标；要求P 的坐标，只要把y=x+n 与一次方程组，可求得含有m 、n 的x 、y 值，即可得P 点的坐标；（2）由四边形PQOB 的面积等于△PAB 的面积减去△AOQ 的面积，可求出m 、n ，从而求出P 点坐标和直线PA 、PB 的关系式．解：（1）在y=x+ n 中，令y=0，得x=－n ，所以A （－n ，0）；在y=－2x+m 中，令y=0，得x=21m ，所以B （21m ，0）；由⎩⎨⎧+-=+=m x y n x y 2，解得⎪⎩⎪⎨⎧+=-=323n m y n m x ，所以P （3n m -，32nm +）． （2）由y=x+ n ，得Q （0，n ），所以QO=n 。

因为A （－n ，0），所以OA=n -= n 。

所以PQOB S 四边形=PAB S ∆－AO Q S ∆=21×2×32n m +－21n 2=65，即2m+4n －3n 2=5。

又OA+OB= n+21m=2，即m=4－2n 。

所以2（4－2n ）+4n －3n 2=5，所以n 2=1，所以n=1（负值舍去），所以m=4－2×1=2，所以P （31，34）。

所以直线PA 的关系式为y=x+1；PB 的关系式为y=－2x+2．点评：对于不规则的几何图形的面积，可以通过转化的思想，化不规则为规则，如本题中将四边形PQOB 的面积，转化为两个规则图形△PAB 与△AOQ 面积的差去解决的．通过以上两道例题可以看出，解决一次函数与面积问题的基本步骤是：（1）确定交点坐标（有时可用待定系数表示）；（2）求出有关线段的长度；（3）将有关图形的面积化归为与坐标轴有联系的几个基本图形的和差倍分，然后根据题目特点利用图象与面积间的关系综合求解．。

一次函數面積問題1、如图，一次函数的图像与X轴交于点B (- 6 , 0),交正比例函数的图像于点A，点A的横坐标为-4，△ ABC的面积为15，求直线OA的解析式。

2、直线y=x+3的图像与X轴、y轴分别交于A B两点，直线a经过原点与线段AB 交于。

，把厶ABO勺面积分为2：1的两部分，求直线a的函数解析式。

3、直线PA是一次函数y=x+n的图像，直线PB是一次函数y=-2x+m (m>n>0的图像，(1) 用m n表示A、B、P的坐标(2) 四边形PQoB勺面积是'，AB=2求点P的坐标4、A AOB的顶点0( 0, 0) A (2, 1)、B (10, 1),直线CDL X 轴且△ AOB面积二等分，若D (m, 0),求m的值5、点B在直线y=-x+1上，且点B在第四象限，点A(2, 0)、0(0, 0),A ABo 的面积为2,求点B的坐标。

6直线y=- x+1与X轴y轴分别交点A B,以线段AB为直角边在第一象限内作等腰直角△ ABC N BAC=90 ,点P( a,])在第二象限，△ ABP勺面积与△ ABC7、如图，已知两直线y=0.5x+2.5和y=-x+1分别与X轴交于A、B两点，这两直线的交点为P(1)求点P的坐标(2)求厶PAB的面积8、已知直线y=ax+b (b>0)与y轴交于点N,与X轴交于点A且与直线y=kx交于点M (2, 3)，如图它们与y轴围成的厶MoN勺面积为5,求(1)这两条直线的函数关系式(2)它们与X轴围成的三角形面积9、已知两条直线y=2x-3和y=5-x(1)求出它们的交点A的坐标(2)求出这两条直线与X轴围成的三角形的面积10、已知直线y=x+3的图像与X轴、y轴交于A B两点，直线I经过原点，与线段AB 交于点。

，把厶AoB的面积分为2：1的两部分，求直线I的解析式。

11、已知直线y=2x+3与直线y=-2x-1与y轴分别交于点A B（1）求两直线交点C的坐标（2）求厶ABe的面积（3）在直线BC上能否找到点P,使得△ APC的面积為6,求出点P的坐标,12、已知直线y=-x+2与X轴、y轴分别交于点A和点B,另一直线y=kx+b（k≠ 0）经过点C（1，0）,且把△ AOB分为两部分，（1）若厶AOB被分成的两部分面积相等，求k和b的值（2）若厶AOB被分成的两部分面积为1：5,求k和b的值13、直线y=- x+3交X, y坐标轴分别为点A B,交直线y=2x-1于点P,直线-Iy=2x-1交X, y坐标轴分别为C。

一次函数面积问题专题
姓名：
一、基本图形识别
求图中各三角形的面积（用坐标表示）
用两种办法求S ∆MLN （用坐标表示）
用两种办法求S ∆AOB （用坐标表示）
二、 基本题型练习
1、在直角坐标系中，O 是坐标原点，点A （3，-2）在一次函数24y x =-+图象上，图象与y 轴的交点为B ，求AOB ∆面积。

x
x
x
变式：(1)在直线AB上找一点P，使得S∆AOB = S∆BOP
变式：(2)在直线AB上找一点P，使得S∆BOP =S∆AOB
变式：(3)在Y轴上找一点P，使得S∆AOP = S∆AOB
1.1如图，直线OC 、BC 的函数关系式分别是x y =1和622+-=x y ，直线BC 与x 轴交于点B ，直线BA 与直线OC 相交于点A ，求:（1）当x 取何值时1y >2y （2）当直线BA 平分△BOC 的面积时,求点A 的坐标.
4
、
如图，已知直线PA 是一次函数)0(>+=n n x y 的图象，直线PB 是一次函数)(2n m m x y +-=的图象。

（1）用m 、n 表示出A 、B 、P 点的坐标；（2）若点Q 是直线PA 与y 轴的交点，且四边形PQOB 的面积6
5，AB=2，试求点P 的坐标，并写出直线PA 与PB 的解析式。

在平面直角坐标系中，点A （4，0），点P （x ，y ）是直线32
1+-
=x y 在第一象限的一点．（1）设△OAP 的面积为S ，用含x 的解析式表示S ，并写出自变量取值范围．（2）在直线321+-=x y 求一点Q ，使△OAQ 是以OA 为底的等腰三角形．（3）若第（2）问变为使△OAQ 是等腰三角形，这样的点。

一次函数中的面积问题（专题）例1：已知一次函数 ，求该函数图象与坐标轴围成的图形的面积.（针对性训练1）已知一次函数 ，求该函数图象与坐标轴围成的图形的面积.例2：若直线 与两坐标轴所围成的图形面积为4，求该直线的解析式.（针对性训练2）若直线 与两坐标轴所围成的图形面积为6，求该直线的解析式.例3：已知一次函数图像经过（0，2）且与两坐标轴围成的三角形面积为1，求一次函数的 解析式.（针对性训练3）已知一次函数图像经过（0，-2）且与两坐标轴围成的三角形面积为3， 求一次函数的解析式.4、如图所示一次函数 的图象经过A（2，4）和B （0，2）两点，且与x 轴相交于C 点，连接AO 。

（1）求此一次函数的解析式；（2）求AOC ∆的面积.b kx y +=121+-=x y b x y +=2231-=x y b x y --=321-5、已知直线 和直线 相交于点P ，且直线分别交x 轴、 轴于点A ，B ，直线 交 轴于点C ，如图所示（1）求点P 的坐标；（2）求PCA ∆的面积.6、如图所示，在平面直角坐标系中，一次函数的图象 分别与x 轴、y 轴和直线4=x 交于点A ，B ，C ，直线4=x 与x 轴交于点D ，梯形OBCD （O 为坐标原点）的面积为10，若点A 的横坐标为 ，求这个一次函数的解析式.7、直线 过点A （0，2），B （2，0），直线 ： 过点C （1，0），且把分成两部分，其中靠近原点的那部分是一个三角形，设此三角形的面积为S ，求S 关于m 的函数解析式.643+-=x y 243-=x y 643+-=x y 243-=x y y y bkx y +=1l 2l bmx y +=AOB ∆。

专题复习：一次函数与面积问题一、忆1.直线y=2x+1与y=2x-3的位置关系是： .2.直线y=2x+5与y=0.5x+5的交点坐标是： .3.直线直线y=x-1与直线y= -0.5 x+2交点坐标是： .4.直线y=x-1与y轴的交点坐标为，与x轴的交点坐标为，此直线与两坐标轴围成的三角形的面积为 .5.一次函数图象经过点（0，2）和（4，0），这个一次函数的解析式为： .二、思例1(根据一次函数求面积)：直线y=x-1交x轴、y轴于点A、B，直线y=-0.5x+2交x轴、y轴于点C、点D，两直线交于点P.(1)你能求出哪些点的坐标?哪些线段的长?哪些图形的面积?(2) 求点O到直线AB的距离OM的长吗？(提示:点的横,纵坐标对求图形面积时用到的底边,高的作用. )例2(根据面积求一次函数表达式)：一次函数y=kx+b 交y=2x 于点A(1,m),交x 轴于点B ，且S △AOB =4.(1)求一次函数y=kx+b 的解析式.(2) 你能求过点(－4，0)且平行于0A 的直线解析式吗？(提示:面积中出现的底,高对点的横,纵坐标的确定作用,分类讨论,数形结合)三、练1.点P 是一次函数y=-2x+8的图象上一点，如果图象与x 轴交于Q 点，且△OPQ 的面积等于6，则P 点的坐标为 . y=-2x+82.如图：正方形ABCD 边长为4，将此正方形置于坐标系中点A 的坐标为（1，0).(1)过点C 的直线 3834-=x y 与x 轴交与E, 求S 四边形AECD ； (2)直线l 经过点E 且将正方形ABCD 分成面积相等的两部分，求直线l 的解析式.四、获---说说自己的收获五、延---复习题单针对训练。

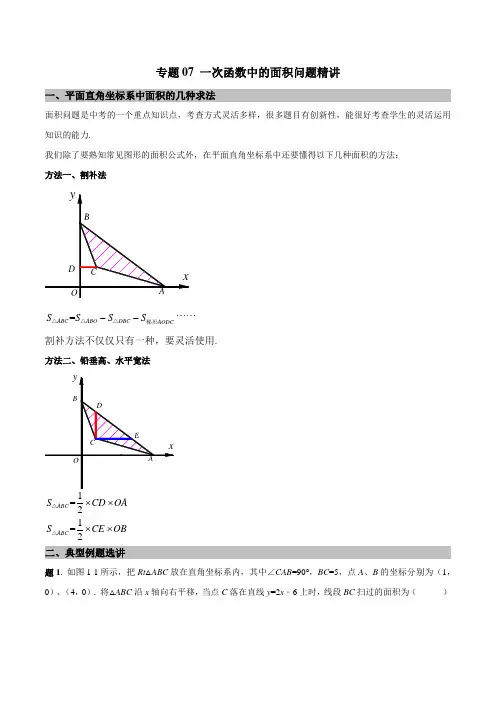
专题07 一次函数中的面积问题精讲一、平面直角坐标系中面积的几种求法面积问题是中考的一个重点知识点，考查方式灵活多样，很多题目有创新性，能很好考查学生的灵活运用知识的能力.我们除了要熟知常见图形的面积公式外，在平面直角坐标系中还要懂得以下几种面积的方法： 方法一、割补法割补方法不仅仅只有一种，要灵活使用.方法二、铅垂高、水平宽法=21=2ABC ABC S CD OAS CE OB⨯⨯⨯⨯△△ 二、典型例题选讲题1. 如图1-1所示，把Rt △ABC 放在直角坐标系内，其中∠CAB =90°，BC =5，点A 、B 的坐标分别为（1，0）、（4，0）．将△ABC 沿x 轴向右平移，当点C 落在直线y =2x ﹣6上时，线段BC 扫过的面积为（ ）图1-1A ．4B ．8C ．16D ．12 【答案】C .【解析】如图1-2所示．图1-2设C 点移动到直线y =2x ﹣6上的点为C ’. ∵点A 、B 的坐标分别为（1，0）、（4，0）， ∴AB =3．∵∠CAB =90°，BC =5，∴在Rt △ABC 中，由勾股定理得：AC =4． ∴A ′C ′=4．∵点C ′在直线y =2x -6上， ∴2x -6=4，解得 x =5．即OA ′=5， ∴CC ′=5-1=4．∴四边形BB ’C ’C 是平行四边形，面积 =4×4=16． 即线段BC 扫过的面积为16，故答案为：C .题2. 已知一次函数2y x a =+与y x b =-+的图象都经过A （2-，0），且与y 轴分别交于B 、C 两点，则△ABC 的面积为 （ ）．A ． 4B ． 5C ． 6D ． 7 【答案】C .【解析】因为y =2x +a 与y =-x +b 的图象都经过A (-2,0), 所以0=2×（-2）+a ， 解得：a =4， 又因为0=2+b 解得：b =-2y =2x +4、y =-x -2与y 轴分别交于B 、C 两点 ∴B (0.4)，C (0,-2)，三角形ABC 的面积=2×6÷2=6. 故答案为：C .题3. (河北中考)如图3-1所示，在平面直角坐标系xOy 中，A (0，5)，直线x ＝－5与x 轴交于点D ，直线y ＝－38x －398与x 轴及直线x ＝－5分别交于点C ，E .点B ，E 关于x 轴对称，连接AB . (1)求点C ，E 的坐标及直线AB 的解析式； (2)若S ＝S △CDE ＋S 四边形ABDO ，求S 的值；(3)在求(2)中S 时，嘉琪有个想法：“将△CDE 沿x 轴翻折到△CDB 的位置，而△CDB 与四边形ABDO 拼接后可看成△AOC ，这样求S 便转化为直接求△AOC 的面积，如此不更快捷吗？”但大家经反复验算，发现S △AOC ≠S ，请通过计算解释他的想法错在哪里．图3-1【答案】见解析【解析】解：（1）y ＝－38x －398，令y ＝0，有0＝－38x －398，解得：x ＝－13，即C (－13，0)．令x ＝－5，则有y ＝－38×(－5)－398＝－3，即E (－5，－3)．∵点B ，E 关于x 轴对称， ∵B (－5，3)． ∵A (0，5)，∵设直线AB 的解析式为y ＝kx ＋5， ∵－5k ＋5＝3， ∵k ＝25，∵直线AB 的解析式为y ＝25x ＋5.（2）由（1）知E (－5，－3)， ∵DE ＝3. ∵C (－13，0)，∵CD ＝－5－(－13)＝8， ∵S ∵CDE ＝12CD ·DE ＝12.由题意知OA ＝5，OD ＝5，BD ＝3， ∵S 四边形ABDO ＝12(BD ＋OA )·OD ＝20，∵S ＝S ∵CDE ＋S 四边形ABDO ＝12＋20＝32.（3）由（2）知S ＝32，在∵AOC 中，OA ＝5，OC ＝13， ∵S ∵AOC ＝12OA ·OC ＝652＝32.5，∵S ≠S ∵AOC .理由：由(1)知直线AB 的解析式为y ＝25x ＋5，令y ＝0，则0＝25x ＋5，∵x ＝－252≠－13，∵点C 不在直线AB 上，即点A ，B ，C 不在同一条直线上， ∵S ∵AOC ≠S .题4. 已知一次函数的图象过点(0,3)，且与两坐标轴所围成的三角形面积为3, 则其表达式为( ) A . y ＝1.5x ＋3B . y ＝－1.5x ＋3C . y ＝1.5x ＋3或y ＝－1.5x ＋3D . y ＝1.5x －3或y ＝－1.5x －3【答案】C .【解析】解：设该一次函数与x 轴的交点坐标为（a ,0）， 由题意得：1332a ⨯⨯=， 解得：a =±2， 当a =2时，设直线解析式为y =kx +3，将（2,0）代入，求得k =-1.5； 同理求得，当a =-2时，k =1.5.所以函数解析式为：y ＝1.5x ＋3或y ＝－1.5x ＋3，故答案为C .题5. 如图5-1所示，已知一次函数y ＝kx ＋b 的图象经过A (－2，－1)，B (1，3)两点，并且交x 轴于点C ，交y 轴于点D .图5-1(1)求该一次函数的解析式；(2)求∵AOB 的面积． 【答案】见解析.【解析】解：(1)把A (－2，－1)，B (1，3)代入y ＝kx ＋b ，得：⎩⎪⎨⎪⎧－2k ＋b ＝－1，k ＋b ＝3. 解得⎩⎨⎧k ＝43，b ＝53.∵一次函数的解析式为y ＝43x ＋53.(2)把x ＝0代入y ＝43x ＋53，得y ＝53，∵D 点坐标为(0，53)．∵S ∵AOB ＝S ∵AOD ＋S ∵BOD ＝12×53×2＋12×53×1＝52.题6. 已知，一次函数y kx b =+的图像与正比例函数13y x =交于点A ，并与y 轴交于点(0,4)B -，△AOB 的面积为6，则kb = 【答案】203-或4. 【解析】解：因为一次函数y kx b =+的图像与y 轴交于点(0,4)B -， ∴b =－4，OB =4， 设A 点横坐标为a ， 因为△AOB 的面积为6， 所以162a OB ⨯⨯=, 即a =3或－3，点A 的坐标为（3,1）或（－3，－1） 将A 点坐标代入4y kx =-，得： k =53或－1 所以kb = 203-或4. 故答案为：203-或4.题7. 如图7-1所示,点G ，D ，C 在直线a 上,点E ,F ,A ,B 在直线b 上,若a ∥b ,Rt △GEF 从如图所示的位置出发,沿直线b 向右匀速运动,直到EG 与BC 重合.运动过程中△GEF 与矩形ABCD 重合部分的面积（S ）随时间（t ）变化的图象大致是（ ）图7-1A B C D【解析】根据题意可得：①F、A重合之前没有重叠面积；②F、A重叠之后，重叠部分面积逐渐增大，且增加的速度越来越快；③△EFG完全进入且F与B重合之前，重叠部分的面积是三角形的面积，不变，④F与B重合之后，重叠部分的面积逐渐减小，减小的速度越来越慢，直至最后重叠部分的面积为0．综上所述，只有B选项图形符合．故答案为：B．题8. 如图8-1所示，已知直线y=2x+3与直线y=-2x-1.(1)求两直线交点C的坐标;(2)求∵ABC的面积.(3)在直线BC上能否找到点P,使得S∵APC=6，若能，请求出点P的坐标，若不能请说明理由。

一次函数面积专题练习1．如图，在平面直角坐标系中，直线1:1l y kx =+交y 轴于点A ，交x 轴于点(4,0)B ，过点(2,0)E 的直线2l 平行于y 轴，交直线1l 于点D ，点P 是直线2l 上一动点(异于点)D ，连接PA 、PB ．(1)直线1l 的表达式为 ，点D 的坐标为 ；(2)设(2,)P m ，当点P 在点D 的下方时，求ABP ∆的面积S 的表达式(用含m 的代数式表示)；(3)当ABP ∆的面积为3时，求点P 的坐标．2．如图，在平面直角坐标系xOy 中，直线443y x =-+与x 轴、y 轴分别交于点A 、点B ，点(0,6)D -在y 轴的负半轴上，若将DAB ∆沿直线AD 折叠，点B 恰好落在x 轴正半轴上的点C 处，直线CD 交AB 于点E ．(1)求点A 、B 、C 的坐标；(2)求ADE ∆的面积；(3)y 轴上是否存在一点P ，使得12PAD ADE S S ∆∆=，若存在，请直接写出点P 的坐标；若不存在，请说明理由．3．如图，直线1:1l y kx =+与x 轴交于点D ，直线2:l y x b =-+与x 轴交于点A ，且经过定点(1,5)B -，直线1l 与2l 交于点(2,)C m ．(1)填空：k = 12；b = ；m = ； (2)在x 轴上是否存在一点E ，使BCE ∆的周长最短？若存在，请求出点E 的坐标；若不存在，请说明理由．(3)若动点P 在射线DC 上从点D 开始以每秒1个单位的速度运动，连接AP ，设点P 的运动时间为t 秒．是否存在t 的值，使ACP ∆和ADP ∆的面积比为1:3？若存在，直接写出t 的值；若不存在，请说明理由．4．如图1，平面直角坐标系中，直线122y x =-与x 轴、y 轴分别交于点A ，B ，直线y x b =-+经过点A ，并与y 轴交于点C ．(1)求A ，B 两点的坐标及b 的值；(2)如图2，动点P 从原点O 出发，以每秒1个单位长度的速度沿x 轴正方向运动．过点P 作x 轴的垂线，分别交直线AC ，AB 于点D ，E ．设点P 运动的时间为t ．点D 的坐标为 ．点E 的坐标为 ；(均用含t 的式子表示)(3)在(2)的条件下，当点P 在线段OA 上时，探究是否存在某一时刻，使DE OB =？若存在，求出此时ADE ∆的面积；若不存在说明理由．。

模型介绍方法点拨☑知识点1两直线平行如图，直线b∥a，那么k b =k a ，若已知k a 及C 的坐标即可求出直线b 的解析式.☑知识点2两直线垂直如图，直线c⊥a，那么k c *k a =-1，若已知k a 及C 或B 的坐标即可求出直线c 的解析式.（针对这一性质，初中不要求掌握，一般用全等、相似的方法求解）例题精讲考点一：一次函数平行问题【例1】．一次函数y＝kx+b与y＝3x+1平行，且经过点（﹣3，4），则这个函数的表达式为y＝3x+13．解：∵一次函数y＝kx+b与y＝3x+1平行，∴k＝3，把（﹣3，4）代入y＝3x+b得﹣9+b＝4，解得b＝13，∴所求一次函数解析式为y＝3x+13．故答案为y＝3x+13．变式训练【变1-1】．一条直线平行于直线y＝2x﹣1，且与两坐标轴围成的三角形面积是4，则直线的解析式是（）A．y＝2x+4B．y＝2x﹣4C．y＝2x±4D．y＝x+2解：∵所求直线与直线y＝2x﹣1平行∴可设所求直线的解析式为y＝2x+b令x＝0可得直线在y轴的截距为b令y＝0可得直线在x轴的截距为由题意可知：b××＝4∴b＝±4，故选：C．【变1-2】．一个一次函数图象与直线y＝x+平行，与x轴、y轴的交点分别为A、B，并且过点（﹣1，﹣20），则在线段AB上（包括端点A、B），横、纵坐标都是整数的点有4个．解：因为一次函数的图象与直线y＝x+平行，所以所求直线的斜率为，又因为所求直线过点（﹣1，﹣20），所以所求直线为5x﹣4y﹣75＝0，所以此直线与x轴、y轴的交点分别为A（15，0）、B（0，﹣），设在直线AB上并且横、纵坐标都是整数的点的横坐标是x＝﹣1+4N，纵坐标是y＝﹣20+5N，（N是整数）．因为在线段AB上这样的点应满足0≤x＝﹣1+4N≤15，且﹣＜y＝﹣20+5N≤0，解得：≤N≤4，所以N＝1，2，3，4，故答案为：4．考点二：一次函数垂直问题【例2】．已知直线y＝kx+b经过点A（3，8），并与直线y＝2x﹣3垂直，则k＝﹣；b＝．解：∵已知直线y＝kx+b与直线y＝2x﹣3垂直，则k＝﹣，∴y＝x+b，将A（3，8）代入，8＝+b，解得b＝，故答案为﹣，．变式训练【变2-1】．如图，在平面直角坐标系中，直线y＝﹣x+4与x轴、y轴分别交于点A、B，直线CD与y轴交于点C（0，﹣8），与直线AB交于点D，若△AOB∽△CDB，则点D的坐标为（，）．解：∵△AOB∽△CDB，∴∠CDB＝∠AOB＝90°，设直线CD的解析式为：y＝2x+b，∵点C的坐标为（0，﹣8），∴b＝﹣8，，解得，，则点D的坐标为：（，），故答案为：（，）．【变2-2】．直线y＝kx+b与抛物线y＝x2交于A（x1，y1），B（x2，y2）两点，当OA⊥OB时，直线AB恒过一个定点，该定点坐标为（0，4）．[提示：直线l1：y＝k1x+b1与直线l2：y＝k2x+b2互相垂直，则k1•k2＝﹣1]解：∵直线y＝kx+b与抛物线y＝x2交于A（x1，y1）、B（x2，y2）两点，∴kx+b＝x2，化简，得x2﹣4kx﹣4b＝0，∴x1+x2＝4k，x1x2＝﹣4b，又∵OA⊥OB，∴×＝＝＝＝＝﹣1，解得，b＝4，即直线y＝kx+4，故直线恒过顶点（0，4），故答案为：（0，4）．考点三：一次函数的面积问题【例3】．已知一次函数y＝mx+2的图象与两坐标轴围成的三角形的面积为1，则常数m＝±2．解：令x＝0，则y＝2，令y＝0，则x＝﹣，∵一次函数y＝mx+2的图象与两坐标轴围成的三角形的面积为1，∴×2×|﹣|＝1，解得m＝±2．故答案为：±2．变式训练【变3-1】．已知直线y＝（n为正整数）与坐标轴围成的三角形的面积为S n．则S1+S2+S3+…+S2020的值为（）A．B．C．D．解：令x＝0，则y＝，令y＝0，则＝0，解得x＝，所以，S n＝••＝（﹣），所以，S1+S2+S3+…+S2020＝（+﹣+﹣+…+﹣）＝（﹣）＝．故选：B．【变3-2】．如图，正比例函数y＝﹣3x的图象与一次函数y＝kx+b的图象交于点P（m，3），一次函数图象经过点B（1，1），与y轴的交点为D，与x轴的交点为C．（1）求一次函数表达式；（2）求△COP的面积．解：（1）∵正比例函数y＝﹣3x的图象过点P（m，3），∴3＝﹣3m，解得：m＝﹣1，∴P（﹣1，3），∵一次函数y＝kx+b的图象过点P（﹣1，3），B（1，1），∴，解得：，∴一次函数表达式为y＝﹣x+2；（2）由（1）知，一次函数表达式为y＝﹣x+2，令y＝0，﹣x+2＝0，解得：x＝2，∴C（2，0），∴OC＝2，∴＝3．1．两直线y1＝k1x+b1与y2＝k2x+b2相交于y轴，则（）A．k1≠k2，b1≠b2B．k1≠k2，b1＝b2C．k1＝k2，b1≠b2D．k1＝k2，b1＝b2解：两直线y1＝k1x+b1与y2＝k2x+b2相交于y轴，则两直线与y轴的交点是同一点，在直线y1＝k1x+b1中，令x＝0，解得y＝b1，与y轴的交点是（0，b1），同理直线y2＝k2x+b2与y轴的交点是（0，b2），则b1＝b2，若k1＝k2，则两直线重合，因而k1≠k2．故选：B．2．若直线x+3y+1＝0与ax+y+1＝0互相垂直，则实数a的值为（）A．﹣3B．﹣C．D．3解：直线x+3y+1＝0的斜率为：﹣，直线ax+y+1的斜率为：﹣a，∵两直线垂直，∴﹣×（﹣a）＝﹣1，∴a＝﹣3，故选：A．3．已知一次函数y＝x+2与y＝﹣2+x，下面说法正确的是（）A．两直线交于点（1，0）B．两直线之间的距离为4个单位C．两直线与x轴的夹角都是30°D．两条已知直线与直线y＝x都平行解：根据一次函数的性质，一次函数y＝x+2与y＝﹣2+x，分别与y轴相交于（0，2）和（0，﹣2）两点，因为x的系数，都为1，因此直线的方向是一样的，都与直线y＝x平行．故选：D．4．如图，直线l1过原点，直线l2解析式为y＝﹣x+2，且直线l1和l2互相垂直，那么直线l1解析式为（）A．y＝x B．y＝x C．y＝x D．y＝x解：∵一次函数经过原点，∴设所求的一次函数为y＝kx，∵一次函数的图象与直线y＝﹣x+2垂直，∴k＝，则直线l1解析式为y＝x，故选：D．5．已知直线y＝mx﹣1上有一点B（1，n），它到原点的距离是，则此直线与两坐标轴围成的三角形的面积为（）A．B．或C．或D．或解：∵点B（1，n）到原点的距离是，∴n2+1＝10，即n＝±3．则B（1，±3），代入一次函数解析式得y＝4x﹣1或y＝﹣2x﹣1．（1）y＝4x﹣1与两坐标轴围成的三角形的面积为：××1＝；（2）y＝﹣2x﹣1与两坐标轴围成的三角形的面积为：××1＝．故选：C．6．如图，一次函数y＝kx+b的图象与正比例函数y＝2x的图象平行且经过点A（1，﹣2），则kb＝﹣8．解：∵一次函数y＝kx+b的图象与正比例函数y＝2x的图象平行，∴k＝2，∴y＝2x+b，把点A（1，﹣2）代入y＝2x+b得2+b＝﹣2，解得b＝﹣4，∴kb＝2×（﹣4）＝﹣8．故答案为﹣8．7．若平行于直线y＝﹣2x的某直线y＝kx+b与两坐标轴所围成的三角形面积为5，则b＝．解：直线y＝kx+b与直线y＝﹣2x平行，因而k＝﹣2，直线y＝﹣2x+b与x轴的交点坐标是，与y轴的交点坐标是（0，b），∴||•|b|＝5，即＝5，解得：b＝±2．8．如图，直线y＝﹣x+2与x，y轴交于A、B两点，以AB为边在第一象限作矩形ABCD，矩形的对称中心为点M，若双曲线y＝（x＞0）恰好过点C、M，则k＝．解：∵y＝﹣x+2，∴x＝0时，y＝2；y＝0时，﹣x+2＝0，解得x＝4，∴A（4，0），B（0，2）．∵四边形ABCD是矩形，∴∠ABC＝90°．设直线BC的解析式为y＝2x+b，将B（0，2）代入得，b＝2，∴直线BC的解析式为y＝2x+2，设C（a，2a+2），∵矩形ABCD的对称中心为点M，∴M为AC的中点，∴M（，a+1）．∵双曲线y＝（x＞0）过点C、M，∴a（2a+2）＝（a+1），解得a1＝，a2＝﹣1（不合题意舍去），∴k＝a（2a+2）＝（2×+2）＝．故答案为．9．在平面直角坐标系xOy中，已知直线AB与x轴交于点A（2，0），与y轴交于点B（0，1）．（1）求直线AB的解析式；＝2，求点C的坐标．（2）若x轴上有一点C，且S△ABC解：（1）设直线AB的解析式为y＝kx+b（k≠0），将点A（2，0），B（0，1）代入，可得，解得，∴直线AB的解析式为y＝﹣x+1；（2）∵x轴上有一点C，设点C（x，0），∴AC＝|2﹣x|，＝2，∵S△ABC∴×|2﹣x|×1＝2，∴x＝﹣2或x＝6，∴C（﹣2，0）或C（6，0）．10．如图，直线l1：y＝x﹣3与x轴交于点A，与y轴交于点B，直线l2：y＝kx+b与x轴交于点C（0.5，0），与y轴交于点D（0，2），直线l1，l2交于点E．（1）求直线l2的函数表达式．（2）试说明CD＝CE．（3）若P为直线l1上一点，当∠POB＝∠BDE时，求点P的坐标．解：（1）将C（0.5，0）．D（0，2）代入y＝kx+b得，，解得，∴直线l2的函数解析式为y＝﹣4x+2；（2）当﹣4x+2＝x﹣3时，∴x＝1，∴E（1，﹣2），过点E作EF⊥x轴于F，∴EF＝OD＝2，∵∠ODC＝∠CEF，∠DCO＝∠ECF，∴△DOC≌△EFC（AAS），∴CD＝CE；（3）∵∠POB＝∠BDE，∴点P在l1上有两个位置，当点P在点B上方时，如图，∴OP∥DE，∴直线OP的函数解析式为y＝﹣4x，∴﹣4x＝x﹣3，∴x＝，当x＝时，y＝﹣，∴P（，﹣），当点P在点B的下方时，设点P关于y轴的对称点为Q，连接OQ交l1为点P'，∴Q（﹣），则直线OQ的函数解析式为y4，∴直线OQ与l1的交点为P'（﹣1，﹣4），综上所述：P（，﹣）或（﹣1，﹣4）．11．如图，在平面直角坐标系中，将一块等腰直角三角板△ABC放在第三象限，斜靠在两坐标轴上，点C坐标为（0，﹣4），直角顶点B坐标为（﹣1，0），一次函数y＝kx+b的图象经过点A、C交x轴于点D．（1）求点A的坐标；（2）求直线AC与坐标轴围成的三角形的面积．解：（1）作AE⊥x轴，垂足为E．∵∠AEB＝90°，∴∠ABE+∠CBO＝90°．在Rt△AEB中，∵∠ABE+∠EAB＝90°，∴∠CBO＝∠EAB，在△AEB和△BOC中，，∴△AEB≌△BOC（AAS）．∴AE＝BO＝1，BE＝OC＝4，∴OE＝OB+BE＝1+4＝5，∴A（﹣5，﹣1）．（2）把A（﹣5，﹣1），C（0，﹣4）代入y＝kx+b，得，解得，函数解析式为：y＝﹣x﹣4，当y＝0时，x＝﹣，D（﹣，0）．S△COD＝××4＝．12．如图，直线l1：y＝x+3分别与直线l2：y＝kx+b（k≠0）、直线l3：y＝k1x+b1（k1≠0）交于A、B两点，直线l1交y轴于点E，直线l2与x轴和y轴分别交于C、D两点，已知点A的纵坐标为，B的横坐标为1，l2∥l3，OD＝1，连BD．（1）求直线l3的解析式；（2）求△ABD的面积．解：（1）在y＝x+3中，令y＝，则x＝﹣，∴A（﹣，），∵OD＝1，∴D（0，﹣1），把点A，D的坐标代入l2：y＝kx+b，可得，解得，∴l2：y＝﹣x﹣1，在y＝x+3中，令x＝1，则y＝4，∴B（1，4），∵l2∥l3，∴k1＝﹣，把B（1，4）代入y＝﹣x+b1可得，4＝﹣+b1，∴b1＝，∴直线l3的解析式为y＝﹣x+；（2）在y＝x+3中，令x＝0，则y＝3，∴E（0，3），∴DE＝3+1＝4，＝DE（|x A|+|x B|）＝（+1）＝5．∴S△ABD13．如图，一次函数y＝x﹣2的图象与x轴交于点A，与反比例函数y＝（x＞0）的图象交于点B，且点B的纵坐标为1．（1）求反比例函数y＝（x＞0）的表达式；（2）过点A作x轴的垂线交反比例函数y＝（x＞0）的图象于点C，平移直线y＝x ﹣2得到过点C的直线l，l的函数表达式为y＝mx+n，结合函数的图象，求＞mx+n对应x的取值范围．解：（1）∵点B在一次函数y＝x﹣2的图象上，且B的纵坐标为1，∴1＝，∴x＝6，∴B（6，1），∵反比例函数y＝（x＞0）的图象过点B，∴，∴k＝6，∴反比例函数的表达式为（x＞0）；（2）∵一次函数y＝x﹣2的图象与x轴交于点A，∴令y＝0得，，∴x＝4，∴A（4，0），∵CA⊥x轴，∴点C的横坐标为4，结合函数图象可知，要求＞mx+n，即反比例函数y＝的图象在一次函数y＝mx+n的图象的上方，∴0＜x＜4．14．已知抛物线y＝ax2﹣a（a＞0）．（1）求抛物线与x轴的交点坐标；（2）设C为抛物线上的一定点，抛物线和x轴交点为E、F，直线l：y＝kx+2k+3与抛物线交于点A、B（点B与点C不重合），与y轴交于点P，直线BD垂直于直线y＝﹣a，垂足为D，且△CEF为等腰直角三角形．①求点C的坐标和抛物线的解析式；②证明：对于每一个给定的实数k，都有DP∥AC．解：（1）在y＝ax2﹣a中，令y＝0，得ax2﹣a＝0，∵a＞0，∴x2﹣1＝0，解得：x＝﹣1或x＝1，∴抛物线与x轴的交点坐标为（﹣1，0）和（1，0）；（2）①∵y＝ax2﹣a，∴E（﹣1，0），F（1，0），∵△CEF为等腰直角三角形，∴CE＝CF，∠ECF＝90°，∠CEF＝∠CFE＝45°，∵∠EOC＝∠FOC＝90°，OE＝OF＝1，∴OC＝OE＝1，∴C（0，﹣1），将C（0，﹣1）代入y＝ax2﹣a中，则﹣a＝﹣1，∴a＝1，∴抛物线的解析式为y＝x2﹣1；②由题意得：，解得：或，∴A（﹣2，3），B（k+2，k2+4k+3），且k+2≠0，∵直线BD垂直于直线y＝﹣1，垂足为D，∴D（k+2，﹣1），在y＝kx+2k+3中，令x＝0，得y＝2k+3，∴P（0，2k+3），设直线AC解析式为y＝mx+n，则，解得：，∴直线AC解析式为y＝﹣2x﹣1，设直线DP的解析式为y＝m′x+n′，则，解得：，∴直线DP的解析式为y＝﹣2x+2k+3，∴AC∥DP．15．定义：已知直线l：y＝kx+b（k≠0），则k叫直线l的斜率．性质：直线l1：y＝k1x+b1．l2：y＝k2x+b2（两直线斜率存在且均不为0），若直线l1⊥l2，则k1k2＝﹣1（1）应用：若直线y＝2x+1与y＝kx﹣1互相垂直，求斜率k的值；（2）探究：一直线过点A（2，3），且与直线y＝﹣x+3互相垂直，求该直线的解析式．解：（1）∵直线y＝2x+1与y＝kx﹣1互相垂直，∴2•k＝﹣1，∴k＝﹣；（2）设该直线的解析式为y＝kx+b，∵直线y＝kx+b与直线y＝﹣x+3互相垂直，∴﹣k＝﹣1，解得k＝3，把A（2，3）代入y＝3x+b得6+b＝3，解得b＝﹣3，∴该直线的解析式为y＝3x﹣3．16．在平面几何中，我们学过两条直线垂直的定义，下面就两个一次函数的图象所确定的两条直线，给出它们垂直的定义：设一次函数y＝k1x+b（k1≠0）的图象为直线l1，一次函数y＝k2x+b2（k≠0）的图象为直线l2，若k1•k2＝﹣1，我们就称直线l1与直线l2互相垂直，如直线y＝3x﹣1与直线y＝﹣x+1，因为3×（﹣）＝﹣1，所以相互垂直．根据以上定义内容，解答下面的问题：（1）求过点P（1，2）且与已知直线y＝0.5x﹣2垂直的直线l的函数表达式，并在如图所示的坐标系中画出直线l的图象．（2）求（1）问中的两条直线与y轴所围的三角形的面积；（3）已知点A（0，2），点B，C分别是（1）问中直线l和x轴上的动点，求出△ABC 周长的最小值．解：（1）设直线l的函数表达式为y＝kx+b，∵直线l与直线y＝0.5x﹣2垂直，∴k＝﹣2，∵直线l过点P（1，2），∴﹣2×1+b＝2，∴b＝4．∴直线l的函数表达式为y＝﹣2x+4；直线l的图象如图；（2）解方程组得，，∵直线y＝0.5x﹣2与y轴的交点为（0，﹣2），直线l的函数表达式为y＝﹣2x+4与y轴的交点为（0，4），∴两条直线与y轴所围的三角形的面积＝×6×＝；（3）∵点A（0，2）关于x轴的对称点为E（0，﹣2），关于直线l的对称点D（，），连接DE交直线l于B，交x轴于C，则此时，△ABC周长的值最小，△ABC周长的最小值＝DE＝＝．17．如图，在平面直角坐标系中，反比例函数的图象经过点A（﹣4，3），将点A向右平移2个单位长度，再向上平移a个单位长度得到点B，点B恰好落在该函数的图象上，过A，B两点的直线与y轴交于点C．（1）求k的值及点C的坐标；（2）在y轴上有一点D（0，4），连接AD，BD，求△ABD的面积．解：（1）设反比例函数表达式为，把A（﹣4，3）代入得，3＝，解得k＝﹣4×3＝﹣12．∴反比例函数的表达式为．∵将点A向右平移2个单位长度，再向上平移a个单位长度得到点B，∴点B的坐标为（﹣2，y）．当x＝﹣2时，．∴点B的坐标为（﹣2，6）．设直线AB的函数表达式为y＝kx+b．由题意，得，解得．∴．∵当x＝0时，y＝9，∴点C的坐标为（0，9）．（2）由（1）知CD＝OC﹣OD＝9﹣4＝5．∴|x A|﹣＝．18．如图在平面直角坐标系中，过点C（0，6）的直线AC与直线OA相交于点A（4，2），动点M在线段OA和射线AC上运动．（1）求直线AB的函数关系式；（2）求△OAB的面积；（3）是否存在点M，使△OMC的面积与△OAB的面积相等？若存在求出此时点M的坐标；若不存在，说明理由．解：（1）设直线AB的解析式是y＝kx+b，根据题意得：，解得：．则直线的解析式是：y＝﹣x+6；（2）∵y＝﹣x+6，当y＝0时，x＝6，∴B（0，6），∴OB＝6，∴△OAB的面积＝×6×2＝6；（3）存在点M，使△OMC的面积与△OAB的面积相等，理由如下：如图所示：设OA的解析式是y＝mx，则42，解得：m＝．则直线OA的解析式是：y＝x，∵点C（0，6），∴OC＝6，∴OB＝OC＝6，∵△OMC的面积与△OAB的面积相等，∴M到y轴的距离＝点A的纵坐标2，∴点M的横坐标为2或﹣2；当M的横坐标为2时，在y＝x中，当x＝2时，y＝1，则M的坐标是（2，1）；在y＝﹣x+6中，当x＝2则y＝4，则M的坐标是（2，4）．则M的坐标为（2，1）或（2，4）．当M的横坐标为﹣2时，在y＝﹣x+6中，当x＝﹣2时，y＝8，则M的坐标是（﹣2，8）．综上所述：点M的坐标为（2，1）或（2，4）或（﹣2，8）．19．如图1，平面直角坐标系中，直线y＝x﹣2与x轴、y轴分别交于点A，B，直线y＝﹣x+b经过点A，并与y轴交于点C．（1）求A，B两点的坐标及b的值；（2）如图2，动点P从原点O出发，以每秒1个单位长度的速度沿x轴正方向运动．过点P作x轴的垂线，分别交直线AC，AB于点D，E．设点P运动的时间为t．点D的坐标为（t，﹣t+4）．点E的坐标为（t，t﹣2）；（均用含t的式子表示）（3）在（2）的条件下，当点P在线段OA上时，探究是否存在某一时刻，使DE＝OB？若存在，求出此时△ADE的面积；若不存在说明理由．解：（1）令y＝0，则x＝4，∴点A的坐标为（4，0），令x＝0，则y＝﹣2，∴点B的坐标为（0，﹣2），将A（4，0）代入y＝﹣x+b，得0＝﹣4+b，解得b＝4；（2）由（1）知，直线AC的表达式为y＝﹣x+4，∵点P（t，0），∵PD⊥x轴，∴D（t，﹣t+4），E（t，t﹣2），故答案为（t，﹣t+4），（t，t﹣2）；（3）存在t，使DE＝OB，理由如下：∵点P在线段OA上，∴0≤t≤4，由（2）知D（t，﹣t+4），E（t，t﹣2），∴DE＝﹣t+4﹣（t﹣2）＝﹣t+6，∵B（0，﹣2），∴OB＝2，∵DE＝OB，∴﹣t+6＝2，解得：t＝，∴AP＝4﹣t＝4﹣＝，＝DE•AP＝×2×＝．∴S△ADE20．如图，已知一次函数y1＝kx+b的图象与函数y2＝（x＞0）的图象交于A（6，﹣），B（，n）两点，与y轴交于点C．将直线AB沿y轴向上平移t个单位长度得到直线DE，DE与y轴交于点F．（1）求y1与y2的解析式；（2）观察图象，直接写出y1＜y2时x的取值范围；（3）连接AD，CD，若△ACD的面积为6，则t的值为2．解：（1）将点A（6，﹣）代入y2＝中，∴y2＝，∵B（，n）在y2＝中，可得n＝﹣6，∴B（，﹣6），将点A、B代入y1＝kx+b，∴，解得，∴y1＝x﹣；（2）∵一次函数与反比例函数交点为A（6，﹣），B（，﹣6），∴＜x＜6时，y1＜y2；（3）在y1＝x﹣中，令x＝0，则y＝﹣，∴C（0，﹣），∵直线AB沿y轴向上平移t个单位长度，∴直线DE的解析式为y＝x﹣+t，∴F点坐标为（0，﹣+t），过点F作GF⊥AB于点G，连接AF，直线AB与x轴交点为（，0），与y轴交点C（0，﹣），∴∠OCA＝45°，∴FG＝CG，∵FC＝t，∴FG＝t，∵A（6，﹣），C（0，﹣），∵AB∥DF，＝S△ACF，∴S△ACD∴×6×t＝6，∴t＝2，故答案为：2．21．如图，抛物线y＝ax2+bx与直线l交于点A（1，5）、B（6，0），点C是l上方的抛物线上的一动点，过C作CD⊥x轴于点D，交直线l于点E．连接AC、BC．（1）求抛物线的解析式；（2）设点C的横坐标为n，△的面积为S，求出S的最大值；（3）在抛物线上是否存在点P，使得△PAB是直角三角形，且始终满足AB边为直角边？若存在，求出所有符合条件的P的坐标；若不存在，简要说明理由．解：（1）∵抛物线y＝ax2+bx与直线l交于点A（1，5）、B（6，0），∴，解得，∴抛物线的解析式为y＝﹣x2+6x；（2）易求直线l的解析式为y＝﹣x+6．由题意，知C（n，﹣n2+6n），E（n，﹣n+6），∴EC＝（﹣n2+6n）﹣（﹣n+6），即EC＝﹣n2+7n﹣6．过A作AF⊥CD于F，则AF＝n﹣1，DB＝6﹣n，+S△BCE∴S＝S△ACE＝×EC×（n﹣1）+×EC×（6﹣n）＝×EC×5＝（﹣n2+7n﹣6），即S＝﹣n2+n﹣15，配方得S＝﹣（n﹣）2+．∵﹣＜0，＝；∴S有最大值，当n＝时，S最大值（3）在抛物线上存在点P，能够使得△PAB是直角三角形，且始终满足AB边为直角边．分两种情况：①当∠PBA＝90°时，∵∠ABO＝45°，∴过点B且垂直于AB y＝x﹣6，解方程组，得，，∵B（6，0），∴P1（﹣1，﹣7）；②当∠PAB＝90°时，∵过点A且垂直于AB的直线解析式为y＝x+4，解方程组，得，，∵A（1，5），∴P2（4，8）．综上所述，符合条件的P点坐标为P1（﹣1，﹣7），P2（4，8）．。

专题12 一次函数-面积问题函数的学习中，自然离不开点、线、面，如求点的坐标、直线、曲线解析式、图形的面积，并且点、线、面之间的相互转化，本专题以一次函数为背景下求多边形面积，即由点或线的条件下求图形的面积，反之，也可以由面积求点的坐标，由面积求直线或曲线的解析式等，本专题的面积问题的巩固，为后面学习函数综合题的面积问题有极大帮助！一、单选题1．（2020·广西博白·期末）如图，矩形ABCD 中，AB =4，BC =3，动点E 从B 点出发，沿B ﹣C ﹣D ﹣A 运动至A 点停止，设运动的路程为x ，△ABE 的面积为y ，则y 与x 的函数关系用图象表示正确的是（ ）A ．B ．C ．D ． 2．（2020·广西灵山·期末）一次函数24y x =-+的图象与x 轴、y 轴的交点分别为A B 、，则OAB ∆的面积是（ ）A ．12B ．1C ．2D ．43．（2020·广西大化·初二期末）若直线4y x b =-+与两坐标轴围成的三角形的面积是5，则b 的值为（ ）A ．±B ．±C ．D ．- 4．（2020·山东枣庄·初三其他）如图，一次函数y ＝2x +1的图象与坐标轴分别交于A ，B 两点，O 为坐标原点，则△AOB 的面积为（ ）A ．14B ．12C ．2D ．4二、填空题5 ．（2020·甘肃省庆阳市第五中学初二期末）已知直线8y kx =+与轴和轴所围成的三角形的面积是4，则k 的值是________．6．（2020·湖南隆回·初三二模）一次函数24y x =-的图象与x 轴，y 轴所围成的三角形面积S =__________．7．（2020·湖北曾都·初二期末）若直线y=kx+b （k≠0）的图象经过点（0，2），且与坐标轴所围成的三角形面积是2，则k 的值为_______8．（2020·长沙市南雅中学初二期末）函数 y=2x+6 的图象与 x 、y 轴分别交于 A 、B 两点，坐标系原点为 O ，求△ABO 的面积___________．9．（2020·湖南渌口·初二期末）已知一次函数y ＝kx +4（k ＜0）的图象与两坐标轴所围成的三角形的面积等于8，则k 的值为_____．10．（2019·山西初二期末）如图所示，点A （﹣3，4）在一次函数y ＝﹣3x +b 的图象上，该一次函数的图象与y 轴的交点为B ，那么△AOB 的面积为_____．三、解答题11．（2020·福建宁化·期中）已知直线l 的表达式为y=﹣x+8，与x 轴交于点B ，点P （x ，y ）在直线l 上，且x >0，y >0，点A 的坐标为（6，0）．（1）求出B 点的坐标；（2）设△OPA 的面积为S ，求S 与x 的函数关系式(并写出自变量的取值范围)．12.（2020·甘肃徽县·初二期末）如图，直线l 1的解析式为y ＝﹣x +2，l 1与x 轴交于点B ，直线l 2经过点D （0，5），与直线l 1交于点C （﹣1，m ），且与x 轴交于点A（1）求点C 的坐标及直线l 2的解析式；（2）求ABC 的面积．13．（2020·湖北下陆·初二期末）在平面直角坐标系中，原点为O ，已知一次函数的图象过点A （0，5），点B （-1，4）和点P （m ，n ）．（1）求这个一次函数的解析式；（2）当n =2时，求直线 AB ，直线 OP 与 x 轴围成的图形的面积；（3）当OAP △的面积等于OAB 的面积的2倍时，求n 的值．14．（2020·昆明市官渡区第一中学初二月考）已知一次函数22y x =--．（1）画出函数图象；（2）求图象与x 轴、y 轴的交点A 、B 的坐标; （3）求图象与坐标轴围成的图形的面积．15．（2018·安徽初二期末）如图，直线PA 是一次函数1y x =+的图象，直线PB 是一次函数24y x =-+的图象.（1）求A 、B 、P 三点坐标；（2）求PAB △的面积；（3）已知过P 点的直线把PAB △分成面积相等的两部分，求该直线解析式.16．（2019·山东初一期末）如图，已知一次函数y =−x +2的图像与y 轴交于点A ，一次函数y =kx +b 的图像过点B(0，4)，且与x 轴及y =−x +2的图像分别交于点C 、D ，D 点坐标为(−23，n). （1）求n 的值及一次函数y =kx +b 的解析式.（2）求四边形AOCD 的面积.17．（2019·内蒙古初二期中）如图，一次函数y=kx+b 的图象经过A 、B 两点，与x 轴交于点C ． （1）写出点A 、B 、C 的坐标；（2）求此一次函数的解析式；（3）求△AOC 的面积．18．（2019·内蒙古初三月考）一次函数CD ：y kx b =-+与一次函数AB ：22y kx b =+，都经过点B （-1,4）.（1）求两条直线的解析式；（2）求四边形ABDO 的面积.19．（2017·山东省济南兴济中学初二单元测试）两个一次函数的图象如图所示，（1）分别求出两个一次函数的解析式；（2）求出两个一次函数图象的交点C 坐标；（3）求这两条直线与y 轴围成△ABC 的面积．20．（2020·安徽初二期末）在平面直角坐标系xOy 中，ABC ∆如图所示，点()()()3,2,1,1,0,4A B C -.（1）求直线AB 的解析式；（2）求ABC ∆的面积；（3）一次函数32y ax a =++（a 为常数）.21．（2020·湖北房县·初二期末）如图1，直线l ：y ＝12x +2与x 轴交于点A ，与y 轴交于点B ．已知点C （﹣2，0）．。

小专题(十二) 一次函数与面积问题 类型1 由一次函数的图象求图形的面积 【例1】 如图，直线l 1的解析式为y ＝x ＋2，直线l 1和直线l 2相交于点A ，直线l 1与x 轴相交于点B，与y 轴相交于点D.直线l 2与x 轴相交于点C(4，0)，与y 轴相交于点E(0，4)．(1)求直线l 2的解析式． (2)求△ABC 的面积．【例2】 已知直线l 1：y 1＝x ＋2与直线l 2：y 2＝kx －1交于A 点，A 点纵坐标为1，且直线l 1与x 轴交于B 点，与y 轴交于D 点，直线l 2与y 轴交于C 点．(1)求直线l 2的解析式． (2)连接BC ，求S △ABC .1．如图，直线y ＝kx ＋b 交x 轴于点A(5，0)，交y 轴于点B ，直线y ＝2x －4交x 轴于点D ，与直线AB 相交于点C(3，2)．(1)点D 的坐标为 ． (2)求直线AB 的解析式． (3)四边形BODC 的面积为 ．当所求三角形的一边在坐标轴上时，直接利用三角形的面积公式计算三角形的面积．如图1，S △ABC ＝12|x C －x B |·|y A |.图1 图2 如图2，S △ABC ＝12|y C －y B |·|x A |.类型2由图形的面积为定值求点的坐标【例3】如图，在平面直角坐标系xOy中，已知一次函数y＝2x＋m与y＝－12x＋n的图象都经过点A(－2，0)，且分别与y轴交于点B和点C.(1)点B的坐标为，点C的坐标为．(2)设点D在直线y＝－12x＋n上，且在y轴右侧，当△ABD的面积为15时，求点D的坐标．【补充设问】在(2)的条件下，将“点D在y轴右侧”这个条件去掉，则点D的坐标为．2．如图，已知直线PA：y＝x＋1交y轴于点Q，直线PB：y＝－2x＋m.若四边形PQOB的面积为56，则m的值为．类型3 由图形间面积的数量关系求点的坐标【例4】如图，在平面直角坐标系xOy中，直线l的解析式为y＝2x－6，点A，B的坐标分别为(1，0)，(0，2)，直线AB与直线l相交于点P.(1)求直线AB的解析式．(2)求点P的坐标．(3)若直线l上存在一点C，使得△APC的面积是△APO的面积的2倍，求出点C的坐标．、【例5】如图，A(－2，0)，B(0，4)，C(5，3)，在y轴负半轴上是否存在点P，使S△PAB＝S△ABC？若存在，求点P的坐标；若不存在，说明理由．由图形的面积为定值求点的坐标的一般解题步骤是：(1)设出要求的点的坐标，一般用一个未知数表示；(2)用含有未知数的式子表示出已知图形的面积；(3)由已知图形的面积为定值列出关于未知数的方程；(4)解方程求出未知数的值，即可得到点的坐标．温馨提示：在解决一次函数与面积问题时，注意分类讨论思想的运用．3．如图，直线y＝－2x－4与坐标轴交于A，B两点，点P为直线y＝2x上一点，PA交y轴于点M，且S△ABM＝2S△BPM，则点P的坐标为．【例1】解：(1)设直线l2的解析式为y＝kx＋b(k≠0)．把点C(4，0)，点E(0，4)代入，得⎩⎪⎨⎪⎧4k＋b＝0，b＝4，解得⎩⎪⎨⎪⎧k＝－1，b＝4.∴直线l2的解析式为y＝－x＋4.(2)对于y＝x＋2，令y＝0，则x＝－2，∴B(－2，0)．∵C(4，0)，∴BC＝6.联立⎩⎪⎨⎪⎧y＝－x＋4，y＝x＋2，解得⎩⎪⎨⎪⎧x＝1，y＝3.∴A(1，3)．∴S△ABC＝12×3×6＝9.【例2】解：(1)点A在y1＝x＋2上，A点纵坐标为1，∴x＋2＝1，解得x＝－1.∴点A的坐标为(－1，1)．∵点A在y2＝kx－1上，∴－k－1＝1，解得k＝－2.∴直线l2的解析式为y2＝－2x－1.(2)∵直线l1与x轴交于点B，∴x＋2＝0，解得x＝－2，即OB＝2.∵直线l2与y轴交于点C，∴点C的坐标为(0，－1)，即OC＝1.∵直线l1与y轴交于点D，∴点D的坐标为(0，2)，即OD＝2.∴DC＝2＋1＝3.∴S△ABC＝S△BCD－S△ACD＝12×3×2－12×3×1＝32.1．(1)点D的坐标为(2，0)．(2)把点A(5，0)，C(3，2)代入y＝kx＋b中，得⎩⎪⎨⎪⎧5k＋b＝0，3k＋b＝2，解得⎩⎪⎨⎪⎧k＝－1，b＝5.∴直线AB的解析式为y＝－x＋5.(3)9.5．【例3】(1)点B的坐标为(0，4)，点C的坐标为(0，－1)．(2)解：过点D作DE⊥BC于点E.易得直线AC的解析式为y＝－12x－1.∵点D在直线y＝－12x－1上，∴设点D的坐标为(a，－12a－1)．当△ABD的面积为15时，即S△ABC＋S△BCD＝15，∴12AO·BC＋12DE·BC＝15.∴12×2×5＋12|x D|×5＝15.∴|x D|＝4.∴a＝4.∴－12a－1＝－3.∴D(4，－3)．【补充设问】(－8，3)或(4，－3)．2．2．【例4】解：(1)设直线AB 的解析式为y ＝kx ＋b. 由点A ，B 的坐标分别为(1，0)，(0，2)，可知⎩⎪⎨⎪⎧k ＋b ＝0，b ＝2，解得⎩⎪⎨⎪⎧k ＝－2，b ＝2. ∴直线AB 的解析式为y ＝－2x ＋2.(2)由题意，得⎩⎪⎨⎪⎧y ＝－2x ＋2，y ＝2x －6，解得⎩⎪⎨⎪⎧x ＝2，y ＝－2.∴点P 的坐标为(2，－2)．(3)直线l 的解析式为y ＝2x －6，令y ＝0，则x ＝3， ∴直线l 与x 轴交于点(3，0)． 设点C 的坐标为(x ，2x －6)，∵△APC 的面积是△APO 的面积的2倍， ∴12×(3－1)×|2x －6－(－2)|＝2×12×1×2， 解得x ＝1或3. ∴C(3，0)或(1，－4)． 【例5】解：在y 轴负半轴上存在点P ，使S △PAB ＝S △ABC .理由： 过点C 作CD ∥AB ，CD 与y 轴的负半轴交于点P ，则△PAB 与△ABC 同底等高，∴S △PAB ＝S △ABC .设直线AB 的解析式为y ＝kx ＋b ，则⎩⎪⎨⎪⎧－2k ＋b ＝0，b ＝4，解得⎩⎪⎨⎪⎧k ＝2，b ＝4. ∴直线AB 的解析式为y ＝2x ＋4.∵CD ∥AB ，∴设直线CD 的解析式为y ＝2x ＋m. 又∵C(5，3)，∴3＝2×5＋m.∴m ＝－7. ∴直线CD 的解析式为y ＝2x －7. 当x ＝0时，y ＝－7. ∴P(0，－7)．3．(1，2)．。

一次函數面積問題1、如图，一次函数的图像与x轴交于点B（-6，0），交正比例函数的图像于点A，点A的横坐标为-4，△ABC的面积为15，求直线OA的解析式。

2、直线y=x+3的图像与x轴、y轴分别交于A、B两点，直线a经过原点与线段AB交于C，把△ABO的面积分为2：1的两部分，求直线a的函数解析式。

3、直线PA是一次函数y=x+n的图像，直线PB是一次函数y=-2x+m（m>n>0）的图像，（1）用m、n表示A、B、P的坐标（2）四边形PQOB的面积是，AB=2，求点P的坐标4、△AOB的顶点O（0，0）、A（2，1）、B（10，1），直线CD⊥x轴且△AOB面积二等分，若D（m，0），求m的值5、点B在直线y=-x+1上，且点B在第四象限，点A（2，0）、O（0，0），△ABO 的面积为2，求点B的坐标。

6、直线y=-x+1与x轴y轴分别交点A、B，以线段AB为直角边在第一象限内作等腰直角△ABC， BAC=90°，点P（a，）在第二象限，△ABP的面积与△A BC 面积相等，求a的值.7、如图，已知两直线y=0.5x+2.5和y=-x+1分别与x轴交于A、B两点，这两直线的交点为P（1）求点P的坐标（2）求△PAB的面积8、已知直线y=ax+b（b>0）与y轴交于点N，与x轴交于点A且与直线y=kx交于点M（2，3），如图它们与y轴围成的△MON的面积为5，求（1）这两条直线的函数关系式（2）它们与x轴围成的三角形面积9、已知两条直线y=2x-3和y=5-x（1）求出它们的交点A的坐标（2）求出这两条直线与x轴围成的三角形的面积10、已知直线y=x+3的图像与x轴、y轴交于A、B两点，直线l经过原点，与线段AB交于点C，把△AOB的面积分为2：1的两部分，求直线l的解析式。

11、已知直线y=2x+3与直线y=-2x-1与y轴分别交于点A、B（1）求两直线交点C的坐标（2）求△ABC的面积（3）在直线BC上能否找到点P，使得△APC的面积為6，求出点P的坐标，若不能请说明理由。

专题33 一次函数与面积结合1．已知O为坐标原点，过点A（1，2）的直线y=kx+b与x轴交于点B，且S△ABO=4，求k的值．2．已知直线y=﹣3x+6与x轴交于A点，与y轴交于B点．（1）求A，B两点的坐标；（2）求直线y=﹣3x+6与坐标轴围成的三角形的面积．【答案】（1）A（2，0），B（0，6）；（2）6．【详解】试题分析：（1）分别令x=0、y=0求解即可得到与坐标轴的交点；（2）根据三角形的面积公式列式计算即可得解．解：（1）当x=0时，y=﹣3x+6=6，当y=0时，0=﹣3x+6，x=2．所以A（2，0），B（0，6）；（2）直线与坐标轴围成的三角形的面积=S△ABO=×2×6=6．考点：一次函数图象上点的坐标特征．3．已知动点P以每秒2 cm的速度沿图(1)的边框按从B⇒C⇒D⇒E⇒F⇒A的路径移动，相应的△ABP 的面积S与时间t之间的关系如图(2)中的图象表示．若AB=6 cm，试回答下列问题∶（1）图（1）中的BC长是多少？（2）图（2）中的a是多少？（3）图（1）中的图形面积是多少？（4）图（2）中的b是多少？4．如图，已知一次函数y kx b=+的图象经过A（－2，－1），B（1，3）两点，并且交x轴于点C，交y轴于点D．(1)求该一次函数的解析式；(2)求△AOB的面积．5．如图，已知一次函数与正比例函数图像相交于点A ，与轴交于点B．（1）求出m、n的值；（2）求出的面积．代入可求得点的坐标代入与轴的交点即可求得的）在函数的图象上，∴）也在函数的图象上，∴解得：∵与轴交于点令，则∴6．如图，一次函数y=kx+b的图象为直线l1，经过A（0，4）和D（4，0）两点；一次函数y=x+1的图象为直线l2，与x轴交于点C；两直线l1，l2相交于点B．（1）求k、b的值；（2）求点B的坐标；（3）求△ABC的面积．7．如图，一条直线经过点A（5，0），B（1，4）．（1）求直线AB 的解析式；（2）若直线2y x b =+与直线AB 相交于点C （3，a ），与x 轴相交于点D ，求a 、b 的值以及△ACD 的面积．8．在平面直角坐标系中，O 为原点，点()4,0A ，()2,0B -，()3,2C -，点D 是y 轴正半轴上的动点，连接CD 交x 轴于点E ．(1)如图①，若点D 的坐标为()0,2，求ACD V 的面积；(2)如图②，若12ABD ABC S S =V V ，求点D 的坐标．(3)如图③，若BDE ACE S S =△△，请直接写出点D 的坐标．9．如图，在直角坐标系中，已知直线332y x =-+与x 轴相交于点A 与y 轴交于点B ．(1)A 、B 两点坐标分别为________，________；(2)点(3,0)M 在x 轴上，若点P 是直线AB 上的一个动点，当PBM AOB S S =△△时，求点P 的坐标．12PBM PAM ABM S S S =+=△△△∴3P y =，∵点P 在x 轴下方，∴3P y =-，当=3y -时，代入32y x =-10．已知，一次函数(2)4y t x =-+与(1)2y t x =-+-的图像相交于点P ，分别与y 轴相交于点A 、B ．其中t 为常数，2t ¹且1t ¹-．(1)求线段AB的长；(2)试探索ABPV的面积是否是一个定值？若是，求出ABPV的面积；若不是，请说明理由；(3)当t为何值时，ABPV周长的最小值．V的周长最小，并求出ABP【点睛】本题考查了一次函数综合，最短路径问题，勾股定理，解题的关键是注意（3）中分析出要ABP+最小．V的周长最小，则要AP BP11．在平面直角坐标系中，原点为O，点P（m，n），已知一次函数的图象过点A（0，5），点B （﹣1，4）．（1）求这个一次函数的解析式；（2）当n＝0时，求PA+PB距离最短时m的值．（3）当点P经过直线AB时，且△OAP的面积等于△OAB的面积的2倍时，求n的值．∵点A的坐标为（0，5），【点睛】本题考查了轴对称中最短路线问题以及待定系数法求一次函数解析式，解题的关键是：（1）利用待定系数法求出一次函数表达式；（2）找出PA +PB 取最小值时点P 的位置；（3）列出关于m 的方程．12．在平面直角坐标系中，原点为O ，已知一次函数的图象过点A （0，5），点B （-1，4）和点P （m ，n ）．（1）求这个一次函数的解析式；（2）当n =2时，求直线 AB ，直线 OP 与 x 轴围成的图形的面积；（3）当OAP △的面积等于OAB V 的面积的2倍时，求n 的值．当x=-2时，y=x+5=3，此时P（-2，3）；综上所述，n的值为7或3．【点睛】本题考查了待定系数法求一次函数解析式：考查了直线与坐标轴围成的图形的面积，掌握以上知识是解题的关键．13．如图，已知直线y=1x+2交x轴于点A，交y轴于点B，2（1）求A，B两点的坐标；S△AOB时，求直线OC的解析式．（2）已知点C是线段AB上的一点，当S△AOC= 1214．如图1，已知直线y＝2x+2与y轴，x轴分别交于A，B两点，以B为直角顶点在第二象限作等腰Rt△ABC（1）求点C的坐标，并求出直线AC的关系式；（2）如图2，直线CB交y轴于E，在直线CB上取一点D，连接AD，若AD＝AC，求证：BE＝DE．（3）如图3，在（1）的条件下，直线AC交x轴于点M，P（﹣52，k）是线段BC上一点，在x轴上是否存在一点N，使△BPN面积等于△BCM面积的一半？若存在，请求出点N的坐标；若不存在，请说明理由．∵∠HCB+∠CBH＝90°，∠CBH+∴∠ABO＝∠BCH，∵∠CHB＝∠BOA＝90°，BC＝BA ∴△CHB≌△BOA（AAS），∴BH＝OA＝2，CH＝OB，则点∵AC=AD，AB⊥CB，∴BC=BD，∵∠CBH=∠FBD，∴△BCH≌△BDF，∴BF=BH，15．如图，在平面直角坐标系中，过点B（4，0）的直线AB与直线OA相交于点A（3，1），动点M 在线段OA和射线AC上运动．（1）求直线AB的解析式；（2）直线AB交y轴于点C，求△OAC的面积；（3）当△OAC的面积是△OMC面积的3倍时，求出这时点M的坐标．16．在平面直角坐标系中，O 为原点，已知直线132y x =+与x 轴交于点A ，与y 轴交于点B ，点C 与点A 关于y 轴对称，如图①．（1）点A 的坐标为________，点B 的坐标为________，点C 的坐标为________，直线BC 的解析式为________．（2）点M 是x 轴上的一个动点（点M 不与点O 重合），过点M 作x 轴的垂线，交直线AB 于点P ．交直线BC 于点Q （图②）．①如图②，当点M 在x 轴的正半轴上时，若PQB △的面积为94，求点M 的坐标；②BM P17．如图，直线1l的解析表达式为：y=－3x＋3，且1l与x轴交于点D，直线2l经过点A，B，直线1l，l交于点C．2（1）求点D的坐标；（2）求直线2l的解析表达式；（3）求△ADC的面积；（4）在直线2l上存在一点P，使得△ADP的面积是△ADC面积的2倍，请直接写出点P的坐标．∵y=1.5x-6，y=6，∴1.5x-6=6，解得x=8，∴P1（8，6）．∵y=1.5x-6，y=-6，∴1.5x-6=-6，解得x=0，∴P2（0，-6）综上所述，P1（8，6）或P2（0，-6）．【点睛】本题考查的是一次函数的性质，与坐标轴的交点坐标，两个一次函数图象的交点，三角形面积的计算等有关知识，难度中等．。