下载文档原格式
天体运动知识点归类解析【问题一】行星运动简史1、两种学说（1）地心说:地球是宇宙的中心，而且是静止不动的，太阳、月亮以及其他行星都绕地球运动。
支持者托勒密。
（2）.日心说：太阳是宇宙的中心，而且是静止不动的，地球和其他行星都绕太阳运动。
（3）.两种学说的局限性都把天体的运动看的很神圣，认为天体的运动必然是最完美，最和谐的圆周运动，而和丹麦天文学家第谷的观测数据不符。
2、开普勒三大定律开普勒1596年出版《宇宙的神秘》一书受到第谷的赏识，应邀到布拉格附近的天文台做研究工作。
1600年，到布拉格成为第谷的助手。
次年第谷去世，开普勒成为第谷事业的继承人。
第谷去世后开普勒用很长时间对第谷遗留下来的观测资料进行了整理与分析他在分析火星的公转时发现，无论用哥白尼还是托勒密或是第谷的计算方法得到的结果都与第谷的观测数据不吻合。
他坚信观测的结果，于是他想到火星可能不是按照人们认为的匀速圆周运动他改用不同现状的几何曲线来表示火星的运动轨迹，终于发现了火星绕太阳沿椭圆轨道运行的事实。
并将老师第谷的数据结果归纳出三条著名定律。
第一定律：所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上。
第二定律：对任意一个行星来说，它与太阳的连线在相等时间内扫过的面积相等。
如图某行星沿椭圆轨道运行，远日点离太阳的距离为a，近日点离太阳的距离为b，过远日点时行星的速率为a v，v过近日点时的速率为b由开普勒第二定律，太阳和行星的连线在相等的时间内扫过相等的面积，取足够短的时间t ，则有：所以b a v v a b = ②②式得出一个推论：行星运动的速率与它距离成反比，也就是我们熟知的近日点快远日点慢的结论。
②式也当之无愧的作为第二定律的数学表达式。
第三定律：所有行星的轨道半长轴的三次方跟它的公转周期平方的比值都相等。
用a 表示半长轴，T 表示周期，第三定律的数学表达式为k T a =23，k 与中心天体的质量有关即k 是中心天体质量的函数)(23M k T a =①。
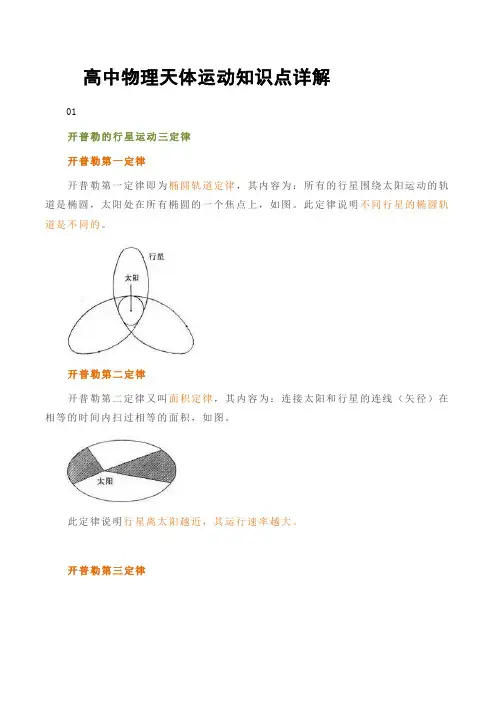
高中物理天体运动知识点详解01开普勒的行星运动三定律开普勒第一定律开普勒第一定律即为椭圆轨道定律，其内容为：所有的行星围绕太阳运动的轨道是椭圆，太阳处在所有椭圆的一个焦点上，如图。
此定律说明不同行星的椭圆轨道是不同的。
开普勒第二定律开普勒第二定律又叫面积定律，其内容为：连接太阳和行星的连线（矢径）在相等的时间内扫过相等的面积，如图。
此定律说明行星离太阳越近，其运行速率越大。
开普勒第三定律开普勒第三定律即为周期定律，其内容为：行星轨道半长轴的三次方与公转周期的二次方的比值是一个常数。
即，其中r代表椭圆轨道的半长轴，T代表行星运动的公转周期，k是一个与行星无关的常量。
对的认识：在图中，半长轴是AB间距的一半，不要认为a等于太阳到A 点的距离；T是公转周期，不要误认为是自转周期，如地球的公转周期是一年，不是一天。
说明（1）在以后的计算问题中，我们都把行星的轨道近似为圆，把卫星的运行轨道也近似为圆，这样就使问题变得简单，计算结果与实际情况也相差不大。
（2）在上述情况下，的表达式中，a就是圆的半径R，利用的结论解决某些问题很方便。
注意①比例系数k是一个与行星无关的常量，但不是恒量，在不同的星系中，k值不相同。
②在太阳系中，不同行星的半长轴都不相同，故其公转周期也不相等。
③卫星绕地球转动、地球绕太阳转动遵循相同的运动规律。
易错点在认识行星做椭圆运动时的向心力大小及速度大小时易错，行星的运动符合能量守恒定律，它们离太阳近时半径小，速度大，向心力也大；离太阳远时半径大，速度小，向心力也小，另一个易错点是找椭圆的半长轴时易错，许多同学在初学时，往往将2倍的半长轴代入题中进行运算。
忽略点本节中的行星运动的轨道为椭圆，是曲线运动，行星在轨道上任一点的速度方向沿该点的切线方向，速度方向易忽略，如：有部分同学认为行星的速度方向垂直于行星与太阳的连线，这种认识是错误的，是将行星的运动视为圆周运动，而实质上其轨道为椭圆。
02卡文迪许扭称实验卡文迪许设计了扭称实验来测量万有引力常量，下图是扭称实验的原理图。
三体运动方程引言三体运动是天体力学中的一个经典问题，指的是三个质点之间相互作用的运动。
这个问题在理论物理和计算科学领域具有重要的意义，因为它涉及到了非线性动力学、混沌理论和数值计算等多个方面。
本文将详细探讨三体运动的基本方程、运动规律以及数值求解方法。
三体运动的基本方程三体运动的基本方程可以通过牛顿第二定律推导得到。
假设三个质点的质量分别为m1、m2和m3，位置矢量分别为r1、r2和r3，根据牛顿第二定律，可以得到以下方程：1.m1 * d2r1/dt2 = G * (m2 * (r2 - r1) / |r2 - r1|^3 + m3 * (r3 - r1) /|r3 - r1|^3)2.m2 * d2r2/dt2 = G * (m1 * (r1 - r2) / |r1 - r2|^3 + m3 * (r3 - r2) /|r3 - r2|^3)3.m3 * d2r3/dt2 = G * (m1 * (r1 - r3) / |r1 - r3|^3 + m2 * (r2 - r3) /|r2 - r3|^3)其中，G为引力常数。
这三个方程描述了三个质点之间的相互作用，是三体运动的基本方程。
运动规律三体运动问题由于其非线性的本质，导致了一系列复杂的运动规律。
根据三体运动的性质，可以将其分为以下几种情况：稳定运动在某些特殊情况下，三体系统可以呈现稳定运动。
例如，当三个质点的质量相等且初始位置形成等边三角形时，它们将以恒定的角速度绕质心旋转。
这种情况下，三体系统的运动是稳定的。
周期性运动在一些特殊的初始条件下，三体系统的运动可以是周期性的。
例如，当两个质点的质量远大于第三个质点的质量时，第三个质点将围绕着前两个质点做椭圆轨道运动。
这种情况下，三体系统的运动是周期性的。
混沌运动大多数情况下，三体系统的运动是混沌的。
混沌运动指的是系统对初始条件极其敏感，微小的初始误差可能导致完全不同的运动轨迹。
三体问题的混沌性质使其成为天体力学中的一个重要研究课题。
N体问题的三百年天体运行的数学原理------N体问题的三百年1。
N体问题的起源和早期发展(希尔伯特-----开普勒-----牛顿-----伯努利)在二十世纪的第一次数学家大会(1900年)上，二十世纪伟大的数学家希尔伯特(David Hilbert)在他著名的演讲中提出了23个困难的数学问题，这些数学问题在二十世纪的数学发展中起了非常重要的作用。
在同一演讲中，希尔伯特也提出了他所认为的完美的数学问题的准则：问题既能被简明清楚的表达出来，然而问题的解决又是如此的困难以至于必须要有全新的思想方法才能够实现。
为了说明他的观点，希尔伯特举了两个最典型的例子：第一个是费尔马(Pierre de Fermat)猜想，即代数方程 xn+yn=zn 在n大于2时是没有整数解的；第二个就是我们这篇文章所要介绍的N体问题的特例------三体问题。
(参看[4]) 值得一提的是，尽管这两个问题在当时还没有被解决，希尔伯特并没有把他们列进他的问题清单。
但是在整整一百年后回顾，这两个问题对于二十世纪数学的整体发展所起的作用恐怕要比希尔伯特提出的23个问题中任何一个都大。
费尔马猜想经过全世界几代数学家几百年的努力，终于在1994年被美国普林斯顿大学(Princeton University)威尔斯(Andrew Wiles)最终解决，这被公认为二十世纪最伟大的数学进展之一，因为除了解决一个重要的问题，更重要的是在解决问题的过程中好几种全新的数学思想诞生了，难怪在问题解决后也有人遗憾地感叹一只会生金蛋的母鸡被杀死了。
正象希尔伯特指出的，费尔马猜想的产生来源于纯粹的数学思维，而N体问题则来源于天体力学，对它的认识也有助于人类对自然界最简单的基本现象的理解。
N体问题可以用一句话写出来：在三维空间中给定N个质点，如果在它们之间只有万有引力的作用，那么在给定它们的初始位置和速度的条件下，它们会怎样在空间中运动。
最简单的例子就是太阳系中太阳，地球和月球的运动。
什么是三体问题？三体问题是指在牛顿力学的框架下，研究三个星体相互之间的引力作用，寻找它们运动轨迹的问题。
这个问题看似简单，但却具有极高的复杂性，直到现在仍未找到通解。
下面，我们将就三体问题展开科普。
一、三体问题的基础知识1.1 牛顿的万有引力定律三体问题的研究基础是牛顿的万有引力定律。
该定律是指两个质点之间的引力与它们质量的乘积成正比，与它们的距离平方成反比。
即F=G(m1m2/r^2)，其中F为引力，G为万有引力常数，m1和m2为两个质量，r为它们之间的距离。
1.2 三体运动的基本形式在三体问题中，三个质点的运动是相互关联的。
它们在互相之间的作用下，各自的运动状态都会发生变化。
根据这种变化的方式，三体运动可以分为封闭运动、开放运动和混沌运动。
1.3 研究三体问题的工具在牛顿力学中，通过建立方程组来求解三体问题。
通常需要借助于数值计算，在计算机的帮助下才能得到比较准确的结果。
此外，为了更好地研究三体问题，人们提出了许多方法，如雅可比坐标系、哈密顿力学和希尔伯特空间等。
二、三体问题的研究历程2.1 初步解决问题的尝试早在17世纪，牛顿便开始了对于三体问题的研究。
他发现，当星体的质量很小时，可以得到比较精确的解。
而当质量增大时，方程就变得复杂起来。
因此，人们开始寻找一些特殊的情况，如相等质量的星体、等边三角形的星体分布等。
2.2 深入研究与新的认识随着科技的发展，人们对于三体问题的理解逐渐深入。
在20世纪初期，有人提出了一个重要的概念——“好的起始条件”。
即在三体运动开始时，如果星体的位置和速度能够得到一定的控制和调整，就有可能获得可解的结果。
此外，二十世纪六、七十年代，科学家们通过计算机对三体问题进行了更深入的研究。
在这一过程中，人们发现了许多令人震惊的现象，如棒球效应、克莱因瓶、麻球等。
2.3 从三体问题到宇宙的研究三体问题的研究不仅仅是为了解决这一个问题本身，更是建立在对宇宙的探索之上。
随着人类的探索不断深入，我们意识到我们所处的宇宙是极其复杂的，三体问题的研究将会给我们更好地理解宇宙带来帮助。
N体问题的三百年作者: dsds 发布日期: 2004-12-07 查看数: 4647 出自: /portal天体运行的数学原理------N体问题的三百年1。
N体问题的起源和早期发展(希尔伯特-----开普勒-----牛顿-----伯努利)在二十世纪的第一次数学家大会(1900年)上，二十世纪伟大的数学家希尔伯特(David Hilbert)在他著名的演讲中提出了23个困难的数学问题，这些数学问题在二十世纪的数学发展中起了非常重要的作用。
在同一演讲中，希尔伯特也提出了他所认为的完美的数学问题的准则：问题既能被简明清楚的表达出来，然而问题的解决又是如此的困难以至于必须要有全新的思想方法才能够实现。
为了说明他的观点，希尔伯特举了两个最典型的例子：第一个是费尔马(Pierre de Fermat)猜想，即代数方程xn+yn=zn 在n大于2时是没有整数解的；第二个就是我们这篇文章所要介绍的N体问题的特例------三体问题。
(参看[4]) 值得一提的是，尽管这两个问题在当时还没有被解决，希尔伯特并没有把他们列进他的问题清单。
但是在整整一百年后回顾，这两个问题对于二十世纪数学的整体发展所起的作用恐怕要比希尔伯特提出的23个问题中任何一个都大。
费尔马猜想经过全世界几代数学家几百年的努力，终于在1994年被美国普林斯顿大学(Princeton University)威尔斯(Andrew Wiles)最终解决，这被公认为二十世纪最伟大的数学进展之一，因为除了解决一个重要的问题，更重要的是在解决问题的过程中好几种全新的数学思想诞生了，难怪在问题解决后也有人遗憾地感叹一只会生金蛋的母鸡被杀死了。
正象希尔伯特指出的，费尔马猜想的产生来源于纯粹的数学思维，而N体问题则来源于天体力学，对它的认识也有助于人类对自然界最简单的基本现象的理解。
N体问题可以用一句话写出来：在三维空间中给定N个质点，如果在它们之间只有万有引力的作用，那么在给定它们的初始位置和速度的条件下，它们会怎样在空间中运动。
天体运行的数学原理------N体问题的三百年1。
N体问题的起源和早期发展(希尔伯特-----开普勒-----牛顿-----伯努利)在二十世纪的第一次数学家大会(1900年)上，二十世纪伟大的数学家希尔伯特(David Hilbert)在他著名的演讲中提出了23个困难的数学问题，这些数学问题在二十世纪的数学发展中起了非常重要的作用。
在同一演讲中，希尔伯特也提出了他所认为的完美的数学问题的准则：问题既能被简明清楚的表达出来，然而问题的解决又是如此的困难以至于必须要有全新的思想方法才能够实现。
为了说明他的观点，希尔伯特举了两个最典型的例子：第一个是费尔马(Pierre de Fermat)猜想，即代数方程x^n+y^n=z^n 在n大于2时是没有整数解的；第二个就是我们这篇文章所要介绍的N体问题的特例------三体问题。
(参看[4]) 值得一提的是，尽管这两个问题在当时还没有被解决，希尔伯特并没有把他们列进他的问题清单。
但是在整整一百年后回顾，这两个问题对于二十世纪数学的整体发展所起的作用恐怕要比希尔伯特提出的23个问题中任何一个都大。
费尔马猜想经过全世界几代数学家几百年的努力，终于在1994年被美国普林斯顿大学(Princeton University)威尔斯(Andrew Wiles)最终解决，这被公认为二十世纪最伟大的数学进展之一，因为除了解决一个重要的问题，更重要的是在解决问题的过程中好几种全新的数学思想诞生了，难怪在问题解决后也有人遗憾地感叹一只会生金蛋的母鸡被杀死了。
正象希尔伯特指出的，费尔马猜想的产生来源于纯粹的数学思维，而N体问题则来源于天体力学，对它的认识也有助于人类对自然界最简单的基本现象的理解。
N体问题可以用一句话写出来：在三维空间中给定N个质点，如果在它们之间只有万有引力的作用，那么在给定它们的初始位置和速度的条件下，它们会怎样在空间中运动。
最简单的例子就是太阳系中太阳，地球和月球的运动。
在浩瀚的宇宙中，星球的大小可以忽略不及，所以我们可以把它们看成质点。
如果不计太阳系其他星球的影响，那么它们的运动就只是在引力的作用下产生的，所以我们就可以把它们的运动看成一个三体问题。
我们知道地球和月球都在进行一种周期性运动，这样我们才有了年，月和日的概念。
所以大家不难想象周期运动可能是三体问题的一种解。
然而对N体问题的全面认识就不是那么简单了，数学家几百年以来的研究证明各种千奇百怪的运动都有可能在N体问题中出现。
等到看完这篇短文，也许你就会庆幸这些奇怪的运动轨道都没有出现在我们的星球身上，否则你就不能在这里舒舒服服地看杂志啦。
初通高中物理和大学微积分的读者都不难推出三体问题的数学方程。
事实上，根据牛顿(Issac Newton)万有引力定理和牛顿第二定律，我们可以得到\begin{equation}&m_1\frac{d^2 q_{1i}}{dt^2}= k m_1 m_2 \frac{q_{2i}-q_{1i}}{r^{3}_{12}}+km_1 m_3 \frac{q_{3i}-q_{1i}}{r^{3}_{13}}\\&m_2 \frac{d^2 q_{2i}}{dt^2}= k m_2 m_1 \frac{q_{1i}-q_{2i}}{r^{3}_{12}}+km_2 m_3 \frac{q_{3i}-q_{2i}}{r^{3}_{23}}\\&m_3 \frac{d^2 q_{3i}}{dt^2}= k m_3 m_1 \frac{q_{1i}-q_{3i}}{r^{3}_{13}}+km_3 m_2 \frac{q_{32i}-q_{3i}}{r^{3}_{23}}, \;\; (i=1,2,3),\end{split}\end{equation}其中$m_i$ 是质点的质量，$k$ 是万有引力常数，$r_{ij}$ 是两个质点$m_i$ 和$m_j$之间的距离，而$(q_{i1},q_{i2},q_{i3})$ 则是质点$m_i$ 的空间坐标。
所以三体问题在数学上就是这样九个方程的二阶常微分方程组再加上相应的初始条件。
(事实上根据方程组本身的对称性和内在的物理原理，方程可被简化以减少变量个数)。
而N体问题的方程也是类似的一个$N^2$ 个方程的二阶常微分方程组。
作者：湍流2006-7-27 00:16 回复此发言--------------------------------------------------------------------------------2 【转】科学史上的三体问题当$N=1$ 时，单体问题是个平凡的方程。
单个质点的运动轨迹只能是直线匀速运动。
当$N=2$ 的时候(二体问题)，问题就不那么简单了。
但是方程组仍然可以化简成一个不太难解的方程，任何优秀的理科大学生大概都能轻易解出来。
简单来说这时两个质点的相对位置始终在一个圆锥曲线上，也就是说如果我们站在其中一个质点上看另一个质点，那么另一个质点的轨道一定是个椭圆，抛物线，双曲线的一支或者直线。
二体问题又叫开普勒(Johannes Kepler)问题，它是在1710年被瑞士数学家约翰伯努利(Johann Bernoulli) 首先解决的。
N体问题的提出大概可以追溯到上千年前，但是这一问题的第一个完整的数学描述(象使用上面这样的微分方程)是出现在牛顿的“自然哲学的数学原理”(Philosophiae Naturalis Prinicipia Mathematica，1687年出版)一书中。
在他的著作中，牛顿成功地运用微积分证明了开普勒的天文学三大定律，但是奇怪的是他的书里并没有给出二体问题的解，尽管这两者是紧密相关的，而且现在的人们还是相信牛顿当时完全有能力自己给出二体问题的解。
http://74.54.200.37/bbsqydz/forumdisplay.php?fid=128###的二百年里，被十八和十九世纪几乎所有著名的数学家都尝试过，但是问题的进展是微乎其微的。
尽管在失败的尝试中微分方程的理论被不断地发展成为一门更成熟的数学分支，但是对于这些发展的源头-----N体问题，人们还是知道的太少了。
终于在十九世纪末期，也就是希尔伯特做他的著名演讲前几年，人们期待的重大突破出现了。
2。
三体问题和瑞典国王的奖金(奥斯卡国王-----米塔格莱夫勒-----庞加莱)1885年，在刚创刊不久的瑞典数学杂志Acta Mathematica的第七卷上出现了一则引人注意的通告：为了庆祝瑞典和挪威国王奥斯卡二世在1889年的六十岁生日，Acta Mathematica将举办一次数学问题比赛，悬赏2500克郎和一块金牌。
而比赛的题目有四个，其中第一个就是找到N体问题的所有解。
参加比赛的各国数学家必须在1888年的6月1日前把他们的参赛论文寄给杂志的创办人和主编，著名的瑞典数学家米塔格莱夫勒(GostaMittag-Leffler)。
所有论文将被匿名地被一个国际委员会评判以决出优胜者，然后优胜者的论文将发表在Acta Mathematica上。
这个委员会由三个当时赫赫有名的数学家组成：德国的维尔斯特拉斯(Karl Weierstrass)，法国的赫密特(Charles Hermite)和米塔格莱夫勒本人组成。
从现代的观点来看，这样的比赛也许有“抄作”和给新杂志做广告的嫌疑。
(事实上当时就有一些数学家这样批评这种比赛，象德国的克隆奈克(Leopold Kronecker))。
但是从历史上看，米塔格莱夫勒和奥斯卡二世的动机是好的，是为了推动科学的发展。
奥斯卡二世本人在大学中数学就学得很好，他和许多当时著名的数学家，象维尔斯特拉斯，科瓦列夫斯卡雅(Sonya Kovalevskaya)等都有亲密的关系。
而米塔格莱夫勒更是雄心勃勃，想把这样的比赛每四年举行一次。
可惜这个设想没有实现，比赛只举办了一次就夭折了，否则的话也许今天数学的最大奖不是菲尔兹(John Charles Fields)奖http://70.86.178.187而是奥斯卡奖了(那样后来美国的电影奖大概也要考虑换个名字了)。
让我们回到比赛本身。
这次比赛在当时轰动一时，虽然奖金不高，这种崇高的荣誉是当时罕见的，要知道瑞典更有名的“炸药奖”诺贝尔(Alfred Bernhard Nobel)奖是在几年后的1896年才开始评选的。
但是由于问题的困难程度，大多数一开始跃跃欲试的数学家后来都知难而退，最后只有四五个数学家真正交了他们的答卷。
而优胜者也并不难选出，虽然还是没有人能完整地解决任何一个问题，但是所有评委一致认为其中一份答卷对于N体问题的解决做出了关键的贡献，应该把奖颁给这位数学家。
这位获胜者就是作者：湍流2006-7-27 00:16 回复此发言--------------------------------------------------------------------------------3 【转】科学史上的三体问题法国数学家，物理学家庞加莱(Jules Henri Poincar\'{e})。
庞加莱在现代数学历史上占有举足轻重的地位，他曾被称为现代数学的两个奠基人之一(另一个是黎曼(Bernhard Riemann))，也有人称他为历史上精通当时所有数学的最后两个人之一(另一个就是希尔伯特))。
而1885年的庞加莱只有31岁，虽然已初露锋芒，但还是一位希望能够一举成名的年轻数学家，所以这次比赛是个大好的机会，这也迫使他先放下手上其他的工作，集中精力投入到天体力学和N体问题的研究中。
庞加莱获奖的论文“关于三体问题的动态方程”(Sur le probl\`{e}me des trois corps et les \'{e}quations de la dynamique) 最后在1890年在Acta Mathematica上发表，论文长达270页，占了整整半卷杂志。
(关于论文发表的一段故事下面还要提到)。
这篇重要论文使原来就已有不小名气的年轻庞加莱更加誉满整个欧洲数学界，也使他得到了新的热情和动力继续进行他在这篇论文中开始的工作。
从1892年到1899年，庞加莱陆续出版了他的三大卷宏伟巨著“天体力学的新方法”(Les M\'{e}thodsNouvelles de la M\'{e}canique C\'{e}leste)。
他的获奖论文和这三卷书可以说奠定了现代天体力学，动力系统，微分方程定性理论，甚至混沌理论的基础，尽管大多数他的思想直到几十年后才被广大的数学工作者所领悟进而发展成现代的数学理论。
下面我们就来简单看一看庞加莱在这一时期的工作究竟给N体问题的解决带来了什么进展。
