当前位置：文档之家 › 复数和实数域上的多项式

复数和实数域上的多项式

  • 格式：ppt
  • 大小：451.50 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

4.8 复数和实数域上的多项式讲解

4.8 复数和实数域上的多项式讲解

数学家的幽默
一名统计学家遇到一位数学家， 统计学家调 侃数学家说道： 你们不是说若Ｘ＝Ｙ且Ｙ＝Ｚ，则Ｘ＝Ｚ 吗！那么想必你若是喜欢一个女孩，那么那个女 孩喜欢的男生你也会喜欢罗！？” 数学家来也没事吧！因为它 们平均不过是五十度而已！ ”
授课时数：2 学时 教学重点：实系数多项式的标准型，代数基本 定理和复数域上多项式的标准型，Vieta 定理及应用。
教学难点：代数基本定理和复数域上多项式的 标准型 ，Vieta定理。
教学过程:
思 考
问题 1 在解一元二次方程时， 有求根公式， 那么三次及以上方程也有吗？
问题 2 一元二次方程有 Vieta 定理，高次方程有吗？
4.8 复数和实数域上的多项式 授课题目： 4.8 复数和实数域上的多项式
教学目标：熟练实系数多项式的标准型，学习一些 解决实系数多项式问题的方法和技巧； 理解代 数基本定理和复数域上多项式的标准型， 熟练 掌握 Vieta 定理， 了解一元三次方程、 四次方 程的根式解法以及 Galois 在根式问题解的重 大贡献。
也是f ( x)的根。
设，的重数分别为 k , l , 且k l , h( x) C[ x], 使得
k l f ( x) （x ） （ x ） h( x), 其中x 不整除h( x), 且
x 也不整除h( x)，由于k l
k k l k f ( x) （x ） （ x ） （ x ） h( x )
思考 我们已解决了实数域、复数域上的多项式的可
约性问题 ，求根问题那么还有哪一个常见数域上的多 项式的可约性问题和求根问题没有解决呢？ 答 常见数域有复数域、实数域和有理数域。还有有理数域 上的多项式的可约性和求根问题尚未解决，同时有理数域
复数域与实数域上多项式的因式分解

复数域与实数域上多项式的因式分解

其中an为f ( x)的首项系数, c1 , , cs , p1 , , pr , q1 , , qr 全是实数, l1 , , ls ,k1 , , kr是正整数,且pi2 4qi 0, i 1, 2, , r;l1 ls 2(k1 kr ) n ( f ( x)).
10
首页 上页 下页 返回 结束
设 f ( x) C[x], 并且( f ( x)) 1, 则存在 C, 使得f ( x) ( x ) f1( x),其中( f1( x)) 0.
2
首页 上页 下页 返回 结束
推论1 设 p( x) C[x], 则p( x)是C上的不可约多 项式 ( p( x)) 1.
即:在复数域C上所有次数大于1的多项式全是 可约的.
an n
a n1 n1
a1 a0 0
即 f ( ) 0, 所以也是 f ( x)的根.
7
首页 上页 下页 返回 结束
因此 f ( x)能被
g( x) ( x )( x ) x2 -( )x
整除.
因 和 都是实数,所以g( x)是实系数多
项式, 故有
f ( x) g( x)h(x),
证 对f ( x)的次数用数学归纳法. 因一次多项式本身不可约,定理成立. 假设定理对次数 n的多项式来说成立.
设f ( x)是n次多项式,由代数基本定理, f ( x)有一复根.
如果是实数, 那么
f ( x) ( x ) f1( x)
其中f1 ( x)是n 1次实系数多项式.
如果不是实数, 那么也是f ( x)的根,于是
次式与二次不可约多项式的乘积. 故f ( x)也可以分解成实系数的一次式与二次不
可约多项式的乘积.
12
首页 上页 下页 返回 结束
高等代数试题

高等代数试题

第一章 多项式§1.1一元多项式的定义和运算1．设),(x f )(x g 和)(x h 是实数域上的多项式．证明：若是(6) 222)()()(x xh x xg x f +=，那么.0)()()(===x h x g x f2．求一组满足（6）式的不全为零的复系数多项式)(),(x g x f 和).(x h 3．证明：!))...(1()1(!)1)...(1()1(!2)1(1n n x x n n x x x x x x nn---=+---+--+-§1.2 多项式的整除性1．求)(x f 被)(x g 除所得的商式和余式：( i );13)(,14)(234--=--=x x x g x x x f (ii);23)(,13)(3235+-=-+-=x x x g x x x x f 2．证明：kx f x )(|必要且只要).(|x f x3．令()()()x g x g x f x f 2121,,),(都是数域F 上的多项式，其中()01≠x f 且()()()()()().|,|112121x g x f x f x f x g x g 证明：()().|22x f x g4．实数q p m ,,满足什么条件时多项式12++mx x 能够整除多项式.4q px x ++ 5．设F 是一个数域，.F a ∈证明：a x -整除.nn a x -6．考虑有理数域上多项式()()()()()(),121211nkn k nk x x x x x x f ++++++=-++这里k 和n 都是非负整数．证明：()()().11|1n k 1+++++-x x f x x k7．证明：1-d x 整除1-nx 必要且只要d 整除.n§1.3 多项式的最大公因式1. 计算以下各组多项式的最大公因式：( i )()();32103,34323234-++=---+=x x x x g x x x x x f (ii) ()().1)21(,1)21()42()22(2234i x i x x g i x i x i x i x x f -+-+=----+-+-+=2. 设()()()()()().,11x g x d x g x f x d x f ==证明：若()()(),),(x d x g x f =且()x f 和()x g 不全为零，则()();1),(11=x g x f 反之，若()(),1),(11=x g x f 则()x d 是()x f 与()x g 的一个最大公因式．3. 令()x f 与()x g 是][x F 的多项式，而d c b a ,,,是F 中的数，并且0≠-bc ad证明：()()()()()()).,(),(x g x f x dg x cf x bg x af =++4． 证明：（i ）h g f ),(是fh 和gh 的最大公因式； （ii ）),,,,(),)(,(212121212211g g f g g f f f g f g f = 此处h g f ,,等都是][x F 的多项式。

不可约多项式的判别

不可约多项式的判别

不可约多项式的判别一个多项式是否可约取决于它的系数所在的域。

下面给出了一些判别不可约多项式的方法。

1. 整数域中的多项式：在整数域中，两个常用的判别方法是Eisenstein 判别法和 Modulus 判别法。

- Eisenstein 判别法：设 P(x) 是一个系数为整数的多项式，且可以表示为 P(x) = a₀ + a₁x + a₂x² + ... + aₙxⁿ。

如果存在一个素数 p，满足以下条件：- p 不能整除 aₙ；- p 能整除 a₀, a₁, ..., aₙ₋₁；- p²不能整除 a₀；那么多项式 P(x) 在整数域中是不可约的。

- Modulus 判别法：设 P(x) 是一个系数为整数的多项式，且可以表示为 P(x) = a₀ + a₁x + a₂x² + ... + aₙxⁿ。

如果存在一个素数 p，使得 P(x) 在有限域 Zₙ 上可约（即 P(x) 在模 p 的意义下有一个非常数的因子），那么多项式 P(x) 在整数域中是不可约的。

2. 实数域、复数域和有理数域中的多项式：在这些域中，不可约多项式的判别较为简单，只需要使用带余除法进行因子分解判别即可。

带余除法即根据多项式除法的原理，如果存在一个多项式 Q(x)和 R(x)，使得 P(x) = Q(x)B(x) + R(x) 并且 R(x) 为零次或者次数小于 B(x) 的多项式。

如果 R(x) 为零次多项式，则 P(x) 是可约的；如果 R(x) 的次数大于等于 1，则 P(x) 是不可约的。

需要注意的是，对于高次多项式，进行带余除法可能会非常复杂，需要借助计算机进行多项式除法运算。

综上所述，对于一个多项式的可约性的判别需要根据具体的域和具体的算法进行分析。

以上只是给出了一些常用的判别方法，实际的判别可能需要更加复杂的计算。

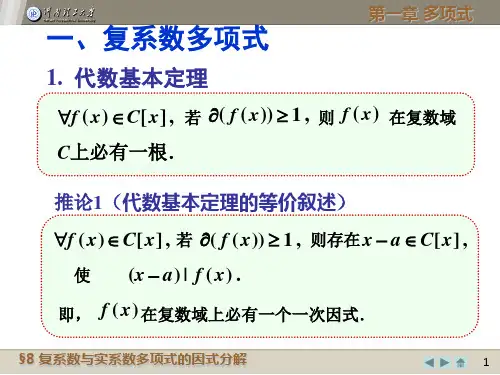
复系数和实系数多项式

复系数和实系数多项式


定理 实系数不可约多项式或为一次或为形如ax2 bx c
的二次多项式, 其中b2 4ac 0.
所以 上一元多项式的标准分解式为
m
r
f ( x) d ( x ai )li ( x2 bj x c j )hj
其中ai
i 1
且两两互异,
li
j1
是正整数(i
1,2,, m);
bj ,cj
的多项式.
解
因0
f
(ci )
ancin
an1cin1
ac 1i
a 且c
0
i
0,
所以
0
cn i
f
(ci
)
an
a c1 n1 i
a c( n1) 1i
a cn 0i
,
令 g(x)
a0 xn
a xn1 1
an1 x an ,
则
g(
1 ci
)
0.
又 c1,c2 ,,cn 非零且两两互异,所以 g(x)为所求.
,
hj
是正整数,
b
2 j
4c
j
0
且x2 bjx cj
两
两互素( j 1,2,,r)
l m
i1 i
2
h r
j1 j
deg
f
( x).
5.6 复系数和实系数多项式
例1
设f
(
x
)
an
x
n
an1
x
n1
a 1
x
a 0
的n个互
异的非零根为 c1,c2 ,,cn ,
求以
1 c1
,
1 c2
实系数多项式

实系数多项式


55
第一章 多项式
若 不为实数，则 也是 f ( x) 的复根，于是
f ( x) ( x )( x ) f2( x) x2 ( )x f2( x)
设 a bi ，则 a bi, 2a R , a2 b2 R 即在R上 x2 ( )x 是 一个二次不可约多项式．
从而 ( f2 ) n 2. 由归纳假设 f1( x) 、f2( x)可分解成一次因式与二次
不可约多项式的乘积． 由归纳原理，定理得证．
§8 复系数与实系数多项式的因式分解 © 2009, Henan Polytechnic University
66
推论1
第一章 多项式
f ( x) R[ x], f ( x) 在R上具有标准分解式 f ( x) an( x c1)k1 ( x c2 )k2 ( x cs )ks ( x2 p1x q1)l1
一、复系数多项式
第一章 多项式
1. 代数基本定理
f ( x) C[x] , 若 ( f ( x)) 1 , 则 f ( x) 在复数域 C上必有一根．
推论1（代数基本定理的等价叙述） f ( x) C[x] , 若 ( f ( x)) 1 , 则存在 x a C[x] ,
f ( x) a( x 1)r1 ( x 2 )r2 ( x s )rs
其中1,2 , ,s是不同的复数，r1,r2, ,rs Z+
推论2 f ( x) C[x]，若 ( f ( x)) n ，则 f ( x) 有n个 复根（重根按重数计算）．
§8 复系数与实系数多项式的因式分解 © 2009, Henan Polytechnic Un多项式
高等代数实系数和复系数多项式的因式分解

高等代数实系数和复系数多项式的因式分解


−
n−2
(ε 2
+
ε
n+2 2
)x
+
1].
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
例题选讲
例 设 f(x), g(x) 是两多项式，且 f(x3) + xg(x3) 可被 x2 + x + 1 整除， 则 f(1) = g(1) = 0.
两边取共轭数，有
f(α¯) = anα¯n + an−1α¯n−1 + · · · + a0 = 0,
这就是说，f(α¯) = 0，α¯ 也是 f(x) 的根.
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
实系数多项式因式分解定理
. .. . . ..
高斯与代数基本定理
代数基本定理在代数乃至整个数学中起着基础作用. 据说，关于 代数学基本定理的证明，现有 200 多种证法. 迄今为止，该定理 尚无纯代数方法的证明. 大数学家 J.P. 塞尔曾经指出：代数基本 定理的所有证明本质上都是拓扑的. 美国数学家 John Willard Milnor 在数学名著《从微分观点看拓扑》一书中给了一个几何直 观的证明，但是其中用到了和临界点测度有关的 sard 定理. 复变 函数论中，对代数基本定理的证明是相当优美的，其中用到了很 多经典的复变函数的理论结果.
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
高斯与代数基本定理
该定理的第一个证明是法国数学家达朗贝尔给出的，但证明不完 整. 接着，欧拉也给出了一个证明，但也有缺陷，拉格朗日于 1772 年又重新证明了该定理，后经高斯分析，证明仍然很不严 格的. 代数基本定理的第一个严格证明通常认为是高斯给出的 (1799 年在哥廷根大学的博士论文)，高斯后来又给出了另外三个 证法，其中第四个证法是他 71 岁公布的，并且在这个证明中他 允许多项式的系数是复数.
复数的基本概念和运算

复数的基本概念和运算

复数的基本概念和运算
1、复数 z=x+iy或 z=x+yi 、
x, y为实数;i 2 = −1
实部： ( z ) = x; 虚部为 Im ( z ) = y Re 若 Im ( z ) = 0，则z为实数； 若 Re ( z ) = 0，则z为纯虚数。
共轭 z = x − iy
z1 z1 i) z1 ± z2 = z1 ± z2, z1z2 = z1z2, = ; z2 z2 ii) z = z; iii) zz =[ R z)] +[ Im z)] ; e( (
x → x0 y → y0
定理四、如果 f ( z )， g ( z )在 z 0处连续，下列函数在 z 0 处都连续。 处连续， 处都连续。 定理四、 f ( z ) ± g ( z ),
w = zn 多 项 式 ： w = P ( z ) = a 0 + a1 z + L + a n z n 有 理 式 ： w= P(z) 在 Q(z) ≠ 0 Q(z)
– 复平面与直角坐标平面上的点一一对应
y
0
z = x + iy (x,y )
x
P
• 向量表示
–模 – 幅角
| z |= r = x 2 + y 2
y
θ
O
z=x+iy
θ = Argz = arg z + 2kπ θ 0 = arg z, −π < θ0 ≤ π
x
z=0时辐角不确定
• 三角表示： z = r (cos θ + i sin θ )
(4) 在除去负实轴(包括原点)的复平面内, 主值支和其它各分支 处处连续, 处处可导, 且 (ln z )′ = 1 , (Lnz )′ = 1 .
一元多项式

一元多项式

3x2 14x 15 x 3 3x 5
所以 r2 x就是 f x与 gx的最大公因式：
f x, gx x 3
定理 1.4.2
若dx 是 P[x] 的多项式 f x与 gx的最大公因 式，那么在 P[x] 里可以求得多项式 ux与vx ，
二、教学目的
1．掌握一元多项式整除的概念及其性质。 2．熟练运用带余除法。
三、重点、难点
多项式的整除概念，带余除法定理
1.3.1 多项式的整除概念
设P是一个数域. P[x]是P上一元多项式.
定义1
设f x, gx P[x] ，如果存在 hx P[x] ，使得
f x gxhx，则称 gx整除 f x ，记为
3
虽然 a1,b1, a2,b2 Z，
不一定属于Z ，所以
不是数域.
a1aa不222 一33bb定122b2属, a于a2b221Z(3ab132b2)2
，因此 Z (
3)
定理1.1 任何数域都包含有理数域 Q. (有理数域是最小的数域).
定理1.2 若数域 P R，则P C. (实数域和复数域之间没有其它的数域).
则 (a1 a2) b1 b2 2 Q 2 ，
a1 b1 2 a2 b2 2
(a1a2 2b1b2 ) a1b2 a2b1 2 Q 2
显然，Q Q( 2) R.
再设 a2 b2 2 0, 即 a2,b2 不全为零，从
而 a2 b2 2 0 ， a1 b1 2 a1 b1 2 a2 b2 2 a2 b2 2 a2 b2 2 a2 b2 2
a 叫做 i 次项, i叫做 i 次项的系数.
注 2：在一个多项式中，可以任意添上或去掉一些系
数为零的项；若是某一个i次项的系数是1 ，那 么这个系数可以省略不写。
复数和实数域上的多项式.

复数和实数域上的多项式.

前页 后页 返回
由归纳假设，
f1 ( x )在C中有n 1个根 2 , 3 ,
f ( x )在C中有n个根1 , 2 ,
推论 1
, n . 因 此 ，
（证毕）
, n .
1） 任意一个 n( n 0)多项式 f ( x )在C [ x ]
中都能分解成一次因式的乘积；
2）C [ x ]中的不可约多项式只有一次的.
*1）可用归纳法证；2）用 1）来证 2）
前页 后页 返回
这样， 任意一个 n( n 0) 多项式 f ( x ) 在 C [ x ] 中的典型分解式为以下形式：
f ( x ) a( x a1 )k1 ( x a2 )k2
其中 k1 k2
kt n.
( x a t ) kt ,
a4 5 ( 2) 3 3 90.
前页 后页 返回
所以
例2
f ( x ) x 4 9 x 3 17 x 2 33 x 90, 或
试求 3 次多项式
f ( x ) ax 4 9ax 3 17ax 2 33ax 90a (a 0).
f ( x ) 2 x 3 6 x 2 3 x 4 的根是α ，β ，γ ，
数域 a F , F 是任意数域。 ）
前页 后页 返回
二、实数域上多项式
1、实系数多项式非复根的重要性质
定理 4.8.3 设 f ( x ) R[ x ]，非实复数
是f ( x )的根，则 的共轭复数
是f ( x )的根，并且 与 有相同的重数。
证
设f ( x ) a0 x n a1 x n1
前页 后页 返回
根据上面韦达定理，由根1 , 2 , n ，可以求出
27复数域和实数域上的多项式

27复数域和实数域上的多项式


定理2.14说明，实系数多项式的虚根（非 实复数根）成对.
例2.13 已知i ( i 2 =-1)是 f ( x) x6 3 x2 2 的一个二重根，求f ( x )在 中的全部根.
定理2.15： 上的不可约多项式只有一次多 项式和含有一对非实共轭复数根的二次多项式.
推论2.15 每个次数大于零的实系数多项式 都可唯一地分解成实系数的一次或二次不可约 因式的乘积.
利用根与系数的关系可以构造一个n次多项式使其恰以事先给定的n个数例212使它以5和2为单根以3为二重根
2.7.1 复数域C上的多项式
对于 一般的数域F上的多项式 f x ，它在F中 未必有根. 那么，它在复数域（这个最大的数域上）
是否有根？ 定理2.13（代数基本定理） 每个次数… 大于零的 复系数多项式在复数域内至少有一个根. 推论2.13.1 每个n（n>0）次复系数多项式在 复数域内恰有n个根（k重根按k个计）.
xn c1
xn1
cn .
1i j n

ci c j xn2
比较系数， 得到根与系数的关系为：
a2 c1c2 c1c3
a1 c1 c2
cn ,
cn1cn ,
cn2cn1cn ,
并且l1 ls 2k1 2kr n.
, r).
注：四次及四次以下的方程可用根号解（公 式解），五次和五次以上的方程不能用根号解.
, cn 为根.
例 2.12 求一个最高次项系数为1的4次多项式， 使它以5和-2为单根，以3为二重根.
2.7.2
定理2.14
实数域R上的多项式
设f ( x ) [ x ], 是一个非实复数.

第二章 多项式 第七节 复数实数域上的多项式课件


其中，1 , 2 ,
f (x) a(x 1)k1 (x s )ks
,s 是不同的复数，k1, k2, , ks 是正整数，并且
k1 k2 ks n.
定理2.7.3
任何n (n > 0)次多项式在复数域中有n个根(重根按 重数计算) . 证 设f (x)是一个次多项式,那么由定理2.7.1,它在复
一、代数基本定理 二、实系数多项式的性质定理
一、代数基本定理
定理2.7.1(代数基本定理) 任何n (n > 0)次多项式在复数域中至少有一个根.
定理2.7.2(复系数多项式因式分解定理) 复数域C上任一n (n > 0)次多项式可以唯一地 分解为n一次因式的乘积.
由定理2.7.2， n (n > 0)次复系数多项式 f (x) 的标准分解式为
二、实系数多项式的性质定理
定理2.7.4
若实系数多项式 f (x)有一个非实的复数根 ,那么 的共轭数 也是f (x)的根, 并且 与 有同一重数.
换句话说,实系数多项式的非实的复数根两两成对.
证 令f (x) a0 xn a1xn1 an . 由假设
a0 xn a1xn1 an 0.
数域C中有一个根 1, 因此在C [x]中
f (x) (x 1) f1(x),
这里 f1(x是) C上的一个n – 1 次多项式.若n – 1 > 0,那
么在C中有一个根 2 , 因而在C [x]中
f (x) (x 1)(x 2 ) f2 (x).
这样继续下去,最后f (x)在C [x]中完全分解成n个一 次因式的乘积,而在f (x) C中有n个根.
整除.由共轭复数的性质知道g (x)的系数都是实数.故 f (x) g(x)h(x), 此处h (x) 也是,那么它一定是h (x)的根,因而根 据方才所证明的, 也是h (x)的一个根.这样也是f (x) 的重根.重复应用这个推理方法,容易看出, 与的重

多项式的因式分解定理

§1-5多项式的因式分解定理多项式44-x 在有理数域、实数域、复数域上的因式分解 ][)2)(2)(2)(2(4][)2)(2)(2(4][)2)(2(4424224x C i x i x x x x x R x x x x x Q x x x +-+-=-++-=-+-=-（不能再分）（不能再分） 在不同的系数域上，具有不同形式的分解式什么叫不能再分平凡因式：零次多项式（不等于零的常数）、多项式自身、前两个的乘积Definition8：（不可约多项式）令][)(x P x f 是的一个次数大于零的多项式，如果][)(x P x f 在中只有平凡因式，就称f(x )为数域P 上（或在P[x]中）的不可约多项式.（p(x)在数域P 上不能表示成两个次数低的多项式的乘积） 若)(x f 除平凡因式外，在P[x]中还有其它因式，f(x )就说是在数域P 上（或在P[x]中）是可约的.如果不是平凡因式)(,)()()(x g x h x g x f =，的次数显然和则)()(x h x g 都小于)(x f 的次数.反之，若)(x f 能写成两个这样多项式的乘积，那么)(x f有非平凡因式；如果P[x]的一个n 次多项式能够分解成P[x]中两个次数都 小于n 的多项式 的乘积和)()(x h x g 即 )()()(x h x g x f 那么)(x f 在P 上可约.由不可约多项式的定义可知：任何一次多项式都是不可约多项式的.不可约多项式的重要性质：一个多项式是否不可约是依赖于系数域；1.如果多项式)(x f 不可约，那么P 中任意不为零的元素c 与)(x f 的乘积c )(x f 都不可约.2.设)(x f 是一个不可约多项式而P(x)是一个任意多项式，那么或者)(x f 与P(x)互素，或者)(x f 整除P(x).3.如果多项式)(x f 与)(x g 的乘积能被不可约多项式P(x)整除，那么至少有一个因式被P(x)整除.Theorem5.如果)(x p 是一个不可约多项式,P(x)整除一些多项式)(,),(),(21x f x f x f s 的乘积,那么)(x p 一定整除这些多项式之中的一个.证明:对被除多项式的个数s 用数学归纳法当s=1时,显然成立;假设s=n-1 时,结论成立;当s=n 时,令)()()()(),()(32211x f x f x f x g x f x g n ==, 如果)(|)(),(|)(11x f x p x g x p 则命题成立,如果1))(),((),(|)(11=/x g x p x g x p 则,从而)(|)(2x g x p ,即)(,),(),()(32x f x f x f x p n 整除 n-1 多项式的乘积,由归纳法假设)(x p 整除其中一个多项式,根据数学归纳法原理,命题得证. 因式分解及唯一性定理：多项式环P[x]的每一个)0(>n n 次多项式)(x f 都可以唯一分解成P[x]的不可约多项式的乘积；)()()()(21x p x p x p x f s =所谓唯一性是说，如果有两个分解式)()()()()()()(2121x q x q x q x p x p x p x f t s ==那么，必有s=t ，并且适当地排列因式的顺序后有),2,1()()(s i x cq x p i i ==标准分解式（典型分解式）：)()()()(2121x p x p x cp x f s r s r r = 其中c 是f(x)的首项系数，)(),(),(21x p x p x p s 是不同的、首项系数为1的不可约多项式，而s r r r ,,21正整数.例1：在有理数域上分解多项式， 22)(23--+=x x x x f . )2)(1)(1()2)(1(22)(223+-+=-++=--+=x x x x x x x x x x f例2：求 的典型分解式内在][122)(2345x Q x x x x x x f -++--=. 23242345)1()1()12)(1(122)(+-=+--=-++--=x x x x x x x x x x x f 例3.求 的典型内在][6141616102)(2345x R x x x x x x f -+-+-= 分解式. )3()1)(1(2)(22--+=x x x x f例4：分别在有理数域、实数域和复数域上分解多项式 15-x 和16-x 为不可约多项式的乘积.解:)1)(1()1(2345++++-=-x x x x x x Q[x]][)154cos 2)(152cos 2)(1()1)(1()1(222345x R x x x x x x x x x +-+--=++++-=-ππ][)52sin 52cos ()1()1)(1()1(412345x C k i k x x x x x x x x k ππ---=++++-=-=在Q[x]上)1)(1)(1)(1()1)(1()1(22336+-+++-=+-=-x x x x x x x x x ; 在R[x]上)1)(1)(1)(1()1)(1()1(22336+-+++-=+-=-x x x x x x x x x ; 在C[x]上)2321)(2321)(1)(2321)(2321)(1(16i x i x x i x i x x x -++++--+--=-。

如何判别一个多项式不可约

定 理 2( 艾 森 斯 坦 (Eisenstein) 判 别 法 ) ： 设 f(x)=a0+a1x+…+anxn 是 整 系 数 多 项 式 ， 若 能 找到一个素数p，使得
(1)p不能整除an； (2)p|a0,a1,┅,an-1； (3)p2不能整除a0； 那么，f(x)在有理数域上不可约。
单位元，结合律，交换律，逆元，零元， 分配律
同态，同构
2.相容
设“~”为S上的等价关系，“*” 为S上 的二元运算。若对任意a,b,c,dS，当a~b， c~d时，必有ac~bd，则称等价关系~与 运算 是相容的，称~为代数系统[S;]的 相容等价关系。
3.半群，拟群，群
有关定理
4.元素的阶和群的阶
定义,结论
5.子群与陪集 概念,定理,陪集的实质 正规子群 6.商群与群同态基本定理 7.环的基本概念 环的零元,环的单位元,交换环 在环中讨论元素可逆 1-un=(1-u)(1+u+u2++un-1) 8.特征数 整环的特征数 9.子环，理想，商环 主理想,主理想环 10.多项式环
定 理 2( 艾 森 斯 坦 (Eisenstein) 判 别 法 ) ： 设 f(x)=a0+a1x+…+anxn 是 整 系 数 多 项 式 ， 若 能 找到一个素数p，使得
(1)p不能整除an； (2)p|a0,a1,┅,an-1； (3)p2不能整除a0； 那么，f(x)在有理数域上不可约。
5.本原元与本原多项式 有关定理和结论的证明 GF(pn)的表述,化简 求出所有本原元,本原多项式
已知为GF(pn)上的本原元，怎样求出 GF(pn)上的所有本原元？

6.7 复数域和实数域上的多项式讲解


mr
其中， a0 为 f x 的首项系数，且 m1 m2 mr 0 f x
3
高等代数与解析几何
6.7 复数域和实数域上的多项式
6.7.2 实数域上的多项式
定理 6.23 设 f x 为实系数多项式， 为 f x 的虚根，则 也是 f x 的根，且 与 的重数相同.
4
高等代数与解析几何
6.7 复数域和实数域上的多项式
从而， x - , x - 都是 f x 的因式.
令 g( x) x x x2 x R x 因 g ( x) f ( x) (?) ，则可令 f ( x) g ( x)h( x), h( x) R x .
5
高等代数与解析几何
6.7 复数域和实数域上的多项式
证 因 p x 不可约，则 0 ( p x )> 0 ，故 p x 在 C 内必有一个根
.若 为实数，则因 x - p x ，令 p x x q x ，但 p x 不可
约，则 q x c c 0 ，可见， p x c x ；若 为虚数，则 也 是 p x 的根， 从而 g x x x x 2 x 为 p x 的因 式，但 p x 不可约，则 p x b[ x 2 x ] (b 0) ，即 p x 是 含共轭虚根的二次多项式.
证 1 n 0 时， f x 有零个根，结论成立；
2 设 n 0 ，且当 n 1 时结论成立，而由定理 6.21 知： f x
必有一个根 .于是， x - f ( x ) .设

复系数多项式.

2 2
R上的不可约多项式.
§1.8 复系数与实系数多项式的因式分解
推论2
实数域上不可约多项式只有一次多项式和某些二 次不可约多项式，所有次数 3的多项式皆可约.
§1.8 复系数与实系数多项式的因式分解
附：单位根、单位原根
定义1 多项式 x n 1 在复数域上的任一根都称为
n 次单位根.
n x 1 的n个复根为 事实上,在复数范围内
复根（重根按重数计算）．
§1.8 复系数与实系数多项式的因式分解
二、实系数多项式
命题：若 是实系数多项式 f ( x ) 的复根，则 的共轭复数 也是 f ( x ) 的复根．
n n1 f ( x ) a x a x a0 , ai R 证：设 n n1
1, , , ,
2
n1
这里
2 2 cos i sin , n 1 n n 2k 2k k cos i sin , k 0,1, , n 1. n n
§1.8 复系数与实系数多项式的因式分解
定义2 若1, , , ,
若 为根，则
f ( ) an n an1 n1 a0 0
两边取共轭有
f ( ) an an1
n
n1
a0 0
∴ 也是为 f ( x ) 复根．
§1.8 复系数与实系数多项式的因式分解
实系数多项式因式分解定理
f ( x ) R[ x ]，若 ( f ( x )) 1， 则 f ( x ) 可唯一
5 2 3 4
x 1 ( x 1)( x )( x )( x )( x )( x )

复系数与实系数

f ( x ) C [ x ], 若 ( f ( x )) 1, 则 f ( x ) 在复数域
C 上可唯一分解成一次因式的乘积．
§1.8 复系数与实系数多项式的因式分解
推论1
f ( x ) C [ x ], 若 ( f ( x )) 1, 则 f ( x ) 在 C
上具有标准分解式
2
n1
n x 是 1 的根）.也就是说
x n 1 的任一根，都可经
易知如下性质:
表示.
k k 1
2k , , 2cos n k 1, 2, , n
k n k
k k
§1.8 复系数与实系数多项式的因式分解
1, , , ,
2
n1
这里
2 2 cos i sin , n 1 n n 2k 2k k cos i sin , k 0,1, , n 1. n n
§1.8 复系数与实系数多项式的因式分解
定义2 若1, , , ,
例1 (1)求 x 5 1 在 C上与在 R上的标准分解式. (2)求 x 6 1 在 C 上与在 R 上的标准分解式. 一般地，给出 x n 1 在 C 上与在 R 上的标准分解式. 解 对（1）、（2）仅给出实数域上的分解
x 1 ( x 1)( x )( x )( x )( x )
§1.8 复系数与实系数多项式的因式分解
若 不为实数，则 也是 f ( x ) 的复根，于是
f ( x ) ( x )( x ) f 2 ( x ) x 2 ( ) x f 2 ( x )


设 a bi ，则
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a4 5 (2) 3 3 90.
前页 后页 返回
所以 f ( x) x4 9x3 17x2 33x 90,或 f ( x) ax4 9ax3 17ax2 33ax 90a (a 0).
例 2 试求 3 次多项式 f ( x) 2x3 6x2 3x 4的根是α ，β ，γ ， 求以 α +β ，β +γ ，α +γ 为根的多项式。 （也可设所求多项式 f ( x) x3 a1x2 a2 x a3
1.代数基本定理及推论 定理 4.8.1（代数基本定理）任何n(n 0)次 多项式在复数域中至少有一个根.
定理 4.8.2 任何次n(n 0)多项式在复数 域中有n个根（k 重根按 k 个计算）.
证 对多项式次[ x]中任何一次多项式ax b显然在C中有一个根, 即 b / a,故结论成立.
是f ( x)的根，则 的共轭复数
是f ( x)的根，并且 与 有相同的重数。
证 设f ( x) a0 xn a1xn1 an1x an , ai R,
由假设是f ( x)的根,于是
f ( ) a0 n a1 n1 an1 an 0, 所 以
124


n2 n1 n ),

an1

a0

( 1)n1 (1 2
n1 13
n
23 n ),
an a0

( 1)n 1 2
n.
前页 后页 返回
根据上面韦达定理，由根1,2 , n，可以求出
1 , 2 ,
前页 后页 返回
这样，任意一个n(n 0)多项式 f ( x)在C[x] 中的典型分解式为以下形式：
f ( x) a( x a1 )k1 ( x a2 )k2 ( x at )kt , 其中k1 k2 kt n.
2. 根与系数的关系（韦达定理）
1) 首1多项式的根与系数的关系 设 f ( x) xn a1 xn1 a2 xn2 an1x an 在C 中首n个根1,2 , ,n ,那么
前页 后页 返回
由归纳假设，
f1( x)在C中有n 1个根2 ,3 , ,n . 因 此 ， f ( x)在C中有n个根1,2 , ,n . （证毕）
推论 1 1）任意一个n(n 0)多项式 f ( x)在C[x] 中都能分解成一次因式的乘积；
2）C[ x]中的不可约多项式只有一次的. *1）可用归纳法证；2）用 1）来证 2）

xn

a1 a0
x n1

a2 a0
x n2

所以：
an1 x an
a0
a0
前页 后页 返回
a1

a0

(1
2

n ),
a2

a0

(1 2
13

1n 23
n1 n ),

a3 a0

(1 2 3
前页 后页 返回
a1 (1 2 n ), a2 (12 13 1n 23
n1 n ),
a3 (123 124 n2 n1 n ),


an1 (1)n1(12 n1 13 an (1)n12 n .
a0 n a1 n1 an1 an 0,
前页 后页 返回
即 a0 n a1 n1 an1 an 0, 因此， 是f ( x)的根. 设 ,的重数分别是k和l,且k l, 则存在h( x) C[ x],使得 f ( x) ( x )k ( x )l h( x), 其中x | h( x), x | h( x),
利用α +β +γ =3， 3 , 2
2 求出a1,a2 ,a3最后乘上a(a 0,a 指定数域，没指定 数域a F ,F 是任意数域。）
前页 后页 返回
二、实数域上多项式
1、实系数多项式非复根的重要性质
定理 4.8.3 设 f ( x) R[x]，非实复数
4.8 复数和实数域上的多项式 授课题目：4.8复数和实数域上的多项式
教学目标：掌握复数域和实数域上多项式因式 分解定理
授课时数：2学时
教学重点：复数域上多项式因式分解定理、根与 系数的关系。实数域上的多项式因式分解定理。
教学难点：复系数多项式根与系数关系的应用
前页 后页 返回
教学过程： 一. 复数域上多项式

为根的多项式。
n
例1 求一个有单根5，-2及重根3的4次多项式。
解 a1 (5 2 3 3) 9, a2 5 (2) 5 3 (2) 3 (2) 3 3 3 17, a3 [5 (2) 3 5 (2) 3 5 3 3 (2) 3 3] 33,
n
23 n ),
2）非首1多项式的根与系数的关系
前页 后页 返回
设 f ( x) a0 xn a1xn1 a2 xn2 an1x an
a0 0,而1,2 , n是f ( x)在C中的n个根,
因 f ( x) a0 f1( x)，其中
f1( x)
假 定 任 意 n 1(n 1 0) 次 多 项 式 在 C中有n 1个根.
令设f ( x)是n次多项式, f ( x) C[x]. 由代数基
本定理， f ( x)在C中至少有一个根1,于是存在
f1( x) C[ x], ( f1( x)) n 1, 使
f ( x) ( x 1) f1( x).