当前位置：文档之家 › 大学物理.力对物体的空间累积效应

大学物理.力对物体的空间累积效应

  • 格式：ppt
  • 大小：924.00 KB
  • 文档页数：35

下载文档原格式

  / 35

合集下载

2-5力对空间的积累效应

2-5力对空间的积累效应


P F v cos
功率的单位 （瓦特） 1W 1J s 1 1kW 10 3 W
第二章 质点力学
2-5 力对空间的积累效应
二 质点的动能定理 A F d r F d r
F d s
1 2
2
F m
mv
2 2
dv dt
m v1
作业题：2-25、26、33
第二章 质点力学
2-5 力对空间的积累效应 例 1 一质量为 m 的小球竖直落入水中， 刚接触 水面时其速率为v0 . 设此球在水中所受的浮力与重力 相等, 水的阻力为Fr=-bv, b 为一常量. 求阻力对球作 的功与时间的函数关系 . 解 如图建立坐标轴 dx W F dr b v d x b v dt dt o 2 W b v d t 即 b
FT v ds P
l
2
(1) 质点由点(0,0)沿x方向到点(2,0)，y=0；dy=0。
A1
F dx
0 x
x dx
2
8 3
(J )
y A2 O A1 x
0
再平行y方向运动到点(2,4)；x=2；dx=0。
A2
F
0
4
y
dy
6 ydy
0
4
48 ( J )
A A1 A2 45
2
A

v2
v1
m
dv dt
ds

v2
v1
m vdv
1 2 mv
1 2
动能(状态函数) E k

p
2
2m
动能定理 合外力对质点所做的功, 等于质点动能的增量。 注意
哈里德大学物理第三章

哈里德大学物理第三章


注意
Fi内 0 I i内 0
i i
W
i
i内
0
二、变力的功
微元分析法：
ds dr
P

P
a
F
r
F r
o
b
取微元过程
以直代曲
以不变代变
再求和
§3-1 功 功率
ds
P

dr
P
r
a
F
r
F
o
b
元功： dW F dr F dr cosθ Fcosθds
F
M
m
r
r
o
以上这些力的共同特点？
保守力
1）做功与路径无关，只与起、末点位置有关；
2）做功等于与相互作用物体的相对位置有关的 某函数在始末位置的值之差。
势能
§3-2 保守力与非保守力 势能
二、保守力与非保守力
势能
1. 保守力与非保守力
• 做功与路径无关，只与起点、终点位置有关
b m L1 a
§3-2 保守力与非保守力 势能
保守力在 x 轴的分力，等于其相关势 能对坐标 x 的导数的负值:
F
dW F dr
x
Fx dx dEp x
m

θ
Fx
Fx
dEp x dx
§3-2 保守力与非保守力 势能
练习3：
一质量为 m 的人造地球卫星沿一圆形轨道运动，
§3-4 功能原理
1. 动能定理与功能原理的区别与联系：
功能原理是从动能定理推出的，完全包含在 动能定理之中； 由于保守力的功已反映在势能的改变中，运 用功能原理时，只需要计算非保守力的功， 而动能定理，则需要计算所有力做的功 。 2. 功与能的联系与区别： 功与能的单位与量纲相同； 功是过程量，能量是状态量； 功是能量传递和转化的一种方式和量度。
大学物理2-6动能定理

大学物理2-6动能定理


ab Fτ
ds
ab maτ
ds
b
a
m
d d
v t
d
s
vb va
mv d v
1 2
m vb2
1 2
m va2
定义质点的动能为：Ek
1 mv2 2
动能定理
质点动能定理:合外力对质点所做的功等于质点 动能的增量。
Aab Ekb Eka Ek
几点注意： a.合力做正功时，质点动能增大；反之，质
点动能减小。
b.动能的量值与参考系有关。
c.动能定理只适用于惯性系。 d.功是一个过程量，而动能是一个状态量。
动能定理
(3)质点系动能定理
多个质点组成的质点系，既要考虑外力，又要 考虑质点间的相互作用力（内力）。
二质点组成的 系统
推 广
多个质点组成 的系统
两个质点在外力及内
力作F用1下如图所示F：2
m1
f1 2
下从a运动到b。
b
a
怎样计算这个力
的功呢？
采用微元分割法
动能定理
第1段近似功： A1 F1 r1
第2段近似功： A2 F2
r2
Δ
r3
Δ
r4
Δ r2
F4
Δ r1
F3
a
F2
F1
Δ ri
b Fi
第i 段近似功：
Δ Ai Fi • ri
总功近似：
Aab Δ Ai Fi • ri
i
i
F
N
F
300
(a)
100
fr
(b)
G
动能定理
解： 木箱所受的力为：拉力F ，方向与斜面成100 角向上；重力G ，方向竖直向下；斜面对木箱的支 持力N ，方向垂直于斜面向上，斜面对木箱的摩擦 力 fr 方向和斜面平行，与木箱运动方向相反， 如图 (b).已知l=3m,每个力所作的功可计算如下。
3.1 力的空间积累效应

3.1 力的空间积累效应

从静止出发， 轴正向作直线运动。 从静止出发，沿 x 轴正向作直线运动。 前三秒内该力所作的功， 时的功率。 求：前三秒内该力所作的功，及 t = 2s 时的功率。
r r 解： A = F ⋅ dr = Fdx （一维运动可以用标量） 一维运动可以用标量） ∫ ∫
dx = ∫F dt = dt
t
∫ F vdt
5
3.1 力的空间积累效应
2、变力曲线运动的功
第3章 机械运动的守恒定律 解决方法： 解决方法：微元积分法
“化整为零，以直代曲，以恒代变，再求和”。 化整为零，以直代曲，以恒代变，再求和” 把路径分成许多微小的位移元； 把路径分成许多微小的位移元； 位移元 在各段位移元上质点受的力可以看成是恒力 恒力， 在各段位移元上质点受的力可以看成是恒力， 在该微过程中的元功 元功为 在该微过程中的元功为：
t
3 3 4 3 0
t 12t F = 0 + ∫ dt = ∫ dt = 3t 2 v = v0 + ∫ adt 0 m 0 2 0
∴ A = ∫ 12 t ⋅ 3 t dt = ∫ 36 t dt = 9 t
2
3
v v 2 P = F ⋅ v = 12t ⋅ 3t = 288W
0
0
= 729 J
3
3.1 力的空间积累效应
第3章 机械运动的守恒定律
3.1
力的空间积累效应 （功 动能定理） 动能定理）
4
3.1 力的空间积累效应 一、功
第3章 机械运动的守恒定律
力对质点所作的功： 力在质点位移方向的分量 力对质点所作的功： 与位移大小的乘积，即为力与质点位移的点积。 位移大小的乘积，即为力与质点位移的点积 力与质点位移的点积。 的乘积 1、恒力直线运动的功： 恒力直线运动的功：
2.5 动能定理和功能原理

2.5 动能定理和功能原理


结论：
成对 保守内力功 特点：只取决于相互作
用质点的始末相对位置，是始末位置的函数。
§2.5 动能定理和功能原理 第二章 质点动力学
4. 成对保守内力 作功特点
《大学物理》教程
讨论
一对
m' m m' m W1 W2 ( G ) ( G ) 万有引力作功 rA rB

ACB
A
D
C
B
Fc dr Fc dr
BDA
Fc dr Fc dr
ACB
ADB
0
§2.5 动能定理和功能原理
始末位置 相同
第二章 质点动力学
3. 成对力作功
《大学物理》教程
有人问：
力是一种 相互作用 力总是成对 出现，满足 牛三律 这对力作功 有特点吗？
§2.5 动能定理和功能原理 第二章 质点动力学
1. 质点 的动能定理
《大学物理》教程

b
a
1 1 2 2 F dr mvb mva 2 2
定义功（过程量）：力对空间的累积量
W
① 元功：
b
a
F dr
dW F dr ② 功率：单位时间内作的功 P F v dt dt
xb
xa
1 2 1 2 kxdx kxa kxb 2 2
小结： 弹簧力做功与路径无关，只与运动 起点和终点的位置有关。
§2.5 动能定理和功能原理 第二章 质点动力学
《大学物理》教程
讨论
定义式法 求功的计算举例
例3 万有引力做功 以 m 2 为参考系
a m
r (t ) F
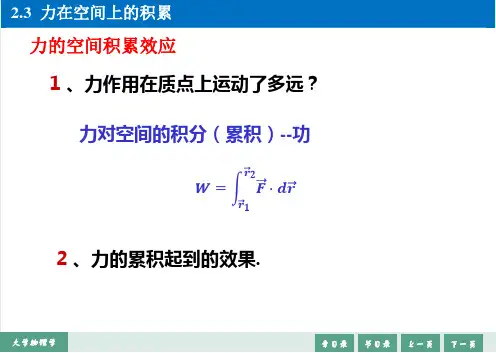
大学物理学-力的空间积累

大学物理学-力的空间积累


质点系的功能原理
W 外 W 内 E k末 E k初
W 外 W 非保守内力 W 保守内力 E K E K 0
W 保守内力 ( E P E P 0 ) E P
W 外 W 非保守内力 ( E K E K 0 ) ( E P E P 0 )
总动量，但增大总动能。
大学物理学
章目录
节目录
上一页
下一页
2.3 力在空间上的积累
质点系的动能定理
质点系的动能
一对内力 做功之和不一定为零
W 外 W 内 E k末 E k初
质点系的动能定理:
质点系总动能的增量等于外力的功和内力的功之和。
大学物理学
章目录
节目录
上一页
下一页
2.3 力在空间上的积累
此势能曲线可分析系统
状态的变化。
大学物理学
势垒
E
ra 势阱 rb
•A
章目录
节目录
rc
上一页
X
下一页
2.3 力在空间上的积累
四、质点系的动能定理和功能原理
内力矢量和为零，但内力做功之和可不为零。
作用于不同质点，质点位移可能不同。
W W 0
f
f
例：物体间摩擦力矢量和为零，对总动量没影响
，但做功可以减小总动能。炸弹爆炸时爆炸力不改变
2GM
c
R
星体即使发光，引力也会把光吸引回来，远处
的观察者根本接收不到该星体发出的任何信息。这
W 外 W 非保守内力 E E0
功能原理:质点系在运动过程中，所受外力的功与系
统内非保守力的功的总和等于其机械能的增量。
大学物理学
大学物理学-力矩的时空积累效应

大学物理学-力矩的时空积累效应

➢ 讨论系统总的角动量改变，只需关注系统所受的外力及外力矩。
当把刚体、质点系或单个质点作为一个研究对象时，角动量定
理具有普适性：一切外力力矩的时间累积的结果是使这个研究
对象的角动量发生改变，数值上满足

න () = −
守恒条件？

大学物理学
章目录
节目录
上一页
下一页
3.3 力矩的时空积累效应
大学物理学


/

2, 由质心运动定理

− =


=


= ? → =

章目录
节目录
上一页
下一页
3.3 力矩的时空积累效应
例5
质量为m的小球A，以速度
沿质量为M的、
半径为R的地球表面水平切向向右飞出（如图）地轴
OO’与 平行，小球A的轨道与轴OO’相交于 3R的C

o

=×=×

=
( × )
=
−
×


对于单个质点，其角动量也可表示为
其大小
L r p s in r m v s in
m
r
Lr p

质点角动量定理的微分形式
0

=

大学物理学
章目录

节目录

v
m
r
上一页
下一页
3.3 力矩的时空积累效应
章目录
节目录
上一页
下一页
3.3 力矩的时空积累效应
Z
m
X
O O’
M地
CY
由（1）式：
由（2）式：
大学物理力对物体的时间累积效应

大学物理力对物体的时间累积效应


i
(4) 动量守恒定律是物理学最普遍、最基
本的定律之一．
14
2.2 力对物体的时间累积效应
例1：一长为l，密度均匀的柔软链条，其单位长度
的质量为，将其卷成一堆放在地面上，如图所示。若 用手握住链条的一端，以加速度a从静止匀加速上提。 当链条端点离地面的高度为x时，求手提力的大小。
解：以链条为系统，向上为X正向，地面为原点 建立坐标系。
L
而已落到桌面上的柔绳的重量为mg=Mgx/L
所以F总=F+mg=2Mgx/L+Mgx/L=3mg
18
证明二：
2.2 力对物体的时间累积效应 o
取如图坐标，设t时刻已有x长的
x
柔绳落至桌面，随后的dt 时间内将有
质量为 dx（Mdx/L)的柔绳以dx/dt
的速率碰到桌面而停止，它的动量变
化为：
x
dp vdm vdx
F ex F1 F2 FN
I
p
p0
8
2.2 力对物体的时间累积效应
注意
➢区分外力和内力 ➢内力仅能改变系统内某个物体的 动量，但不能改变系统的总动量.
9
2.2 力对物体的时间累积效应
讨论
F
（1） F 为恒力
I Ft
O t1
（2） F 为变力
F
I
t2 t1
Fdt F (t2
t1)
dt
F xg 3xa
x xg
N
O (l x)g
16
2.2 力对物体的时间累积效应
例2、 一质量均匀分布的柔软细
o
绳铅直地悬挂着，绳的下端刚好触到水
平桌面上，如果把绳的上端放开，绳将
x
力矩的空间累积效应公式

力矩的空间累积效应公式

力矩的空间累积效应公式
力矩是描述物体围绕一个轴旋转的物理量，通常用符号M表示。

力矩的大小等于施加在物体上的力的大小与力臂的乘积，即M= F ×d，其中F是力的大小，d是力臂的长度。

在三维空间中，如果一个物体在不同的轴上受到多个力矩的作用，那么这些力矩的效应将会叠加，形成一个空间累积效应。

这个效应可以表示为：
M = (Mx²+ My²+ Mz²)^(1/2)
其中，Mx、My、Mz分别代表三个力矩在x、y、z轴上的分量。

这个公式可以用来计算一个物体所受到的总力矩，并且可以帮助我们理解一个物体在空间中受力的情况。

需要注意的是，在计算力矩的空间累积效应时，必须使用向量运算，而不是简单的加法。

CH3-1力的空间累积效应

CH3-1力的空间累积效应


v2 m2 v4 m3 v3
v1 m4
v f1
v v f 1=−f 2
v ∑f =0
B A
v f2
B A S L
A1 = − f 1L
A2 = f 2S
∑A = − f 1(L − S)
例 质量为 的质点作平面曲线运动，其运动方程为 质量为m的质点作平面曲线运动， 的质点作平面曲线运动 v v v 其中a、 、 为正的常量 为正的常量。 r = a cosωt i + bsin ωt j 其中 、b、ω为正的常量。 求 解 时间内， 从t=0 到 t=π/2ω时间内，合外力所作的功。 时间内 合外力所作的功。 由速度的定义可得： 由速度的定义可得：
例 一轻弹簧的劲度系数为 =100N/m，用手推一质量 m =0.1 一轻弹簧的劲度系数为k ， kg 的物体把弹簧压缩到离平衡位置为 1=0.02m处, 如图所 的物体把弹簧压缩到离平衡位置为x 处 放手后，物体沿水平面移动到x 而停止。 示。放手后，物体沿水平面移动到 2=0.1m而停止。 而停止 求 物体与水平面间的滑动摩擦系数。 物体与水平面间的滑动摩擦系数。 解 放手后，物体运动到 x 1 处和弹簧分离。在整个过程中， 放手后， 处和弹簧分离。在整个过程中，
3. 质点系动能定律
把质点动能定理应用于质点系内所有质点 并把所得方程相加有: 并把所得方程相加有:
1 1 2 A = ∑ mivi2 − ∑ mivi2 ∑i i2 1 i i 2
m1
∑Ai = ∑Ai外 + ∑Ai内 i i i
讨论 (1) 内力和为零,内力功的和 内力和为零, 是否为零？ 是否为零？ 不一定为零
作用于质点的合力在某一路程中对质点所作的功， 作用于质点的合力在某一路程中对质点所作的功，等于质 点在同一路程的始、末两个状态动能的增量。 点在同一路程的始、末两个状态动能的增量。 说明 (1) Ek 是一个状态量, 是一个状态量, A 是过程量。 是过程量。 (2) 动能定律只适用于惯性系。 动能定律只适用于惯性系。
大学物理功和能

大学物理功和能


例4-4、一质量为m的质点，在xoy平面上运动。
其r位置a矢c量os为：ti
b
sin
tj
y
b
B
r
m
t A
x
其中a , b , 为正值常数，a > b 。 o
a
(1)求质点在A (a,0)点和B(0,b)点时的动能。
(2)求质点所受的作用力以及当质点从A运动到B的
解：(过1)程由中分r力
Fx
a
、Fy
cos
rdr
G rb ra 0
Mm r3
rdr
b
Mm
Mm
确定 (两G个0 质r点a ，) 则(MG、0 mrb
1 2
kx22
1 2
kx12
4 8102 (J )
例2：用铁锤把钉子敲入墙面木板。设木板对钉子的阻力
与钉子进入木板的深度成正比。若第一次敲击，能把钉
子钉入木板1cm。第二次敲击时，保持第一次敲击钉子
的速度，那么第二次能把钉子钉入多深？
分析：由于两次锤击的条件相同，锤击后钉子获得的速
度也相同，所具有的初动能也相同；由动能定理
两式相加得：
即： 外力的功之和＋内力的功之和 ＝系统末动能－系统初动能
记作：W外＋W内＝EKB - EKA
质点系动能定理
所有外力对质点系做的功和内力对质点系做的功 之和等于质点系总动能的增量。
注意：内力能改变系统的总动能， 但不能改变系统的总动量。
说明： 1、动能是状态量，任一运动状态对应一 定的动能。 2、功是过程量，它与能量的改变有联系。 3、动能是质点因运动而具有的做功本领。 4、动能与动量的异同：
F cos
S ab Fdr cos

物理学原理及工程应用104力的空间累积效应


保守力学系统 —— 能量守恒表现为机械能守恒 热力学系统 —— 表达形式是热力学第一定律
相对论性力学 —— 质能守恒定律
WL
物理学原理及工程应用
When a cheetah gallops, its back flexes and extends by an exceptional amount. Flexion of the back stretches elastic tendons and muscles along the top of the spine and also compresses the spine, storing mechanical energy. When the cheetah launches into its next bound, this energy helps to extend the spine, enabling the cheetah to run more efficiently.
WL

mg k
1


e
2 ky m

物理学原理及工程应用
【例1-23】质量为m、速度为 的子弹，射入置于光滑平面上 的质量为M的静止木块，木块滑行一段距离后，与子弹取得共 同速度继续向前运动。测得子弹入木深度为L，求：（1）子弹
对木块的平均冲击力 ；F（2）子弹与木块发生强烈挤擦内耗的
功 ；（3）子弹和木块的能量变化关系。
WL
物理学原理及工程应用
取子弹、木块为系统，它在水平方向不受外力的作用，动量守恒
m0 M m
m0
M m
——子弹和木块的共同速度
WL
物理学原理及工程应用
m0

大学物理 第二章 质点动力学


A Fs cos
A F s
（2-27）
式中为力F与位移 s之间的夹角。 根据矢量标积的定义，上式可以写成：
（2-28） 注意：如果力为变力，或质点作曲线运动，力作的功就不 能用上式来计算,而应该应用微积分的方法来计算力作的功。
设质点在变力 F 的作用下，沿曲线从A点运动到B点。将A 到B 的路径分成许多小段，任取一小段位移，用 d r 来表示。由 于 d r 非常微小，可以认为质点在这段位移元上所受的力为恒 力，则力对质点作的元功为：
A
在直角坐标系中:
A Fx dx Fy dy Fz dz Fx dx Fy dy Fz dz
二、质点的动能定理：
dr vB B 1 2 1 2 dv A m dr m dv mvdv mvB mvA A A vA dt dt 2 2 即：合力对质点所作的功等于质点始、末两状态的动能 的增量。 所以说：功是动能变化的量度。
F dv 解： 6t m dt
dx v 3t dt
2
dx 3t 2dt
A
x
0
3 36 t F 3 t d t Fdx dt 144J
2 0
t
2
0
2 P F v 12t 3t 288W
补充例题
例4 已知用力 F从竖直方向缓慢拉质量为m 的小球，且 F 保持方向不变。 求 = 0 时，F 作的功。 L θ 解： F T sin θ 0 T cosθ mg 0 T
B

课后思考及作业
阅读：P60-68 作业：习题2-25、习题2-26
2 2 2 4 2 2
由点(2，0) 到点（2，4）由于x=2为常量，dx=0，所以:

第1章 1.5 力的时间和空间积累效应

i i
P系2 ( pi 2 ) (mi 2vi 2 )
i i
F1外
m1.v11
m1.v11
dr1
F1外
④ 质点系动量定理
m1 :
f1内
过程
m1.v12
I
f 2内
II
m2 .v22
dr2
f1内
（f1内 F1,外 )dt d (m1v1 ) （f2内 F2,外 )dt d (m2v2 )
五. 动量定理与动量守恒定律（矢量角度） (conservation of momentum)
（§1.5.1）
■过程
F ma

2

1
力作用的积累
过程
1 2
按时间
按空间 功
冲量
■三个定理与三个守恒定律（过程）
*. 动量定理与动量守恒定律 (conservation of momentum) *. 动能定理与能量（机械能）守恒定律 (conservation of mechanical energy *. 角动量定理与角动量守恒定律 (conservation of angular momentum)
m M
R
（零）
（4）保守力与保守力的功
① 保守力 如果力作用在物体上，当物体沿闭合路径移动 一周时，力做的功为零，这样的力叫保守力。

f
a
f dr 0
f
●m
f
●
●
b
② 一对保守内力的功
如果一对内力的功与相对路径无关,只决定于相
互作用的质点的始末位置,这样一对力叫保守内力。
f f M m
Fi外1
成对出现； 大小相等方向相反。

功的定义及物理意义

功的定义及物理意义
如果一个力作用在物体上，且物体在这个力的方向上移动了一段距离，我们就说这个力对物体做了功。

物理意义：功是用来描写力对物体的空间累积效应，是物体运动状态变化的一种量度。

功，也叫机械功，是物理学中表示力对物体作用的空间的累积的物理量，功是标量，其大小等于力与其作用点位移的乘积，国际单位制单位为焦耳。

判断一个力对物体是否做功，可根据该力和物体位移方向的夹角是否为90°，或力与物体速度方向的夹角是否总是90°来确认力是否对物体做功。

夹角大于90°时功为负，夹角小于90°时功为正。

所以力的作用是相互的。

一个物体对外做了多少功，它就减少了多少能量。

反之，外界对一个物体做了多少功，这个物体的能量就增加了多少。

ch4-3力的空间累积效应

讨论工科物理教程43力的空间累积效应势能势能势能的定义势能的定义mgymgy万有引力的功万有引力的功重力的功重力的功kxkx保守力的功可写成保守力的功可写成对照动能定理对照动能定理弹性力的功弹性力的功势能势能eepp是与位置函数相关联的能量是与位置函数相关联的能量动能势能差工科物理教程43力的空间累积效应质点在任一位置时的势能等于质点从该位置经任意路径质点在任一位置时的势能等于质点从该位置经任意路径移动到势能零点时保守力所作的功移动到势能零点时保守力所作的功势能的讨论势能的讨论只有在保守力的情况下才能引入势能的概念
xi
m
x2
O
x1
x
A ( Fcos )s F x cos A F (xi ) F r
F (x) 示功图
★ 功是标量； ★ 功的数值在 F-x 示功图上， 是
A
O ★ 功有正功、负功之分 ，功的正负取决于 。
《工科物理教程》 R
Q
曲线下所包围的面积；
万有引力的功仅与始末位 置有关，而与路径无关
《工科物理教程》 R
Q
F
dl
m
r
m
rb
b
且有 A F dl 0
L
e
↑
↓
第4章
★ 弹性力的功
§4.3 力的空间累积效应
元功
dA F dr F dr cosπ
k
m x
O
x2
x1
kxdx
R
Q
《工科物理教程》
e
↑
↓
第4章
§4.3 力的空间累积效应
A外 A内 Ekb Eka Ek
推广到n个质点的质点系
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3
12t

3t
2dt

336t3dt 9t4 729(J )
0
0
2.3.1 质点的功与能
例2 质量为10kg 的质点，在外力作用下做平
面曲线运动，该质点的速度为
v

4t 2i
16
j
开始时质点位于坐标原点。求在质点从 y =
16m 到 y = 32m 的过程中，外力做的功。
解 W Fxdx Fydy
2.3.1 质点的功与能
力的空间累积效应：
F
对
r
积累
W，动能定理
一功
1
恒力作用下的功
W F cos r
F

r
F
r
2.3.1 质点的功与能
2 变力的功
dW F cos dr
dW

F
dr
dr ds
dW F cos ds
dri B
2.3.1 质点的功与能 例3 小球在水平变力 F 作用下缓慢移动，即在
所 与有 竖位 直置方上向均成近 角似。处于求力：平(1F)衡状的态功，，直(到2)绳重子力
的功。
解： l
m
2.3.1 质点的功与能
l
变力
m
恒力曲线运动
2.3.1 质点的功与能

例4 作用在质点上的力为 F 2 yi 4 j(N ) 在下列情况下求质点从 x1 2(m) 处运动到 x2 3(m) 处该力作的功：
4y x6
1
W1
x2 x1 ,
,y2 y1
(
Fx
dx

Fy
dy
)

x2 2 ydx
x1
y2 4dy 2
y1
O 3X 做

3 ( x2 / 2)dx
94
4dy 10 . 8J
2
1
功 与
W2
x2 x1 ,
,y2 y1
(
Fx
dx

Fy
dy
)

x2 2ydx
例1、质量为2kg的质点在力 F =12ti (SI)
的作用下，从静止出发，沿x轴正向作直线运 动。求前三秒内该力所作的功。
解：
W＝ F d r Fxdx 12tvdt
v v0
t
adt 0
0
tF dt
0m
t 12t dt 3t 2 02
W
dr
i * Fi
dr1 1
*A
F1
F
W
B F dr
B
F cos ds
A
A
2.3.1 质点的功与能
在直角系下

F dr

Fx
i
Fy
j
dxi dyj

Fz k dzk
W
B
F

dr

A
A（B Fxdx Fydy Fzdz）
在自然系下
B
B
W
F cosds
A
A F ds
2.3.1 质点的功与能
讨论
(1) 功的正、负
0o 90o , dW 0
90 o


90 o

180
o
,
F dr
dW 0 dW 0
(2) 作功的图示
F cos
W s2 F cos ds s1
Fx

m
dv x dt
80t
dx vxdt 4t2dt
Fy

m dv y dt

0
W
320t3dt
2.3.1 质点的功与能
ay 0
y vyt 16t
y 16时 t 1
y 32时 t 2
W Fxdx Fydy
2 320t3dt 1200 J 1

1 2
k x12
)
2 保守力与非保守力 势能
F
dW
O x1
x2 x
dx
W
x2 Fdx
x1
x2 x1

kxdx
( 1 2
k x22

1 2
k x12
)
2 保守力与非保守力 势能
保守力作功的数学表达式
保守力所作的功与路径无关，仅决定 于始、末位置．
引力的功
W

(G

m'm) (G rB
r dr
m'
rB
B
dW

F
dr

G
m'm r2
er
dr
2 保守力与非保守力 势能
m从A到B的过程中 F作功：
B m'm
W
F dr
G
A
r2
er dr
er
dr

er

dr
cos
dr
A
rA
r

m dr dr
x1
y2 4dy
y1
路 径 有
3
94
( x 6) / 2dx 4dy 21 .25J
2
1
关
2 保守力与非保守力 势能
二 万有引力和弹性力作功的特点
(1) 万有引力作功
m' 对m 的万有引力为
F

G
m'm r2
er
m移动dr时，F作元功为
rA
Ar
m
dr
m'm rA
)
弹力的功
W

(
1 2
kxB2

1 2
kx
2 A
)
2 保守力与非保守力 势能
F

d r

W W1 W2 W3
2.3.1 质点的功与能
功的单位（焦耳）
1J 1Nm
平均功率 P W
t
瞬时功率 P
lim
ΔW

dW

F

v
t0 Δt
dt
P Fvcos
功率的单位（瓦特）
1 W 1 J s1 1 kW 103 W
2.3.1 质点的功与能
1. 质点的运动轨道为抛物线 x2 4 y
2. 质点的运动轨道为直线4 y x 6
Y x2 4y
2.25
4y x6
1
ቤተ መጻሕፍቲ ባይዱ
2 O 3 X
B
W A F dr
2.3.1 质点的功与能
Y x2 4y
b
a Fxdx Fydy Fzdz
2.25
F 2 yi 4 j(N )
W rB G m'm dr
rA
r2
r dr
m'
rB
B
W Gmm( 1 1 ) rB rA
2 保守力与非保守力 势能
(2) 弹性力作功 F F'
o x Px


F kxi
dW kxdx
W
x2 Fdx
x1
x2 x1

kxdx
( 1 2
k x22
s
o s1 ds s2
2.3.1 质点的功与能
（3）功是一个过程量，与路径有关．
（4）合力的功，等于各分力的功的代数和．
F F1 F2 F3
W
B
F dr
A
A（B F1 dr F2 dr F3 dr）
B
B
B
W1 A F1 dr W2 A F2 dr W3 A F3 dr