七下数学每日一练：估算无理数的大小练习题及答案_2020年单选题版

C．7
D．8
6．（2019 秋•沙坪坝区期末）实数 23 在数轴上位于两个连续整数之间，这两个连续整数为
()
A．3 和 4
B．4 和 5
C．5 和 6
D．6 和 7
7．（2019 秋•余杭区期末）估计 21 的大小应在 ( )
A．3.5 与 4 之间 B．4 与 4.5 之间．【解答】解： 4 7 9 ， 2 7 3， 点 Q 在这两个数之间， 故选： B ．
2．【解答】解： A.1 2 2 ，不符合题意； B.1 3 2 ，不符合题意； C.2 7 3 ，符合题意； D.3 10 4 ，不符合题意． 故选： C ．
3．【解答】解： 3 11 4 ， 1 11 2 2 ， 那么与实数 11 2 对应的点在线段 CD 上， 故选： C ．
11．【解答】解： 25 29 36 ， 5 29 6 ， 根据题意得： x 5 ， y 29 5 ， 则原式 ( 29 5)( 29 5) 29 25 4 ．
3a b 1的平方根是 4 ， 3a b 1 16 ， 解得： b 2 ，
c 是 2 5 的整数部分， c 4 ， a 2b c 5 4 4 5 ， 故 a 2b c 的平方根为： 5 ．
二、解题方法或注意事项 1．无理数估算的基本方法，多用逼近法，用有理数逼近无理数，求无理数的近似值．若 a x b ，则 a x b （ a 、 x 、 b 为非负数）， 3 a 3 x 3b ，因此，当 a 与 b 为平 方数或立方数时，则可知无理数的大致范围；
2．无理数的整数部分与小数部分：逼近法确定大致范围后，整数部分向前取一位，小数部 分为 无理数-整数部分； 3．易错提醒：负无理数（或含无理数的减法式子）在确定整数部分时，可借用数轴．

七下数学每日一练：估算无理数的大小练习题及答案_2020年填空题版答案答案答案答案答案答案答案答案答案答案2020年七下数学：数与式_无理数与实数_估算无理数的大小练习题~~第1题~~(2019.七下期末) 任何实数a ，可用[a]表示不超过a 的最大整数，如[2]=2，[3.7]=3，现对72进行如下操作：，这样对72只需进行3次操作后变为1，类似地：对325只需进行________次操作后变为考点： 估算无理数的大小;定义新运算;~~第2题~~(2019龙岩.七下期末) 请写出一个比2大且比4小的无理数：________.考点： 估算无理数的大小;~~第3题~~(2019滨州.七下期中) 写出一个比－2 小的无理数________．考点： 估算无理数的大小;~~第4题~~(2019十堰.七下期末)对于有理数a ，b ，定义min{a ，b}的含义为：当a ＜b 时，min{a ，b}＝a ，例如：min{1，－2}＝－2.已知min{ ，a}＝ ，min{ ，b}＝b，且a 和b为两个连续正整数，则a －b 的平方根为________.考点： 估算无理数的大小;代数式求值;~~第5题~~(2019通化.七下期中) 是的整数部分， 是的小数部分。

则 ________考点： 估算无理数的大小;~~第6题~~(2019白城.七下期中) 已知5+小数部分为m ，11﹣ 为小数部分为n ，则m+n ＝________．考点： 估算无理数的大小;~~第7题~~(2019谢家集.七下期中) 规定用符号[m ]表示一个实数m 的整数部分，例如[ ]＝0，[3.14]＝3．按此规定 的值为________．考点： 估算无理数的大小;~~第8题~~(2019贵池.七下期中) 设的整数部分和小数部分分别是 、 ，则 ________， ________。

考点： 估算无理数的大小;~~第9题~~(2019博兴.七下期中) 已知a，b 为两个连续整数，且a<<b ，则a+b 的值为________．考点： 估算无理数的大小;~~第10题~~(2019黄石.七下期中) 已知x 是 的整数部分，y 是 的小数部分，则 的平方根为________.考点： 估算无理数的大小;代数式求值;2020年七下数学：数与式_无理数与实数_估算无理数的大小练习题答案1.答案：2.答案：3.答案：4.答案：5.答案：6.答案：7.答案：8.答案：9.答案：10.答案：。

七上数学每日一练：估算无理数的大小练习题及答案_2020年填空题版答案解析答案解析答案解析答案解析答案解析答案解析答案解析答案解析答案解析2020年七上数学：数与式_无理数与实数_估算无理数的大小练习题1.(2020苍南.七上期末) 已知一个无理数a ，满足1<a<2，则这个无理数a 可以是________(写出一个即可)。

考点： 估算无理数的大小;2.(2020西湖.七上期末) 已知：，则 ________.考点： 估算无理数的大小;实数的绝对值;3.(2019萧山.七上期末) 已知则 可取的整数值为________.考点： 估算无理数的大小;4.(2019江干.七上期末) 如图,在4×4方格中阴影正方形的边长是________，这个长度介于两个相邻整数________之间(小正方格的边长为1个长度单位）。

考点： 估算无理数的大小;几何图形的面积计算-割补法;5.(2019嘉兴.七上期末) 已知a ，b 是正整数，且a<<b ，则a -b 的最大值是 ________ ．考点： 估算无理数的大小;代数式求值;6.(2020.七上期中) 已知a 为 的整数部分，b ﹣1是400的算术平方根，则 的值为________．考点： 估算无理数的大小;代数式求值;7.(2017萧山.七上期中) 把5的平方根和立方根按从小到大的顺序排列为________．考点： 平方根;立方根及开立方;估算无理数的大小;8.(2016长兴.七上期末) 任何实数a ，可用[a]表示不超过a 的最大整数，如[4]=4，[]=1，现对72进行如下操作：72 [ ]=8 [ ]=2 []=1，这样对72只需进行3次操作后变为1，类似地，对81只需进行3次操作后变为1；那么只需进行3次操作后变为1的所有正整数中，最大的是________．考点： 估算无理数的大小;9.(2016新泰.七上期末) (2016七上·新泰期末) 满足﹣＜x ＜ 的整数是________．考点： 估算无理数的大小;实数大小的比较;一元一次不等式组的特殊解;10.(2017金华.七上期中) 写出一个比﹣1小的无理数是________22考点：估算无理数的大小;答案解析2020年七上数学：数与式_无理数与实数_估算无理数的大小练习题答案1.答案：2.答案：3.答案：4.答案：5.答案：6.答案：7.答案：8.答案：9.答案：10.答案：。

七下数学每日一练：无理数的认识练习题及答案_2020年单选题版
2020年 七 下 数 学 ： 数 与 式 _无 理 数 与 实 数 _无 理 数 的 认 识 练 习 题
~~第1题~~ (2018防城港.七下期末) 下列实数中是无理数的是（ ）
A. B. C. D.0
考点： 无理数的认识;
答案
~~第2题~~ (2019景.七下期末) 已知一组数据
考点： 无理数的认识;
答案
2020年 七 下 数 学 ： 数 与 式 _无 理 数 与 实 数 _无 理 数 的 认 识 练 习 题 答 案
1.答 案 ： C 2.答 案 ： C 3.答 案 ： B 4.答 案 ： C 5.答 案 ： D 6.答 案 ： A 7.答 案 ： A 8.答 案 ： C 9.答 案 ： B 10.答 案 ： B
A.1B.2C.3D.4 考点： 无理数的认识;
，π，
，0．0456， ，1．010010003…，则无理数的个数是( )
答案
~~第3题~~ (2019端州.七下期中) 实数－2，0.3， ， ，－π中，无理数的个数有（ ）.
A . 1个 B . 2个 C . 3个 D . 4个
考点： 无理数的认识;
答案
~~第4题~~ (2019阜阳.七下期中) 在实数 ，
， ，0，π，
中，无理数的个数是（ ）数的认识;
答案
~~第5题~~ (2019监利.七下期末) 以下各数中， 、﹣2、0、3 、 、﹣1.732、
无理数的个数有（ ） A . 1个 B . 2个 C . 3个 D . 4个 考点： 无理数的认识;
答案
~~第8题~~ (2019廉江.七下期末) 下列个数： ， ，

考点： 估算无理数的大小;
答案解析
2020年 七 上 数 学 ： 数 与 式 _无 理 数 与 实 数 _估 算 无 理 数 的 大 小 练 习 题 答 案
1.答案：
2.答案： 3.答案： 4.答案： 5.答案：
． 答案解析
2. (2020吴兴.七上期中) 大家知道 是无理数，而无理数是无限不循环小数，因此 的小数部分我们不可能全部地写 出来，于是小明用 ﹣2来表示 的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理，因为 ＜ ＜ ，即2＜ ＜3，故 的整数部分是2，将这个数减去其整数部分，差就是小数部分． ∴ 的整数部分为2，小数部分为（ ﹣2）．
答案解析
4. (2018城.七上期中) 阅读：通过探究知道：
，小数部分可以用
来表示．
已知
，其中 是一个整数，
，它是值．
考点： 估算无理数的大小;实数的运算;
答案解析
5. (2017瑞安.七上期中) 数学张老师在课堂上提出一个问题：“通过探究知道： ≈1.414…，它是个无限不循环小数，也 叫无理数，它的整数部分是1，那么有谁能说出它的小数部分是多少”，小明举手回答：它的小数部分我们无法全部写出来 ，但可以用 ﹣1来表示它的小数部分，张老师夸奖小明真聪明，肯定了他的说法．现请你根据小明的说法解答： 已知8+ =x+y，其中x是一个整数，0＜y＜1，求2x+（y﹣ ）2016的值．
七上数学每日一练：估算无理数的大小练习题及答案_2020年解答题版
2020年 七 上 数 学 ： 数 与 式 _无 理 数 与 实 数 _估 算 无 理 数 的 大 小 练 习 题
1. (2016广饶.七上期末) 已知a 考点： 估算无理数的大小;

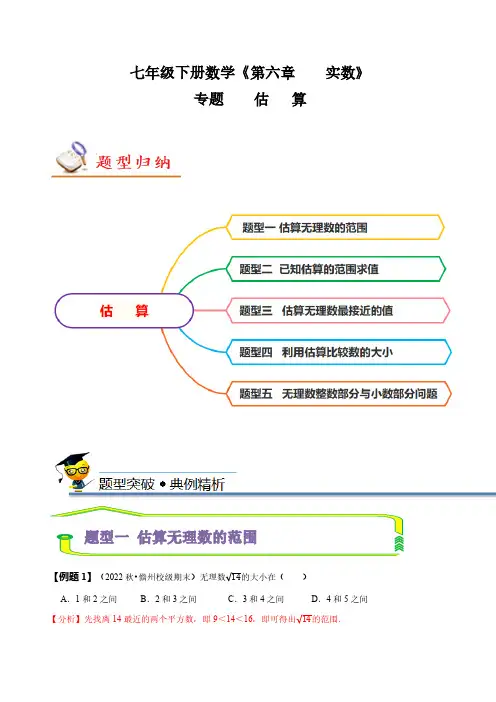
七年级下册数学《第六章实数》专题估算【例题1】（2022秋•A．1和2之间B．2和3之间C．3和4之间D．4和5之间【分析】先找离14最近的两个平方数，即9＜14＜16【解答】解：∵9＜14＜16，∴34；故选：C．【点评】本题考查的是无理数的估值，解题关键找到离14最近的两个平方数．【变式1-2】（2022秋•A．3和4之间B．4和5之间C．5和6之间D．6和7之间【分析】本题考查了估算无理数的大小：利用完全平方数和算术平方根对无理数的大小进行估算．也考查了算术平方根．【解答】解：∵25＜27＜36，∴56，5和6之间，故选：C．【点评】本题考查了估算无理数的大小，熟练掌握平方数是解题的关键．【变式1-3】（2011秋•A．2与3之间B．3与4之间C．4与5之间D．5与6之间∴45，4和5之间．故选：C．【变式1-4】（2022秋•+1的值在（ ）A．4到5之间B．5到6之间C．6到7之间D．7到8之间56，可得．【解答】解：∵56，∴6+1＜7，故选：C．【点评】本题考查的是无理数大小的估算，解题的关键是会用夹逼法进行估算．【变式1-5】（2023•南岸区校级开学）估计3+A．5和6之间B．6和7之间C．7和8之间D．8和9之间3+【解答】解：∵34，∴6＜37．故估计3+6和7之间．故选：B．【点评】本题考查了无理数的估算，估算无理数大小要用逼近法．用有理数逼近无理数，求无理数的近似值．【变式1-6】（2022秋•3的值在（ ）A．3到4 之间B．4到5之间C．1到2 之间D．2到3 之间【分析】首先得出45，进而求出结论．∴45，3的值在1到2之间．故选：C．【变式1-7】（2022秋•5的值（ ）A．在1和2之间B．在2和3之间C．在3和4之间D．在4和5之间【分析】根据完全平方数，进行计算即可解答．【解答】解：∵49＜56＜64，∴78，∴2―5＜3，―5的值在2和3之间，故选：B．【点评】本题考查了估算无理数的大小，熟练掌握完全平方数是解题的关键．【变式1-8】（2022秋•雁塔区校级期末）2A．0和1之间B．1和2之间C．0和﹣1之间D．﹣1和﹣2之间【解答】解：∵23，∴﹣1＜2―0，∴2―1和0之间．故选：C．【点评】本题考查估算无理数的大小，掌握算术平方根的定义是正确解答的前提．【变式1-9】（2022•庐阳区校级三模）若无理数x=x的范围正确的是（ ）A．1＜x＜2B．2＜x＜3C．3＜x＜4D．4＜x＜5【分析】根据算术平方根的性质（被开方数越大，其算术平方根越大）解决此题．【解答】解：∵4＜5＜9，∴23．+2，∴4＜25．∵x=∴4＜x＜5．故选：D．【点评】本题主要考查算术平方根的性质，熟练掌握被开方数越大，其算术平方根越大是解决本题的关键．【变式1-10】（2022秋•双牌县期末）满足xA．4个B．3个C．2个D．1个【分析】先估算出―【解答】解：∵12，∴﹣2＜―1，∵12，∴满足x1，0，1，共3个，故选：B．【点评】本题考查了估算无理数的大小，能估算出―【变式1-11】（2022秋•萧山区期中）设面积为31的正方形的边长为x，则x的取值范围是（ ）A．5.0＜x＜5.2B．5.2＜x＜5.5C．5.5＜x＜5.7D．5.7＜x＜6.0【分析】利用正方形的面积＝边长×边长可得正方形边长x=【解答】解：正方形边长x∵5.52＝30.25，5.62＝31.36，∵5.55.6．故选：C．【点评】此题主要考查了估算无理数的大小，思维方法：用有理数逼近无理数．【变式1-12】（2022秋•江北区校级期末）如果m＝1，那么m的取值范围是（ ）A．4＜m＜5B．4＜m＜6C．5＜m＜6D．5＜m＜73与4之间，再根据m＝―1，即可得出m的取值范围．【解答】解：∵34，∴2×3﹣1＜―1＜2×4﹣1，即5＜―1＜7，∴m的取值范围是5＜m＜7．故选：D．【点评】本题考查了估算无理数的大小，掌握题意确定无理数的整数部分是关键．【例题2】（2022秋•鄞州区期末）若整数aaa是（ ）A．2B．3C．4D．5【分析】先计算2=7，2=15，然后看哪个平方数在7和15之间即可．【解答】解：∵7＜9＜15，3∴如果整数a a a的值是：3．故选：B．【点评】本题考查了估算无理数的大小，熟练掌握平方数是解题的关键．【变式2-1】（2022秋•衡山县期末）已知n n n等于（ ）A．5B．6C．7D．8【解答】解：∵36＜40＜49，∴67，∵49＜50＜64，∴78，∵n n∴n＝7，故选：C．【点评】本题考查了估算无理数的大小，熟练掌握平方数是解题的关键．【变式2-2】（2022秋•aa的值不可能为（ ）A．2B．3C．4D．56，23a a的整数．=6aa＜6，∵23，∴整数a的值可为3或4或5，∴整数a的值不可能为2．故选：A．【点评】本题考查了估算无理数的大小，熟练掌握根式的运算是解本题的关键，综合性较强，难度适中．【变式2-3】（2022秋•南关区校级期末）若n为整数，n n+1，则n的值为（ ）A．1B．0C．2D．3【分析】利用完全平方数，进行计算即可解答．【解答】解：∵9＜13＜16，∴34，∵n为整数，n n+1，∴n＝3，故选：D．【点评】本题考查了估算无理数的大小，熟练掌握完全平方数是解题的关键．【变式2-4】（2022秋•九龙坡区期末）若自然数n满足n＜―2＜n+1，则n的值为（ ）A．4B．5C．6D．7【分析】根据算术平方根的定义估算无理数2的大小即可．【解答】解：=78，∴5―2＜6，即5＜―2＜6，∵n＜―2＜n+1，而n是自然数，∴n＝5，故选：B．【点评】本题考查估算无理数的大小，理解算术平方根的定义是正确估算的前提．【变式2-5】（2022秋•福田区期末）若m，n是两个连续的整数且m n，则m+n＝（ ）A．5B．6C．7D．8m，n的值，然后代入式子中，进行计算即可解答．【解答】解：∵9＜14＜16，∴34，∵m，n是两个连续的整数且m n，∴m＝3，n＝4，∴m+n＝3+4＝7，故选：C．【点评】本题考查了估算无理数的大小，熟练掌握完全平方数是解题的关键．【变式2-6】（2022春•新罗区校级月考）在― ．【分析】根据估算――【解答】解：∵22＞3＞12，32＜10＜42，∴―2＜――1，34，∴―1、0、1、2，3；﹣1+0+1+2+3＝5．故答案为：5．【点评】本题考查了无理数的近似值，正确估计出无理数的近似值是解题关键．【变式2-7】（2022秋•桂平市期末）已知m，n为两个连续的整数，且m n，则（m﹣n）2023的值是（ ）A．2023B．﹣2023C．1D．﹣1m、n的值，再代入计算即可．【解答】解：∵34，而m n，其中m，n为两个连续的整数，∴m＝3，n＝4，∴（m﹣n）2023＝（3﹣4）2023＝﹣1，故选：D．【点评】本题考查估算无理数的大小，理解算术平方根的定义是正确解答的前提．【变式2-8】（2022秋•通川区校级期末）已知整数x2≤x―1，则x＝ ．―2―1的值的范围，即可解答．【解答】解：∵4＜5＜9，∴23，∴02＜1，∵4＜7＜9，∴23，∴11＜2，∵整数x2≤x―1，∴x＝1，故答案为：1．【点评】本题考查了估算无理数的大小，熟练掌握估算无理数的大小是解题的关键．【变式2-9】（2022秋•辉县市校级期末）若a b，且a，b是（ ）A．9B．5C．4D．3a，b的值，进而得出答案．【解答】解：∵a b，且a，b为两个连续的正整数，∴a＝4，b＝5，==3．故选：D．【变式2-10】（2022秋•莱阳市期末）若a b，且a、b为两个连续的正整数，则a+b的平方根是　．∴45，∴a＝4，b＝5，∴a+b＝4+5＝9，∴a+b的平方根是±3．【点评】本题考查了平方根，求出a、b的值是解题的关键．【变式2-11】（2022春•蓬江区校级月考）已知a，b为两个相连的整数，满足a+11＜b，则a+b的立方根为 ．【分析】11的值的范围，然后求出a，b的值，最后代入式子中，进行计算即可解答．【解答】解：∵4＜6＜9，∴23，∴13+11＜14，∵a，b为两个相连的整数，满足a+11＜b，∴a＝13，b＝14，∴a+b＝27，∴a+b的立方根为3，故答案为：3．【点评】本题考查了估算无理数的大小，熟练掌握完全平方数是解题的关键．【变式2-12】（2022秋•古田县期中）已知a，b为两个连续的整数，且a＜―b，则2a﹣3b＝ ．【分析】首先估算―5和﹣6之间，然后可得a、b的值，进而可得答案．【解答】解：∵――∴﹣6＜―5，∴a＝﹣6，b＝﹣5，∴2a﹣3b＝﹣12+15＝3，故答案为：3．【点评】此题主要考查了估算无理数，用有理数逼近无理数，求无理数的近似值．【变式2-13】（2022秋•海曙区期中）若整数x满足3+x2，则x的值是 ．3+2+小即可．【解答】解：∵43＝64，，53＝125，而64＜65＜125，∴45，∴7＜3+8，又：∵82＝64，，92＝81，而64＜65＜81，∴89，∴10+2＜11，又∵整数x满足3+≤x≤+2，∴x＝8或x＝9或x＝10，故答案为：8或9或10．【点评】本题考查估算无理数的大小，掌握算术平方根、立方根的定义是正确估算的前提．【例题3】（2022秋•A．5B．6C．7D．86．故选：B．【点评】此题主要考查了估算无理数的大小，正确得出最接近的有理数是解题关键．【变式3-1】（2022春• ．【分析】用夹逼法估算无理数的大小即可得出答案．【解答】解：∵4＜5＜6.25，∴22.5，2．故答案为：2．【点评】本题考查了估算无理数的大小，无理数的估算常用夹逼法，用有理数夹逼无理数是解题的关键．【变式3-2】（2021春•A．5B．6C．7D．851距离哪个整数的平方接近即可确定答案．【解答】解：∵49＜51＜64，即78，∵7.52＝56.25，51＜56.25，7．故选：C．【点评】本题考查了无理数的估算，解题关键是确定无理数的整数部分即可解决问题．【变式3-3】（2022•三门峡二模）数轴上与最接近的整数是．1.7，由此可得出本题的答案．【解答】解：﹣1.7，∴最接近的整数为-2．故答案为：-2．【点评】本题主要考查了无理数的估算，解题关键是确定无理数的整数部分即可解决问题．【变式3-4】（2022秋•A．﹣1B．0C．1D．2【分析】由π﹣4＜0=4―π1．【解答】解：∵π﹣4＜0，4―π．∵4﹣π最接近1，1．故选：C．a(a≥0)―a(a＜0)是解题关键．【变式3-5】（2022秋•南岸区期末）与2A．5B．6C．7D．8【分析】根据完全平方数，进行计算即可解答．【解答】解：∵9＜10＜16，∴34，∵3.52＝12.25，∴3 3.5，∴5＜2 5.5，∴与25，故选：A．【点评】本题考查了估算无理数的大小，熟练掌握完全平方数是解题的关键．【变式3-6】（2022春•1最接近的整数是（ ）A．5B．6C．7D．8【分析】用夹逼法估算无理数的大小即可得出答案．【解答】解：∵36＜40＜42.25，∴6 6.5，∴5―1＜5.5，∴最接近的整数是5，故选：A．【点评】本题考查了估算无理数的大小，无理数的估算常用夹逼法，用有理数夹逼无理数是解题的关键．【变式3-7】3最接近的是（ ）A．5B．6C．7D．8的取值范围即可．【解答】解：∵3.62＜13＜3.72，∴3.6 3.7，∴3.6+33＜3.7+3，即6.63＜6.7，+3最接近的是7．故选：C．【点评】此题主要考查了估算无理数的大小，正确得出无理数的取值范围是解题关键．A．1B．2C．3D．4【变式3-9】（2022秋•宁德期末）定义[x]为不大于x的最大整数，如[2]＝2，=1，[4.1]＝4，则满足=5，则n的最大整数为　．【分析】由题意得：56，然后利用平方运算，进行计算即可解答．【解答】解：由题意得：∵5≤6，∴25≤n＜36，∴n的最大整数为35．故答案为：35．【点评】本题考查了无理数的估算，掌握夹逼法，用有理数夹逼无理数是关键．【变式3-10】（2022春•香洲区期末）如图，用边长为3的两个小正方形拼成一个面积为18的大正方形，则大正方形的边长最接近的整数是（ ）A．4B．5C．6D．7【分析】根据算术平方根的概念结合正方形的性质得出其边长，进而得出答案．【解答】解：∵用边长为3的两个小正方形拼成一个大正方形，∴大正方形的面积为：9+9=18，∴4 4.5，∴大正方形的边长最接近的整数是4．故选：A．【点评】此题主要考查了算术平方根，正确掌握算术平方根的定义是解题的关键．【例题4】（2022•惠水县模拟）下列各数中比―A．﹣2B．﹣1C．―12D．0【分析】根据实数比较大小的方法分析得出答案．【解答】解：A、∵|﹣2|＝2，|=由2∴﹣2＜B、∵|﹣1|＝1，|―=由1∴﹣1＞C、∵|―12|=12，|―=由1 2＜∴―12＞―D、0＞―故选：A．【点评】此题主要考查了实数比较大小，正确掌握比较方法是解题关键．【变式4-1】（2021秋•乳山市期末）通过估算比较大小，下列结论不正确的是（ ）AB．―C ＜12D【分析】根据算术平方根的定义和立方根的定义估算各根式的大小，然后再比较大小即可．【解答】解：A、因为64＜69，所以44A正确，与要求不符；B―3，―=―3，故―B错误，与要求相符；C32＜1＜12，则C正确，与要求不符；D、=D正确，与要求不符．故选：B．【点评】本题主要考查的是实数大小比较，掌握无理数的大小的方法是解题的关键．【变式4-2】（2022春•铁东区校级月考）若将被如图所示的墨迹覆盖的数是（ ）A．B．C D【分析】先估算出各数，再根据实数与数轴的关系即可得出结论．【解答】解：―=3，在墨迹覆盖处的右边，不符合题意；23，符合题意；，3，在墨迹覆盖处的右边，不符合题意；故选：C．【点评】本题考查无理数的大小比较；熟练掌握数轴上点的特点，能够准确判断无理数的范围是解题的关键．【变式4-3】（2021秋•灌云县月考）已知：a=―1，b=2a、b的大小关系为：a b（填“＞”、“＜”或“＝”）．【分析】先判断a、b的正负，再比较它们的大小．【解答】解：∵12，∴a=―1＞0，∵23，∴b＝20，∴a＞b，故答案为：＞．【点评】本题考查实数大小比较，解答本题的关键是明确实数的意义，会比较实数的大小．【变式4-4】 13； 1 89．（填“＜”或“＞”）【分析】先估算出各个数的范围，再比较大小．【解答】解：∵23，∴02＜1，＜13；∵12，∴21＜3，1；∵34，∴2―1＜3，1，∵89＜1，＞89，故答案为：＜，＞，＞．【点评】本题考查了实数大小比较的方法，估算出无理数的大小是解决本题的关键．【变式4-5】通过估算，比较下面各组数的大小：（1，12； （2 3.85．【分析】（1（2）首先求出3.852，进而比较即可．【解答】解：（1 1.73，1＜1，＜12；（2）∵3.852≈14.8，3.85．【变式4-6】通过估算比较大小：（1与85（2与13．【分析】（1＜32，再比较32与85的大小，即可得出与85的大小，（2＞13．【解答】解：（1＜32，∵32=1510，85=1610，∴32＜1610，＜85，（2＞13．【点评】此题主要考查了的是实数的大小比较，解题的关键是选择合适的被开方数．【例题5】（2022春•鼓楼区校级期中）已知=x+y，其中x是整数，且0＜y＜1，则xy ＝ ．x的值，再根据已知条件得出y的值，然后代入要求的式子进行计算即可．【解答】解：∵12，x是整数，∴x＝1，x+y，∴xy=1．1．【变式5-1】（2022秋•+2的小数部分是 ．22减去它的整数部分，即可求出小数部分．【解答】解：∵23，∴42＜5，2的整数部分是4，22﹣4=2；2．【点评】此题主要考查了估算无理数的大小，掌握估算的能力是解题的关键，经常用逼近法确定无理数的整数部分．【变式5-2】（2022秋•a b，则a+b―= ．a、b的值，再代入求出即可．【解答】解：∵12，34，∴a=―1，b＝3，∴a+b―=1+3＝2．故答案为：2．【变式5-3】（2022秋•金牛区校级期末）已知：2+m，小数部分为n，则2m﹣n＝ ．2+m、n的值，再代【解答】解：∵12，∴3＜24，∴2+m＝3，小数部分n＝2―3=―1，∴2m﹣n＝6+1＝7故答案为：7―【点评】本题考查估算无理数的大小，掌握算术平方根的定义是正确解答的前提，确定m、n的值是正确计算的关键．【变式5-4】（2022秋•双峰县期末）若x y表示它的小数部分，则+x)y的值为 ．x、y的值，再代入计算即可．【解答】解：∵23，x＝2，小数部分y=2，∴+x)y22）＝5﹣4＝1，故答案为：1．【点评】本题考查估算无理数的大小，掌握算术平方根的定义是正确解答的前提．【变式5-5】（2022秋•东港市期末）若55a，b，则a+b＝ ．a，b，然后代入计算即可．【解答】解：∵34，∴8＜5+9，1＜5―2，∴a=5+8=―3，b=5―1=4―∴a+b=―3+4―1．故答案为：1．【点评】本题主要考查了估算无理数的大小、代数式求值以及二次根式的加减运算，求得a，b的值是解题的关键．【变式5-6】（2022秋•商水县期末）已知a的立方根是2，b c是9的平方根，则a+b+c的算术平方根是 ．【分析】根据平方根、立方根、估算无理数的大小确定a、b、c的值，再代入计算即可．【解答】解：∵a的立方根是2，b c是9的平方根，∴a＝8，b＝3，c＝±3，当a＝8，b＝3，c＝3时，a+b+c＝14，∴a+b+c的算术平方根是当a＝8，b＝3，c＝﹣3，a+b+c＝8，∴a+b+c的算术平方根是=【点评】本题考查平方根、立方根、估算无理数的大小，理解平方根、立方根的定义、掌握估算无理数的大小的方法是正确解答的前提．【变式5-7】（2022•南谯区校级模拟）已知﹣2m是64的负的平方根，3n mn的立方根为 ．【分析】根据平方根的意义可得﹣2m＝﹣8，从而可得：m＝43n＝6，进而求出n的值，然后代入式子中进行计算即可解答．【解答】解：∵﹣2m是64的负的平方根，∴﹣2m＝﹣8，解得：m＝4，∵36＜37＜49，∴67，6，∴3n＝6，解得：n＝2，∴mn＝4×2＝8，∴mn的立方根为2，故答案为：2．【点评】本题考查了估算无理数的大小，平方根，熟练掌握估算无理数的大小是解题的关键．【变式5-8】（2022春•玉州区期中）阅读下面文字，然后回答问题．的整数部分是11表示．由x+y，其中x是整数，且0＜y＜1，那么x＝1，y=1．请解答下列问题：（1a+b，其中a是整数，且0＜b＜1，求a，b的值；（2）如果―c+d，其中c是整数，且0＜d＜1，求c，d的值；（3）已知3+m+n，其中m是整数，且0＜n＜1，求|m﹣n|的值．【分析】（1）估算出23，依此即可确定出a，b的值；（2）估算出23，可得﹣3＜――2，依此即可确定出c，d的值；（3）根据题意确定出m与n的值，代入求出|m﹣n|即可．【解答】解：（1a+b，其中a是整数，且0＜b＜1，23，∴a＝2，b=2；（2）∵c+d，其中c是整数，且0＜d＜1，23，﹣3＜―2，∴c＝﹣3，d＝3（3）∵2+m+n，其中m是整数，且0＜n＜1，∴m＝4，n―2，则|m﹣n|＝|4―2|＝6―【点评】此题考查了估算无理数的大小，解题关键是确定无理数的整数部分即可解决问题．【变式5-9】（2022春•乐昌市校级期中）阅读下面的文字，解答问题：11，将这个数减去其整数部分，差就是小数部分．23，2―2；请解答：（1 ，小数部分是 ；（2a b，求|a﹣b|+的值；（3）已知：9+x+y，其中x是整数，且0＜y＜1，求x﹣y的相反数．【分析】（1（2）分别确定出a与b的值，代入原式计算即可求出值；（3）根据题意确定出等式左边的整数部分得到y的值，进而求出y的值，即可求出所求．【解答】解：（1）∵78，77．故答案为：77．（2）∵34，∴a3，∵23，∴b＝2，∴|a﹣b|=―3―2|+=5―＝5．（3）∵23，∴11＜9+12，∵9=x+y，其中x是整数，且0＜y＜1，∴x＝11，y=9+11=2，∴x﹣y=11―2)=13―∴x﹣y13．【点评】此题考查了估算无理数的大小，以及实数的运算，熟练掌握运算法则是解本题的关键．【变式5-10】（2022秋•沧州期末）已知一个正数a的平方根分别是2a﹣5和2a+1，另一个实数b的立方根是2，c（1）a，b，c的值；（2）求2a+4b﹣c2的平方根．【分析】（1）由平方根的性质知2a﹣5和2a+1互为相反数，可列式，解之可求得a的值；根据立方根定义可得b的值；根据34可得c的值；（2）分别将a，b，c的值代入2a+4b﹣c2中，即可求得它的值及平方根．【解答】解：（1）∵一个正数的平方根分别是2a﹣5和2a+1，另一个实数b的立方根是2，∴2a﹣5+2a+1＝0，b＝8，解得：a＝1，则a的值是1，b的值是8；∵9＜15＜16，∴34，3，∴c＝3，综上所述，a＝1，b＝8，c＝3；（2）∵a＝1，b＝8，c＝3，∴2a+4b﹣c2＝2+32﹣9＝25，∵25的平方根±5，∴2a+4b﹣c2的平方根±5．【点评】本题主要考查了立方根、平方根及无理数的估算，解题的关键是熟练掌握平方根和立方根的定义．【变式5-11】（2022秋•兴化市校级期末）材料1：2.5的整数部分是2，小数部分是0.5，小数部分可以看成是2.5﹣2得来的，而12，1，1材料2：若10―a+a，b要满足a＝10，b=―1．2根据以上材料，完成下列问题：（1 ，小数部分是　；（2）3a＜3+b，求a+b的算术平方根．【分析】（1）根据完全平方数，进行计算即可解答；（23+a，b的值，然后代入式子中进行计算即可解答．【解答】解：（1）∵16＜17＜25，∴45，4―4，故答案为：4―4；（2）∵1＜3＜4，∴12，∴4＜35，∵3+a＜3+b，∴a＝4，b＝5，∴a+b＝4+5＝9，∴a+b的算术平方根是3．【点评】本题考查了估算无理数的大小，熟练掌握完全平方数是解题的关键．【变式5-12】（2022秋•232―2．请解答下列各题：（1的整数部分是　，小数部分是 ．（2）已知9―m，9+n，且x2＝m+n，请求出满足条件的x的值．【分析】（1）类比题目中方法进行估算；（2）先通过估算确定出m，n的值，再求解x．【解答】解：（1即45，4―4，故答案为：4―4；（24，∴9―m＝9――4＝5―9+n＝913=4，∴x2＝m+n＝5―4＝1，∴x＝±1，即满足条件的x的值是±1．【点评】此题考查了对无理数大小的估算能力，关键是能准确理解并运用该方法．。

填空题：1．（2011•芜湖）已知a、b为两个连续的整数，且，则a+b=11．考点：估算无理数的大小。

分析：根据无理数的性质，得出接近无理数的整数，即可得出a，b的值，即可得出答案．解答：解：∵，a、b为两个连续的整数，∴＜＜，∴a=5，b=6，∴a+b=11．故答案为：11．点评：此题主要考查了无理数的大小，得出比较无理数的方法是解决问题的关键．2．（2011•无锡）写出一个大于1且小于2的无理数．考点：估算无理数的大小。

专题：开放型。

分析：由于所求无理数大于1且小于2，两数平方得大于2小于4，所以可选其中的任意一个数开平方即可．解答：解：大于1且小于2的无理数是，答案不唯一．点评：此题主要考查了无理数的估算，现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．3．（2011•六盘水）一个正方形的面积是20，通过估算，它的边长在整数4与5之间．考点：估算无理数的大小；算术平方根。

分析：本题需要先按要求找到4与5相乘，得出正方形的面积是20，即可求出答案．解答：解：∵正方形的面积是20，∴它的边长在整数：在4与5之间．故答案为：4，5．点评：本题主要考查了估算无理数的大小，解题关键是确定无理数的整数部分即可解决问题．4．（2011•抚顺）若两个连续的整数a、b满足a＜＜b，则的值为．考点：估算无理数的大小。

分析：＜＜，由此可确定a和b的值，进而可得出的值．解答：解：∵3=＜＜=4，∴a=3，b=4，即=．故答案为：．点评：本题考查无理数的估算，注意夹逼法的运用．5．（2011•崇文区）与最接近的整数是4．考点：估算无理数的大小；二次根式的性质与化简。

专题：推理填空题。

分析：根据无理数的意义和二次根式的性质得出＜＜，即可求出答案．解答：解：∵＜＜，∴最接近的整数是，=4，故答案为：4．点评：本题考查了二次根式的性质和估计无理数的大小等知识点，主要考查学生能否知道在4和5之间，题目比较典型．6．（2010•呼和浩特）已知a、b为两个连续整数，且a＜＜b，则a+b=5．考点：估算无理数的大小。

（1） 的整数部分是，小数部分是
（2） 如果 的小数部分为a， 的整数部分为b，求a+b﹣ 的值．
考点： 估算无理数的大小;
答案
~~第4题~~ (2017梁子湖.七下期中) 我们知道 是无理数，其整数部分是1，于是小明用 ： （1） 如果 的小数部分为a， +2的整数部分为b，求a+b﹣ 的值； （2） 已知10+ =x+y，其中x是整数，且0＜y＜1，求x﹣y的相反数． 考点： 无理数的认识;估算无理数的大小;实数的相反数;
~~第3题~~ (2017定州.七下期中) 阅读下面的文字，解答问题：大家知道 是无理数，而无理数是无限不循环小数，因此 的 小数部分我们不可能全部地写出来，于是小明用 ﹣1来表示 的小数部分，你同意小明的表示方法吗？事实上，小明 的表示方法是有道理的，因为 的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：∵22＜（ ）2 ＜32 ， 即2＜ ＜3，∴ 的整数部分为2，小数部分为（ ﹣2）． 请解答：
七下数学每日一练：估算无理数的大小练习题及答案_2020年综合题版
2020年 七 下 数 学 ： 数 与 式 _无 理 数 与 实 数 _估 算 无 理 数 的 大 小 练 习 题
~~第1a+b-1的算术平方根是4，c是 的整数部分．
（1） 求a，b，c的值；
1.答案：
2.答案：
3.答案：
4.答案：
5.答案：
﹣1米表示
的小数部分．请解答 答案
~~第5题~~ (2017东莞.七下期中) 阅读下面的文字，解答问题： 大家知道 是无理数，而无理数是无限不循环小数，因此 的小数部分我们不可能全部地写出来，于是小明用 1来表示 的小数部分，你同意小明的表示方法吗？

2021年中考数学估算无理数的大小专题（附答案）一、单选题1.估计的值应在（）A. 4和5之间B. 5和6之间C. 6和7之间D. 7和8之间2.已知a＝﹣1，a介于两个连续自然数之间，则下列结论正确的是（）A. 1＜a＜2B. 2＜a＜3C. 3＜a＜4D. 4＜a＜53.某款国产手机上有科学计算器，依次按键：，显示的结果在哪两个相邻整数之间（）A. 2～3B. 3～4C. 4～5D. 5～64.估计的值在（）A. 3和4之间B. 4和5之间C. 5和6之间D. 6和7之间5.下列各数中，比3大比4小的无理数是（）A. 3.14B.C.D.6.实数2 介于（）A. 4和5之间B. 5和6之间C. 6和7之间D. 7和8之间7.无理数在（）A. 2和3之间B. 3和4之间C. 4和5之间D. 5和6之间8.估计的值在（）A. 2和3之间B. 3和4之间C. 4和5之间D. 5和6之间9.设，则x的取值范围是（）A. B. C. D. 无法确定10.小明学了在数轴上画出表示无理数的点的方法后，进行练习：首先画数轴，原点为O，在数轴上找到表示数2的点A，然后过点A作AB⊥OA，使AB=3(如图).以O为圆心，OB的长为半径作弧，交数轴正半轴于点P，则点P所表示的数介于( )A. 1和2之间B. 2和3之间C. 3和4之间D. 4和5之间二、填空题11.若m＜2 ＜m+1，且m为整数，则m＝________.12.与最接近的自然数是________．13.的整数部分是________.14.估算：________.（结果精确到）15.如图，M、N、P、Q是数轴上的四个点，这四个点中最适合表示的点是________．16.写出一个大于1且小于2的无理数________．17.写一个比大的整数是________18.若的值在两个整数a与a+1之间，则a=________．19.任何实数a，可用[a]表示不超过a的最大整数，如[4]=4，[ ]=1．现对72进行如下操作：72[ ]=8 [ ]=2 [ ]=1，这样对72只需进行3次操作后变为1，类似的，①对81只需进行________次操作后变为1；②只需进行3次操作后变为1的所有正整数中，最大的是________．20.5﹣的小数部分是 ________．三、计算题（共2题；共10分）21.先化简÷（﹣x+1），然后从﹣＜x＜的范围内选取一个合适的整数作为x的值代入求值．22.先化简，再求值：，其中x为0＜x＜的整数．答案一、单选题1. A2. C3. B4. B5. C6. C7. B8. D9. B 10. C二、填空题11. 5 12. 2 13. 4 14. 6 15. P 16. 17. 2（答案不唯一）18. 2 19. 3；255 20.三、计算题21. 解：÷（﹣x+1）= = = = ，∵﹣＜x＜且x+1≠0，x﹣1≠0，x≠0，x是整数，∴x=﹣2时，原式=﹣22. 解：原式= = = = ，∵x为0＜x＜的整数，∴x=1（舍去）或x=2，则x=2时，原式=。

初一数学下册知识点《估算无理数的大小》150题和解析初一数学下册知识点《估算无理数的大小》150题及解析副标题一、选择题（本大题共77小题，共231.0分）1.估计√7+1的值()．A. 在1和2之间B. 在2和3之间C. 在3和4之间D. 在4和5之间【答案】C【解析】【分析】此题主要考查了估算无理数大小，正确得出√7的取值范围是解题关键．直接利用已知无理数得出√7的取值范围，进而得出答案．【解答】解：∵2<√7<3，∴3<√7+1<4，∴√7+1在3和4之间．故选C．2.若√3<a<√10，则下列结论中正确的是()A. 1<a<3B. 1<a<4C. 2<a<3D. 2<a<4【答案】B【解析】【分析】首先估算√3和√10的大小，再做选择．本题主要考查了估算无理数的大小，首先估算√3和√10的大小是解答此题的关键．【解答】解：∵1<√3<2，3<√10<4，又∵√3<a<√10，∴1.732<a<3.162，各选项中，只有B，1<a<4符合题意；故选B．3.估计√19的值在()A. 2和3之间B. 3和4之间C. 4和5之间D. 5和6之间【答案】C【解析】解：∵√16<√19<√25，∴√19的值在4和5之间．故选：C．直接利用二次根式的性质得出√19的取值范围．此题主要考查了估算无理数大小，正确把握最接近√19的有理数是解题关键．4.估计√10+1的值应在()A. 3和4之间B. 4和5之间C. 5和6之间D. 6和7之间【答案】B【解析】【分析】此题主要考查了估算无理数的大小，正确得出√10的取值范围是解题关键．首先得出√10的取值范围，进而得出答案．【解答】解：∵3<√10<4，∴4<√10+1<5．故选B．5.估计√13+1的值在()A. 2和3之间B. 3和4之间C. 4和5之间D. 5和6之间【答案】C【解析】【分析】本题考查了估算无理数的大小，能估算出√13的范围是解此题的关键．先估算出√13的范围，即可得出答案．【解答】解：∵3<√13<4，∴4<√13+1<5，即√13+1在4和5之间．故选C．6.估计√6+1的值在()A. 2到3之间B. 3到4之间C. 4到5之间D. 5到6之间【答案】B【解析】解：∵2=√4<√6<√9=3，∴3<√6+1<4，故选：B．利用”夹逼法“得出√6的范围，继而也可得出√6+1的范围．此题考查了估算无理数的大小的知识，属于基础题，解答本题的关键是掌握夹逼法的运用．7.估计5√6−√24的值应在()A. 5和6之间B. 6和7之间C. 7和8之间D. 8和9之间【答案】C【解析】解：5√6−√24=5√6−2√6=3√6=√54，∵7<√54<8，∴5√6−√24的值应在7和8之间，故选：C．先合并后，再根据无理数的估计解答即可．本题考查了估算无理数的大小，解决本题的关键是估算出无理数的大小．8.估计√38的值在()A. 4和5之间B. 5和6之间C. 6和7之间D. 7和8之间【答案】C【解析】解：∵√36<√38<√49，∴6<√38<7，∴√38的值在整数6和7之间．故选：C．初一数学下册知识点《估算无理数的大小》150题和解析利用二次根式的性质，得出√36<√38<√49，进而得出答案．此题主要考查了估计无理数的大小，得出√36<√38<√49是解题关键．9.估计√10+1的值应在()A. 3和4之间B. 4和5之间C. 5和6之间D. 6和7之间【答案】B【解析】解：∵3<√10<4，∴4<√10+1<5，故选：B．根据被开方数越大算术平方根越大，可得答案．本题考查了估算无理数的大小，利用被开方数越大算术平方根越大得出3<√10<4是解题关键，又利用了不等式的性质．10.已知整数m满足m<√38<m+1，则m的值为()A. 4B. 5C. 6D. 7【答案】C【解析】【分析】本题考查了无理数的大小问题，从√38的整数大小范围出发，然后确定m的大小．【解答】解：由题意∵√62<√38<√72∴当m=6时，则m+1=7适合．故选C．11.下列选项中的整数，与√17最接近的是()A. 3B. 4C. 5D. 6【答案】B【解析】解：∵16<17<20.25，∴4<√17<4.5，∴与√17最接近的是4．故选：B．依据被开方数越大对应的算术平方根越大进行解答即可．本题主要考查的是估算无理数的大小，掌握算术平方根的性质是解题的关键．12.估计√11的值在()A. 在1和2之间B. 在2和3之间C. 在3和4之间D. 在4和5之间【答案】C【解析】解：∵9<11<16，∴√9<√11<√16，∴3<√11<4．故选：C．由于9<11<16，于是√9<√11<√16，从而有3<√11<4．本题考查了无理数的估算，解题关键是确定无理数的整数部分即可解决问题．13.如图，表示√7的点在数轴上表示时，所在哪两个字母之间()A. C与DB. A与BC. A与CD. B与C【答案】A【解析】解：∵6.25<7<9，∴2.5<√7<3，则表示√7的点在数轴上表示时，所在C和D两个字母之间．故选：A．确定出7的范围，利用算术平方根求出√7的范围，即可得到结果．此题考查了估算无理数的大小，以及实数与数轴，解题关键是确定无理数的整数部分即可解决问题．14.面积为2的正方形的边长在()A. 0和1之间B. 1和2之间C. 2和3之间D. 3和4之间【答案】B【解析】【分析】本题考查了算术平方根的定义和估算无理数的大小，运用“夹逼法”是解答此题的关键．面积为2的正方形边长是2的算术平方根，再利用夹逼法求得√2的取值范围即可．【解答】解：面积为2的正方形边长是√2，∵1<2<4，∴1<√2<2故选：B．15.若一正方形的面积为20平方公分，周长为x公分，则x的值介于下列哪两个整数之间？()A. 16，17B. 17，18C. 18，19D. 19，20【答案】B【解析】【分析】本题主要考查了无理数大小的估计．注意利用数的平方大小比较是解此题的方法．【解答】解：∵周长为x公分，∴边长为x公分，4)2=20，∴(x4∴x2=20，16∴x2=320，又∵172=289，182=324，∴172<320<182，即172<x2<182，又∵x为正整数，∴x介于17和18之间，故选B．初一数学下册知识点《估算无理数的大小》150题和解析16.与√37最接近的整数是()A. 5B. 6C. 7D. 8【答案】B【解析】解：∵36<37<49，∴√36<√37<√49，即6<√37<7，∵37与36最接近，∴与√37最接近的是6．故选：B．由题意可知36与37最接近，即√36与√37最接近，从而得出答案．此题主要考查了无理数的估算能力，关键是整数与√37最接近，所以√36=6最接近．17.下列无理数中，与4最接近的是()A. √11B. √13C. √17D. √19【答案】C【解析】解：∵√16=4，∴与4最接近的是：√17．故选：C．直接利用估算无理数的大小方法得出最接近4的无理数．此题主要考查了估算无理数的大小，正确得出接近4的无理数是解题关键．18.估计2+√7的值A. 在2和3之间B. 在3和4之间C. 在4和5之间D. 在5和6之间【答案】C【解析】解：∵2<√7<3，∴4<2+√7<5，∴2+√7的值在4和5之间，故选：C．直接得出2<√7<3，进而得出2+√7的取值范围．此题主要考查了估算无理数的大小，正确得出√7的范围是解题关键．19.估算√27−2的值()A. 在1到2之间B. 在2到3之间C. 在3到4之间D. 在4到5之间【答案】C【解析】解：∵5<√27<6，∴3<√27−2<4．故选：C．首先估计√27的整数部分，然后即可判断√27−2的近似值．本题主要考查了无理数的估算能力，现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．20.判断2√11−1之值介于下列哪两个整数之间？()A. 3，4B. 4，5C. 5，6D. 6，7【答案】C【解析】解：∵2√11=√44，且√36<√44<√49，即6<2√11<7，∴5<2√11−1<6，故选：C．由√36<2√11<√49即6<2√11<7，由不等式性质可得2√11−1的范围可得答案．本题考查了估算无理数大小的知识，注意夹逼法的运用是解题关键．21.如图，已知数轴上的点A、B、C、D分别表示数−2、1、2、3，则表示数3−√5的点P应落在线段()A. AO上B. OB上C. BC上D. CD上【答案】B【解析】解：∵2<√5<3，∴0<3−√5<1，故表示数3−√5的点P应落在线段OB上．故选：B．根据估计无理数的方法得出0<3−√5<1，进而得出答案．此题主要考查了估算无理数的大小，得出√5的取值范围是解题关键．22.与无理数√31最接近的整数是()A. 4B. 5C. 6D. 7【答案】C【解析】解：∵√25<√31<√36，∴√31最接近的整数是√36，√36=6，故选：C．根据无理数的意义和二次根式的性质得出√25<√31<√36，即可求出答案．本题考查了二次根式的性质和估计无理数的大小等知识点，主要考查学生能否知道√31在5和6之间，题目比较典型．23.若3+√5的小数部分为a，3−√5的小数部分为b，则a+b的值为()A. 0B. 1C. −1D. 2【答案】B【解析】【分析】本题考查了估算无理数的大小，解题的关键是用有理数逼近无理数，求无理数的近似值．运用有理数逼近无理数，求无理数的近似值求解．【解答】解：∵2<√5<3，∴5<3+√5<6，0<3−√5<1∴a=3+√5−5=√5−2.b=3−√5，∴a+b=√5−2+3−√5=1，故选B．24.估计√41−2的值()A. 在4和5之间B. 在3和4之间C. 在2和3之间D. 在1和2之间【答案】A【解析】【分析】本题考查了估算无理数的大小的应用，关键是确定√41的范围．求出√41的范围，都减去2即可得出答案．【解答】解：∵36<41<49，∴√36<√41<√49，初一数学下册知识点《估算无理数的大小》150题和解析∴6<√41<7，∴4<√41−2<5，故选A．25.实数√2的值在()A. 0和1之间B. 1和2之间C. 2和3之间D. 3和4之间【答案】B【解析】解：∵1<√2<2，∴实数√2的值在：1和2之间．故选：B．直接利用估算无理数大小，正确得出√2接近的有理数，进而得出答案．此题主要考查了估算无理数大小，正确得出无理数接近的有理数是解题关键．26.估算√19的值是在()A. 3和4之间B. 4和5之间C. 5和6之间D. 6和7之间【答案】B【解析】【分析】本题主要考查了估计无理数大小的方法，找出最接近的有理数，再进行比较是解决问题的关键．找出比较接近√19的有理数，即√16与√25，从而确定它的取值范围．【解答】解：∵√16<√19<√25，∴4<√19<5．故选B．27.估计√40的值在()A. 4和5之间B. 5和6之间C. 6和7之间D. 7和8之间【答案】C【解析】解：∵√36<√40<√49，即6<√40<7，故选：C．根据√40，可以估算出位于哪两个整数之间，从而可以解答本题．本题考查估算无理数的大小，解题的关键是明确估算无理数大小的方法．28.式子√13+1的整数部分是a，小数部分是b，则a−b的值是()A. √13−7B. 1−√13C. 5−√13D. 7−√13【答案】D【解析】【分析】此题考查无理数的估算和代数式的值，注意找出最接近的整数范围是解决本题的关键．因为3<√13<4，所以4<√13+1<5，由此求得整数部分与小数部分，代入a−b 即可即可得到结果．【解答】解：∵3<√13<4，∴4<√13+1<5，∴a=4，b=√13+1−4，∴a−b=4−(√13−3)=7−√13．故选D．29.一个正方形的面积是15，估计它的边长在()A. 1和2之间B. 2和3之间C. 3和4之间D. 4和5之间【答案】C【解析】解：∵一个正方形的面积是15，∴其边长=√15．∵9<15<16，∴3<√15<4．故选C．先求出正方形的边长，再估算出其大小即可．本题考查的是估算无理数的大小，熟知估算无理数大小要用逼近法是解答此题的关键．30.已知a是√17−3的整数部分，b是√17−3的小数部分，那么(−a)3+(b+4)2的平方根是()A. 4B. ±2C. ±8D. ±4【答案】D【解析】【分析】此题考查了估算无理数的大小，代数式的值，平方根，正确得出a，b的值是解题关键，根据4<√17<5，得到1<√17−3<2，求出a、b的值，再代入(−a)3+(b+4)2计算，根据平方根的定义求解，即可得到答案．【解答】解：∵4<√17<5，∴1<√17−3<2，∴a=1，b=√17−4，∴(−a)3+(b+4)2=(−1)3+(√17−4+4)2=−1+17=16，∴16的平方根是±4，故选D．31.估计√7+1的值在()A. 2到3之间B. 3到4之间C. 4到5之间D. 5到6之间【答案】B【解析】【分析】本题考查了估算无理数的大小，能估算出√7的范围是解此题的关键．解答此题先求出√7的范围，然后再加1可得√7+1的范围．【解答】解：∵2<√7<3，∴3<√7+1<4，即√7+1在3和4之间，故选B．32.已知a是√17−3的整数部分，b是√17−3的小数部分，那么(−a)3+(b+4)2的平方根是()A. 4B. ±2C. ±8D. ±4【答案】D【解析】解：∵4<√17<5，∴1<√17−3<2，初一数学下册知识点《估算无理数的大小》150题和解析∴a=1，b=√17−4，∴(−a)3+(b+4)2=(−1)3+(√17−4+4)2=−1+17=16，∴16的平方根是±4．故选D．根据4<√17<5，利用不等式的性质可得1<√17−3<2，求出a、b的值，再代入(−a)3+(b+4)2计算，根据平方根的定义求解．此题主要考查了估算无理数的大小，正确得出a，b的值是解题关键．33.√43在两个连续整数a和b之间，a<√43<b，那么a+b的值是()A. 11B. 13C. 14D. 15【答案】B【解析】解：∵6<√43<7，∴a=6，b=7，∴a+b=6+7=13．故选：B．首先用“夹逼法”确定a、b的值，进而可得a+b的值．此题主要考查了估算无理数的大小，关键是正确确定a、b的值．34.实数√28界于哪两个相邻的整数之间()A. 3和4B. 5和6C. 7和8D. 9和10【答案】B【解析】解：∵5<√28<6，∴√28在5和6之间．故选：B．先估算出√28的范围，即可得出答案．本题考查了估算无理数的大小，能估算出√28的范围是解此题的关键．35.实数√3的值在()A. 0与1之间B. 1与2之间C. 2与3之间D. 3与4之间【答案】B【解析】解：∵1<√3<√4，∴实数√3的值在1与2之间．故选：B．直接利用无理数最接近的有理数进而答案．此题主要考查了估算无理数大小，正确得出接近的有理数是解题关键．36.下列说法：①−1是1的平方根；②√10在两个连续整数a和b之间，那么a+b=7；③所有的有理数都可以用数轴上的点表示，反过来，数轴上的所有点都表示有理数；④无理数就是开放开不尽的数；正确的个数为()A. 1个B. 2个C. 3个D. 4个【答案】B【解析】【分析】此题考查了估算无理数的大小、实数与数轴、实数，熟知有关定义和性质是本题的关键．根据估算无理数的大小、实数与数轴、无理数的定义和特点分别对每一项进行分析，即可得出答案．【解答】解：①−1是1的平方根是正确的；②√10在两个连续整数a和b之间，那么a+b=3+4=7是正确的；③所有的实数都可以用数轴上的点表示，反过来，数轴上的所有点都表示实数，题目中的说法是错误的；④无理数就是无限不循环的小数，题目中说法是错误的．故选B．37.估计√6+1的值在()A. 2 到3 之间B. 3 到4 之间C. 4 到5 之间D. 5 到6 之间【答案】B【解析】解：∵2<√6<3，∴3<√6+1<4，故选：B．首先确定√6在整数2和3之间，然后可得√6+1的值在3到4之间．此题主要考查了估算无理数，关键是掌握用有理数逼近无理数，求无理数的近似值．38.估计√16+√20的运算结果应在()A. 6与7之间B. 7与8之间C. 8与9之间D. 9与10之间【答案】C【解析】解：∵√16+√20=4+√20，而4<√20<5，∴原式运算的结果在8到9之间；故选C．首先计算出√16，再估算出√20即可得结果．本题考查了无理数的近似值问题，关键是利用“夹逼法”是估算的一般方法，也是常用方法．39.若a<1−√7<b，且a、b是两个连续整数，则a+b的值是()A. −1B. −2C. −3D. −4【答案】C【解析】解：∵2<√7<3，∴−2>−√7>−3，∴−1>1−√7>−2，∴a=−2，b=−1，∴a+b=−3，故选C．先求出√7的范围，再求出1−√7的范围，求出a、b的值，代入求出即可．本题考查了估算无理数的大小，能求出1−√7的范围是解此题的关键．40.设a=√13−1，a在两个相邻整数之间，则这两个整数是()A. 0和1B. 1和2C. 2和3D. 3和4【答案】C【解析】解：∵9<13<16，∴3<√13<4，即2<a=√13−1<3，则这两整数是2和3，故选C估算√13大小，即可得到结果．此题考查了估算无理数的大小，估算出√13大小是解本题的关键．41.估计√21的值()A. 1到2之间B. 2到3之间C. 3和4之间D. 4和5之间初一数学下册知识点《估算无理数的大小》150题和解析11 / 45第11页，共45页【答案】D【解析】解：∵√16<√21<√25， ∴4<√21<5，即√21在4到5之间， 故选：D ．根据√16<√21<√25得出4<√21<5，即可得出答案．本题考查了估算无理数的大小的应用，关键是能求出√21的范围．42. 估计√76的值在哪两个整数之间( )A. 75和77B. 6和7C. 7和8D. 8和9【答案】D【解析】解：∵√64<√76<√81， ∴8<√76<9，∴√76在两个相邻整数8和9之间． 故选：D ．先对√76进行估算，再确定√76是在哪两个相邻的整数之间．此题主要考查了估算无理数的大小，注意首先估算无理数的值，再根据不等式的性质进行计算．现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．43. 定义：对任意实数x ，[x]表示不超过x 的最大整数，如[3.14]=3，[1]=1，[−1.2}=−2.对数字65进行如下运算：①[√65]=8：②[√8]=2：③[√2]=1，这样对数字65运算3次后的值就为1，像这样对一个正整数总可以经过若干次运算后值为1，则数字255经过( )次运算后的结果为1． A. 3 B. 4 C. 5 D. 6 【答案】A【解析】解：255→第一次[√255]=15→第二次[√15]=3→第三次[√3]=1， 则数字255经过3次运算后的结果为1． 故选：A ．根据[x]表示不超过x 的最大整数计算，可得答案．本题考查了估算无理数的大小的应用，主要考查学生的阅读能力和逆推思维能力．44. 黄金分割数√5−12是一个很奇妙的数，大量应用于艺术、建筑和统计决策等方面，请你估算√5−1的值( ) A. 在1.1和1.2之间 B. 在1.2和1.3之间 C. 在1.3和1.4之间 D. 在1.4和1.5之间【答案】B【解析】解：∵√5≈2.236， ∴√5−1≈1.236， 故选：B ．根据√5≈2.236，可得答案．本题考查了估算无理数的大小，利用√5≈2.236是解题关键．45. 8的负的平方根介于( )A. −5与−4之间B. −4与−3之间C. −3与−2之间D. −2与−1之间【答案】C第12页，共45页【解析】解：∵4<8<9， ∴2<√8<3．∴−2>−√8>−3． 故选：C ．先求得√8的范围，然后再求得−√8的范围即可．本题主要考查的是估算无理数的大小，利用夹逼法求得√8的大致范围是解题的关键．46. 通过估算，估计√193+1的值应在( )A. 2～3之间B. 3～4之间C. 4～5之间D. 5～6之间【答案】B【解析】解：∵8<19<27，∴√83<√193<√273，即2<√193<3，∴3<√193+1<4， 故选：B ．根据8<19<27得出：2<√193<3，进而可得答案．本题考查了估算无理数的大小，利用了正数的被开方数越大立方根越大的关系．47. 估计√13的值在( )A. 1和2之间B. 2和3之间C. 3和4之间D. 4和5之间【答案】C【解析】解：∵9<13<16， ∴3<√13<4，则√13的值在3和4之间， 故选：C ．估算得出√13的范围即可．此题考查估算无理数的大小，熟练掌握算术平方根定义是解本题的关键．48. 如图，数轴上A ，B ，C ，D 四点中，与−√3对应的点距离最近的是( )A. 点AB. 点BC. 点CD. 点D【答案】B【解析】【分析】本题考查的是实数与数轴，熟知实数与数轴上各点是一一对应关系是解答此题的关键． 先估算出−√3的范围，结合数轴可得答案． 【解答】解：∵√1<√3<√4，即1<√3<2， ∴−2<−√3<−1，∴由数轴知，与−√3对应的点距离最近的是点B ． 故选B ．49. 下列各数中，介于正整数6和7之间的数是( )A. √41B. √52C. √26D. √383初一数学下册知识点《估算无理数的大小》150题和解析13 / 45第13页，共45页【答案】A【解析】解：∵36<41<49， ∴6<√41<7，故A 正确． ∵52>49，∴√52>7，故B 错误． ∵36>26，∴6>√26，故C 错误． ∵27<38<64，∴3<√383<4，故D 错误． 故选：A ．依据被开方数越大对应的算术平方根(立方根)越大进行求解即可． 本题主要考查的是估算无理数的大小，夹逼法的应用是解题的关键．50. 若n −1<√45<n ，则整数n =( )A. 5B. 6C. 7D. 8【答案】C【解析】解：∵6<√45<7， ∴n =7， 故选：C ．先估算出√45的范围，再得出选项即可．本题考查了估算无理数的大小，能估算出√45的范围是解此题的关键．51. 在数轴上有一块墨迹，被覆盖住的无理数可能是( )A. √17B. √11C. √5D. −√3【答案】B【解析】【分析】此题主要考查了估算无理数的大小，数轴的有关知识，应先找到所求的无理数在哪两个和它接近的整数之间，然后判断出所求的无理数的范围即可求解． 【解答】解：由图可知：被覆盖的数在3和4之间； ∴被墨迹覆盖的无理数有可能是√11． 故选B ．52. 对于实数x ，我们规定[x]表示不大于x 的最大整数，如[4]=4，[√3]=1，[−2.5]=−3.现对82进行如下操作： 82→第1次[√82]=9→第2次[93]=3→第3次[√3]=1，这样对82只需进行3次操作后变为1，类似地，对121只需进行多少次操作后变为1( )A. 1B. 2C. 3D. 4【答案】C【解析】解：121→第1次[12111]=11→第2次[√11]=3→第3次[√3]=1，∴对121只需进行3次操作后变为1，故选：C ．[x]表示不大于x 的最大整数，依据题目中提供的操作进行计算即可．本题考查了估算无理数的大小，解决本题的关键是明确[x]表示不大于x的最大整数．53.估计√10的值在哪两个整数之间()A. 9和10B. 7和8C. 5和6D. 3和4【答案】D【解析】解：∵3<√10<4，∴√10在3和4之间．故选D．先估算出√10的范围，即可得出选项．本题考查了估算无理数的大小的应用，能估算出√10的范围是解此题的关键．54.与1+√5最接近的整数是()A. 1B. 2C. 3D. 4【答案】C【解析】解：∵2.22=4.84，2.32=5.29，∴2.22<5<2.32．∴2.2<√5<2.3．∴3.2<1+√5<3.3．∴与1+√5最接近的整数是3．故选：C．先依据被开方数越大对应的算术平方根也越大估算出√5的大小，然后即可做出判断．本题主要考查的是估算无理数的大小，利用夹逼法估算出√5的大小是解题的关键．55.在数轴上标注了四段范围，如图，表示√8的点落在()A. 段①B. 段②C. 段③D. 段④【答案】C【解析】【分析】根据数的平方，即可解答．本题考查了估算无理数的大小，解决本题的关键是计算出各数的平方．【解答】解：2.62=6.76，2.72=7.29，2.82=7.84，2.92=8.41，32=9，∵7.84<8<8.41，∴2.8<√8<2.9，∴√8的点落在段③，故选：C．56.如图，数轴上点N表示的数可能是()A. √10B. √5C. √3D. √2【答案】A【解析】解：∵√10≈3.16，√5≈2.24，√3≈1.73，√2≈1.41，根据点N在数轴上的位置，知：3<N<4，∴四个选项中只有3<3.16<4，即3<√10<4．故选：A．第14页，共45页初一数学下册知识点《估算无理数的大小》150题和解析先对四个选项中的无理数进行估算，再根据N点的位置即可求解．本题考查了同学们估算无理数大小的能力，及能够根据点在数轴的位置确定数的大小．57.数轴上表示√21−1的点A的位置应该在()A. 2与3之间B. 3与4之间C. 4与5之间D. 7与8之间【答案】B【解析】【分析】本题考查了实数与数轴的对应关系，以及估算无理数大小的能力，难度一般．先估算无理数√21的大小，然后求解即可．【解答】解：∵4=√16<√21<5=√25，∴3<√21−1<4，故数轴上表示√21−1的点A的位置应在3与4之间．故选：B．58.估计√6的值在()A. 2到3之间B. 3到4之间C. 4到5之间D. 5到6之间【答案】A【解析】解：∵√4<√6<√9，∴2<√6<3，故选：A．根据估算无理数的大小，即可解答．本题考查了估算无理数的大小，解决本题的关键是估算无理数的大小．59.如图，已知数轴上的点A、B、C、D分别表示数−2、−1、1、2，则表示1−√7的点P应落在线段()A. AB上B. OB上C. OC上D. CD上【答案】A【解析】解：∵2<√7<3，∴−2<1−√7<−1，∴表示1−√7的点P应落在线段AB上．故选：A．直接根据题意得出−2<1−√7<−1进而得出答案．此题主要考查了估算无理数的大小，正确得出√7的取值范围是解题关键．60.a与b是两个连续整数，若a<√7<b，则a，b分别是()A. 6，8B. 3，2C. 2，3D. 3，4【答案】C【解析】解：∵4<7<9，∴2<√7<3，∵a<√7<b，且a与b是两个连续整数，∴a=2，b=3．故选C．根据4<7<9，结合a<√7<b，即可得出a、b的值．本题考查了估算无理数的大小，解题的关键是找出2<√7<3．15/ 45第15页，共45页61.估计√7+1的值在()A. 2和3之间B. 3和4之间C. 4和5之间D. 5和6之间【答案】B【解析】解：∵2<√7<3，∴3<√7+1<4，故选：B．直接利用2<√7<3，进而得出答案．此题主要考查了估算无理数的大小，正确得出√7的取值范围是解题关键．62.若m<√14<n，且m、n为连续正整数，则n2−m2的值为()A. 5B. 7C. 9D. 11【答案】B【解析】解：∵m<√14<n，且m、n为连续正整数，∴m=3，n=4，则原式=7，故选：B．根据题意确定出m与n的值，代入原式计算即可求出值．此题考查了估算无理数的大小，设实数为a，a的整数部分A为不大于a的最大整数，小数部分B为实数a减去其整数部分，即B=a−A；理解概念是解题的关键．63.估计√30的值在两个整数()A. 3与4之间B. 5与6之间C. 6与7之间D. 3与10之间【答案】B【解析】解：∵√25<√30<√36，∴5<√30<6，∴√30的值在5与6之间．故选：B．直接利用估算无理数的方法得出接近无理数的整数进而得出答案．此题主要考查了估算无理数的大小，正确掌握无理数的估算方法是解题关键．64.3+√10的结果在下列哪两个整数之间()．A. 6和7B. 5和6C. 4和5D. 3和4【答案】A【解析】解：∵3<√10<4，∴6<3+√10<7，故选：A．直接利用3<√10<4，进而得出答案．此题主要考查了估算无理数的大小，正确得出无理数接近的整数是解题关键．65.关于“√19”，下列说法不正确的是()A. 它是一个无理数B. 它可以用数轴上的一个点来表示C. 它可以表示面积为19的正方形的边长D. 若为整数)，则n=5【答案】D第16页，共45页初一数学下册知识点《估算无理数的大小》150题和解析17 / 45第17页，共45页【解析】【分析】本题主要考查了无理数的定义、数轴的意义以及无理数的估算，无理数的估算关键是确定无理数的整数部分．“夹逼法”是估算的一般方法，也是常用方法． 分别根据无理数的定义、数轴的意义、正方形面积公式以及无理数的估算方法判断即可． 【解答】解：A ．√19是一个无理数，说法正确，故选项A 不合题意；B .√19可以用数轴上的一个点来表示，说法正确，故选项B 不合题意；C .它可以表示面积为19的正方形的边长，说法正确，故选项C 不合题意；D .4<√19<5，n =4，故选项D 符合题意． 故选D ．66. 如图，数轴上点P 表示的数可能是( ) A. √2 B. √3C. √5D. √73【答案】C【解析】解：从数轴可知：P 点表示数在2和3之间，A 、1<√2<2，故本选项不符合题意；B 、1<√3<2，故本选项不符合题意；C 、2<√3<3，故本选项符合题意；D 、1<√73<2，故本选项不符合题意； 故选C ．从数轴可知P 点表示数在2和3之间，先估算出每个无理数的范围，即可得出答案． 本题考查了估算无理数的大小，能估算出每个无理数的范围是解此题的关键．67. 估计√5在( )A. 0～1之间B. 1～2之间C. 2～3之间D. 3～4之间【答案】C【解析】解：∵√4<√5<√9， 即：2<√5<3， ∴√5在2到3之间． 故选：C ．根据二次根式的性质得出√4<√5<√9，即：2<√5<3，可得答案．本题考查了估算无理数的大小和二次根式的性质，解此题的关键是知道√5在√4和√9之间．68. 若√13的整数部分是a ，小数部分是b ，则式子3(a +b)−ab 的值是( )A. −9B. 9C. 19D. 3√13 【答案】B【解析】解：∵√9<√13<√16， ∴3<√13<4，∴a =3，b =√13−3，∴3(a +b)−ab =3×(3+√13−3)−3×(√13−3)=3√13−3√13+9=9． 故选：B ．先进行估算√13的范围，确定a ，b 的值，再代入代数式即可解答． 本题考查了估算无理数的大小，解决本题的关键是估算√13的范围．69. 关于“√10”，下列说法不正确的是( )A. 它是数轴上唯一一个距离原点√10个单位长度的点表示的数B. 它是一个无理数C. 若a<√10<a+1，则整数a的值为3D. 它可以表示面积为10的正方形的边长【答案】A【解析】解：数轴上距离原点√10个单位长度的点表示的数是±√10，故A错误，符合题目要求√10它是一个无理数，故B正确，不符合题目要求∵9<10<16，∴3<√10<4，故整数a的值为3，故C正确，不故符合题目要求√10它可以表示面积为10的正方形的边长，故D正确，不符合题目要求．故选：A．依据绝对值的定义、无理数的概念，依据夹逼法估算无理数大小的方法、依据算术平方根的定义进行判断即可．本题主要考查的是估算无理数的大小，实数与数轴，熟练掌握相关知识是解题的关键．70.若a<√5<b，且a、b是两个连续整数，则a+b的值是()A. 2B. 3C. 4D. 5【答案】D【解析】解：∵4<5<9，∴2<√5<3，由a<√5<b，且a、b是两个连续的整数，得到a=2，b=3，则a+b=5，故选：D．由被开方数5的范围确定出√5的范围，进而求出a与b的值，代入原式计算即可得到结果．71.设面积为6的正方形的边长为a.下列关于a的四种说法：①a是有理数；②a是无理数；③a可以用数轴上的一个点来表示；④2<a<3.其中说法正确的有()A. 1个B. 2个C. 3个D. 4个【答案】C【解析】解：∵面积为3的正方形的边长为a，∴a=√6，故①a是有理数，错误；②a是无理数，正确；③a可以用数轴上的一个点来表示，正确；④2<a<3，正确，则说法正确的是：②③④共3个．故选：C．直接利用得出正方形的边长，再利用实数的性质分析得出答案．此题主要考查了实数的性质以及无理数的估算，正确掌握实数有关性质是解题关键．72.有下列说法：①实数与数轴上的点一一对应；②2−√7的相反数是√7−2；③在1和3之间的无理数有且只有√2，√3，√5，√7这4个；④2+3x−4x2是三次三项式；第18页，共45页。

七下数学| 月测必考专练【估算】4大常考重难题型题型1 估算无理数的范围【例1】估计√11.6的值在（C）A．3.2和3.3之间B．3.3和3.4之间C．3.4和3.5之间D．3.5和3.6 之间【解题思路】估算11.6的算术平方根，即可得出答案．【解答过程】解：∵3.52＝12.25，3.42＝11.56，而12.25＞11.6＞11.56∴3.4＜√11.6＜3.5【例2】已知m=√8+√9，则以下对m的估算正确的是（C）A．3＜m＜4 B．4＜m＜5 C．5＜m＜6 D．6＜m＜7【解题思路】估算确定出√8的范围，计算√9=3，进而确定出m的范围即可．【解答过程】解：∵2＜√8＜3，√9=3，∴5＜√8+3＜6，∵m=√8+√9=3+√8，∴m的范围为5＜m＜6．题型2 已知无理数的范围求值【例1】若两个连续整数x，y满足x＜√5+2＜y，则x+y的值是（C）A．5 B．7 C．9 D．11【解题思路】先利用“夹逼法”√5的整数部分，再利用不等式的性质可得√5+2在哪两个整数之间，进而求解．【解答过程】解：∵4＜5＜9，∴2＜√5＜3，∴4＜√5+2＜5，∵两个连续整数x、y满足x＜√5+2＜y，∴x＝4，y＝5，∴x+y＝4+5＝9．【例2】若a＜√28-√7＜a+1，其中a为整数，则a的值是（B）A．1 B．2 C．3 D．4【解题思路】先把√28-√7化简，再估算√7的范围即可．【解答过程】解：√28-√7=2√7-√7=√7，∵22＜7＜32，∴2＜√7＜3，∵a＜√28-√7＜a+1，其中a为整数，∴a＝2．题型3 估算无理数最接近的值【例1】下列整数中，与10-√30最接近的是（C）A．3 B．4 C．5 D．6【解题思路】先估算出√30的范围，再估算10-√30的范围即可．【解答过程】解：∵25＜30＜36，30离25更近，∴5＜√30＜6，且更接近5，∴-6＜-√30＜-5，且更接近﹣5，∴4＜10-√30＜5，且更接近5．【例2】若m＝5n（m、n是正整数），且10＜√m＜12，则与实数√n的最大值最接近的数是（B）A．4 B．5 C．6 D．7【解题思路】根据m的取值范围确定n的取值，再根据m、n为整数，确定n 的最大值，再估算即可．【解答过程】解：∵10＜√m＜12，∴100＜m＜144，∴20＜m/5＜28.8，即20＜n＜28.8，又∵m、n是正整数，∴n的最大值为28，∵25比36更接近28，∴√n的值比较接近√25，即比较接近5，题型4 无理数整数、小数部分问题【例1】我们知道√2是一个无限不循环小数，因此√2的小数部分我们不可能全部写出来．因为√2的整数部分为1，所以√2减去其整数部分，差就是√2的小数部分，所以用√2-1来表示√2的小数部分．根据这个方法完成下列问题：（1）√43的整数部分为，小数部分为；（2）已知√17的整数部分a，6-√3的整数部分为b，求a+b的立方根．【解题思路】（1）根据6＜√43＜7求√43的整数部分和小数部分；（2）求√17的整数部分4，6-√3的整数部分为4，得a+b的立方根．【解答过程】解：（1）∵6＜√43＜7，∴整数部分为6，小数部分为√43-6．（2）∵4＜√17＜5，∴a＝4．∵4＜6-√3＜5，∴b＝4．∴³√a+b=2．。

选择题：1．（2011•遵义）若a、b均为正整数，且，则a+b的最小值是（）A．3 B．4 C．5 D．6考点：估算无理数的大小。

分析：本题需先根据已知条件分别求出a、b的最小值，即可求出a+b的最小值．解答：解：a、b均为正整数，且，∴a的最小值是3，b的最小值是：1，则a+b的最小值4．故选B．点评：本题主要考查了如何估算无理数的大小，在解题时要能根据题意求出a、b的值是本题的关键．2．（2011•资阳）如图，在数轴上表示实数的点可能是（）A．点M B．点N C．点P D．点Q考点：估算无理数的大小；实数与数轴。

专题：应用题。

分析：先对进行估算，再确定是在哪两个相邻的整数之间，然后确定对应的点即可解决问题．解答：解：∵12.25＜14＜16，∴3.5＜＜4，∴在数轴上表示实数的点可能是点P．故选C．点评：本题考查实数与数轴上的点的对应关系，应先看这个无理数在哪两个有理数之间，进而求解．3．（2011•徐州）估计的值（）A．在2到3之间B．在3到4之间C．在4到5之间D．在5到6之间考点：估算无理数的大小。

专题：计算题。

分析：先确定的平方的范围，进而估算的值的范围．解答：解：9＜=11＜16，故3＜＜4；故选B．点评：本题主要考查了无理数的估算，解题关键是确定无理数的整数部分即可解决问题，属于基础题．4．（2011•天津）估计的值在（）A．1到2之间B．2到3之间C．3到4之间D．4到5之间考点：估算无理数的大小。

专题：计算题。

分析：根据特殊有理数找出最接近的完全平方数，从而求出即可．解答：解：∵＜＜，∴3＜＜4，故选：C．点评：此题主要考查了估计无理数的大小，根据已知得出最接近的完全平方数是解决问题的关键．5．（2011•台湾）如图数轴上有O，A，B，C，D五点，根据图中各点所表示的数，判断在数轴上的位置会落在下列哪一线段上（）A．OA B．AB C．BC D．CD考点：估算无理数的大小；实数与数轴。

【考点训练】估算无理数的大小-1一、选择题（共5小题）4．（2013•淮安）如图，数轴上A、B两点表示的数分别为和5.1，则A、B两点之间表示整数的点共有（）二、填空题（共3小题）（除非特别说明，请填准确值）6．（2013•呼和浩特）大于且小于的整数是_________．7．（2013•抚顺）已知a、b为两个连续整数，且a＜＜b，则a+b=_________．8．（2013•台州）任何实数a，可用[a]表示不超过a的最大整数，如[4]=4，[]=1．现对72进行如下操作：72[]=8[]=2[]=1，这样对72只需进行3次操作后变为1，类似的，①对81只需进行_________此操作后变为1；②只需进行3次操作后变为1的所有正整数中，最大的是_________．三、解答题（共2小题）（选答题，不自动判卷）9．小丽想用一块面积为400平方厘米的正方形纸片，沿着边的方向裁出一块面积为300平方厘米的长方形纸片，使它的长宽之比为3：2．不知能否裁出来，正在发愁．小明见了说：“别发愁，一定能用一块面积大的纸片裁出一块面积小的纸片．”你同意小明的说法吗？请说明理由．10．（1）如图1，小明想剪一块面积为25cm2的正方形纸板，你能帮他求出正方形纸板的边长吗？（2）若小明想将两块边长都为3cm的正方形纸板沿对角线剪开，拼成如图2所示的一个大正方形，你能帮他求出这个大正方形的面积吗？它的边长是整数吗？若不是整数，那么请你估计这个边长的值在哪两个整数之间．【考点训练】估算无理数的大小-1参考答案与试题解析一、选择题（共5小题）＜，即与的积，再根据所得的值估算出在哪两个整数之间，即可得出答案．×=×的大约值是解题的关键，是一道基础题．先估算出24．（2013•淮安）如图，数轴上A、B两点表示的数分别为和5.1，则A、B两点之间表示整数的点共有（）比1的范围，继而也可得出2=二、填空题（共3小题）（除非特别说明，请填准确值）6．（2013•呼和浩特）大于且小于的整数是2．=2＜＜=2＜＜且小于7．（2013•抚顺）已知a、b为两个连续整数，且a＜＜b，则a+b=9．＜＜8．（2013•台州）任何实数a，可用[a]表示不超过a的最大整数，如[4]=4，[]=1．现对72进行如下操作：72[]=8[]=2[]=1，这样对72只需进行3次操作后变为1，类似的，①对81只需进行3此操作后变为1；②只需进行3次操作后变为1的所有正整数中，最大的是255．[][][][[[][[[]三、解答题（共2小题）（选答题，不自动判卷）9．小丽想用一块面积为400平方厘米的正方形纸片，沿着边的方向裁出一块面积为300平方厘米的长方形纸片，使它的长宽之比为3：2．不知能否裁出来，正在发愁．小明见了说：“别发愁，一定能用一块面积大的纸片裁出一块面积小的纸片．”你同意小明的说法吗？请说明理由．x=515，15cm1510．（1）如图1，小明想剪一块面积为25cm2的正方形纸板，你能帮他求出正方形纸板的边长吗？（2）若小明想将两块边长都为3cm的正方形纸板沿对角线剪开，拼成如图2所示的一个大正方形，你能帮他求出这个大正方形的面积吗？它的边长是整数吗？若不是整数，那么请你估计这个边长的值在哪两个整数之间．，边长为的边长不是整数，然后估算出的大小，从而求出与相邻的两个整数．，∴边长不是整数，关注中学生习题网官方微信公众号，免费学习资源、学习方法、学习资讯第一时间掌握。

初一数学下册知识点《估算无理数的大小》150题及解析副标题一、选择题（本大题共77小题，共231.0分）1.估计的值．A. 在1和2之间B. 在2和3之间C. 在3和4之间D. 在4和5之间【答案】C【解析】【分析】此题主要考查了估算无理数大小，正确得出的取值范围是解题关键．直接利用已知无理数得出的取值范围，进而得出答案．【解答】解：，，在3和4之间．故选C．2.若，则下列结论中正确的是A. B. C. D.【答案】B【解析】【分析】首先估算和的大小，再做选择．本题主要考查了估算无理数的大小，首先估算和的大小是解答此题的关键．【解答】解：，，又，，各选项中，只有B，符合题意；故选B．3.估计的值在A. 2和3之间B. 3和4之间C. 4和5之间D. 5和6之间【答案】C【解析】解：，的值在4和5之间．故选：C．直接利用二次根式的性质得出的取值范围．此题主要考查了估算无理数大小，正确把握最接近的有理数是解题关键．4.估计的值应在A. 3和4之间B. 4和5之间C. 5和6之间D. 6和7之间【答案】B【解析】【分析】此题主要考查了估算无理数的大小，正确得出的取值范围是解题关键．首先得出的取值范围，进而得出答案．【解答】解：，．故选B．5.估计的值在A. 2和3之间B. 3和4之间C. 4和5之间D. 5和6之间【答案】C【解析】【分析】本题考查了估算无理数的大小，能估算出的范围是解此题的关键．先估算出的范围，即可得出答案．【解答】解：，，即在4和5之间．故选C．6.估计的值在A. 2到3之间B. 3到4之间C. 4到5之间D. 5到6之间【答案】B【解析】解：，，故选：B．利用”夹逼法“得出的范围，继而也可得出的范围．此题考查了估算无理数的大小的知识，属于基础题，解答本题的关键是掌握夹逼法的运用．7.估计的值应在A. 5和6之间B. 6和7之间C. 7和8之间D. 8和9之间【答案】C【解析】解：，，的值应在7和8之间，故选：C．先合并后，再根据无理数的估计解答即可．本题考查了估算无理数的大小，解决本题的关键是估算出无理数的大小．8.估计的值在A. 4和5之间B. 5和6之间C. 6和7之间D. 7和8之间【答案】C【解析】解：，，的值在整数6和7之间．故选：C．利用二次根式的性质，得出，进而得出答案．此题主要考查了估计无理数的大小，得出是解题关键．9.估计的值应在A. 3和4之间B. 4和5之间C. 5和6之间D. 6和7之间【答案】B【解析】解：，，故选：B．根据被开方数越大算术平方根越大，可得答案．本题考查了估算无理数的大小，利用被开方数越大算术平方根越大得出是解题关键，又利用了不等式的性质．10.已知整数m满足，则m的值为A. 4B. 5C. 6D. 7【答案】C【解析】【分析】本题考查了无理数的大小问题，从的整数大小范围出发，然后确定m的大小．【解答】解：由题意当时，则适合．故选C．11.下列选项中的整数，与最接近的是A. 3B. 4C. 5D. 6【答案】B【解析】解：，，与最接近的是4．故选：B．依据被开方数越大对应的算术平方根越大进行解答即可．本题主要考查的是估算无理数的大小，掌握算术平方根的性质是解题的关键．12.估计的值在A. 在1和2之间B. 在2和3之间C. 在3和4之间D. 在4和5之间【答案】C【解析】解：，，．故选：C．由于，于是，从而有．本题考查了无理数的估算，解题关键是确定无理数的整数部分即可解决问题．13.如图，表示的点在数轴上表示时，所在哪两个字母之间A. C与DB. A与BC. A与CD. B与C【答案】A【解析】解：，，则表示的点在数轴上表示时，所在C和D两个字母之间．故选：A．确定出7的范围，利用算术平方根求出的范围，即可得到结果．此题考查了估算无理数的大小，以及实数与数轴，解题关键是确定无理数的整数部分即可解决问题．14.面积为2的正方形的边长在A. 0和1之间B. 1和2之间C. 2和3之间D. 3和4之间【答案】B【解析】【分析】本题考查了算术平方根的定义和估算无理数的大小，运用“夹逼法”是解答此题的关键．面积为2的正方形边长是2的算术平方根，再利用夹逼法求得的取值范围即可．【解答】解：面积为2的正方形边长是，，故选：B．15.若一正方形的面积为20平方公分，周长为x公分，则x的值介于下列哪两个整数之间？A. 16，17B. 17，18C. 18，19D. 19，20【答案】B【解析】【分析】本题主要考查了无理数大小的估计．注意利用数的平方大小比较是解此题的方法．【解答】解：周长为x公分，边长为公分，，，，又，，，即，又为正整数，介于17和18之间，故选B．16.与最接近的整数是A. 5B. 6C. 7D. 8【答案】B【解析】解：，，即，与36最接近，与最接近的是6．故选：B．由题意可知36与37最接近，即与最接近，从而得出答案．此题主要考查了无理数的估算能力，关键是整数与最接近，所以最接近．17.下列无理数中，与4最接近的是A. B. C. D.【答案】C【解析】解：，与4最接近的是：．故选：C．直接利用估算无理数的大小方法得出最接近4的无理数．此题主要考查了估算无理数的大小，正确得出接近4的无理数是解题关键．18.估计的值A. 在2和3之间B. 在3和4之间C. 在4和5之间D. 在5和6之间【答案】C【解析】解：，，的值在4和5之间，故选：C．直接得出，进而得出的取值范围．此题主要考查了估算无理数的大小，正确得出的范围是解题关键．19.估算的值A. 在1到2之间B. 在2到3之间C. 在3到4之间D. 在4到5之间【答案】C【解析】解：，．故选：C．首先估计的整数部分，然后即可判断的近似值．本题主要考查了无理数的估算能力，现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．20.判断之值介于下列哪两个整数之间？A. 3，4B. 4，5C. 5，6D. 6，7【答案】C【解析】解：，且，即，，故选：C．由即，由不等式性质可得的范围可得答案．本题考查了估算无理数大小的知识，注意夹逼法的运用是解题关键．21.如图，已知数轴上的点A、B、C、D分别表示数、1、2、3，则表示数的点P应落在线段A. AO上B. OB上C. BC上D. CD上【答案】B【解析】解：，，故表示数的点P应落在线段OB上．故选：B．根据估计无理数的方法得出，进而得出答案．此题主要考查了估算无理数的大小，得出的取值范围是解题关键．22.与无理数最接近的整数是A. 4B. 5C. 6D. 7【答案】C【解析】解：，最接近的整数是，，故选：C．根据无理数的意义和二次根式的性质得出，即可求出答案．本题考查了二次根式的性质和估计无理数的大小等知识点，主要考查学生能否知道在5和6之间，题目比较典型．23.若的小数部分为a，的小数部分为b，则的值为A. 0B. 1C.D. 2【答案】B【解析】【分析】本题考查了估算无理数的大小，解题的关键是用有理数逼近无理数，求无理数的近似值．运用有理数逼近无理数，求无理数的近似值求解．【解答】解：，，，，故选B．24.估计的值A. 在4和5之间B. 在3和4之间C. 在2和3之间D. 在1和2之间【答案】A【解析】【分析】本题考查了估算无理数的大小的应用，关键是确定的范围．求出的范围，都减去2即可得出答案．【解答】解：，，，，故选A．25.实数的值在A. 0和1之间B. 1和2之间C. 2和3之间D. 3和4之间【答案】B【解析】解：，实数的值在：1和2之间．故选：B．直接利用估算无理数大小，正确得出接近的有理数，进而得出答案．此题主要考查了估算无理数大小，正确得出无理数接近的有理数是解题关键．26.估算的值是在A. 3和4之间B. 4和5之间C. 5和6之间D. 6和7之间【答案】B【解析】【分析】本题主要考查了估计无理数大小的方法，找出最接近的有理数，再进行比较是解决问题的关键．找出比较接近的有理数，即与，从而确定它的取值范围．【解答】解：，．故选B．27.估计的值在A. 4和5之间B. 5和6之间C. 6和7之间D. 7和8之间【答案】C【解析】解：，即，故选：C．根据，可以估算出位于哪两个整数之间，从而可以解答本题．本题考查估算无理数的大小，解题的关键是明确估算无理数大小的方法．28.式子的整数部分是a，小数部分是b，则的值是A. B. C. D.【答案】D【解析】【分析】此题考查无理数的估算和代数式的值，注意找出最接近的整数范围是解决本题的关键．因为，所以，由此求得整数部分与小数部分，代入即可即可得到结果．【解答】解：，，，，．故选D．29.一个正方形的面积是15，估计它的边长在A. 1和2之间B. 2和3之间C. 3和4之间D. 4和5之间【答案】C【解析】解：一个正方形的面积是15，其边长．，．故选C．先求出正方形的边长，再估算出其大小即可．本题考查的是估算无理数的大小，熟知估算无理数大小要用逼近法是解答此题的关键．30.已知a是的整数部分，b是的小数部分，那么的平方根是A. 4B.C.D.【答案】D【解析】【分析】此题考查了估算无理数的大小，代数式的值，平方根，正确得出a，b的值是解题关键，根据，得到，求出a、b的值，再代入计算，根据平方根的定义求解，即可得到答案．【解答】解：，，，，，的平方根是，故选D．31.估计的值在A. 2到3之间B. 3到4之间C. 4到5之间D. 5到6之间【答案】B【解析】【分析】本题考查了估算无理数的大小，能估算出的范围是解此题的关键．解答此题先求出的范围，然后再加1可得的范围．【解答】解：，，即在3和4之间，故选B．32.已知a是的整数部分，b是的小数部分，那么的平方根是A. 4B.C.D.【答案】D【解析】解：，，，，，的平方根是．根据，利用不等式的性质可得，求出a、b的值，再代入计算，根据平方根的定义求解．此题主要考查了估算无理数的大小，正确得出a，b的值是解题关键．33.在两个连续整数a和b之间，，那么的值是A. 11B. 13C. 14D. 15【答案】B【解析】解：，，，．故选：B．首先用“夹逼法”确定a、b的值，进而可得的值．此题主要考查了估算无理数的大小，关键是正确确定a、b的值．34.实数界于哪两个相邻的整数之间A. 3和4B. 5和6C. 7和8D. 9和10【答案】B【解析】解：，在5和6之间．故选：B．先估算出的范围，即可得出答案．本题考查了估算无理数的大小，能估算出的范围是解此题的关键．35.实数的值在A. 0与1之间B. 1与2之间C. 2与3之间D. 3与4之间【答案】B【解析】解：，实数的值在1与2之间．故选：B．直接利用无理数最接近的有理数进而答案．此题主要考查了估算无理数大小，正确得出接近的有理数是解题关键．36.下列说法：是1的平方根；在两个连续整数a和b之间，那么；所有的有理数都可以用数轴上的点表示，反过来，数轴上的所有点都表示有理数；无理数就是开放开不尽的数；正确的个数为A. 1个B. 2个C. 3个D. 4个【答案】B【解析】【分析】此题考查了估算无理数的大小、实数与数轴、实数，熟知有关定义和性质是本题的关键．根据估算无理数的大小、实数与数轴、无理数的定义和特点分别对每一项进行分析，即可得出答案．【解答】解：是1的平方根是正确的；在两个连续整数a和b之间，那么是正确的；所有的实数都可以用数轴上的点表示，反过来，数轴上的所有点都表示实数，题目中的说法是错误的；无理数就是无限不循环的小数，题目中说法是错误的．37.估计的值在A. 2 到3 之间B. 3 到4 之间C. 4 到5 之间D. 5 到6 之间【答案】B【解析】解：，，故选：B．首先确定在整数2和3之间，然后可得的值在3到4之间．此题主要考查了估算无理数，关键是掌握用有理数逼近无理数，求无理数的近似值．38.估计的运算结果应在A. 6与7之间B. 7与8之间C. 8与9之间D. 9与10之间【答案】C【解析】解：，而，原式运算的结果在8到9之间；故选C．首先计算出，再估算出即可得结果．本题考查了无理数的近似值问题，关键是利用“夹逼法”是估算的一般方法，也是常用方法．39.若，且a、b是两个连续整数，则的值是A. B. C. D.【答案】C【解析】解：，，，，，，故选C．先求出的范围，再求出的范围，求出a、b的值，代入求出即可．本题考查了估算无理数的大小，能求出的范围是解此题的关键．40.设，a在两个相邻整数之间，则这两个整数是A. 0和1B. 1和2C. 2和3D. 3和4【答案】C【解析】解：，，即，则这两整数是2和3，故选C估算大小，即可得到结果．此题考查了估算无理数的大小，估算出大小是解本题的关键．41.估计的值A. 1到2之间B. 2到3之间C. 3和4之间D. 4和5之间【答案】D【解析】解：，，即在4到5之间，故选：D．根据得出，即可得出答案．本题考查了估算无理数的大小的应用，关键是能求出的范围．42.估计的值在哪两个整数之间A. 75和77B. 6和7C. 7和8D. 8和9【答案】D【解析】解：，，在两个相邻整数8和9之间．故选：D．先对进行估算，再确定是在哪两个相邻的整数之间．此题主要考查了估算无理数的大小，注意首先估算无理数的值，再根据不等式的性质进行计算．现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．43.定义：对任意实数x，表示不超过x的最大整数，如，，对数字65进行如下运算：：：，这样对数字65运算3次后的值就为1，像这样对一个正整数总可以经过若干次运算后值为1，则数字255经过次运算后的结果为1．A. 3B. 4C. 5D. 6【答案】A【解析】解：第一次第二次第三次，则数字255经过3次运算后的结果为1．故选：A．根据表示不超过x的最大整数计算，可得答案．本题考查了估算无理数的大小的应用，主要考查学生的阅读能力和逆推思维能力．44.黄金分割数是一个很奇妙的数，大量应用于艺术、建筑和统计决策等方面，请你估算的值A. 在和之间B. 在和之间C. 在和之间D. 在和之间【答案】B【解析】解：，，故选：B．根据，可得答案．本题考查了估算无理数的大小，利用是解题关键．45.8的负的平方根介于A. 与之间B. 与之间C. 与之间D. 与之间【答案】C【解析】解：，．．故选：C．先求得的范围，然后再求得的范围即可．本题主要考查的是估算无理数的大小，利用夹逼法求得的大致范围是解题的关键．46.通过估算，估计的值应在A. ～之间B. ～之间C. ～之间D. ～之间【答案】B【解析】解：，，即，，故选：B．根据得出：，进而可得答案．本题考查了估算无理数的大小，利用了正数的被开方数越大立方根越大的关系．47.估计的值在A. 1和2之间B. 2和3之间C. 3和4之间D. 4和5之间【答案】C【解析】解：，，则的值在3和4之间，故选：C．估算得出的范围即可．此题考查估算无理数的大小，熟练掌握算术平方根定义是解本题的关键．48.如图，数轴上A，B，C，D四点中，与对应的点距离最近的是A. 点AB. 点BC. 点CD. 点D【答案】B【解析】【分析】本题考查的是实数与数轴，熟知实数与数轴上各点是一一对应关系是解答此题的关键．先估算出的范围，结合数轴可得答案．【解答】解：，即，，由数轴知，与对应的点距离最近的是点B．故选B．49.下列各数中，介于正整数6和7之间的数是A. B. C. D.【答案】A【解析】解：，，故A正确．，，故B错误．，，故C错误．，，故D错误．故选：A．依据被开方数越大对应的算术平方根立方根越大进行求解即可．本题主要考查的是估算无理数的大小，夹逼法的应用是解题的关键．50.若，则整数A. 5B. 6C. 7D. 8【答案】C【解析】解：，，故选：C．先估算出的范围，再得出选项即可．本题考查了估算无理数的大小，能估算出的范围是解此题的关键．51.在数轴上有一块墨迹，被覆盖住的无理数可能是A. B. C. D.【答案】B【解析】【分析】此题主要考查了估算无理数的大小，数轴的有关知识，应先找到所求的无理数在哪两个和它接近的整数之间，然后判断出所求的无理数的范围即可求解．【解答】解：由图可知：被覆盖的数在3和4之间；被墨迹覆盖的无理数有可能是．故选B．52.对于实数x，我们规定表示不大于x的最大整数，如，，现对82进行如下操作：第次第次第次，这样对82只需进行3次操作后变为1，类似地，对121只需进行多少次操作后变为A. 1B. 2C. 3D. 4【答案】C【解析】解：第次第次第次，对121只需进行3次操作后变为1，故选：C．表示不大于x的最大整数，依据题目中提供的操作进行计算即可．本题考查了估算无理数的大小，解决本题的关键是明确表示不大于x的最大整数．53.估计的值在哪两个整数之间A. 9和10B. 7和8C. 5和6D. 3和4【答案】D【解析】解：，在3和4之间．故选D．先估算出的范围，即可得出选项．本题考查了估算无理数的大小的应用，能估算出的范围是解此题的关键．54.与最接近的整数是A. 1B. 2C. 3D. 4【答案】C【解析】解：，，．．．与最接近的整数是3．故选：C．先依据被开方数越大对应的算术平方根也越大估算出的大小，然后即可做出判断．本题主要考查的是估算无理数的大小，利用夹逼法估算出的大小是解题的关键．55.在数轴上标注了四段范围，如图，表示的点落在A. 段B. 段C. 段D. 段【答案】C【解析】【分析】根据数的平方，即可解答．本题考查了估算无理数的大小，解决本题的关键是计算出各数的平方．【解答】解：，，，，，，，的点落在段，故选：C．56.如图，数轴上点N表示的数可能是A. B. C. D.【答案】A【解析】解：，，，，根据点N在数轴上的位置，知：，四个选项中只有，即．故选：A．先对四个选项中的无理数进行估算，再根据N点的位置即可求解．本题考查了同学们估算无理数大小的能力，及能够根据点在数轴的位置确定数的大小．57.数轴上表示的点A的位置应该在A. 2与3之间B. 3与4之间C. 4与5之间D. 7与8之间【解析】【分析】本题考查了实数与数轴的对应关系，以及估算无理数大小的能力，难度一般．先估算无理数的大小，然后求解即可．【解答】解：，，故数轴上表示的点A的位置应在3与4之间．故选：B．58.估计的值在A. 2到3之间B. 3到4之间C. 4到5之间D. 5到6之间【答案】A【解析】解：，，故选：A．根据估算无理数的大小，即可解答．本题考查了估算无理数的大小，解决本题的关键是估算无理数的大小．59.如图，已知数轴上的点A、B、C、D分别表示数、、1、2，则表示的点P应落在线段A. AB上B. OB上C. OC上D. CD上【答案】A【解析】解：，，表示的点P应落在线段AB上．故选：A．直接根据题意得出进而得出答案．此题主要考查了估算无理数的大小，正确得出的取值范围是解题关键．60.a与b是两个连续整数，若，则a，b分别是A. 6，8B. 3，2C. 2，3D. 3，4【答案】C【解析】解：，，，且a与b是两个连续整数，，．故选C．根据，结合，即可得出a、b的值．本题考查了估算无理数的大小，解题的关键是找出．61.估计的值在A. 2和3之间B. 3和4之间C. 4和5之间D. 5和6之间【答案】B【解析】解：，，直接利用，进而得出答案．此题主要考查了估算无理数的大小，正确得出的取值范围是解题关键．62.若，且m、n为连续正整数，则的值为A. 5B. 7C. 9D. 11【答案】B【解析】解：，且m、n为连续正整数，，，则原式，故选：B．根据题意确定出m与n的值，代入原式计算即可求出值．此题考查了估算无理数的大小，设实数为a，a的整数部分A为不大于a的最大整数，小数部分B为实数a减去其整数部分，即；理解概念是解题的关键．63.估计的值在两个整数A. 3与4之间B. 5与6之间C. 6与7之间D. 3与10之间【答案】B【解析】解：，，的值在5与6之间．故选：B．直接利用估算无理数的方法得出接近无理数的整数进而得出答案．此题主要考查了估算无理数的大小，正确掌握无理数的估算方法是解题关键．64.的结果在下列哪两个整数之间．A. 6和7B. 5和6C. 4和5D. 3和4【答案】A【解析】解：，，故选：A．直接利用，进而得出答案．此题主要考查了估算无理数的大小，正确得出无理数接近的整数是解题关键．65.关于“”，下列说法不正确的是A. 它是一个无理数B. 它可以用数轴上的一个点来表示C. 它可以表示面积为19的正方形的边长D. 若为整数，则【答案】D【解析】【分析】本题主要考查了无理数的定义、数轴的意义以及无理数的估算，无理数的估算关键是确定无理数的整数部分．“夹逼法”是估算的一般方法，也是常用方法．分别根据无理数的定义、数轴的意义、正方形面积公式以及无理数的估算方法判断即可．【解答】解：A．是一个无理数，说法正确，故选项A不合题意；B.可以用数轴上的一个点来表示，说法正确，故选项B不合题意；C.它可以表示面积为19的正方形的边长，说法正确，故选项C不合题意；D.，，故选项D符合题意．故选D．66.如图，数轴上点P表示的数可能是A. B. C. D.【答案】C【解析】解：从数轴可知：P点表示数在2和3之间，A、，故本选项不符合题意；B、，故本选项不符合题意；C、，故本选项符合题意；D、，故本选项不符合题意；故选C．从数轴可知P点表示数在2和3之间，先估算出每个无理数的范围，即可得出答案．本题考查了估算无理数的大小，能估算出每个无理数的范围是解此题的关键．67.估计在A. ～之间B. ～之间C. ～之间D. ～之间【答案】C【解析】解：，即：，在2到3之间．故选：C．根据二次根式的性质得出，即：，可得答案．本题考查了估算无理数的大小和二次根式的性质，解此题的关键是知道在和之间．68.若的整数部分是a，小数部分是b，则式子的值是A. B. 9 C. 19 D.【答案】B【解析】解：，，，，．故选：B．先进行估算的范围，确定a，b的值，再代入代数式即可解答．本题考查了估算无理数的大小，解决本题的关键是估算的范围．69.关于“”，下列说法不正确的是A. 它是数轴上唯一一个距离原点个单位长度的点表示的数B. 它是一个无理数C. 若，则整数a的值为3D. 它可以表示面积为10的正方形的边长【答案】A【解析】解：数轴上距离原点个单位长度的点表示的数是，故A错误，符合题目要求它是一个无理数，故B正确，不符合题目要求，，故整数a的值为3，故C正确，不故符合题目要求它可以表示面积为10的正方形的边长，故D正确，不符合题目要求．故选：A．依据绝对值的定义、无理数的概念，依据夹逼法估算无理数大小的方法、依据算术平方根的定义进行判断即可．本题主要考查的是估算无理数的大小，实数与数轴，熟练掌握相关知识是解题的关键．70.若，且a、b是两个连续整数，则的值是A. 2B. 3C. 4D. 5【答案】D【解析】解：，，由，且a、b是两个连续的整数，得到，，则，故选：D．由被开方数5的范围确定出的范围，进而求出a与b的值，代入原式计算即可得到结果．71.设面积为6的正方形的边长为下列关于a的四种说法：是有理数；是无理数；可以用数轴上的一个点来表示；其中说法正确的有A. 1个B. 2个C. 3个D. 4个【答案】C【解析】解：面积为3的正方形的边长为a，，故是有理数，错误；是无理数，正确；可以用数轴上的一个点来表示，正确；，正确，则说法正确的是：共3个．故选：C．直接利用得出正方形的边长，再利用实数的性质分析得出答案．此题主要考查了实数的性质以及无理数的估算，正确掌握实数有关性质是解题关键．72.有下列说法：实数与数轴上的点一一对应；的相反数是；在1和3之间的无理数有且只有，，，这4个；是三次三项式；绝对值等于本身的数是正数；其中错误的个数为A. 1B. 2C. 3D. 4【答案】C【解析】解：实数与数轴上的点一一对应，正确；的相反数是，正确；在1和3之间的无理数有无数个，错误；是二次三项式，错误；绝对值等于本身的数是正数和0，错误；故选：C．根据估算无理数的大小、相反数的概念、绝对值的概念、多项式的概念、实数与数轴判断即可．本题考查的是估算无理数的大小、相反数的概念、绝对值的概念、多项式的概念、实数与数轴，掌握相关的概念和性质是解题的关键．73.估计的值在两个整数A. 3与4之间B. 5与6之间C. 6与7之间D. 3与10之间【答案】B【解析】解：，，的值在5与6之间．故选：B．直接利用估算无理数的方法得出接近无理数的整数进而得出答案．此题主要考查了估算无理数的大小，正确掌握二次根式的性质是解题关键．74.估算的值是A. 在0和1平之间B. 在1和2之间C. 在2和3之间D. 在3和4之间【答案】C【解析】解：，，在 2 和 3 之间．故选C直接得出的取值范围进而得出答案．此题主要考查了估算无理数的大小，正确得出的取值范围是解题关键．75.已知a为实数，若，则下列结论中正确的是A. B. C. D.【答案】D【解析】【分析】本题主要考查了估算无理数的大小，首先估算和的大小是解答此题的关键．首先估算和的大小，再做选择．【解答】解：，，又，，故选D．76.如图，在数轴上，与表示的点最接近的点是。

第三章实数（解析板）5、估算无理数的大小知识点梳理估算无理数的大小估算无理数大小要用逼近法．思维方法：用有理数逼近无理数，求无理数的近似值同步练习一．选择题（共10小题）1．若k＜＜k+1（k是整数），则k＝（）A．6B．7C．8D．9【考点】估算无理数的大小．【分析】根据＝9，＝10，可知9＜＜10，依此即可得到k的值．【解答】解：∵k＜＜k+1（k是整数），9＜＜10，∴k＝9．故选：D．【点评】本题考查了估算无理数的大小，解题关键是估算的取值范围，从而解决问题．2．估计的值在（）A．2到3之间B．3到4之间C．4到5之间D．5到6之间【考点】估算无理数的大小．【分析】利用”夹逼法“得出的范围，继而也可得出的范围．【解答】解：∵2＝＜＝3，∴3＜＜4，故选：B．【点评】此题考查了估算无理数的大小的知识，属于基础题，解答本题的关键是掌握夹逼法的运用．3．对于实数x，我们规定[x]表示不大于x的最大整数，如[4]＝4，[]＝1，[﹣2.5]＝﹣3．现对82进行如下操作：82[]＝9[]＝3[]＝1，这样对82只需进行3次操作后变为1，类似地，对121只需进行多少次操作后变为1（）A．1B．2C．3D．4【考点】估算无理数的大小．【分析】[x]表示不大于x的最大整数，依据题目中提供的操作进行计算即可．【解答】解：121[]＝11[]＝3[]＝1，∴对121只需进行3次操作后变为1，故选：C．【点评】本题考查了估算无理数的大小，解决本题的关键是明确[x]表示不大于x的最大整数．4．估计+1的值在（）A．2和3之间B．3和4之间C．4和5之间D．5和6之间【考点】估算无理数的大小．【分析】先估算出的范围，即可得出答案．【解答】解：∵3＜＜4，∴4＜+1＜5，即+1在4和5之间，故选：C．【点评】本题考查了估算无理数的大小，能估算出的范围是解此题的关键．5．估计+1的值（）A．在1和2之间B．在2和3之间C．在3和4之间D．在4和5之间【考点】估算无理数的大小．【分析】直接利用已知无理数得出的取值范围，进而得出答案．【解答】解：∵2＜＜3，∴3＜+1＜4，∴+1在3和4之间．故选：C．【点评】此题主要考查了估算无理数大小，正确得出的取值范围是解题关键．6．与最接近的整数是（）A．5B．6C．7D．8【考点】实数；估算无理数的大小．【分析】由题意可知36与37最接近，即与最接近，从而得出答案．【解答】解：∵36＜37＜49，∴＜＜，即6＜＜7，∵37与36最接近，∴与最接近的是6．故选：B．【点评】此题主要考查了无理数的估算能力，关键是整数与最接近，所以＝6最接近．7．已知a为整数，且，则a等于（）A．1B．2C．3D．4【考点】估算无理数的大小．【分析】直接利用，接近的整数是2，进而得出答案．【解答】解：∵a为整数，且，∴a＝2．故选：B．【点评】此题主要考查了估算无理数大小，正确得出无理数接近的有理数是解题关键．8．下列整数中，与10﹣最接近的是（）A．4B．5C．6D．7【考点】估算无理数的大小．【分析】解法一：由于9＜13＜16，可判断与4最接近，从而可判断与10﹣最接近的整数为6．解法二：计算3.5的平方与13作比较，再得10﹣＜6.5，可作判断．【解答】解：解法一：∵9＜13＜16，∴3＜＜4，∵3.62＝12.96，3.72＝13.69，∴3.6＜＜3.7，∴﹣3.7＜﹣＜﹣3.6，∴10﹣3.7＜10﹣＜10﹣3.6，∴6.3＜10﹣＜6.4，∴与10﹣最接近的是6．解法二：∵3＜＜4，∴6＜10﹣＜7，∵3.52＝12.25，且12.25＜13，∴＞3.5，∴10﹣＜6.5，∴与10﹣最接近的是6．故选：C．【点评】此题考查了估算无理数的大小，熟练掌握估算无理数的方法是解本题的关键．9．估计a＝×﹣1的值应在（）A．2到3之间B．3到4之间C．4到5之间D．5到6之间【考点】估算无理数的大小．【分析】先求出×＝，因为5＜＜6，所以×﹣1在4到5之间．【解答】解：a＝×﹣1＝﹣1，∵5＜＜6，∴在5到6之间，∴﹣1在4到5之间，故选：C．【点评】本题考查了二次根式的乘法，估算无理数的大小等，比较简单，理解二次根式的意义是解题的关键．10．如图，数轴上的点A，B，O，C，D分别表示数﹣2，﹣1，0，1，2，则表示数2﹣的点P应落在（）A．线段AB上B．线段BO上C．线段OC上D．线段CD上【考点】实数与数轴；估算无理数的大小．【分析】根据2＜＜3，得到﹣1＜2﹣＜0，根据数轴与实数的关系解答．【解答】解：2＜＜3，∴﹣1＜2﹣＜0，∴表示数2﹣的点P应落在线段BO上，故选：B．【点评】本题考查的是无理数的估算、实数与数轴，正确估算无理数的大小是解题的关键．二．填空题（共14小题）11．若5+的小数部分是a，5﹣的小数部分是b，则ab+5b＝2．【考点】估算无理数的大小．【分析】由于2＜＜3，所以7＜5+＜8，由此找到所求的无理数在哪两个和它接近的整数之间，然后判断出所求的无理数的整数部分，小数部分让原数减去整数部分，代入求值即可．【解答】解：∵2＜＜3，∴2+5＜5+＜3+5，﹣2＞﹣＞﹣3，∴7＜5+＜8，5﹣2＞5﹣＞5﹣3，∴2＜5﹣＜3∴a＝﹣2，b＝3﹣；将a、b的值，代入可得ab+5b＝2．故答案为：2．【点评】此题主要考查了无理数的估算能力，现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．估算出整数部分后，小数部分＝原数﹣整数部分．12．已知a，b为两个连续整数，且a＜＜b，则a+b＝7．【考点】估算无理数的大小．【分析】根据被开方数越大对应的算术平方根越大求得a、b的值，然后利用加法法则计算即可．【解答】解：∵9＜11＜16，∴3＜＜4．∵a，b为两个连续整数，且a＜＜b，∴a＝3，b＝4．∴a+b＝3+4＝7．故答案为：7．【点评】本题主要考查的是估算无理数的大小，求得a、b的值是解题的关键．13．已知m是的整数部分，n是的小数部分，则m2﹣n＝12﹣．【考点】估算无理数的大小．【分析】由于3＜＜4，由此找到所求的无理数在哪两个和它接近的整数之间，然后判断出所求的无理数的整数部分，小数部分让原数减去整数部分，代入求值即可．【解答】解：∵3＜＜4，∴m＝3；又∵3＜＜4，∴n＝﹣3；则m2﹣n＝9﹣+3＝12﹣．故答案为：12﹣．【点评】此题主要考查了无理数的估算能力，现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．估算出整数部分后，小数部分＝原数﹣整数部分．14．已知：m、n为两个连续的整数，且m＜＜n，则m+n＝7．【考点】估算无理数的大小．【分析】先估算出的取值范围，得出m、n的值，进而可得出结论．【解答】解：∵9＜11＜16，∴3＜＜4，∴m＝3，n＝4，∴m+n＝3+4＝7．故答案为：7．【点评】本题考查的是估算无理数的大小，先根据题意算出的取值范围是解答此题的关键．15．规定用符号[x]表示一个实数的整数部分，例如[3.69]＝3．[]＝1，按此规定，[﹣1]＝2．【考点】估算无理数的大小．【分析】先求出（﹣1）的范围，再根据范围求出即可．【解答】解：∵9＜13＜16，∴3＜＜4，∴2＜﹣1＜3，∴[﹣1]＝2．故答案是：2．【点评】本题主要考查了无理数的估算，解题关键是确定无理数的整数部分即可解决问题．16．已知a、b为两个连续的整数，且，则a+b＝11．【考点】估算无理数的大小．【分析】根据无理数的性质，得出接近无理数的整数，即可得出a，b的值，即可得出答案．【解答】解：∵，a、b为两个连续的整数，∴＜＜，∴a＝5，b＝6，∴a+b＝11．故答案为：11．【点评】此题主要考查了无理数的大小，得出比较无理数的方法是解决问题的关键．17．规定：用符号[x]表示一个不大于实数x的最大整数，例如：[3.69]＝3，[+1]＝2，[﹣2.56]＝﹣3，[﹣]＝﹣2．按这个规定，[﹣﹣1]＝﹣5．【考点】估算无理数的大小．【分析】先求出的范围，求出﹣1的范围，即可得出答案．【解答】解：∵，∴，∴，∴[﹣﹣1]＝﹣5．故答案为：﹣5．【点评】本题考查了估算无理数的大小的应用，解此题的关键是求的范围．18．设m＝，那么m+的整数部分是2．【考点】估算无理数的大小．【分析】根据2＜＜3，可得答案．【解答】解：m+＝＝＝．∵2＜＜2.5，∴12＜6＜15，∴2＜m+＝＜3，故答案为：2．【点评】本题考查了估算无理数的大小，利用算术平方根越大被开方数越大得出2＜＜3是解题关键．19．已知的小数部分是a，的整数部分是b，则a+b＝．【考点】估算无理数的大小．【分析】先分别求出和的范围，得到a、b的值，再代入a+b计算即可．【解答】解：∵2＜＜3，2＜＜3，∴a＝﹣2，b＝2，a+b＝﹣2+2＝，故答案为．【点评】本题考查了估算无理数的大小，利用夹值法估算出和的范围是解此题的关键．20．已知，则的值约为0.048．【考点】估算无理数的大小．【分析】由于当被开方数两位两位地移，它的算术平方根相应的向相同方向就一位一位地移，由此即可求解．【解答】解：把0.0023向右移动4位，即可得到23，显然只需对4.80向左移动2位得到0.048．故答案为：0.048．【点评】此题主要考查了算术平方根的性质和无理数的估算，关键是利用了被开方数与其算术平方根之间位数的移动关系．21．若x＜﹣1＜y且x，y是两个连续的整数，则x+y的值是3．【考点】估算无理数的大小．【分析】估算得出的范围，进而求出x与y的值，即可求出所求．【解答】解：∵4＜6＜9，∴2＜＜3，即1＜﹣1＜2，∴x＝1，y＝2，则x+y＝1+2＝3，故答案为：3【点评】此题考查了估算无理数的大小，弄清估算的方法是解本题的关键．22．已知a，b为两个连续整数，且，则a+b＝7．【考点】估算无理数的大小．【分析】因为32＜13＜42，所以3＜＜4，求得a、b的数值，进一步求得问题的答案即可．【解答】解：∵32＜13＜42，∴3＜＜4，即a＝3，b＝b，所以a+b＝7．故答案为：7．【点评】此题考查无理数的估算，利用平方估算出根号下的数值的取值，进一步得出无理数的取值范围，是解决这一类问题的常用方法．23．若的整数部分是a，小数部分是b，则2a﹣b＝24﹣．【考点】估算无理数的大小．【分析】首先确定的范围，即可推出ab的值，把ab的值代入求出即可．【解答】解：∵8＜＜9，∴a＝8，b＝﹣8，∴2a﹣b＝2×8﹣（﹣8）＝24﹣．故答案为：24﹣．【点评】考查了估算无理数的大小，解此题的关键是确定的范围．8＜＜9，得出a，b的值．24．的整数部分是a，小数部分是b，则a﹣b＝2﹣．【考点】估算无理数的大小．【分析】根据无理数大小可得出a，b的值，进而得出答案．【解答】解：∵的整数部分是a，小数部分是b，∴a＝1，b＝﹣1，则a﹣b＝1﹣（﹣1）＝2﹣．故答案为：2﹣．【点评】此题主要考查了估计无理数，得出a，b的值是解题关键．三．解答题（共7小题）25．已知5a+2的立方根是3，3a+b﹣1的算术平方根是4，c是的整数部分，求3a﹣b+c 的平方根．【考点】平方根；算术平方根；立方根；估算无理数的大小．【分析】利用立方根的意义、算术平方根的意义、无理数的估算方法，求出a、b、c的值，代入代数式求出值后，进一步求得平方根即可．【解答】解：∵5a+2的立方根是3，3a+b﹣1的算术平方根是4，∴5a+2＝27，3a+b﹣1＝16，∴a＝5，b＝2，∵c是的整数部分，∴c＝3，∴3a﹣b+c＝16，3a﹣b+c的平方根是±4．【点评】此题考查立方根的意义、算术平方根的意义、无理数的估算方法、平方根的意义、代数式求值等知识点，读懂题意，掌握解答顺序，正确计算即可．26．对于实数a，我们规定：用符号表示不大于的最大整数，称为a的根整数，例如：，．（1）仿照以上方法计算：＝2；＝5．（2）若，写出满足题意的x的整数值1，2，3．如果我们对a连续求根整数，直到结果为1为止．例如：对10连续求根整数2次，这时候结果为1．（3）对100连续求根整数，3次之后结果为1．（4）只需进行3次连续求根整数运算后结果为1的所有正整数中，最大的是255．【考点】估算无理数的大小；实数的运算．【分析】（1）先估算和的大小，再由并新定义可得结果；（2）根据定义可知x＜4，可得满足题意的x的整数值；（3）根据定义对100进行连续求根整数，可得3次之后结果为1；（4）最大的正整数是255，根据操作过程分别求出255和256进行几次操作，即可得出答案．【解答】解：（1）∵22＝4，52＝25，62＝36，∴5＜＜6，∴＝[2]＝2，[]＝5，故答案为：2，5；（2）∵12＝1，22＝4，且，∴x＝1，2，3，故答案为：1，2，3；（3）第一次：[]＝10，第二次：[]＝3，第三次：[]＝1，故答案为：3；（4）最大的正整数是255，理由是：∵[]＝15，[]＝3，[]＝1，∴对255只需进行3次操作后变为1，∵[]＝16，[]＝4，[]＝2，[]＝1，∴对256只需进行4次操作后变为1，∴只需进行3次操作后变为1的所有正整数中，最大的是255，故答案为：255．【点评】本题考查了估算无理数的大小的应用，主要考查学生的阅读能力和猜想能力，同时也考查了一个数的平方数的计算能力．27．阅读下面的文字，解答问题，例如：∵＜＜，即2＜＜3，∴的整数部分为2，小数部分为（﹣2）．请解答：（1）的整数部分是4，小数部分是﹣4．（2）已知：9﹣小数部分是m，9+小数部分是n，且（x+1）2＝m+n，请求出满足条件的x的值【考点】估算无理数的大小．【分析】（1）根据夹逼法可求的整数部分和小数部分；（2）首先估算出m，n的值，进而得出m+n的值，可求满足条件的x的值．【解答】解：（1）∵4＜＜5，∴的整数部分是4，小数部分是﹣4．（2）∵9﹣小数部分是m，9+小数部分是n，∴m＝9﹣﹣4＝5﹣，n＝9+﹣13＝﹣4，∵（x+1）2＝m+n＝5﹣+﹣4＝1，∴x+1＝±1，解得x1＝﹣2，x2＝0．故满足条件的x的值为x1＝﹣2，x2＝0．故答案为：4，﹣4．【点评】此题主要考查了估算无理数的大小，正确得出各数的小数部分是解题关键．28．阅读下面的文字，解答问题：大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，于是小明用﹣1来表示的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理，因为的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：∵＜＜，即2＜＜3，∴的整数部分为2，小数部分为（﹣2）．请解答：（1）的整数部分是4，小数部分是﹣4．（2）如果的小数部分为a，的整数部分为b，求a+b﹣的值；（3）已知：10+＝x+y，其中x是整数，且0＜y＜1，求x﹣y的相反数．【考点】估算无理数的大小．【分析】（1）先估算出的范围，即可得出答案；（2）先估算出、的范围，求出a、b的值，再代入求出即可；（3）先估算出的范围，求出x、y的值，再代入求出即可．【解答】解：（1）∵4＜＜5，∴的整数部分是4，小数部分是，故答案为：4，﹣4；（2）∵2＜＜3，∴a＝﹣2，∵3＜＜4，∴b＝3，∴a+b﹣＝﹣2+3﹣＝1；（3）∵1＜3＜4，∴1＜＜2，∴11＜10+＜12，∵10+＝x+y，其中x是整数，且0＜y＜1，∴x＝11，y＝10+﹣11＝﹣1，∴x﹣y＝11﹣（﹣1）＝12﹣，∴x﹣y的相反数是﹣12+；【点评】本题考查了估算无理数的大小，能估算出、、、的范围是解此题的关键．29．已知5a+2的立方根是3，3a+b﹣1的算术平方根是4，c是的整数部分．（1）求a，b，c的值；（2）求3a﹣b+c的平方根．【考点】估算无理数的大小．【分析】（1）利用立方根的意义、算术平方根的意义、无理数的估算方法，求出a、b、c 的值；（2）将a、b、c的值代入代数式求出值后，进一步求得平方根即可．【解答】解：（1）∵5a+2的立方根是3，3a+b﹣1的算术平方根是4，∴5a+2＝27，3a+b﹣1＝16，∴a＝5，b＝2，∵c是的整数部分，∴c＝3．（2）将a＝5，b＝2，c＝3代入得：3a﹣b+c＝16，∴3a﹣b+c的平方根是±4．【点评】此题考查立方根的意义、算术平方根的意义、无理数的估算方法、平方根的意义、代数式求值等知识点，读懂题意，掌握解答顺序，正确计算即可．30．阅读下面的文字，解答问题：大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部写出来，而1＜＜2，于是可用﹣1来表示的小数部分．请解答下列问题：（1）的整数部分是4，小数部分是﹣4．（2）如果的小数部分为a，的整数部分为b，求a+b﹣的值（3）已知：100+＝x+y，其中x是整数，且0＜y＜1，求x++24﹣y的平方根．【考点】平方根；估算无理数的大小．【分析】（1）先估算出的范围，即可得出答案；（2）先估算出、的范围，求出a、b的值，再代入求出即可；（3）先估算出的范围，求出x、y的值，再代入求出即可．【解答】解：（1）∵4＜＜5，∴的整数部分是4，小数部分是﹣4，故答案为：4，﹣4；（2）∵2＜＜3，∴a＝﹣2，∵3＜＜4，∴b＝3，∴a+b﹣＝﹣2+3﹣＝1；（3）∵100＜110＜121，∴10＜＜11，∴110＜100+＜111，∵100+＝x+y，其中x是整数，且0＜y＜1，∴x＝110，y＝100+﹣110＝﹣10，∴x++24﹣y＝110++24﹣+10＝144，x++24﹣y的平方根是±12．．【点评】本题考查了估算无理数的大小，能估算出、、、的范围是解此题的关键．31．已知2a﹣1的算术平方根是3，3a+b﹣9的立方根是2，c是的整数部分，求7a﹣2b﹣2c的平方根．【考点】平方根；估算无理数的大小．【分析】根据平方根、立方根、算术平方根，即可解答．【解答】解：∵2a﹣1的算术平方根是3，∴2a﹣1＝9，∴a＝5，∵3a+b﹣9的立方根是2，∴3a+b﹣9＝8，∴b＝2，∵c是的整数部分，，∴c＝3，∴7a﹣2b﹣2c＝35﹣4﹣6＝25，∴7a﹣2b﹣2c的平方根是±5．【点评】本题考查了平方根、立方根、算术平方根，解决本题的关键是熟记平方根、立方根、算术平方根的定义。

考点： 估算无理数的大小;
答案
~~第4题~~ (2019象山.七上期末) 已知a，b为两个连续整数，且
，则 的值为
A.9B.8C.7D.6
考点： 估算无理数的大小;代数式求值;
答案
~~第5题~~
(2019拱墅.七上期末) 若一个正方形的面积为 7 ，它的周长介于两个相邻整数之间，这两个相邻整数是（ ）
A . -3 B . -2 C . -4 D . -1
考点： 估算无理数的大小;
答案
~~第8题~~ (2019长兴.七上期末) 若k<
<k+1(k是整数)，则k的值为（ ）
A.6B.7C.8D.9
考点： 估算无理数的大小;
答案
~~第9题~~ (2019鄞州.七上期末) 如图，在数轴上表示无理数 的点落在( )
考点： 估算无理数的大小;
答案
~~第2题~~
(2019余杭.七上期末) 估计 -1在哪两个整数之间（ ）
A . 0和1 B . 1和2 C . 2和3 D . 3和4
考点： 估算无理数的大小;
答案
~~第3题~~
(2019江北.七上期末) 与50的算术平方根最接近的整数是
A . 7 B . 8 C . 10 D . 25
1.答 案 ： C 2.答 案 ： B 3.答 案 ： A 4.答 案 ： C 5.答 案 ： B 6.答 案 ： D 7.答 案 ： B 8.答 案 ： C 9.答 案 ： C 10.答 案 ： C
A . 线段AB上 B . 线段BC上 C . 线段CD上 D . 线段DE上
考点： 估算无理数的大小;
答案
~~第10题~~
(2017金华.七上期中) 估计 的大小在（ ）

估算无理数的大小（北京习题集）（教师版）一．选择题（共4小题）1．（2015秋•门头沟区期末）若13m =，估计m 的值所在的范围是( ) A ．01m <<B ．12m <<C ．23m <<D ．34m <<2．（2016春•西城区期末）如图，在数轴上，与表示2的点最接近的点是( )A ．点AB ．点BC ．点CD ．点D3．（2016春•西城区校级期中）已知：212.5156.25=，212.6158.76=，212.7161.29=，212.8163.84=，下列说法正确的是( ) A ．12.616012.7<< B 16040= C ．12.515612.6<D 158.7612.6=± 4．（2016116282的结果估计在( ) A ．6至7之间B ．7至8之间C ．8至9之间D ．9至10之间二．填空题（共8小题）5．（20175的整数部分是x ，小数部分是y ，则x y -= ．6．（2016秋•西城区期末）对于实数p ，我们规定：用p <>表示不小于p 的最小整数，例如：44<>=，32<>=．现对72进行如下操作： 727299332===第一次第二次第三次．即对72只需进行3次操作后变为2，类似地：（1）对36只需进行 次操作后变为2；（2）只需进行3次操作后变为2的所有正整数中，最大的是 ．7．（201613的整数部分为a ，小数部分为b ，则2a b -的值为 ． 8．（2016春•海淀区校级期中）若56a b <<且a 、b 为连续整数，则a b += ． 9．（2016(0)m m >近似值的方法，回答问题： ①任取正数1a m <②令2111()2ma a a =+，则22m m a a <；③3221()2m a a a =+，则33mm a a <<；⋯以此类推n次，得到n nma a <． 其中n an 阶过剩近似值，nman 阶不足近似值．的近似值． ①取正数12a =<②于是2a = ；则2a <．③3阶过剩近似值3a 是 ，3阶不足近似值是 ． 10．（2016秋•海淀区校级期中）大于的整数有 ．（写出所有符合条件的整数）11．（2016春•海淀区校级期中）已知ab则a b -= ． 12．（2015秋•平谷区期末）若a ，b为两个连续的正整数，且a b ，则a b += ． 三．解答题（共3小题）13．（2014秋•房山区校级期中）阅读材料：学习了无理数后，的近似值：，2(01)k k +<<，所以22(2)k =+，可得2644k k =++．由01k <<可知201k <<，所以644k ≈+，解得12k ≈12 2.502+≈． 依照小红的方法解决下列问题： （1≈ ；（精确到0.01)（2）已知非负整数a 、b 、m，若1a a <+，且2m a b =+．（用含a 、b 的代数式表示） 14．（2013春•西城区期末）在没有带开方功能的计算器的情况下，n 为正整数）的近似值(k a k 为正整数），并通过迭代逐渐减小|k a -的值来提高k a如下：（11:a，23∴<<，取1322 2.52a -=+=； （2）通过计算2()2k k ka nm a -=和1k k k a a m +=-得到精确度更高的近似值1:k a +（说明 2.6458≈，此题中记2.6458，以下结果都要求写成小数形式）:1k =时，2111()72a m a -== ，211a a m =-=，2|a = ； 1k =时，2()()m =≈ （精确到0.001)，3a = - =，3|a -= ； ⋯15．（2011秋•海淀区期末）阅读材料：的近似值． 小明的方法：，3(01)k k =+<<．∴22(3)k =+．21396k k ∴=++． 1396k ∴≈+．解得46k ≈．∴43 3.676≈+≈． 问题：（1（2a 、b 、m，若1a a <+，且2m a b =+，≈ （用含a 、b 的代数式表示）； （3）请用（2估算无理数的大小（北京习题集）（教师版）参考答案与试题解析一．选择题（共4小题）1．（2015秋•门头沟区期末）若13m =，估计m 的值所在的范围是( ) A ．01m <<B ．12m <<C ．23m <<D ．34m <<【分析】根据91316<<，得出3134<<，从而估算出m 所在的范围． 【解答】解：91316<<，∴91316<<，3134∴<<，m ∴的值所在的范围是：34m <<；故选：D ．【点评】本题考查了估算无理数的大小，解决本题的关键是估算出13的范围． 2．（2016春•西城区期末）如图，在数轴上，与表示2的点最接近的点是( )A ．点AB ．点BC ．点CD ．点D【分析】依据被开放数越大对应的算术平方根越大进行比较即可． 【解答】解：21.4 1.96=，21.5 2.25=， 221.42 1.5∴<<． 1.42 1.5∴<．∴2D ．故选：D ．【点评】2的大致范围是解题的关键．3．（2016春•西城区校级期中）已知：212.5156.25=，212.6158.76=，212.7161.29=，212.8163.84=，下列说法正确的是( ) A ．12.616012.7<< B 16040= C ．12.515612.6<D 158.7612.6=±【分析】根据二次根式的性质解答即可．【解答】解：因为212.5156.25=，212.6158.76=，212.7161.29=，212.8163.84=，所以12.612.7<<12.512.6=． 故选：A ．【点评】此题考查实数的估算问题，关键是根据已知中的数值进行解答．4．（2016的结果估计在( ) A ．6至7之间B ．7至8之间C ．8至9之间D ．9至10之间【分析】先根据二次根式的乘法计算得到原式4=，由于489<<，则23，于是有647<<．【解答】解：原式4=， 489<<，23∴<，647∴<<．故选：A ．【点评】本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，在进行二次根式的乘除运算，然后合并同类二次根式．也考查了估算无理数的大小． 二．填空题（共8小题）5．（2017的整数部分是x ，小数部分是y ，则x y -= 4【分析】因为23<的整数部分是22，由此代入求得数值即可． 【解答】解：253<<，∴的整数部分是22，则22)4x y -=-=-故答案为：4．【点评】此题考查无理数的估算与代数式求值，关键是得到x ，y 的值．6．（2016秋•西城区期末）对于实数p ，我们规定：用p <>表示不小于p 的最小整数，例如：44<>=，2<>=．现对72进行如下操作： 727299332===第一次第二次第三次．即对72只需进行3次操作后变为2，类似地：（1）对36只需进行 3 次操作后变为2；（2）只需进行3次操作后变为2的所有正整数中，最大的是．【分析】（1）根据题目中的例子可以解答本题；（2）根据题意可以求得只需进行3次操作后变为2的所有正整数中，最大的是哪个整数．【解答】解：（1）由题意可得，第一次第二次第三次，===363666332故答案为：3；（2）由题意可得，===第一次第二次第三次，2562561616442故只需进行3次操作后变为2的所有正整数中，最大的是256，故答案为：256．【点评】本题考查估计无理数的大小、实数大小的比较，解答本题的关键是明确题意，找出所求问题需要的条件．7．（2016的整数部分为a，小数部分为b，则2a b-的值为9-【分析】a、b的值，最后代入求出即可．【解答】解：3134<<，b=，a3∴=，3∴-=⨯-=-2233)9a b故答案为：9【点评】8．（2016春•海淀区校级期中）若a b<<且a、b为连续整数，则a b+=15．【分析】a、b的值，再代入求出即可．【解答】解：7568<，∴=，8b=，a7∴+=，a b15故答案为：15．【点评】m>近似值的方法，回答问题：9．（20160)a<①任取正数1②令2111()2ma a a =+，则22m a a <；③3221()2m a a a =+，则33ma a <<；⋯以此类推n次，得到n nma a <． 其中n an 阶过剩近似值，nman 阶不足近似值．的近似值． ①取正数12a =< ②于是2a =52；则2a <．③3阶过剩近似值3a 是 ，3阶不足近似值是 ． 【分析】根据材料中的公式，将1a 的值代入求出2a ，3a 即可解答． 【解答】解：2111165()(2)2222m a a a =+=+=，2612552m a ==， 3151249()22520a =+=， 36120494920m a ==， 故答案为：②52，125；③4920，12049．【点评】本题主要考查估算无理数的大小，是阅读型问题，解决此类问题时，要认真阅读材料，根据材料中的步骤逐步计算．10．（2016秋•海淀区校级期中）大于的整数有 1-，0，1，2，3 ．（写出所有符合条件的整数）【分析】【解答】==+1.732≈2.236≈，∴估算出符合条件的数的范围是 1.7-到3.9之间，可得有整数：1-，0，1，2，3， 故答案为：1-，0，1，2，3．【点评】本题考查了有理数的大小比较，求出取值范围是解答此题关键．11．（2016春•海淀区校级期中）已知a 表示的整数部分，b 表示的小数部分， 则a b -=3【分析】<<<<，确定a 、b ，计算即可 ．【解答】解：<<<，23∴<<，12<<，2a ∴=，1b =，21)3a b ∴-=-=，故答案为：3．【点评】本题考查了实数的整数部分及小数部分， 设实数为a ，a 的整数部分A 为不大于a 的最大整数， 小数部分B 为实数a 减去其整数部分， 即B a A =-．12．（2015秋•平谷区期末）若a ，b 为两个连续的正整数，且a b ，则a b += 9 ．【分析】a 、b 的值，最后代入求出即可． 【解答】解：4205<， 4a ∴=，5b =， 9a b ∴+=，故答案为：9．【点评】 三．解答题（共3小题）13．（2014秋•房山区校级期中）阅读材料：学习了无理数后，的近似值：，2(01)k k +<<，所以22(2)k =+，可得2644k k =++．由01k <<可知201k <<，所以644k ≈+，解得12k ≈12 2.502+≈． 依照小红的方法解决下列问题：（1≈ 3.67 ；（精确到0.01)（2）已知非负整数a 、b 、m ，若1a a <+，且2m a b =+ ．（用含a 、b 的代数式表示）【分析】（1）根据题目信息，找出133(01)k k +<<，再根据题目信息近似求解即可；（2）根据题目提供的求法，先求出k 值，再加上a 即可． 【解答】解：（1），3(01)k k =+<<，则22(3)k =+． 21396k k ∴=++， 201k <<， 1396k ∴≈+．解得23k ≈，∴23 3.673≈+≈；（2(01)a k k +<<， 22222m a ak k a ak ∴=++≈+， 2m a b =+， 222a ak a b ∴+=+，解得2b k a =，∴2b a a≈+． 故答案为：（1）3.67；（2）2ba a+． 【点评】本题考查了无理数的估算，读懂题目提供信息，然后根据信息中的方法改变数据即可．14．（2013春•西城区期末）在没有带开方功能的计算器的情况下，n 为正整数）的近似值(k a k 为正整数），并通过迭代逐渐减小|k a -的值来提高k a如下：（11:a，23∴<<，取1322 2.52a -=+=； （2）通过计算2()2k k ka nm a -=和1k k k a a m +=-得到精确度更高的近似值1:k a +（说明 2.6458≈，此题中记2.6458，以下结果都要求写成小数形式）:1k =时，2111()72a m a -== 0.15- ，211a a m =-=，2|a -= ； 1k =时，2()()m =≈ （精确到0.001)，3a = - =，3|a -= ； ⋯【分析】根据（1【解答】解：（2）273<<， 1322 2.52a -∴=+=， 212570.152 2.5m -∴==-⨯，211 2.5(0.15) 2.65a am =-=--=，2||2.65 2.6458|0.0042a ≈-=，222227 2.6570.00422 2.65a m a --==≈⨯，322 2.650.004 2.646a a m =-=-=，3||2.646 2.6458|0.0002a ≈-=，故答案为：0.15-，2.65，0.0042，0.004，2a ，2m ，2.646，0.0002．【点评】本题考查了估算无理数的大小的应用，主要考查学生的理解能力和计算能力． 15．（2011秋•海淀区期末）阅读材料：的近似值． 小明的方法：，3(01)k k =+<<．∴22(3)k =+．21396k k ∴=++． 1396k ∴≈+．解得46k ≈． ∴43 3.676≈+≈． 问题：第11页（共11页）（1（2a 、b 、m，若1a a <+，且2m a b =+，≈ 2b a a+ （用含a 、b 的代数式表示）； （3）请用（2【分析】（1）根据题目信息，找出416(01)k k =+<<，再根据题目信息近似求解即可；（2）根据题目提供的求法，先求出k 值，然后再加上a 即可；（3）把a 换成6，b 换成1代入公式进行计算即可得解．【解答】解：（1）设6(01)k k +<<，∴22(6)k =+，2413612k k ∴=++，413612k ∴≈+． 解得512k ≈，∴5660.42 6.4212≈+≈+=；（2(01)a k k +<<，22222m a ak k a ak ∴=++≈+，2m a b =+，222a ak a b ∴+=+， 解得2b k a=，∴2b a a ≈+；（316 6.0812≈+≈． 【点评】本题考查了无理数的估算，读懂题目提供信息，然后根据信息中的方法改变数据即可，难度不大，很有趣味性．。