结构力学(李廉锟第五版)
- 格式:pdf
- 大小:9.56 MB
- 文档页数:50

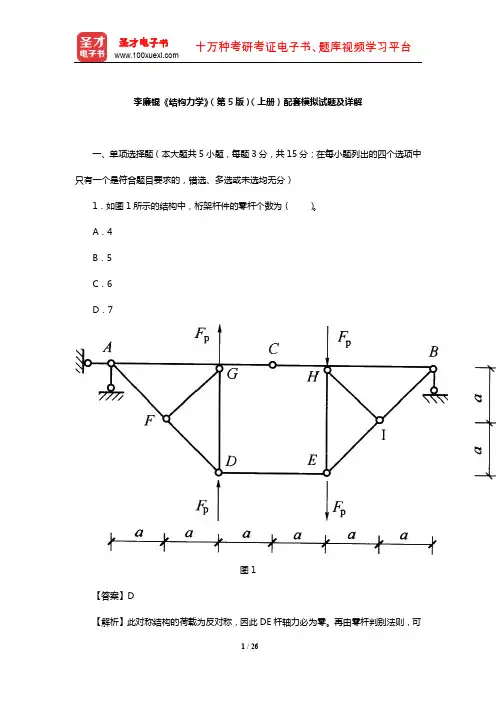
李廉锟《结构力学》(第5版)(上册)配套模拟试题及详解一、单项选择题(本大题共5小题,每题3分,共15分;在每小题列出的四个选项中只有一个是符合题目要求的,错选、多选或未选均无分)1.如图1所示的结构中,桁架杆件的零杆个数为()。
A.4B.5C.6D.7图1【答案】D【解析】此对称结构的荷载为反对称,因此DE杆轴力必为零。
再由零杆判别法则,可知DF、AF、FG、HI、EI、BI六杆也为零杆,总共此结构有7根零杆。
2.如图2所示结构,A支座发生沉降∆后,则()。
A.AB杆无内力,BD杆有内力B.AB杆有内力,BD杆无内力C.AB、BD杆均无内力产生D.AB、BD杆均有内力产生图2【答案】C【解析】AB为静定梁,支座移动不引起内力,因此铰B对AB杆的约束力为零,对BD 杆的约束力也为零。
BD杆上又无其他荷载,其内力也等于零。
3.如图3所示结构为对称抛物线三铰拱,铰C右侧截面的轴力(受压为正)为()。
图3A.64kN B .32kN C .24kN D .16kN 【答案】C【解析】由于该结构为对称抛物线拱,截面的轴力必是水平方向,其等于支座的水平反力F H 。
求得F VA =10kN ,F H =24kN ,因此,'24NC H F F kN ==。
4.如图4所示结构,各杆为矩形截面,在温度变化t 1>t 2时,其轴力为( )。
图4【答案】C【解析】因为当温度变化时,AB杆、DC杆可自由伸缩,故F NAB=F NCD=0。
由于BC 杆在B、C结点处有轴向约束,且,故其轴线伸长受阻,则必有F NBC<O,为压力。
5.如图5所示结构为对称刚架,利用对称性简化后的计算简图为()。
图5【答案】A【解析】刚架有两个对称轴AB、AD,此刚架纵横均为两跨,可以取四分之一结构BCD 计算,由于荷载对称,因此,B、D两处有弯矩,无转角和线位移,AB、AD杆无弯矩。
二、填空题(本大题共5小题,每题3分,共15分)1.如图6(a)所示体系的几何组成为______。



目 录第12章 结构动力学12.1 复习笔记12.2 课后习题详解12.3 名校考研真题详解第13章 结构弹性稳定13.1 复习笔记13.2 课后习题详解13.3 名校考研真题详解第14章 结构的极限荷载14.1 复习笔记14.2 课后习题详解14.3 名校考研真题详解第15章 悬索计算15.1 复习笔记15.2 课后习题详解15.3 名校考研真题详解第12章 结构动力学12.1 复习笔记【知识框架】动力荷载与静力荷载基本概念自由振动和强迫振动 结构动力计算的目的 振动自由度的定义结构振动的自由度 结构按自由度的数目分类:单自由度结构和多自由度结构 确定结构的振动自由度 无限自由度结构 自由振动的原因:初始位移、初始速度单自由度结构的自由振动 不考虑阻尼时的自由振动 考虑阻尼时的自由振动 简谐荷载作用下单自由度受迫振动单自由度结构在简谐荷载作用下的受迫振动 不考虑阻尼的纯受迫振动考虑阻尼的纯受迫振动 瞬时冲量作用于质点单自由度结构在任意荷载作用下的受迫振动 任意动力载荷作用下的质点位移公式 振动微分方程 两种特殊载荷作用下的质点位移公式 按柔度法求解多自由度结构的自由振动按刚度法求解主振型的正交性多自由度结构在筒谐荷载作用下的的受迫振动 按柔度法求解振型分解法的优点 按刚度法求解振型分解法振型分解法的步骤 振动微分方程组的建立多自由度结构在任意荷载作用下的受迫振动 振动微分方程组的解耦待定常数的确定求解的具体步骤 地震作用的基本概念 地震作用的定义地震作用的计算 地震作用的分类:水平地震和竖向地震地震作用的实质单自由度结构的地震作用计算 多自由度结构的地震作用计算 梁的自由振动无限自由度结构的振动简谐均布干扰力作用下的受迫振动计算频率的近似计算方法:能量法、集中质量法、用相当梁法计算桁架的最低频率【重点难点归纳】一、基本概念1.动力载荷与静力载荷(1)静力载荷静力荷载是指施力过程缓慢,不致使结构产生显著的加速度,因而可以略去惯性力影响的荷载。


第13章 结构弹性稳定一、选择题1.用能量法求得的临界荷载值()。
A.总是等于其精确解B.总是小于其精确解C.总是大于其精确解D.总是大于或等于其精确解【答案】D2.如图13-1所示各结构中,F Pcri(i=1,2,3,4)为临界荷载,EI=常数,k为弹簧刚度,则()。
A.F Pcr1>F Pcr2>F Pcr3>F Pcr4B.F Pcr2>F Pcr3>F Pcr4>F Pc1C.F Pcr1>F Pcr4>F Pcr3>F Pcr2D.F Pcr4>F Pcr3>F Pcr2>F Pcr1图13-1【答案】B【解析】当其他条件相同时,约束越强,则临界荷载越大。
3.用能量法求图13-2所示压杆的临界荷载时,设挠曲线用正弦级数表示,若只取两项,则应采用()。
图13-2A .B .C .D .【答案】B【解析】从压杆两端的边界条件:当x =0,y =0,y"=0;当x =l 时,y =0,y"=0,判定。
4.解稳定问题时,将图13-3(a )所示弹性杆件体系,简化为图13-3(b )所示弹性支承单个杆件,其弹性支承刚度系数为( )。
A .33EIk l =B .312EI k l=C .33EI EA k l l =+D .()31/3/k l EI l EA=+图13-3【答案】D【解析】方法一:由于BCD 部分相当于两个串联的弹簧,串联后的等效刚度计算式为111CD BCk k k =+由位移法的形常数可知,33CD EI k l =BC EA k l=所以弹性支承刚度系数()31/3/k l EI l EA=+方法二:根据弹簧刚度是的定义,k 就是8点(去除AB 杆)产生单位水平位移时需要施加的力,如图13-3(c )所示,由整体平衡条件得到33EI k l∆=再取结点C 为隔离体,如图13-3(d )所示,由水平方向平衡可得将Δ代入到,即得33EI k l∆=()31/3/k l EI l EA=+5.用能量法求图13-4所示排架的临界荷载P cr 时,失稳时柱的变形曲线可设为( )。

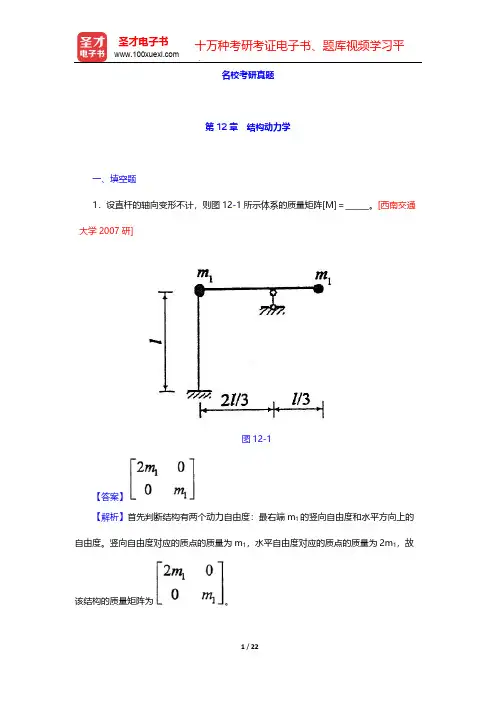


目 录第一部分 名校考研真题第12章 结构动力学第13章 结构弹性稳定第14章 结构的极限荷载第15章 悬索计算第二部分 课后习题第12章 结构动力学第13章 结构弹性稳定第14章 结构的极限荷载第15章 悬索计算第三部分 章节题库第12章 结构动力学第13章 结构弹性稳定第14章 结构的极限荷载第15章 悬索计算第四部分 模拟试题李廉锟《结构力学》(第5版)(下册)配套模拟试题及详解第一部分 名校考研真题第12章 结构动力学一、填空题1.设直杆的轴向变形不计,则图12-1所示体系的质量矩阵[M]=]______。
[西南交通大学2007研【答案】【解析】首先判断结构有两个动力自由度:最右端m1的竖向自由度和水平方向上的自由度。
竖向自由度对应的质点的质量为m1,水平自由度对应的质点的质量为2m1,故该结构的质量矩阵为。
2.如图12-2所示结构的动力自由度为______(不计杆件质量)。
[中南大学2003研]图12-2二、选择题1.如图12-3所示结构,不计阻尼与杆件质量,若要发生共振,θ应等于( )。
[天津大学2005研]A .B .3【答案】一个自由质点的动力自由度为两个(不考虑转动自由度),本题所示结构中有三个质点,第一层的两个质点只有一个水平自由度,第二层的质点有水平和竖向两个自由度,故一共有三个动力自由度。
【解析】C .D.图12-3【解析】当体系的自振频率与外部激励荷载的频率相同时,体系发生共振。
首先求该结构的自振频率,设m 处的位移为u (t ),质量m 处的惯性力向下为,质量3m 处的惯性力向下,弹性力向上为,向左端铰支座处取矩,列运动方程为:。
所以体系的自振频率为。
2.如图12-4所示体系(不计阻尼)的稳态最大动位移y max =4Pl 3/9EI ,则最大的动力弯矩为( )。
[浙江大学2007研]A .7Pl/3 B .4Pl/3C .Pl D .Pl/3B【答案】图12-4【解析】在质点m 处的静位移为:,则动力放大系数R d =;最大静力弯矩为Pl ,故最大动力弯矩为。