下载文档原格式
概率论与数理统计习题 第三章 多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球，在其中任取4只球.以X 表示取到黑球的只数，以Y 表示取到红球的只数，求X 和Y 的联合分布律.（X ，Y ）的可能取值为(i , j )，i =0，1，2，3， j =0，12，i + j ≥2，联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f（1） 确定常数k ； （2） 求{}3,1<<Y X P （3） 求{}5.1<X P ； （4） 求{}4≤+Y X P . 分析：利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分，其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解：（1）∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ，∴81=k （2）83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P （3）3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P （4）32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次，以X 表示前2次出现H 的次数，以Y 表示3次中出现H 的次数，求Y X ,的联合分布律以及),(Y X 的边缘分布律。
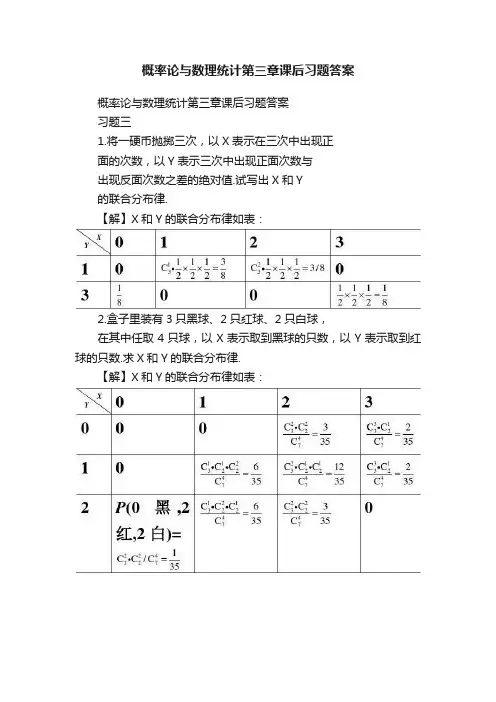
概率论与数理统计第三章课后习题答案概率论与数理统计第三章课后习题答案习题三1.将一硬币抛掷三次，以X表示在三次中出现正面的次数，以Y表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X和Y的联合分布律.【解】X和Y的联合分布律如表：2.盒子里装有3只黑球、2只红球、2只白球，在其中任取4只球，以X表示取到黑球的只数，以Y表示取到红球的只数.求X和Y的联合分布律.【解】X和Y的联合分布律如表：（2）随机变量（X ，Y ）的分布函数；（3）P {0≤X <1，0≤Y <2}.【解】（1）由-(34)0(,)d d e d d 112x y Af x y x y A x y +∞+∞+∞+∞+-∞-∞===??得 A =12（2）由定义，有(,)(,)d d yx F x y f u v u v -∞-∞=??(34)340012ed d (1e )(1e )0,0,0,0,y yu v x y u v y x -+--??-->>?==?? 其他(3){01,02}P X Y ≤<≤<12(34)3800{01,02}12ed d (1e )(1e)0.9499.x y P X Y x y -+--=<≤<≤==--≈?5.设随机变量（X ，Y ）的概率密度为f （x ，y ）=<<<<--.,0,42,20),6(其他y x y x k（1）确定常数k ；（2）求P {X ＜1，Y ＜3}；（3）求P {X <1.5}；（4）求P {X +Y ≤4}. 【解】（1）由性质有242(,)d d (6)d d 81,f x y x y k x y y x k +∞+∞-∞-∞=--==??故18R =（2） 13{1,3}(,)d d P X Y f x y y x -∞-∞<<=??130213(6)d d 88k x y y x =--=?? (3)11.5{ 1.5}(,)d d a (,)d d x D P X f x y x y f x y x y<<=如图 1.542127d (6)d .832x x y y =--=?(4)24{4}(,)d d (,)d d X Y D P X Y f x y x y f x y x y+≤+≤=如图b 240212d (6)d .83xx x y y -=--=??题5图6.设X 和Y 是两个相互独立的随机变量，X 在（0，0.2）上服从均匀分布，Y 的密度函数为f Y （y ）=>-.,0,0,55其他y y e求：（1） X 与Y 的联合分布密度；（2）P {Y ≤X }.题6图【解】（1）因X 在（0，0.2）上服从均匀分布，所以X 的密度函数为1,00.2,()0.20,.X x f x ?<而55e ,0,()0,.y Y y f y -?>=?其他所以(,),()()XY f x y X Y f x f y g 独立5515e25e ,00.20,0.20,0,yy x y --<<>?==??且其他.5()(,)d d 25e d d y y xDP Y X f x y x y x y-≤≤=如图0.20.2-550-1d 25e d (5e 5)d =e 0.3679.xy x x y x-==-+≈7.设二维随机变量（X ，Y ）的联合分布函数为F （x ，y ）=>>----.,0,0,0),1)(1(24其他y x y x e e求（X ，Y ）的联合分布密度. 【解】(42)28e ,0,0,(,)(,)0,x y x y F x y f x y x y -+?>>?==?其他.8.设二维随机变量（X ，Y ）的概率密度为f （x ，y ）=4.8(2),01,0,0,.y x x y x -≤≤≤≤??求边缘概率密度.【解】()(,)d X fx f x y y+∞-∞=?x204.8(2)d 2.4(2),01,=0,.0,y x y x x x ??--≤≤?=??其他()(,)d Y f y f x y x+∞-∞=?12y 4.8(2)d 2.4(34),01,=0,.0,y x x y y y y ?-?-+≤≤?=??其他题8图题9图9.设二维随机变量（X ，Y ）的概率密度为f （x ，y ）=<<-.,0,0,其他e y x y求边缘概率密度.【解】()(,)d Xf x f x y y +∞-∞=?e d e ,0,=0,.0,y x x y x +∞--??>?=??其他()(,)d Y f y f x y x+∞-∞=?0e d e ,0,=0,.0,yy x x y y --??>?=??其他题10图10.设二维随机变量（X ，Y ）的概率密度为f （x ，y ）=≤≤.,0,1,22其他y x y cx（1）试确定常数c ；（2）求边缘概率密度. 【解】（1） (,)d d (,)d d Df x y x y f x y xy+∞+∞-∞-∞如图2112-14=d d 1.21xx cx y y c ==??得214c =.(2)()(,)d X f x f x y y+∞-∞=?212422121(1),11,d 840,0,.x x x x x y y ??--≤≤??==其他()(,)d Y f y f x y x+∞-∞=?522217d ,01,420,0,.y y x y x y y -??≤≤??==其他11.设随机变量（X ，Y ）的概率密度为f （x ，y ）=?<<<.,0,1其他x x y求条件概率密度f Y ｜X （y ｜x ），f X ｜Y （x ｜y ）.题11图【解】()(,)d Xf x f x y y +∞-∞=?1d 2,01,0,.x x y x x -?=<111d 1,10,()(,)d 1d 1,01,0,.y Y y x y y f y f x y x x y y -+∞-∞=+-<<??其他所以|1,||1,(,)(|)2()0,.Y X X y x f x y f y x xf x ?<其他, 1,1(,)1(|),1,()10,.X Y Y y x y f x y f x y y x f y y<<?-?==-<<?+其他12.袋中有五个号码1，2，3，4，5，从中任取三个，记这三个号码中最小的号码为X ，最大的号码为Y .（1）求X 与Y 的联合概率分布；（2） X 与Y 是否相互独立？【解】（1） X 与Y 的联合分布律如下表1 3511C 10=3522C 10= 3533C 10= 610 2 0 3511C 10=3522C 10= 310 30 02511C 10=110{}i P Y y =110310(2) 因6161{1}{3}{1,3},101010010P X P Y P X Y ===?=≠===g 故X 与Y 不独立13.设二维随机变量（X ，Y ）的联合分布律为2 5 80.4 0.80.15 0.30 0.35 0.05 0.12 0.03 （1）求关于X 和关于Y 的边缘分布；（2） X 与Y 是否相互独立？【解】（1）X 和Y 的边缘分布如下表2 5 8 P {Y=y i } 0.4 0.15 0.30 0.35 0.8 0.80.05 0.12 0.03 0.2{}i P X x =0.20.420.38(2) 因{2}{0.4}0.20.8P X P Y ===?g 0.160.15(2,0.4),P X Y =≠=== 故X 与Y 不独立.XYX Y14.设X 和Y 是两个相互独立的随机变量，X 在（0，1）上服从均匀分布，Y 的概率密度为f Y （y ）=>-.,0,0,212/其他y y e（1）求X 和Y 的联合概率密度；（2）设含有a 的二次方程为a 2+2Xa +Y =0，试求a 有实根的概率. 【解】（1）因1,01,()0,Xx fx <21e ,1,()20,yY y f y -?>?==其他.故/21e01,0,(,),()()20,.y X Y x y f x y X Y f x f y -?<<>?=g 独立其他题14图(2) 方程220aXa Y ++=有实根的条件是 2(2)40X Y ?=-≥故X 2≥Y ，从而方程有实根的概率为：22{}(,)d d x yP X Y f x y x y ≥≥=??21/2001d e d 212[(1)(0)]0.1445.x yx yπ-==-Φ-Φ=??15.设X 和Y 分别表示两个不同电子器件的寿命（以小时计），并设X 和Y 相互独立，且服从同一分布，其概率密度为f （x ）=>.,0,1000,10002其他x x求Z =X /Y 的概率密度.【解】如图,Z 的分布函数(){}{}ZXF z P Z z P z Y =≤=≤(1) 当z ≤0时，()0ZF z =（2）当0<="" p="">）(如图a) 3366102222101010()d d d d yz Z zxy zF z x y y x x y x y +∞≥==??33610231010=d 2z zy yzy +∞-=题15图(3) 当z ≥1时，（这时当y =103时，x =103z ）（如图b ）3366222210101010()d d d d zy Z xy zF z x y y xx y x y +∞≥==??336231010101=d 12y yzy z +∞-=-即11,1,2(),01,20,.Z z z zf z z ?-≥=<<??其他故21,1,21(),01,20,.Z z z f z z ?≥=<<??其他16.设某种型号的电子管的寿命（以小时计）近似地服从N （160，202）分布.随机地选取4 只，求其中没有一只寿命小于180的概率. 【解】设这四只寿命为X i (i =1,2,3,4)，则X i ~N （160，202），从而123412{min(,,,)180}{180}{180}i P X X X X X P X P X ≥≥≥g 之间独立34{180}{180}P X P X ≥≥g1234[1{180}][1{180}][1{180}][1{180}]P X P X P X P X =-<-<-<-<="" p="">44144180160[1{180}]120[1(1)](0.158)0.00063.P X ?-=-<=-Φ=-Φ==17.设X ，Y 是相互独立的随机变量，其分布律分别为P {X =k }=p （k ），k =0，1，2，…， P {Y =r }=q （r ），r =0，1，2，…. 证明随机变量Z =X +Y 的分布律为P {Z =i }=∑=-ik k i q k p 0)()(，i =0，1，2，….【证明】因X 和Y 所有可能值都是非负整数，所以{}{}Z i X Y i ==+={0,}{1,1}{,0}X Y i X Y i X i Y =====-==U UL U于是{}{,},ik P Z i P X k Y i k X Y =====-∑相互独立0{}{}ik P X k P Y i k ===-∑g()()ik p k q i k ==-∑18.设X ，Y 是相互独立的随机变量，它们都服从参数为n ，p 的二项分布.证明Z =X +Y 服从参数为2n ，p 的二项分布.【证明】方法一：X +Y 可能取值为0，1，2，…，2n .0{}{,}ki P X Y k P X i Y k i =+====-∑00202(){}2ki k i n i k i n k ii kk n ki k n k P X i P Y k i n n p q p q i k i n n p q i k i n p q k =---+=-=-===-= ? ?-= ???-??= ???∑∑∑g方法二：设μ1,μ2,…,μn ;μ1′,μ2′,…，μn ′均服从两点分布（参数为p ），则X =μ1+μ2+…+μn，Y =μ1′+μ2′+…+μn ′,X +Y =μ1+μ2+…+μn +μ1′+μ2′+…+μn ′,所以，X +Y 服从参数为（2n ,p )的二项分布.19.设随机变量（X ，Y ）的分布律为(1) 求P {X =2｜Y =2}，P {Y =3｜X =0}；（2）求V =max （X ，Y ）的分布律；（3）求U =min （X ，Y ）的分布律；（4）求W =X +Y 的分布律.【解】（1）{2,2}{2|2}{2}P X Y P X Y P Y ======5{2,2}0.051,0.252{,2}i P X Y P X i Y ========∑{3,0}{3|0}{0}P Y X P Y X P X ======3{0,3}0.011;0.033{0,}j P X Y P X Y j ========∑（2）{}{max(,)}{,}{,}P V i P X Y i P X i Y i P X i Y i =====<+≤= 10{,}{,},i ik k P X i Y k P X k Y i -=====+==∑∑0,1,2,3,4,5i =所以V 的分布律为(3){}{min(,)}P U i P X Y i ===351{,}{,}{,}{,}k i k i P X i Y i P X i Y i P X i Y k P X k Y i ==+==≥+>====+==∑∑0,1,2,3,i =于是 (4)类似上述过程，有26 3 9 4 9 2 520.雷达的圆形屏幕半径为R ，设目标出现点（X ，Y ）在屏幕上服从均匀分布. （1）求P {Y ＞0｜Y ＞X }；（2）设M =max{X ，Y }，求P {M ＞0}.题20图【解】因（X ，Y ）的联合概率密度为22221,,(,)π0,.x y R f x y R+≤?=其他（1）{0,}{0|}{}P Y Y X P Y Y X P Y X >>>>=> 0(,)d (,)d y y xy xf x y f x y σσ>>>=π2π/405π42π/401d d π1d d πRR r r R r r R θθ=??3/83;1/24==(2){0}{max(,)0}1{max(,)0}P M P X Y P X Y >=>=-≤00131{0,0}1(,)d 1.44x y P X Y f x y σ≤≤=-≤≤=-=-=??21.设平面区域D 由曲线y =1/x 及直线y =0，x =1,x=e 2所围成，二维随机变量（X ，Y ）在区域D 上服从均匀分布，求（X ，Y ）关于X 的边缘概率密度在x =2处的值为多少？题21图【解】区域D 的面积为 22e e 0111d ln 2.S x x x===?（X ,Y ）的联合密度函数为211,1e ,0,(,)20,.x y f x y x≤≤<≤?=其他（X ，Y ）关于X 的边缘密度函数为1/2011d ,1e ,()220,.x X y x f x x=≤≤?=其他所以1(2).4Xf=22.设随机变量X 和Y 相互独立，下表列出了二维随机变量（X ，Y ）联合分布律及关于X 和Y 的边缘分布律中的部分数值.试将其余。
第三章连续型随机变量3、1设随机变量 ξ 的分布函数为F(x),试以F(x)表示下列概率: 。
)()4();()3();()2();()1(a P a P a P a P >≥≤=ξξξξ 。
）（解：)0(1)()4();(1)()3();0()(P 2);()0()()1(+-=>-=≥+=≤-+==a F a P a F a P a F a a F a F a P ξξξξ3、2函数x211F(x)+=就是否可以作为某一随机变量的分布函数,如果在其它场合恰当定义。
在其它场合恰当定义；）（,0)3(,0)2(1<<∞-∞<<∞<<∞-x x x 解:(1)F(x)在),(∞-∞内不单调,因而不可能就是随机变量的分布函数; (2)F(x)在)0∞，（内单调下降,因而也不可能就是随机变量的分布函数; (3)F(x)在），（－0∞内单调上升、连续且,若定义 ⎩⎨⎧≥<<∞=01)()(~x x X F x F －则)(~x F 可以就是某一随机变量的分布函数。
3、3函数 sinx 就是不就是某个随机变量ξ的分布函数？如果ξ的取值范围为[]。
，）；（，）；（，）（⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡πππ230302201 解:(1)当⎥⎦⎤⎢⎣⎡∈2,0πx 时,sinx 0≥且1sin 20=⎰πxdx ,所以 sinx 可以就是某个随机变量的分布密度; (2) 因为12sin 0≠=⎰πxdx ,所以sinx 不就是随机变量的分布密度; (3) 当 ⎥⎦⎤⎢⎣⎡∈23,ππx 时,sinx<=0所以sinx 不就是随机变量的分布密度。
3、4设随机变量ξ具有对称的分布函数p(x),即p(x)=p(-x) 证明:对任意的a>0,有[][]。
－－故上式右端＝知由证：）1)(21a)P(1a)(3)P(1;-2F(a))(21)(1)1(,)(2)()()2(;)(21)()(1)(1)(1)(1)(1)()()1(.)(F 12)()3(;1)(2)()2(;(p 21)(1)()1(00000-=<=>-=-==<-=--=-=-=+=-==--=>-=<-=-=-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰-∞-∞-∞-∞--∞-a F dxx p a F dx x p dx x p a P dx x p dx x p dx x p a F dx x p dxx p dx x p dx x p a F a a P a F a P dx x a F a F a a a a a aaaaaa ξξξξξ3、5设)(1x F 与)(2x F都就是分布函数,证明F(x)=aF(x)+bF(x)也就是一个分布函数,并由此讨论,分布函数就是否只有离散型与连续型这两种类型？ 证:因为)(1x F与 )(2x F 都就是分布函数,于就是F(x1)＝aF1(x1)+bF2(x2)<= aF1(x1)+bF2(x2)= F(x2) 又F(x-0)= aF1(x1-0)+bF2(x2-0) = aF1(x)+bF2(x)= F(x) 所以,F(x)也就是分布函数。
概率论与数理统计第三章课后习题及参考答案1．设二维随机变量),(Y X 只能取下列数组中的值：)0,0(，)1,1(-，31,1(-及)0,2(，且取这几组值的概率依次为61，31，121和125，求二维随机变量),(Y X 的联合分布律．解：由二维离散型随机变量分布律的定义知，),(Y X 的联合分布律为2．某高校学生会有8名委员，其中来自理科的2名，来自工科和文科的各3名．现从8名委员中随机地指定3名担任学生会主席．设X ，Y 分别为主席来自理科、工科的人数，求：(1)),(Y X 的联合分布律；(2)X 和Y 的边缘分布律．解：(1)由题意，X 的可能取值为0，1，2，Y 的可能取值为0，1，2，3，则561)0,0(3833====C C Y X P ，569)1,0(381323====C C C Y X P ，569)2,0(382313====C C C Y X P ，561)3,0(3833====C C Y X P ，283)0,1(382312====C C C Y X P ，289)1,1(38131312====C C C C Y X P ，283)2,1(382312====C C C Y X P ，0)3,1(===Y X P ，563)0,2(381322====C C C Y X P ，563)1,2(381322====C C C Y X P ，0)2,2(===Y X P ，0)3,2(===Y X P ．),(Y X 的联合分布律为：(2)X 的边缘分布律为X 012P1452815283Y 的边缘分布律为Y 0123P285281528155613．设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其他．,0,42,20),6(),(y x y x k y x f 求：(1)常数k ；(2))3,1(<<Y X P ；(3))5.1(<Y P ；(4))4(≤+Y X P ．解：方法1：(1)⎰⎰⎰⎰--==∞+∞-∞+∞-422d d )6(d d ),(1yx y x k y x y x f ⎰--=42202d |)216(y yx x x k k y y k 8d )210(42=-=⎰，∴81=k ．(2)⎰⎰∞-∞-=<<31d d ),()3,1(y x y x f Y X P ⎰⎰--=32102d d )216(yx yx x x ⎰--=32102d |)216(81y yx x x 83|)21211(81322=-=y y ．(3)),5.1()5.1(+∞<<=<Y X P X P ⎰⎰∞+∞-∞---=5.1d d )6(81yx y x ⎰⎰--=425.10d d )6(81y x y x y yx x x d )216(81422⎰--=3227|)43863(81422=-=y y ．(4)⎰⎰≤+=≤+4d d ),()4(y x y x y x f Y X P ⎰⎰---=2042d )6(d 81x y y x x ⎰+-⋅=202d )812(2181x x x 32|)31412(1612032=+-=x x x ．方法2：(1)同方法1．(2)20<<x ，42<<y 时，⎰⎰∞-∞-=yxv u v u f y x F d d ),(),(⎰⎰--=y xv u v u 20d d )6(81⎰--=y xv uv u u 202d |)216(81⎰--=y v xv x x 22d )216(81y xv v x xv 222|)21216(81--=)1021216(81222x xy y x xy +---=，其他，0),,(=y x F ，∴⎪⎩⎪⎨⎧<<<<+---=其他．,0,42,20),1021216(81),(222y x x x xy y x xy y x F 83)3,1()3,1(==<<F Y X P ．(3))42,5.1(),5.1()5.1(<<<=+∞<<=<Y X P Y X P X P )2,5.1()4,5.1(<<-<<=Y X P Y X P 3227)2,5.1()4,5.1(=-=F F ．(4)同方法1．4．设随机变量),(Y X 的概率密度为⎩⎨⎧>>=--其他．,0,0,0,e ),(2y x A y x f y x 求：(1)常数A ；(2)),(Y X 的联合分布函数．解：(1)⎰⎰⎰⎰∞+∞+--∞+∞-∞+∞-==02d d e d d ),(1yx A y x y x f y x ⎰⎰∞+∞+--=02d e d e y x A y x2|)e 21(|)e (020A A y x =-⋅-=∞+-∞+-，∴2=A ．(2)0>x ，0>y 时，⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰--=yxv u vu 02d d e 2yv x u 020|)e 21(|)e (2---⋅-=)e 1)(e 1(2y x ----=，其他，0),(=y x F ，∴⎩⎨⎧>>--=--其他．,0,0,0),e 1)(e 1(),(2y x y x F y x ．5．设随机变量),(Y X 的概率密度为⎩⎨⎧≤≤≤≤=其他．,0,10,10,),(y x Axy y x f 求：(1)常数A ；(2)),(Y X 的联合分布函数．解：(1)2121d d d d ),(11010⋅⋅===⎰⎰⎰⎰∞+∞-∞+∞-A y y x x A y x y x f ，∴4=A ．(2)10≤≤x ，10≤≤y 时，⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰=yxv u uv 0d d 4220202||y x v u yx =⋅=，10≤≤x ，1>y 时，⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4xv u uv 210202||x v u x =⋅=，10≤≤y ，1>x 时，⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4yu v uv 202102||y v u y =⋅=，1>x ，1>y 时，⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=101d d 4v u uv 1||102102=⋅=v u ，其他，0),(=y x F ，∴⎪⎪⎪⎩⎪⎪⎪⎨⎧>>≤≤>>≤≤≤≤≤≤=其他．,0,1,1,1,10,1,,1,10,,10,10,),(2222y x y x y y x x y x y x y x F ．6．把一枚均匀硬币掷3次，设X 为3次抛掷中正面出现的次数，Y 表示3次抛掷中正面出现次数与反面出现次数之差的绝对值，求：(1)),(Y X 的联合分布律；(2)X 和Y 的边缘分布律．解：由题意知，X 的可能取值为0，1，2，3；Y 的可能取值为1，3．易知0)1,0(===Y X P ，81)3,0(===Y X P ，83)1,1(===Y X P ，0)3,1(===Y X P 83)1,2(===Y X P ，0)3,2(===Y X P ，0)1,3(===Y X P ，81)3,3(===Y X P 故),(Y X 得联合分布律和边缘分布律为：7．在汽车厂，一辆汽车有两道工序是由机器人完成的：一是紧固3只螺栓；二是焊接2处焊点，以X 表示由机器人紧固的螺栓紧固得不牢的数目，以Y 表示由机器人焊接的不良焊点的数目，且),(Y X 具有联合分布律如下表：求：(1)在1=Y 的条件下，X 的条件分布律；(2)在2=X 的条件下，Y 的条件分布律．解：(1)因为)1,3()1,2()1,1()1,0()1(==+==+==+====Y X P Y X P Y X P Y X P Y P 08.0002.0008.001.006.0=+++=，所以43)1()1,0()1|0(=======Y P Y X P Y X P ，81)1()1,1()1|1(=======Y P Y X P Y X P ，101)1()1,2()1|2(=======Y P Y X P Y X P ，401)1()1,3()1|3(=======Y P Y X P Y X P ，故在1=Y 的条件下，X 的条件分布律为X 0123P4381101401(2)因为)2,2()1,2()0,2()2(==+==+====Y X P Y X P Y X P X P 032.0004.0008.002.0=++=，所以85)2()0,2()2,0(=======X P Y X P X Y P ，41)2()1,2()2,1(=======X P Y X P X Y P ，81)2()2,2()2,2(=======X P Y X P X Y P ，故在2=X 的条件下，Y 的分布律为：Y 012P8541818．设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧>>=+-其他．,0,0,0,e ),()2(y x c y x f y x 求：(1)常数c ；(2)X 的边缘概率密度函数；(3))2(<+Y X P ；(4)条件概率密度函数)|(|y x f Y X ，)|(|x y f X Y ．解：(1)⎰⎰⎰⎰∞+∞++-∞+∞-∞+∞-==0)2(d d e d d ),(1yx c y x y x f y x⎰⎰∞+∞+--=02d e d ey x c y x2|)e (|)e 21(002c c y x =-⋅-=∞+-∞+-，∴2=c ．(2)0>x 时，⎰∞+∞-=y y x f x f X d ),()(⎰∞++-=0)2(d e 2y y x x y x 202e 2|)e (e 2-+∞--=-=，0≤x 时，0)(=x f X ，∴⎩⎨⎧≤>=-．0,0,0,e 2)(2x x x f x X ，同理⎩⎨⎧≤>=-．0,0,0,e )(y y y f y Y ．(3)⎰⎰<+=<+2d d ),()2(y x y x y x f Y X P ⎰⎰---=20202d d e 2xy x yx 422202e e 21d e d e 2-----+-==⎰⎰xy x y x ．(4)由条件概率密度公式得，当0>y 时，有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他．其他．,0,0,e 2,0,0,e e 2)(),()|(22|x x y f y x f y x f xy y x Y Y X ，同理，当0>x 时，有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他．其他．,0,0,e ,0,0,2e e 2)(),()|(22|y y x f y x f x y f yx y x X X Y ．9．设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧<<<<=其他．,0,0,10,3),(x y x x y x f 求：(1)关于X 、Y 的边缘概率密度函数；(2)条件概率密度函数)|(|y x f Y X ，)|(|x y f X Y ．解：(1)10<<x 时，⎰∞+∞-=y y x f x f X d ),()(203d 3x y x x==⎰，其他，0)(=x f X ，∴⎩⎨⎧<<=其他．,0,10,3)(2x x x f X ，密度函数的非零区域为}1,10|),{(}0,10|),{(<<<<=<<<<x y y y x x y x y x ，∴10<<y 时，⎰∞+∞-=x y x f y f Y d ),()()1(23d 321y x x y-==⎰，其他，0)(=y f Y ，∴⎪⎩⎪⎨⎧<<-=其他．,0,10),1(23)(2y y y f Y ．(2)当10<<y 时，有⎪⎩⎪⎨⎧<<-=⎪⎪⎩⎪⎪⎨⎧<<-==其他．其他．,0,1,12,0,1,)1(233)(),()|(22|x y y x x y y xy f y x f y x f Y Y X ．当10<<x 时，有⎪⎩⎪⎨⎧<<=⎪⎩⎪⎨⎧<<==其他．其他．,0,0,1,0,0,33)(),()|(2|x y x x y x x x f y x f x y f X X Y ．10．设条件密度函数为⎪⎩⎪⎨⎧<<<=其他．,0,10,3)|(32|y x y x y x f Y X Y 的概率密度函数为⎩⎨⎧<<=其他．,0,10,5)(4y y y f Y 求21(>X P ．解：⎩⎨⎧<<<==其他．,0,10,15)|()(),(2|y x y x y x f y f y x f Y X Y ，则6447d )(215d d 15d d ),(21(121421211221=-===>⎰⎰⎰⎰⎰>x x x x y y x y x y x f X P xx ．11．设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧<<<<+=其他．,0,20,10,3),(2y x xyx y x f 求：(1)),(Y X 的边缘概率密度；(2)X 与Y 是否独立；(3))),((D Y X P ∈，其中D 为曲线22x y =与x y 2=所围区域．解：(1)10<<x 时，x x y xy x y y x f x f X 322d )3(d ),()(222+=+==⎰⎰∞+∞-，其他，0)(=x f X ，∴⎪⎩⎪⎨⎧<<+=其他．,0,10,322)(2x x x x f X ，20<<y 时，⎰∞+∞-=x y x f y f Y d ),()(316)d 3(12+=+=⎰y x xy x ，其他，0)(=y f Y ，∴⎪⎩⎪⎨⎧<<+=其他．,0,20,316)(y y y f Y ．(2)∵),()()(y x f y f x f Y X ≠，∴X 与Y 不独立．(3)}22,10|),{(2x y x x y x D ≤≤<<=，∴⎰⎰+=∈102222d d 3()),((xxx y xy x D Y X P 457d )32238(10543=--=⎰x x x x ．12．设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=-其他．,0,0,0,e )1(),(2y x y xy x f x试讨论X ，Y 的独立性．解：当0>x 时，xx x X x yx y y x y y x f x f -∞+-∞+-∞+∞-=+-=+==⎰⎰e |11e d )1(e d ),()(002，当0≤x 时，0)(=x f X ，故⎩⎨⎧≤>=-．0,0,0,e )(x x x x f x X ，同理，可得⎪⎩⎪⎨⎧≤>+=．0,0,0,)1(1)(2y y y y f Y ，因为)()(),(y f x f y x f Y X =，所以X 与Y 相互独立．13．设随机变量),(Y X 在区域}|),{(a y x y x g ≤+=上服从均匀分布，求X 与Y 的边缘概率密度，并判断X 与Y 是否相互独立．解：由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤+=其他．,0,,21),(2a y x a y x f ，当0<<-x a 时，有)(1d 21d ),()(2)(2x a a y a y y x f x f xa x a X +===⎰⎰++-∞+∞-，当a x <≤0时，有)(1d 21d ),()(2)(2x a a y a y y x f x f x a x a X -===⎰⎰---∞+∞-，当a x ≥时，0d ),()(==⎰+∞∞-y y x f x f X ，故⎪⎩⎪⎨⎧≥<-=．a x a x x a a x f X ,0,),(1)(2，同理，由轮换对称性，可得⎪⎩⎪⎨⎧≥<-=．a y a y y a a y f Y ,0,),(1)(2，显然)()(),(y f x f y x f Y X ≠，所以X 与Y 不相互独立．14．设X 和Y 时两个相互独立的随机变量，X 在)1,0(上服从均匀分布，Y 的概率密度为⎪⎩⎪⎨⎧≤>=-．0,0,0,e 21)(2y y y f yY (1)求X 和Y 的联合概率密度；(2)设含有a 的二次方程为022=++Y aX a ，试求a 有实根的概率．解：(1)由题可知X 的概率密度函数为⎩⎨⎧<<=其他．,0,10,1)(x x f X ，因为X 与Y 相互独立，所以),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧><<==-其他．,0,0,10,e 21)()(),(2y x y f x f y x f y Y X ，(2)题设方程有实根等价于}|),{(2X Y Y X ≤，记为D ，即}|),{(2X Y Y X D ≤=，设=A {a 有实根}，则⎰⎰=∈=Dy x y x f D Y X P A P d d ),()),(()(⎰⎰⎰---==1021002d )e 1(d d e 2122xx y x x y⎰--=12d e12x x ⎰--=12d e 21212x x ππππ23413.01)]0()1([21-=Φ-Φ-=．15．设i X ～)4.0,1(b ，4,3,2,1=i ，且1X ，2X ，3X ，4X 相互独立，求行列式4321X X X X X =的分布律．解：由i X ～)4.0,1(b ，4,3,2,1=i ，且1X ，2X ，3X ，4X 相互独立，易知41X X ～)84.0,16.0(b ，32X X ～)84.0,16.0(b ．因为1X ，2X ，3X ，4X 相互独立，所以41X X 与32X X 也相互独立，又32414321X X X X X X X X X -==，则X 的所有可能取值为1-，0，1，有)1()0()1,0()1(32413241======-=X X P X X P X X X X P X P 1344.016.084.0=⨯=，)1,1()0,0()0(32413241==+====X X X X P X X X X P X P )1()1()0()0(32413241==+===X X P X X P X X P X X P 7312.016.016.084.084.0=⨯+⨯=，)0()1()0,1()1(32413241=======X X P X X P X X X X P X P 1344.084.016.0=⨯=，故X 的分布律为X 1-01P1344.07312.01344.016．设二维随机变量),(Y X 的概率密度为⎩⎨⎧>>=+-其他．,0,0,0,e 2),()2(y x y x f y x 求Y X Z 2+=的分布函数及概率密度函数．解：0≤z 时，若0≤x ，则0),(=y x f ；若0>x ，则0<-=x z y ，也有0),(=y x f ，即0≤z 时，0),(=y x f ，此时，0d d ),()2()()(2==≤+=≤=⎰⎰≤+zy x Z y x y x f z Y X P z Z P z F ．0>z 时，若0≤x ，则0),(=y x f ；只有当z x ≤<0且02>-=xz y 时，0),(≠y x f ，此时，⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 2d d ),()2()()(⎰⎰-+-=zx z y x y x 020)2(d e 2d z z z ----=e e 1．综上⎩⎨⎧≤>--=--．0,0,0,e e 1)(z z z z F z z Z ，所以⎩⎨⎧≤<='=-．0,0,0,e )()(z z z z F z f z Z Z ．17．设X ，Y 是相互独立的随机变量，其概率密度分别为⎩⎨⎧≤≤=其他．,0,10,1)(x x f X ，⎩⎨⎧≤>=-．0,0,0,e )(y y y f y Y 求Y X Z +=的概率密度．解：0<z 时，若0<x ，则0)(=x f X ；若0≥x ，则0<-=x z y ，0)(=-x z f Y ，即0<z 时，0)()(=-x z f x f Y X ，此时，0d )()()(=-=⎰∞+∞-x x z f x f z f Y X Z ．10≤≤z 时，若0<x ，则0)(=x f X ；只有当z x ≤≤0且0>-=x z y 时0)()(≠-x z f x f Y X ，此时，z zx z Y X Z x x x z f x f z f ---∞+∞--==-=⎰⎰e 1d e d )()()(0)(．1>z 时，若0<x ，0)(=x f X ；若1>x ，0)(=x f X ；若10≤≤x ，则0>-=x z y ，此时，0)()(≠-x z f x f Y X ，z x z Y X Z x x x z f x f z f ---∞+∞--==-=⎰⎰e )1e (d e d )()()(1)(．综上，⎪⎩⎪⎨⎧<>-≤≤-=--．0,0,1,e )1e (,10,e 1)(z z z z f z z Z ．18．设随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=+-其他．,0,0,0,e)(21),()(y x y x y x f y x (1)X 和Y 是否相互独立？(2)求Y X Z +=的概率密度．解：(1)),()()(y x f y f x f Y X ≠，∴X 与Y 不独立．(2)0≤z 时，若0≤x ，则0)(=x f X ；若0>x ，则0<-=x z y ，0),(=y x f ，此时，0d ),()(=-=⎰∞+∞-x x z x f z f Z ．0≥z 时，若0≤x ，则0)(=x f X ；只有当z x <<0且0>-=x z y 时0),(≠y x f ，此时，⎰∞+∞--=x x z x f z f Z d ),()(⎰+-+=zy x x y x 0)(d e)(21⎰-=z z x z 0d e 21z z -=e 212，所以⎪⎩⎪⎨⎧≤>=-．0,0,0,e 21)(2z z z z f zZ ．19．设X 和Y 时相互独立的随机变量，它们都服从正态分布),0(2σN ．证明：随机变量22Y X Z +=具有概率密度函数⎪⎩⎪⎨⎧<≥=-．0,0,0,e )(2222z z z z f z Z σσ．证：因为X 与Y 相互独立，均服从正态分布),0(2σN ，所以其联合密度函数为2222)(2e 121),(σσπy x y x f +-⋅=，(+∞<<∞-y x ,)当0≥z 时，有⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 22d d ),()()()(22⎰⎰≤++-⋅=zy x y x y x 22222d e 1212)(2σσπ⎰⎰-⋅=πσθσπ2022d ed 12122zr r r ⎰-=zr r r 022d e122σσ，此时，2222e)(σσz Z z z f -=；当0<z 时，=≤+}{22z Y X ∅，所以0)()()(22=≤+=≤=z Y X P z Z P z F Z ，此时，0)(=z f Z ，综上，⎪⎩⎪⎨⎧<≥=-．0,0,0,e )(2222z z z z f z Z σσ．20．设),(Y X 在矩形区域}10,10|),{(≤≤≤≤=y x Y X G 上服从均匀分布，求},min{Y X Z =的概率密度．解：由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤≤≤≤=其他．,0,20,10,21),(y x y x f ，易证，X ～]1,0[U ，Y ～]2,0[U ，且X 与Y 相互独立，⎪⎩⎪⎨⎧≥<≤<=．1,1,10,,0,0)(x x x x x F X ，⎪⎪⎩⎪⎪⎨⎧≥<≤<=．2,1,20,2,0,0)(y y yy y F Y ，可得)](1)][(1[1)(z F z F z F Y X Z ---=)()()()(z F z F z F z F Y X Y X -+=⎪⎪⎩⎪⎪⎨⎧≥<≤-<=．1,1,10,223,0,02z z z z z ，求导，得⎪⎩⎪⎨⎧<<-=其他．,0,10,23)(z z z f Z ．21．设随机变量),(Y X 的概率密度为⎩⎨⎧+∞<<<<=+-其他．,0,0,10,e ),()(y x b y x f y x (1)试确定常数b ；(2)求边缘概率密度)(x f X 及)(y f Y ；(3)求函数},max{Y X U =的分布函数．解：(1)⎰⎰⎰⎰∞++-∞+∞-∞+∞-==01)(d d e d d ),(1yx b y x y x f y x⎰⎰∞+--=1d e d e y x b y x )e 1(|)e (|)e (1102-+∞---=-⋅=b b y x ，∴1e11--=b ．(2)10<<x 时，1)(1e1e d e e 11d ),()(--∞++--∞+∞--=-==⎰⎰x y x X y y y x f x f ，其他，0)(=x f X ，∴⎪⎩⎪⎨⎧<<-=--其他．,0,10,e 1e )(1x x f xX ，0>y 时，⎰∞+∞-=x y x f y f Y d ),()(y y x x -+--=-=⎰e d e e1110)(1，0≤y 时，0)(=y f Y ，∴⎩⎨⎧≤>=-．0,0,0,e )(y y y f y Y ．(3)0≤x 时，0)(=x F X ，10<<x 时，101e 1e 1d e 1e d )()(----∞---=-==⎰⎰xxt xX X t t t f x F ，1≥x 时，1)(=x F X ，∴⎪⎪⎩⎪⎪⎨⎧≥<<--≤=--．1,1,10,e1e1,0,0)(1x x x x F x X ；0≤y 时，0)(=y F Y ，0>y 时，y yv y Y Y v v v f y F --∞--===⎰⎰e 1d e d )()(0，∴⎩⎨⎧≤>-=-．0,0,0,e 1)(y y y F y Y ，故有)()()(y F x F u F Y X U =⎪⎪⎩⎪⎪⎨⎧≥-<≤--<=---．1,e 1,10,e1e1,0,01u u u uu ．。
第三章 离散型随机变量率分布。
，试写出命中次数的概标的命中率为目；设已知射手每次射击射击中命中目标的次数指示射手在这三次独立以本空间上定义一个函数验的样本空间；试在样作为试验，试写出此试察这些次射击是否命中三次独立射击，现将观一射手对某目标进行了7.0.1.343.0441.0189.0027.03210027.0)7.01()()0()0(189.0)7.01()7.01(7.03)(3)1()1()1()1(441.0)7.01(7.07.03)(3)2()2()2()2(343.0)7.0()()3()3()(0)(1)()()(2)()()(3)(},,,{)},,(),,,(),,,(),,,(),,,(),,,(),,,(),,,{(3,2,1332183217653214323321187654321821321321321321321321321321⎪⎪⎭⎫ ⎝⎛=-======-⨯-⨯⨯===+=+====-⨯⨯⨯===+=+===================Ω==的分布列为所以，，则简记为将，，则代表击中目标的次数，令则次射中”，“第解：设ξξξξξξξξξξξξξξωξωξωξωξωξωξωξωξωξξωωωA A A P P P A A A P P P P P A A A P P P P P A A A P P P A A A A A A A A A A A A A A A A A A A A A A A A i i A i i i。
出的废品数的概率分布前已取个，求在取得合格品之不再放回而再取来使用，若取得废品就个这批零件中任取个废品，安装机器时从个合格品、一批零件中有1139.2118805499101112123)3(132054109112123)2(13227119123)1(129)0(32101919110111111211213110191111211213111191121311219=⨯⨯⨯=⋅⋅⋅===⨯⨯=⋅⋅===⨯=⋅=====C C C C C C C C P C C C C C C P C C C C P C C P ξξξξξξ，，，可能取值为：代表废品数，则解：令.1188054132054132271293210⎪⎪⎭⎫ ⎝⎛的分布列为所以，ξ废品数的概率分布。
第三章 习题参考答案1.计算习题二第2题中随机变量的期望值。
解：由习题二第2题计算结果0112{0}={1}=33p p p p ξξ====，得12201333E ξ=⨯+⨯= 一般对0-1分布的随机变量ξ有{1}E p p ξξ===2．用两种方法计算习题二第30题中周长的期望值，一种是利用矩形长与宽的期望计算，另一种是利用周长期望的分布计算。
解：方法一：先按定义计算长的数学期望290.3300.5310.229.9E ξ=⨯+⨯+⨯=和宽的数学期望190.3200.4210.320E η=⨯+⨯+⨯=再利用数学期望的性质计算周长的数学期望(22)229.922099.8E E ζξη=+=⨯+⨯=方法二：利用习题二地30题的计算结果(见下表)，按定义计算周长的数学期望960.09980.271000.351020.231040.0698.8E ξ=⨯+⨯+⨯+⨯+⨯=3.对习题二第31题，（1）计算圆半径的期望值；（2）(2)E R π是否等于2ER π？（3）能否用2()ER π来计算远面积的期望值，如果不能用，又该如何计算？其结果是什么？解（1）100.1110.4120.3130.211.6ER =⨯+⨯+⨯+⨯=（2）由数学期望的性质有(2)223.2E R ER πππ==（3）因为22()()E R E R ππ≠，所以不能用2()E R π来计算圆面积的期望值。
利用随机变量函数的期望公式可求得222222()()(100.1110.4120.3130.2)135.4E R E R ππππ==⨯+⨯+⨯+⨯= 或者由习题二第31题计算结果，按求圆面积的数学期望1000.11210.41440.31690.2)135.4E ηπππ=⨯+⨯+⨯+⨯=4． 连续随机变量ξ的概率密度为,01(,0)()0,a kx x k a x ϕ⎧<<>=⎨⎩其它又知0.75E ξ= ，求k 和a 的值 解 由1010()11324a a kx dx kx dx a k E kx x dx a ϕξ+∞-∞===+=⋅==+⎰⎰⎰解得 2,3a k ==5．计算服从拉普拉斯分布的随机变量的期望和方差（参看习题二第16题）。
概率论第三章习题参考解答1. 如果ξ服从0-1分布, 又知ξ取1的概率为它取0的概率的两倍, 求ξ的期望值 解：由习题二第2题算出ξ的分布率为ξ0 1 P1/32/3因此有E ξ=0×P (ξ=0)+1×P (ξ=1)=2/3+2η, ξ与η的分布律如下表所示:: 求周长的期望值, 用两种方法计算, 一种是利用矩形长与宽的期望计算, 另一种是利用周长的分布计算.解: 由长和宽的分布率可以算得E ξ=29×P (ξ=29)+30×P (ξ=30)+31×P (ξ=31) =29×0.3+30×0.5+31×0.2=29.9E η=19×P (η=19)+20×P (η=20)+21×P (η=21) =19×0.3+20×0.4+21×0.3=20 由期望的性质可得E ζ=2(E ξ+E η)=2×(29.9+20)=99.8而如果按ζ的分布律计算它的期望值, 也可以得E ζ=96×0.09+98×0.27+100×0.35+102×0.23+104×0.06=99.8 验证了期望的性质.4. 连续型随机变量ξ的概率密度为⎩⎨⎧><<=其它)0,(10)(a k x kx x aϕ又知Eξ=0.75, 求k 和a 的值。
解: 由性质⎰+∞∞-=1)(dx x ϕ得111)(|10110=+=+==++∞∞-⎰⎰a kx a k dx kx dx x a aϕ即k =a +1(1)又知75.022)(|10211=+=+===+++∞∞-⎰⎰a kx a k dx kx dx x x E a a ϕξ得k =0.75a +1.5(2)由(1)与(2)解得0.25a =0.5, 即a =2, k =36. 下表是某公共汽车公司的188辆汽车行驶到发生一次引擎故障的里程数的分布数列.若表中各以组中值为代表. 从188辆汽车中, 任意抽选15辆, 得出下列数字: 90, 50, 150, 110, 90, 90, 110, 90, 50, 110, 90, 70, 50, 70, 150. (1)求这15个数字的平均数; (2) 计算表3-9中的期望并与(1)相比较.解: (1) 15个数的平均数为(90+50+150+110+90+90+110+90+50+110+90+70+50+70+150)/15 = 91.33 (2) 按上表计算期望值为(10×5+30×11+50×16+70×25+90×34+110×46+130×33+150×16+170×2)/188 =96.177. 两种种子各播种300公顷地, 调查其收获量, 如下表所示, 分别求出它们产量的平均值解: 假设种子甲的每公顷产量数为, 种子乙的每公顷产量数为, 则 E ξ=(4500×12+4800×38+5100×40+5400×10)/100=4944 E η=(4500×23+4800×24+5100×30+5400×23)/100=49598. 一个螺丝钉的重量是随机变量, 期望值为10g , 标准差为1g . 100个一盒的同型号螺丝钉重量的期望值和标准差各为多少?(假设各个螺丝钉的重量相互之间独立) 解: 假设这100个螺丝钉的重量分别为ξ1, ξ2,…, ξ100, 因此有E ξi =10, Dξi =102=12=1, (i =1,2,…,100), 设ξ为这100个螺丝钉的总重量，因此∑==1001i i ξξ，则ξ的数学期望和标准差为gD D D kgg E E E i ii i i i i i 1011001)(1000101001001100110011001=⨯==⎪⎭⎫⎝⎛====⨯==⎪⎭⎫ ⎝⎛=∑∑∑∑====ξξξσξξξξ9. 已知100个产品中有10个次品，求任意取出的5个产品中次品数的期望值.解: 假设ξ为取出5个产品中的次品数, 又假设ξi 为第i 次取出的次品数, 即, 如果第i 次取到的是次品, 则ξi =1否则ξi =0, i =1,2,3,4,5, ξi 服从0-1分布,而且有 P {ξi =0}=90/100, P {ξi =1}=10/100, i =1,2,3,4,5因此, E ξi =10/100=1/10, 因为∑==51i iξξ因此有5.010155151=⨯==⎪⎭⎫ ⎝⎛=∑∑==i i i i E E E ξξξ10. 一批零件中有9个合格品和3个废品, 在安装机器时, 从这批零件中任取一个, 如果取出的是废品就不再放回去. 求取得第一个合格品之前, 已经取出的废品数的数学期望和方差. 解: 假设在取到第一个合格品之前已取出的废品数为ξ, 则可算出0045.02201101112123}3{041.02209109112123}2{2045.0119123}1{75.0129}0{==⋅⋅====⋅⋅===⋅=====ξξξξP P P P因此有319.009.0409.0)(409.090045.04041.02045.03.030045.02041.02045.0222===-==⨯+⨯+==⨯+⨯+=ξξξξξE E D E E11. 假定每人生日在各个月份的机会是同样的, 求3个人中生日在第一个季度的平均人数. 解: 设三个随机变量ξi ,(i =1,2,3), 如果3个人中的第i 个人在第一季度出生, 则ξi =1, 否则ξi =0, 则ξi 服从0-1分布, 且有 P (ξi =1)=1/4, 因此E ξi =1/4, (i =1,2,3)设ξ为3个人在第一季度出生的人数, 则ξ=ξ1+ξ2+ξ3, 因此Eξ=E (ξ1+ξ2+ξ3)=3Eξi =3/4=0.7512. ξ有分布函数⎩⎨⎧>-=-其它1)(x e x F xλ, 求E ξ及D ξ. 解: 因ξ的概率密度为⎩⎨⎧>='=-其它)()(x e x F x xλλϕ, 因此 ()λλλϕξλλλλλ11)(0=-=+-=-===∞+-∞+-∞+-+∞-+∞-+∞∞-⎰⎰⎰⎰xx xxxe dx e xe e xd dx ex dx x x E()2220222222)(|λξλλϕξλλλλ==+-=-===⎰⎰⎰⎰∞+-∞+-+∞-+∞-+∞∞-E dx xe ex e d x dx ex dx x x E x x x x22222112)(λλλξξξ=-=-=E E D13. ⎪⎩⎪⎨⎧<-=其它1||11)(~2x x x πϕξ, 求E ξ和D ξ.解: 因φ(x )是偶函数, 因此Eξ=0,则D ξ=Eξ2-(Eξ)2=Eξ2 因此有⎰⎰-===+∞∞-1222212)(dx xx dx x x E D πϕξξ令θθθd dx x cos ,sin ==则上式=2112sin 21212cos 2sin 12||20202022=+=+=⎰⎰ππππθπθπθθπθθπd d 即D ξ=1/2=0.516. 如果ξ与η独立, 不求出ξη的分布直接从ξ的分布和η的分布能否计算出D (ξη), 怎样计算?解: 因ξ与η独立, 因此ξ2与η2也独立, 则有[]()()222222)()()(ηξηξξηξηξηE E E E E E D -=-=17. 随机变量η是另一个随机变量ξ的函数, 并且η=e λξ(λ>0), 若E η存在, 求证对于任何实数a 都有λξλξEe ea P a⋅≤≥-}{.证: 分别就离散型和连续型两种情况证. 在ξ为离散型的情况: 假设P (ξ=x i )=p i , 则λξλξλλλξEe e e E p e p ep a P a a i i a x ax i a x ax i i i i i --∞=-≥-≥==≤≤=≥∑∑∑][){)(1)()(在ξ为连续型的情况假设ξ的概率密度为φ(x ), 则λξλξλλλϕϕϕξEe e Ee dx x e dx x edx x a P a a a x aa x a--+∞∞--+∞-+∞==≤≤=≥⎰⎰⎰)()()()()()(}{证毕.18. 证明事件在一次试验中发生次数的方差不超过1/4.证: 设ξ为一次试验中事件A 发生的次数, 当然最多只能发生1次, 最少为0次, 即ξ服从0-1分布, P {ξ=1}=P (A )=p , P {ξ=0}=1-p =q ,则4121412124141)1(222≤⎪⎭⎫ ⎝⎛--=-⋅+-=-=-=p p p p p p p D ξ19. 证明对于任何常数c , 随机变量ξ有 D ξ=E (ξ-c )2-(Eξ-c )2证: 由方差的性质可知D (ξ-c )=Dξ, 而2222)()()]([)()(c E c E c E c E c D ---=---=-ξξξξξ证毕.20. (ξ,η)的联合概率密度φ(x ,y )=e -(x +y )(x ,y >0), 计算它们的协方差cov (ξ,η). 解: 由φ(x ,y )=e -(x +y )(x ,y >0)可知ξ与η相互独立, 因此必有cov (ξ,η)=0.21. 袋中装有标上号码1,2,2的3个球, 从中任取一个并且不再放回, 然后再从袋中任取一球, 以ξ, η分别记为第一,二次取到球上的号码数, 求ξ与η的协方差.,P {ξ=2}=P {η=2}=2/3, P {ξ=1}=P {η=1}=1/3, E ξ=E η=35322311=⨯+⨯38314312312},{)(2121=⨯+⨯+⨯====∑∑==i j j i ijP E ηξξη则913538)(),cov(22-=-=⋅-=ηξξηηξE E E22. (ξ , η)只取下列数组中的值：)0,2()31,1()1,1()0,0(--且相应的概率依次为1/6, 1/3, 1/12, 5/12. 求ξ与η的相关系数ρ, 并判断ξ与η是否独立? 解: ξ与的联合分布表及各边缘分布计算表如下表所示: 因此1212260121=⨯+⨯+⨯-=ξE 1225125412512=⨯+⨯=ξE 144275144251225)(22=-=-=ξξξE E D 3613311121311270=⨯+⨯+⨯=ηE 1083731121912=+⨯=ηE 129627512961691237129616910837)(22=-⨯=-=-=ηηηE E D 36133112131)(-=-⨯-=ξηE则4322211236171336131253613)(),cov(-=⨯⨯-=⋅--=⋅-=ηξξηηξE E E 相关系数804.027522127543236122211296275144275432221),cov(-=-=⨯⨯⨯-=⨯-==ηξηξρD D, 计算ξ与η的相关系数ρ, 并判断ξ与η是否独立? 解: 由上表的数据的对称性可知与η的边缘分布一样, 算出为 P (ξ=-1)=P (η=-1)=3/8 P (ξ=0)=P (η=-0)=2/8P (ξ=1)=P (η=1)=3/8 由对称性可知Eξ=Eη=0831831=⨯+⨯-. 081818181)(=+--=ξηE 因此cov (ξ,η)=E (ξη)-E (ξ)E (η)=0 则ρ=0而P (ξ=0,η=0)=0≠P {ξ=0}P {η=0}=1/16因此ξ与η不独立. 这是一个随机变量间不相关也不独立的例子.24. 两个随机变量ξ与η, 已知Dξ=25, Dη=36, ρξη=0.4, 计算D (ξ+η)与D (ξ-η). 解:374.065236252),cov(2)]()[()]([)(854.065236252),cov(2)]()[()]([)(2222=⨯⨯⨯-+=-+=-+=---==---=-=⨯⨯⨯++=++=++=-+-==+-+=+ξηξηρηξηξηξηξηηξξηξηξηξρηξηξηξηξηηξξηξηξηξD D D D D D E E E E E D D D D D D D E E E E E D《概率论与数理统计》复习资料一、填空题（15分）题型一：概率分布的考察 【相关公式】（P379）【相关例题】 1、设(,)XU a b ，()2E X =，1()3D Z =，则求a ，b 的值。
