识别结构模态阻尼比的一种新方法_黄方林

格式：pdf
大小：174.05 KB
文档页数：5

下载文档原格式

/ 5

模态阻尼系数

模态阻尼系数模态阻尼系数（modal damping ratio）是一个用于描述结构震动时能量逐渐衰减的参数。

该系数表示每个模态振动中能量在一个周期内衰减的速率，常用符号为ζ（zeta）。

在结构设计和地震工程中，模态阻尼系数是非常重要的参数。

本文将介绍模态阻尼系数的定义、计算方法、以及其在设计和分析中的作用。

1. 定义结构物在受到外力时会发生震动。

由于结构有阻尼，震动能量不可能无限地保存下去，而是会逐渐减少。

这是振动能量转化为其他形式，比如热能。

模态阻尼系数就是用来描述这种能量衰减的参数。

简单来说，它表示结构物振动能随时间的波动幅度下降的快慢。

2. 计算方法通常，模态阻尼系数可以通过实验和理论计算两种方法获得。

目前常用的实验方法是采用反应振型法（modal identification）进行模态参数辨识。

该方法是基于加速度传感器测量物体的振动响应，利用模态分析算法计算模态阻尼比。

理论计算方法包括基于能量守恒原理或基于成对振型的经验公式两种。

前者利用结构的自由振动响应方程，通过分析结构物振动系统的动能和势能之间的能量转换关系，计算出每个模态的振动能量随时间的衰减速度。

后者则利用计算机模拟和试验结果对成对振型的阻尼系数进行拟合获得相应的经验公式。

3. 作用模态阻尼系数是结构设计和分析中非常重要的参数。

一方面，它可以用于评估结构的动态特性和稳定性。

一般而言，模态阻尼系数越大，震动能量衰减越快，结构的振动响应越稳定，耐震性能越好。

因此，模态阻尼系数对地震工程的结构抗震能力评估至关重要，特别是对于高层建筑和大型桥梁等重点工程。

另一方面，模态阻尼系数也可以用于优化结构设计。

在某些情况下，通过改变结构材料、截面形状或支座设置等方式，可以提高结构阻尼，从而达到减小震动能量和避免结构破坏的目的。

因此，在结构设计和改进过程中，模态阻尼系数的计算和分析具有重要的意义。

综上所述，模态阻尼系数是一个重要而复杂的参数，它既可以用于评估结构的动态特性和抗震性能，又可以用于优化结构设计和改进过程。

HHT法识别结构模态频率和阻尼比的改进_汪家慰

图 3 采用标准 EM D 分解的固有模态函数
图 4 带通滤波后应用 EM D 分解的固有模态函数
从图 4 中可以看出 , 经过带通滤波再应用 EMD 方法分解 , 可以将 4 阶振动模态信号从原信号中分离出来 , 并且避免了直接应用 EM D 分解过程中产生的模态混淆现象。
对图 4 的各阶固有模态函数进行 H ilbert 变换得到瞬时幅值图和瞬时相位图 , 然后对瞬时幅值和瞬时相位用最小二乘法进行线性拟合获得结构的各阶模态频率和模态阻尼比。
由度系统响应的叠加。
单自由度系统的位移响应为 :
x(t)=a0 e-ζωnt co s(ωn 1 -ζ2 t +θ0)=
a
0
e-ζω n
t
cos(ωd t
+θ0 )
(10)
其中 , ξ、ωn 、ωd 为系统的阻尼比、无阻尼固有频率
和有阻尼固有频率。令
a(t)=a0 e-ζωnt
(11)
θ(t)= ωd t +θ0
(12)
对(11)式两边取对数 , 得
l n a(t)=ln a0 +ζωn t
令 An =ln a(t), A0 =ln a0 , 则
An = A0 +ζωn t
(13)
利用(12)式、(13)式 , 对相位-时间曲线和对
数幅值-时间曲线进行最小二乘拟合 , 即可得到
ξ、ωn 。 2.2 滤波
1.2 H i lbert 变换
IM F 是瞬时频率唯一的信号 , 且其瞬时频率
可以通过 H T 计算[ 5] 。即假设 c(t)是一个 IM F ,
对 c(t)作 H T 得 :

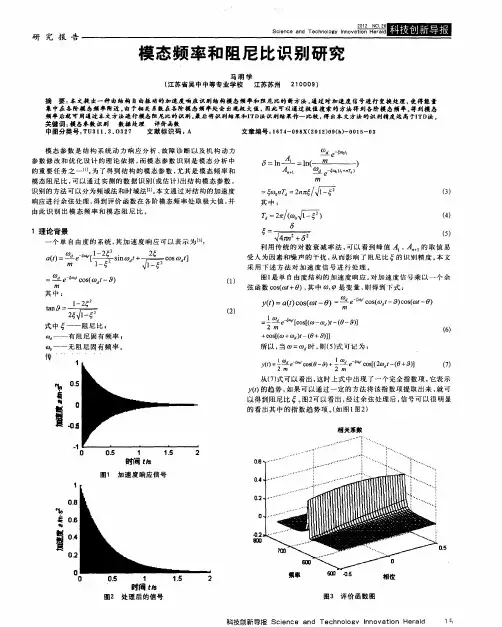
模态频率和阻尼比识别研究

模态频率和阻尼比识别研究摘要：本文提出一种由结构自由振动的加速度响应识别结构模态频率和阻尼比的新方法。

通过对加速度信号进行变换处理，使得能量集中在各阶模态频率附近。

由于相关系数在各阶模态频率处会出现极大值，因此可以通过极值搜索的方法得到各阶模态频率。

得到模态频率后就可用通过本文方法进行模态阻尼比的识别。

最后将识别结果和ITD法识别结果作一比较，得出本文方法的识别精度远高于ITD法。

关键词: 模态参数识别数据处理评价函数模态参数是结构系统动力响应分析、故障诊断以及机构动力参数修改和优化设计的理论依据，而模态参数识别是模态分析中的重要任务之一[1]。

为了得到结构的模态参数，尤其是模态频率和模态阻尼比，可以通过实测的数据识别（或估计）出结构模态参数，识别的方法可以分为频域法和时域法[2]。

本文通过对结构的加速度响应进行余弦处理，得到评价函数在各阶模态频率处取极大值，并由此识别出模态频率和模态阻尼比。

1 理论背景一个单自由度的系统，其加速度响应可以表示为[3]：2.2 参数搜索通过以上分析，知道多自由度系统的相关函数在处取极大值，因此可以通过参数搜索的方法直接搜索得到。

参数搜索的过程如图4所示。

3 提取指数趋势项和仿真3.1 提取指数趋势项我们知道，通过参数搜索得到，然后再乘以为固频率和初始相位的余弦函数，这时就会得到一个含有指数趋势项的信号。

如何从该信号中提取指数趋势项呢？（1）低通滤波。

由于上述信号中除了指数趋势项外，其余分量都是伪简谐信号，因此可以通过滤波的方法将非指数项滤除。

（2）小波变换。

对上述信号进行多尺度分解，得到信号的高频系数和低频系数，然后对低频系数进行重建，得到信号的低频部分，即指数趋势项。

3.2 Matlab仿真下面采用小波变换的方法提取指数趋势项，进行参数识别的算例仿真。

设一个加速度响应信号：用ITD方法识别模态频率和阻尼比时，识别过程中由于虚假模态的存在，因此有可能将噪声模态误认为结构的模态，造成模态识别的错误。

利用粒子群优化算法实现阻尼比和频率的精确识别

。ξ i 为第 i 阶的阻尼比； Ai′ 为脉冲
响应信号幅值谱图中 ωi 处的幅值， ωi 为固有频率； Ai′′ 为脉冲响应信号向后平移
其中： Ak 、ωk 、ξ k 、ϕ k ( k = 1,2,L, m ) 分别表示振幅、固有频率、阻尼比和相位；
m 为模态阶数； n(t ) 为白噪声； t 为时间。
∗
[2]
和Eberhart 提出的一种仿生优化算法[8]，广泛应用于神经网络构建[9]、车间调度[10]、模糊控制[11]等领域。目前，学者主要从提高粒子群的收敛速度和开拓能力两个方面来完善PSO算法。2006 年，Chatterjee等[12] 将非线性权重惯量引入PSO模型，提高收敛速度。2007 年，Yan Jiang等[13]将粒子群分成若干个子粒子群。每个子粒子群单独进化。迭代一定次数后，合并子粒子群，并打乱顺序，再重新分成若干个子粒子群，达到提高粒子开拓能力的目的。同年，Ali 等[14]对PSO的效率和可靠性进行研究，分析了PSO算法收敛缓慢的原因。通过修改位置更新准则提高 PSO 算法收敛速度。 2008 年，Arumugam等[15]将遗传算法中的交叉算法和均方根变量引入PSO算法，提高了PSO算法的收敛速度。基于 PSO 算法的阻尼比和频率辨识方法是一种不需要测量激励信号的模态辨识方法。它将脉冲响应信号数学模型与实
利用粒子群优化算法实现阻尼比和频率的精确识别 ∗
胡峰吴波胡友民史铁林 (华中科技大学,数字制造装备与技术国家重点试验室,湖北武汉，430074)
摘要：本文提出了一种利用粒子群优化算法辨识阻尼比和频率的方法。该方法将系统频率、阻尼比、幅
值和相位的辨识问题转化为非线性优化问题，引入粒子群优化算法寻找全局最优解。基于粒子群优化的阻尼比和频率辨识方法不需要测量激励信号，原理简单，实现容易。仿真和实验结果表明：基于粒子群优化算法的阻尼比和频率辨识方法不受邻近模态耦合的影响。在无噪声条件下具有较高的辨识精度，随着信噪比的逐步降低，辨识精度开始逐步下降。用低通滤波器滤除高阶模态后，得到的脉冲响应信号对频率、阻尼比、幅值的辨识精度影响很小，对相位的辨识精度影响很大。

识别结构模态阻尼比的一种新方法

识别结构模态阻尼比的一种新方法黄方林何旭辉陈政清高赞明倪一清(中南大学)(香港理工大学)摘要提出一种新的由结构自由振动响应识别结构阻尼比的方法。

对于单自由度振动系统,推导出响应历程与时轴所围各面积之间的确定性关系后,利用各面积之间的关系来确定自由衰减振动的阻尼比系数。

与传统的对数衰减率法比较,它具有抗噪声干扰能力强、精度高、稳定性好及简便实用等特点。

对于多自由度振动系统,先将结构上某测点的自由振动响应表达为一理论解析式x(t),以e at相乘x(t),预给a初值范围,通过牛顿二分法(或黄金分割法)搜索a值,直至e a t x(t)做等幅振荡,则该阶模态的各模态参数得以确定。

从总响应中扣除该阶模态对总响应的贡献后,重复这一过程,则可识别出响应信号中各阶模态的模态阻尼比。

仿真计算与岳阳洞庭湖斜拉桥拉索实测试验结果表明了本文方法的有效性和实用性。

关键词模态阻尼比参数识别斜拉桥拉索中图分类号:T U31114文献标识码:A文章编号:1000O131X(2002)06O0020O051引言在结构故障诊断、振动实时监控、响应预测、荷载识别等结构动力学前沿课题研究方面,建立一精确的动力学模型是至关重要的环节。

由于实际工程结构大型、复杂及测量误差的存在,理论计算与实际测量获得的系统动力学特性有时相差甚远。

在进行结构动力学计算时,往往需要用到结构阻尼这一参数。

为便于计算,人们经常理想地将结构阻尼取为比例阻尼,但即使这样,比例系数的选取仍很大程度上取决于工程经验。

为此,人们通过参数识别理论,由实测的试验数据识别(或估计)出结构模态参数,识别的方法可分为时域法和频域法两种。

常见的频域法有半功率带宽法、峰值法、导纳圆法等方法[1],时域法有对数衰减率法、ITD 法[2]、S TD法[3]、随机减量法[4]等。

在结构模态参数中,阻尼比的识别精度远比固有频率、振型的识别精度低,测试数据受噪声干扰时更为糟糕,100%的阻尼比误差被认为是司空见惯的事情。

基于信号能量分析的结构阻尼比识别方法

振动与冲击第22卷第2期J OURNA L OF VIBR ATION AND SHOCK Vol.22No.22003基于信号能量分析的结构阻尼比识别方法*曾储惠黄方林柳成荫陈政清(中南大学土木建筑学院,长沙410075)摘要本文提出一种基于信号能量分析计算结构阻尼比的新方法。

推导出自由振动响应信号能量与阻尼比关系的理论表达式后,求出阻尼比。

与传统的对数衰减率法相比,此法精度、抗噪声干扰能力强、稳定性好。

振动系统信号的能量之所以会衰减,是因为阻尼的存在。

本文提出的这种识别阻尼比的方法物理概念清晰,易于理解。

仿真计算和洞庭桥实测试验结果表明所提出的方法有效、可行。

关键词:能量分析,参数识别,阻尼比中图分类号:O324,TH1130引言在结构损伤检测、安全评估、振动实时监控、荷载识别等结构动力学的课题研究当中,往往要用到结构阻尼比这一参数。

在工程实际中,人们通常通过参数识别理论由实测的试验数据识别出结构的模态阻尼比。

识别方法有:对数衰减率法[1]、用功率谱求阻尼的精确方法[2]、时域峰值法[2]、半功率带宽法[3]、修正半功率带宽法、导纳圆法、神经网络和优化方法[4]、I TD、STD、随机减量法以及时序法[5]等。

文[6]、[7]介绍了由反应谱识别阻尼比的方法,及由频响函数识别模态参数[8]。

在结构模态参数识别中,阻尼比的识别精度远比固有频率和振型的识别精度低,且测试数据易受噪声的干扰。

因此,提高阻尼比的识别精度是结构动力学研究者需要解决的难题之一。

传统的对数衰减率法由于受到噪声的干扰,识别效果有时很差,难以达到预期目的。

半功率带宽法、导纳圆法、RFP[5]等频域方法要求测量输入,这在土木工程应用中有时很困难或不能实现。

本文提出的能量分析是一时域方法,它通过计算振动响应的时域能量,分析系统能量衰减与系统阻尼比之间的确定性关系,由一段时间内的信号能量的确定性关系推导出系统阻尼比。

这种方法在识别结构的阻尼比时,信号能量定义为自由振动响应x2(t)的积分,即Q t2t1x2(t)dt。

材料结构阻尼系数测量方法

材料结构阻尼系数测量方法
材料的结构阻尼系数是指材料对振动能量的吸收能力，是衡量材料阻尼性能的重要参数。

测量材料结构阻尼系数的方法有多种，下面我会从不同角度来介绍几种常见的测量方法。

首先，一种常见的方法是通过动态力学分析仪器（DMA）来测量材料的阻尼性能。

DMA是一种精密的实验仪器，能够在一定频率范围内施加振动力或应变，然后测量材料的应力和变形响应。

通过对材料在不同频率下的阻尼能力进行测试，可以得到材料的结构阻尼系数。

其次，另一种常见的方法是使用振动台进行振动试验来测量材料的阻尼性能。

在振动台上，可以将材料样品固定在不同的位置，然后施加不同频率和幅度的振动力，通过测量振动台和材料的振动响应，可以计算出材料的阻尼系数。

此外，还可以利用谐振频率法来测量材料的阻尼系数。

这种方法通过在材料上施加谐振频率的振动，然后测量振动的幅度和相位差，从而计算出材料的结构阻尼系数。

除此之外，还有一些其他间接的测量方法，例如利用声学谐振法或者模态分析法来推断材料的阻尼性能。

综上所述，测量材料的结构阻尼系数有多种方法，每种方法都有其适用的场景和局限性。

选择合适的测量方法需要根据具体的材料特性和实验要求来进行综合考虑。

希望以上介绍能够对你有所帮助。

基于Hilbert_Huang变换和自然激励技术的模态参数识别_韩建平

第27卷第8期V ol.27 No.8 工程力学2010年8 月Aug. 2010 ENGINEERING MECHANICS 54 文章编号：1000-4750(2010)08-0054-06基于Hilbert-Huang变换和自然激励技术的模态参数识别*韩建平1,2，李达文3(1. 兰州理工大学防震减灾研究所，甘肃，兰州 730050；2. 同济大学土木工程防灾国家重点实验室，上海 200092；3. 湖南中大设计院有限公司，湖南，长沙 410075)摘要：基于工程结构振动信号的分析与处理识别结构的模态参数，是结构健康监测和损伤诊断的重要手段之一。

基于傅里叶分析的信号处理方法对非线性、非稳态信号的处理能力差，传统的模态参数识别方法也存在阻尼比识别精度不高的问题。

基于Hilbert-Huang变换和自然激励技术，提出了一种新的模态参数识别方法，首先通过经验模态分解和Hilbert变换提取信号的瞬时特性，进而利用自然激励技术和模态分析的基本理论识别结构的模态频率和模态阻尼比。

利用这一方法，对12层钢筋混凝土框架模型振动台试验一测点的加速度记录进行了处理，识别了模态参数，识别结果与其它识别方法及有限元分析结果的对比表明该方法识别模态频率是可靠的，而模态阻尼比的识别虽然较传统的基于傅里叶变换的半功率带宽法有所改进，但识别的精准性仍然难以确认。

关键词：Hilbert-Huang变换；经验模态分解；自然激励技术；模态参数识别；振动台试验中图分类号：TB122; TU311.3文献标识码：AMODAL PARAMETER IDENTIFICATION BASED ON HILBERT-HUANG TRANSFORM AND NATURAL EXCITATION TECHNIQUE*HAN Jian-ping1,2 , LI Da-wen3(1. Institute of Earthquake Protection and Disaster Mitigation, Lanzhou University of Technology, Lanzhou, Gansu 730050, China;2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China;3. Hunan Zhongda Design Institute Limited Corporation, Changsha, Hunan 410075, China)Abstract:Identifying modal parameters via processing vibration signals is one of the mainstream approaches for structural health monitoring and damage diagnosis. The processing approaches based on Fourier analysis are not able to process nonlinear and non-stationary signals. In addition, most of traditional identification methods suffer from low precision to identify damping. Therefore, a new approach is proposed for identifying modal parameters based on Hilbert-Huang transform (HHT) and natural excitation technique (NExT). First, the instantaneous characteristics of the original signal are extracted by means of empirical mode decomposition (EMD) and Hilbert transform (HT). Then, NExT and basic modal analysis theory are used to identify modal frequencies and modal damping ratios. Furthermore, the original acceleration record from the shaking table test of a 12-storey RC frame model is processed and modal parameters are identified by the proposed approach. And identification results are compared with the results from other identification algorithms and finite element analysis.———————————————收稿日期：2009-03-02；修改日期：2009-08-03基金项目：甘肃省科技攻关项目(2GS057-A52-008)作者简介：*韩建平(1970―)，男，甘肃宕昌人，教授，博士生，从事结构抗震减振、结构健康监测及结构检测鉴定加固方面的教学与研究(E-mail: jphan@)；Comparison indicates that the proposed approach is reliable to identify modal frequencies. Although identification of modal damping ratios gets improved by comparison with half-power bandwidth method, it is still difficult to confirm the precision of the results.Key words: Hilbert-Huang transform; empirical mode decomposition; natural excitation technique; modal parameter identification; shaking table test基于工程结构振动信号的分析与处理识别结构的模态参数，是结构健康监测和损伤诊断的重要手段之一，也是当前国内外研究的热点问题之一[1]。

阻尼对结构模态测试精度影响的试验研究_1053

第35卷第3期 201 5年6月
地震 T 程与 T 程振动
EARTHQUAKE EI\GINEERING AND ENGINEERING DYNAMICS
Vol.35 No.3 Jun. 201 5
文章编号: 1000 - 1301 (2015 ) 03 - 0086 - 08
DOT : 10.13197/j.eeev. 211
们往往忽略了试验模态测试采用的方法及测试结果的准确性。对于某特定结构模态的试验测试，主观上由于激励方法、参数设置、数据采集及分析系统等诸多方面缺乏统一的理论技术指导其结果可靠性完伞依赖于技术人员的经验和尝试υ 另一方面，简单、理想的线弹性多自由度体系各 |占|有模态之间有正交忡，不相合。从能量角度表现为每一个固有模态都对应着一种特定能量平衡状态，各状态之间无能量交换，也就互不相合。理论上在实际测试中要激山"纯模态"响应是不可能的任何一种形式的振动必将激山多个模态响应，使被测的振动为多个模态混叠。兰;向、工程中在阻尼较大时， )\�I生阻尼的囚素众多，大多数属于菇滞阻尼等关于振型正交的阻尼体系，但仍有其他阻尼网素，系统振型关于阻尼矩阵也不完全正交，则表示结构振动时振型之间能量可以互相传递[4J。以罔1 (a)巾举出的缩尺比为1:5 的四层钢筋棍凝土框架结构模型:5J为例，其结构一阶阻尼比大小为2.4%(由脉冲激励测试的自谱计算得到)，模态测试结果见图 1 ( L)所示，图l ( h)巾同有频率峰值周围多其他干扰频率，且频率阶次越高振功能量越低使得频率识别用难。如以上的实际T程中测试模态频域无法分辨的情况是再由于阻尼过大造成呢。本文为考察阻尼造成模态混叠时，实际结构振动测试结果与理论的同有模态相比精度如何。为重点考察阻尼因素对结构模态测试结果的影响，设计了专层剪切型钢框架模型及可调硅油阻尼器以3 种常用模态测试方法为例对其在阻尼比由小到大逐渐增大的各种工况下的频率和振型进行测试。

HHT法识别结构模态频率和阻尼比的改进

ｐｓｉｌｏｉｅｔｙｔｅｍｏａａａｅｅｓｏｈｓｕｍｅｇｄｌｗｅ－ｎｒｙｍｏｅ．Ｔｏｉｃｅｓｈｏｓｂｅｔｄｎｉｈｄｌｐｒｍｔｒｆｔｏｅｓｂｒｅｏｒｅｅｇｄｓｆｎｒａｅｔｅｐｅｉｉｎｏｈｔｕｔｒｌｏａａａｔｒｎｏｍｏｅｐｅｉｅｙｉｅｔｙｍｏａａａｅｅｓｏｏｒｃｓｏｆｔｅｓｒｃｕａｄｌｒｍｅｅｓａｄｔｒｒｃｓｌｄｎｉｄｌｐｒｍｔｒｆｌｗ－ｍｐｆｆｅｕｎｙａｄｌｗｅ－ｎｒｙｍｏｅ，ｂｎｐｓｉｅｓａｅａｏｔｄｔｒｃｓｈｅｐｎｅｓｇａｓｉｈｓｒｑｅｃｎｏｒｅｅｇｄｓａｄａｓｆｔｒｒｄｐｅｏｐｏｅｓｔｅｒｓｏｓｉｎｌｎｔｉｌｐｐｒｈｎｔｅＥＤｓａｐｉｄｔｈｉｅｅｉｎｌ，ａｄｔｅｍｏａｒｑｅｃｎａｉｇｒｔｏｏａｅ，ｔｅｈＭｉｐｌｏｔｅｆｔｒｄｓｇａｓｎｈｄｌｅｕｎｙａｄｄｍｐｎａｉｆｅｌｆ
ＡｂｔａｔＴｈｒｒｏｓｂｌｉｓｔａｈｉｆｒｎｉｒｔｎｍｏｅｒｉｅｎｉｔｉｓｃｍｏｅｆｎ — ｓｒｃ：ｅｅａｅｐｓｉｉｔｅｈｔｔｅｄｆｅｅｔｖｂａｉｄｓａｅｍｘｄｉｎｒｎｉｉｏｄｕｃ

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

收稿日期 :2001 04 12 国家自然科学基金资助项目 ( 编号 50178013)
[ 1]
时域方法 , 不需测量输入 , 只需测量某点的自由振动响应( 位移、速度、加速度均可) , 适用于单、多自由度系统。在处理噪声干扰时 , ITD 、 STD 法考虑噪声模态 , 不得不描述毫无用处的噪声特性 , 造成计算机时的增加 , 这是通过扩阶提供噪声出口的弊端。本文识别阻尼比系数时 , 是通过响应时间历程与时间轴所围面积之间的关系来确定的。实际处理时 , 面积均是通过对响应采样后与时间轴所形成的各小块梯形面积求和得到。噪声虽然对采样值局部 ( 如峰值) 污染严重 , 但对信号的整体求和影响不大 , 特别是对零均值高斯白噪声干扰的情况 , 求和运算可产生正负抵消效应。因而 , 本文方法抗噪声干扰能力强、精度高、结果稳定。对于多自由度振动系统 , 其自由衰减振动响应随着时间的推移会逐渐衰减至零 , 衰减是按照指数关系 -ξω t e i ni 规律进行的。将自由振动响应 x ( t) 乘上 ei
DO I : 10 . 15951 / j. tmgcxb . 2002 . 06 . 004 第 35 卷第 6 期
2 0 0 2 年 12 月
土木工程学报 CHINA CIVIL ENGINEERING JOUR NAL
Vol. 35 No. 6 Dec . 2002
( a -ξ ω ) t
1 nl
3 仿真计算与实测试验
3. 1 单自由度系统考虑一单自由度系统
· ·
2
2
x+ 0. 5x + 25 x = 0
识别结构模态阻尼比的一种新方法
黄方林何旭辉陈政清
( 中南大学)
高赞明倪一清
( 香港理工大学)
摘要提出一种新的由结构自由振动响应识别结构阻尼比的方法。对于单自由度振动系统 , 推导出响应历程与时轴所围各面积之间的确定性关系后 , 利用各面积之间的关系来确定自由衰减振动的阻尼比系数。与传统的对数衰减率法比较 , 它具有抗噪声干扰能力强、精度高、稳定性好及简便实用等特点。对于多自由度振动系统 , 先将结构上某测点的自由振动响应表达为一理论解析式 x (t), 以 eat 相乘 x (t), 预给 a 初值范围 , 通过牛顿二分法 ( 或黄金分割法) 搜索 a 值 , 直至 eat x ( t) 做等幅振荡 , 则该阶模态的各模态参数得以确定。从总响应中扣除该阶模态对总响应的贡献后 , 重复这一过程 , 则可识别出响应信号中各阶模态的模态阻尼比。仿真计算与岳阳洞庭湖斜拉桥拉索实测试验结果表明了本文方法的有效性和实用性。关键词模态阻尼比参数识别斜拉桥拉索中图分类号 :TU311. 4 文献标识码 :A 文章编号 :1000 131X ( 2002) 06 0020 05
( 2)
式中 ξ — — — 阻尼比系数 ;ω — — 无阻尼固有频率 ; n — 1ξ— — — 有阻尼固有频率 ;A , φ — — —由
·
则 S 1 +S 3 +… +S 2N -1 S 1 +S 3 +…+S 2 N -1 = T S 2 +S 4 +…+S 2 N -ξ ω d ( S 1 +S 3 +… +S 2N +1 ) e n2 = e n 2 =e 两边取自然对数 , 可解得阻尼比系数 ξ = 1 2 1+ ( π E)
T t +d 1 2 t
1
= e
2 nπ ξ
1ξ
2
( 9)
式中 E =ln ( ΢ Sk ΢ S k +N ) , 即前 N 个面积之和与后 N 个面积之和之比的自然对数。 2. 2 多自由度系统情况考虑一 N 自由度振动系统 [ M] { x }+[ C] { x }+[ K] { x }={ 0} 某一测点响应
( a -ξ ω ) t
1 nl
t +T
d
T t +d 1 2
Td |x( t) |d t = ∫ |x t + t 1 + | dt 2
T
=A e
-ξ ωt
n 1
e
∫
0
2
d
e
-ξ ωt
nห้องสมุดไป่ตู้
at
sin( ω d t +φ -ω d t1 ) d t ( 6)
at
N
( ξω -α ) t
i ni
sin( ω 13) di t +φ i) ( 将发散 , 一定时间
N · · ·
T
( 11)
∫ ∫
1
x ( t ) dt =
T
∫ x (t +t ) d t
0 1
2
d
=Ae S2 =
-ξ ωt
n 1
∫e
0 T -ξ ω d n 2
2
d
x( t )= ( 5)
-ξ ωt
n
i =1
∑A e
i
-ξ ωt
i ni
sin( ω di t + φ i)
( 12)
sin ( ω -ω d t +φ d t 1) d t
( 2) a =ξ 1 ω nl 时 , e
N
( a -ξ ω ) t
1 nl
= 1,
单自由度振动系统是多自由度振动系统的特例 , 由搜索的方法同样可以识别单自由度系统的模态阻尼比ξ 。
y( t)= i ΢ Ai e = 2
( ξω -a) t
i ni
sin( ω di t +φ i )+
A 1 sin( ω dl t +φ 1) 显然 , 在 t 足够大后 , y ( t ) 将做幅值为 A1 , 频率为 ω d1 的等幅振荡 , 即 A 1 、 ω d1 完全确定 , 则 ξ 1 a a = = ω n1 1 -ξ , 解得 ω d1 ξ 1 1 = 1+ ( ω d1 a)
ξω t
ni
则x ( t) e i
ξω t
ni
在经过一段时间后 , 将做等幅振
荡 , 而且永远振荡下去。当然 , 事先我们并不知道 ξ iω ni 的值为多少 , 但我们可以通过搜索的方法确定它。ξ iω ni 值确定后 , 对等幅振荡信号做频谱分析 , 即可确定 ω ni , 因而 ξ i 值也值之确定。数字仿真与实测试验结果表明了本文的有效性。
ξ ωnT
n d
= 2 n πξ 1 ξ
2
2π 式中 T d = — — —自然周期。由上式可求得阻尼比 ω d 系数 ξ 。存在的问题 : ( 1) 实测响应中 , 对数衰减率法中峰值 A1 , A n 是响应的采样值 , 不一定刚好与实际极大值相等 ;( 2) 易受噪声干扰。若 x ( t) 受噪声干扰后 , A1 、 A n 的峰值可能在局部有很大的变化 , 从而影响了阻尼比系数 ξ 值的识别结果。现在做如下的改进 : 如图 1 所示 , 设该响应曲线与时间 t 轴分别交于 t1 , t2 … …, t 2N +1 点 , 与 t 轴所围的面积的绝对值分别为 S 1 , S 2 … …, S 2N ( 以下的面积均指绝对值) ,则 S1 =
后, y ( t ) 与 t 所围的面积的绝对值将越来越大 , 即后一面积大于前一面积 ;
图 1 响应时程曲线
Td
由( 5) 、 ( 6) 两式知 , S 2 =S 1 e
T -ξ ω d n 2
-ξ ω
n 2
。同理可推
T -ξ ω d n 2
得x ( t) 与 t 轴所围的各部分面积的绝对值 S 2N = S 2N -1e , 即后一面积总为前一面积的 e 倍。
图 2 响应曲线
· 22 ·
土木工程学报表 1 仿真结果比较 ( %)
本文方法阻尼比 ( 不滤波) 误差 0 0. 2 0. 4 1. 0 对数衰减率法 ( 不滤波) 误差阻尼比 5 . 0 4. 31 2. 73 1. 24 0 13. 8 45. 4 75. 4 本文方法阻尼比 5. 0 4. 99 4. 99 4. 98 ( 带通滤波) 误差 0 0 . 1 0. 19 0. 36 对数衰减率法阻尼比 5. 0 4 . 88 4 . 66 4. 5
1 引言
在结构故障诊断、振动实时监控、响应预测、荷载识别等结构动力学前沿课题研究方面 , 建立一精确的动力学模型是至关重要的环节。由于实际工程结构大型、复杂及测量误差的存在 , 理论计算与实际测量获得的系统动力学特性有时相差甚远。在进行结构动力学计算时 , 往往需要用到结构阻尼这一参数。为便于计算 , 人们经常理想地将结构阻尼取为比例阻尼 , 但即使这样 , 比例系数的选取仍很大程度上取决于工程经验。为此 , 人们通过参数识别理论 , 由实测的试验数据识别 ( 或估计) 出结构模态参数 , 识别的方法可分为时域法和频域法两种。常见的频域法有半功率带宽法、峰值法、导纳圆法等方法 , 时域法有对数衰减率法、ITD [ 2] [ 3] [ 4] 法、 STD 法、随机减量法等。在结构模态参数中 , 阻尼比的识别精度远比固有频率、振型的识别精度低 , 测试数据受噪声干扰时更为糟糕 , 100 %的阻尼比误差被认为是司空见惯的事情。因而 , 提高结构阻尼比的识别精度一直是结构动力学研究者追寻的目标 , 也是一难度很大的课题。为进一步提高阻尼比的识别精度 , 文献[ 5 , 6] 提出了不依赖质量和刚度矩阵单独识别阻尼矩阵的方法 , 这是一种频域方法 , 需测量频响函数。对于大型结构( 如桥梁) , 其频响函数的获得是一件很困难的事情。故此 , 本文提出了一种新的由结构自由振动响应识别结构模态阻尼比的方法 , 这是一种