神经网络(BP网)—鸢尾花分类问题

基于多层感知机（Multilayer Perceptron, MLP）的鸢尾花分类是一种监督学习方法，用于解决多类别分类问题。

在处理鸢尾花数据集时，MLP能够根据鸢尾花四个特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度）来区分三种不同的鸢尾花品种（山鸢尾、变色鸢尾、维吉尼亚鸢尾）。

以下是使用PyTorch框架实现一个多层感知机进行鸢尾花分类的基本步骤：1.数据准备：o加载鸢尾花数据集（Iris dataset），通常可以从sklearn.datasets 或直接下载CSV文件获取。

o将数据划分为训练集和测试集，如使用train_test_split函数划分。

o数据预处理，将数据归一化或标准化到同一尺度。

2.构建模型：o定义一个神经网络模型，包含输入层、隐藏层和输出层。

例如，输入层的大小应与特征数量相同，输出层的大小应与类别数相同（对于鸢尾花分类是3）。

Pythonimport torch.nn as nnclass IrisMLP(nn.Module):def__init__(self):super(IrisMLP, self).__init__()yer1 = nn.Linear(4, 16) # 输入层到第一隐藏层 self.relu = nn.ReLU()self.dropout = nn.Dropout(p=0.2)yer2 = nn.Linear(16, 3) # 第一隐藏层到输出层def forward(self, x):x = self.relu(yer1(x))x = self.dropout(x)x = yer2(x)return x3.损失函数与优化器设置：o使用合适的多类别损失函数，如交叉熵损失（CrossEntropyLoss）。

Pythoncriterion = nn.CrossEntropyLoss()optimizer = torch.optim.Adam(model.parameters(),lr=0.001)4.训练循环：o遍历训练集样本，执行前向传播得到预测结果，计算损失并反向传播更新权重。

习题2.1什么是感知机？感知机的基本结构是什么样的？解答：感知机是Frank Rosenblatt在1957年就职于Cornell航空实验室时发明的一种人工神经网络。

它可以被视为一种最简单形式的前馈人工神经网络，是一种二元线性分类器。

感知机结构：2.2单层感知机与多层感知机之间的差异是什么？请举例说明。

解答：单层感知机与多层感知机的区别：1. 单层感知机只有输入层和输出层，多层感知机在输入与输出层之间还有若干隐藏层；2. 单层感知机只能解决线性可分问题，多层感知机还可以解决非线性可分问题。

2.3证明定理：样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点集构成的凸壳互不相交.解答：首先给出凸壳与线性可分的定义凸壳定义1：设集合S⊂R n，是由R n中的k个点所组成的集合，即S={x1,x2,⋯,x k}。

定义S的凸壳为conv(S)为：conv(S)={x=∑λi x iki=1|∑λi=1,λi≥0,i=1,2,⋯,k ki=1}线性可分定义2：给定一个数据集T={(x1,y1),(x2,y2),⋯,(x n,y n)}其中x i∈X=R n , y i∈Y={+1,−1} , i=1,2,⋯,n ,如果存在在某个超平面S：w∙x+b=0能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧，即对所有的正例点即y i=+1的实例i，有w∙x+b>0，对所有负实例点即y i=−1的实例i，有w∙x+b<0，则称数据集T为线性可分数据集；否则，称数据集T线性不可分。

必要性：线性可分→凸壳不相交设数据集T中的正例点集为S+，S+的凸壳为conv(S+)，负实例点集为S−，S−的凸壳为conv(S−)，若T是线性可分的，则存在一个超平面：w ∙x +b =0能够将S +和S −完全分离。

假设对于所有的正例点x i ，有：w ∙x i +b =εi易知εi >0，i =1，2，⋯，|S +|。

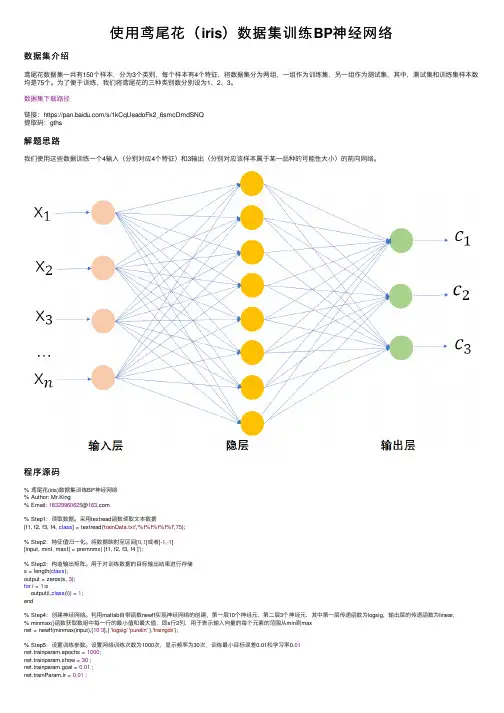
使⽤鸢尾花（iris）数据集训练BP神经⽹络数据集介绍鸢尾花数据集⼀共有150个样本，分为3个类别，每个样本有4个特征，将数据集分为两组，⼀组作为训练集，另⼀组作为测试集，其中，测试集和训练集样本数均是75个。

为了便于训练，我们将鸢尾花的三种类别数分别设为1、2、3。

数据集下载路径链接：https:///s/1kCqUeadoFk2_6smcDmdSNQ提取码：gths解题思路我们使⽤这些数据训练⼀个4输⼊（分别对应4个特征）和3输出（分别对应该样本属于某⼀品种的可能性⼤⼩）的前向⽹络。

程序源码% 鸢尾花(iris)数据集训练BP神经⽹络% Author: Mr.King% Email: 183********@% Step1：读取数据。

采⽤textread函数读取⽂本数据[f1, f2, f3, f4, class] = textread('trainData.txt','%f%f%f%f%f',75);% Step2：特征值归⼀化。

将数据映射⾄区间[0,1]或者[-1,-1][input, minI, maxI] = premnmx( [f1, f2, f3, f4 ]');% Step3：构造输出矩阵。

⽤于对训练数据的⽬标输出结果进⾏存储s = length(class);output = zeros(s, 3);for i = 1:soutput(i,class(i)) = 1;end% Step4：创建神经⽹络。

利⽤matlab⾃带函数newff实现神经⽹络的创建，第⼀层10个神经元，第⼆层3个神经元，其中第⼀层传递函数为logsig，输出层的传递函数为linear，% minmax()函数获取数组中每⼀⾏的最⼩值和最⼤值，即s⾏2列，⽤于表⽰输⼊向量的每个元素的范围从min到maxnet = newff(minmax(input),[103],{ 'logsig''purelin' },'traingdx');% Step5：设置训练参数。

K最近邻（K-Nearest Neighbors，KNN）是一种简单而直观的机器学习算法，用于分类和回归。

下面是KNN算法在鸢尾花分类问题中的基本原理和实现步骤：KNN 算法原理：
1.数据准备：收集带有标签的训练数据，这些数据包括输入特征和对应的标
签（类别）。

2.选择 K 值：确定要使用的邻居数量 K。

K值的选择可能会影响分类的准确
性，一般通过交叉验证等方式来确定。

3.计算距离：对于给定的未标记样本，计算它与训练集中所有样本的距离。

常用的距离度量包括欧氏距离、曼哈顿距离等。

4.排序：将距离按升序排列，选择前 K 个距离最近的训练样本。

5.投票：统计 K 个最近邻居中每个类别的数量，选择数量最多的类别作为未
标记样本的预测类别。

鸢尾花分类问题的实现：
下面是使用Python和scikit-learn库实现鸢尾花分类的简单示例：
在这个示例中，我们首先加载鸢尾花数据集，然后将数据集分为训练集和测试集。

接着，我们创建一个KNN分类器，使用训练集训练模型，并在测试集上进行预测。

最后，计算模型的准确性。

这是一个简单的KNN分类器的实现，可以在更复杂的
数据集和应用中进行进一步的调整和优化。

鸢尾花分类所用的算法
鸢尾花分类是机器学习领域中一个经典的问题，常用的算法包括K近邻算法（K-Nearest Neighbors, KNN）、支持向量机（Support Vector Machine, SVM）、决策树（Decision Tree）、随机森林（Random Forest）、朴素贝叶斯（Naive Bayes）和神经网络等。

K近邻算法是一种基于实例的学习方法，它根据新样本与已知样本的距离来进行分类，选择距离最近的K个样本进行投票决定分类结果。

支持向量机是一种监督学习算法，它通过将数据映射到高维空间，找到一个最优的超平面来进行分类。

决策树是一种树形结构的分类器，通过一系列的规则对数据进行划分，最终得到分类结果。

随机森林是一种集成学习方法，它由多个决策树组成，通过对多个决策树的结果进行投票来进行分类。

朴素贝叶斯是一种基于贝叶斯定理的分类算法，它假设特征之间相互独立，通过计算样本属于每个类别的概率来进行分类。

神经网络是一种模仿人脑神经元网络结构的算法，通过多层神经元的连接和权重调整来进行分类。

这些算法在鸢尾花分类问题中都有较好的表现，选择合适的算法取决于数据集的特征、样本量、计算资源和准确度要求等因素。

同时，也可以通过交叉验证等方法来评估不同算法的性能，以选择最适合的算法进行鸢尾花分类。

《大数据基础》基于简单神经网络的鸢尾花分类预测与分析一、选题的目的及要求选题（5）;尝试使用简单神经网络模型对鸢尾花数据集进行分类预测，对模型的设计、训练和预测结果进行综合分析。

选题的目的是通过使用简单神经网络模型对鸢尾花数据集进行分类预测，并对模型的设计、训练和预测结果进行综合分析。

以下是选题的要求：1、目的：了解和应用简单神经网络模型对实际数据集的分类预测能力。

2、数据集：使用经典的鸢尾花数据集（Iris dataset），该数据集包含了150个样本，分为3个不同种类的鸢尾花（Setosa、Versicolor、Virginica），每个样本有4个特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度）。

3、模型设计：采用简单神经网络模型，包括输入层、隐藏层和输出层，选择合适的激活函数、损失函数和优化算法。

4、模型训练：将数据集分为训练集和测试集，使用训练集对模型进行训练，并通过验证集进行模型优化调整。

5、模型预测与评估：使用测试集进行分类预测，并使用准确率等评估指标对模型进行评估。

6、结果分析：对模型的设计、训练和预测结果进行综合分析，包括模型表现、特征重要性、潜在的改进空间等方面。

总之，本选题旨在通过实际案例，深入了解简单神经网络模型的分类预测能力，在分析模型性能的基础上，提供对模型改进和应用的思考和建议。

二、设计思路1、数据准备：下载鸢尾花数据集（Iris dataset）并加载到程序中。

对数据集进行数据预处理，包括数据清洗、缺失值处理、特征标准化等。

2、简单神经网络模型设计：确定输入层的维度，即特征的数量。

设计隐藏层的数量和神经元个数，可以根据经验或者进行调优。

确定输出层的维度，即鸢尾花类别的数量。

选择适当的激活函数、损失函数和优化算法，如ReLU激活函数、交叉熵损失函数和梯度下降优化算法。

3、数据集划分：将数据集划分为训练集和测试集，一般可以采用70%的数据作为训练集，30%的数据作为测试集。

tensorflow karas 鸢尾花的分类-概述说明以及解释1.引言1.1 概述概述部分将介绍本篇文章的主题和背景信息。

本文正是基于TensorFlow和Keras两个流行的深度学习框架，针对鸢尾花分类问题展开研究和实验。

深度学习已经在各个领域取得了巨大的成功，它是模仿人脑结构和工作原理，通过大量的神经网络层进行学习和推理的一种人工智能方法。

TensorFlow和Keras作为深度学习的两个重要工具，分别提供了高效的张量计算框架和简易的深度学习接口。

鸢尾花数据集是分类问题中的经典案例，也是深度学习入门者常用的练习数据集。

该数据集包含了150个样本，涵盖了鸢尾花的三个不同种类：山鸢尾（setosa）、变色鸢尾（versicolor）和维吉尼亚鸢尾（virginica）。

通过测量花朵的四个特征（花萼长度、花萼宽度、花瓣长度以及花瓣宽度），我们的目标是根据这些特征对鸢尾花进行准确地分类。

本文将介绍如何利用TensorFlow和Keras进行鸢尾花的分类任务，具体包括数据准备、模型构建、模型训练和性能评估等。

同时，本文还会比较TensorFlow和Keras在解决鸢尾花分类问题上的优劣，分析它们在使用过程中的不同特点和适用场景。

最后，我们还会探讨鸢尾花分类问题的应用前景，展望深度学习在生物学、农业和生态研究等领域的潜在应用价值。

通过本文的介绍和实验，读者将能够了解TensorFlow和Keras的基本概念和使用方法，并且具备在鸢尾花分类问题上应用这两个工具进行深度学习的能力。

本文的目的是帮助读者快速入门深度学习，并为深度学习在实际问题中的应用提供一个实例。

最后，希望本文的内容和实验结果能对读者深入理解深度学习的过程和原理，同时为其他相关研究提供一个参考和借鉴。

1.2 文章结构文章结构部分的内容可以包括以下内容：文章结构是指整篇文章的组织形式和各个部分之间的关系。

一个清晰的文章结构可以帮助读者更好地理解和掌握文章的内容。

基于支持向量机的鸢尾花类别预测作者：孙萌月张奥丽曾进成来源：《智富时代》2018年第12期【摘要】支持向量机是基于统计学习理论发展起来的一种新的机器学习方法，应用于解决各种小样本分类问题。

经文献报道，鸢尾花自身的固有属性可以作为输入指标用来预测鸢尾花的种类。

本文以鸢尾花的属性数据建立分类模型，结果表明支持向量机分类方法具有很好的泛化性能，为自动判定鸢尾花种类提供了一种有效的方法。

【关键词】支持向量机；分类问题；核函数鸢尾花属于鸢尾科，是一类具有较高观赏价值的草本植物，其萼片是绚丽多彩的，和向上的花瓣不同，花萼是下垂的。

通过鸢尾花的属性来判断鸢尾花的种类，可以更高效率的培育出相应需要的鸢尾花，来满足现实需求量。

人工智能的快速发展带动了基于数据挖掘的人工神经网络和支持向量机智能分类方法。

人工神经网络具有非线性、自学习、自适应，能够大规模并行处理等特征，同时内部训练过程是在黑箱中进行的，只要直接输入数据即可得出结果[1]。

但缺点也很明显，神经网络中参数无法解释，同时训练过程在黑箱中进行，具有一定的盲目性，由于它是基于经验风险最小化原则，容易出现“过拟合”现象，即有可能出现陷入局部最优解而无法得到全局最优解的现象。

而支持向量机（SVM）借助最优化方法来解决机器学习问题[2]，依赖结构风险最小化原则，针对小样本得到全局最优解，解决了在神经网络方法中无法避免的局部极值问题。

因此，本文将目标数据集的三种鸢尾花的花萼长度、花萼宽度、花瓣长度、花瓣宽度四个属性用来做样本的定量分析，建立模型，通过SVM分类的方法，根据给定的训练集，通过大量的训练点，寻找实值函数，由此得到决策函数，以便用决策函数推断任意模式（输入指标向量或称输入）相对应的输出指标。

一、基于支持向量机的鸢尾花类别预测1.支持向量机支持向量机分类方法是一种基于结构风险最小化的原理，针对一个给定的有限数量训练集样本的学习任务，通过在原空间或经投影后的高维空间中构造最佳分类超平面作为决策面。

[Python机器学习]鸢尾花分类机器学习应⽤1、问题简述 假设有⼀名植物学爱好者对她发现的鸢尾花的品种很感兴趣。

她收集了每朵鸢尾花的⼀些测量数据：花瓣的长度和宽度以及花萼的长度和宽度，所有测量结果的单位都是厘⽶。

她还有⼀些鸢尾花的测量数据，这些花之前已经被植物学专家鉴定为属于 setosa、versicolor 或 virginica 三个品种之⼀。

对于这些测量数据，她可以确定每朵鸢尾花所属的品种。

我们假设这位植物学爱好者在野外只会遇到这三种鸢尾花。

我们的⽬标是构建⼀个机器学习模型，可以从这些已知品种的鸢尾花测量数据中进⾏学习，从⽽能够预测新鸢尾花的品种。

因为我们有已知品种的鸢尾花的测量数据，所以这是⼀个监督学习问题。

在这个问题中，我们要在多个选项中预测其中⼀个（鸢尾花的品种）。

这是⼀个分类（classifification）问题的⽰例。

可能的输出（鸢尾花的不同品种）叫作类别（class）。

数据集中的每朵鸢尾花都属于三个类别之⼀，所以这是⼀个三分类问题。

2、测试代码1#!/usr/bin/env python2# -*- coding: utf-8 -*-3# @File : Iris.py4# @Author: 赵路仓5# @Date : 2020/2/266# @Desc :7# @Contact : 398333404@89import numpy as np10import matplotlib.pyplot as plt11import pandas as pd12import mglearn13import pandas as pd14from sklearn.datasets import load_iris # 鸢尾花（Iris）数据集，这是机器学习和统计学中⼀个经典的数据集15from sklearn.model_selection import train_test_split1617 iris_dataset = load_iris() # load_iris 返回的 iris 对象是⼀个 Bunch 对象，与字典⾮常相似，⾥⾯包含键和值18print("Key or iris_dataset:\n{}".format(iris_dataset.keys())) # 打印19print(iris_dataset['DESCR'][:193] + "\n...") # DESCR 键对应的值是数据集的简要说明。

ANN算法分类实例引言人工神经网络（Artificial Neural Network，简称ANN）是一种模拟人脑神经网络思维的计算模型。

它由输入层、隐藏层和输出层构成，每个神经元通过权重与其他神经元连接，进行信息传递和处理。

ANN算法可以应用于各种分类问题，包括图像识别、语音识别、自然语言处理等。

本文将以一个ANN算法分类实例为例，深入探讨ANN算法的分类原理和应用。

一、数据集介绍我们选取的数据集是关于鸢尾花的信息。

该数据集包含了150个样本，每个样本有四个输入特征：花萼长度、花萼宽度、花瓣长度和花瓣宽度，以及一个输出标签：鸢尾花的种类（Setosa、Versicolor和Virginica）。

我们的目标是根据输入特征预测鸢尾花的种类。

二、数据预处理在应用ANN算法之前，我们需要对数据进行预处理。

首先，我们将数据集分为训练集和测试集，一般情况下，我们将数据集的70%-80%作为训练集，剩余的20%-30%作为测试集。

然后，我们对数据进行归一化处理，将每个输入特征缩放到0到1的范围内，以避免某些特征对模型训练的影响过大。

三、神经网络模型在本实例中，我们将使用一个三层的前馈神经网络模型。

输入层有四个神经元，隐藏层有两个神经元，输出层有三个神经元，每个输出神经元对应一种鸢尾花的种类。

3.1 网络结构图下图展示了我们的神经网络模型的结构：输入层：4个神经元隐藏层：2个神经元输出层：3个神经元3.2 激活函数激活函数是神经网络模型中的一个重要组成部分，用于引入非线性特征。

在隐藏层和输出层的神经元上，我们选择常用的Sigmoid函数作为激活函数，它可以将神经元的输出限制在0到1之间。

3.3 权重和偏置在神经网络模型中，每个连接都有一个对应的权重，用于调整信息传递的强度。

此外，每个神经元还有一个偏置项，用于调整神经元的激活阈值。

我们将根据训练数据通过梯度下降算法来调整权重和偏置，以使得神经网络模型能够更好地拟合训练数据。

对鸢尾花数据进⾏分类的思路对鸢尾花数据进⾏分类1 数据集处理加载数据集，IRIS 数据集在 sklearn 模块中已经提供from sklearn import datasetsiris = datasets.load_iris()iris_feature = iris.datairis_target = iris.target将150个样本分割为90个训练集和60个测试集feature_train, feature_test, target_train, target_test = train_test_split(iris_feature, iris_target, test_size=0.4,random_state=40)2 决策树分类（实现）这⾥选⽤CART算法。

算法从根节点开始，⽤训练集递归构建分类树。

在决策树的构建中，有时会造成决策树分⽀过多，这是就需要去掉⼀些分⽀，降低过度拟合。

通过决策树的复杂度来避免过度拟合的过程称为剪枝。

创建决策树：步骤1：选择GiniIndex最⼩的维度作为分割特征。

（GiniIndex计算⽅式见PPT）步骤2：如果数据集不能再分割，即GiniIndex为0或只有⼀个数据，该数据集作为⼀个叶⼦节点。

步骤3：对数据集进⾏⼆分割步骤4：对分割的数据集1重复步骤1、2、3，创建true⼦树步骤5：对分割的数据集2重复步骤1、2、3，创建false⼦树明显的递归算法。

剪枝：需要从训练集⽣成⼀棵完整的决策树，然后⾃底向上对⾮叶⼦节点进⾏考察。

判断是否将该节点对应的⼦树替换成叶节点。

当节点的gain⼩于给定的 mini Gain时则合并这两个节点.。

测试：通过对测试集的预测来验证准确性。

对于不同的划分⽅式，即选取不同随机数种⼦且保持90:60的⽐例，训练集准确率为：100 %，测试集准确率为：91.67 %3 SVM分类（调库）⽀持向量机的基本模型是定义在特征空间上的间隔最⼤的线性分类器，即求⼀个分离超平⾯，这个超平⾯使得离它最近的点能够最远。

鸢尾花分类实验报告引言鸢尾花是一种常见的植物，由于其花朵形态的多样性，成为了许多植物分类学研究的对象。

本实验旨在通过机器学习算法对鸢尾花的特征进行分类，以提高对鸢尾花分类的准确性和效率。

实验设计与方法本实验使用了鸢尾花数据集，该数据集包含150个样本，每个样本具有四个特征：花萼长度、花萼宽度、花瓣长度和花瓣宽度。

同时，每个样本还有一个类别标签，分别对应三个鸢尾花的品种：山鸢尾（setosa）、变色鸢尾（versicolor）和维吉尼亚鸢尾（virginica）。

我们对数据集进行了预处理，包括数据清洗、缺失值处理和特征标准化。

接着，我们将数据集分为训练集和测试集，其中训练集占总样本数的70%，测试集占30%。

在实验中，我们采用了三种常见的机器学习算法进行鸢尾花分类：K 近邻算法、支持向量机算法和决策树算法。

结果与分析在使用K近邻算法进行鸢尾花分类时，我们选择了K值为3，即选择最近的3个邻居作为分类依据。

在测试集上进行分类准确率的评估，结果显示准确率达到了97%。

接下来，我们使用支持向量机算法进行分类。

通过调整核函数和正则化参数，我们得到了不同的分类结果。

最终，在测试集上，我们选择了径向基核函数和适当的正则化参数，分类准确率达到了95%。

我们使用决策树算法进行分类。

通过调整树的深度和节点划分准则，我们得到了不同的分类结果。

在测试集上，我们选择了树的深度为3和基尼系数作为节点划分准则，分类准确率达到了92%。

讨论与总结本实验通过机器学习算法对鸢尾花进行了分类实验。

结果显示，K 近邻算法在本实验中表现最好，其次是支持向量机算法和决策树算法。

这表明K近邻算法对于鸢尾花的特征分类具有较好的效果。

然而，本实验也存在一些不足之处。

首先，鸢尾花数据集的样本量相对较小，可能导致结果的泛化能力不强。

其次，我们只使用了部分特征进行分类，可能忽略了一些重要的特征信息。

因此，后续的研究可以尝试增加样本量，选择更多的特征进行分类，以提高分类的准确性和鲁棒性。

基于k-means算法的鸢尾花的分类
鸢尾花分类问题是机器学习领域中的一个经典问题。

K-means算法是一种聚类算法，可以被用来解决鸢尾花的分类问题。

下面我将详细解释这些术语和它们的应用。

首先，鸢尾花是一种植物，常见于欧洲和北非地区。

鸢尾花的特征包括花瓣长度、花瓣宽度、萼片长度和萼片宽度等。

这些特征可以用来对鸢尾花进行分类。

其次，机器学习是一种通过数据训练模型来自动化完成任务的方法。

在鸢尾花分类问题中，我们使用机器学习算法来训练模型，自动地将鸢尾花分为不同的类别。

K-means算法是一种聚类算法，可以被用来解决鸢尾花分类问题。

在k-means 算法中，我们首先需要确定要将鸢尾花分为多少个类别。

然后，算法会随机选择一些数据点作为中心点，然后将其他数据点分配到最近的中心点。

在下一步中，中心点会被更新为其所包含数据点的平均值。

这个过程会不断迭代，直到中心点不再改变。

最终，每个数据点都会被分配到一个类别中。

最后，为了实现鸢尾花的分类，我们需要使用K-means算法来训练一个模型。

我们首先需要将鸢尾花数据集分为训练集和测试集。

然后，我们使用训练集的数据来训练模型，找到最佳的中心点，并使用测试集的数据来测试模型的准确度。

如果模型的准确度高，那么我们可以使用它来将新的鸢尾花数据点分类到不同的
类别中。

综上所述，通过K-means算法和机器学习技术，我们可以将鸢尾花自动地分为不同的类别，为进一步研究鸢尾花提供了方便和帮助。

基于逻辑回归的鸢尾花二分类和三分类问题实验报告模板标题：基于逻辑回归的鸢尾花分类问题实验报告模板引言逻辑回归是一种常见的分类算法，在机器学习和数据科学领域被广泛应用。

本实验旨在使用逻辑回归算法解决鸢尾花数据集的二分类和三分类问题。

通过本文，将为您介绍实验的背景和目的、数据集的描述、逻辑回归算法的原理及其在二分类和三分类问题上的应用，并分享个人观点和理解。

1. 实验背景和目的逻辑回归是一种广义线性模型，用于预测离散型目标变量的概率。

在鸢尾花分类问题中，我们的目标是根据鸢尾花的四个特征（萼片长度、萼片宽度、花瓣长度、花瓣宽度）来预测鸢尾花的类别（Setosa、Versicolor、Virginica）。

通过实验，我们旨在评估使用逻辑回归算法解决鸢尾花分类问题的实际表现。

2. 数据集描述本实验使用的数据集是著名的鸢尾花数据集（Iris Dataset）。

该数据集包含150个样本，每个样本有4个特征和一个类别标签。

特征包括萼片长度、萼片宽度、花瓣长度和花瓣宽度。

类别标签为三个类别之一：Setosa、Versicolor和Virginica。

数据集通过分割样本集为训练集和测试集，以便评估模型的性能。

3. 逻辑回归算法原理逻辑回归算法基于逻辑函数对样本进行分类。

逻辑函数将线性函数的输出映射到一个[0,1]的区间内，代表样本属于某个类别的概率。

逻辑回归通过最大似然估计来拟合模型参数，并使用梯度下降来优化模型。

在二分类问题中，我们使用二元逻辑回归模型；而在三分类问题中，我们使用多项逻辑回归模型。

4. 二分类问题实验4.1 数据预处理在二分类问题中，我们将鸢尾花数据集中的类别标签转换为二进制变量，将Setosa类别标记为0，其他类别标记为1。

我们将数据集分为训练集和测试集，以便进行模型的训练和评估。

4.2 特征缩放为了提高模型的性能，我们对特征进行标准化处理，以确保各特征具有相同的尺度。

4.3 模型训练及评估我们使用训练集来拟合逻辑回归模型，并使用测试集来评估模型的性能。

keras 鸢尾花分类的实验步骤
Keras 是一种高级神经网络API，它可以帮助我们在深度学习任务（包括图像分类、文本
分类和序列标记）中使用强大的建模技术。

本文将介绍使用Keras进行鸢尾花分类的实验
步骤。

第一步，下载鸢尾花数据集。

数据集可以从UCI机器学习知识库下载，包含三类鸢尾花的150条记录，每类50条，其中五个属性是花萼长度、花萼宽度、花瓣长度、花瓣宽度和
花的类别。

第二步，将数据集拆分成训练集和测试集。

将数据分为训练数据集和测试数据集可以帮助
我们评估模型性能和精度。

第三步，预处理数据。

我们必须以某种形式处理数据，以便模型能够正确地操作它们。

在这里，我们可以将输入数据转换为单位矩阵，以使模型能够更好地处理它们，此外，还可以将因变量转换为类别标签。

第四步，准备模型。

使用Keras创建和编译模型。

在这种情况下，多项式函数方程可用于
模型。

第五步，训练模型。

使用训练数据集训练模型。

第六步，结果评估。

使用测试数据集验证模型效果，计算准确率、查准率、查全率和F1
分数。

第七步，模型诊断。

如果性能不佳，可以使用模型诊断方法，运行关于训练的可视化报告，以调整模型参数和优化模型性能。

由于它简单易用，易于使用高级神经网络API（如Keras）来帮助你更好地深入建模和解
决机器学习问题，因此Keras在机器学习应用方面得到了普遍认可。

本文介绍了使用Keras进行鸢尾花分类的实验步骤，希望对您有所帮助。