水力学第三章3
- 格式:ppt
- 大小:2.27 MB
- 文档页数:93









第三章:液体运动学思考题1.区别:(1)拉格朗日法:拉格朗日法是一液体质点为研究对象,研究每个液体质点所具有的运动要素(速度,加速度,压强)时间变化的规律。
(2)欧拉法:欧拉法是研究流场中某些固定空间点上的运动要素随时间的变化规律。
联系:二者都是描述液体的运动的基本方法du2.(茨)反映了在同一空间上液体质点运动速度随时间的变化,称为du du duu — + u — + u —时变加速度;("X ydy Z dz)反映了同一时刻位于不同空间点上液体质点的速度变化,称为位变加速度。
3•液体质点的运动形式:由平移、线变形.角变形及旋转运动等四种基本形式所组成。
(1)位置平移:u x dt > u y dt > u7dt(2)线变形:瓦;e yy~W;严er/r/~~dz .' 2( dy 炭丿显(些+些:2(氐勿丿 1 du x 加・、 dx )4•按照液体运动中质点本身有无旋转,将液体运动分为有旋或无旋。
若液体运动时每个质点都不存在着绕自身轴的旋转运动,即角速度为0,称为无旋流;反之为有旋流。
无旋流:叭二3=叫=0,无旋必有势函数。
5•使用条件:不可压缩液体;物理意义:液体的体积变形率为零,即体积不会随时间发生变化。
3、= 06•答:Q = 0 T < 0 = 09=0定义:设流场中有流速势函数况rj 和),设函数满足:1 ( du, du -—+一(4)旋转:(3)角变形:du x _ du z dzdx v du.■ — ____________________dz dydu x du y dydx0) = < co x ■—dx + — dy + — dz = u X dx+u dy + u.dz (= d (p ) dx dy dz d (p= u x dx + u v dy + u.dz7•意义:给分析液体带了很大的方便,更能辨别液体属于有旋或无旋Oily dUya = u ---------- F u -------- F uyX dx T Uy °y T U z 3z%=°2・解:当t=l 时aux 3u x au x dux% - u x g x + u y Qy + Uy dz + dt =z 2x + yz dUy Oily OilydUy% - u x Qx + 勺 Qy + % Qz + dt =z 2y + xz % = °在(1,2,1)得:a x = 3m/s2; a y = 3m/S 2 . 3z = 0dx dy dx dy 1 23解:龙可所以口 =三即+ = £1 1 2当t“时,在(0, 0)点的流线方程为:x= t (y■ 2y )则函数称为流速势函数,若流速已知,可利用上式求出势流的流速势函du5ux% =畑 4-u — + u-所以 液体质点有变形运动du_2莎=-k(x 2 + y 2)+ ky(x 2 +『)*2 du_2- = k(x 2 + y 2)- kx(x 2 + y 2)* 2x所以 液体质点有角变形1 k(y2 + x 2)叭-2( ax " dy )=k(x 2 + y 2)所以液体质点自身无旋转运动dx dydx dy% u y ,所以即:流线方程为J + y2 = C 5•解:(1) 因为为不可压缩液体°P/°t=o叫 du y du zdx + dy + dz _ °所以满足流动连续函数(2)因为为不可压缩液体°P/°t=O所以不满足流动连续函数du 2xykdx2 2 2 (X 2 +y 2)°Uy 2xyk dy / 22、2(x + y );k(y 2 - x 2) (x 2 4- y 2)2duxdxduzdz =4工0l/aux Eyx = W 历7 +(3)因为为不可压缩液体°P/°t=Ou= u J + U y j + u z k =6X - + 6y f _7tk时变加速度dt =-7^ dux u -------- F u 位变加速度x dx全加速度 a = 36xi + 36yj‘ -7k7% = 6 + 2xy + t 2 u y =- (xy 2 + lOt) u z = 25du x du x du x du xa = u ---------- 1- u ------- 1- u ---- ------ = 2t + 2v(6 + 2xv + t 2)x u x dx y dy 7 dz + at y< (xy 2 + lOt) * 2xdUy du y du y dUy av = U ^~dx + 勺石 + 吗冠*页“0+(6 + 2xy +『)*(- y 2)+ (xy 2 + lOt) * 2xy当t“在(3,0,2)时a x =- 58m/s 2 a y =- 10m/s 2 a z = 08. (1)aux dUy au z所以满足流动连续函数OUy dUy 3u zdz丿du du \X z|dz dx jdu duy Xdx oy丿=0fax -y1O)=—y 2U)=—x 2U maxr o13 =—z 2所以9.解有旋流为无势流au xF- -T— = 2xy(1) fc xx - dx当x=l ,y=2 时&xx — °£ =yy=一4yy £zz = O(2)32=一2/7。
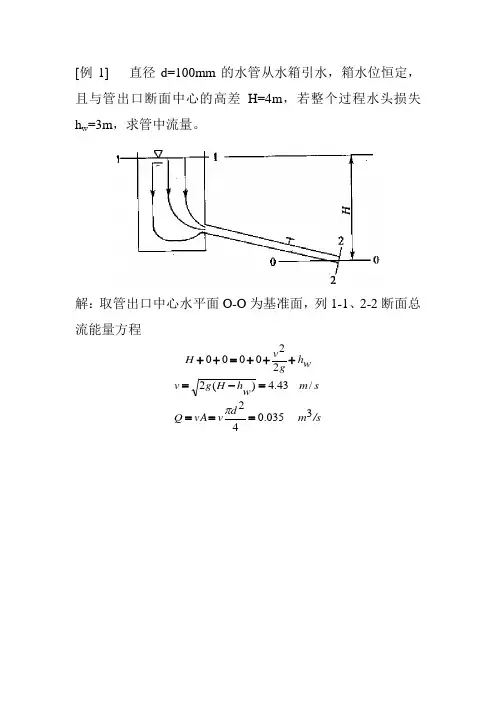
第三章 水动力学基础本章研究液体机械运动的基本规律及其在工程中的初步应用。
根据物理学和理论力学中的质量守恒原律、牛顿运动定律及动量定理等,建立水动力学的基本方程,为以后各章的学习奠定理论基础。
液体的机械运动规律也适用于流速远小于音速(约340 m/s )的低速运动气体。
因为当气体的运动速度不大于约50m/s 时,其密度变化率不超过1%,这种情况下的气体也可认为是不可压缩流体,其运动规律与液体相同。
研究液体的运动规律,也就是要确定描述液体运动状态的物理量,如速度、加速度、压强、切应力等运动要素随空间与时间的变化规律以及相互关系。
由于实际液体存在粘性,使得水流运动分析十分复杂,所以工程上通常先以忽略粘性的理想液体为研究对象,然后进一步研究实际液体。
在某些工程问题上,也可将实际液体近似地按理想液体估算。
§3-1 描述液体运动的两种方法描述液体运动的方法有拉格朗日(grange )法和欧拉(L.Euler )法两种。
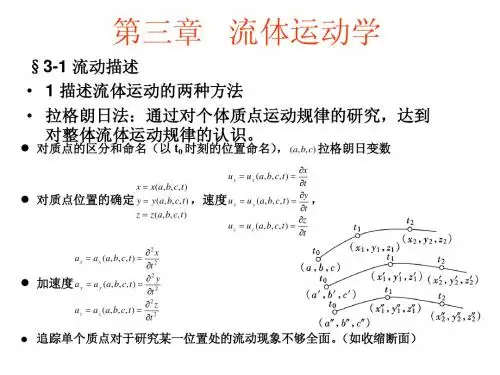
1.拉格朗日法(Lagrangian View ) 拉格朗日法是以液体运动质点为对象,研究这些质点在整个运动过程中的轨迹(称为迹线)以及运动要素(Kinematic Parameter)随时间的变化规律。
每个质点运动状况的总和就构成了整个液体的运动。
所以,这种方法与一般力学中研究质点与质点系运动的方法是一样的。
用拉格朗日法描述液体的运动时,运动坐标不是独立变量,设某质点在初始时刻t =t 0时的空间坐标为a 、b 、c (称为起始坐标),则它在任意时刻t 的运动坐标x 、y 、z 可表示为确定这个质点的起始坐标与时间变量的函数,即⎪⎭⎪⎬⎫===),,,(),,,(),,,(t c b a z z t c b a y y t c b a x x(3-1-1)变量a ,b ,c ,t 统称为拉格朗日变量。
显然,对于不同的质点,起始坐标a ,b ,c 是不同的。
根据式(3-1-1),将某质点运动坐标时间历程描绘出来就得到该质点的迹线(Trace)。