牵连速度

牵连加速度和相对加速度1.引言1.1 概述概述：牵连加速度和相对加速度是物理学中重要的概念，用于描述物体运动时的加速情况。

牵连加速度指的是物体在运动中发生的加速度变化，而相对加速度则描述了两个物体之间的相对运动时的加速度。

在物体运动中，加速度是描述物体加速或减速的物理量。

而牵连加速度则是指在物体运动的过程中，由于某种原因而导致物体加速度发生变化的情况。

这种变化可能是由于外力的作用、摩擦力的影响或者其他因素导致的。

相对加速度则是指两个物体之间的相对运动时的加速度，它描述了物体之间在相对运动中的速度变化情况。

当两个物体相对运动时，它们的相对加速度可以用于描述它们之间的运动关系和速度变化情况。

在本文中，我们将详细介绍牵连加速度和相对加速度的定义和概念，并且阐述它们的计算方法和关系。

我们还将讨论牵连加速度和相对加速度在物理学领域中的应用和意义，以及它们在实际问题中的重要性。

通过对牵连加速度和相对加速度的深入理解，我们可以更好地解释物体运动的加速度变化和相对运动的速度变化，从而为物理学的研究和应用提供更加准确和全面的描述模型。

同时，对于解决实际问题和优化物体运动过程也具有重要的指导意义。

接下来的章节将详细探讨牵连加速度和相对加速度的定义、计算方法以及它们之间的关系。

我们将重点介绍它们在实际问题中的应用案例，并分析其对解决实际问题和优化物体运动的意义和作用。

通过对这些内容的学习和理解，我们将能够更好地应用牵连加速度和相对加速度的概念和理论，为物体运动提供更加准确和全面的解释和分析。

1.2文章结构1.2 文章结构本文将分为三个部分来探讨牵连加速度和相对加速度的相关内容。

首先，在引言部分中会对牵连加速度和相对加速度的概念进行概述，并介绍文章的整体结构和目的。

接下来，在正文部分的第二节中，将详细讨论牵连加速度的定义、概念以及计算方法。

然后，在正文部分的第三节中，将同样讨论相对加速度的定义、概念以及计算方法。

最后，在结论部分中，将探讨牵连加速度和相对加速度之间的关系，并讨论它们的应用和意义。

va
α vb
【例题2】如图所示，纤绳以恒定速率v沿水平方向
通过定滑轮牵引小船靠岸，绳与水面夹角为θ时，则
船靠岸的速度是
，若使船匀速靠岸，则
纤绳的速度是
。（填：匀速、加速、减
速）
v
答案：变长
运动的合成和分解的应用 2.绳拉物牵连速度问题
【例题1】如图所示，汽车沿水平路面以恒定速度v
前进，则当拉绳与水平方向成θ角时，被吊起的物
体B的速度为vB=
，物体上升的运动是_____
(填“加速”、“减速”、“匀速”）
B
方法一：微元法
v物t
θ
v车t
cos v物 v物＝v车 cos
B A
B
A
重物M沿细杆竖直下滑，并通过绳带动小车 m沿斜面升高。则：当滑轮右侧的绳与竖直 方向成θ角，且重物下滑的速率为v时，小 车的速度为多少？
θ
v
• 两根光滑的杆互相垂直地固定在一起。上 面分别穿有一个小球。小球a、b间用一细 直棒相连如图。当细直棒与竖直杆夹角为α 时，求两小球实际速度之比va∶vb
v车
方法二：运动的合成与分解
绳拉物体或物体拉绳问题的主要思路： （1）物体的实际运动为合运动； （2）沿绳的运动为一个分运动； （3）垂直于绳的运动为另一个分运动。
方法二：运动的合成与分解
v绳
θ
v车
cos
v
v绳 v车
v物＝v绳＝v车 cos
变大，cos变小
v物变小, 减速下降
【例题3】光滑水平面上有A、B两个 物体，通过一根跨过定滑轮的轻绳 子相连，如图，它们的质量分别为 mA和mB，当水平力F拉着A且绳子 与水平面夹角为θA＝45O， θB＝ 30O时，A、B两物体的速度之比VA： VB应该是________

牵连角速度引言角速度是物体绕某个固定点旋转的速度，并且与旋转半径有关。

在物理学中，存在一种现象被称为牵连角速度，即当一个物体绕固定轴旋转时，由于与之相连的其他物体的牵连作用，在旋转过程中也会产生一定的角速度。

本文将探讨牵连角速度的原理、应用以及相关实验。

牵连角速度的原理当一个物体绕固定轴旋转时，如果与之相连的其他物体也同时产生旋转，那么相连物体的旋转速度即为牵连角速度。

可以通过以下实例来说明。

假设有一个长杆，在其中心位置固定一个轴，将长杆做旋转运动。

如果长杆两端均绑有质量较小的质点A和B，并且质点A离轴的距离大于质点B离轴的距离。

当长杆旋转时，轴会施加力矩在杆上，并使质点A的转速大于质点B的转速。

这是由于杆的角速度相同，而物体的线速度与转速成正比，质点A所受的线速度较大，因此其角速度也较大。

这就是牵连角速度的原理。

牵连角速度的应用牵连角速度在实际应用中有着广泛的应用。

以下是一些常见的应用场景。

汽车转弯在汽车转弯的过程中，车轮与地面之间存在着牵连角速度。

当车辆转弯时，由于车轮与地面之间的摩擦力，车轮会产生滑动，而滑动的速度与转速之间的比值即为牵连角速度。

牵连角速度的存在使得转弯过程更加平稳，并且能够提供更好的转弯性能。

旋转木马旋转木马是儿童游乐场中非常受欢迎的游乐设施之一。

当木马开始旋转时，木马上的座椅也会随之旋转。

由于座椅与木马轴之间存在牵连作用，座椅会产生自己的角速度。

这使得坐在座椅上的孩子们能够感受到旋转的乐趣，同时也保证了座椅的相对稳定性。

地球自转地球自转是地球围绕自己的轴旋转的运动。

在地球自转的过程中，由于地球上的大气、海洋和陆地与地球相连，它们也会受到地球自转的影响而产生牵连角速度。

这种牵连角速度的存在使得地球上各种自然现象如风、潮汐等能够发生，并对生态系统产生影响。

实验验证为了验证牵连角速度的存在，科学家们进行了一系列的实验。

旋转操场实验一项实验使用了一个旋转的操场和一些附着在操场上的质点。

相关名词：
1
点的合成运动：
2
绝对运动
3
相对运动
4
牵连运动
5
速度合成定理
亦称点的复合运动.质点简单运动的复合,即动点相对固定坐标系的运动、相对运动坐标系的运动以及运动坐 标系本身的运动三者存在关系,通过相对运动和运动坐标系的运动来求质点相对固定坐标系的运动称为运动的合成. 主要说明速度的合成关系和加速度的合成关系.从具有相对运动的二坐标系考察同一点的运动,必不相同.不妨设 其中一个坐标系为定系,另一个为动系。相对定系的速度(加速度)为绝对速度va(绝对加速度aa),相对动系的速度 (加速度)为相对速度vr(相对加速度ar);动系上动点瞬时重合点相对定系的速度(加速度)为牵连速度ve(牵连加速 度ae).
牵连速度
运动学中的基本物理量
目录
01 应用范畴：
03 相关名词：
02 单位：
牵连速度，又称动点的牵连速度，即指定瞬时动系上与动点相重合之点（牵连点）的速度。
应用范畴：
牵连运动是在运动学的中进行点的合成运动描述和计算的一个基本物理量，主要存在及应用于合成运动中的 速度合成定理。
单位：
牵连速度的单位和速度相同，在国际单位制的最基本单位是米每秒，国际符号是m/s，中文符号是米/秒。 常用单位：千米/小时，国际符号是km/h。 单位换算：1 m/s=3.6 km/h
动点相对定系的运动为绝对运动。Βιβλιοθήκη 动点相对动系的运动为相对运动。
动系相对定系的运动为牵连运动。
动点在某瞬时的绝对速度等于它在该瞬时的牵连速度与相对速度的矢量和。即动点的绝对速度可由牵连速度 和相对速度构成的平行四边形的对角线来确定，这个平行四边形称为速度平行四边形。
谢谢观看

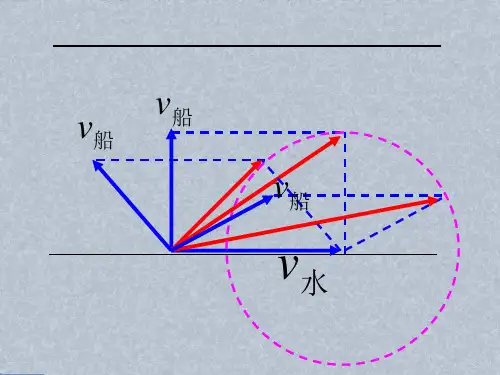
牵连速度牵连速度如图所示如图所示,,有一光滑的T 字形支架字形支架,,在它的竖直杆上套有一个质量为m 1的物体A ,用长为l 的不可伸长的细绳将A 悬挂在套于水平杆上的小环B 下,B 的质量m 2=m 1=m 开始时A 处于静止状态状态,,细绳处于竖直状态细绳处于竖直状态..今用水平恒力F =3mg 拉小环B ,使A 上升上升..求当拉至细绳与水平杆成3737°时°时°时,,A 的速度为多大的速度为多大? ?答案gl 58如图37所示，物块M 和m 用一不可伸长的轻绳通过定滑轮连接，m 放在倾角q =300的固定的光滑斜面上，而穿过竖直杆PQ 的物块M 可沿杆无摩擦地下滑，M=3m ，开始时将M 抬高到A 点，使细绳水平，此时OA 段的绳长为L=4.0m ，现将M 由静止开始下滑，求当M 下滑到3．0m 至B 点时的速度？（g=10m/s 2）解:为使小球能绕O ’点做完整的圆周运动，则小球在最高点D 对绳的拉力F 1应该大于或等于零，即有：d L V m mg D -£2○1根据机械能守恒定律可得：[])(c o s 212d L d mg mVD --=q ○2因为小球在最低点C 对绳的拉力F 2应该小于或等于7mg ，即有：，即有：mg mg d L V m mg F c -£-=-722○3 根据机械能守恒定律可得：[])(cos 212d L d mg mV c -+=q ○4 由○1○2○3○4式解得：qq cos 22cos 233+££+L d L 。

如图2-7-14所示，质量为m 的物体静放在水平光滑平台上，系在物体上的绳子跨过光滑的定滑轮由地面以速度v 0向右匀速走动的人拉着，设人从地面上且从平台的边缘开始向右行至绳和水平方向成3030°角处，在此过程中人所做的功为°角处，在此过程中人所做的功为°角处，在此过程中人所做的功为( ( )A.mv 02／2B.mv 02C.2mv 02／3D.3mv 02／8图37 如图所示，套在竖直细杆上的环A 由跨过定滑轮的不可伸长的轻绳与重物B 相连，由于B的质量较大，故在释放B 后，A 将沿杆上升当A 上升至环与定滑轮的连线处于水平位置时，其上升速度v A ≠0，这时B 的速度为v B ，则（），则（）A.v A ＞v B ＞0 B.v A =v BC.v A ＜v B D.vB =0 如图所示如图所示,,小船用绳索拉向岸边小船用绳索拉向岸边,,设船在水中运动时所受水的阻力不变设船在水中运动时所受水的阻力不变,,那么小船在匀速靠岸过程中过程中,,下面说法哪些是正确的下面说法哪些是正确的 （（ ））A.A.绳子的拉力绳子的拉力F 不断增大不断增大B. B. B.绳子的拉力绳子的拉力F 不变不变C.C.船所受的浮力不断减小船所受的浮力不断减小船所受的浮力不断减小D. D. D.船所受的浮力不断增大船所受的浮力不断增大船所受的浮力不断增大答案答案 AC AC江苏省扬州中学2010届高三综合练习如图所示，一根长为L 的轻杆OA ，O 端用铰链固定，另一端固定着一个小球A ，轻杆靠在一个质量为M 、高为h 的物块上．若物块与地面摩擦不计，则当物块以速度v 向右运动至杆与水平方向夹角为θ时，小球A 的线速度大小为（ A A ））A ．B B．．C ．D D．．hvL q 2sin h vL q2sin h vL q 2cos h vq cos。

（1）根据运动的独立性原理、合运动 与分运动等时性原理，如河水是静止
的则船以由A到B历时10min；由A到 D历时12.5min。
A
cos AB v1t1 10 4 37或 arccos 4
AD v1t2 12.5 5
5
（2）根据分运动、合运动等时性原理，
v2
BC t1
120 600
度为v2=3m/s, 河宽为d=100m. 2.(1)使小船渡河时间最短,小船朝什么方向开 行?渡河时间是多少? 到达对岸的什么位置？
(2)若水流的速度增大到v2′=4m/s,渡河时间是
多少?到达对岸的什么位置？
模型一：小船渡河问题
例2：小船在静水中的速度为v1=5m/s,水流的速
度为v2=3m/s, 河宽为d=100m. 3.(1)使小船渡河路程最短,小船朝什么方向开 行? 渡河时间是多少?
答：过河路程由实际运动轨迹
的方向决定，故最短路程为d。 d V船 V实际
条件：v水＜v船，且满足： cos
水
V水
船
模型一：小船渡河问题
例2：小船在静水中的速度为v1=5m/s,水流的速
度为v2=3m/s, 河宽为d=100m. 3.(1)使小船渡河路程最短,小船朝什么方向开 行? 渡河时间是多少?
运动时，系A,B的绳分别与水平方向成a、β角，
此时B物体的速度大小为
，方向如
何？
小船过河
如右图所示，若用v水表示水速，v船 v⊥ v实际
d
v船表示船速，则过河时间仅由
v水
v船的垂直于岸的分量v⊥决定，
即 ，t与 vvd水无关。
所以当v船垂直于岸时，过
V船
V实际
河所用时间最短，最短时间 d

而有 ４ Ｌ＝Ａ ｃ ｓ ， 边 同除 以 Ａｔ ｘ ｏＯ两 得 ： 一 ｃ 嘲 即 收 绳 速 率 Ｖ 一 ｃ ， 此 Ｏ ０ 因
船的速率为 ｖ 一 ｖ Ａ ０ －
．
的时机 ， 将这些精彩 的方法提供 给学生 可以获得 丰富 的
收 获 ： 生 可 以有 更 开 阔 的解 题 思 路 ， 师 可 以获 得 更 学 老 好的学 生评价 等等． 不过教师 在掌握 了某 个 问题 的多种
总结 ： 由于 教 材将 动 力 学 中的 能 量 问题 放 在 了运 动
合成和分解知识之后 ， 所以在 最初 涉及 牵连物体 速度分 解 问题 时学生并不能使 用该方 法， 不过 在 学习能量知识 后 ， 师 可 重 新 安 排 练 习该 问题 ， 引 导 学 生使 用该 方 教 并
法 解 题 ， 样 既 可 以 复 习 旧 知 识 ， 时 叉 可 以 练 习使 用 这 同
解 法 四 （ 导法 ） 求 ：
总结 ： 牵连 速 度 问题 是 指 物拉 绳 （ ） 绳 （ ） 物 杆 或 杆 拉 问题 ， 人 教 版 高 中物 理 实验 教 材 必 修 二 中 关 于速 度 矢 是
量 的合 成和 分 解 的典 型应 用 问题 ． 究 此 类 问题 的 目的 研
如 图 ３ 示 ， 勾 股 定 理 所 由
出 牵连 物 体 间速 度 大 小 的 关 系．
解法时 ， 如何寻 找恰 当的时机 ， 引导学 生独 立寻得 各种 不同的解题思路 和方法 呢？下面笔者谈谈具体的做法．
【 例题 】 如 图 １所 示 ， 人 用 绳 子 通 过 定 滑 轮 以 不
由于在人教版必修一 中 已经练 习使用过该方 法 ， 因
度 变 化 ｑ ／， ， Ａ Ｃ 可 近 似 看 作 是 一 直 角 三 角 形 ， ｔ Ｊｔ △ Ｂ ｌ ＇？ Ｉ ， 因

绝对速度,相对速度,牵连速度的关系《绝对速度：风驰电掣的追求》你知道吗？在这个世界上，有一种速度叫绝对速度。

就说短跑运动员吧，他们在赛道上全力冲刺，那一瞬间爆发出来的速度，就是绝对速度。

比如博尔特，他那飞一般的身影，让全世界都为之惊叹。

他的绝对速度，仿佛能突破时间和空间的限制。

在赛车场上，那些赛车呼啸而过，速度快得让人看不清。

车手们追求的，也是绝对速度。

他们不断地改进赛车，提升技术，就为了能在那一瞬间冲过终点线，成为绝对速度的王者。

想象一下，一只猎豹在草原上追捕猎物。

它瞬间爆发的速度，那就是绝对速度。

它必须足够快，才能在激烈的竞争中生存下来。

绝对速度，是一种极致的追求，是对自身潜能的不断挑战。

它让我们看到了人类和动物的无限可能。

《感受绝对速度》提起绝对速度，我就想起那次坐高铁的经历。

车一启动，速度越来越快，窗外的景色都变得模糊了。

那种感觉，就像是被一股强大的力量推着向前飞奔。

这就是绝对速度啊，又快又稳。

还有飞机起飞的时候，引擎轰鸣，速度不断提升，一下子就冲向蓝天。

那速度，真的让人惊叹不已。

在游乐场里，坐过山车也是一种体验绝对速度的方式。

风在耳边呼啸，心都提到了嗓子眼儿，那种刺激，就是绝对速度带来的。

绝对速度，它能让我们在短时间内去到很远的地方，也能给我们带来无与伦比的刺激和快乐。

《绝对速度的魅力》绝对速度，有着让人无法抗拒的魅力。

你看那些参加奥运会的运动员，为了那零点几秒的提升，付出了无数的汗水和努力。

他们追求的，就是在赛场上展现出惊人的绝对速度。

就像摩托车比赛，车手们在赛道上飞驰，引擎的轰鸣声震耳欲聋。

他们的目标就是以最快的速度冲过终点，那种激情和速度的结合，太吸引人了。

我曾经看过一场火箭发射，那火箭升空的速度，简直快得让人不敢相信。

这就是绝对速度的力量，带着人类的梦想冲向太空。

绝对速度，它不仅仅是快，更是一种突破，一种对未知的探索。

《生活中的绝对速度》在我们的生活中，也有很多绝对速度的例子。

运动学牵连速度相对速度绝对速度运动学是物理学中研究物体运动的学科，其中牵连速度、相对速度和绝对速度是运动学中常见的概念。

本文将对这三个概念进行解释和比较。

一、牵连速度牵连速度是指在同一直线上两个物体之间的速度差。

当两个物体在同一直线上运动时，它们的牵连速度可以通过一个物体相对于另一个物体的速度来计算。

具体而言，若物体A的速度为v1，物体B的速度为v2，则物体A相对于物体B的牵连速度为v1-v2，物体B相对于物体A的牵连速度为v2-v1。

牵连速度的正负表示相对运动的方向。

二、相对速度相对速度是指两个物体相对于彼此的速度。

当两个物体不在同一直线上运动时，它们的相对速度可以通过它们各自的速度的矢量和来计算。

具体而言，若物体A的速度为v1，物体B的速度为v2，则物体A相对于物体B的相对速度为v1-v2，物体B相对于物体A的相对速度为v2-v1。

相对速度的正负表示相对运动的方向。

相对速度的概念在实际生活中有很多应用。

例如，两辆车以不同的速度在同一方向行驶，它们之间的相对速度就是它们速度之差。

如果两辆车以相同的速度行驶，它们之间的相对速度就是零。

相对速度的概念还可以应用于飞机与地面之间的相对速度、船只在河流中的相对速度等。

三、绝对速度绝对速度是指物体相对于参考点的速度。

参考点可以是固定的地面，也可以是其他物体。

绝对速度与物体本身的运动状态有关，并且无论其他物体是否存在，绝对速度都是相对于参考点来计算的。

绝对速度的概念在物理学中有广泛的应用。

在工程领域，我们常常需要计算物体相对于地面的速度，例如飞机的空速、汽车的速度等。

在天文学中，我们需要计算天体相对于地球的速度，例如行星的速度、彗星的速度等。

绝对速度的概念还可以应用于机器人的运动控制、物体的轨迹分析等领域。

运动学中的牵连速度、相对速度和绝对速度是描述物体运动的重要概念。

牵连速度用于描述同一直线上两个物体之间的速度差，相对速度用于描述两个物体相对于彼此的速度，而绝对速度则是指物体相对于参考点的速度。

3一辆车通过一根跨过定滑轮的轻绳PQ 提升井中质量为m的物体，开始时，车 在A点,左右两侧绳都已绷紧并且是竖直 的,左侧绳长为H.提升时，车向左加速运 动，沿水平方向从A经过B驶向C.设A到 B的距离也为H，车过B点时速度为vB。 求车由A移到B的过程中,绳Q端的拉力 对物体做的功是多少?
4如图所示，跨过同一高度处的定滑轮的细线连接 着质量相同的物体A和B，A套在光滑水 平杆上， 定滑轮离水平杆的高度h=0．2 m，开始时让连着 A的细线与水平杆的夹角θ=37°，由静止释放B， 在运动过程中，A所获得的最大速度为多大?(设BБайду номын сангаас不会碰到水平杆，sin37°=0．6，sin 53°=0．8， 取g=10 m／s2)
1、一根长度为L的轻绳一端固定，另一端拴一 质量为m的小球，若在悬点O的正下方钉一小钉， 拉起小球至细绳水平位置时，由静止释放小球， 如图所示．当绳碰到小钉后，小球刚好能在以钉 子C为圆心的竖直面内做圆周运动．若不考虑细 绳碰钉子时的能量损失及空气阻力，求小钉的位 置C距悬点O的距离．
2、如图所示，物块M和m用一不可伸长的轻绳通过 定滑轮连接，m放在倾角 =300的固定的光滑斜面 上，而穿过竖直杆PQ的物块M可沿杆无摩擦地下滑， M=3m，开始时将M抬高到A点，使细绳水平，此时 OA段的绳长为L=4.0m，现将M由静止开始下滑，求 当M下滑到3m至B点时的速度？（g=10m/s2）
5如图，在竖直平面内有一半径为R 的半圆形圆柱截面，用轻质不可伸长 的细绳连接的A、B两球，悬挂在圆柱 面边缘两侧，A球质量为B球质量的2 倍，现将A球从圆柱边缘处由静止释放， 已知A始终不离开球面，且细绳足够长， 圆柱固定．若不计一切摩擦．求：A球 沿圆柱截面滑至最低点时速度的大小

牵连速度（两物体交点速度）分解专题两个各种形状物体在运动过程中，其交点速度问题一直以来比较棘手推荐几个有梯度的题帮助理解：分析：交点的速度实际是滑AC 斜向上的，可以认为是，MN 棒上的P 点一方向沿自己本来的速度向左运动，同时再沿自身的杆向上运动，两个合运动即为交点的运动。

所以，交点的速度应该为：0v 1.39/cos30m s分析：先假设右边方框不动，求一下交点的速度V 1，再假设左边方框不动，求一下交点的速度V 2，二者一起动的话，就是两个速度的合速度。

先假设两个方框原来是重合的，而且右边方框静止不动，左侧方框向左匀速的速度为V ，交点实际速度是沿着图中1的方向运动，可以看作在沿自身的速度2的方向向左以速度V 运动，同时沿着自身杆的方向3运动到交点位置，所以速度V 1应该为22v 。

同理，如果左框不动的话，右框速度为2V ，可求出交点的V 2速度为222v 。

所以二者一起运动的话，是两个的合速度，即102v同理，再看我们最近刚作的这一道题目：分析：先假设右框不动，左框以速度V 向右运动，交点沿右框上移。

如图交点处速度的合成关系放大一些如下图右框不动情况下，交点逐渐升高的情况下，交点的实际速度是V 1，可以看作左框在沿着自身的速度V 向右运动，同时沿自身的圆弧切线方向2运动，由于1、2的对称性，设V 1与水平方向成θ角，由三形关系可得，12cos V v θ=12cos v V θ=，同理，左框不动可框动时，此速度也是也速度V 1大小相等、左右对称的速度。

二者一起运动的时候，合速度为1sin 2sin tan cos v V v θθθθ==，方向竖直向上，因为θ角是越来越小，所以交点越过最高点前，交点的合速度是向上，逐渐减小。

所以此题答案是向上，向减小后增大。

同理，如果两个圆框的速度不相等，同理可以计算。

并且此方向可以推广到其它题。

总结，交点的速度可看作：在沿自身的实际速度方向运动，同时沿自身杆的方向运动到交点位置此为个人拙见，大家共同讨论，看看是否还有不同的例子，可以更进一步完善。

相对速度：这个好理解，物理里面的速度定义永远都需要参照系，把B物体假定为不动，A物体离B位移的变化率，就是A相对于B的速度。
绝对速度：我们平常研究物理运动的时候，一定要把一个大的参考系当成是不动的，所有研究都不会超越这个参考系的范围。相对于这个大的参考系的速度就是绝对速度。由此可见，绝对速度也是一种相对速度，只不过参考系很大。
牵连速度：如果已经把B定义为参考系，A相对于B有速度，同时B相对于某个大参考系C也有速度，我们就把B相对于C（也就是参考系相对于更大参考系的速度）定义为牵连速度，叫参考系B的牵连速度。由此可见，牵连速A的绝对速度=A相对于B的相对速度+B的牵连速度
上面说的太抽象，举个例子比较好。比如车B在公路C上走，人A在车里走。不向窗外看的话，人会感觉车不动，只有自己在走，这个就是人相对于车的速度，是人的相对速度；公路（地面）包含了我们研究的所有东西（车、人），它是我们认为铁定不动的，因此车在公路上走，相对于公路的速度就是牵连速度；如果车外的观察者看车内的人，能看到人整个相对于地面的速度，这就是人的绝对速度。我们也知道，假如车子15m/s在走（牵连速度），人相对于车在车内走1m/s，方向相同的话人实际上速度是15+1=16m/s，这就是绝对速度=相对速度+牵连速度。

运 动 学一、知识点击1．直线运动和曲线运动⑴匀变速直线运动：匀变速直线运动包括匀加速直线运动和匀减速直线运动两种情况，它的特点是加速度a=恒量，并与速度υ在同一直线上．匀变速运动的基本公式为：0at υυ=+ ①2012s t at υ=+ ② ⑵匀变速曲线运动：匀变速曲线运动的特点是a=恒量，但与速度υ的方向不在同一直线上，如斜抛运动，研究斜抛运动可以有多种方法，既可以将它看成是水平方向的匀速运动和竖直方向的（上或下）抛运动的合成；也可以看做是抛出方向的匀速运动和一个自由落体运动的合成．⑶匀速圆周运动：匀速圆周运动的特点是a 与υ的大小为恒量，但它们的方向无时无刻不在改变，它是一种特殊的曲线运动，但却是研究曲线运动的基础，一般曲线运动的任何一个位置，都可以作为一个瞬时的圆周运动来研究。

我们经常将圆周运动分解成法向和切向两个方向来研究，法向加速度22n a R R υω==，对于匀速圆周运动，其切向的加速度为零，如果是变速圆周运动，那么它在切向上也有加速度i a ．此时它的合加速度是：n i a a a =+ 。

2．相对运动：在大多数情况下，我们都习惯于以地面作为参照物，但在某些场合，我们选择其他一些相对地面有速度的物体作为参照物，这样会给解决问题带来方便，所以相对运动就是研究物体对于不同参考系的运动以及它们之间的联系，比如A 物体相对于地面的速度为A υ地，如果取另一个相对地面有速度υB 地的B 物体作参照物，那么A 物体相对B 物体的速度为：AB A B υυυ=+ 地地或AB A B υυυ=-地地通常把物体相对“固定”参考系的速度称为绝对速度，把相对于“运动”参考系的速度称为相对速度，而把运动参考系相对固定参考系的速度称为牵连速度，所以上式我们可以表述为“相对速度等于绝对速度和牵连速度之差”．速度的合成必须用平行四边形定则进行计算．3．刚体的平动和转动刚体：刚体是指在任何条件下，形状和大小不发生变化的物体。

2023年1月第4期Jan. 2023No.4教育教学论坛EDUCATION AND TEACHING FORUM浅析“理论力学”中的牵连速度与牵连加速度王沿朝，谢惠祥，郭剑峰，杜海霞（火箭军工程大学 基础部，陕西 西安 710025）［摘 要］ “理论力学”是工科专业重要的专业基础课程，而点的加速度合成定理是其重点及难点内容之一。

针对学员在学习“理论力学”中点的加速度合成定理中对牵连速度和牵连加速度概念理解及分析中存在的难点与疑惑，从基本定义出发并基于具体案例，阐述了牵连速度的导数与牵连加速度的物理意义及其概念上的差异，厘清了牵连运动含转动时牵连速度与牵连加速度之间的关系，明确了牵连点随动点发生改变而导致的牵连速度的变化对牵连速度导数的影响，使学员更好地理解和掌握点的加速度合成定理的内容。

［关键词］ 理论力学；牵连速度；牵连加速度；加速度合成定理；求导［基金项目］ 2022年度火箭军工程大学教育改革项目“基于OBE理念下的理论力学教学改革与探索”（HJJKTB2021028）［作者简介］ 王沿朝（1991—），男，湖北应城人，博士，火箭军工程大学基础部讲师，主要从事结构抗震与减震、工程力学研究；谢惠祥（1985—），男，广西贵港人，博士，火箭军工程大学基础部讲师，主要从事智能机械与数字化设计研究；郭剑锋（1981—），男，湖南桃源人，硕士，火箭军工程大学基础部副教授，主要从事工程力学研究。

［中图分类号］ G642.41 ［文献标识码］ A ［文章编号］ 1674-9324（2023）04-0073-04 ［收稿日期］ 2022-01-24“理论力学”是大学工科专业非常重要的专业基础课程，其架起了大学基础课与专业课之间的桥梁［1-3］。

“理论力学”主要研究的是物体机械运动的一般规律，其内容包含静力学、运动学及动力学三个部分［4-5］。

点的加速度合成定理是运动学篇章中的重点及难点内容之一，也是后续动力学内容的基础。

牵连速度的名词解释牵连速度是一个相对较为抽象和复杂的概念，它常常在各个领域中被提及和讨论，比如物理、社会科学、心理学等。

虽然没有一个固定的定义，但我们可以尝试解释并理解这个概念。

1. 牵连速度的物理解释在物理学中，牵连速度通常指的是物体的运动速度或变化速度。

它可以用来描述物体在空间中的移动情况，或者描述物体在运动过程中某个属性（如温度、压力等）的变化速度。

牵连速度通常以单位时间内物体所经过的距离或属性发生的变化量来表示。

举例来说，当我们谈论车辆的速度时，我们可以使用牵连速度来描述车辆在单位时间内行驶的距离。

同样地，当我们研究物体的温度变化时，我们可以使用牵连速度来表达单位时间内温度的变化量。

2. 牵连速度的社会科学解释在社会科学领域，牵连速度常常涉及到信息传播、社会变迁和技术发展等方面的现象。

它可以指社会中信息传播的速度或社会变迁的迅猛程度。

例如，在当代社会中，信息传播速度的快慢对个体和社会都产生了极大的影响。

互联网和社交媒体的普及使得信息传播变得更为迅捷和广泛。

一条消息可以在短时间内以指数级速度传播开来，令人感叹不已。

牵连速度的快慢不仅影响了信息的传播效果，也对个体和社会带来了各种政治、经济和文化的变化。

3. 牵连速度的心理学解释在心理学中，牵连速度与人们的思维过程和认知能力有关。

它可以指一个人处理信息或解决问题的速度。

牵连速度在认知心理学中也常被称为反应时间，是指从接受某个刺激到做出相应反应所需要的时间。

例如，在认知心理学的实验中，研究者会通过观察被试者对特定刺激的反应来推断他们的认知能力和信息处理速度。

反应时间的长短可以反映出一个人在特定任务中的牵连速度，以及其在认知加工上的效率。

总结：牵连速度作为一个概念，有不同的解释和应用。

在物理学中，它可以表示物体运动的速度和变化的速度；在社会科学中，它涉及信息传播和社会变迁的速度；在心理学中，它表示人们处理信息和解决问题的速度。

牵连速度的深入研究有助于我们更好地理解各个领域中的相关现象，并能够应用于实际问题的解决和决策-making。

动点的牵连速度一、引言在相对运动的研究中，动点的牵连速度是一个重要的概念。

牵连速度是指动点相对于固定参考系的速度。

它反映了物体在运动过程中，相对于参考系的位置和方向的变化。

牵连速度在许多领域都有广泛的应用，如物理学、工程学、天文学等。

本文将详细介绍牵连速度的定义、性质、计算方法以及应用领域。

二、牵连速度的定义与性质1.定义牵连速度是指动点相对于固定参考系的速度。

它是矢量，既有大小又有方向。

在二维空间中，牵连速度的大小表示动点在参考系中的位移，方向表示动点的运动方向。

在三维空间中，牵连速度的大小和方向分别表示动点的三维位移和运动方向。

2.性质（1）相对性：牵连速度的大小和方向会随着参考系的改变而改变。

同一动点相对于不同的参考系有不同的牵连速度。

（2）方向性：牵连速度的方向始终与动点的运动方向一致，反映了动点的运动状态。

（3）独立性：牵连速度的大小和方向不受其他物体运动状态的影响，仅与动点自身的运动状态有关。

三、牵连速度的计算计算牵连速度需要确定动点和参考系的位置矢量，然后进行速度的矢量运算。

具体步骤如下：1.确定动点和参考系的位置矢量：在二维空间中，设动点的位置矢量为r(x, y)，参考系的位置矢量为 R(X, Y)。

在三维空间中，设动点的位置矢量为 r(x, y, z)，参考系的位置矢量为 R(X, Y, Z)。

2.计算动点和参考系的相对位置矢量：在二维空间中，相对位置矢量为Δr(Δx, Δy) = r(x, y) - R(X, Y)。

在三维空间中，相对位置矢量为Δr(Δx, Δy, Δz) = r(x, y, z) - R(X, Y, Z)。

3.计算相对位置矢量的时间导数：根据相对运动方程，可以得到相对位置矢量的时间导数为 dr/dt = v。

其中 v 是动点的速度矢量。

4.计算牵连速度：在二维空间中，牵连速度的大小为|v| = |dr/dt| = |v|。

在三维空间中，牵连速度的大小和方向分别为 |v| 和θ，其中θ是相对位置矢量和时间导数的夹角。

精品
【例1】如图所示，纤绳以恒定速率v沿水平方向通
过定滑轮牵引小船靠岸，绳与水面夹角为θ时，则船
靠岸的速度是
，若使船匀速靠岸，则纤
绳的速度是
。（填：匀速、加速、减速）
v
精品
v
v1Βιβλιοθήκη V合v2人拉船产生了两个效果，相当于有两个分运 动，一个是使连接船的绳子的运动，由于绳子不 可伸长所以，人拉绳的快慢与绳缩短的快慢相同； 另一个效果是使θ变大，这个效果相当于按住滑 轮O点不动，使绳头绕滑轮O点做圆周运动，且这 两个分运动互不影响。拉绳的分运动不会改变θ 角的大小，而按住O点时绕O点转动的分运动又不 会使绳变短，符合独立性原理。
精品
【例题2】如图所示，汽车沿水平路面以恒定速度v
向右前进，则当拉绳与水平方向成θ角时，被吊起
的物体B的速度为vB=
，物体下降的运动是
_____(填“加速”、“减速”、“匀速”）
B
精品
v绳
θ
v车
cos
v
v绳 v车
v物 ＝ v绳 ＝ v车cos
变大co， s变小
v精物品变小,减速下降
• 【例题3】两根光滑的 杆互相垂直地固定在一起。 上面分别穿有一个小球。小球a、b间用一细直棒 相连如图。当细直棒与竖直杆夹角为α时，求两小 球实际速度之比va∶vb
（A）大小和方向均不变 （B）大小不变，方向改变 （C）大小改变，方向不变 （D）大小和方向均改变
精品
va
α vb
精品
练习：光滑水平面上有A、B两个物体，
通过一根跨过定滑轮的轻绳子相连，如
图，它们的质量分别为mA和mB，当水平 力F拉着A且绳子与水平面夹角为θA＝ 45O， θB＝30O时，A、B两物体的速度 之比VA：VB应该是________