当前位置：文档之家 › 第四节 反常积分 无穷限广义积分 无界函数的广义积分 习题 例题小结

第四节 反常积分 无穷限广义积分 无界函数的广义积分 习题 例题小结

  • 格式：ppt
  • 大小：204.50 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

高等数学课件5第四节 反常积分ppt

高等数学课件5第四节 反常积分ppt

lim
t b
t a
f
(
x
)
dx
b
a
f (x) 在 [a , b) 上的反常积分(或瑕积分).
这时称反常积分
收敛;
否则, 称反常积分 发散.
定义6. 设函数 f ( x)在[a, b]上除点c (a c b)外连续,
点 c 为f (x)的瑕点.
若 瑕 积 分ac
f
(
解:
原式
1 p
0
td(e
pt
)
1 p
([te
pt
]0
e
0
pt dt )
a
udv
[uv]a
a
vdu
1 p
( lim te t
pt
0
[
1 p
e
pt
]0
)
0
1 p2
( lim e
t
pt
1)
1 p2
.
定义2. 设 f ( x)在(, b)上连续.
b
f
( x) dx
lim
t
tb
f
( x) dx
若极限存在,则称无穷限积分
2
1)3
]13
1
1
lim 3( x 1)3+ 3 3 3 4 lim 3( x 1)3
x1
x1
3(1 3 4 ).
例12.
讨
论
反
常
积
分
1 1
dx x2
的
收
敛
性.
解:
lim
x0
1 x2
,
x
0是
1 x2
的瑕点.

高等数学@5-4反常积分

高等数学@5-4反常积分

( x)dx
发散
.
y f (x)
s
a
b
x
b
定义
b
f ( x)dx lim f ( x)dx .

a a
右端极限存在,
则称 反 广常 义积分
b

f
( x)dx
收敛
,
否则
,
则称
b

f
( x)dx
发散
.
2

f ( x)dx
定义
0
f ( x)dx
F () lim F (x) ; F () lim F (x)
x
x
则有类似牛 – 莱公式的计算表达式 :

a f (x) dx F (x)
F () F (a)
b
f (x) dx F (x)

f (x) dx F (x)
F (b) F () F () F ()
(a 0)
解.
x
3a 是
x 3a2
x
2
的无穷间断点
.
3a x dx
0
3a2 x2

( 3a)
3a2 x2
0
(0 3a) 3a . #
上限 (
3 a)
代入的含义是
lim
x( 3 a)

3a2 x2 .
13
例6.
1 1 1 x
解:
[ arctan x ]|0

[ arctan x ]|



0 22
思考:
分析:
原积分发散 !

第四节 反常积分

第四节 反常积分

f ( x) dx lim
f ( x ) dx a a
a
v.p. f ( x) dx (c 为瑕点, a c b)
a
c b lim f ( x ) dx f ( x ) dx c a 0
注意: 主值意义下反常积分存在不等于一般意义下反


Biblioteka x 1 x2
dx lim
A
x 1 x
2
A A
dx 0
解: 不正确 因为
x 1 x
2
dx lim
2 b
a a b

b
x 1 x2
dx lim
b
1 2 1 x2
a a b
d 1 x 2
lim 1 x lim 1 b 2 lim 1 a 2 a a a b
例9 解
计算广义积分

0
dx . 3 x( x 1)
此题为混合型广义积分, 积分上限为 ,
下限 x 0 为被积函数的瑕点. 令 x t , 则 x t 2 , x 0 时 t 0, x 时
t , 于是 dx 2 tdt dt . 2 0 x( x 1)3 0 t (t 2 1)3 / 2 0 (t 2 1)3 / 2

1 1 x2 0 x2 1 x2
1
dt
1
d( x 1 ) x 2
0 ( x 1)2 x
dt 2 t 2 (2) 当一题同时含两类反常积分时, 应划分积分区间,
0
分别讨论每一区间上的反常积分.
(3) 有时需考虑主值意义下的反常积分. 其定义为

反常积分

反常积分


1 x
b 1
y

1 x2
A
1b

lim 1 b

1 b


1
2
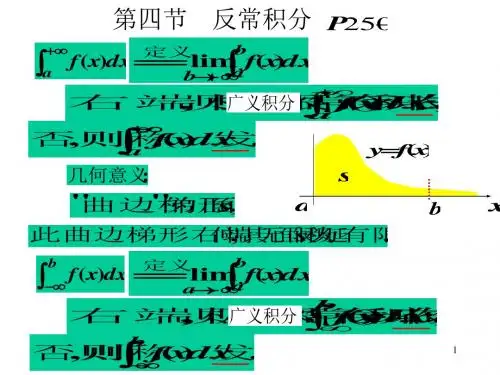
定义1. 设 f (x)C[a, ), 取b a, 若
存在 , 则称此极限为 f (x) 的无穷限反常积分, 记作
这时称反常积分
收敛 ; 如果上述极限不存在,
就称反常积分
发散 .
类似地 , 若 f (x) C (, b], 则定义
若极限
存在 , 则称此极限为函
数 f (x) 在 [a , b] 上的反常积分, 记作
这时称反常积分
收敛 ; 如果上述极限不存在,
就称反常积分
发散 .
类似地 , 若 f (x) C[a, b), 而在 b 的左邻域内无界,
则定义
12
而在点 c 的
邻域内无界 , 则定义
c
b
a f (x) dx c f (x) dx
二、无界函数的反常积分
引例:曲线
与 x 轴, y 轴和直线
开口曲边梯形的面积 可记作
y
所围成的
其含义可理解为
A lim 0
1 dx

lim 2 x 0
x
1

lim 2(1 ) 2
0
y 1 x
A
0
x
11
定义2. 设 f (x) C (a, b], 而在点 a 的右邻域内无界,
1 0
1 dx 。 1 x2
y
y 1 1 x2
解：∵ lim 1 ， x1 1 x2
(0, 1)
o ∴ 1
1
1

第四节 反常积分

第四节 反常积分
0 +∞
f ( x )dx 都收敛，则称
+∞
上述两反常积分之和为函数 f ( x ) 在无穷区间
( −∞ ,+∞ ) 上的反常积分，记作 ∫− ∞ f ( x )dx .
∫−∞ f ( x )dx = ∫−∞ f ( x )dx + ∫0
= lim f ( x )dx + lim ∫0 ∫ a a → −∞ b→ +∞
高等数学
17/17
1 1 1 Q e ⋅ x = 1− s ⋅ x < 1− s , x e x 而 1 − s < 1, 根据比较审敛法 2, I1 收敛 .
−x s −1 s +1 x ( 2) Q lim x 2 ⋅ ( e − x x s −1 ) = lim x = 0, x → +∞ x → +∞ e
+∞
f ( x )dx .
b b→ +∞
∫a
+∞
f ( x )dx = lim ∫a f ( x )dx
当极限存在时，称反常积分收敛；当极限不存在 时，称反常积分发散.
高等数学
3/17
类似地，设函数 f ( x ) 在区间 ( −∞ , b] 上连续，取
a < b ，如果极限 lim
b
f ( x )dx 存在，则称此极 ∫ a a → −∞
b
限 为函数 f ( x ) 在 无穷区间 ( −∞ , b] 上 的反 常积 分，记作 ∫− ∞ f ( x )dx .
∫−∞ f ( x )dx
b
= lim
f ( x )dx ∫ a a → −∞
b
当极限存在时，称反常积分收敛；当极限不存在 时，称反常积分发散.

反常积分法课件

反常积分法课件

3、
0
x ne xdx（
n 为自然数
）；4、
2 dx 0 (1 x)2
；
5 、 2 xdx ； 1 x1
6 、
x ln x 0 (1 x 2 )2
dx
；
7 、
1
ln
n
xdx
.
0
三 、 求 当 k 为何值时
， 广 义 积 分 b dx a (x a)k
(b a)
收 敛 ？ 又 k 为何值时 ， 这 广 义 积 分 发 散 ？
的瑕点是哪几点？
01
02
思考题解答
1
ln
x
0
x
dx 1
积分
x0,可能x 的 瑕1 点是
lim lnx lim1 1, x1
x014x 1 x1 x
03
的瑕1点l是nx dx
0 x1
x0.
不是瑕点,
练习题
一、填空题：
1、广义积分 dx 当_______时收敛；当______ 时
1 xp 发散；
0 1x2
6、 广 义 积 分x f(t)d的 t 几 何 意 义 是 ______________
________________________.
二、判别下列各广义积分的收敛性，如果收敛，则计
算广义积分的值：
1、 e pt cosh tdt 0
( p 1) ； 2、 dx
；
x2 2x 2
1
因此当q 1时反常积分收敛，其值为 1 ； 1q
当q 1时反常积分发散.
例6 计算反常积分
2 dx .
1 x ln x
2
1
dx x ln x

广义反常积分简单提

广义反常积分简单提

a
dx
a
lim
dx
0 a2 x2 0 0 a2x2
l im 0arcsaxina0 l im 0arcas ain0
2
.
例 6证 明 广 义 积 分 01x1qd当 xq1时 收 敛 ， 当
q1时 发 散 .
证 (1)q1,
11
0 x q
dx
1
0
1 x
dx
lnx10
,
(2)q1,
1
0
1 xq
1
dx x2
.
解
dx 1 x2
0 dx 1 x2
dx 0 1 x2
al ima011x2dxbl im0b11x2dx
al im arctxa 0 anbl im arctxab0n
al im arctaanbl im arctban22.
例2
计算广义积分
2
1 x2
c
b
l i0a m f(x )d x l i0c m f(x )dx
否 则 ， 就 称 广 义 积 分 a b f ( x ) d 发 散 . x
定义中C为瑕点，以上积分称为瑕积分.
a dx
例5
计算广义积分 0
a2x2
(a0).
解
lim 1 , xa0 a2x2
x a 为 被 积 函 数 的 无 穷 间 断 点 .
第四节 广义（反常）积分
• 一、无穷限的广义积分 • 二、无界函数的广义积分 • 三、小结
一、无穷限的广义积分
定义 1 设函数f (x)在区间[a,)上连续，取
ba，如果极限lim b b a
f
(x)dx存在，则称此极

5(4)反常积分

5(4)反常积分

反常积分
注 为了方便起见, 规定:
f ( x) C(a, b], 如a为瑕点, F( x) f ( x),
由N—L公式, 则反常积分
b
a f ( x)dx F (b) F (a ) F(b)
lim F( x)
xa
[F
(
x
)]
b a
f ( x) C[a, b),如b为瑕点,
边梯形的面积 可记作
A
dx 1 x2
其含义可理解为
A
lim
b
b 1
dx x2

lim b

1 x
b 1

lim 1 b

1 b


1
y

1 x2
A
1b
7
机动 目录 上页 下页 返回 结束
反常积分
定义1 (1) 设f ( x)在[a,)上连续, 取t a,

2

lim cos 1 cos
x
x
2
1.
13
反常积分
例
讨论积分

sin
xdx的敛散性.

解 考虑 由于被积函数为奇函数,
积分区间又为对称区间, 因而

sin xdx 0

由定义可知

sin xdx

[
cos
x
]

lim cos x lim cos x
dx
dx
1
4. 当 x 为何值时，函数 I x x tet2 dt有极值。 0 解 Ix xex2 令 Ix 0 得唯一驻点 x 0 当x 0时I x 0, 当x 0时I x 0, 故 x 0 为函数 I x的惟一 的极值点（极小值点）。

高等数学第四节反常积分-精品文档

高等数学第四节反常积分-精品文档
2. ( 1 0 ) ( 0 1 )
dx arctan x 1 x2

. 2 2
3

(k0 ) 例 2 .I x dx e sin
0
kx
kx 1 e cos x

D ekx
第四节 反常积分
P 250
a

f (x)dx lim ) dx . f(x
a b


定义
b
右端极限存在 , 则称 反常积分 ( x ) dx 收敛 , 广义积分 f
a
否则 ,则称 ( x ) dx 发散 . f
a
y f( x )
b 此曲边梯形右端无限延 伸 ,其面积 s为有限值 .


y f( x )
a
y f( x )
s b s
s
b

f(x )dx
x
s

f(x )dx
2
a
b
x
例 1 .
e
x
0 x dx edx ex dx 0


x0 x e e 0
0 x x 0 e lim e lim e e x x
a 0 3
0
( 0 3 a ) 3 a .#
2 2 上限 a 代入的含义 lim 3 a x . 3 x 0 3
9
a

1 1 例 6 . dx ln x 0 . x 1 1
1
错 !
1
忽视了 x0是被积函数的无穷间 点 .

高数 反常积分 知识点与例题精讲

高数 反常积分 知识点与例题精讲

例1
计算广义积分

2
1 x2
sin
1 x
dx.
解

2
1 x2
sin
1 x
dx


2

sin
1 x
d

1 x

lim b
b
2
sin
1 x
d

1 x


lim
b
cos
1b x 2


lim
b
cos
1 b

cos
2

1.
例2
计算广义积分

1
dx x
2
.
解法1:
dx 1 x2

0
dx 1 x2

dx 0 1 x2
lim a
0
a1
1 x2
dx

lim
b
b1 0 1 x2 dx

lim arctan
1 p

0

e
pt
d
t
机动 目录 上页 下页 返回 结束
二、无界函数的广义积分
引例:曲线
与 x 轴, y 轴和直线
开口曲边梯形的面积 可记作
所围成的
其含义可理解为
A

lim
0
1
dx x

lim
0
2
1 x

lim 2(1 ) 2
0

机动 目录 上页 下页 返回 结束
注意: 对反常积分, 只有在收敛的条件下才能使用 “偶倍奇零” 的性质否, 则会出现错误 .

5-4 反常积分

5-4 反常积分

b
2
sin
1 x
d
1 x
lim
b
cos
1 x
b 2
blimcos
1 b
cos
2
1.
如果 F ( x)是 f ( x) 的原函数, 引入记号
F() lim F( x) ; F() lim F( x)
x
x
则这类积分有类似的基本积分公式 :
a f ( x)d x F ( x) a F() F(a)
第四节 广义积分
积分区间有限 常义积分
被积函数有界 推广
无穷区间上的广义积分 常义积分的极限
无界函数的广义积分
一、无穷区间上的广义积分
定义 1 设函数 f ( x)在区间[a,)上连续，取
b
a
，如果极限
lim
b
b
a
f
(
x
)dx
存在，则称此极
限为函数 f ( x) 在无穷区间[a,) 上的广义积
分，记作 a

f ( x)d x F(b) F(c ) F(c ) F(a) a
例5 计算广义积分 a dx 0 a2 x2
解 lim 1 , xa0 a2 x2
(a 0).
x a 为被积函数的无穷间断点.
a dx
t
lim
dx
0 a2 x2 ta 0 a2 x2
lim
t a
b p
p
e
ap
p
,
,
p0 p0
即当 p 0时收敛，当p 0 时发散.
二. 无界函数的广义积分
曲线 y 1 与x轴,y轴和直线 x 1所围成的
x
开口曲边梯形的面积 可记作

反常积分

反常积分

a

f ( x )dx lim a f ( x )dx

当极限存在时，称反常积分收敛；当极限不存在 时，称反常积分发散．此时 a
f ( x )dx无意义．
类似地，设函数 f ( x ) 在区间 ( , b]上连续，取
a b ，如果极限 lim a f ( x )dx 存在，则称此极
第四Байду номын сангаас 反常积分
一、无穷限的反常积分
定义 1 设函数 f ( x ) 在区间[a , ) 上连续，取
b b
b a ，如果极限 lim a f ( x )dx 存在，则称此极
限为函数 f ( x ) 在无穷区间 [a , ) 上的反常积 分，记作 a

f ( x )dx.
b b
a
b
限为函数 f ( x ) 在无穷区间 ( , b] 上的反常积 分，记作 f ( x )dx .
b
f ( x )dx
b
lim a f ( x )dx
a
b
当极限存在时，称反常积分收敛；当极限不存在 时，称反常积分发散．
设函数 f ( x ) 在区间 ( , ) 上连续,如果 广义积分 f ( x )dx 和 0
a f ( x )dx lim0 a
b
b
f ( x )dx
当极限存在时，称反常积分收敛；当极限不存在 时，称反常积分发散.
类似地，设函数 f ( x ) 在区间[a , b )上连续， 而在点 b 的左邻域内无界.取 0 ，如果极限
0
lim a
b
f ( x )dx 存在，则称此极限为函数 f ( x )
1 1 dx dx ln x 1 , (1) p 1, 1 证 1 xp x , p 1 1 p 1 x ( 2) p 1, dx p 1 , p1 1 x 1 p 1 p1 1 因此当 p 1 时广义积分收敛，其值为 ； p1 当 p 1 时广义积分发散.

第四节 反常积分 无穷限广义积分 无界函数的广义积分

第四节 反常积分 无穷限广义积分 无界函数的广义积分

例 3 证明广义积分 当 p 1 时发散.

1 x
p
1
dx 当 p 1 时收敛，
证 (1) p 1,1

1 x
dx p
1

1 x
dx ln x 1 ,

, p 1 1 x ( 2) p 1, dx p 1 , p1 1 x 1 p 1 p1 1 因此当 p 1 时广义积分收敛，其值为 ； p1 当 p 1 时广义积分发散.
即当 p 0 时收敛，当 p 0 时发散.
二、无界函数的广义积分
定义 2 设函数 f ( x ) 在区间( a , b] 上连续，而在 点 a 的 右 邻 域 内 无 界 ． 取 0 ， 如 果 极 限
0 a
lim
b
f ( x )dx 存在，则称此极限为函数 f ( x )
2
sin
1 x
dx .


1 x
2
sin 2
b
1 x
dx 2 sin


1 1 d x x
b
lim
b

2
1 1 1 sin d lim cos b x2 x x

1 lim cos cos 1. b b 2
a
f ( x )dx .
a

f ( x )dx lim
a f ( x )dx b
b
当极限存在时，称广义积分收敛；当极限不存在 时，称广义积分发散.
类似地，设函数 f ( x ) 在区间( , b] 上连续，取

反常积分法课件省名师优质课赛课获奖课件市赛课一等奖课件

反常积分法课件省名师优质课赛课获奖课件市赛课一等奖课件
当q 1时反常积分发散.
2 dx
例6
计算反常积分
1
. x ln x
解
2 dx
1 x ln x
lim t 1
2 t
dx x ln x
lim 2 d(ln x) lim ln(ln x) 2
t1 t ln x
t 1
t
lim ln(ln 2) ln(ln t) t 1
. 故原反常积分发散.
类似地，设函数 f ( x)在区间[a,b)上连续，
t
点b
为
f
(
x)的瑕点.若极限
lim
t b
a f ( x)dx 存在，
则称此极限为函数 f ( x)在区间[a,b)上的反常
积分，记作
b
t
a
f ( x)dx lim t b
a f ( x)dx .
当极限存在时，称反常积分收敛；当极限不存在
2
2
.
例2
计算反常积分
2
1 x2
sin
1 x
dx.
解
2
1 x2
sin
1 x
dx
2
sin
1 x
d
1 x
lim b
b
2
sin
1 x
d
1 x
lim
b
cos
1 x
b 2
lim
b
cos
1 b
cos
2
1.
例3
证明反常积分 1
1 xp
dx
当
p
1时收敛，
当 p 1时发散.
1 xp 发散；
2、广义积分 1 dx 当_______时收敛；当_______时发

反常积分

反常积分

1 y 2 x A
1
b
1 lim 1 1 b b
定义1. 设 f ( x) C [a , ) , 取 b a , 若
存在 , 则称此极限为 f (x) 的无穷限反常积分, 记作
这时称反常积分 就称反常积分
收敛 ; 如果上述极限不存在, 发散 .
0
x
定义2. 设 f ( x) C (a , b] , 而在点 a 的右邻域内无界,
若极限 存在 , 则称此极限为函
数 f (x) 在 [a , b] 上的反常积分, 记作
这时称反常积分 就称反常积分
收敛 ; 如果上述极限不存在, 发散 .
类似地 , 若 f ( x) C [a , b) , 而在 b 的左邻域内无界,
0
0 dx 1 dx 1 1 1 下述解法是否正确 : 2 2 解: 1 x 0x x 1 x 0 1 1 dx 2 1 1 1 2 , ∴积分收敛 1 x x 发散 1 所以反常积分 .
f ( x) dx F ( x) f ( x) dx F ( x)

b
例1. 计算反常积分
解:
[ arctan x ]


y
y

( ) 2 2

1 1 x 2
o
x
例2: 分析: 原积分发散 !
例3. 计算反常积分
t pt 解: 原式 e p
则也有类似牛 – 莱公式的
的计算表达式 :
若 b 为瑕点, 则
若 a 为瑕点, 则
a a
b
f ( x) dx F (b ) F (a) f ( x) dx F (b) F (a )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1
1 x
q
0
dx 当q 1 时收敛，当
q 1时发散.
证 (1) q 1,
0 x q dx 0 x dx ln x
1 1
1 q 1
1
1
1 0
,
, q 1 1 1 x ( 2) q 1, q dx 1 ,q1 0 x 1 q 0 1 q 1 因此当q 1时广义积分收敛，其值为 ； 1 q 当q 1时广义积分发散.
2
x 1 x
2

dx =____；
5、广义积分
1
xdx 1 x
2
________；
f ( t )dt
0
6、广 义 积 分

x

的 几 何 意 义 是
______________ ________________________.
二、 判别下列各广义积分的收敛性，如果收敛，则计算 广义积分的值： dx pt ( p 1) ； 2、 1、 e cosh tdt 0 x 2 2 x 2 ； 3、 0
练 习 题
一、填空题： 1、广义积分 散； 2、广义积分 散； 3、广 义 积 分 _______ 时发散；
4、广义积分


dx x
p
当_______时收敛； 当______时发
1
1
dx x
q
当_______时收敛； 当_______时发
0


dx x (ln x )
k
在 ______ 时 收 敛 ； 在
a
(b a )

x

f ( t )dt .
练习题答案
一、1、 p 1, p 1 ；2、q 1 , q 1 ； 3、k 1 , k 1 ； 4、发散； 5、1； 6、过点 x 平行于 y 轴 的直 线左边,曲线 y f ( x ) 和 x 轴 所围图形的面积 . p n 二、1、 2 ； 2、 ； 3、 ! ； 4、发散； p 1 2 n 5、2 ； 6、0； 7、( 1) n! . 3 1 1 k k 1 时收敛于 ( b a ) ； 当k 1 时发散. 三、当 1 k 0 , x 0 1 x 2 四、 f ( t )dt x , 0 x 2 . 4 x 1 , 2 x
.
故原广义积分发散.
思考题
积分 0
1
ln x x 1
dx 的瑕点是哪几点？
思考题解答
积分 0
lim
x 1
1
ln x x 1
dx 可能的瑕点是 x 0,
1 x 1,
x 1
ln x x 1
lim
x 1
x 1 不是瑕点,

1
ln x x 1
0
dx 的瑕点是 x 0.

x e
n
x
dx （ n 为自然数 ） ；4、
2
dx (1 x )
2
；
0
5、 7、
2
xdx x 1
1 n 0
；
6、
1


x ln x (1 x )
2 2
dx ；
0

ln xdx .
b
三、 求 当 k 为何值时 ， 广义 积分
dx
k
( x a) 收敛？又 k 为何值时 ，这广义积分发散？ 0 , x 0 1 四、 已知 f ( x ) x , 0 x 2 ，试用分段函数表示 2 1 , 2 x
例7 计算广义积分 解

2
dx x ln x
2
.
1
1
2
dx x ln x
2
lim
dx x ln x
0 1
lim
0
d (ln x ) ln x
0 1
lim ln(ln x )1
2
0
lim ln(ln 2) ln(ln( 1 ))
三、小结
无穷限的广义积分
f ( x )dx

f( x )dx
b
无界函数的广义积分（瑕积分）a f ( x )dx
（注意：不能忽略内部的瑕点）
b c b
a f ( x )dx a f ( x )dx c
f ( x )dx
例 6 证明广义积分