西安交大西工大 考研备考期末复习 概率论与数理统计 第三部分 二维随机变量(答案)

第一部分 随机事件及其概率基础练习一． 填空1 设====)(,7.0)(,5.0)(,4.0)(B A P B A P B P A P 则若 答案：0.552 三次独立重复射击中，至少有一次击中的概率为则每次击,6437中的概率为 答案：1/43箱中盛有8个白球6个黑球，从其中任意地接连取出8个球，若每球被取出后不放还，则最后取出的球是白球的概率等于_________________。

答案：8144 任取两个正整数，则它们之和为偶数的概率是_______ 答案：1/25 设10件产品中有3件不合格品，从中任取两件，已知两件中有一件是不合格品，则另一件也是不合格品的概率为__________答案：2/96已知P （A ）=0.8,P(A-B)=0.5,且A 与B 独立，则P （B ）= 答案：3/87从1，2，…，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于___________ 答案：9876104⨯⨯⨯=0.3024 8箱中盛有8个白球6个黑球，从其中任意地接连取出8个球，若每球被取出后不放还，则最后取出的球是白球的概率等于_________________ 答案：8149平面上有10个点，其中任何三点都不在一直线上，这些点可以确定_____个三角形。

答案：12010设样本空间U={1，2， 10}，A={2，3，4，}，B={3，4，5，}，C={5，6，7}，则()C B A 表示的集合=______________________。

答案：{1,2,5,6,7,8,9,10} 二． 计算题1 一打靶场备有5支某种型号的枪,其中3支已经校正,2支未经校正.某人使用已校正的枪击中目标的概率为1p ,使用未经校正的枪击中目标的概率为2p .他随机地取一支枪进行射击,已知他射击了5次,都未击中,求他使用的是已校正的枪的概率(设各次射击的结果相互独立).解 以M 表示事件“射击了5次均未击中”,以C 表示事件“取得的枪是已经校正的”，则,5/3)(=C P,5/2)(=C P 又,按题设,)1()|(51p C M P -=52)1()|(p C M P -=,由贝叶斯公式 ,)()()|(M P MC P M C P =)()|()()|()()|(C P C M P C P C M P C P C M P +=52)1(53)1(53)1(525151⨯-+⨯-⨯-=p p p.)1(2)1(3)1(3525151p p p -+--= 2 某人共买了11只水果,其中有3只是二级品,8只是一级品.随机地将水果分给C B A 、、三人,各人分别得到4只、6只、1只. (1)求C 未拿到二级品的概率.(2)已知C 未拿到二级品,求B A ,均拿到二级品的概率. (3)求B A ,均拿到二级品而C 未拿到二级品的概率.解 以，，，C B A 分别表示事件C B A ，，取到二级品,则C B A ，，表示事件C B A ，，未取到二级品.(1).11/8)(=C P(2)就是需要求).|(C AB P 已知C 未取到二级品,这时B A ,将7只一级品和3只二级品全部分掉.而B A 、均取到二级品,只需A取到1只至2只二级品,其它的为一级品.于是.5441027234103713)|(=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=C AB P(3).55/32)()|()(==C P C AB P C AB P3 一系统L 由两个只能传输字符0和1的独立工作的子系统1L 和2L 串联而成(如图13-1),每个子系统输入为0输出为0的概率为)10(<<p p ;而输入为1输出为1的概率也是p .今在图中a 端输入字符1,求系统L 的b 端输出字符0的概率.ab解 “系统L 的输入为1输出为0”这一事件(记)01(→L )是两个不相容事件之和,即),00()01()01()11()01(2121→→→→=→L L L L L 这里的记号“)11(1→L ”表示事件“子系统1L 的输入为1输出为1,其余3个记号的含义类似.于是由子系统工作的独立性得)}00()01({)}01()11({)}01({2121→→+→→=→L L P L L P L P)}00({)}01({)}01({)}11({2121→→+→→=L P L P L P L P).1(2)1()1(p p p p p p -=-+-=4 甲乙二人轮流掷一骰子,每轮掷一次,谁先掷得6点谁得胜,从甲开始掷,问甲、乙得胜的概率各为多少?解 以i A 表示事件“第i 次投掷时投掷者才得6点”.事件i A 发生,表示在前1-i 次甲或乙均未得6点,而在第i 次投掷甲或乙得6点.因各次投掷相互独立,故有.6165)(1-⎪⎭⎫⎝⎛=i i A P 因甲为首掷,故甲掷奇数轮次,从而甲胜的概率为}{}{531 A A A P P =甲胜+++=)()()(531A P A P A P ),(21两两不相容因 A A⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+= 426565161.116)6/5(11612=-=同样,乙胜的概率为}{}{642 A A A P P =乙胜+++=)()()(642A P A P A P.1156565656153=⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+=5 将一颗骰子掷两次,考虑事件=A “第一次掷得点数2或5”,=B “两次点数之和至少为7”，求),(),(B P A P 并问事件B A ,是否相互独立.解 将骰子掷一次共有6种等可能结果,故.3/16/2)(==A P 设以i X 表示第i 次掷出骰子的点数,则}).6({1})7({)(2121≤+-=≥+=X X P X X P B P因将骰子掷两次共有36个样本点,其中621≤+X X 有6,5,4,3,221=+X X 共5种情况,这5种情况分别含有1,2,3,4,5个样本点,故.12/712/5136/)54321(1)(=-=++++-=B P以),(21X X 记两次投掷的结果,则AB 共有(2,5),(2,6),(5,2),(5,3)(5,4),(5,5),(5,6)这7个样本点.故 .36/7)(=AB P今有).(36/7)12/7)(3/1()()(AB P B P A P === 按定义B A ,相互独立.6 B A ，两人轮流射击,每次各人射击一枪,射击的次序为A B A B A ,,,,,射击直至击中两枪为止.设各人击中的概率均为p ,且各次击中与否相互独立.求击中的两枪是由同一人射击的概率.解 A 总是在奇数轮射击,B 在偶数轮射击.先考虑A 击中两枪的情况.以12+n A 表示事件“A 在第12+n 轮),2,1( =n 射击时又一次击中,射击在此时结束”. 12+n A 发生表示“前n 2轮中A 共射击n 枪而其中击中一枪,且A 在第12+n 轮时击中第二枪”（这一事件记为C ），同时“B 在前n 2轮中共射击n 枪但一枪未中”(这一事件记为D )，因此)()()()(12D P C P CD P A P n ==+nn p p p p n )1()1(11-⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛=- .)1(122--=n p np注意到 ,,,753A A A 两两互不相容,故由A 击中了两枪而结束射击(这一事件仍记为A )的概率为∑∑∞=-∞=++∞=-===1122112121)1()()()(n n n n n n p np A P A P A P1122])1[()1(-∞=∑--=n n p n p p.)2(1])1(1[1)1(2222p pP p p --=---(此处级数求和用到公式.1,)1(1112<=-∑∞=-x nx x n n 这一公式可自等比级数1,11<=-∑∞=x x x n n 两边求导而得到.) 若两枪均由B 击中,以)1(2+n B 表示事件 “B 在第)1(2+n 轮),2,1( =n 射击时又一次击中,射击在此时结束”. )1(2+n B 发生表示在前12+n 轮中B 射击n 枪其中击中一枪,且B 在第)1(2+n 轮时击中第2枪，同时A 在前12+n 轮中共射击1+n 枪,但一枪未中.注意到 ,,,864A A A 两两互不相容,故B 击中了两枪而结束射击(这一事件仍记为B )的概率为∑∞=+-+∞=--⎪⎪⎭⎫ ⎝⎛==111)1(21)1()1(1)()(n n n n n p p p p n B P B P 12112222])1[()1()1(-∞=∞=--=-=∑∑n n n np n p p p np.)2()1(])1(1[1)1(222222p p p p p --=---= 因此,由一人击中两枪的概率为222)2()1()2(1)()()(p p p p B P A P B A P --+--=+= .21pp --= 7 有3个独立工作的元件1,元件2,元件3,它们的可靠性分别为.,,321p p p 设由它们组成一个“3个元件取2个元件的表决系统”,记为2/3].[G 这一系统的运行方式是当且仅当3个元件中至少有2个正常工作时这一系统正常工作.求这一2/3][G 系统的可靠性. 解 以i A 表示事件“第i 个元件正常工作”，以G 表示事件“2/3][G 系统正常工作”，则G 可表示为下述两两互不相容的事件之和： 321321321321A A A A A A A A A A A A G = 因321,,A A A 相互独立,故有)()()()()(321321321321A A A P A A A P A A A P A A A P G P +++=)()()()()()()()()()()()(321321321321A P A P A P A P A P A P A P A P A P A P A P A P +++=.)1()1()1(321321321321p p p p p p p p p p p p +-+-+-= 8 甲、乙、丙三部机床独立工作由一名工人照看，某段时间内甲、乙、丙三部机床不需要照看的概率依次为3/4、2/3、1/2，求在这段时间内有机床需要工人照看的概率及恰有1台机床需要工人照看的概率。

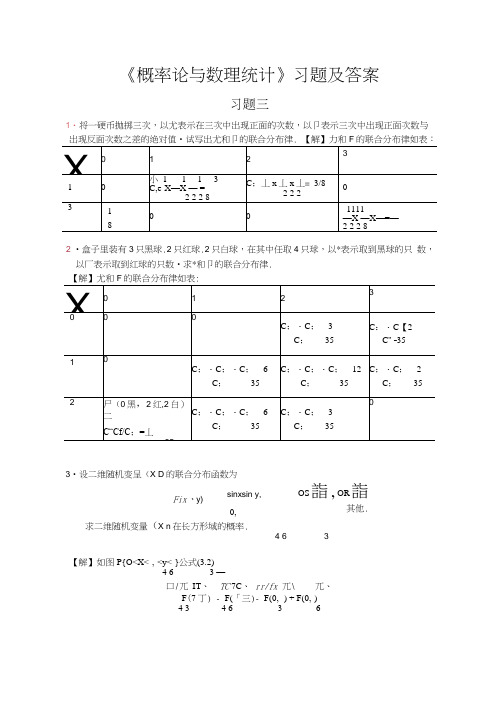
《概率论与数理统计》习题及答案习题三1・将一硬币抛掷三次，以尤表示在三次中出现正面的次数，以卩表示三次中出现正面次数与2 •盒子里装有3只黑球.2只红球.2只白球，在其中任取4只球，以*表示取到黑球的只 数，以厂表示取到红球的只数•求*和卩的联合分布律.3•设二维随机变呈（X D 的联合分布函数为求二维随机变量（X n 在长方形域的概率.4 63【解】如图P{O<X<-,-<y<-}公式(3.2)4 6 3 —口/兀 IT 、 TC 7C 、 rr/fx 兀\ 兀、F (7 丁) - F(「三)- F(0, -) + F(0,-) 4 3 4 6 3 6Fix 、y)sinxsin y,0,OS詣,OR 詣其他.=sin —>sin — 一 sin —•sin — 一 sin O ・sin — + sin 0>sin= ^(73-1).4说明：也可先求出密度函数，再求概率。

4•设随机变量（匕D 的分布密度Ae H3r+4v \ x>0,y>0, 0, 其他.£' £' 12e _(3M+4v,di/dv _J(l-e _3x )(1-e -4-) y > 0,x > 0,0° ° =| o,其他(3) P{0<X<l,0<y<2)= p{o<x<i,o<y<2}=fj ： 12e _<3t *4v,d.vdy = (l-e-3 )(l-e _8)« 0.9499.5.设随机变量(X D 的概率密度为k(6 一兀一 y), 0 < x < 2, 2 <f (儿 y)=<0,(1) 确定常数k; (2) 求 P{X<\. K3}； (3) 求 HK1.5}； (4)求 PUHW4}.【解】(1)由性质有fix. y)=<求：(1)(2) (3) 常数川随机变量（x n 的分布函数;P{owg 0WK2}・【解】（1）由匚匚 fg y)dxdy =门「Ae 「'i &dy =£ = 1得(2)J=12由定义，有j* J f(x, y)dvdy = J ( J k(6 - x - y)dydx =8k = 1,故 R = -8(2) P{X v 1, Y v 3} = J ：/(x,y)dydx一 曲•皿 €⑶ P{ X v 1.5} = JJ /(x, y)dAdy如图a [J/(x, y)d.vdyATP 曲 i —y)dy = ||.⑷ P{X+r<4}= JJ /(x,y)dxdy 如图y)dxdyX+YS4Dy6•设尤和F 是两个相互独立的随机变量，尤在（0, 0.2）上服从均匀分布，卩的密度函数为—r求:（1） X 与卩的联合分布密度；（2） P{Y^X\.【解】（1）因尤在（0, 0.2）上服从均匀分布，所以X 的密度函数为0, 其他.x<1.5fx(x )= 0 210<x<0.2,所以f(^y)X.Y 独立办(x)M(y)(2) P (y<X)= JJ fg y)dvdy 如图［f25e"5v dvdyy<x D=£'2 dxj ： 25e® dy = J (「(一5e 亠 + 5)<Lv =e _l a 0.3679・7•设二维随机变疑(x n 的联合分布函数为求(上D 的联合分布密度.&设二维随机变呈(儿力的概率密度为求边缘概率密度. 【解】办(X )=匚/'(X,刃dy「4・8y(2-x)dy \lAx 2(l-x)y 0 <x< h o. 1°， 其他f Y (y) =匚/(兀刃 dxJ 4.8y(2 -x)dx _ J2.4y(3 -4y + y 2), 0 < y < 1, o =|o, 其他,y > o. 其他.0,25e _5v ,0,0<x<0.2且y >0, 其他.F5刃屮十*严)0.x > 0, y > 0,其他【解】oxdy0、 x >0,y> 0,其他.4.8y(2-A 0,0<x<l,0<y<x,其他y)=<求边缘概率密度.【解】办（尤）=匚f（x，y）dyI e~v dy=Jx ・=<0, ・A(y) = JJ/GvoOdx10.设二维随机变量（X D的概率密度为cFy, X2 < y < 1,0, 其他匚匚 /(也y )^2如图|7 fg y)dxdy1)=f dvj1, ex2 ydy = * c = 1.21c = —•4fx W =匚/a，y)dyy)=<fix、e0,0<x< ”其他(1)(2)试确定常数c；求边缘概率密度.x> 0,其他.0,f S e'v cLv=< Jo0,y>0, a 其他.yiw o Xf (x、y)=<【解】（1）题10图【解】办（兀）=匚/（血刃⑪f ldy = 2x.= J-x 0.ildv = 1 + y,一1 vy <0,所以丄，I y l< x < 1,2x 0, 其他J ；pyd ），0,—x~(l — %4), —lSxSl,8 0,其他.0,7 ?0<y<t 厶0,其他.11 •设随机变量（上D 的概率密度为 1, 0,f (%, y)=<|y| < x, 0 < x < 1,其他求条件概率密度fnx （y I X ）,A (y) =匚/(""nf ldx = 1 -y, 0,0<y<h 其他.0< x< 1, 其他.AirCviy) =/g)A(y)1o,-y < A： <1,其他.345P{X=x t} 11 _ 1 c[ = To2 _ 2 c[ = io3 _ 3 c[ = lo610201 _ 1 cf ~io2 _ 2 c[_lo310 3001 _ 1 c[= 10110P{y = y i}1To3 To61012•袋中有五个1, 2. 3, 4, 5,从中任取三个，记这三个中最小的为兀最大的为X （1）求X与『的联合概率分布；（2）X与卩是否相互独立？【解】（1）尤与卩的联合分布律如下表⑵因吩=啊一3}=劭存侖工存吟+ = 3}故尤与卩不独立（2）尤与卩是否相互独立？(2)因P{X= 2}.P{Y = 0.4} = 0.2x0.8 = 0.160.15 = P(X = 2,K = 0.4),1）上服从均匀分布，F 的概率密度为y > 0,其他.（1） 求尤和卩的联合概率密度；（2）设含有日的二次方程为才+2炉扫0,试求臼有实根的概率.（2）方程a 2+2Xa + Y = 0有实根的条件是△ = (2X)2-43 0故斤2 K,从而方程有实根的概率为：P{X 2>r )= JJ /(x,y)drdyA 2>V= I -V^[①⑴-①(0)]= 0.1445.15 •设才和F 分别表示两个不同电子器件的寿命（以小时计），并设X 和卩相互独立，且服从同一分布，其概率密度为[1000f 3 ==〔0,求Z^X/Y 的概率密度.故尤与卩不独立.【解】（1） 14•设*和卩是两个相互独立的随机变量，*在（0,0,x > 1000, 其他fi (y)=【解】如图,z 的分布函数巧⑵= P{Z<z} = P[—<z}当O 〈z<l 时，（这时当尸1000时，尸型2）（如图a ） 106Fz ⑵=”詈"dy =打dy 打毎dx〉•注(1) 当zWO 时，巧（z ）= o2zz> 1, /z ⑵£2y0,0<z<l, 其他.ZT 5 Z ' I ， 2z—,0 < z < h 2 0, 其他.16 •设某种型号的电子管的寿命（以小时计）近似地服从M160,20‘）分布•随机地选取4 求其中没有一只寿命小于180的概率.【解】设这四只寿命为上（住123,4）,则尤二2（160 , 202）,只,(2)当时，（这时当尸10’时，尸102）（如图b ）传⑵=JI 詈dg ，=叵呱；詈"103 106 12z从而P{minCX,, X 2, X 3, X 4) > 180)X.之间独AtPfX, > 180}<P{X 2 > 180}P{X 3>180)eP{X 4>180)=[1 一P{XV80}]・[1 一P{X? v 180}]41-P{X 3<180}J41-P{X 4<180}]= [1-0(1)]4=(O 」58『 =0・00063・17•设匕F 是相互独立的随机变量，其分布律分别为P{X-k} =p (&), A=0, L 2,…，P{JM=g (r), r=0, U 2,….证明随机变疑卅卩的分布律为PC}二工 p (k)q(i -灯,，二0, 1> 2, •••・【证明】因X 和卩所有可能值都是非负整数，所以^Z = i} = {X + Y = i]= {X=0,Y = i}U{X = l" = i — l}U ・・・U{X=/』= 0}于是P{Z = i} = y P{X =k,Y = i-k}X.Y 相互独立 y P{X = k}.P{Y = i-k}R.O'女.0= ±P(k)q(i -k)£■(>1&设兀卩是相互独立的随机变量，它们都服从参数为”，p 的二项分布.证明Z=X+Y 服从参 数为2m, p 的二项分布•【证明】方法一：贰F 可能取值为0, 1, 2,…，2n.kP {X +Y = R } =工p{xf-0= [1-P{X 1 <180)]4=180-160H20 jjk= ^P(X =i^P{Y = k-i}J-0方法二：设“】，“2,・「"n ； “J , P2 ，…，"J 均服从两点分布(参数为P ),则 於 “l+“2+・・・+〃m U +"/ +•••+“/ •於片 “|+〃2+・・・+“/"「+"/ +•••+“/ ,所以，卅F 服从参数为(2/7.P )的二项分布.X0 1 2 3 4 5 0 0 0.01 0. 03 0. 05 0. 07 0. 09 1 0.01 0. 02 0. 04 0. 05 0. 06 0. 08 2 0.01 0. 03 0. 05 0. 05 0. 05 0. 06 30.010. 020. 040. 060. 060. 05(1)求 刊后2 I 比2}, P{K=3 I 后0}(2) 求J^max (X JO 的分布律； (3) 求itmin (X JO 的分布律； (4)求炉卅卩的分布律.【解】⑴吩—J ；/二「P{X=2,Y = 2} j^P{X=i,Y = 2} J-0P{X=0V = 3} £p{X=0，UI(2) P{V=i} = P{max(X.Y) = i} = P{X=i,Y<i} + P{X <i.Y = i]r-li=》P{X =i,Y = £} +》P{X =«Y = f},7 = 0,1,2,3,4.5 JO10P F2n-k(2n\J >0.05 ~ 0^25P{Y = 3IX =0}=P{Y = 3,X =0) P{X=0}0.01 _ 1 0^03~3p"q 21所以J/的分布律为J^max (Z Y)0 1 2 3 4 5p0. 040. 160. 28 0. 240. 28(3) P{U=i} = P{min(X,Y) = i}= P{X =i.Y>i} + P{X >i,Y = i]35= ^P{X=i y Y = k}+ Z P{X=k,Y = i} k7(4) 类似上述过程，有1 2 3 4 56780?020?06 6773671902467196712 676520•雷达的圆形屛幕半径为乩设目标出现点(上力在屏幕上服从均匀分布. (1)求 P{J>0 I (2)设 JhnaxU ； y\9【解】因(上力的联合概率密度为Jj/(’y)dby>0 y>x ___________jj/(A-,y)do-i = 0J,2,3,于是V0. 280. 30 0. 25 0. 17/(儿 y)= < 1TI R 20, X 1 + y 2 <R\其他.(1) P{Y>0\Y>X} =P{Y>0”>X}P{Y>X}y>x3/8 _ 3172 "4(2) P{M>Q] = P{max(X.y )>0} = l-P{max(X,Y)<0}= l-P{X<0,r<0} = l-JJ f(x. y)db.r<0 y<021 •设平面区域〃由曲线y-\/x 及直线尸0, A=l,x=e 2所围成，二维随机变量(上力 在区域〃上服从均匀分布，求(尤D 关于尤的边缘概率密度在齐2处的值为多少？r c 2 1【解】区域〃的面枳为S o = | -cLv = lnx f =2. (XK)的联合密度函数为 J1 V1 <x<e 2,0< y < —,x 其他.(X D 关于才的边缘密度函数为所以人⑵冷22•设随机变量尤和卩相互独立，下表列出了二维随机变量(儿 力联合分布律及关于/和 卩的边/3P{F 对二P ：X\ Xz1/8 1/8"{y=y.} =P >1/61【解】因P{Y = y j } = P j =XP{X=x i ,Y = y j },(-1故 P{Y = y }} = P{X=x r Y = y {} + P{X=x 2.Y = yi }.从而 P{X=x v Y = y,}丄1 _ 1 "6^8" 24* 而才与卩独立，故 P{X =x i ]^P{Y = yj} = P{X =x p y = y.). 从而 P{X=x l }x- = P{X=x }>Y = y }] = —.624即：P{X 十眾 又 P{X=x }} = P{X=x }.Y = y }} + P{X=x^Y = y 2} + P{X=x {.Y = y 3}.£/(x,y)= 20,1 <x<e 2, 其他.即丄=-L + l + P{X=xr = yJ,4 24 8 i••狎从而P{X=x r Y = y3} = ^. 丄乙13同理P{Y = y2} = -. P{X=x2.Y = y2} = -2o3 1 1 1 又工卩{丫=儿} = 1・故川丫=儿} =1_7_3 = ?3同理P{X=x2} = -.从而P{X=x2,Y = y i} = P{Y = y i}-P{X=x r Y = y.} = L-^ = L 故23•设某班车起点站上客人数才服从参数为人（/1>0）的泊松分布，每位乘客在中途下车的概率为p（o<p<l）,且中途下车与否相互独立，以F表示在中途下车的人数，求：（1）在发车时有”个乘客的条件下，中途有刃人下车的概率；（2）二维随机变量（尤，力的概率分布. 【解】仃)P{Y = m\X=n} = C；；p m(1 -p)n'm,0</n</?,H = 0J,2,• • •.(2) P{X=mY = m} = P{X=n}>P{Y = m\X= n}A 1', n < m <n,n = 0,1,2,・・・・1 2 )24•设随机变量*和卩独立，其中才的概率分布为FL 而卩的概率密度为fg(0.3 0.7；求随机变量決於F 的概率密度g(u).【解】设尸(刃 是F 的分布函数，则由全概率公式，知作於卩的分布函数为G(u) = P{X +Y <u} = 0.3P{X +Y <u \ X = \} + 0.7P{X + Y <u \ X = 2}= 0・3P{mX=l} + 0・7P{YS — 2IX=2} 由于才和卩独立，可见G(w) = 0・3P{ y<z/-l} + 0.7P{y<M-2} = 0・3F (M —l) + 0・7F(" — 2)・由此，得〃的概率密度为g(“)= G f(u) = 0.3F\u -1) + 0.7F (“ 一 2)=0・3/(" — 1) + 0・7/(“一2)・25. 25.设随机变量*与F 相互独立，且均服从区间［0.3］上的均匀分布，求/^{max(X H W1}.解：因为随即变量服从［0, 3］上的均匀分布，于是有因为兀卩相互独立，所以0<x<3,0<y<3,x<0, y<0,x>3, y>3.推得 P{max{X,y}<l)=l.26.设二维随机变量(尢力的概率分布为10 1 1 a0.2 0 0. 1 b0.210. 1c其中a 、b 、c 为常数，且X 的数学期望Eg 0.2/{卩冬0|辰0}二0・5,记Z-X^Y.求://!£fM = <30<x<3,(X x<0,x>3;£/(>') = * 30,0<y<3, y < 0,y > 3.fg y)=1-9（1） a 、b 、c 的值；（2） Z 的概率分布；（3） P{X^ ・解 （1）由概率分布的性质知，0“心0・6=1由 E （X ） = -0.2,可得-a + c = -OA.得a +b = 0.3.解以上关于血b 9 c 的三个方程得a = 0・2,b = 0・l,c = 0.1.(2) Z 的可能取值为2, L 0, h 2,P{Z = _2} = P{X =_1,丫 = _1} = 0.2,P{Z = —1} = P{X=—1" = O} + P{X=O,Y = —1}=O ・1,P{Z = O} = P{X=—1,Y = 1} + P{X=OV = O} + P{X=1V = —1} = O ・3,P{Z = 1} = P{X =1V = O} + P{X=OV = 1} = O ・3,P{Z = 2} = P{X=l" = l} = 0.1,即z 的概率分布为P{X=Z} = P{Y = 0}=0」+b + 0・2 = 0・l + 0・l + 0・2 = 0・4.即 a+b+c = 0. 4.再由p{r<o|x<o ( =p{x<o,r<o )P{X<0}= 0.5a +b + 0.5。

第三部分 二维随机变量基础练习一． 填空1设二维随机变量,X Y 相互独立，且()()120,133P X P X ====，()103P Y ==，()213P Y == 则()P X Y == 。

答案：59；2若二维随机变量,X Y 相互独立， 且都服从正态分布，则(),X Y 服从________。

答案：二维正态分布；3若二维随机变量(),X Y 的联合分布密度为(),f x y ，则Y 的边缘分布密度为___________。

答案：()(,)Y f y f x y dx +∞-∞=⎰；4. (),()()X Y f x y f x f y =⋅ 是连续型随机变量X,Y 相互独立的______条件.答案：充要；5. 已知随机变量(),ξη的联合分布函数(){},,F x y P x y ξη=<<用它表示概率{},P a y ξη=<=__________________.答案：()()0,,F a y F a y +-6. 设二维随机变量(),ξη在由曲线2y x =和y x =所围成的区域G 上服从均匀分布，则(),ξη的联合概率密度(),x y ϕ_______________.答案：{6 (, )0x y G∈其它7. 若(52)0,0(,)0x y Ae x y x y ϕ-+⎧>>=⎨⎩ 其它为随机变量(),ξη的联合概率密度,则常数A =__________. 答案：108. 若(),ξη的联合概率密度为() 0, 0(,)0 x y e x y x y ϕ-+⎧⎪>>=⎨⎪⎩其它则有{}1P ξ>=_______________.答案：1e -9. 设(),ξη互相独立，并服从区间[]0,a 上的均匀分布，且0a >，则(),ξη的联合概率密度为(),f x y =_________.答案：21,0,00,x a y a a ⎧≤≤≤≤⎪⎨⎪⎩ 其它10. 设随机变量(),ξη的联合概率密度函数为：() 0, 0(,)0 x y e x y x y ϕ-+⎧≥≥=⎨⎩其它则(),ξη落在区域:0,0,1G x y x y >>+<内的概率(){},P G ξη∈=____________________. 答案：21e-二． 计算题1. 假设某校学生的数学能力测试成绩X 与音乐能力测试成绩Y 具有如下形式的概率密度函数:⎪⎩⎪⎨⎧≤≤≤≤+=其它,010,10),32(52),(y x y x y x f试求：)(x f X 与)(y f Y ，并判断X 与Y 是否相互独立？ 答案：解:⎪⎩⎪⎨⎧≤≤+=+=⎰其它,1,5354)32(5201)(o x o x dy y x x f x ⎪⎪⎩⎪⎪⎨⎧≤≤+=+=⎰其它,010,5652)32(5201)(y y dx y x y f Y )()(),(y f x f y x f Y x ≠ )2('故，X 与Y 不独立.2. 设随机变量X 与Y 独立，且均在()1,1-区间上服从均匀分布，求：()0.5,0.5F 的值.答案：由题意，⎩⎨⎧<<=⎩⎨⎧<<=其它其它0101)(,0101)(y y f x x f Y X 且X 与Y 独立， 故⎩⎨⎧<<<<=其它010,101),(y x y x f}5.0,5.0{)5.0,5.0(<<=Y X P F 415.005.00==⎰⎰dy dx 3. 设某昆虫的产卵数X 服从参数为50的泊松分布，又设一个虫卵能孵化成虫的概率为0.8，且各卵的孵化是相互独立的，求此昆虫的产卵数X 与孵化为成虫数Y 的联合分布律.答案：解：本题已知随机变量X 的分布律为{}50!50-==e i i X P i , ,2,1,0=i由题意知，该昆虫下一代只数Y 在i X =的条件下服从参数为0.8的二项分布，故有j i i j i C i X j Y P -===2.08.0}|{，i j ,...,1,0=由{}{}{}i X P i X i Y P j Y i X P ======|,， 得),(Y X 的联合分布律为：50!502.08.0},{--===e j C j Y i X P i ji j j i ，i j i ,,1,0;,1,0 ==. 4.设二维随机变量),(Y X 的概率密度为⎩⎨⎧<<=其它,01,),(22y x y cx y x f , （1）确定常数c 的值;（2）Y X ,是否相互独立?为什么? 答案：解：（1）⎰⎰<<=121),(y x dxdy y x f ,即⎰⎰-12112x ydy cx dx =dx x x c )1(214112-⋅⎰-=121821=⋅⋅c 421=∴c . （2）⎪⎩⎪⎨⎧<<=其它,01,421),(22y x y x y x f ,1,)1(821421),()(214222<-===∴⎰⎰∞+∞-x x x ydy x dy y x f x f xX即⎪⎩⎪⎨⎧<-=其它,01),1(821)(242x x x x f X .同理，10,27421),()(25<<===⎰⎰∞+∞--y y xydx dx y x f y f yyY , 即⎪⎩⎪⎨⎧≤≤=其它1027)(25y y y f Y . 显然有)()(),(y f x f y x f Y X ⋅≠ 从而X 与Y 不独立.5. 已知,X Y 相互独立，),(Y X 的分布律为：{}31,118P X Y ===，{}21,218P X Y ===，{}11,318P X Y ===，{}62,118P X Y ===，{}2,2P X Y α===，{}2,3P X Y β===，试求：(1),αβ的值； (2),X Y 的边缘分布. 答案：(1)92；91（2）{}113P X ==,{}223P X ==, {}112P Y ==，{}123P Y ==,{}136P Y ==6. 设袋中有3个球，其标号为1，2，2，今从中不放回地任取2个球，记,X Y 为第1，2次抽得球的标号，试求： (1) ),(Y X 的联合概率分布律； (2) ,X Y 的边缘分布律.答案：(1)0，1/3，1/3，1/3；(2)1/3，2/3；1/3，2/3. 7. 设),(Y X 的联合密度为⎩⎨⎧+∞<<<=-其它,00,),(y x Cxe y x f y (1) 求参数C 的值；(2) 求X 与Y 的边缘密度函数)(),(y f x f Y X . 答案：解：（1）由1),(=⎰⎰+∞∞-+∞∞-dxdy y x f ，可得1C =.(2)20,0()0,01(),020,0y x x X y yyY xe dy xe x f x x xe dx f y y e y y +∞----⎧=>⎪=⎨⎪≤⎩⎧=⎪=>⎨⎪≤⎩⎰⎰8. 已知随机向量(),X Y 的联合概率分布为（1）求,X Y 的边缘分布；（2）判断X 与Y 是否独立. 答案：解：（1）()()()()()()()()()()11101,11,01,1 0.300.30.61,11,01,1 0.10.20.10.41,11,1 0.30.10.41,01,0 p P X Y P X Y P X Y p P X Y P X Y P X Y p P X Y P X Y p P X Y P X Y --==-=-+=-=+=-==++====-+==+===++===-=-+==-=+===-=+==()()1 00.20.21,11,1 0.30.10.4p P X Y P X Y =+===-=+===+=∴综合有下表（2）111,10.60.40.240.3p p p ----⋅=⨯=≠=，,X Y ∴不独立。